Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges
Abstract
1. Introduction
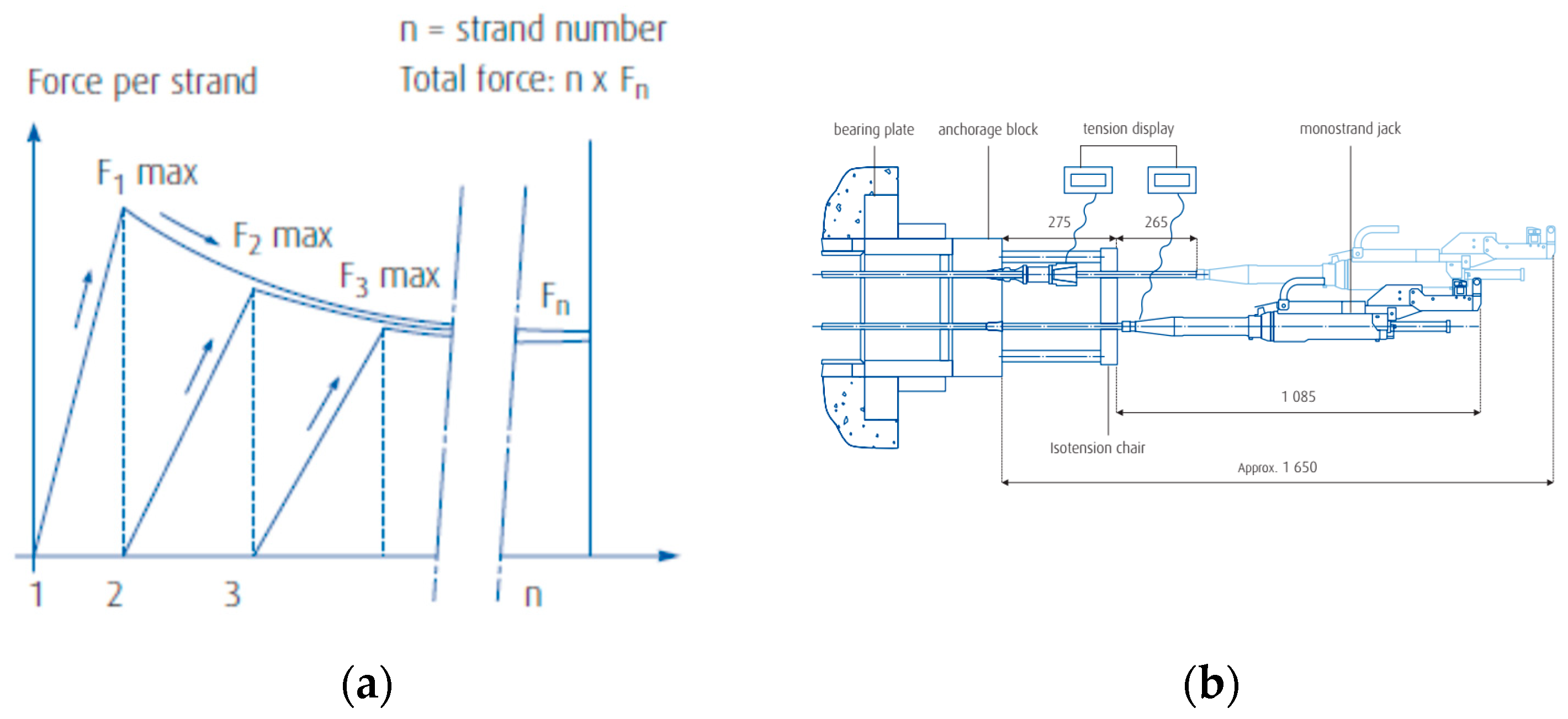
2. Modeling of Stay Cable
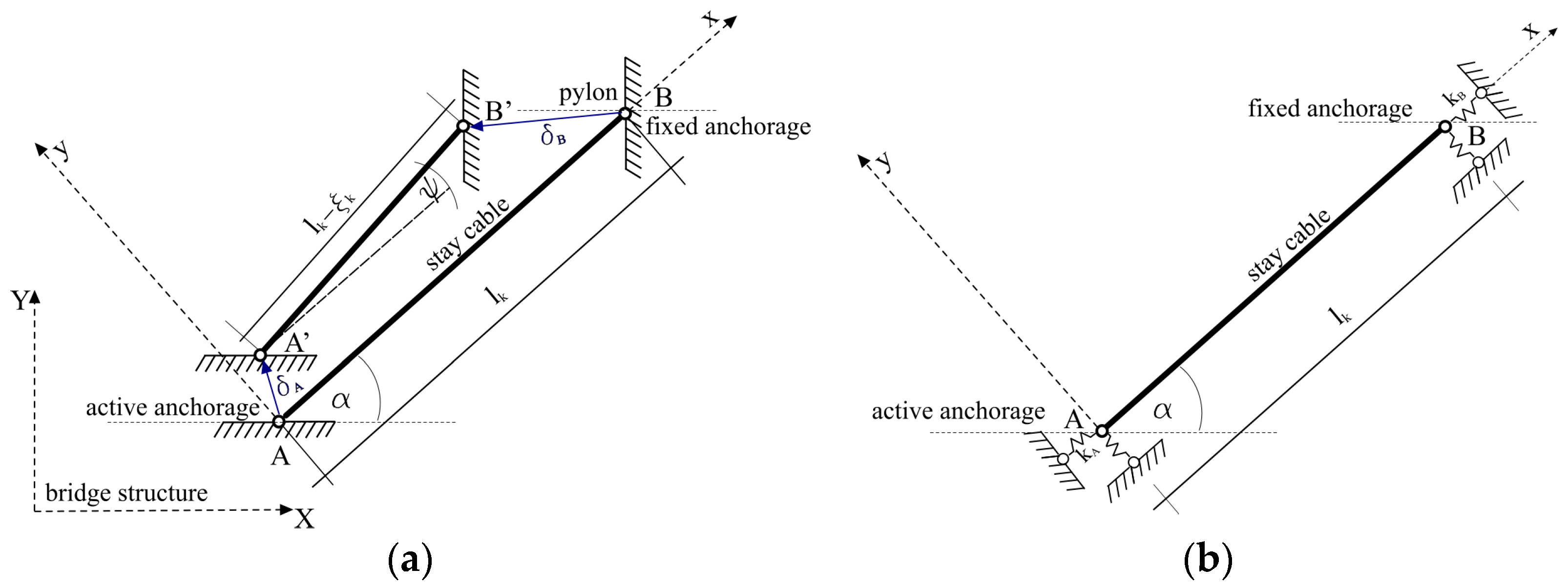
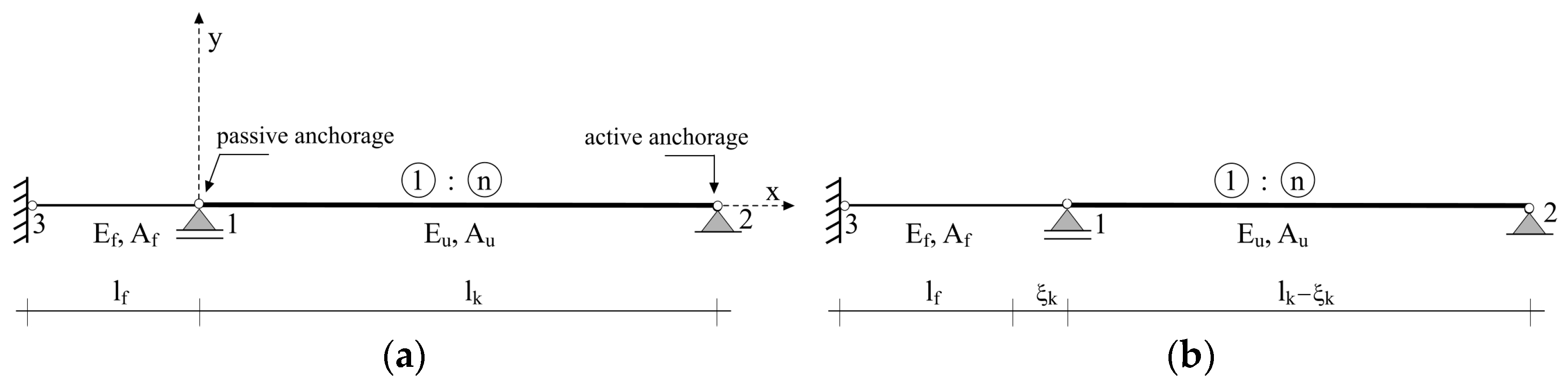
3. Algorithms for Calculation
3.1. Strand Tensioning in Single Cycle
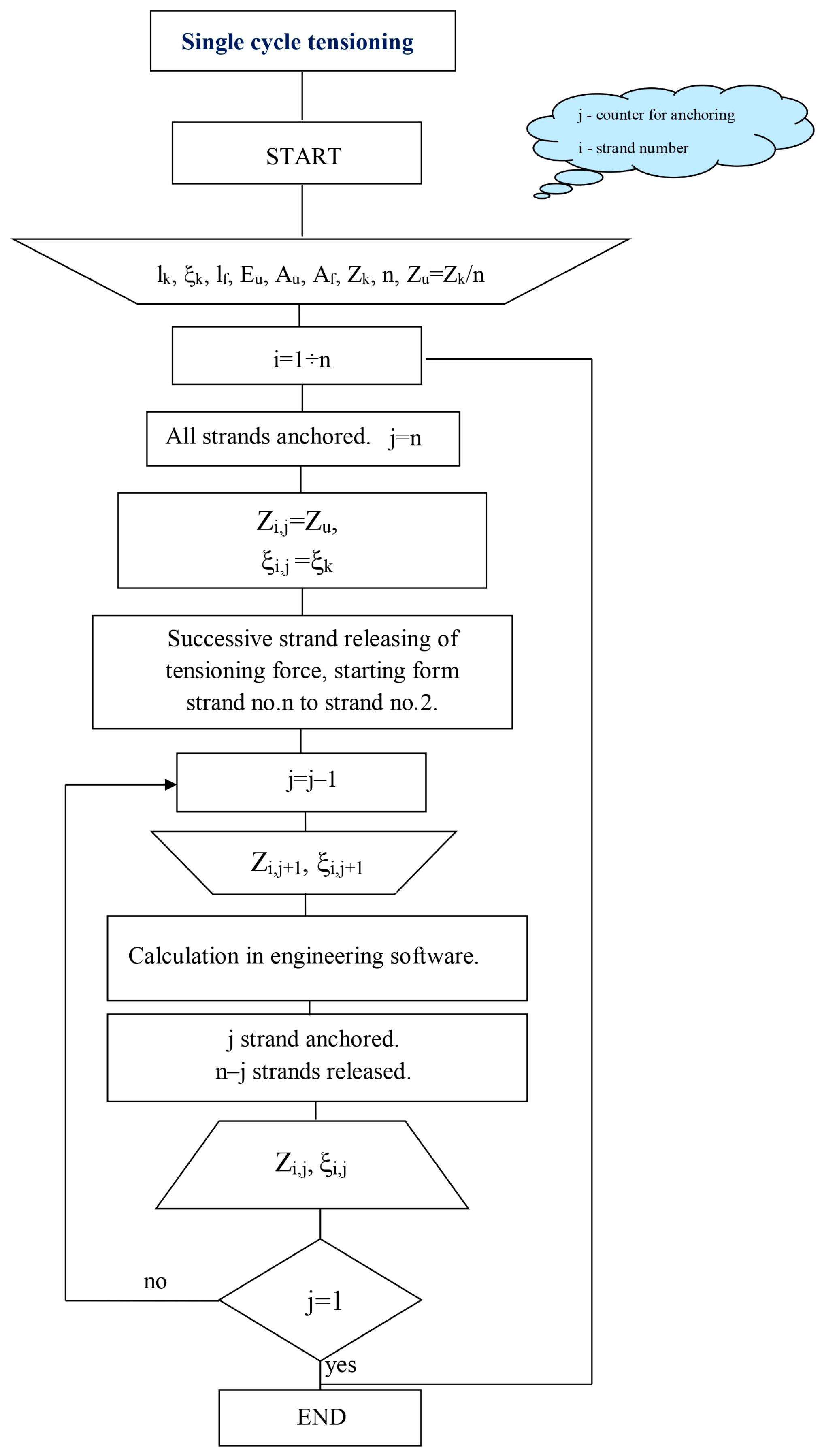
3.2. Partial Tensioning of Strands over Multiple Cycles
3.2.1. First Cycle (c = 1)
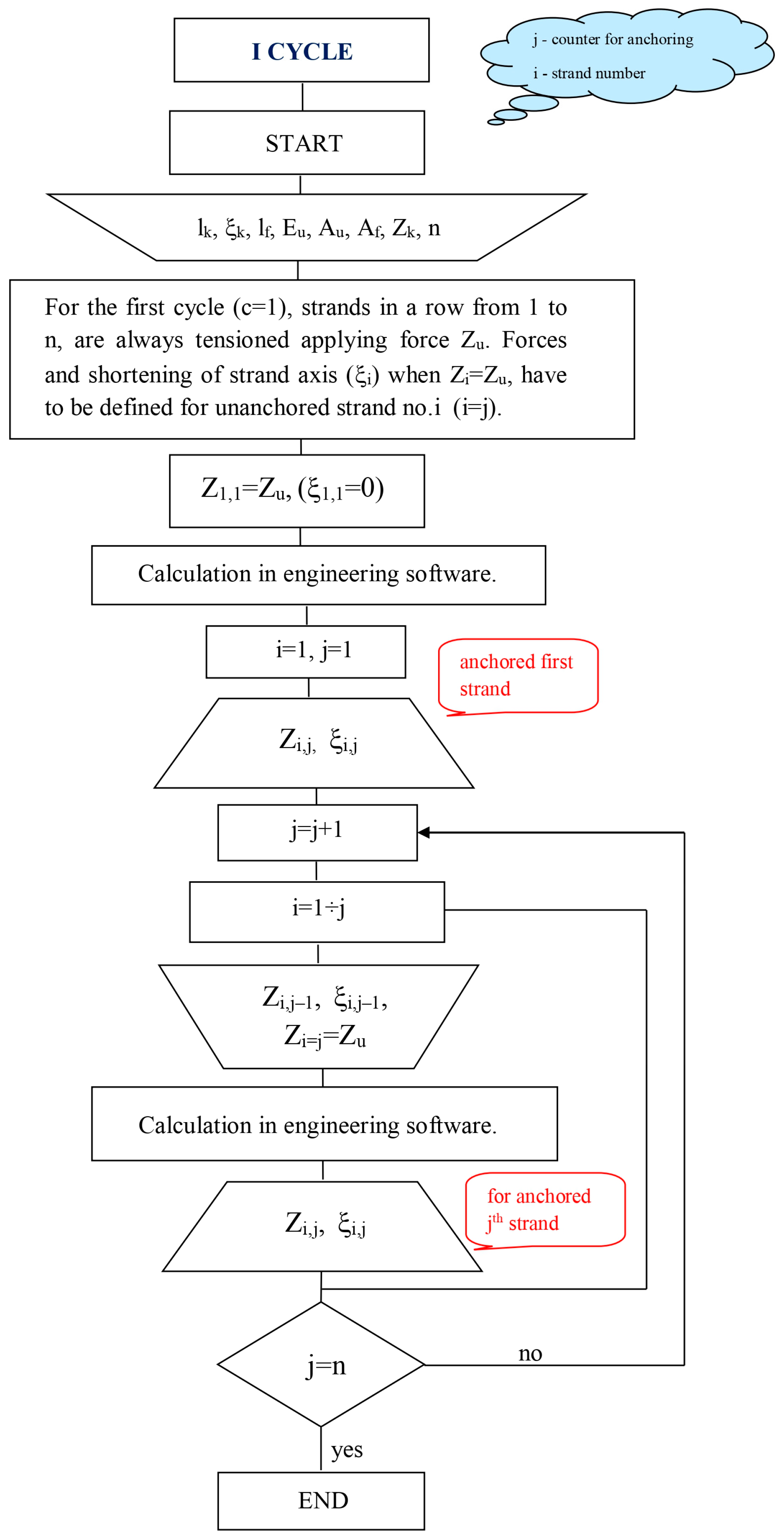
3.2.2. Subsequent (Higher) Cycles (c > 1)
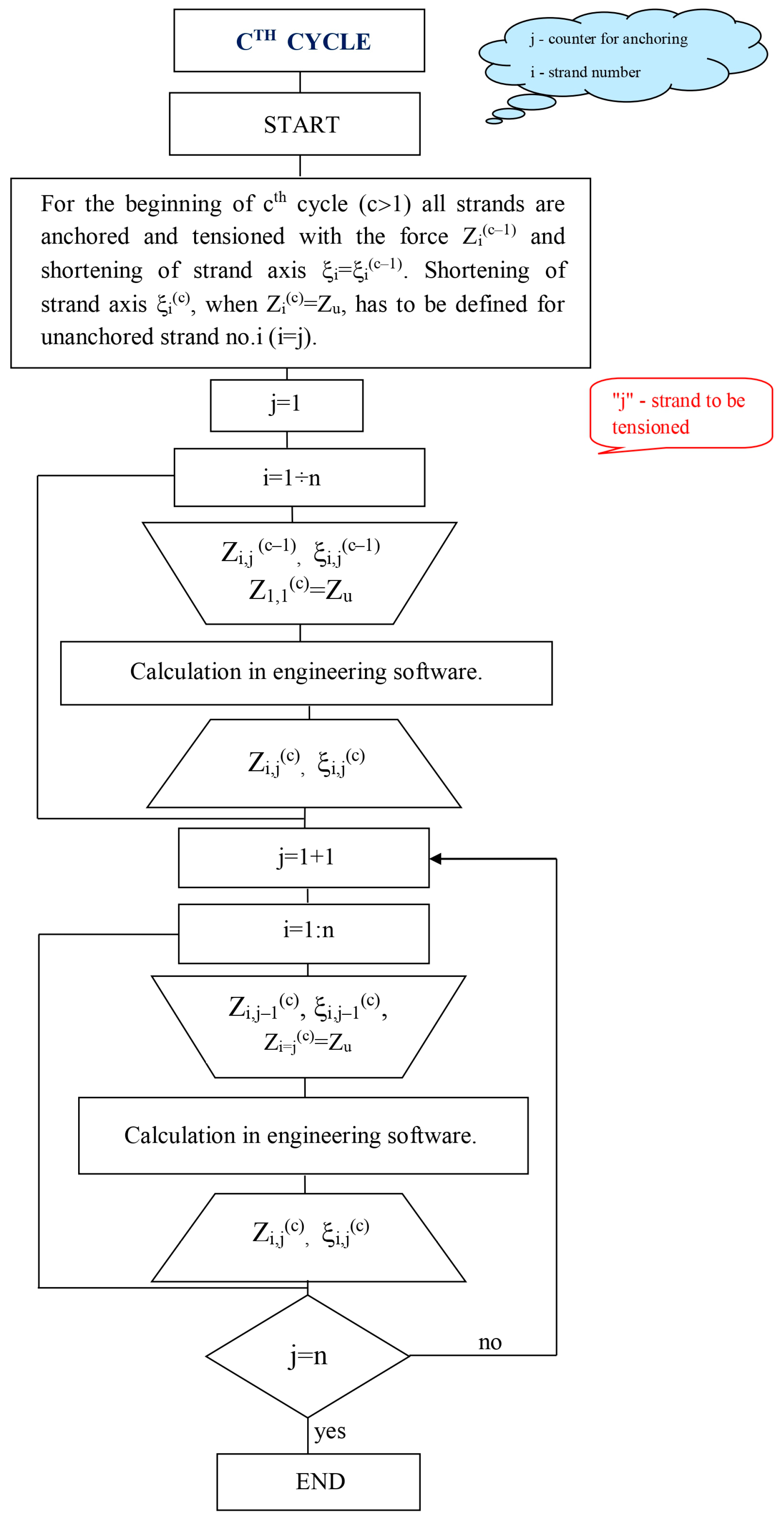
4. Numerical Example
5. Results
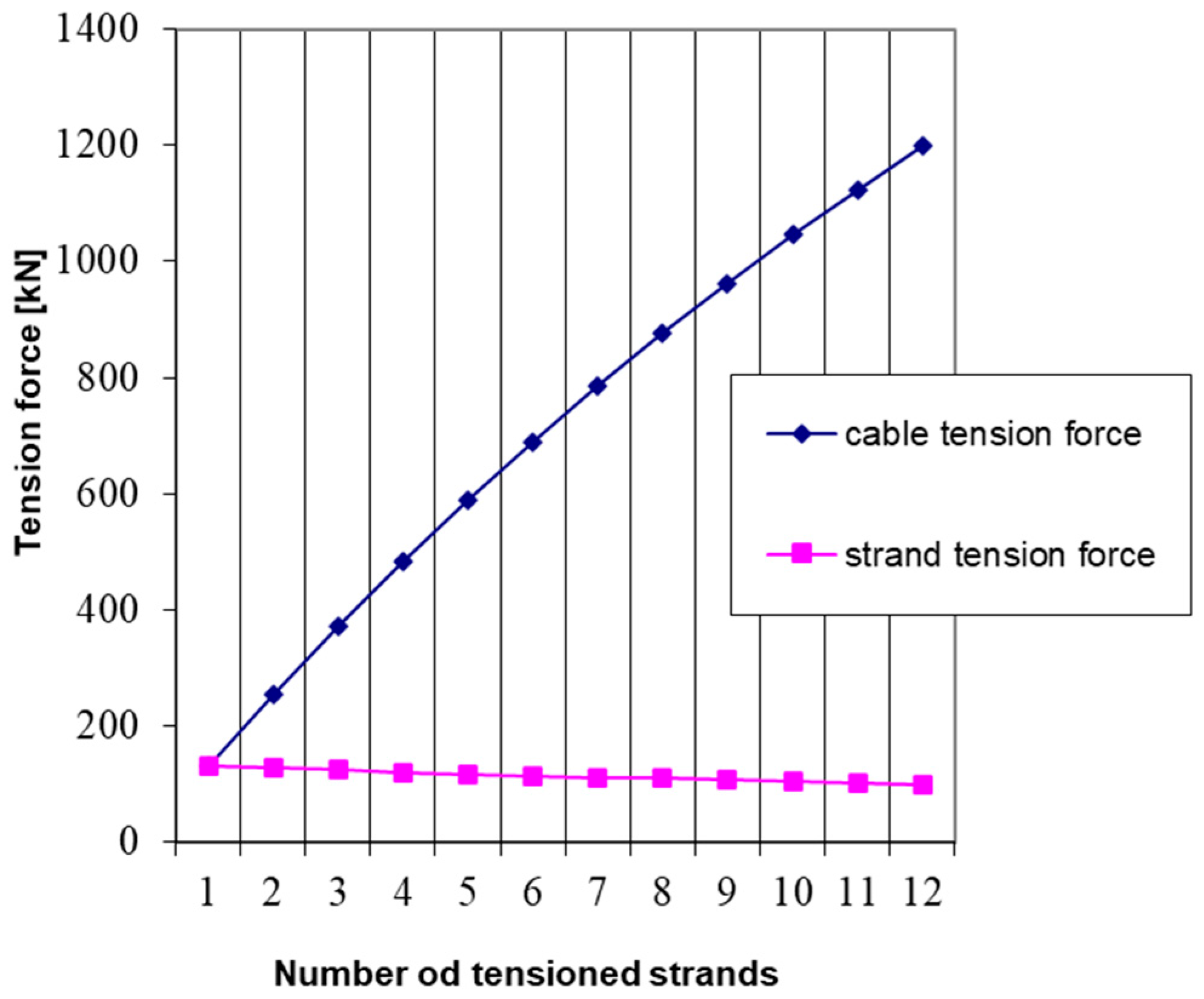
5.1. Single-Cycle Tensioning of Strands
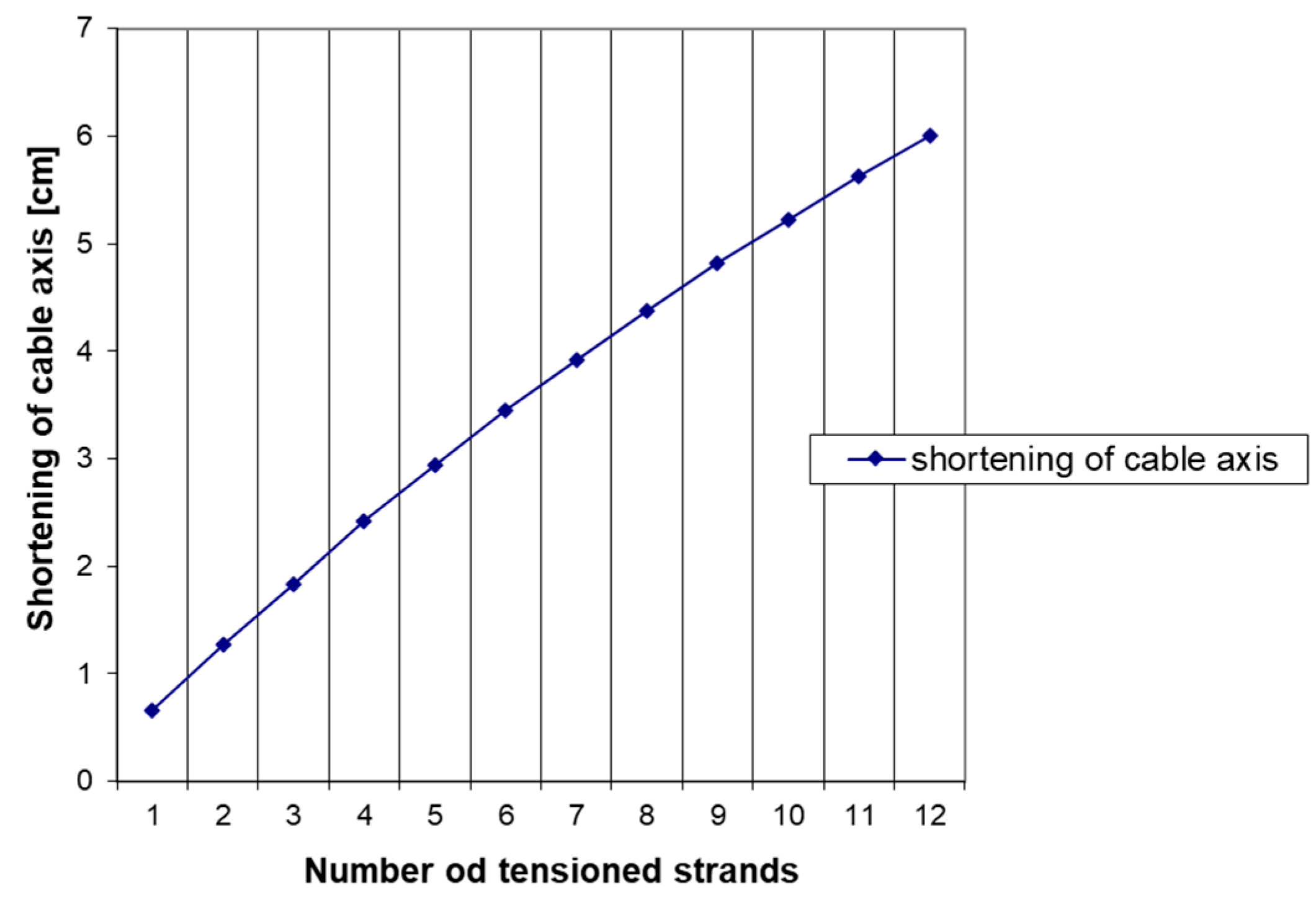
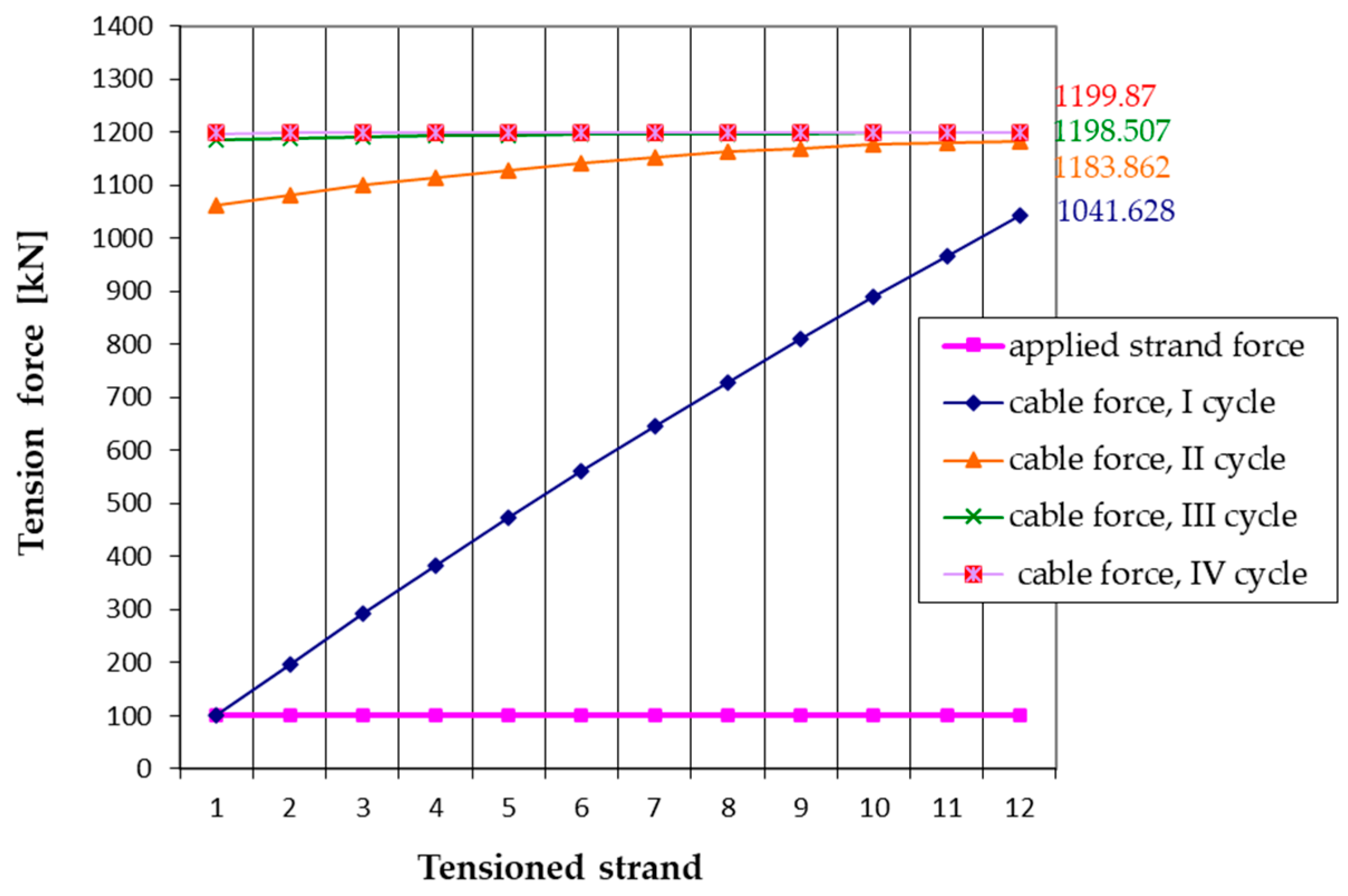
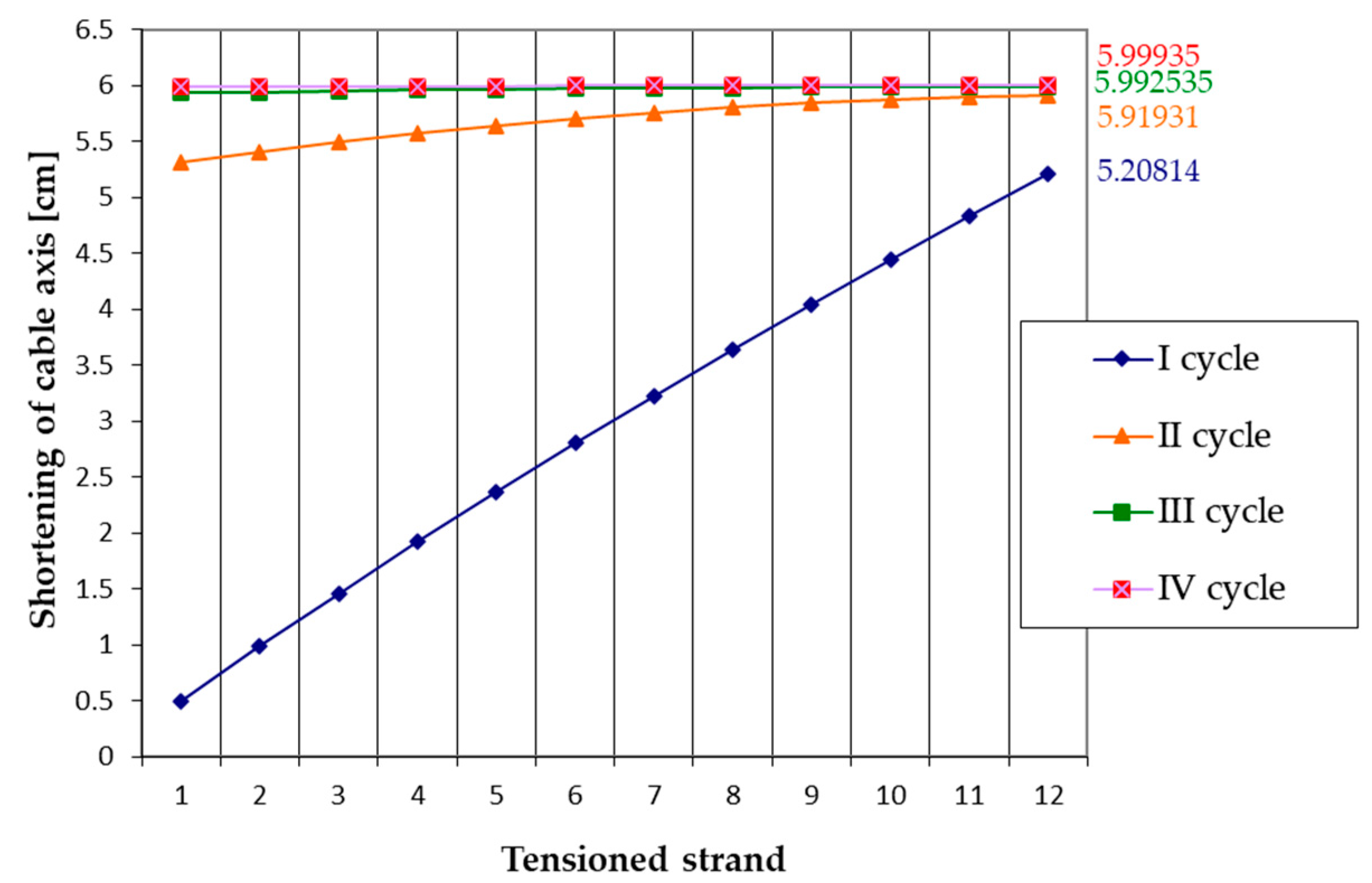
5.2. Multi-Cycle Tensioning of Strands
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Wang, S.; Huang, K.; Zhong, J.; Cheng, H. Research on Dynamic Response of a Single-Tower Cable-Stayed Bridge with Successive Cable Breaks Based on a 3D Index. Appl. Sci. 2023, 13, 9197. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, J.Y.; Cao, M.S.; Damjanovic, D.; Ostachowicz, W. Identification of instantaneous tension of bridge cables from dynamic responses: Strict algorithm and applications. Mech. Syst. Signal Process. 2020, 142, 106729. [Google Scholar] [CrossRef]
- Podolny, W., Jr.; Asce, M.; Fleming, J.F. Historical Development of Cable-Stayed Bridges. J. Struct. Div. 1972, 98. [Google Scholar] [CrossRef]
- Gimsing, N.J.; Georgiakis, C.T. Cable Supported Bridges Concept and Design, 3rd ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Walther, R.; Houriet, B.; Isler, W.; Moia, P.; Klein, J.F. Cable Stayed Bridges, 2nd ed.; Thomas Telford Publishing: London, UK, 1999. [Google Scholar]
- Huang, D.; Chen, W. Cable Structures in Bridge Engineering. J. Bridge Eng. 2019, 24, 02019001. [Google Scholar] [CrossRef]
- Wilson, J.C.; Gravelle, W. Modelling of a cable-stayed bridge for dynamic analysis. Earthq. Eng. Struct. Dyn. 1991, 20, 707–721. [Google Scholar] [CrossRef]
- Wang, P.H.; Tang, T.Y.; Zheng, H.N. Analysis of cable-stayed bridges during construction by cantilever methods. Comput. Struct. 2004, 82, 329–346. [Google Scholar] [CrossRef]
- Shen, G.; Macdonald, J.; Coules, H.E. Nonlinear cable-deck interaction vibrations of cable-stayed bridges. J. Sound Vib. 2023, 544, 117428. [Google Scholar] [CrossRef]
- Fragassa, C.; Minak, G.; Pavlovic, A. Measuring deformations in the telescopic boom under static and dynamic load conditions. Facta Univ. Ser. Mech. Eng. 2020, 18, 315–328. [Google Scholar] [CrossRef]
- Cho, S.; Lynch, J.P.; Lee, J.J.; Yun, C.B. Development of an Automated Wireless Tension Force Estimation System for Cable-stayed Bridges. J. Intell. Mater. Syst. Struct. 2010, 21, 361–367. [Google Scholar] [CrossRef]
- Wang, P.H.; Tseng, T.C.; Yang, C.G. Initial shape of cable-stayed bridges. Comput. Struct. 1993, 47, 111–123. [Google Scholar] [CrossRef]
- Chen, D.W.; Au, F.T.K.; Tham, L.G.; Lee, P.K.K. Determination of initial cable forces in prestressed concrete cable-stayed bridges for given design deck profiles using the force equilibrium method. Comput. Struct. 2000, 74, 1–9. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, Z.; Li, M.; Fu, N. Cable Force Optimization of Cable-Stayed Bridge Based on Multiobjective Particle Swarm Optimization Algorithm with Mutation Operation and the Influence Matrix. Appl. Sci. 2023, 13, 2611. [Google Scholar] [CrossRef]
- Martins, A.M.; Simões, L.M.; Negrão, J.H. Optimization of cable-stayed bridges: A literature survey. Adv. Eng. Softw. 2020, 149, 102829. [Google Scholar] [CrossRef]
- Xiao, F.; Hulsey, J.L.; Chen, G.S.; Xiang, Y. Optimal static strain sensor placement for truss bridges. Int. J. Distrib. Sens. Netw. 2017, 13. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The Current Development of Structural Health Monitoring for Bridges: A Review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Xiao, F.; Hulsey, J.L.; Balasubramanian, R. Fiber optic health monitoring and temperature behavior of bridge in cold region. Struct. Control Health Monit. 2017, 24, e2020. [Google Scholar] [CrossRef]
- Suangga, M.; Hidayat, I.; Celine, J. Temperature effect on cable tension forces of cable-stayed bridge. IOP Conf. Ser. Earth Environ. Sci. 2018, 195, 012009. [Google Scholar] [CrossRef]
- Xiao, F.; Sun, H.; Mao, Y.; Chen, G.S. Damage identification of large-scale space truss structures based on stiffness separation method. Structures 2023, 53, 109–118. [Google Scholar] [CrossRef]
- Hou, S.; Dong, B.; Wang, H.; Wu, G. Inspection of surface defects on stay cables using a robot and transfer learning. Autom. Constr. 2020, 119, 103382. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Xiao, Z.; Liu, L. A tensioning control method for stay cables with super large tonnage cable force. Int. J. Struct. Integr. 2024, 15, 613–630. [Google Scholar] [CrossRef]
- Li, T.; Liu, Z. An improved continuum model for determining the behavior of suspension bridges during construction. Autom. Constr. 2021, 127, 103715. [Google Scholar] [CrossRef]
- Spasojević Šurdilović, M. Modeling and Sterss and Starin Analysis of Cable-Stayed Bridges during the Phase Formation of the Structaral System Using Temporary Supports. Master’s Thesis, Faculty of Civil Engineering and Architecture, University of Niš, Niš, Serbia, 2007. (In Serbian). [Google Scholar]
- Spasojević Šurdilović, M.; Spasojević, A.; Spasojević, N. Specifična problematika projektovanja i izvođenja pešačkog mosta preko reke Nišave u Nišu. In Proceedings of the Third International Scientific-Expert Conference, GNP 2010, Žabljak, Montenegro, 15–19 February 2010; Volume 1, pp. 643–648. (In Serbian). [Google Scholar]
- Spasojević Šurdilović, M.; Spasojević, A.; Stojić, D. Modelling of a bridge stay cable for individual strand tensioning. Građevinar 2014, 66, 549–554. [Google Scholar] [CrossRef]
- Freyssinet Commercial Brochure. Freyssinet HD Stay Cable. Available online: www.freyssinet.com (accessed on 20 March 2024).
- El Shenawy, E.A. Form Finding for Cable-Stayed and Extradosed Bridges. Ph.D. Thesis, Technischen Universität Berlin, Berlin, Germany, 2013. [Google Scholar]
- Spasojević Šurdilović, M.; Spasojević, A. Analytical solutions for determining tension force in strands of bridge stay-cable in isotension procedure. In Proceedings of the International Conference Innovation as a Function of Engineering Development-IDE 2011, Nis, Serbia, 25–26 November 2011; pp. 319–324. [Google Scholar]
- He, W.Y.; Meng, F.C.; Ren, W.X. Cable force estimation of cables with small sag considering inclination angle effect. Adv. Bridge Eng. 2021, 2, 15. [Google Scholar] [CrossRef]
- Croce, P. Non-linear behavior of heavy stays. Int. J. Solids Struct. 2013, 50, 1093–1107. [Google Scholar] [CrossRef]
- Feng, X.H.; Zhu, Z.Q.; He, X.Q. Geometrical Nonlinear Analysis for Multi-Parameters of Four Tower Cable-Stayed Bridge Based on The Bar Element Model. In Proceedings of the International Conference on Structural, Mechanical and Materials Engineering (ICSMME 2015), Dalian, China, 6–8 November 2015. [Google Scholar]
- Irvine, H.M. Free vibration of inclined cables. ASCE J. Struct. Div. 1978, 104, 343–347. [Google Scholar] [CrossRef]
- Hajdin, N.; Michaltsos, G.T.; Konstantakopulus, T.G. About the equivalent elastic modulus of elasticity of cables of cable-stayed bridges. Facta Univ. 1998, 1, 569–575. [Google Scholar]
- Wang, L.-Z.; Guo, Z.; Yuan, F. Quasi-static three-dimensional analysis of suction anchor mooring system. Ocean Eng. 2010, 37, 1127–1138. [Google Scholar] [CrossRef]
- Ernst, J.H. Der E-modul von seilen under berücksichtigung des durchhanges. Bauing 1965, 40, 52–55. (In German) [Google Scholar]
- The Centre for Structures and Prestressing–IMS Institute. Available online: https://institutims.rs/ (accessed on 9 June 2024).
- Stanković, M.; Đorđević, Đ. Stress, Software System for Static Calculation of Engineering Structures; Trion Computers: Niš, Serbia, 1991. (In Serbian) [Google Scholar]
- Spasojević Šurdilović, M.; Spasojević, A. Analytical Solutions for Deformations of Bridge Stay Cables. Proc. Fac. Civ. Eng. Archit. Niš 2010, 25, 207–214. (In Serbian) [Google Scholar]


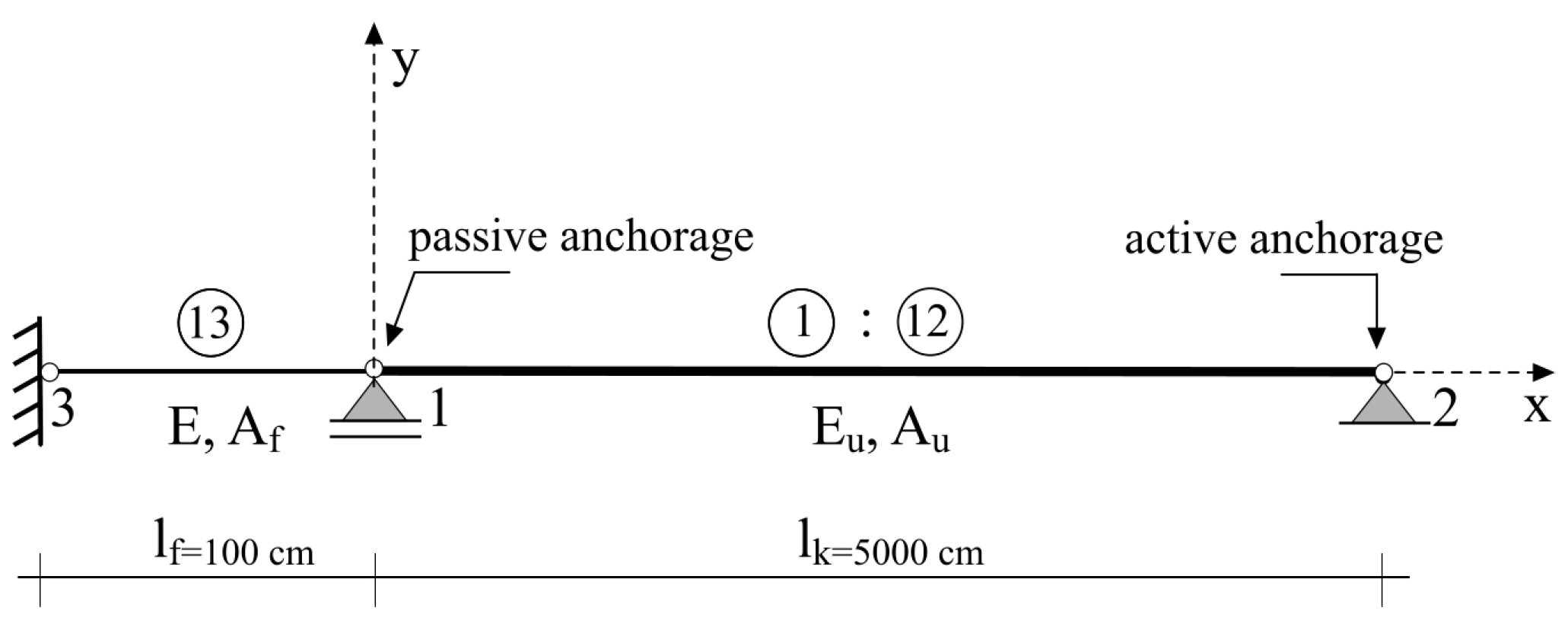
| Characteristic | Symbol | Value |
|---|---|---|
| Diameter (steel) | d | 15.7 mm |
| Total diameter (steel + grease + HDPE) | D | 19.1 mm |
| Area of strand (steel) | Au | 150 mm2 |
| Strand mass (steel + grease + HDPE) | ms | 1.29 kg/m |
| Relaxation class | - | 2 (low relaxation level: <2.5%) |
| Characteristic tensile strength | fpk | 1860 N/mm2 |
| Characteristic failure force | Fpk = Au · fpk | 279 kN |
| Characteristic value of yield force at which permanent 0.1% elongation occurs | Fp 0.1 | 246 kN |
| Allowed force in strand (for considered case) | 0.45 Fpk | 12.55 kN |
| Modulus of elasticity | E | 1.94 (±0.01) × 105 MPa |
| Property | Symbol | Value |
|---|---|---|
| External diameter of pipe | dp | 110 mm (Ddp = +1.0 mm) |
| Pipe wall thickness | s | 6.6 mm (Ds= +0.9 mm) |
| Mass of the HDPE pipe | mp | 2.166 kg/m1 |
| Strand | Tension Force in Strand Zi * [kN] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 131.26 | 127.633 | 124.201 | 120.948 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 |
| 2 | 127.633 | 124.201 | 120.948 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | |
| 3 | 124.201 | 120.948 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | ||
| 4 | 120.948 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | |||
| 5 | 117.862 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | ||||
| 6 | 114.929 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | |||||
| 7 | 112.139 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | ||||||
| 8 | 109.481 | 106.946 | 104.526 | 102.213 | 100 | |||||||
| 9 | 106.946 | 104.526 | 102.213 | 100 | ||||||||
| 10 | 104.526 | 102.213 | 100 | |||||||||
| 11 | 102.213 | 100 | ||||||||||
| 12 | 100 | |||||||||||
| Zki [kN] ** | 131.26 | 255.266 | 372.603 | 483.792 | 589.31 | 689.574 | 784.973 | 875.848 | 962.514 | 1045.26 | 1124.34 | 1200 |
| ξki [cm] *** | 0.6563 | 1.2763 | 1.8630 | 2.4190 | 2.9465 | 3.4479 | 3.9249 | 4.3792 | 4.8126 | 5.2263 | 5.6217 | 6.000 |
| Strand (i) | Zu [kN] | Zi(c) * [kN] | |||
|---|---|---|---|---|---|
| Zi(1) | Zi(2) | Zi(3) | Zi(4) | ||
| 1 | 100 | 72.457 | 96.450 | 99.620 | 99.967 |
| 2 | 100 | 75.299 | 97.010 | 99.716 | 99.975 |
| 3 | 100 | 78.062 | 97.521 | 99.773 | 99.980 |
| 4 | 100 | 80.751 | 97.984 | 99.822 | 99.985 |
| 5 | 100 | 83.370 | 98.400 | 99.863 | 99.988 |
| 6 | 100 | 85.922 | 98.768 | 99.897 | 99.991 |
| 7 | 100 | 88.410 | 99.089 | 99.925 | 99.993 |
| 8 | 100 | 90.838 | 99.364 | 99.947 | 99.995 |
| 9 | 100 | 93.208 | 99.592 | 99.965 | 99.997 |
| 10 | 100 | 95.524 | 99.774 | 99.979 | 100 |
| 11 | 100 | 97.787 | 99.910 | 100 | 100 |
| 12 | 100 | 100 | 100 | 100 | 100 |
| Zk(c) [kN] ** | 1041.628 | 1183.862 | 1198.507 | 1199.870 | |
| ξk(c) [cm] *** | 5.208 | 5.920 | 5.993 | 6.000 | |
| γk(c) **** | 86.8% | 98.66% | 99.88% | 100% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spasojević Šurdilović, M.; Živković, S.; Turnić, D. Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges. Appl. Sci. 2024, 14, 5410. https://doi.org/10.3390/app14135410
Spasojević Šurdilović M, Živković S, Turnić D. Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges. Applied Sciences. 2024; 14(13):5410. https://doi.org/10.3390/app14135410
Chicago/Turabian StyleSpasojević Šurdilović, Marija, Srđan Živković, and Dragana Turnić. 2024. "Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges" Applied Sciences 14, no. 13: 5410. https://doi.org/10.3390/app14135410
APA StyleSpasojević Šurdilović, M., Živković, S., & Turnić, D. (2024). Algorithms for Computer-Based Calculation of Individual Strand Tensioning in the Stay Cables of Cable-Stayed Bridges. Applied Sciences, 14(13), 5410. https://doi.org/10.3390/app14135410








