Robot Grasp Detection with Loss-Guided Collaborative Attention Mechanism and Multi-Scale Feature Fusion
Abstract
1. Introduction
- We propose a novel grasp detection network that integrates a loss-guided collaborative attention mechanism with multi-scale feature fusion to enhance the network’s focus on object grasp regions.
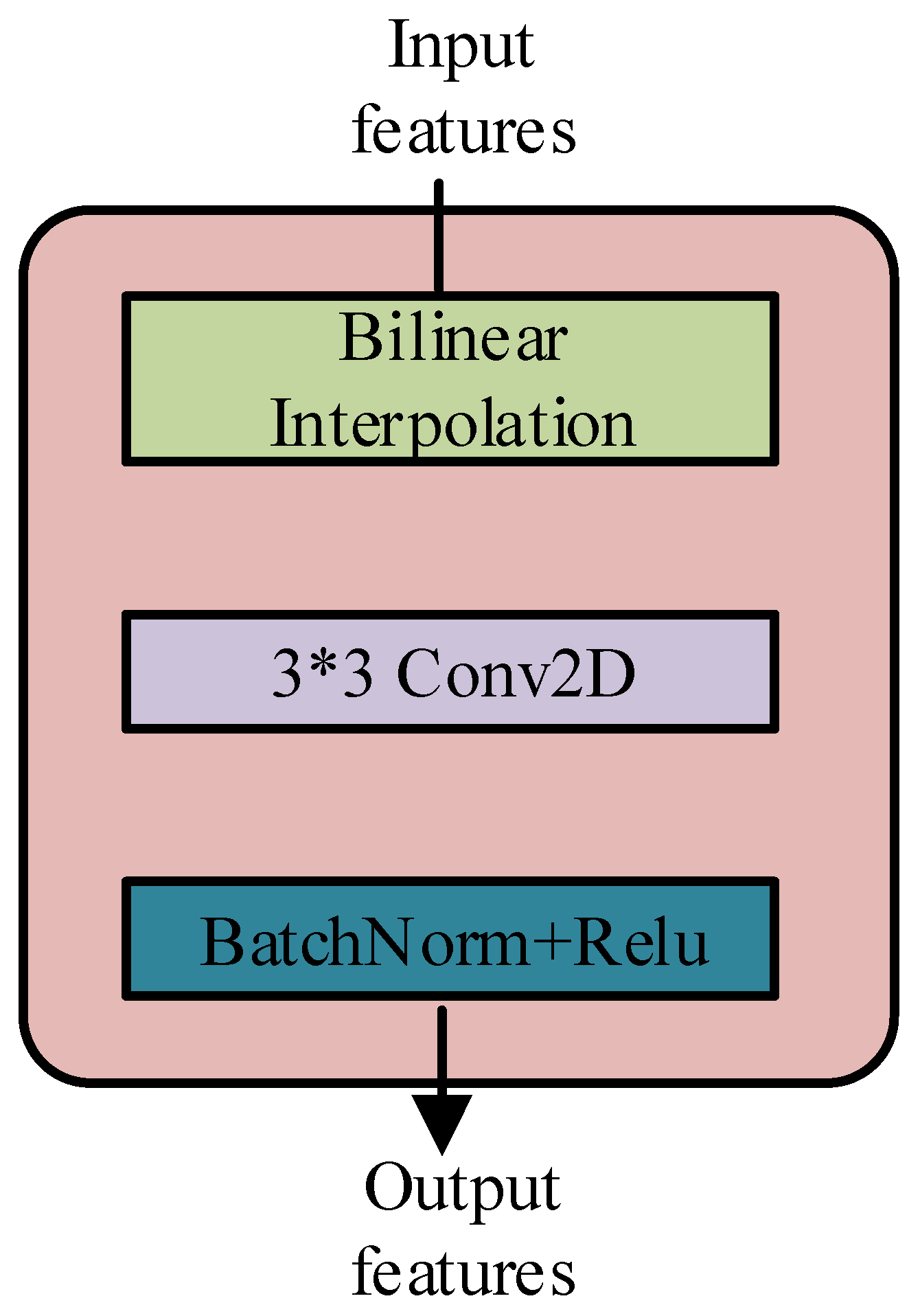
- In order to address the checkerboard artifacts in the upper sampling layer and improve the grasping accuracy, an effective convolutional decoding block is proposed.
- The grasping network LGAR-Net2 built with the proposed module achieved 97.7% performance in both open datasets and simulated robot grasping. And an ROS simulation environment is established for the real-time prediction of grasping poses using LGAR-Net2, achieving a processing speed of 15 ms per piece with an accuracy rate of 93.3%.
2. Related Works
2.1. Grasp Detection Using Deep Learning
2.2. Encoder–Decoder Regression
2.3. Attention Mechanisms for Grasp Detection
3. Problem Statement
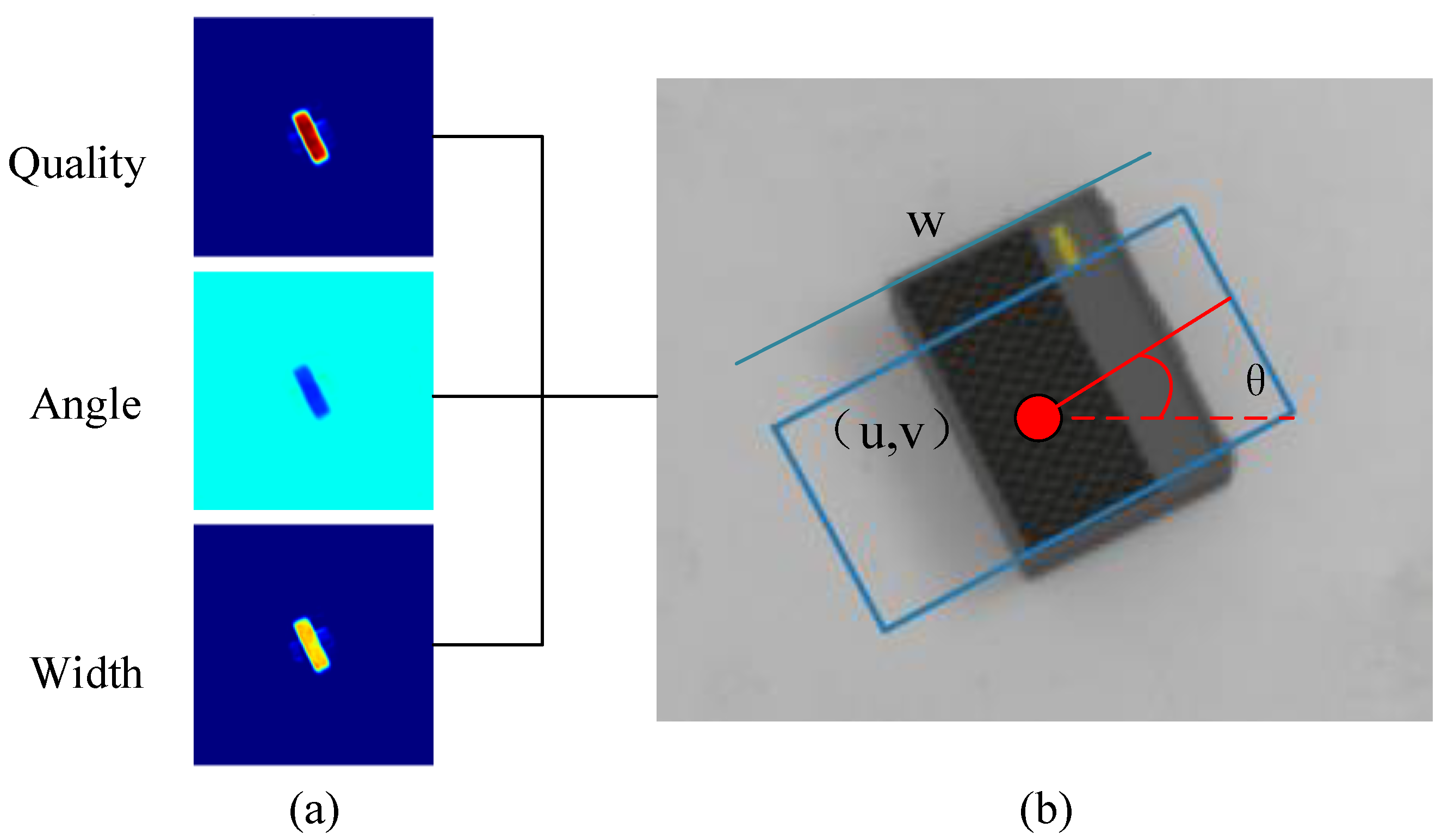
3.1. Grasp Pose Definition
3.2. The Chessboard Artifacts Problem Description
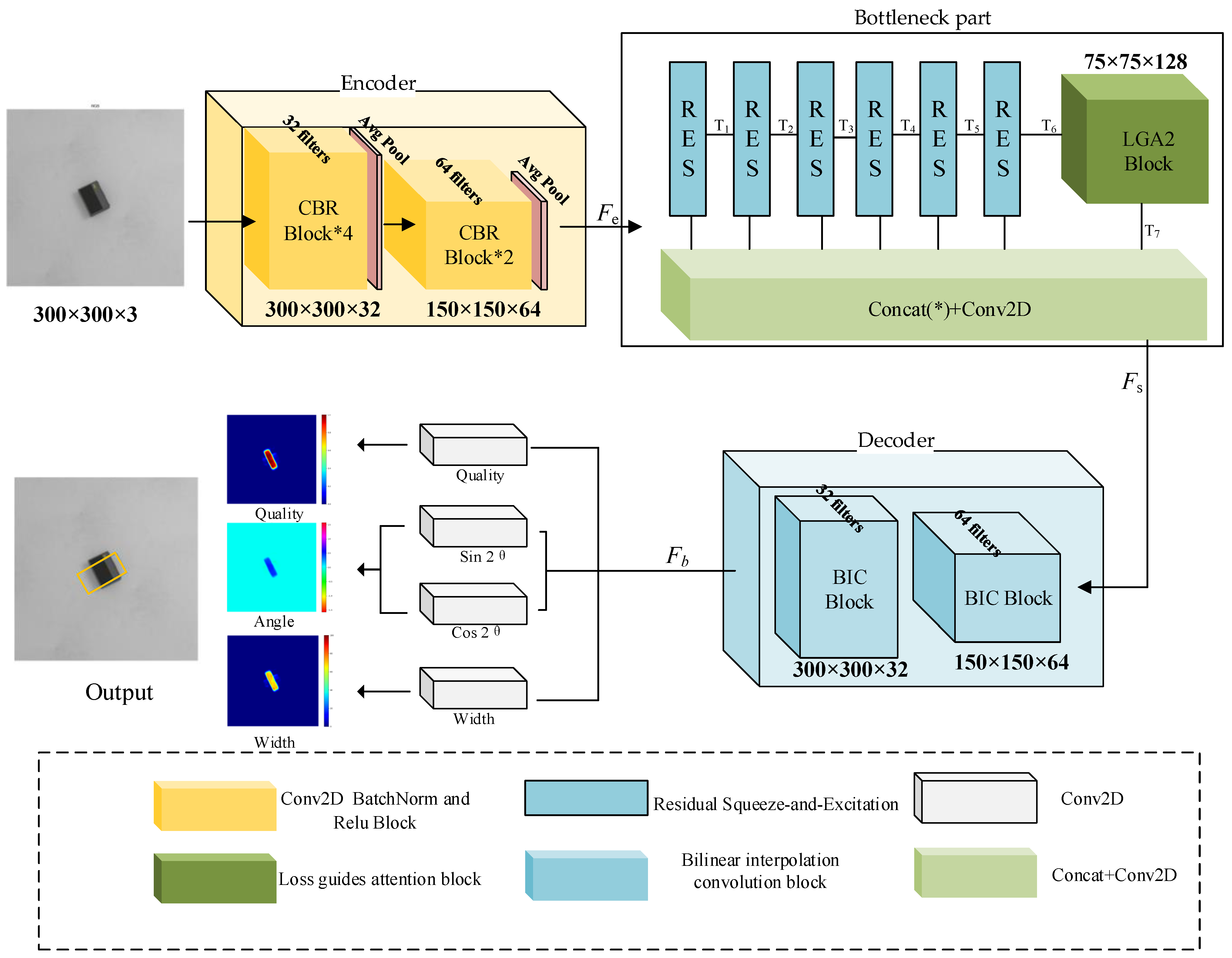
4. Method
4.1. Encoder
4.2. Bottleneck Part
4.2.1. Residual Squeeze Excitation Block (RSE Block)
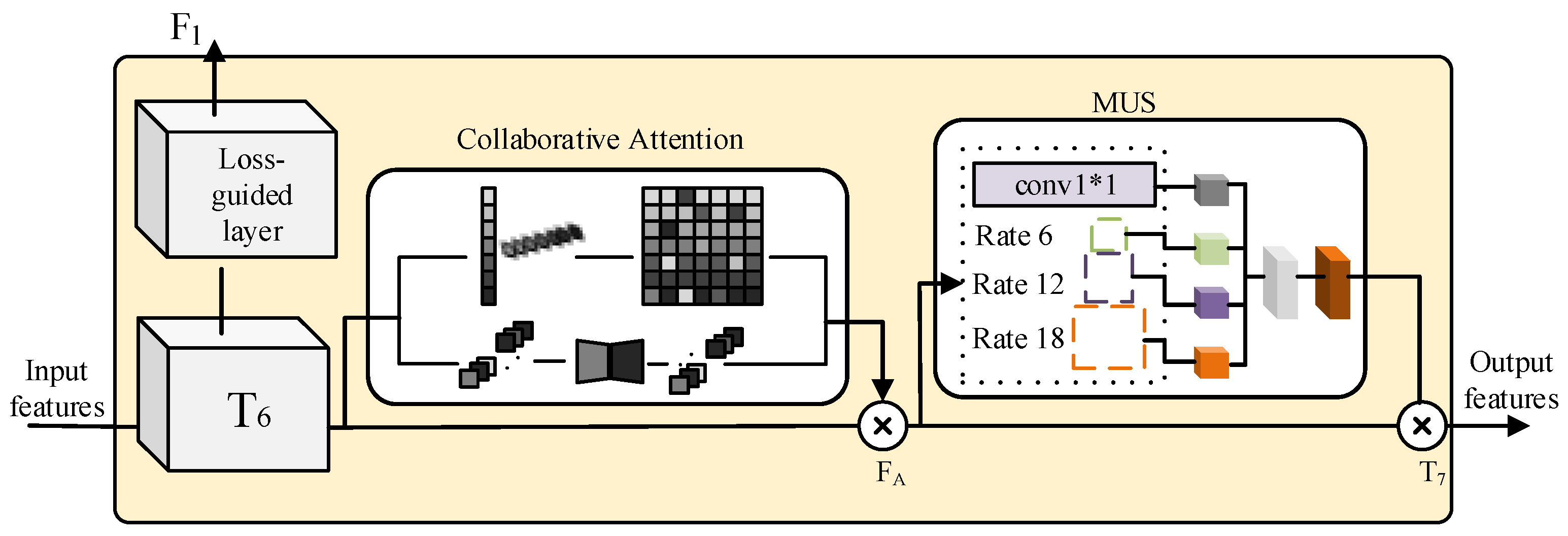
4.2.2. Loss-Guided Collaborative Attention Block (LGCA Block)
- 1.
- Loss guide block
- 2.
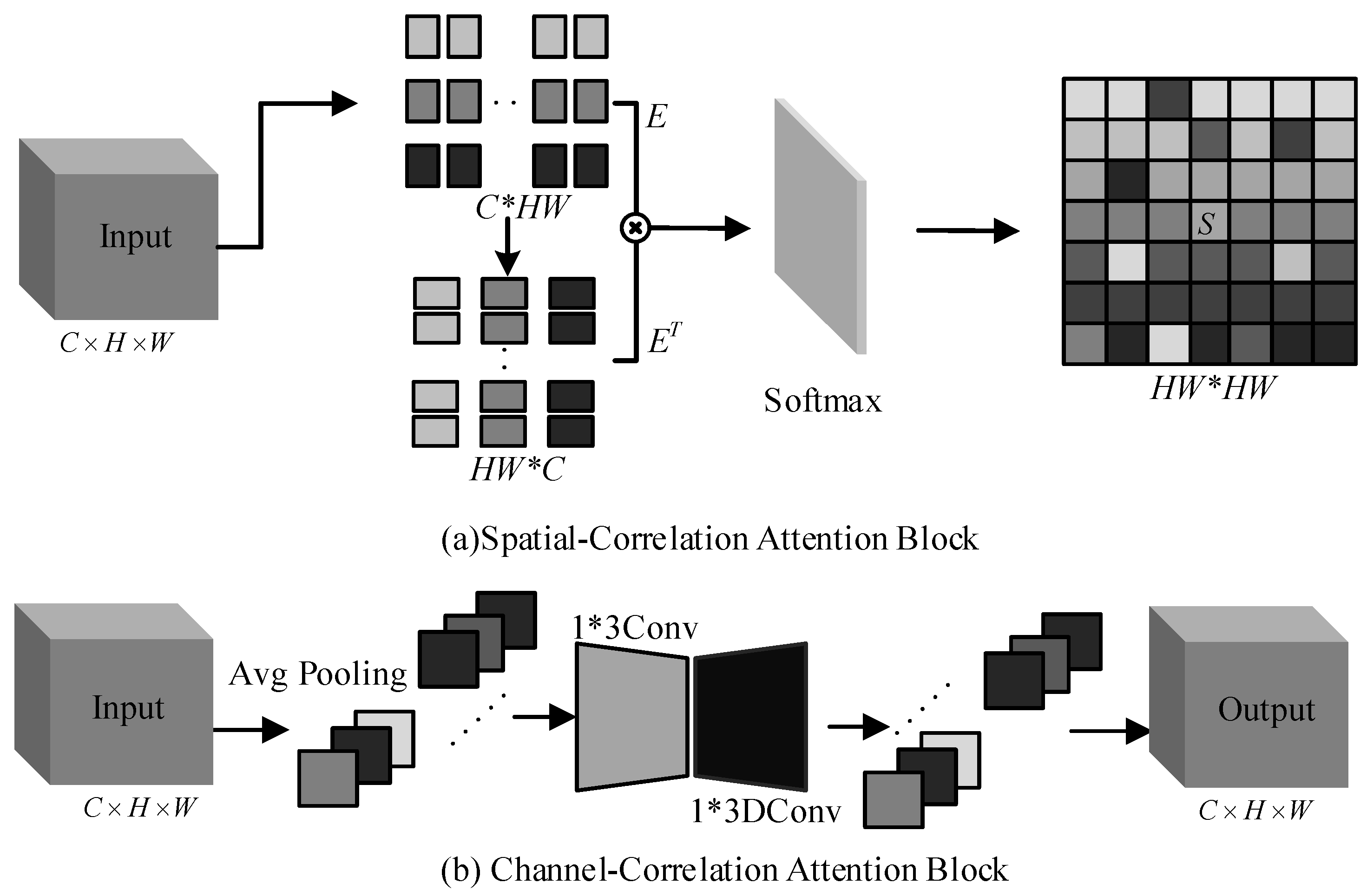
- Collaborative attention block
- 3.
- Multi-Scale Module
4.3. Feature Fusion Module
4.4. Decoder
4.5. Loss Function
- (1)
- LGCA auxiliary losses: The function is defined, where represents the predicted value image of the network’s grabber region and denotes the label for the grabber region.
- (2)
- Regression loss estimation for the confidence, angle, and width of a crawlable region: The definitions of , , , and are equivalent to , where represents the ground truth image of the graspable region mapping for the i-th sample, while denotes the predicted value image of the graspable region for the i-th sample.
5. Results
5.1. Experimental Details
- Model training implementation: We employ the Xavier normal distribution for initializing network parameters and utilize the Adam optimization algorithm for network optimization. The number of epochs is 50, 1000 batches of data are processed in each epoch, and the number of samples per input is set to eight.
- Evaluation metrics: The angle difference and Jaccard index are two commonly employed criteria for assessing grasping performance. According to the angle difference criterion, a successful grasp is defined as having a deviation of less than 30° between the predicted grasping area and its corresponding label. Under the Jaccard index, a grasp is deemed successful if the overlap between the predicted and labeled grasping areas exceeds 25%. The mathematical expression of the Jaccard index is as follows:
- In the formula, and denote the predicted grasping area and true grasping area value, respectively. The intersection of predicted grasping area and grasping area label is represented by , while the union of predicted grasping area and grasping area label is denoted by .
5.2. Comparative Study
5.2.1. Attention Mechanism Experiment
5.2.2. Checkerboard Artifact Experiment
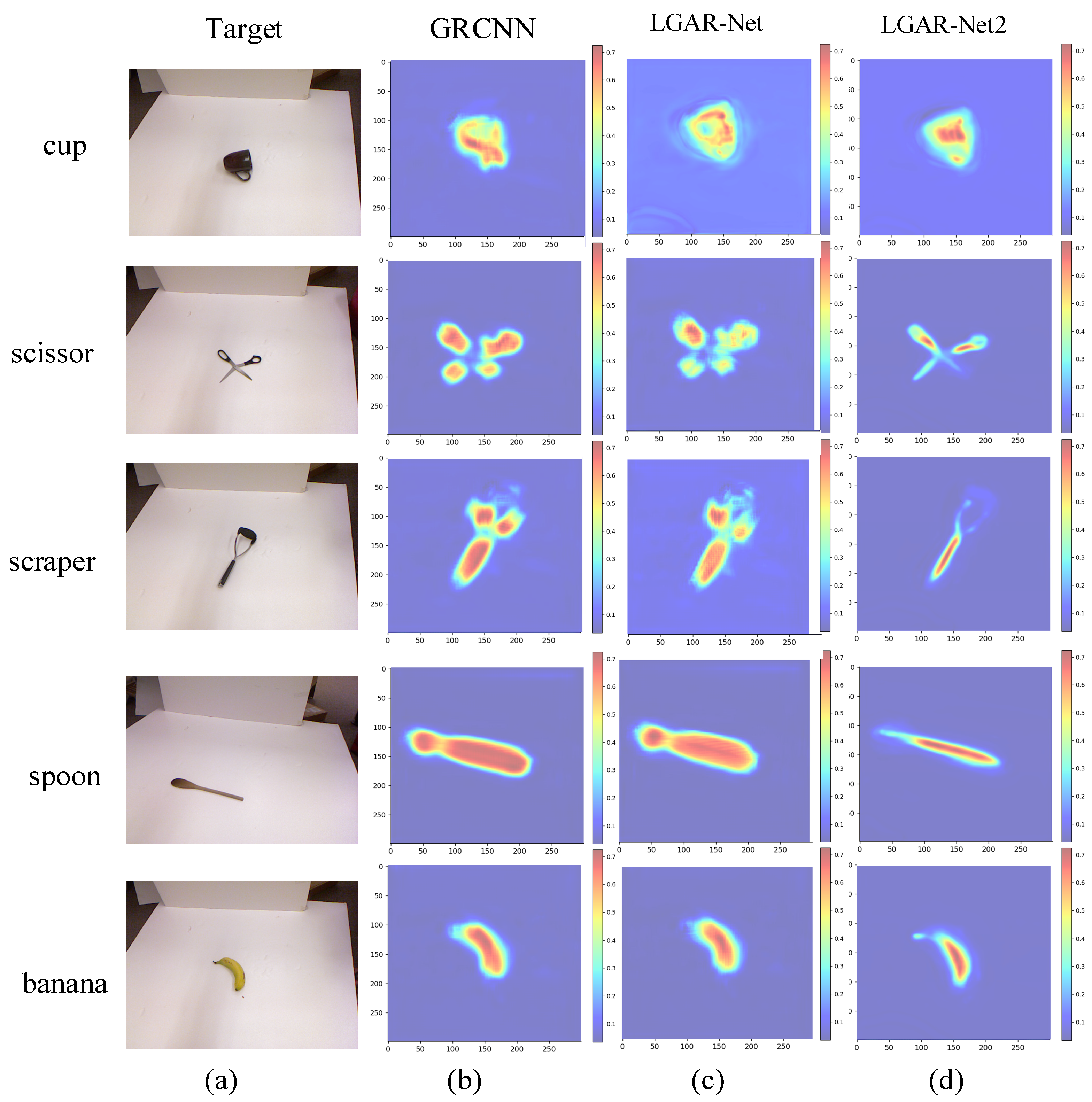
5.2.3. Experimental Verification on Datasets
5.3. Simulation Experiment Capture Detection
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ni, P.; Zhang, W.; Zhu, X.; Cao, Q. PointNet++ grasping: Learning an end-to-end spatial grasp generation algorithm from sparse point clouds. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 3619–3625. [Google Scholar]
- Jiang, Y.; Moseson, S.; Saxena, A. Efficient grasping from RGBD images: Learning using a new rectangle representation. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3304–3311. [Google Scholar]
- Lenz, I.; Saxena, A. Deep learning for detecting robotic grasps. Int. J. Robot. Res. 2015, 34, 705–724. [Google Scholar] [CrossRef]
- Redmon, J.; Angelova, A. Real-time grasp detection using convolutional neural networks. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1316–1322. [Google Scholar]
- Morrison, D.; Corke, P.; Leitner, J. Learning robust, real-time, reactive robotic grasping. Int. J. Robot. Res. 2020, 39, 183–201. [Google Scholar] [CrossRef]
- Kumra, S.; Joshi, S.; Sahin, F. Antipodal robotic grasping using generative residual convolutional neural network. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2020; pp. 9626–9633. [Google Scholar]
- Bicchi, A.; Kumar, V. Robotic grasping and contact: A review. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat.No. 00CH37065), San Francisco, CA, USA, 24–28 April 2000; IEEE: New York, NY, USA, 2000; Volume 1, pp. 348–353. [Google Scholar]
- Guo, D.; Sun, F.; Liu, H.; Kong, T.; Fang, B.; Xi, N. A hybrid deep architecture for robotic grasp detection. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1609–1614. [Google Scholar]
- Pinto, L.; Gupta, A. Supersizing self-supervision: Learning to grasp from 50k tries and 700 robot hours. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: New York, NY, USA, 2016; p. 34063413. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Mahajan, M.; Bhattacharjee, T.; Krishnan, A.; Shukla, P.; Nandi, G.C. Robotic grasp detection by learning representation in a vector quantized manifold. In Proceedings of the 2020 International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 19–24 July 2020; pp. 1–5. [Google Scholar]
- Yu, Y.; Cao, Z.; Liu, Z.; Geng, W.; Yu, J.; Zhang, W. A twostream CNN with simultaneous detection and segmentation for robotic grasping. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1167–1181. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Zhou, Z.; Zhu, X.; Cao, Q. AAGDN: Attention-Augmented Grasp Detection Network Based on Coordinate Attention and Effective Feature Fusion Method. IEEE Robot. Autom. Lett. 2023, 8, 3462–3469. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Wang, X.; Ross, G.; Abhinav, G.; Kaiming, H. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; p. 77947803. [Google Scholar]
- Luo, C.; Shi, C.; Zhang, X.; Peng, J.; Li, X.; Chen, Y. AMCNet: Attention-Based Multiscale Convolutional Network for DCM MRI Segmentation. In Proceedings of the 2019 IEEE 43rd Annual Computer Software and Applications Conference (COMPSAC), Milwaukee, WI, USA, 15–19 July 2019; pp. 434–439. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, X.; Ran, L.; Han, Y.; Chu, H. DSC-GraspNet: A Lightweight Convolutional Neural Network for Robotic Grasp Detection. In Proceedings of the 2023 9th International Conference on Virtual Reality (ICVR), Xianyang, China, 12–14 May 2023. [Google Scholar]
- Denavit, J.; Hartenberg, R.S. A kinematic notation for lower-pair mechanisms based on matrices. Asme J. Appl. Mech. 1995, 22, 215–221. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.; Wang, C.; Chen, Y. Grasping Pose Detection Based on Loss-Guided Attention Mechanism and Residual Network. In Proceedings of the 2023 IEEE 5th International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Dali, China, 11–13 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 921–924. [Google Scholar]
- Depierre, A.; Dellandrea, E.; Chen, L. Jacquard: A large scale dataset for robotic grasp detection. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3511–3516. [Google Scholar]
- Karaoguz, H.; Jensfelt, P. Object Detection Approach for Robot Grasp Detection. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4953–4959. [Google Scholar]






| Author | Method | Input | Accuracy (%) | Times (ms) |
|---|---|---|---|---|
| Jiang [2] | Fast Search | RGB-D | 60.5 | 5000 |
| Lenz [3] | SAE, struct. reg. | RGB-D | 73.9 | 1350 |
| Wang [18] | Two-stage closed-loop | RGB-D | 85.3 | 140 |
| Redmon [4] | AlexNet, MultiGrasp | RGB-D | 88.0 | 76 |
| Morrison [5] | GG-CNN | D | 73.0 | - |
| Karaoguz [25] | GRPN | RGB | 88.7 | 200 |
| Kumra [6] | GRCNN | RGB | 96.6 | 19 |
| Ours | LGAR-Net2 | RGB | 97.7 | 15 |
| Author | Method | Input | Accuracy (%) | Times (ms) |
|---|---|---|---|---|
| Depierre [24] | Jacquard | RGD | 93.6 | - |
| Morrison [5] | GG-CNN2 | D | 84 | 19 |
| Kumra [6] | GRCNN | RGB | 91.8 | 19 |
| Ours | LGAR-Net2 | RGB | 94.4 | 17 |
| Target Object | Grasp Pose Detection Accuracy (%) | Success/Attempt | Accuracy (%) |
|---|---|---|---|
| Coke Bottle | 87.5 | 13/15 | 86.7 |
| Wood Block | 88.1 | 13/15 | 86.7 |
| Screwdriver | 93.5 | 14/15 | 93.3 |
| Remote | 90.1 | 13/15 | 86.7 |
| Hexagon Nut | 93.2 | 13/15 | 86.7 |
| Weight | 88.7 | 13/15 | 86.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, H.; Wang, C.; Chen, Y. Robot Grasp Detection with Loss-Guided Collaborative Attention Mechanism and Multi-Scale Feature Fusion. Appl. Sci. 2024, 14, 5193. https://doi.org/10.3390/app14125193
Fang H, Wang C, Chen Y. Robot Grasp Detection with Loss-Guided Collaborative Attention Mechanism and Multi-Scale Feature Fusion. Applied Sciences. 2024; 14(12):5193. https://doi.org/10.3390/app14125193
Chicago/Turabian StyleFang, Haibing, Caixia Wang, and Yong Chen. 2024. "Robot Grasp Detection with Loss-Guided Collaborative Attention Mechanism and Multi-Scale Feature Fusion" Applied Sciences 14, no. 12: 5193. https://doi.org/10.3390/app14125193
APA StyleFang, H., Wang, C., & Chen, Y. (2024). Robot Grasp Detection with Loss-Guided Collaborative Attention Mechanism and Multi-Scale Feature Fusion. Applied Sciences, 14(12), 5193. https://doi.org/10.3390/app14125193




