Research on the Strategy for the Flexible Configuration of Chaotic Signal Probability Distribution and Its Application
Abstract
1. Introduction
2. Strategy for Flexible Setting Probability Distribution of Chaotic Signals Based on Graphical Language
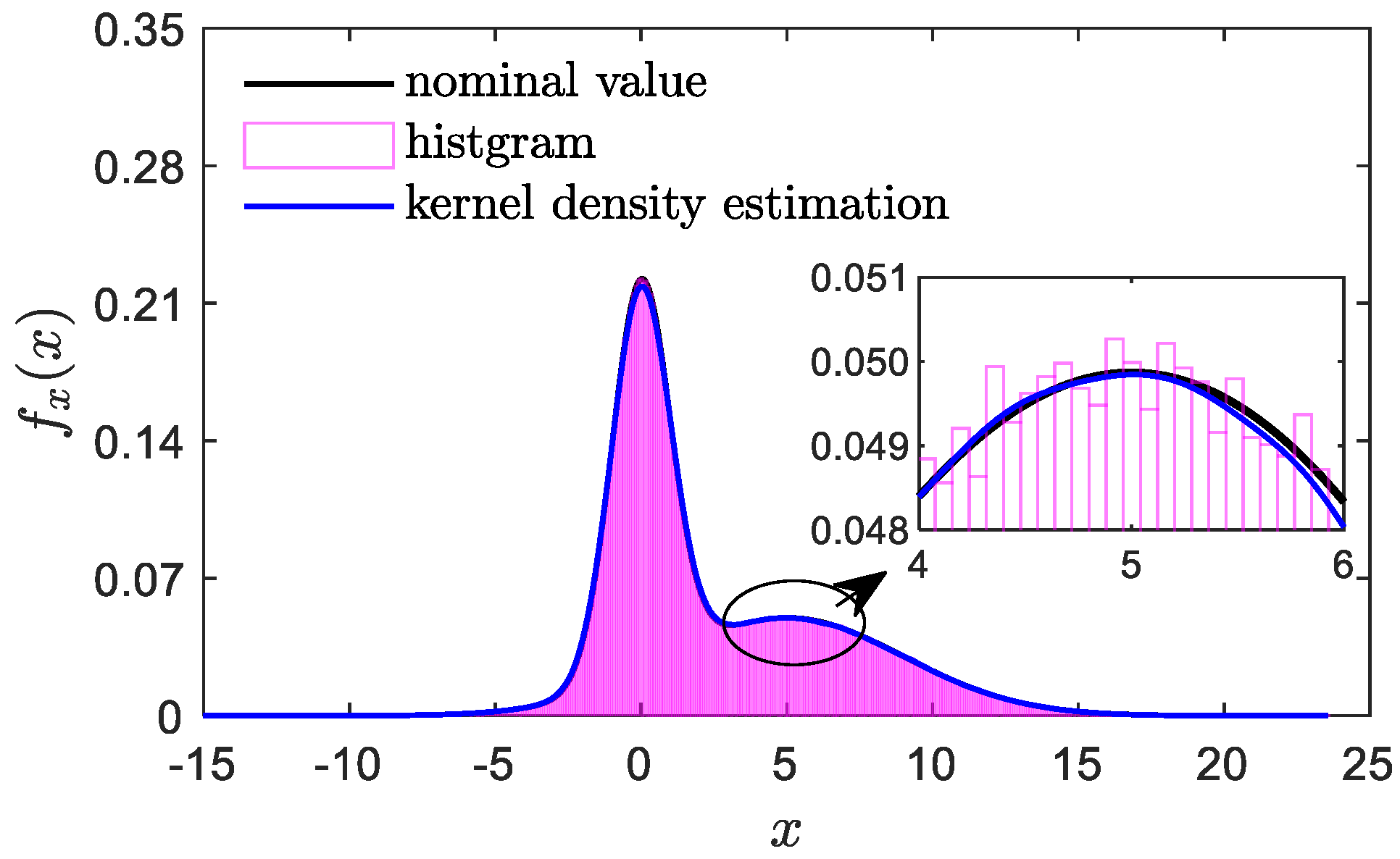
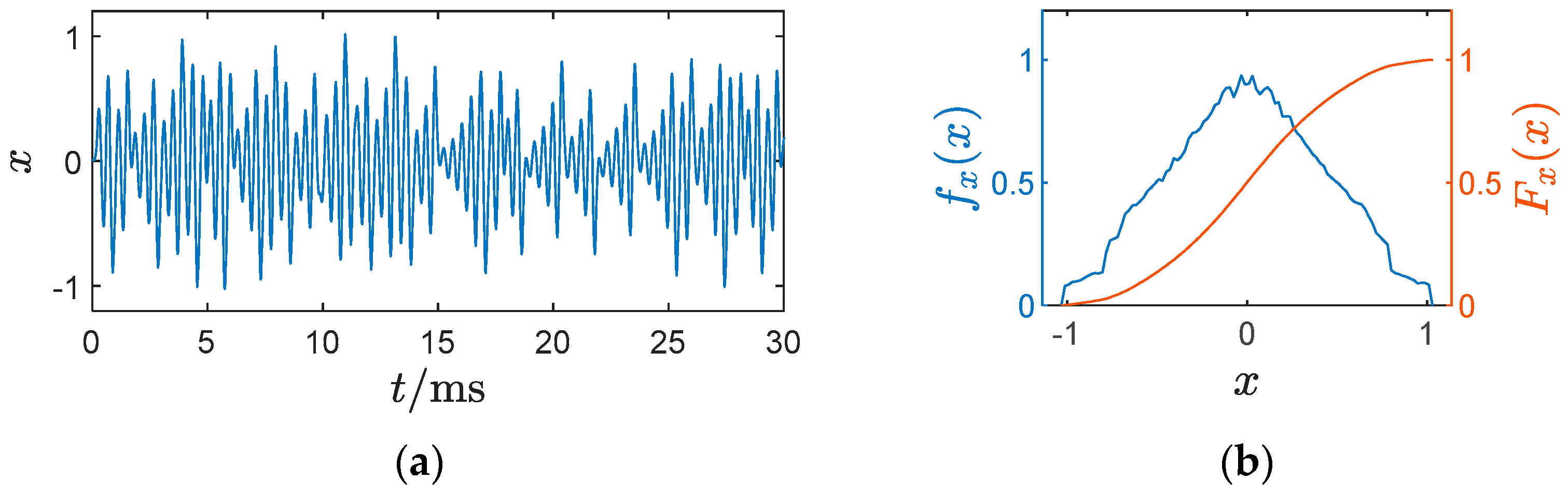
2.1. Kernel Density Estimation for Solving the Probability Density Function of Chaotic Signals
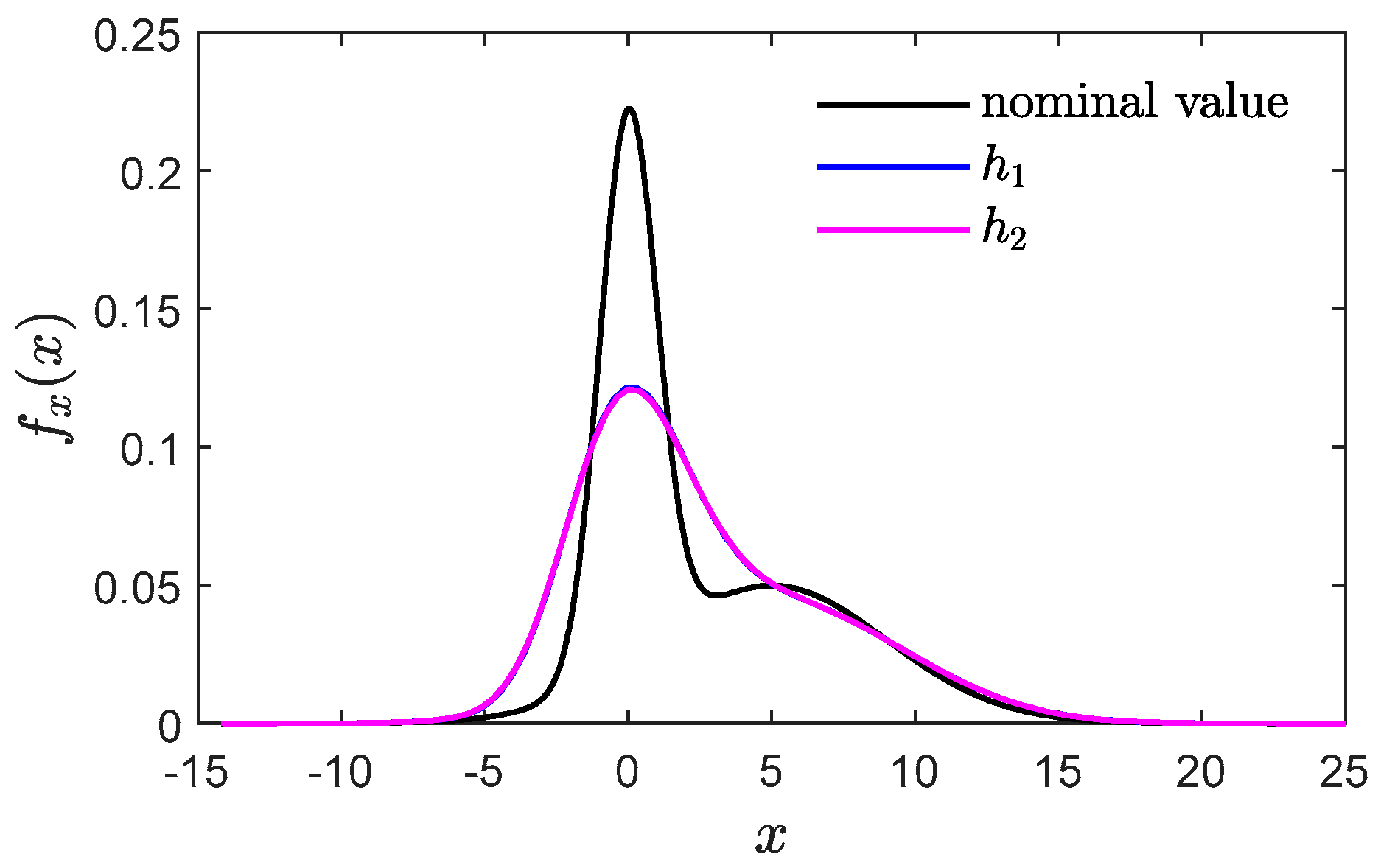
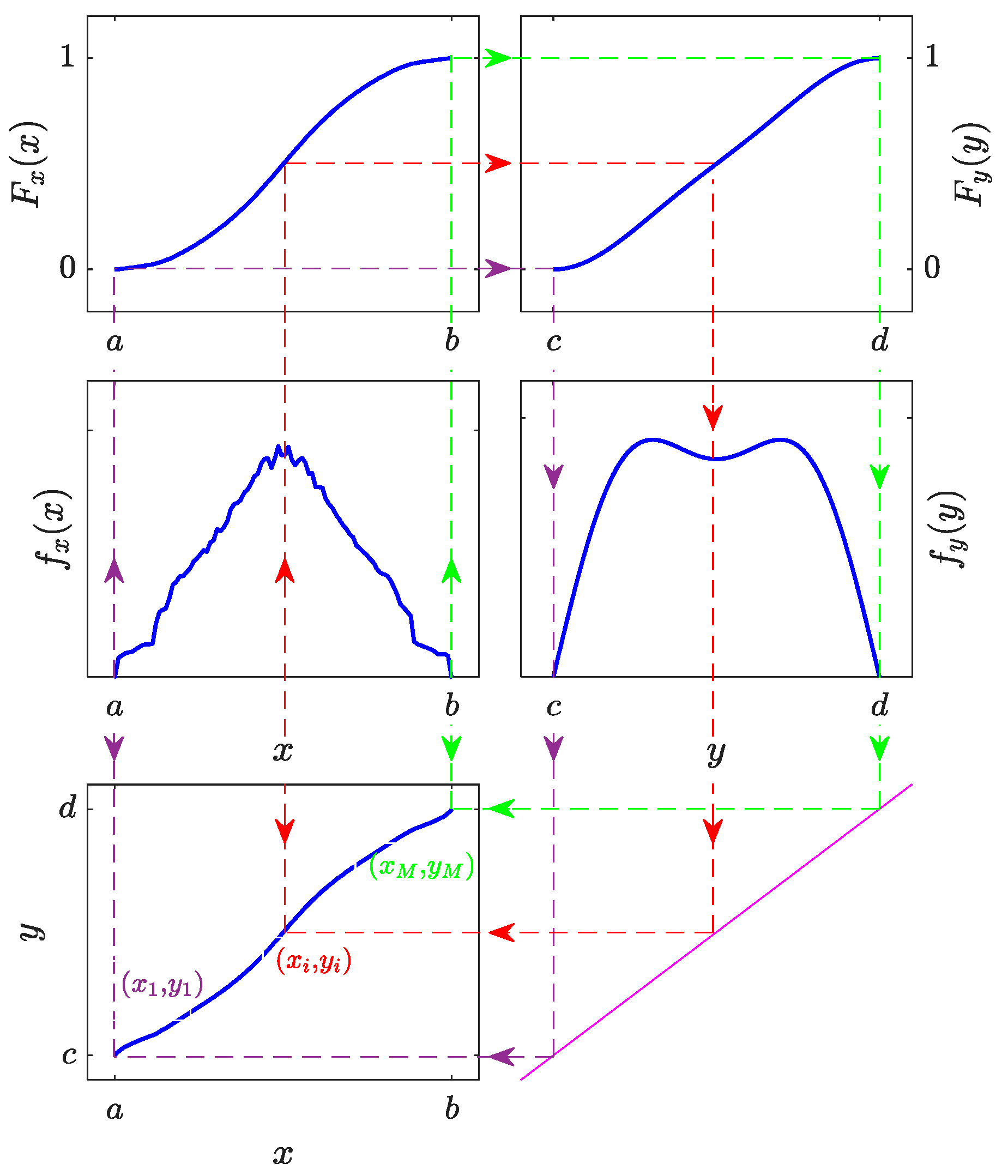
2.2. Algorithm for Probability Distribution Variation Based on Graphical Language
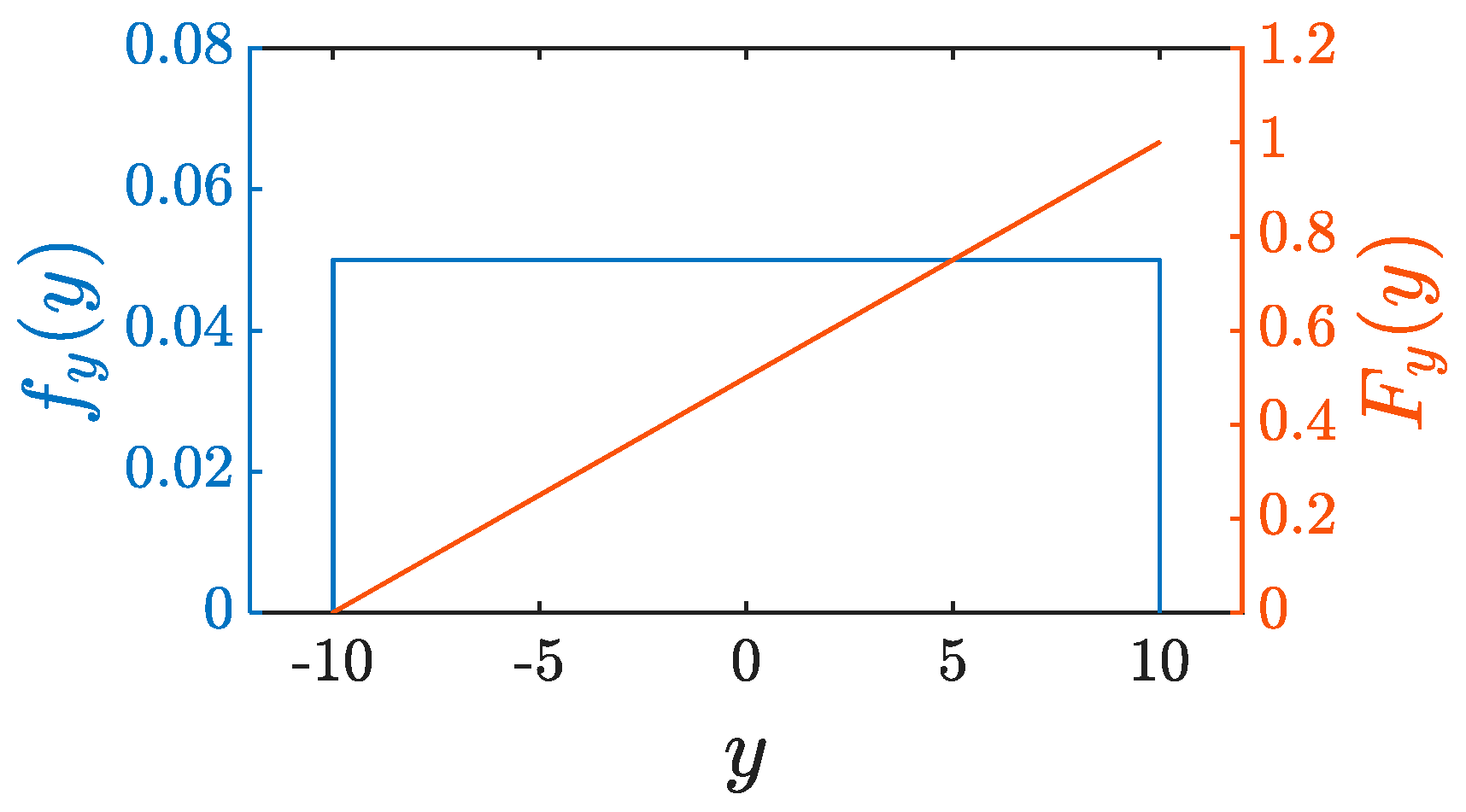
2.3. Implementation of Uniformly Distributed Chaotic Signals
3. Results and Discussion
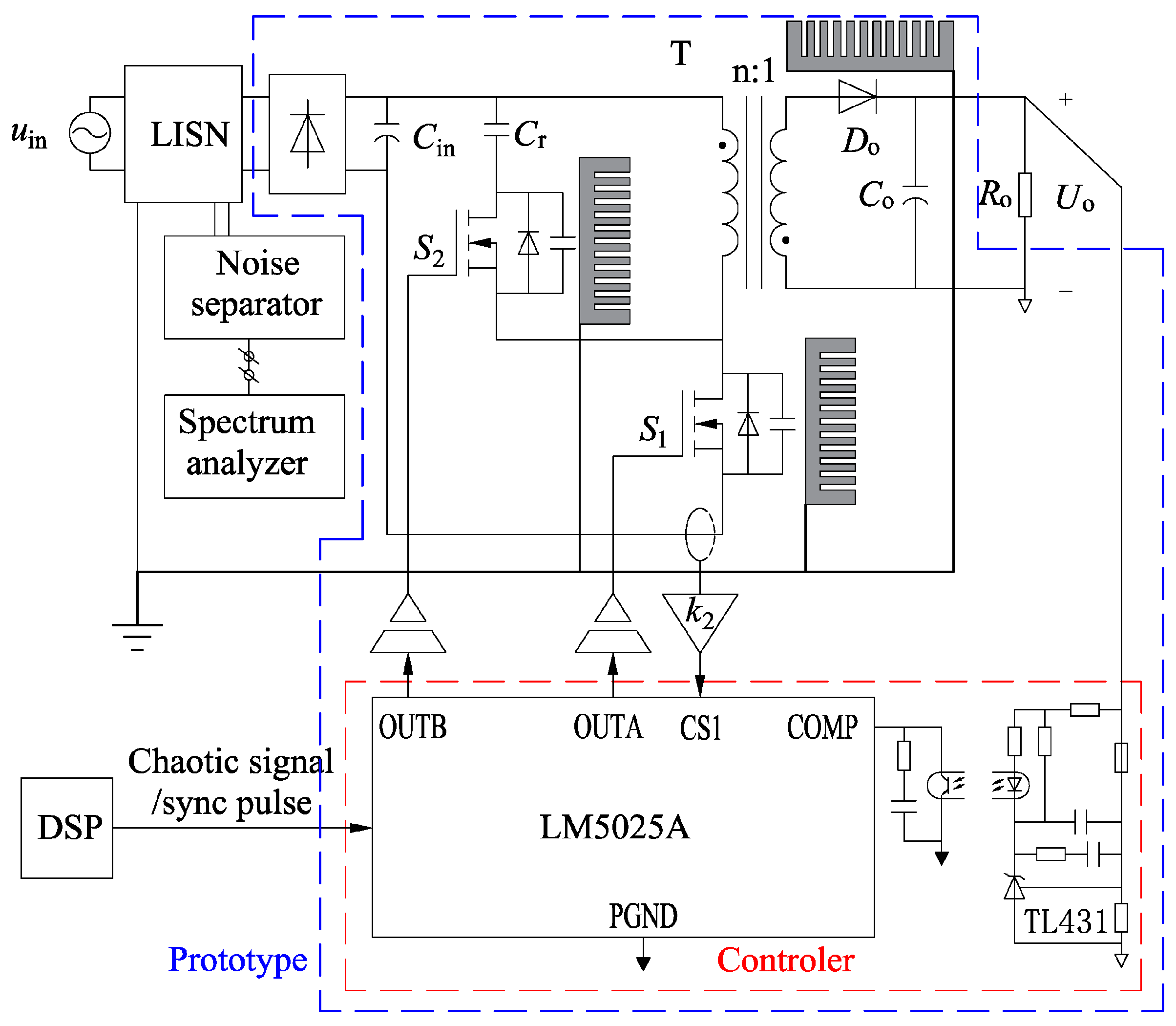
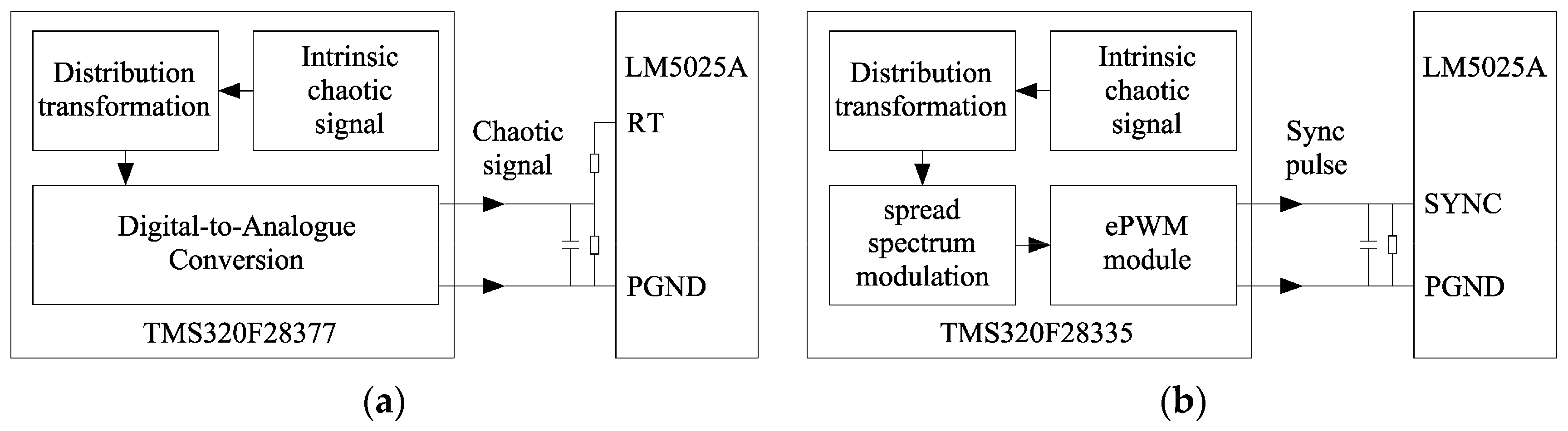
3.1. Construction of Experimental Prototype and Implementation Scheme of Chaotic Spread Spectrum Modulation PWM
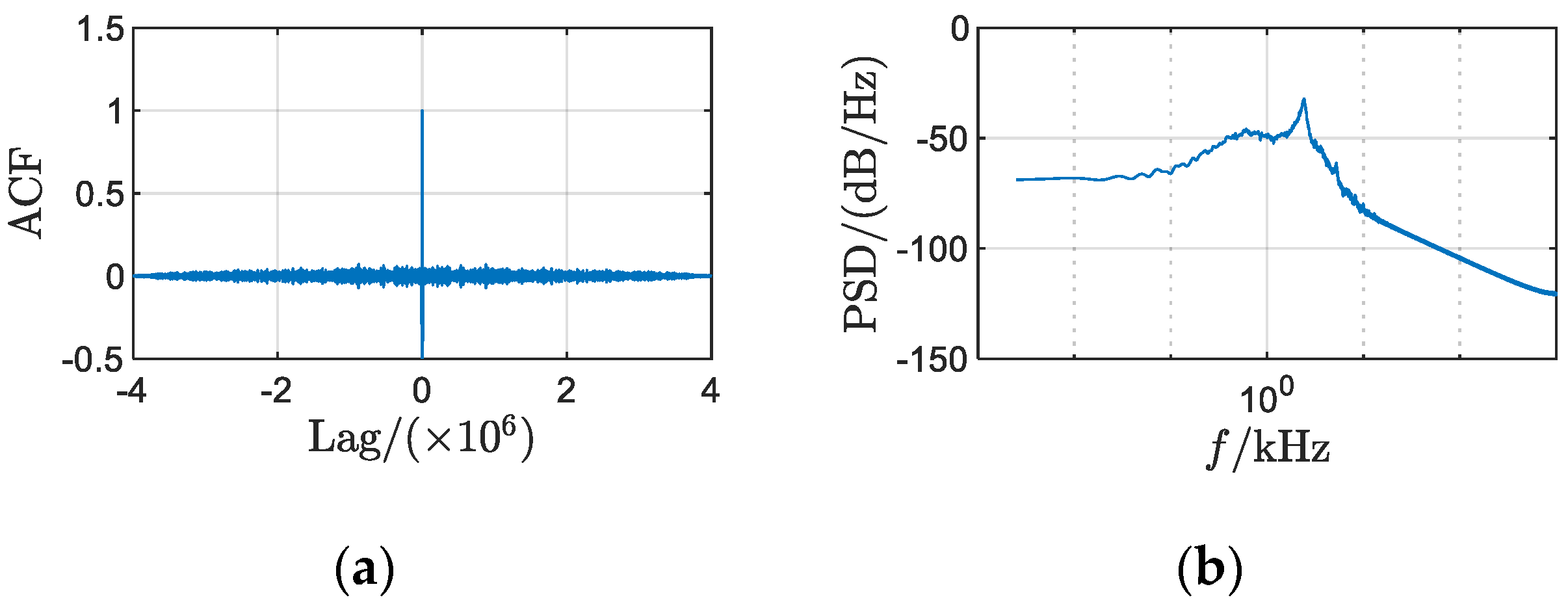
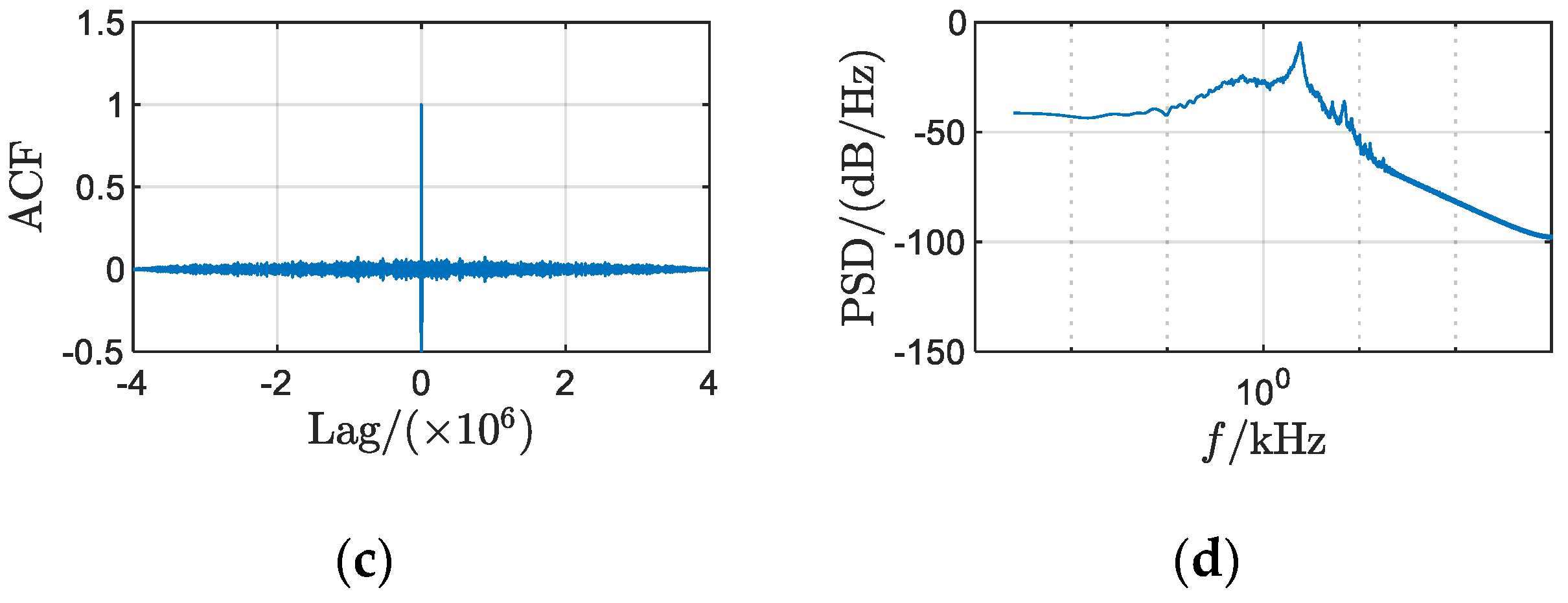
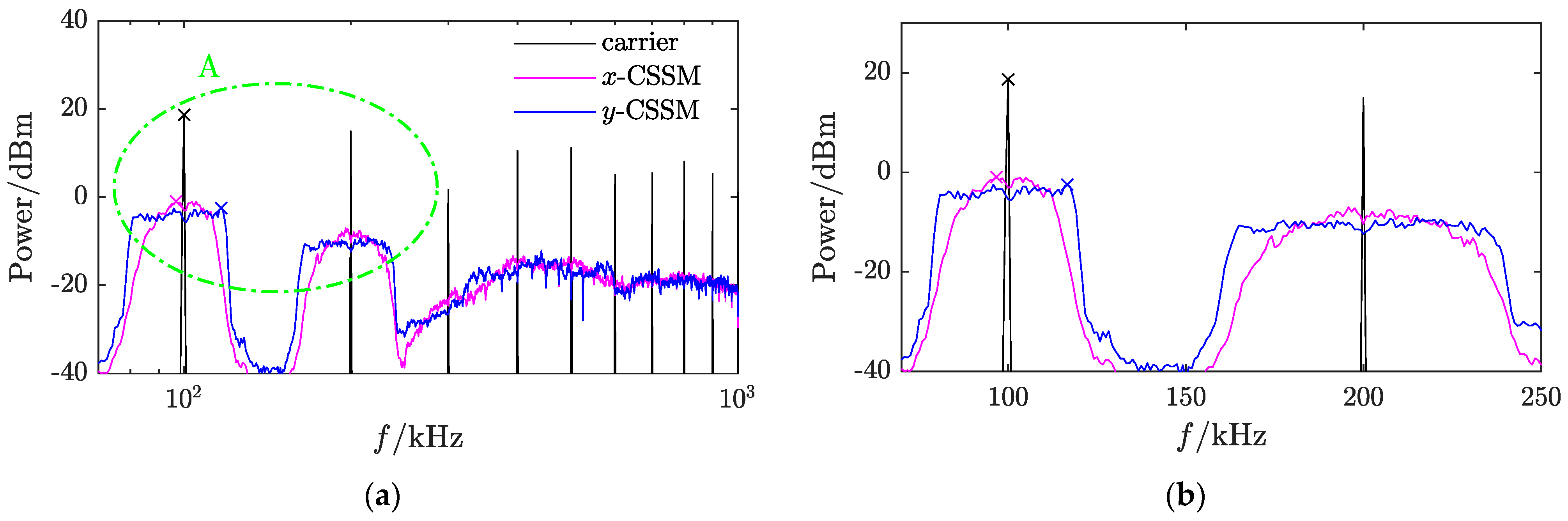
3.2. Uniformly Distributed Chaotic Signal for Uniform Shaping of Conventional PWM Power Spectrum
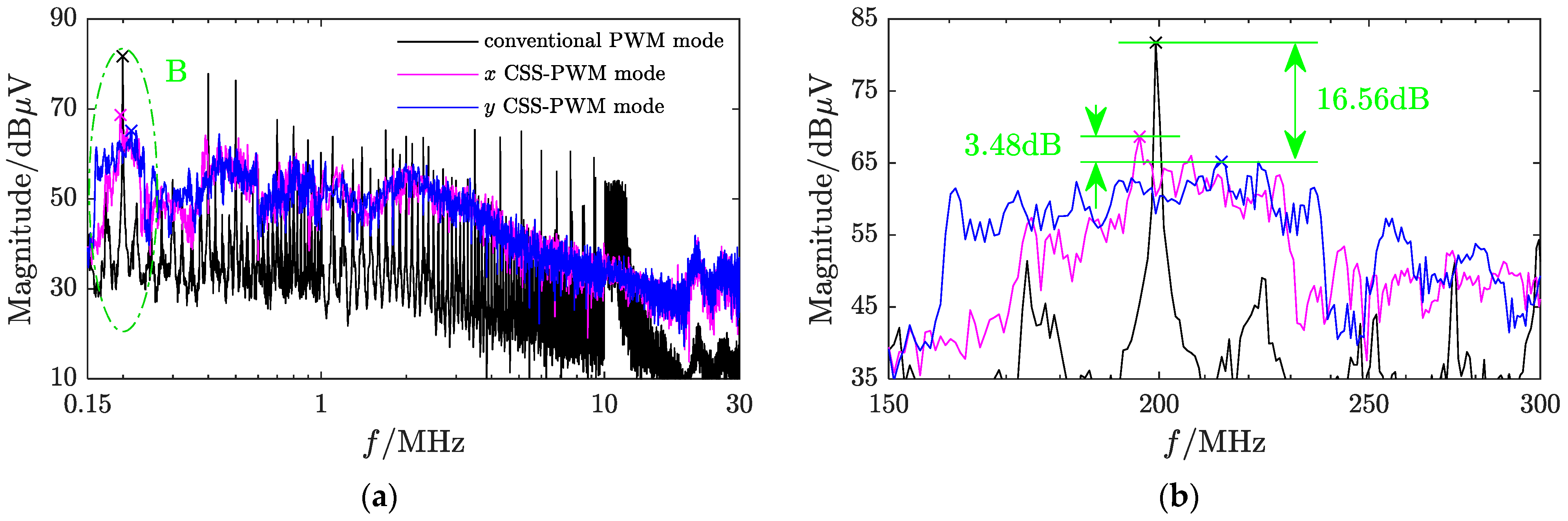
3.3. Uniformly Distributed Chaotic Signal for Uniform Shaping of Power Spectrum of Common-Mode Conducted EMI
4. Conclusions
- (1)
- The issue of obtaining smooth probability density functions for high-dimensional chaotic signals is addressed through the use of kernel density estimation algorithms.
- (2)
- The 2A transformation algorithm based on graphical language is introduced, allowing the transformation of intrinsic chaotic signals into chaotic signals with arbitrary probability distributions. This enables the flexible configuration of chaotic signal probability distribution types, offering feasible solutions for obtaining chaotic signals with specific probability distributions.
- (3)
- Applying the obtained uniformly distributed chaotic signals for chaotic spread spectrum modulation achieves uniform shaping of the power spectrum. Experimental results demonstrate that compared to traditional Chua’s chaotic spread spectrum modulation techniques, the proposed strategy exhibits superior performance in suppressing high-frequency converter common-mode conducted EMI.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| −1.0345 | −1.0136 | −0.9927 | −0.9719 | −0.9510 | −0.9301 | −0.9092 | −0.8883 | −0.8674 | −0.8465 | |
| −0.8257 | −0.8048 | −0.7839 | −0.7630 | −0.7421 | −0.7212 | −0.7003 | −0.6794 | −0.6586 | −0.6377 | |
| −0.6168 | −0.5959 | −0.5750 | −0.5541 | −0.5332 | −0.5124 | −0.4915 | −0.4706 | −0.4497 | −0.4288 | |
| −0.4079 | −0.3870 | −0.3662 | −0.3453 | −0.3244 | −0.3035 | −0.2826 | −0.2617 | −0.2408 | −0.2199 | |
| −0.1991 | −0.1782 | −0.1573 | −0.1364 | −0.1155 | −0.0946 | −0.0737 | −0.0529 | −0.0320 | −0.0111 | |
| 0.0098 | 0.0307 | 0.0516 | 0.0725 | 0.0933 | 0.1142 | 0.1351 | 0.1560 | 0.1769 | 0.1978 | |
| 0.2187 | 0.2395 | 0.2604 | 0.2813 | 0.3022 | 0.3231 | 0.3440 | 0.3649 | 0.3858 | 0.4066 | |
| 0.4275 | 0.4484 | 0.4693 | 0.4902 | 0.5111 | 0.5320 | 0.5528 | 0.5737 | 0.5946 | 0.6155 | |
| 0.6364 | 0.6573 | 0.6782 | 0.6990 | 0.7199 | 0.7408 | 0.7617 | 0.7826 | 0.8035 | 0.8244 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| −10.0000 | −9.9856 | −9.9511 | −9.9132 | −9.8738 | −9.8318 | −9.7866 | −9.7400 | −9.6901 | −9.6374 | |
| −9.5824 | −9.5265 | −9.4600 | −9.3550 | −9.2434 | −9.1292 | −9.0064 | −8.8603 | −8.7031 | −8.5355 | |
| −8.3647 | −8.1874 | −8.0048 | −7.8156 | −7.6175 | −7.4130 | −7.2036 | −6.9892 | −6.7697 | −6.5397 | |
| −6.2994 | −6.0524 | −5.8014 | −5.5429 | −5.2698 | −4.9833 | −4.6915 | −4.3963 | −4.0937 | −3.7777 | |
| −3.4583 | −3.1235 | −2.7815 | −2.4320 | −2.0662 | −1.6889 | −1.3285 | −0.9667 | −0.5894 | −0.2003 | |
| 0.1738 | 0.5621 | 0.9396 | 1.3026 | 1.6635 | 2.0382 | 2.4027 | 2.7535 | 3.0977 | 3.4315 | |
| 3.7520 | 4.0748 | 4.3835 | 4.6801 | 4.9723 | 5.2522 | 5.5229 | 5.7822 | 6.0373 | 6.2875 | |
| 6.5292 | 6.7612 | 6.9822 | 7.1960 | 7.4033 | 7.6069 | 7.8041 | 7.9925 | 8.1758 | 8.3511 | |
| 8.5220 | 8.6891 | 8.8495 | 8.9962 | 9.1223 | 9.2421 | 9.3537 | 9.4588 | 9.5288 | 9.5848 | |
| 9.6394 | 9.6912 | 9.7394 | 9.7877 | 9.8308 | 9.8709 | 9.9096 | 9.9478 | 9.9838 | 10.0000 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0031 | 0.0076 | 0.0086 | 0.0091 | 0.0099 | 0.0109 | 0.0115 | 0.0126 | 0.0136 | 0.0146 | |
| 0.0152 | 0.0185 | 0.0300 | 0.0327 | 0.0344 | 0.0381 | 0.0467 | 0.0518 | 0.0569 | 0.0599 | |
| 0.0643 | 0.0685 | 0.0735 | 0.0799 | 0.0856 | 0.0913 | 0.0974 | 0.1041 | 0.1141 | 0.1250 | |
| 0.1349 | 0.1445 | 0.1572 | 0.1760 | 0.1964 | 0.2138 | 0.2319 | 0.2565 | 0.2908 | 0.3214 | |
| 0.3716 | 0.4233 | 0.4888 | 0.5881 | 0.7130 | 0.8260 | 1.0538 | 1.5070 | 2.4712 | 5.7961 | |
| −13.6799 | −3.1122 | −1.6946 | −1.1749 | −0.9366 | −0.7394 | −0.5988 | −0.5069 | −0.4325 | −0.3707 | |
| −0.3371 | −0.2939 | −0.2594 | −0.2363 | −0.2106 | −0.1904 | −0.1711 | −0.1586 | −0.1471 | −0.1348 | |
| −0.1230 | −0.1116 | −0.1031 | −0.0957 | −0.0901 | −0.0839 | −0.0771 | −0.0722 | −0.0667 | −0.0627 | |
| −0.0593 | −0.0551 | −0.0489 | −0.0407 | −0.0376 | −0.0340 | −0.0312 | −0.0202 | −0.0157 | −0.0149 | |
| −0.0138 | −0.0126 | −0.0123 | −0.0107 | −0.0097 | −0.0092 | −0.0089 | −0.0082 | −0.0036 | −0.0036 |
References
- Dong, Y.; Xu, J.; Nie, Z.; Liu, Y.; Zhu, J. Summary and Prospect of Random Pulse Width Modulation in the Field of Power Transformation. Electr. Mach. Control. Appl. 2021, 48, 1–9. [Google Scholar] [CrossRef]
- Jiang, D.; Shen, Z.; Liu, Z.; Han, X.; Wang, Q.; He, Z. Progress in active mitigation technologies of power electronics noise for electrical propulsion system. Proc. CSEE 2020, 40, 5291–5302. [Google Scholar] [CrossRef]
- Xue, J.; Nie, Z.; Zhu, J.; Zhang, Y.; Li, Y. Restudy on the Random Pulse Width Modulation. Electr. Mach. Control. Appl. 2016, 43, 45–51. [Google Scholar]
- Trzynadlowski, A.M.; Blaabjerg, F.; Pedersen, J.K.; Kirlin, R.L.; Legowski, S. Random pulse width modulation techniques for converter-fed drive systems-a review. IEEE Trans. Ind. Appl. 1994, 30, 1166–1175. [Google Scholar] [CrossRef]
- Morales-Leal, T.; Moreno-Munoz, A.; Ortiz-López, M.A.; Geninatti, S.R.; Quiles-Latorre, F.J. New Random PWM Method at Constant Switching Frequency and Maximum Harmonic Reduction Created with a Flexible FPGA-Based Test Bench. IEEE Access 2023, 11, 19385–19394. [Google Scholar] [CrossRef]
- Stakovic, A.M.; Lev-Ari, H. Randomized modulation in power electronic converters. Proc. IEEE 2002, 90, 782–799. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, S.; Zhang, J.; Yao, Y. Review of Conducted Noise Suppression Method for Power Electronic and Electrical Equipment. Trans. China Electrotech. 2017, 32, 77–86. [Google Scholar] [CrossRef]
- Yang, W.; Chiu, S.; Kuo, C.; Lin, Y.; Lai, Y.; Chen, H.; Ma, Y.; Chen, K.; Lin, Y.; Lin, S.; et al. A True-Random-Number-Based Pseudohysteresis Controller for Buck DC–DC Converter in High-Security Inter-Net-of-Everything Devices. IEEE Trans. Power Electron. 2020, 35, 2969–2978. [Google Scholar] [CrossRef]
- Nguyen, N.; Kaddoum, G.; Pareschi, F.; Rovatti, R.; Setti, G. A fully CMOS true random number generator based on hidden attractor hyperchaotic system. Nonlinear Dyn. 2020, 102, 2887–2904. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, D.B. EMI-Regulated GaN-Based Switching Power Converter with Markov Continuous Random Spread-Spectrum Modulation and One-Cycle on-Time Rebalancing. IEEE J. Solid-State Circuits 2019, 54, 3306–3315. [Google Scholar] [CrossRef]
- Cui, K.; Adrian, V.; Gwee, B.; Chang, J.S. A Noise-Shaped Randomized Modulation for Switched-Mode DC-DC Converters. IEEE Trans. Circuits Syst. I Reg. Pap. 2018, 65, 394–405. [Google Scholar] [CrossRef]
- Ho, E.N.Y.; Mok, P.K.T. Design of PWM Ramp Signal in Voltage-Mode CCM Random Switching Frequency Buck Converter for Conductive EMI Reduction. IEEE Trans. Circuits Syst. I Reg. Pap. 2013, 60, 505–515. [Google Scholar] [CrossRef]
- Ming, X.; Chen, Z.; Zhou, Z.; Zhang, B. An Advanced Spread Spectrum Architecture Using Pseudorandom Modulation to Improve EMI in Class D Amplifier. IEEE Trans. Power Electron. 2011, 26, 638–646. [Google Scholar] [CrossRef]
- Callegari, S.; Setti, G.; Langlois, P.J. A CMOS tailed tent map for the generation of uniformly distributed chaotic sequences. In Proceedings of the 1997 IEEE International Symposium on Circuits and Systems (ISCAS), Hong Kong, China, 12 June 1997. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, B. Experiment and mechanism research of chaotic PWM of converter in EMI suppressing. Proc. CSEE 2007, 27, 114–119. [Google Scholar] [CrossRef]
- Li, H.; Zhang, B. Calculation of invariant probability distribution for chaotic map in DC-DC converter and its application. Proc. CSEE 2005, 25, 54–60. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, B. Quantification descriptions of the chaotic PWM spectrum of the switching converter. Chin. Phys. Soc. 2006, 55, 5667–5673. [Google Scholar] [CrossRef]
- Pareschi, F.; Setti, G.; Rovatti, R.; Frattini, G. Short-term Optimized Spread Spectrum Clock Generator for EMI Reduction in Switching DC/DC Con-verters. IEEE Trans. Circuits Syst. I Reg. Pap. 2014, 61, 3044–3053. [Google Scholar] [CrossRef]
- Pareschi, F.; Setti, G.; Rovatti, R. A 3-GHz Serial ATA Spread-Spectrum Clock Generator Employing a Chaotic PAM Modulation. IEEE Trans. Circuits Syst. I Reg. Pap. 2010, 57, 2577–2587. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, B. Spectrum Characteristics and Spectrum Optimizing Design of Chaotic PWM Based on Invariable Distribution. Acta Electron. Sin. 2007, 35, 2150–2155. [Google Scholar]
- Li, Z.; Qiu, S.; Chen, Y. Experimental study on the suppressing EMI level of DC-DC converter with chaotic map. Proc. CSEE 2006, 26, 76–81. [Google Scholar] [CrossRef]
- Lian, S.; Sun, J.; Wang, Z. A block cipher based on a suitable use of the chaotic standard map. Chaos Solitons Fractals 2005, 26, 117–129. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vision Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Xie, T.; He, X. New color image encryption scheme based on chaos. Appl. Res. Comput. 2013, 30, 318–320. [Google Scholar] [CrossRef]
- Fu, C.; Chen, J.; Zou, H.; Meng, W.; Zhan, Y.; Yu, Y. Chaos-based digital image encryption scheme with an improved diffusion strategy. Opt. Express 2012, 20, 2363–2378. [Google Scholar] [CrossRef] [PubMed]
- Setti, G.; Mazzini, G.; Riccardo, R.; Callegari, S. Statistical modeling of discrete-time chaotic processes-basic finite-dimensional tools and applications. Proc. IEEE 2002, 90, 662–690. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C.L.P. A new 1D chaotic system for image encryption. Signal Process. 2014, 97, 172–182. [Google Scholar] [CrossRef]
- Tang, X.; Xu, Z.; Li, F.; Li, Z.; Liu, L.; Yang, C.; Huang, H.; Chen, L.; Zhang, X. A Physical Layer Security-Enhanced Scheme in CO-OFDM System Based on CIJS Encryption and 3D-LSCM Chaos. J. Light. Technol. 2022, 40, 3567–3575. [Google Scholar] [CrossRef]
- Rovatti, R.; Setti, G.; Callegari, S. Limit properties of folded sums of chaotic trajectories. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 1736–1744. [Google Scholar] [CrossRef]
- Callegari, S.; Rovatti, R.; Setti, G. Chaos-based FM signals: Application and implementation issues. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 1141–1147. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Zhang, L.; Pareschi, F.; Setti, G.; Chen, G. From Chaos to Pseudorandomness: A Case Study on the 2-D Coupled Map Lattice. IEEE Trans. Cybern. 2023, 53, 1324–1334. [Google Scholar] [CrossRef]
- Bauer, J.D.; Graziani, F.R. Statistical closure and the logistic map. Phys. Rev. E 1994, 49, 192–198. [Google Scholar] [CrossRef] [PubMed]
- An, C.; Zhou, T. Generating binary-phase chaotic spread-spectrum sequences and behavior of the sequences. J. Harbin Inst. Technol. 2003, 35, 1117–1120. [Google Scholar]
- Lawnik, M. The approximation of the normal distribution by means of chaotic expression. J. Phys. Conf. Ser. 2014, 490, 12072. [Google Scholar] [CrossRef]
- Eisencraft, M.; Monteiro, L.H.A.; Soriano, D.C. White Gaussian Chaos. IEEE Commun. Lett. 2017, 21, 1719–1722. [Google Scholar] [CrossRef]
- Flores, B.C.; Verdin, B.; Thomas, G.; Ashtari, A. Generation of quasi-normal variables using chaotic maps. Radar Sens. Technol. 1X 2005, 5788, 108–115. [Google Scholar] [CrossRef]
- Balestra, M.; Bellini, A.; Callegari, S.; Rovatti, R.; Setti, G. Chaos-Based Generation of PWM-like Signals for Low-EMI Induction Motor Drives: Analysis and Experimental Results. IEICE Trans. Electron. 2004, E87-C, 66–75. [Google Scholar]
- Callegari, S.; Rovatti, R.; Setti, G. Spectral properties of chaos-based FM signals: Theory and simulation results. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 3–15. [Google Scholar] [CrossRef]
- Fan, W.; Shi, Y.; Chen, Y. A Method for CM EMI Suppression on PFC Converter Using Lossless Snubber with Chaotic Spread Spectrum. Energies 2023, 16, 3583. [Google Scholar] [CrossRef]





| Parameter | Specification or Value |
|---|---|
| Controller | LM5025A |
| Optocoupler | TLP250H |
| Precision Programmable Reference IC | TL431C |
| CS9N90 | |
| SMF5N60 | |
| AIDW10S65C5 | |
| 180 V~235 V alternating current | |
| 15 V direct current | |
| 45 W | |
| transformer magnetic core | PQ3535 |
| 509.02 μH | |
| 9.74 μH | |
| 0.1 μF | |
| voltage sensor | LV25-P |
| current sensor | FC-SCT4.6-1:100 |
| 100 μF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Liu, B.; Chen, B.; Liang, Q.; Zhang, Y.; Chen, Y. Research on the Strategy for the Flexible Configuration of Chaotic Signal Probability Distribution and Its Application. Appl. Sci. 2024, 14, 5181. https://doi.org/10.3390/app14125181
Yang Z, Liu B, Chen B, Liang Q, Zhang Y, Chen Y. Research on the Strategy for the Flexible Configuration of Chaotic Signal Probability Distribution and Its Application. Applied Sciences. 2024; 14(12):5181. https://doi.org/10.3390/app14125181
Chicago/Turabian StyleYang, Zaixue, Bin Liu, Bing Chen, Qian Liang, Yao Zhang, and Yanming Chen. 2024. "Research on the Strategy for the Flexible Configuration of Chaotic Signal Probability Distribution and Its Application" Applied Sciences 14, no. 12: 5181. https://doi.org/10.3390/app14125181
APA StyleYang, Z., Liu, B., Chen, B., Liang, Q., Zhang, Y., & Chen, Y. (2024). Research on the Strategy for the Flexible Configuration of Chaotic Signal Probability Distribution and Its Application. Applied Sciences, 14(12), 5181. https://doi.org/10.3390/app14125181






