Solving Optimal Electric Vehicle Charger Deployment Problem
Abstract
1. Introduction
- Building a comprehensive mathematical framework accommodating the particular complexity,
- Demonstrating our numerical computational framework for solving the facility location problem (FLP) representing the optimal location;
- Laying out an extensive comparative study among the optimization solving techniques as an effort to find the most efficient solver;
- Applying the findings to two real-world case studies representing an average and high density of EVs.
2. Related Work
2.1. Problem Formulation Approaches
2.1.1. Facility Location Problem (FLP)
2.1.2. Distance Optimization
2.1.3. Weight Assignment Techniques
2.1.4. Machine Learning Techniques
2.2. Solving Techniques
3. Problem Formulation
3.1. Spatial Setup
3.2. Formulation to Capacitated FLP
- i and j are indexes for an EV charging facility and a demanding area (or, equivalently, a customer), respectively.
- gives the variable cost to obtain the electricity supplied to serve customer j.
- gauges the demand from customer j.
- quantifies the fraction of the demand made by customer j and fulfilled by facility i.
- indicates whether facility i opens or not.
- denotes the sunken cost (also known as “fixed” cost) of opening a charging facility i.
- defines the equity achieved at customer j via service from facility i.
- and indicate the capacity of facility i and the required minimum capacity of any facility, respectively, both in the unit of kWh.
3.3. Unique Challenges
- C1: Large search spaces for domain and other variables;
- C2: Inexistence of polynomial-time numerical solving. techniques
4. Solving Techniques Development
4.1. Unique Challenges and Proposed Approaches
4.2. Comparison among Solving Techniques
4.3. Alternative Techniques
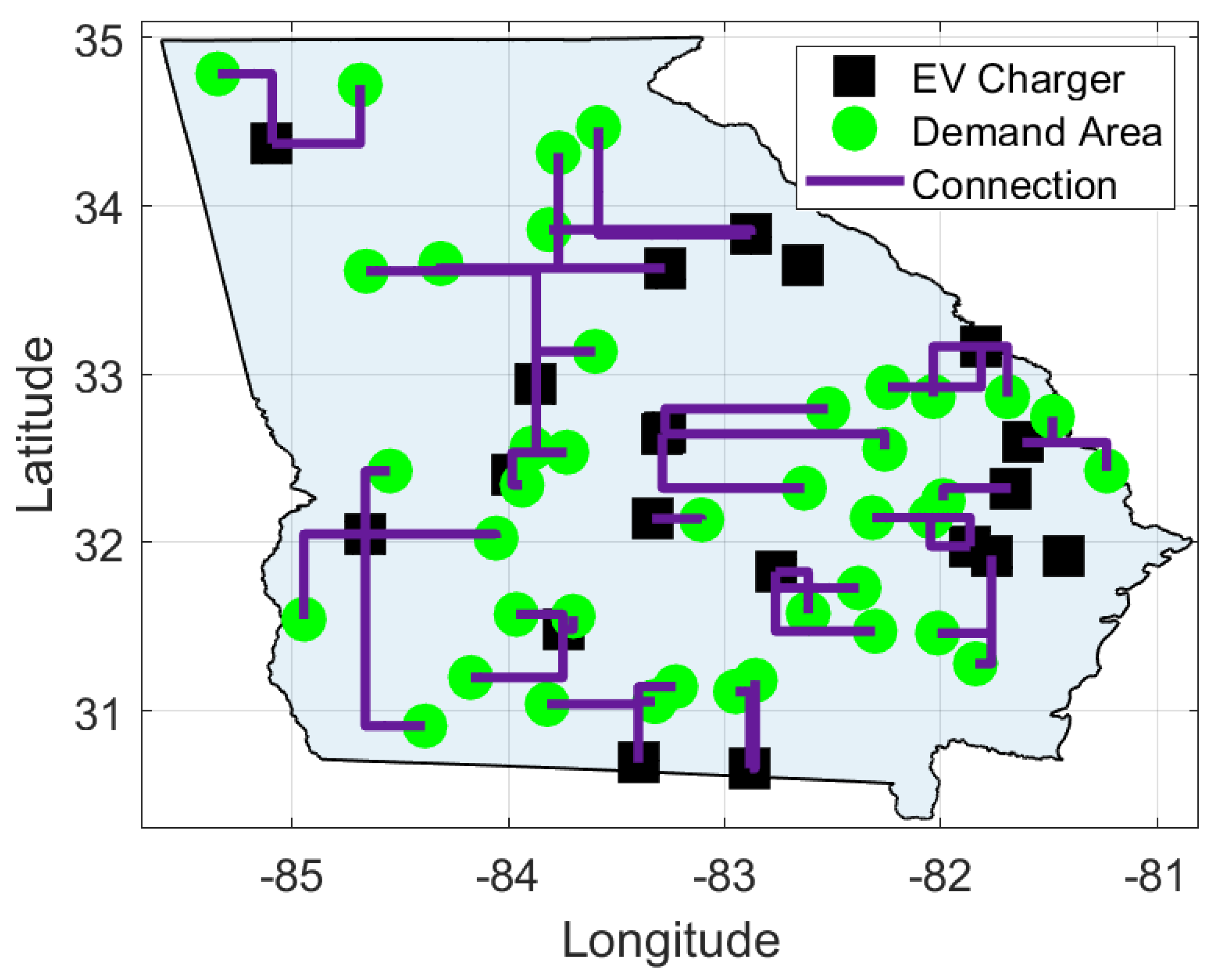
5. Case Study 1: Region with Average EV Density
5.1. Case-Specific Refinement of Solving Method
5.2. Results and Discussion
| Algorithm 1 SA implemented in this work |
|
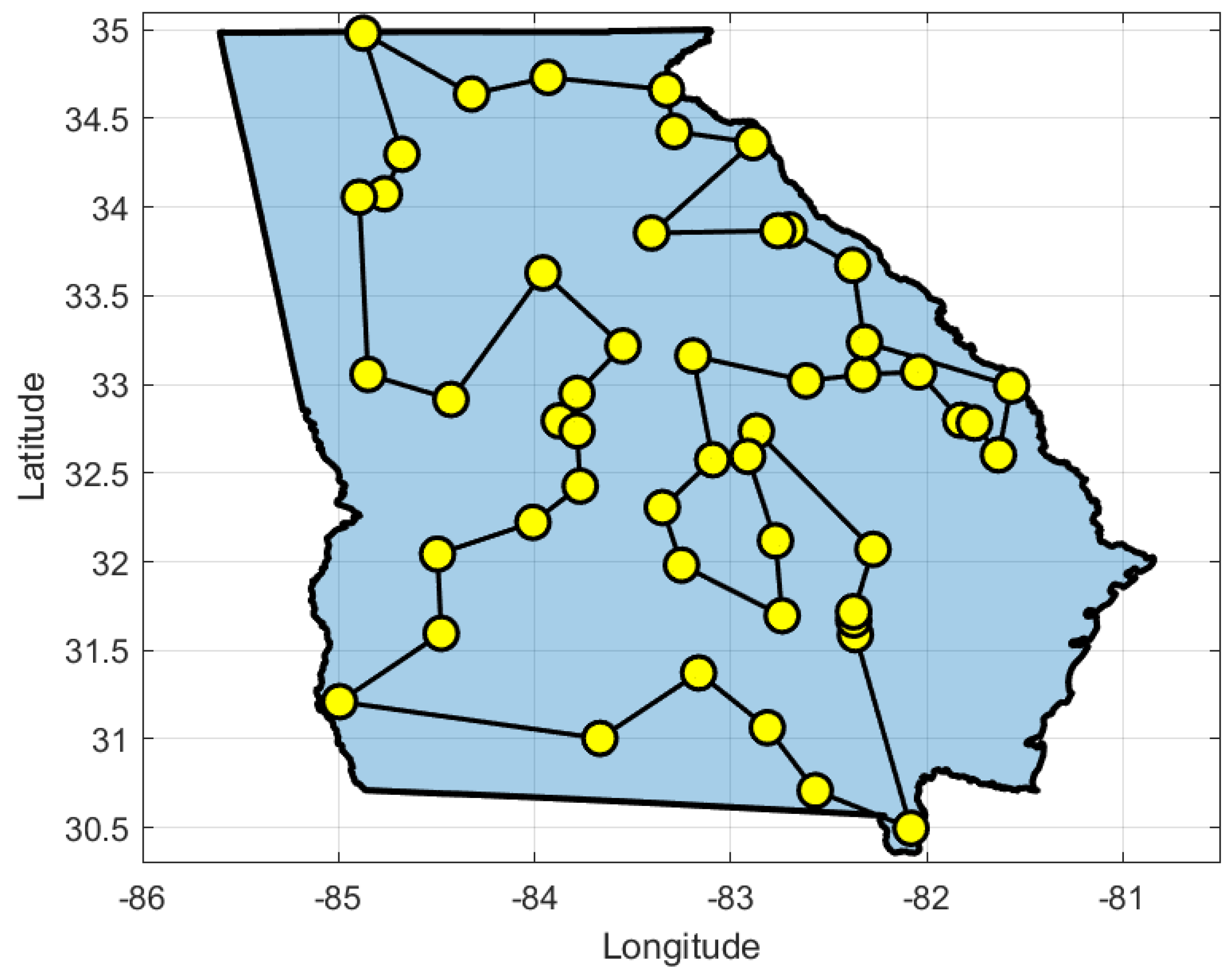
6. Case Study 2: Region with High EV Density
6.1. Case-Specific Refinement of Solving Method
6.1.1. Data Collection and Preprocessing
6.1.2. Data Integration
6.1.3. Training Methods
- Data Preparation: The collected and merged dataset undergoes preprocessing to ensure its suitability for training, including handling missing values, data normalization, and feature engineering.
- Training Process: Each selected model is trained using the prepared dataset, which is divided into training and validation sets. Performance evaluation metrics such as accuracy, precision, recall, and F1 score are utilized to assess the model’s performance during training.
- Model Evaluation: After training, the models are evaluated using the validation set to assess their predictive capabilities. The evaluation metrics are used to compare the models’ performance and identify the model with the highest accuracy or other desired performance metrics.
- Model Selection: Based on the evaluation results, the model demonstrating the best performance is selected as the final machine learning model for the site selection task.
6.2. Results and Discussions
- Installation criteria differ between DC fast chargers and level-2 chargers. Significant differences in consistency are observed when training separately based on each charging station type or when training with both types together. Consequently, it can be concluded that chargers have been installed at locations that meet their respective criteria for both DC fast chargers and level-2 chargers.
- Non-uniform distribution of reference data does not significantly affect training results. There is no significant difference in consistency between training based on non-uniformly distributed chargers and training based on grid points uniformly distributed at regular intervals. Thus, it can be concluded that the non-uniform distribution of data does not impact the training results.
- Buffer size influences data consistency. Decreasing the buffer size results in increased consistency. The reason for the decrease in consistency at buffer sizes below 125 m is that the polygon data used for learning is 250 m × 250 m grid data, resulting in buffers that do not contain data from the 125 m radius buffer size. This problem can be solved by using smaller grid data than 250 m × 250 m grid data during data preprocessing. In conclusion, this result shows that larger buffer sizes increase data redundancy and affect consistency.
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gersdorf, T.; Hensley, R.; Hertzke, P.; Schaufuss, P.; Tschiesner, A. The Road Ahead for E-Mobility; McKinsey: Chicago, IL, USA, 2020. [Google Scholar]
- The White House. Fact sheet: The Biden-Harris electric vehicle charging action plan. In Statements and Releases; The White House: Washington, DC, USA, 2021. [Google Scholar]
- United States Department of Transportation. Biden-Harris Administration Announces $1.5 Billion Available through the 2023 RAISE Grant Program; United States Department of Transportation: Washington, DC, USA, 2022.
- Mitchell, R. U.S. government will pay Tesla to open its charger network to non-Tesla EVs. Los Angeles Times, 15 February 2023. [Google Scholar]
- Newburger, E. All 50 States Get Green Light to Build EV Charging Stations Covering 75,000 Miles of Highways; CNBC: Englewood Cliffs, NJ, USA, 2022. [Google Scholar]
- LNG2019. The Average Distance between Gas Stations in the United States. November 2022. Available online: https://www.linkedin.com/pulse/how-many-gas-stations-united-states-timothy-ohagan/ (accessed on 1 May 2024).
- Bauer, G.; Hsu, C.; Lutsey, N. When Might Lower-Income Drivers Benefit from Electric Vehicles? Quantifying the Economic Equity Implications of Electric Vehicle Adoption; ICCT Working Paper; International Council on Clean Transportation: Washington, DC, USA, 2021. [Google Scholar]
- Moghaddam, V.; Ahmad, I.; Habibi, D.; Masoum, M. Dispatch management of portable charging stations in electric vehicle networks. ETransportation 2021, 8, 100112. [Google Scholar] [CrossRef]
- Onat, N.; Kucukvar, M.; Aboushaqrah, N.; Jabbar, R. How sustainable is electric mobility? A comprehensive sustainability assessment approach for the case of Qatar. Appl. Energy 2019, 250, 461–477. [Google Scholar] [CrossRef]
- Qiao, B.; Liu, J. Multi-objective dynamic economic emission dispatch based on electric vehicles and wind power integrated system using differential evolution algorithm. Renew. Energy 2020, 154, 316–336. [Google Scholar] [CrossRef]
- Jakob, K.; Pruzan, P. The simple plant location problem: Survey and synthesis. Eur. J. Oper. Res. 1983, 12, 41. [Google Scholar]
- Ayazi, S.; Askarzadeh, A. Finding optimal path of feeder routing problem in power distribution network by an efficient and new methodology. Int. Trans. Elect. Energy Syst. 2021, 31, e13196. [Google Scholar] [CrossRef]
- Floudas, C.; Lin, X. Mixed integer linear programming in process scheduling: Modeling, algorithms, and applications. Ann. Operat. Res. 2005, 139, 131–162. [Google Scholar] [CrossRef]
- Shen, X.; Shahidehpour, M.; Zhu, S.; Han, Y.; Zheng, J. Multi-stage planning of active distribution networks considering the co-optimization of operation strategies. IEEE Trans. Smart Grid 2016, 9, 1425–1433. [Google Scholar] [CrossRef]
- Kim, K.; Goo, Y. Optimizing fast EV charging infrastructure location with traffic flow data. Innov. Stud. 2020, 15, 61–91. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.; Kim, S. A study to determine the optimized location for fast electric vehicle charging station considering charging demand in seoul. J. Korea Inst. Intell. Transp. Syst. 2022, 21. [Google Scholar] [CrossRef]
- Yun, C. The case study of priority installation area of electric vehicle charging infrastructure using bigdata standard reference analysis model. Proc. Symp. Korean Inst. Commun. Inform. Sci. 2019, 23–26. [Google Scholar]
- Jo, J.; Kim, S. A Study on the optimal location selection for hydrogen refueling stations on a highway using machine learning. J. Cadastre Land InformatiX 2021, 51, 83–106. [Google Scholar]
- Hernandez, A.; Perez, M.; Gupta, S.; Muntes-Mulero, V. Using machine learning to optimize parallelism in big data applications. Future Gener. Comput. Syst. 2018, 86, 1076–1092. [Google Scholar] [CrossRef]
- Klotz, E.; Newman, A. Practical guidelines for solving difficult mixed integer linear programs. Surv. Operat. Res. Manag. Sci. 2013, 18, 18–32. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; Rashad, H.; Zaied, A. A comprehensive review of quadratic assignment problem: Variants, hybrids and applications. J. Ambient Intell. Human Comput. 2018. [Google Scholar] [CrossRef]
- Zhang, H.; Beltran-Royo, C.; Ma, L. Solving the quadratic assignment problem by means of general purpose mixed integer linear programming solvers. Ann. Operat. Res. 2013, 207, 261–278. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Bianchi, L.; Dorigo, M.; Gambardella, L.; Gutjahr, W. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2008, 8, 239–287. [Google Scholar] [CrossRef]
- Drezner, Z. The extended concentric tabu for the quadratic assignment problem. Eur. J. Operat. Res. 2005, 160, 416–422. [Google Scholar] [CrossRef]
- Misevicius, A. An implementation of the iterated tabu search algorithm for the quadratic assignment problem. Operat. Res. Spectrum 2012, 34, 665–690. [Google Scholar] [CrossRef]
- Drezner, Z. Compounded genetic algorithms for the quadratic assignment problem. Operat. Res. Lett. 2005, 33, 475–480. [Google Scholar] [CrossRef]
- Misevicius, A. An improved hybrid optimization algorithm for the quadratic assignment problem. Math. Model. Anal. 2004, 9, 149–168. [Google Scholar] [CrossRef]
- Talbi, E.; Roux, O.; Fonlupt, C.; Robillard, D. Parallel ant colonies for the quadratic assignment problem. Future Gener. Comput. Syst. 2001, 17, 441–449. [Google Scholar] [CrossRef]
- Benlic, U.; Hao, J. Memetic search for the quadratic assignment problem. Expert Syst. Appl. 2015, 42, 584–595. [Google Scholar] [CrossRef]
- Gini, C. Variability and mutability. J. Roy. Statist. Soc. 1913, 76, 476–477. [Google Scholar]
- Dai, L.; Jia, Y.; Liang, L.; Chang, Z. Metric and control of system fairness in heterogeneous networks. In Proceedings of the 2017 23rd Asia-Pacific Conference on Communications (APCC), Perth, Australia, 11–13 December 2017. [Google Scholar]
- Williams, D. Feds Approve Georgia DOT Plan for EV Charging Stations; Georgia Public Broadcasting: Atlanta, GA, USA, 2022. [Google Scholar]
- Nicholas, M. Estimating Electric Vehicle Charging Infrastructure Costs across Major US Metropolitan Areas; Working Paper 2019-14; ICCT: Washington, DC, USA, 2019. [Google Scholar]
- Kleinert, T.; Labbe, M.; Ljubic, I.; Schmidt, M. A survey on mixed-integer programming techniques in bilevel optimization. EURO J. Comput. Optim. 2021, 9, 100007. [Google Scholar] [CrossRef]
- Deng, X.; Lv, T. Power system planning with increasing variable renewable energy: A review of optimization models. J. Clean. Prod. 2020, 246, 118962. [Google Scholar] [CrossRef]
- Schenker, C.; Cohen, J.; Acar, E. A flexible optimization framework for regularized matrix-tensor factorizations with linear couplings. IEEE J. Sel. Topics Signal Process. 2020, 15, 506–521. [Google Scholar] [CrossRef]
- Burkard, R.; Fortuna, T.; Hurkens, C. Makespan minimization for chemical batch processes using non-uniform time grids. Comput. Chem. Eng. 2002, 26, 1321–1332. [Google Scholar] [CrossRef]
- Asghari, M.; Fathollahi-Fard, A.; Al-e-hashem, S.M.; Dulebenets, M. Transformation and linearization techniques in optimization: A state-of-the-art survey. Mathematics 2022, 10, 283. [Google Scholar] [CrossRef]
- Hardman, S.; Fleming, K.; Khare, E.; Ramadan, M. A perspective on equity in the transition to electric vehicle. MIT Sci. Policy Rev. 2021, 2, 46–54. [Google Scholar] [CrossRef]
- Mandi, J.; Stuckey, P.; Guns, T. Smart predict-and-optimize for hard combinatorial optimization problems. Proc. AAAI Conf. Artificial Intell. 2020, 34, 1603–1610. [Google Scholar] [CrossRef]
- Baluja, S.; Davies, S. Using Optimal Dependency-Trees for Combinatorial Optimization: Learning the Structure of the Search Space; Carnegie-Mellon University: Pittsburgh, PA, USA, 1997. [Google Scholar]
- Hyde, K.; Maier, H.; Colby, C. A distance-based uncertainty analysis approach to multi-criteria decision analysis for water resource decision making. J. Environ. Manag. 2005, 77, 278–290. [Google Scholar] [CrossRef]
- Estalaki, W.M.; Kerachian, R.; Nikoo, M. Developing water quality management policies for the Chitgar urban lake: Application of fuzzy social choice and evidential reasoning methods. Environ. Earth Sci. 2016, 75, 1–16. [Google Scholar] [CrossRef]
- Madani, K.; Read, L.; Shalikarian, L. Voting under uncertainty: A stochastic framework for analyzing group decision-making problems. Water Resour. Manag. 2014, 28, 1839–1856. [Google Scholar] [CrossRef]
- Fowler, R.; Paterson, M.; Tanimoto, S. Optimal packing and covering in the plane are NP-complete. Inform. Proc. Lett. 1981, 12, 133–137. [Google Scholar] [CrossRef]
- Megiddo, N.; Tamir, A. On the complexity of locating linear facilities in the plane. Operat. Res. Lett. 1993, 1, 194–197. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C., Jr.; Vecchi, M. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Clausen, J.; Perregaard, M. Solving large quadratic assignment problems in parallel. Comput. Opt. Appl. 1997, 8, 111–127. [Google Scholar] [CrossRef]
- Luong, T.; Melab, N.; Talbi, E. GPU computing for parallel local search metaheuristic algorithms. IEEE Trans. Comput. 2011, 62, 173–185. [Google Scholar] [CrossRef]
- Sonuc, E.; Sen, B.; Bayir, S. A cooperative GPU-based parallel multistart simulated annealing algorithm for quadratic assignment problem. Eng. Sci. Technol., Int. J. 2018, 21, 843–849. [Google Scholar] [CrossRef]
- Website of NVIDIA’s CUDA Zone. Available online: https://developer.nvidia.com/cuda-zone (accessed on 10 October 2023).
- Zhu, W.; Curry, J.; Marquez, A. SIMD tabu search for the quadratic assignment problem with graphics hardware acceleration. Int. J. Prod. Res. 2010, 48, 1035–1047. [Google Scholar] [CrossRef]
- Abdelkafi, O.; Derbel, B.; Liefooghe, A. A parallel tabu search for the large-scale quadratic assignment problem. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019. [Google Scholar]
- Ghosh, D.; Goldengorin, B.; Sierksma, G. Data correcting algorithms in combinatorial optimization. In Handbook Combinatorial Optimization; Springer: Boston, MA, USA, 2004; Volume 5, pp. 1–53. [Google Scholar]
- Dantzig, G. Linear Programming and Extensions, 6th ed.; Princeton University Press: Princeton, NJ, USA, 1974; pp. 545–547. [Google Scholar]
- Rastrigin, L. Systems of Extremal Control; Nauka: Moscow, Russia, 1974. [Google Scholar]
- Katoch, S.; Chauhan, S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools App. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Dupanloup, I.; Schneider, S.; Excoffier, L. A simulated annealing approach to define the genetic structure of populations. Mol. Ecol. 2002, 11, 2571–2581. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Website of MATLAB Parallel Server. Available online: https://www.mathworks.com/products/matlab-parallel-server.html (accessed on 1 February 2023).
- Website of Georgia State Government. Available online: https://www.georgia.org/mobility-infrastructure#/analyze?show_map=true®ion=US-GA (accessed on 12 May 2023).
- Power Planning Department Demand Forecast Team. Electric Vehicle and Charger Supply and Use Analysis; Korea Power Exchange: Naju-si, Republic of Korea, 2021. [Google Scholar]
- Kang, C.; Jeon, S. A Study on Establishment of Proper Installation Criteria of Electric Vehicle Charging Station in Gyeonggi-Do; Gyeonggi Research Institute: Suwon, Republic of Korea, 2017. [Google Scholar]
- Website of QGIS 3.36. Available online: https://www.qgis.org/en/site/ (accessed on 12 October 2023).
- Jeon, H.; Park, J.; Kim, H. A Study on the optimum location selection of electric vehicle fast charging station using GIS. KSCE 2022 Conv. 2022, 558–562. [Google Scholar]
- Charbuty, B.; Abdulazeez, A. Classification based on decision tree algorithm for machine learning. J. Appl. Sci. Technol. Trends 2021, 2, 20–28. [Google Scholar] [CrossRef]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their App. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 5–32. [Google Scholar] [CrossRef]








| Literature | Contribution |
|---|---|
| FLP | Formulation into MINLP for various real-world problems |
| Distance Optimization | Stochastic analyses for location selection |
| Weight Assignment Techniques | Demand prediction by assigning weights to data |
| Machine Learning Techniques | More efficient weight assignment via priority prediction |
| Solving Techniques | Exact or heuristic approaches to solve NP-hard problems |
| This Paper | Comprehensive feasibility study encompassing the aforementioned numerical techniques |
| Solver | ⋯ | Objective Value | Number of Iterations | |||
|---|---|---|---|---|---|---|
| Integer Linear Programming | ⋯ | 0 | 0 | |||
| Pattern Search | 0 | 0 | ⋯ | 0 | 0 | 204 |
| Genetic Algorithm | −0.062657 | 0.042974 | ⋯ | −0.041941 | 1.4801 | 3907 |
| Particle Swarm | ⋯ | 4320 | ||||
| Simulated Annealing | −1.99 | ⋯ | 0.00018799 | 3.9798 | 3008 | |
| Surrogate Optimization | 0.99678 | 1.9937 | ⋯ | 1.9832 | 8.9671 | 200 |
| Model Name | Decision Tree | Support Vector Machine | Random Forest |
|---|---|---|---|
| Consistency | 0.6583 | 0.4295 | 0.7580 |
| Precision | 0.6712 | 0.1845 | 0.7580 |
| Recall | 0.6583 | 0.4295 | 0.7580 |
| F1-Score | 0.6593 | 0.2581 | 0.7509 |
| Setting Condition | Buffer Size | Consistency | |
|---|---|---|---|
| Baseline | Public DC fast chargers and random point | 1.13 km | 0.7580 |
| a. Charging Station Type | Public level-2 chargers and random point | 1.13 km | 0.7678 |
| Public DC fast chargers and public level-2 chargers and random point | 1.13 km | 0.6284 | |
| b. Uniform Distribution of Reference Data | Center point of grid data | 1.13 km | 0.7649 |
| c. Buffer size | Public DC fast chargers and random point | 700 m | 0.8176 |
| 600 m | 0.8355 | ||
| 500 m | 0.8611 | ||
| 400 m | 0.8743 | ||
| 300 m | 0.9003 | ||
| 200 m | 0.9182 | ||
| 150 m | 0.9348 | ||
| 125 m | 0.9395 | ||
| 100 m | 0.9293 | ||
| 50 m | 0.8969 |
| Data | Variable Importance [%] |
|---|---|
| POI | 16.9264 |
| Surface | 12.9745 |
| Building0 | 11.3435 |
| Work_Population | 9.4463 |
| Building3 | 8.1137 |
| Traffic | 7.3983 |
| Building1 | 6.768 |
| Flow_Population | 5.7931 |
| Car | 5.4492 |
| EV_Car | 5.3769 |
| Parking | 4.2025 |
| Tour | 3.563 |
| Building2 | 2.6447 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Jeong, Y.; Nam, J.-W. Solving Optimal Electric Vehicle Charger Deployment Problem. Appl. Sci. 2024, 14, 5092. https://doi.org/10.3390/app14125092
Kim S, Jeong Y, Nam J-W. Solving Optimal Electric Vehicle Charger Deployment Problem. Applied Sciences. 2024; 14(12):5092. https://doi.org/10.3390/app14125092
Chicago/Turabian StyleKim, Seungmo, Yeonho Jeong, and Jae-Won Nam. 2024. "Solving Optimal Electric Vehicle Charger Deployment Problem" Applied Sciences 14, no. 12: 5092. https://doi.org/10.3390/app14125092
APA StyleKim, S., Jeong, Y., & Nam, J.-W. (2024). Solving Optimal Electric Vehicle Charger Deployment Problem. Applied Sciences, 14(12), 5092. https://doi.org/10.3390/app14125092







