Application of a Novel Weighted Essentially Non-Oscillatory Scheme for Reynolds-Averaged Stress Model and Reynolds-Averaged Stress Model/Large Eddy Simulation (RANS/LES) Coupled Simulations in Turbomachinery Flows
Abstract
Featured Application
Abstract
1. Introduction
- The computational cost is very high, and the calculation process is complex.
- The optimal (linear) weights depend on the geometry of the mesh and may become negative in some cases, meaning they lack robustness.
- The drawbacks become more pronounced with an increase in spatial dimension.
2. WENO-ZQ Schemes
- Choose the big central spatial stencil and the other two smaller stencils and to reconstruct the polynomials , , and . Additionally, the generalized expression for the reconstructed polynomial on nonuniform meshes provided by Shu [25] is adopted in this paper.
- Compute the smoothness indicators , which are obtained through a multiple of the local grid spacing and the difference in polynomial values at adjacent points:
- Calculate the nonlinear weights based on the linear weights and the smoothness indicators. An adaptive formula for is written based on the difference between , , and as follows:The nonlinear weights , l = 1, 2, 3 in the expression are then expressed aswhere represents the positive linear weights, with the only requirement being that + + = 1 (). Here, is a small positive number to avoid the denominator becoming zero.
- The final reconstruction formulation of conservative values at the point of the target cell is given by .
- Choose the big spatial stencil and the other three equidistant stencils ,, and to reconstruct the polynomials .
- Compute the linear weights based on the polynomials as follows:are linear weights in the WENO-JS5 scheme. In a uniform grid, and .
- Compute the smoothness indicators based on Formula (4):
- Calculate the nonlinear weights based on the linear weights and the smoothness indicators.
- The final reconstruction formulation of conservative values at the point of the target cell is given by
3. Classic Numerical Scheme Test Cases
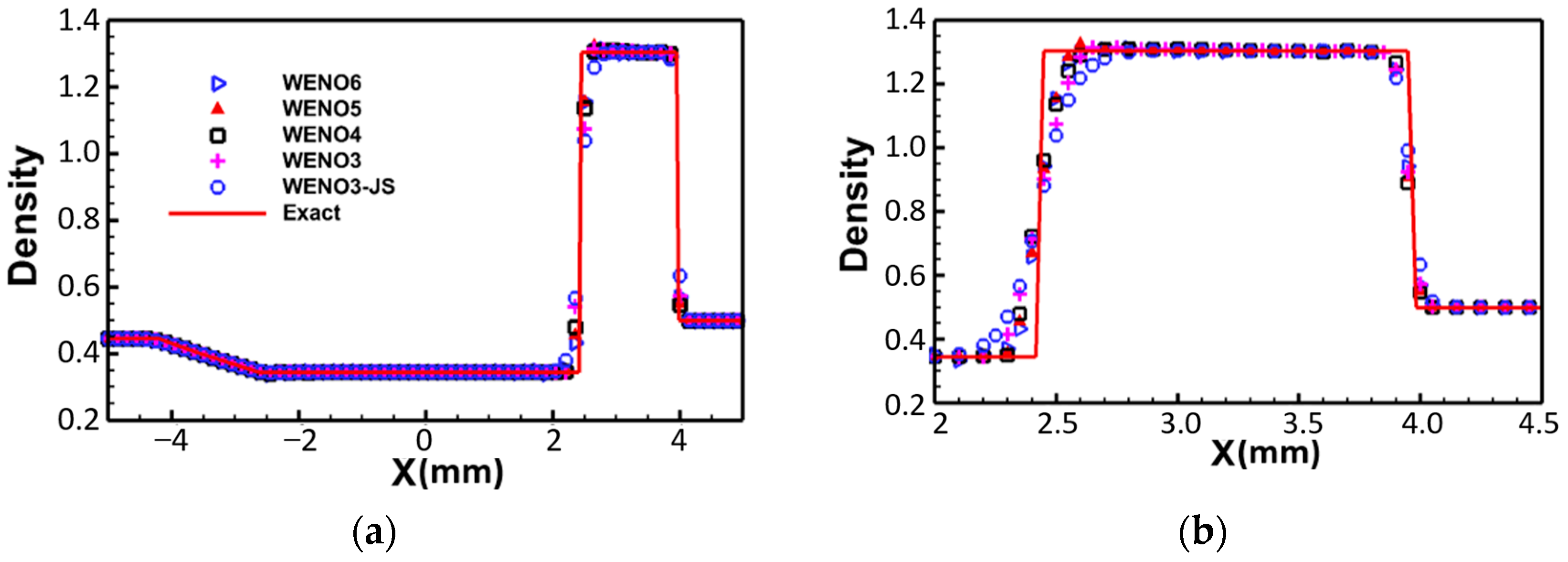
3.1. Solving the One-Dimensional Euler Equations under Riemann Initial Conditions
3.2. Numerical Simulation of the Double Mach Reflection Problem
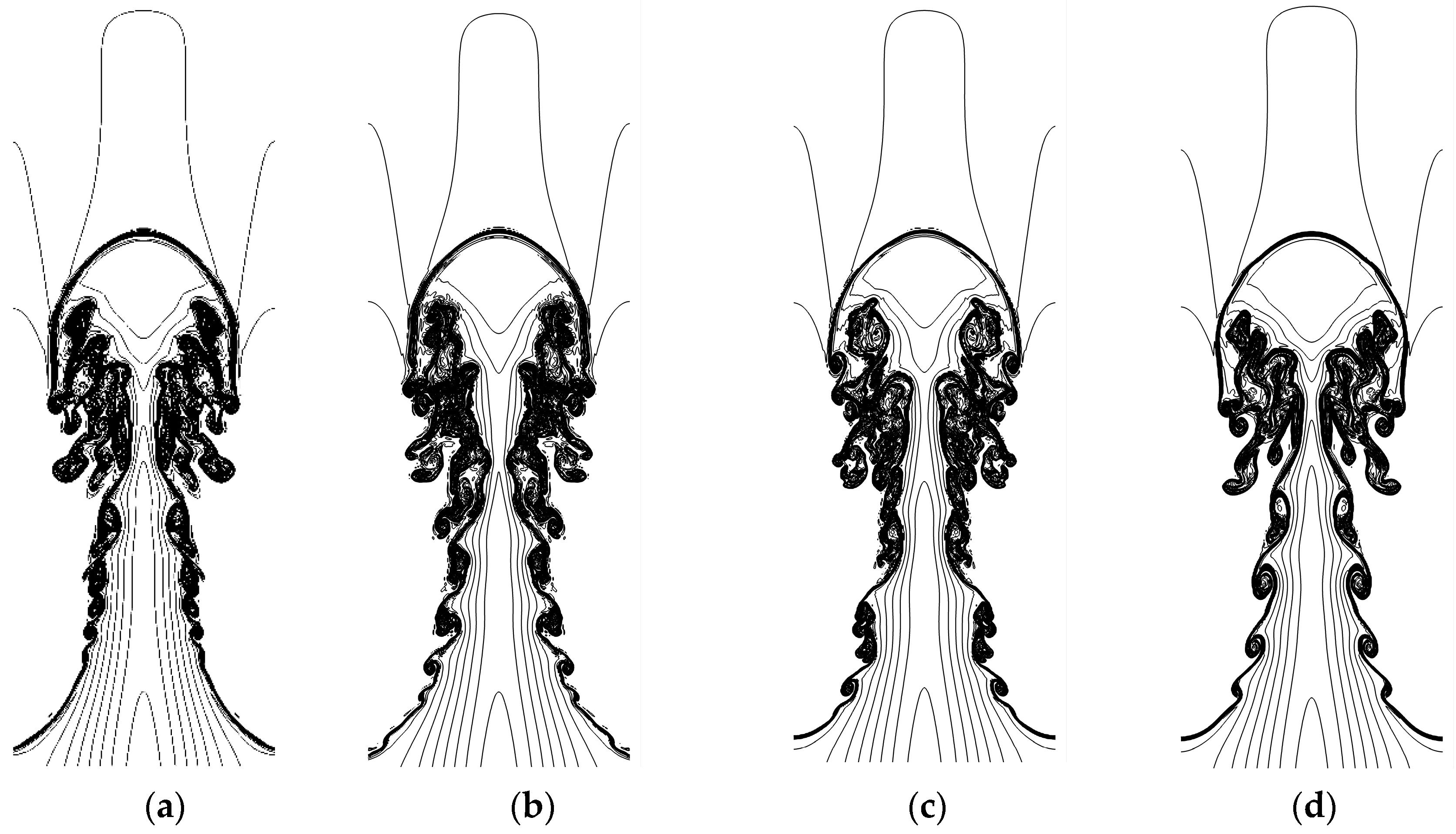
3.3. Numerical Simulation of Rayleigh–Taylor Instability (RT Problem)
- Left and right boundaries: anti-symmetric boundary conditions.
- Bottom boundary: .
- Top boundary: .
4. Application Examples for Turbomachinery
4.1. RANS
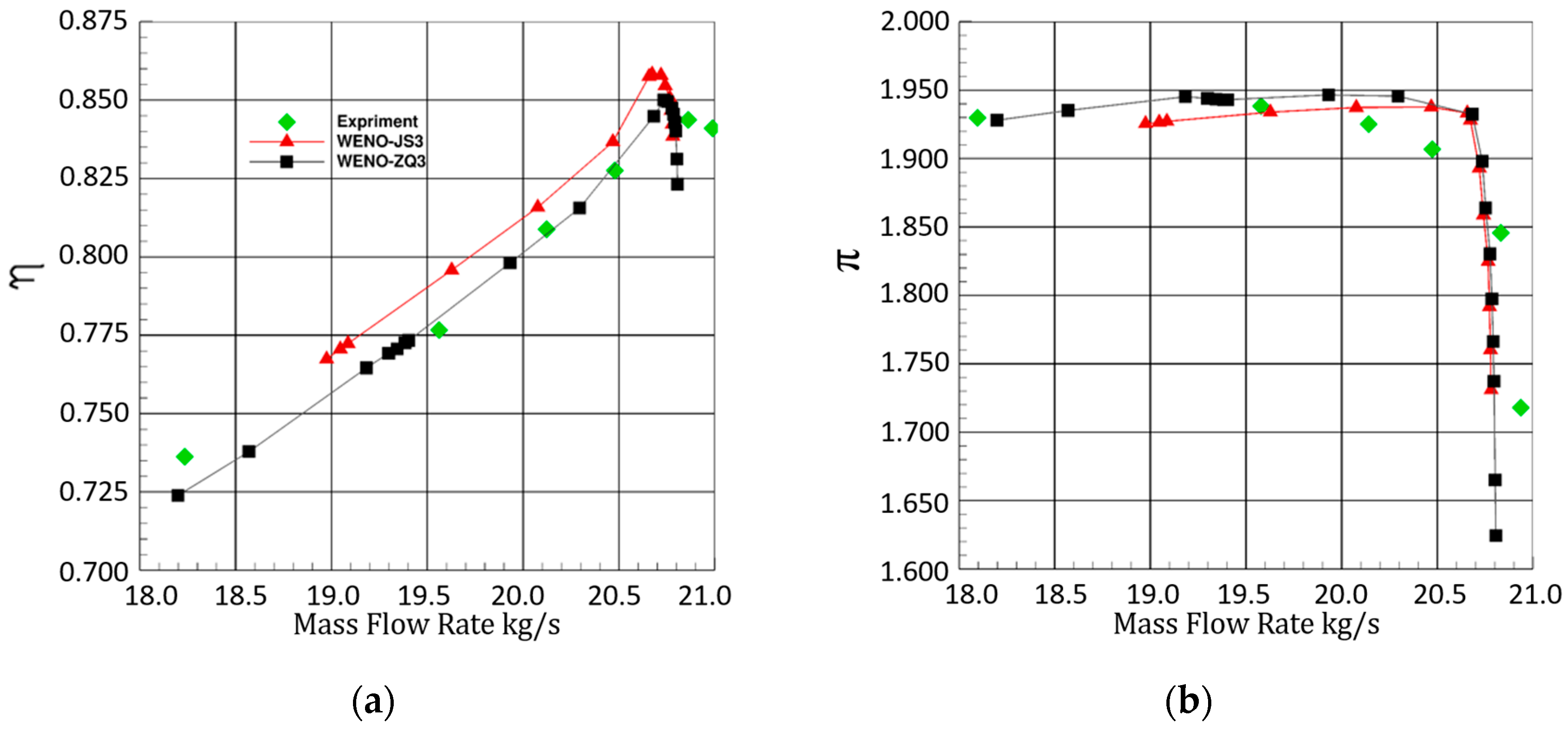
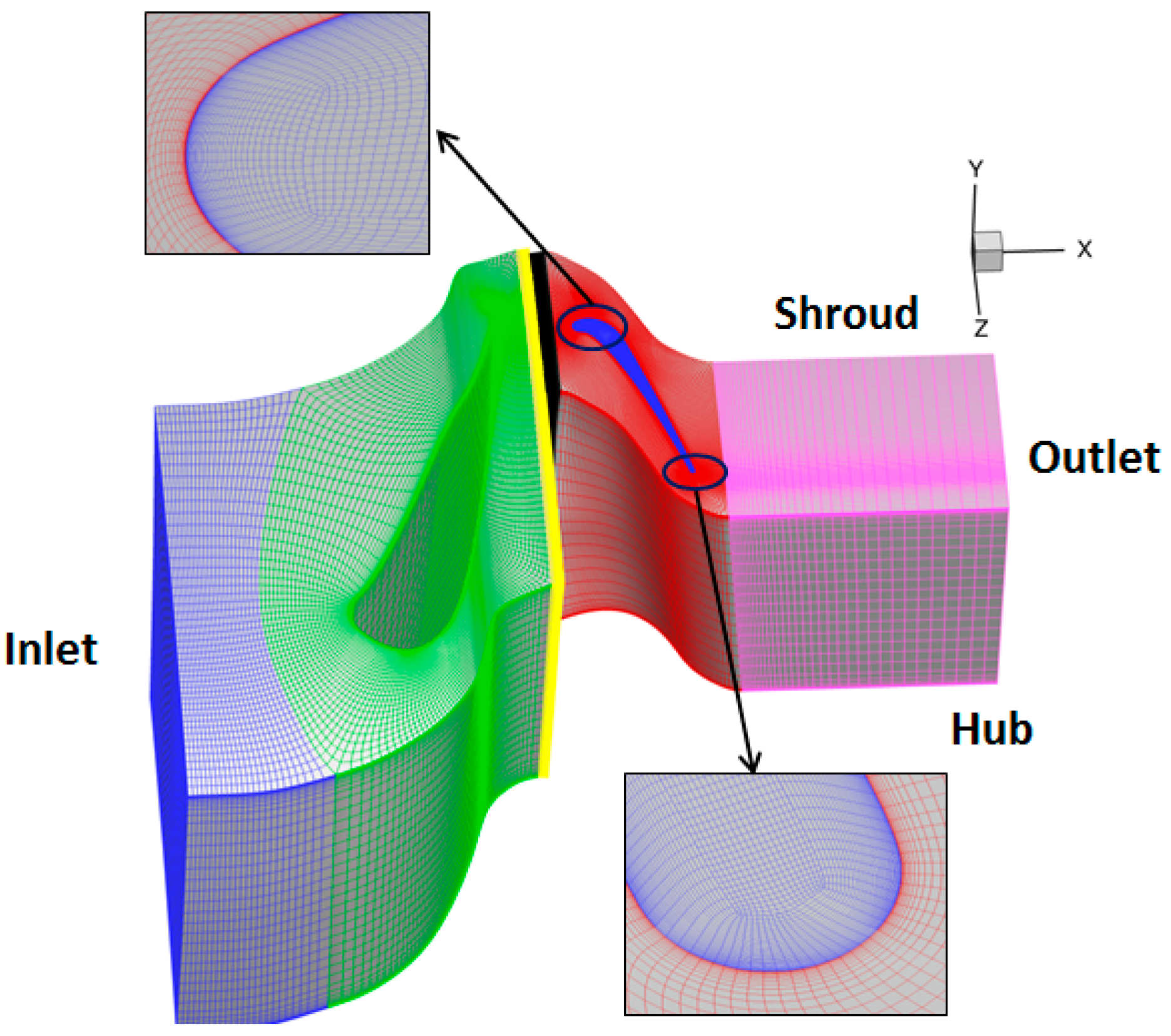
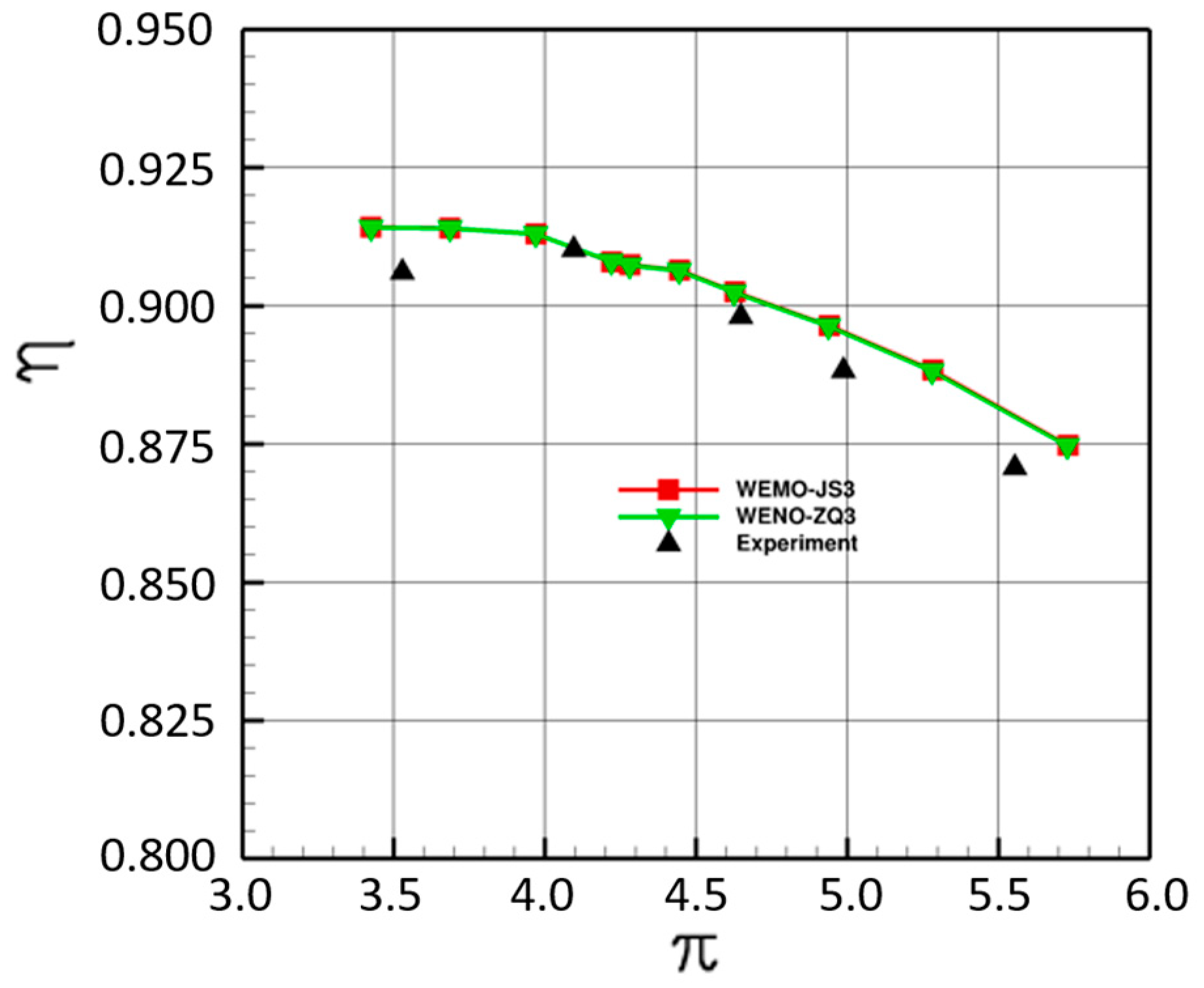
4.1.1. NASA Stage 35
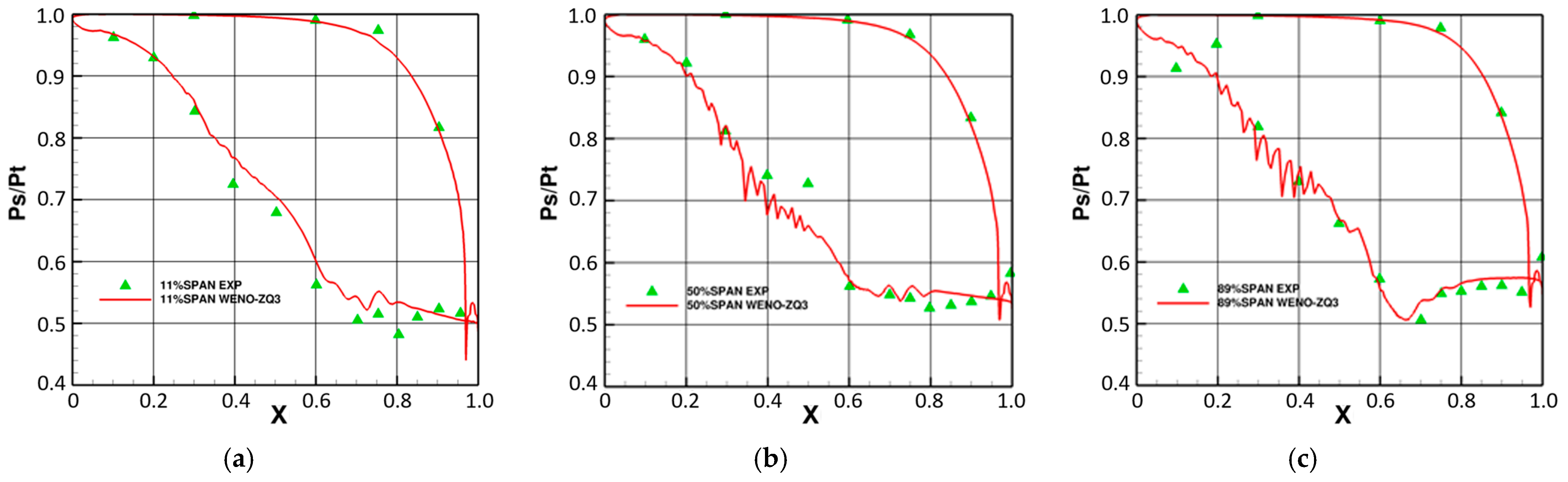
4.1.2. Pratt and Whitney Energy-Efficient Engine High-Pressure Turbine
4.2. Hybrid RANS/LES Model Menter SST-SAS
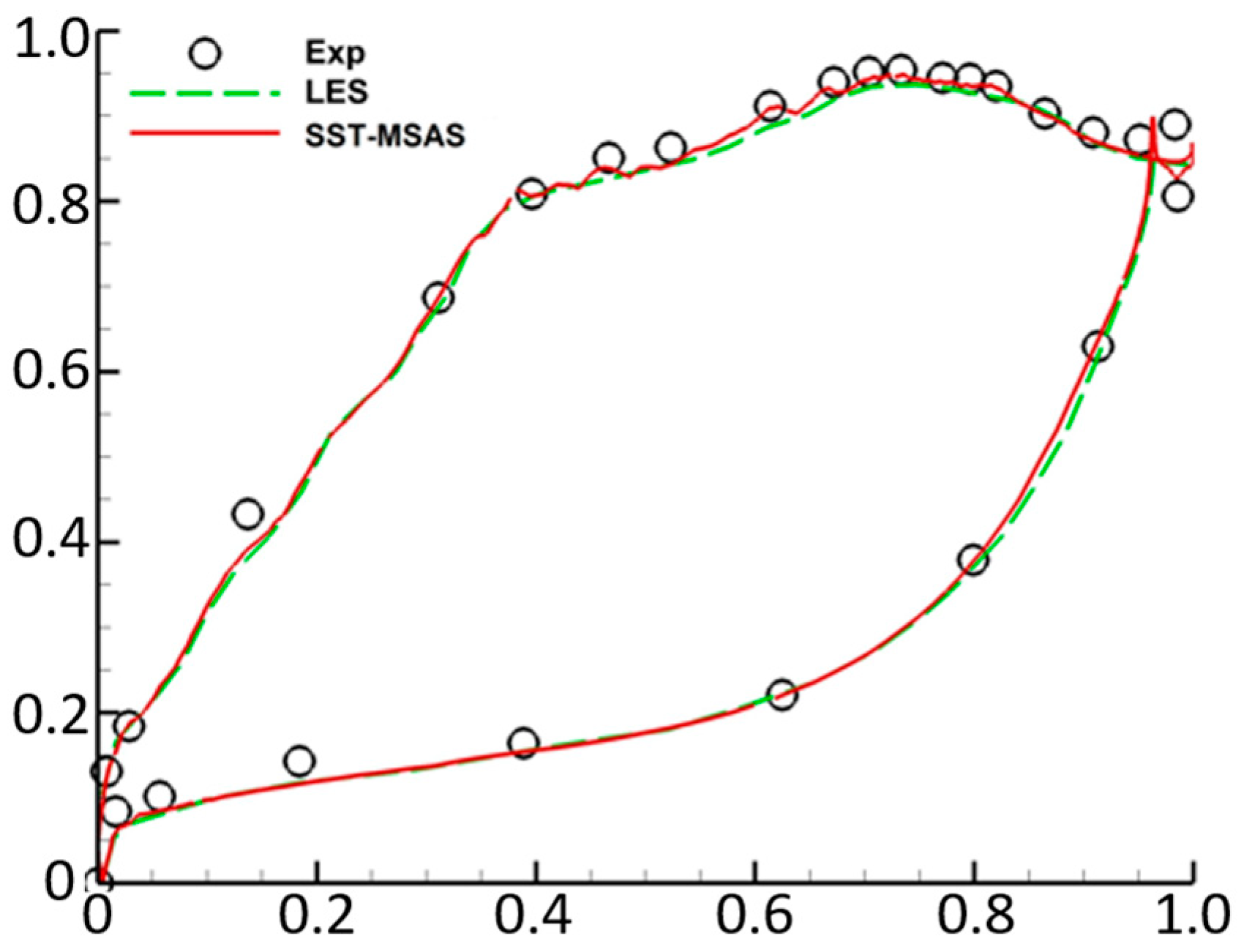
4.2.1. Numerical Calculation of LS89
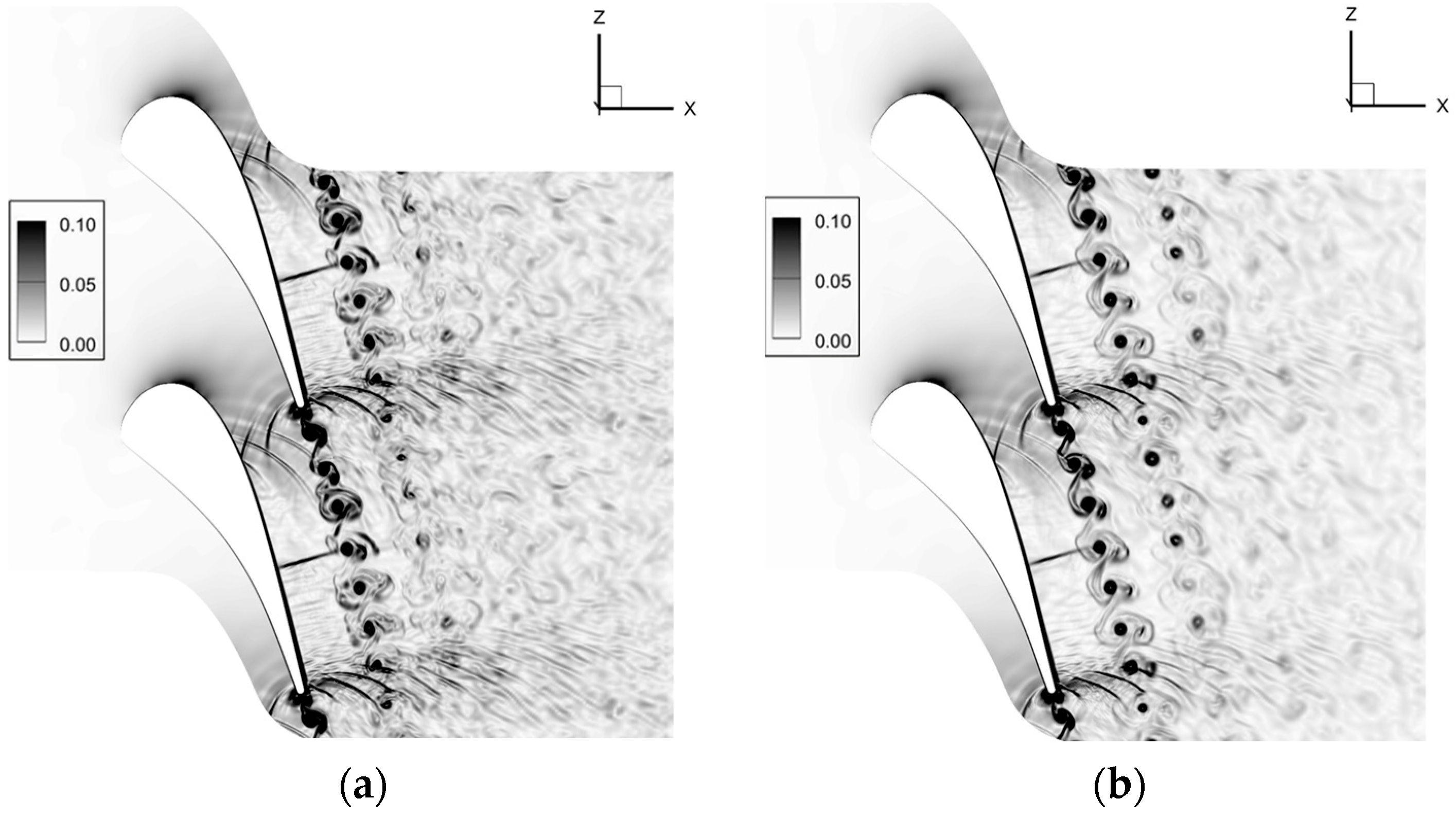
4.2.2. Simulation of Film Cooling Based on C3X Cascade
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Harten, A.; Engquist, B.; Osher, S.; Chakravarthy, S.R. Uniformly high order accurate essentially non-oscillatory schemes, iii. J. Comput. Phys. 1987, 71, 231–303. [Google Scholar] [CrossRef]
- Zhong, D.; Sheng, C. A new method towards high-order weno schemes on structured and unstructured grids. Comput. Fluids 2020, 200, 104453. [Google Scholar] [CrossRef]
- Liu, H.; Qiu, J. Finite difference hermite weno schemes for hyperbolic conservation laws. J. Sci. Comput. 2015, 63, 548–572. [Google Scholar] [CrossRef]
- Balsara, D.S.; Garain, S.; Florinski, V.; Boscheri, W. An efficient class of WENO schemes with adaptive order for unstructured meshes. J. Comput. Phys. 2020, 404, 109062. [Google Scholar] [CrossRef]
- Liu, X.D.; Osher, S.; Chan, T. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Hu, C.; Shu, C.W. Weighted essentially non-oscillatory schemes on triangular meshes. J. Comput. Phys. 1999, 150, 97–127. [Google Scholar] [CrossRef]
- Shi, J.; Hu, C.; Shu, C.W. A technique of treating negative weights in weno schemes. J. Comput. Phys. 2002, 175, 108–127. [Google Scholar] [CrossRef]
- Friedrich, O. Weighted essentially non-oscillatory schemes for the interpolation of mean values on unstructured grids. J. Comput. Phys. 1998, 144, 194–212. [Google Scholar] [CrossRef]
- Zhu, J.; Qiu, J. Academic Lecture on High Order Accuracy Numerical Methods: A Simple and Efficient Finite Volume Weno Method; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2020. [Google Scholar]
- Zhu, J.; Qiu, J. A new fifth order finite difference weno scheme for solving hyperbolic conservation laws. J. Comput. Phys. 2016, 318, 110–121. [Google Scholar] [CrossRef]
- Zhu, J.; Qiu, J. A new type of finite volume weno schemes for hyperbolic conservation laws. J. Sci. Comput. 2017, 73, 1338–1359. [Google Scholar] [CrossRef]
- Zhu, J.; Shu, C.-W. Numerical study on the convergence to steady state solutions of a new class of high order weno schemes. J. Comput. Phys. 2017, 349, 80–96. [Google Scholar] [CrossRef]
- Sheng, C.; Zhao, Q.; Zhong, D.; Ge, N. A strategy to implement high-order weno schemes on unstructured grids. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 2955. [Google Scholar]
- Sheng, C.; Zhao, Q.; Baugher, S. Numerical investigation of rotor aerodynamics using high-order unstructured grid schemes. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0528. [Google Scholar]
- Sheng, C. Improving predictions of transitional and separated flows using rans modeling. Aerosp. Sci. Technol. 2020, 106, 106067. [Google Scholar] [CrossRef]
- Balsara, D.S.; Garain, S.; Shu, C.-W. An efficient class of weno schemes with adaptive order. J. Comput. Phys. 2016, 326, 780–804. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhu, J.; Chen, Y.; Qiu, J. A new hybrid weno scheme for hyperbolic conservation laws. Comput. Fluids 2019, 179, 422–436. [Google Scholar] [CrossRef]
- Zhu, J.; Qiu, J. A new type of modified weno schemes for solving hyperbolic conservation laws. SIAM J. Sci.Comput. 2017, 39, A1089–A1113. [Google Scholar] [CrossRef]
- Lin, J.; Abgrall, R.; Qiu, J. High order residual distribution for steady state problems for hyperbolic conservation laws. J. Sci. Comput. 2019, 79, 891–913. [Google Scholar] [CrossRef]
- Ji, Z.; Liang, T.; Fu, L. A class of new high-order finite-volume TENO schemes for hyperbolic conservation laws with unstructured meshes. J. Sci. Comput. 2022, 92, 61. [Google Scholar] [CrossRef]
- De Vanna, F.; Avanzi, F.; Cogo, M.; Sandrin, S.; Bettencourt, M.; Picano, F.; Benini, E. URANOS: A GPU accelerated Navier-Stokes solver for compressible wall-bounded flows. Comput. Phys. Commun. 2023, 287, 108717. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Liou, M.S. A sequel to ausm, part ii: Ausm-up for all speeds. J. Comput. Phys. 2006, 214, 137–170. [Google Scholar] [CrossRef]
- Shu, C.-W. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws; Springer: Berlin/Heidelberg, Germany, 2007; pp. 325–432. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Sheng, C. A preconditioned method for rotating flows at arbitrary Mach number. Model. Simul. Eng. 2011, 2011, 29. [Google Scholar] [CrossRef]
- Moore, R.; Reid, L. Performance of Single-Stage Axial-Flow Transonic Compressor with Rotor and Stator Aspect Ratios of 1.63 and 1.78, Respectively, and with Design Pressure Ratio of 1.82; NASA Technical Paper; Natbonal Aeronautics and Space Admtnislration: Washington, DC, USA, 1982.
- Reid, L.; Moore, R.D. Design and Overall Performance of four Highly Loaded, High Speed Inlet Stages for an Advanced High-Pressure-Ratio Core Compressor; No. NASA-TP-1337, Natbonal Aeronautics and Space Admtnislration: Washington, DC, USA, 1978. [Google Scholar]
- Gardner, W.B. Energy Efficient Engine: High Pressure Turbine Uncooled Rig Technology Report; No. NASA-CR-165149; Natbonal Aeronautics and Space Admtnislration: Washington, DC, USA, 1979.
- Thulin, R.D.; Howe, D.C.; Singer, I.D. Energy Efficient Engine High-Pressure Turbine Detailed Design Report; No. NASA-CR-165608; Natbonal Aeronautics and Space Admtnislration: Washington, DC, USA, 1982.
- Spalart, P.R. Strategies for turbulence modelling and simulations. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F. Development and application of SST-SAS turbulence model in the DESIDER project. In Advances in Hybrid RANS-LES Modelling, Proceedings of the 2007 Symposium of Hybrid RANS-LES Methods, Corfu, Greece, 17–18 June 2007; Springer: Berlin/Heidelberg, Germany, 2008; pp. 261–270. [Google Scholar]
- Wang, G.; Ge, N.; Zhong, D. Numerical investigation of the wake vortex-related flow mechanisms in transonic turbines. Int. J. Aerosp. Eng. 2020, 2020, 1–18. [Google Scholar] [CrossRef]
- Lin, D.; Yuan, X.; Su, X. Local entropy generation in compressible flow through a high-pressure turbine with delayed detached eddy simulation. Entropy 2017, 19, 29. [Google Scholar] [CrossRef]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th AIAA Fluid Dynamics Conference and Exhibit, Reno, NV, USA, 8–11 January 2001; pp. 1–18. [Google Scholar]
- Liu, J.; Xiao, Z.; Fu, S. Unsteady Flow Around Two Tandem Cylinders Using Advanced Turbulence Modeling Method. In Computational Fluid Dynamics 2010, Proceedings of the Sixth International Conference on Computational Fluid Dynamics, ICCFD6, St. Petersburg, Russia, 12–16 July 2010; Springer: Berlin/Heidelberg, Germany, 2011; pp. 879–881. [Google Scholar]
- Ames, F.E. Aspects of vane film cooling with high turbulence: Part I—Heat transfer. J. Turbomach. 1998, 120, 768–776. [Google Scholar] [CrossRef]




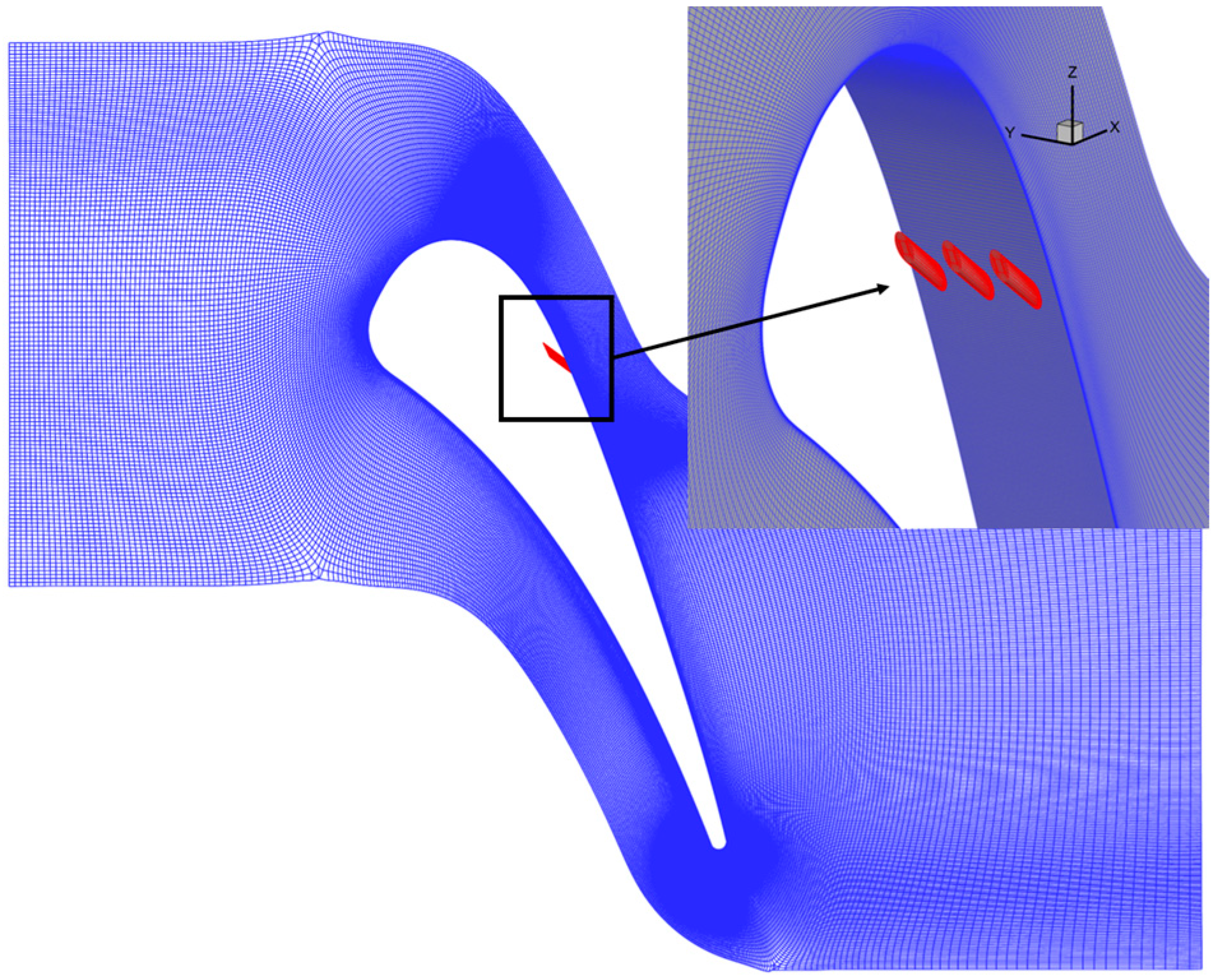
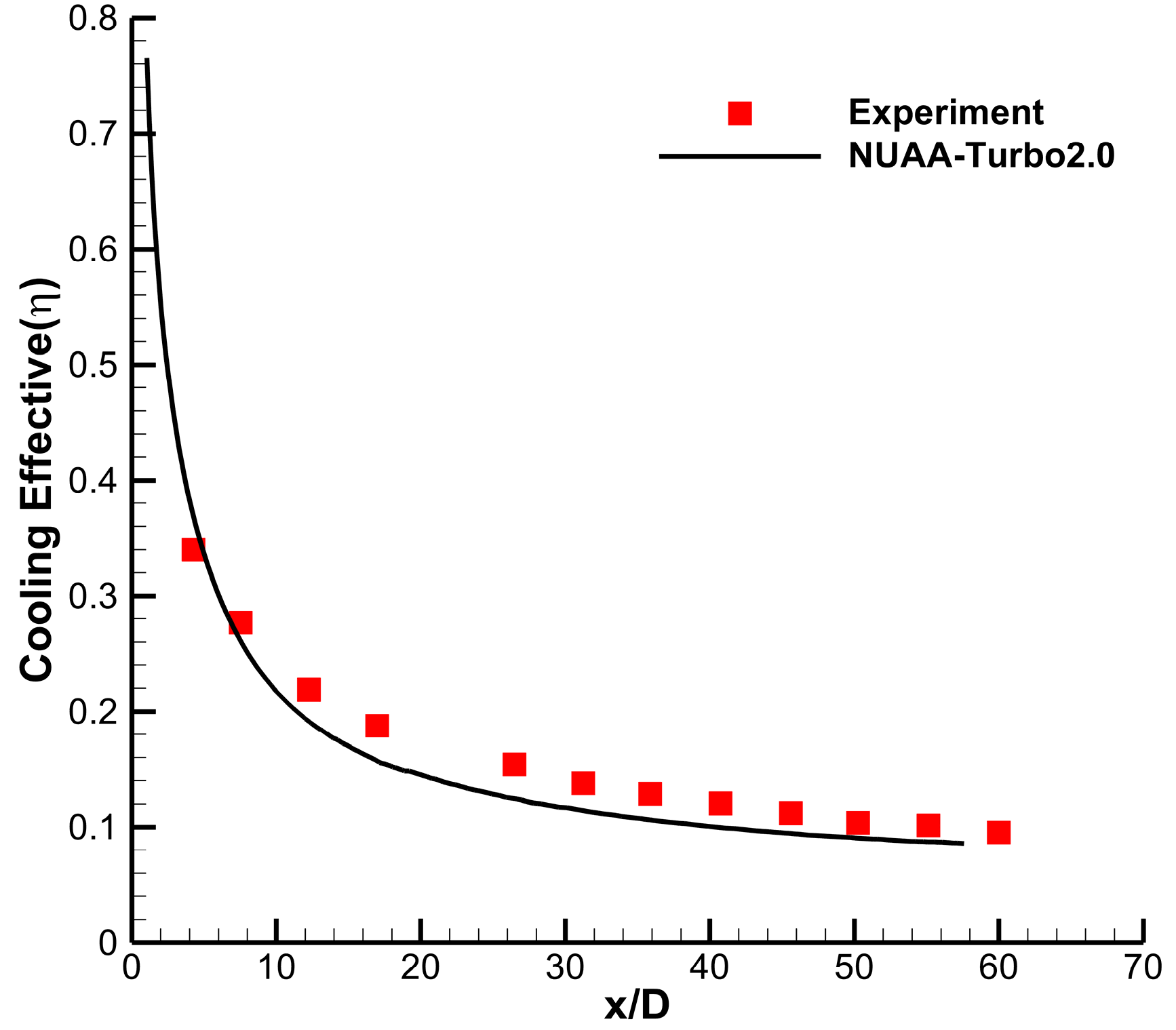
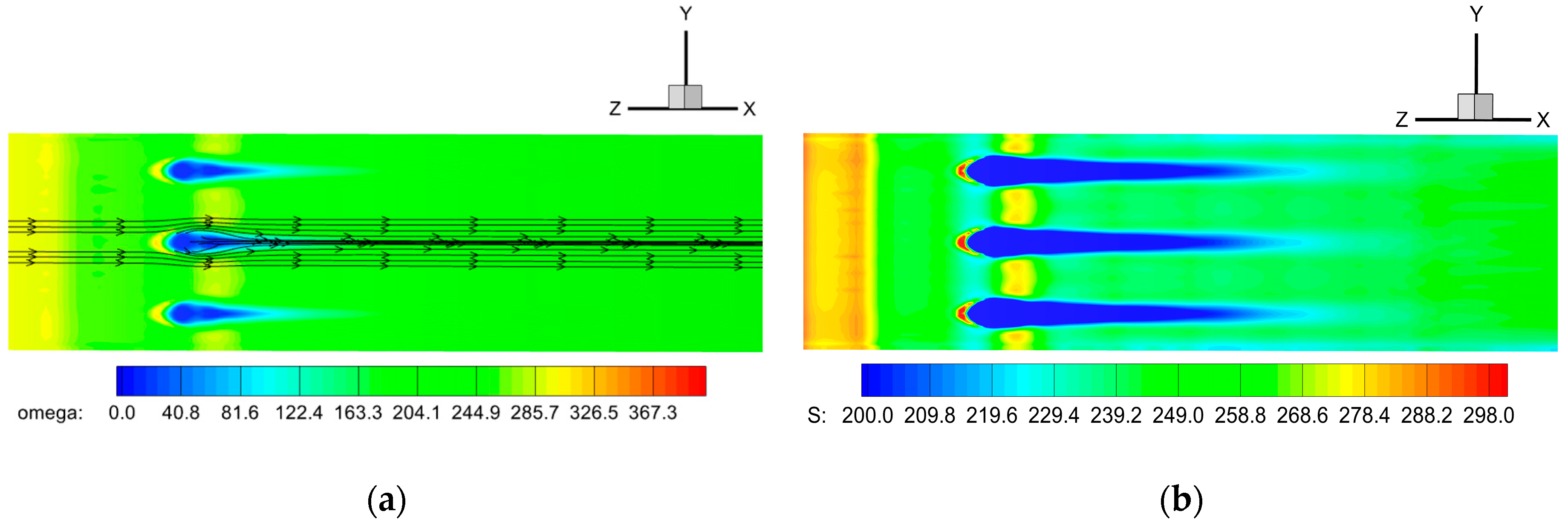
| Parameters | Values |
|---|---|
| Rotor rpm at 100% speed | 17,188.7 rpm |
| Rotor aspect ratio | 1.19 |
| Stator aspect ratio | 1.26 |
| Number of rotor blades | 36 |
| Number of stator blades | 46 |
| Mass flow rate | 20.2 kg/s |
| Total pressure ratio | 1.8 |
| Parameters | Values |
|---|---|
| Total inlet temperature | 431.17 K |
| Total inlet pressure | 375.56 Kpa |
| Speed | 9789 rpm |
| Total pressure ratio | 4.12 |
| Efficiency | 90.8% |
| Correct rotor clearance | 0.3683 mm |
| Parameters | Values |
|---|---|
| Chord length (mm) | 67.647 |
| Axial chord length (mm) | 36.985 |
| Pitch-to-chord ratio (-) | 0.850 |
| Throat-to-chord ratio (-) | 0.2207 |
| Flow inlet angle (degree) | 0 |
| Stagger angle (degree) | 55.0 |
| Trailing-edge diameter (mm) | 1.42 |
| Flow Conditions | |||||
|---|---|---|---|---|---|
| MUR129 | 409.2 | 184,900 | 0 | 116,500 | 0.84 |
| MUR235 | 413.3 | 182,800 | 0 | 104,900 | 0.927 |
| Parameters | Values |
|---|---|
| Chord length (mm) | 144.93 |
| Axial chord length (mm) | 78.16 |
| Pitch-to-chord ratio (-) | 0.812 |
| Throat-to-chord ratio (-) | 0.227 |
| Flow inlet angle (degree) | 0 |
| Stagger angle (degree) | 55.47 |
| Exit flow angle (degree) | 72.4 |
| VR | DR | ||||||
|---|---|---|---|---|---|---|---|
| 0.0793 | 297.34 | 97262 | 0.2702 | 92451 | 317.39 | 0.49 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhong, D.; Zhang, S.; Wu, X.; Ge, N. Application of a Novel Weighted Essentially Non-Oscillatory Scheme for Reynolds-Averaged Stress Model and Reynolds-Averaged Stress Model/Large Eddy Simulation (RANS/LES) Coupled Simulations in Turbomachinery Flows. Appl. Sci. 2024, 14, 5085. https://doi.org/10.3390/app14125085
Wang H, Zhong D, Zhang S, Wu X, Ge N. Application of a Novel Weighted Essentially Non-Oscillatory Scheme for Reynolds-Averaged Stress Model and Reynolds-Averaged Stress Model/Large Eddy Simulation (RANS/LES) Coupled Simulations in Turbomachinery Flows. Applied Sciences. 2024; 14(12):5085. https://doi.org/10.3390/app14125085
Chicago/Turabian StyleWang, Hao, Dongdong Zhong, Shuo Zhang, Xingshuang Wu, and Ning Ge. 2024. "Application of a Novel Weighted Essentially Non-Oscillatory Scheme for Reynolds-Averaged Stress Model and Reynolds-Averaged Stress Model/Large Eddy Simulation (RANS/LES) Coupled Simulations in Turbomachinery Flows" Applied Sciences 14, no. 12: 5085. https://doi.org/10.3390/app14125085
APA StyleWang, H., Zhong, D., Zhang, S., Wu, X., & Ge, N. (2024). Application of a Novel Weighted Essentially Non-Oscillatory Scheme for Reynolds-Averaged Stress Model and Reynolds-Averaged Stress Model/Large Eddy Simulation (RANS/LES) Coupled Simulations in Turbomachinery Flows. Applied Sciences, 14(12), 5085. https://doi.org/10.3390/app14125085






