Abstract
Dynamic stiffness is a parameter of great importance for the assessment of the sound insulation properties of resilient materials commonly used under floating floors in dwellings. This work proposes a simplified approach that relies on an electro-mechanical circuit model for the determination of this parameter using a two-degree-of-freedom system of masses and springs. Unlike the method described in the standard ISO 9052-1, the proposed approach uses a single electrodynamic actuator both as an impulser and vibration sensor, thus reducing the instrumental requirements and yielding a more stable arrangement. By measuring the input electrical impedance of the mass-loaded actuator when coupled to a slab–material system it was possible to retrieve the mechanical mobility function thereof and thus obtain the dynamic stiffness of the material. Several materials were tested following the proposed approach, with results showing good agreement when compared to those obtained following the standardized procedure. In general, the preliminary research encourages the use of the proposed approach for characterization purposes.
1. Introduction
Impact noise in buildings is a problem of major concern for the wellbeing and comfort of their users [1]. In this context, the use of floating floors constitutes a constructive solution to reduce sound vibrations and therefore improve the habitability thereof. To estimate the acoustical performance of these solutions, it is necessary to determine the dynamic stiffness of the materials used as resilient layers [2]. ISO 9052-1 [3] specifies a test method for the determination of the dynamic stiffness of resilient materials commonly used under floating floors in dwellings. Although initially intended for comparing production samples of similar materials used in a continuous layer under floating floors in dwellings, this method has been extensively used for the analysis of many different materials [4]. In this method, the fundamental mode of vibration of a mass–spring system consisting of a loading slab placed over the resilient material under test is excited using a suitable impulser. Once this resonance frequency is determined, it is straightforward to calculate the dynamic stiffness of the specimen using fundamental dynamics formulas [5].
According to the experimental procedure detailed in the standard, the measurements are typically performed through a contact (e.g., piezoelectric sensor or accelerometer) or contactless (e.g., laser vibrometer or microphone) transducer, an impact hammer or a vibration shaker being used as an impulser. Nevertheless, Urban et al. [6] pointed out the uncertainty of dynamic measurements depending on the type of impulser used, hammer or shaker, the former being more influenced by the impact point and the latter by the mounting conditions. Alternatively, electrodynamic actuators can provide a more compact and stable excitation system for the analysis of the dynamic behavior of vibrating structures. These transducers have been widely used as a part of distributed mode loudspeakers [7] or in the active control of vibration in structures [8]. Some authors have dealt with their design [9], the assessment of their performance as self-sensing actuators when compared to piezoelectric technology [10], or their use in thin panels for laboratory vibroacoustic tests [11].
In a recent work by the authors [12], it was shown that electrodynamic actuators can be successfully used to determine the dynamic elastic modulus of materials under a state of simple stresses in beam-type mechanical elements. Similarly to the work by Alba et al. [13], in which a band-pass loudspeaker system coupled to porous sound-absorbing materials was used to determine the airflow resistivity of the latter, the electrical input impedance of the actuator coupled to the beam was measured. By generating a random signal excitation, the fundamental flexural mode of vibration of a beam-type cylindrical element was identified in the electrical input impedance of the actuator, being the dynamic elastic modulus, and then determined using classical beam theory. More recently, some authors have highlighted the usefulness of using an impedance approach for the detection and classification of indoor events by measuring the loudspeaker impedance [14] or for characterization purposes as the determination of the dynamic modulus of elasticity of pine wood [15]. In the present work, a similar approach that measures the electrical input impedance of a mass-loaded actuator coupled to a slab–material system is used to determine the dynamic stiffness of the resilient material. By using an electro-mechanical circuit model, the mechanical mobility function of the system under test can be retrieved from the impedance data and the dynamic stiffness of the material thus obtained. Unlike the standard-based configurations, the proposed approach requires a single transducer, thus reducing the instrumental requirements and further simplifying the characterization procedure. Experiments were performed over different resilient materials, with results showing good agreement when compared to those obtained following ISO 9052-1.
This paper is organized as follows. In Section 2, details of the resilient materials under test and the measurement equipment used for the experiments are given. Section 3 briefly recalls the method described in the standard ISO 9052-1 and the basic background theory of two-degree-of-freedom systems, along with a description of the electro-mechanical circuit model used to determine the dynamic stiffness of resilient materials. In Section 4, measured vibratory response and electrical input impedance data are shown for the analyzed materials, the former showing good agreement when compared to that retrieved using the circuit model. Moreover, a comparison in terms of the dynamic stiffness between this approach and the standardized procedure was carried out, and a discussion on the advantages of the proposed approach along with some remarks on its applicability was also given. Finally, Section 5 summarizes the main conclusions of this work.
2. Materials
2.1. Resilient Materials and Loading Slab
Five different resilient material samples were tested using both the procedure described in ISO 9052-1 [3] and the proposed approach. The type of material was recycled polyurethane foam (RPF) made from polyurethane foam waste, this latter being a residue of great concern in the manufacturing processes in the textile industry. All the specimens and the loading slab were square, with dimensions 200 mm × 200 mm, the latter having a thickness of 30 mm and a weight of 2.341 kg. Moreover, an extra loading mass with a total weight of 0.976 kg was used in both experiments to achieve a more stable setup in the proposed approach, as will be explained later. A summary of the thicknesses, h (in mm), and densities, ρ (in kg/m3), of the tested materials is given in Table 1.

Table 1.
Characteristics of the resilient materials under study.
2.2. Measurement Equipment
The method described in ISO 9052-1 was performed using Brüel & Kjær equipment, Virum, Denmark. Specifically, an accelerometer, type 4534-B-002, and an impact hammer, type 8202, were both connected to a signal conditioner, type 1704-A-002. The outputs of the signal conditioner were then plugged into the acquisition platform OR34 Compact Analyzer, which recorded the responses of each transducer and calculated the mechanical mobility function necessary to identify the resonance frequency. All the measurements were performed with excitation force amplitudes in the interval from 0.21 N to 0.47 N.
As for the proposed approach, the acquisition platform used to perform the electrical input impedance measurements consisted of the USB two-channel audio interface TASCAM US-2 × 2 connected to a laptop running the software LIMP v.1.9.2. This experiment was easy to perform by just connecting the transducer whose electrical impedance was to be measured (the electrodynamic actuator TEAX32C20-8 from Tectonic Audio Labs, Woodinville, WA, USA) in series, with a resistor of 47 ohms yielding a voltage divider configuration (see the instructions described in the software help for details). The input channels were used for recording the total voltage and the voltage in the actuator, respectively, whereas the output channel was used to generate an exponential swept sine (EES) signal of 1 V peak to peak to excite it. This signal type was chosen because EES signals have been successfully used to measure the dynamic stiffness of resilient materials following the standardized procedure but using a shaker as an excitatory device instead [16]. A synchronous time domain averaging of 10 FFT blocks of 131.072 sample size each was applied during the recording to obtain the electrical input impedance spectrums. The manufacturer parameters of the electrodynamic actuator TEAX32C20-8 necessary for the subsequent calculations are summarized in Table 2.

Table 2.
Parameters of the electrodynamic actuator TEAX32C20-8 from Tectonic Audio Labs.
3. Methods
3.1. ISO 9052-1
Dynamic stiffness is an important parameter for the assessment of resilient materials commonly used in floating floors for sound insulation in dwellings. The standard ISO 9052-1 [3] proposes the use of a resonance method for the determination of the dynamic stiffness of resilient materials with smooth surfaces. From the resonance frequency of a single-degree-of-freedom mass–spring system composed of a loading mass (i.e., the mass, m) and the sample of resilient material (i.e., the spring with stiffness s) mounted on a rigid floor, the dynamic stiffness of the material under test can be calculated (see Figure 1a, where damping r was included, although the standard does not take it into account). For this purpose, the vertical vibration of the loading mass when subjected to an external excitation was obtained in terms of the mechanical mobility function frequency response (velocity–force ratio). In the current work, a contact accelerometer and an impact hammer were used as a vibration sensor and impulser, respectively (see Figure 1b). Note that both an extra load and the electrodynamic actuator were also placed over the loading slab to reproduce the same mounting conditions as in the proposed approach to be described next.
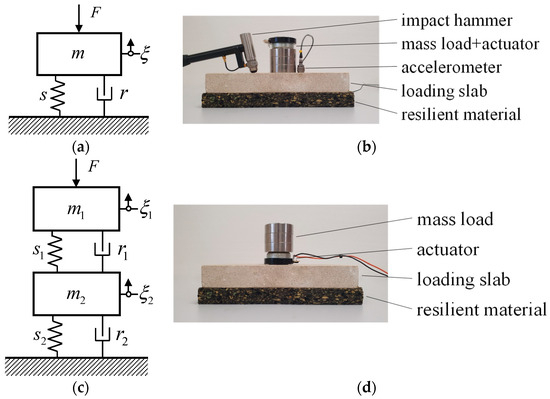
Figure 1.
Schematic representation of the mechanical systems (left) and pictures of the corresponding experimental setups (right) used to determine the dynamic stiffness of resilient materials from the ISO 9052-1 standard (top) and the proposed approach (bottom).
The dynamic stiffness of the material, s′ (in N/m3), can then be obtained from [3]
where ρS is the total mass per unit area (in kg/m2) during the test, and f0 is the resonance frequency (in Hz) identified in the vibratory response.
3.2. Proposed Approach
The proposed approach uses the same arrangement as the standard described above, but the mass-loaded electrodynamic actuator is now directly coupled to the loading slab. The electrodynamic actuator consists of a coiled wire embedded in a uniform magnetic field so that when an electrical current is flowing, a mechanic force is produced in its moving assembly. By measuring its electrical input impedance, it is possible to capture the loading effect on the transducer vibratory frequency response when coupled to other elements or structures. Consequently, instead of using an accelerometer and an impact hammer, the electrodynamic actuator is used both as an impulse exciter and a vibration sensor simultaneously. On the other hand, by using the extra loading mass, the need to glue the actuator to achieve a stable dynamic behavior thereof was avoided. Moreover, the resonance frequencies of the resulting coupled two-degree-of-freedom system (i.e., the slab–material and the mass-loaded actuator) are closer in the frequency spectrum, thus easing the analysis to be explained next.
Let us therefore consider the coupled mechanical system in Figure 1c composed of two masses, m1 and m2 (in kg), and two springs with damping, r1 and r2 (in Ns/m), and stiffness, s1 and s2 (in N/m). Such a system can be linked to the proposed measurement system as follows: m1, r1, and s1 correspond to the mass (including the extra load), damping, and suspension of the loaded electrodynamic actuator, respectively, m2 stands for the mass of the loading slab, and r2 and s2 represents the damping and dynamic stiffness of the resilient material under test, respectively (see Figure 1d).
From the free vibration analysis of such a two-degree-of-freedom system, the equations of motion of each mass can be written as
where ξ1 and ξ2 are the harmonic displacements (in m) from the equilibrium of masses m1 and m2, respectively, whereas • and •• stand for the first- and second-time derivatives.
The above linear differential equations can be written in terms of a matrix product as
where ω is the angular frequency (in rad/s) resulting from the time derivatives.
The eigenvalues of that matrix system can be obtained for those values of ω2 for which the determinant of the matrix is equal to zero from
The frequencies corresponding to these eigenvalues (i.e., the natural frequencies of vibration, ω1,2 = 2πf1,2) correspond to the solutions of the so-called characteristic equation (Equation (5)). These frequencies can be easily obtained by identifying the resonance peak frequencies f1 and f2 (in Hz) on the measured electrical input impedance spectrum of the actuator when an electrical voltage is applied to it (see [12] for a very similar example of the measurement procedure). In this regard, as it was pointed out above, it is of great importance that both resonances lie below the coil inductance region of the electrical input impedance spectrum to avoid the masking effect and ease its identification, the use of impedance compensation networks [17] being necessary otherwise. As is shown in the circuit model, to obtain the dynamic stiffness, the mechanical properties of the remaining elements must be known beforehand. In this regard, a simple weighting procedure can be used to determine m1 and m2, whereas the stiffness of the actuator, s1, can be easily obtained by substituting m1 and the resonance frequency of its electrical input impedance when just mounted on a rigid floor in Equation (1).
3.3. Electro-Mechanical Circuit Model
Figure 2a shows a cross-sectional sketch of an electrodynamic actuator, which may be represented by the electro-mechanical equivalent circuit schematic diagram shown in Figure 2b, which accounts both for its electrical and mechanical parts [11].
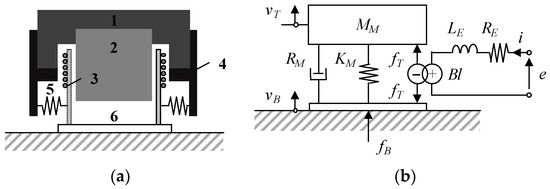
Figure 2.
Electrodynamic actuator: (a) schematic representation (parts: (1) magnet, (2) iron piece, (3) coil, (4) chassis, (5) suspension, (6) base); (b) electro-mechanical equivalent circuit.
The equation that governs the electrical behavior of such actuators is given by [18]
where RE and LE are the resistance (in Ω) and inductance (in H) of the coil, respectively, i is the electrical current (in A), e is the open-circuit applied voltage (in V), Bl is the electro-mechanical transformation factor or force factor (in Tm), and vT and vB are the velocities (in m/s) on the top mass (i.e., the magnet) and base of the actuator, respectively (i.e., vB = 0 m/s when the actuator is mounted on a rigid floor).
On the other hand, the equation of motion that governs the dynamic behavior of the actuator mass can be written as
where MM is the mechanical mass of the actuator (in kg) including the extra load, RM and KM are the mechanical resistance (in Ns/m) and stiffness of the suspension (in N/m), respectively, and the Bli term corresponds to the electromagnetic force (in N).
Both the velocity on the top mass and base of the actuator can in turn be related to the corresponding mechanical forces fT = vT/YT and fB = vB/YB (both in N) from fT = −fB so that
where YT = 1/jωMM is the mobility of the loaded actuator mass and YB is the mobility function of the system at the base of the actuator (both in ms−1/N).
The electrical input impedance of the whole system can thus be derived as [10]
where ZE = RE + jωLE (in Ω) and ZM = RM + jωMM + KM/jω (in Ns/m) are the electrical and mechanical impedances of the electrodynamic transducer, respectively [19].
After some algebraic manipulations of Equations (6)–(9), the mobility function of the same slab–material arrangement used in the standard procedure (including the extra load and the actuator) can be obtained from
where ZET,0 stands for the electrical input impedance (in Ω) of the mass-loaded actuator when mounted on a rigid floor.
4. Results and Discussion
4.1. Proposed Approach vs. ISO 9052-1
First, electrical input impedance was measured for the mass-loaded actuator when mounted on a rigid floor, ZET,0 (i.e., w/o resilient material), and when coupled to the slab–material system, ZET, for different materials. A single measurement was sufficient, provided the location of the actuator was centered as much as possible to minimize the excitation of higher-order modes of vibration in the resulting coupled system. The measured spectrums are plotted in Figure 3 for three of the five specimens under test, M#1, M#3, and M#5, being straightforward to identify the resonance peak frequencies f1 and f2 (blue dots) of the two-degree-of-freedom system resulting from the proposed approach. Secondly, experiments according to the standardized procedure were performed, the measurements being taken three times for each sample to minimize deviations linked to the hammer impact point and the average results being used in the subsequent dynamic stiffness calculations. In Figure 4, the mechanical mobility function was normalized with respect to its maximum value for each tested material is depicted. These curves were obtained both following the standard ISO 9052-1 and predicted using the electrical input impedance data of Figure 3 in the electro-mechanical circuit model (Equation (10)). The results clearly indicate that there is good agreement between the standard measurements and the predictions to identify the resonance frequency f0 (blue dots) necessary to calculate the dynamic stiffness from Equation (1) using the material data in Table 1. Table 3 summarizes the dynamic stiffness results obtained from both procedures and the relative error of the proposed approach with respect to the standard for the analyzed samples.
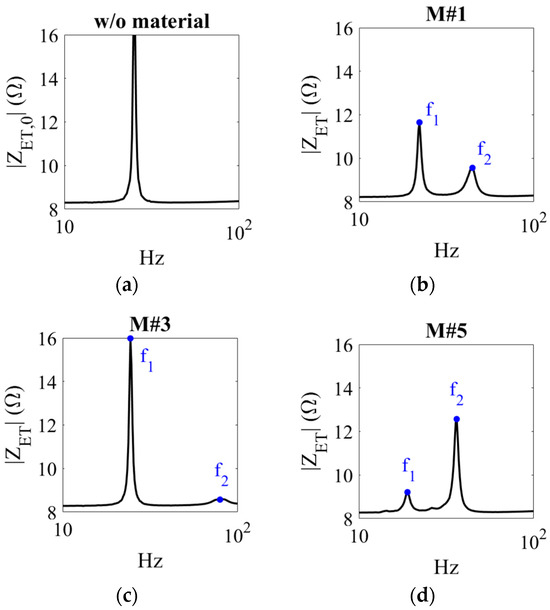
Figure 3.
Measured electrical input impedance: (a) mass-loaded actuator when mounted on a rigid floor (ZET,0); (b) M#1; (c) M#3; and (d) M#5 (ZET). The blue dots indicate the resonance peak frequencies f1 and f2 of the two-degree-of-freedom system resulting from the proposed approach.
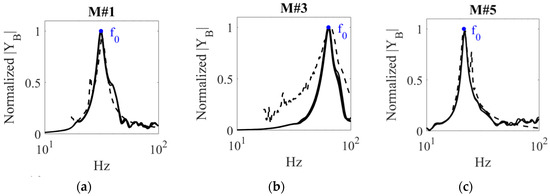
Figure 4.
Normalized mechanical mobility function frequency response for three of the tested materials: (a) M#1; (b) M#3; and (c) M#5. Continuous lines: experimental data obtained following the standard ISO 9052-1; discontinuous lines: predicted data obtained using the electro-mechanical circuit model (Equation (10)). Blue dots indicate the resonance frequency f0 necessary to calculate the dynamic stiffness of each sample material.

Table 3.
Dynamic stiffness results obtained from both methods and relative error of the proposed approach with respect to the standard for the resilient materials under study.
Nevertheless, some points are worth mentioning regarding the proposed approach. On the one hand, the mechanical mobility function derived using the proposed approach shows a secondary spurious peak close to f0 for materials M#1 and M#5 which may mislead the identification of the resonance frequency. This spurious peak (around 25 Hz) corresponds to the resonance of ZET,0 (see Figure 3a) and must therefore be disregarded, not only because of its lower amplitude and narrow bandwidth but also because it has the same value in all measurements. On the other hand, the predicted mechanical mobility function frequency response exhibits differences when compared to that obtained with the standard. In this regard, it should be noted that the proposed approach is focused on successfully identifying the resonance frequency f0 necessary to determine the dynamic stiffness, the extra loss mechanisms linked to the suspension of the actuator and responsible for these differences not being considered.
4.2. Remarks on the Applicability of the Proposed Approach
The above preliminary results showed the proposed approach to be a valid methodology for obtaining the dynamic stiffness of resilient materials using cost-effective laboratory equipment. The use of a stationary source exhibited more stable results than the transient impulser, which required three measurements for each sample to reduce uncertainties linked to point force excitation (as recommended in the standard [3]). Moreover, the proposed arrangement is easier to implement than those using a supported shaker and an impedance head with acceleration and force sensors [5]. Also, the above approach may serve to provide additional data such as the mechanical mobility function of the mechanical system to which the actuator is coupled, thus serving as an alternative to ISO 7626-2 [20]. In this regard, as mentioned above, further research is necessary to account for the loss mechanisms linked to the actuator for a proper determination thereof. Even though other approaches can be also found in the literature, such as the equations derived by Segovia et al. [21], a modified dynamic stiffness calculation method for rubber isolators [22], or empirical formulas for lightweight laminate floors [23], the proposed approach was shown to be a simple and straightforward procedure for the determination of the dynamic stiffness of resilient materials.
Notwithstanding these advantages, it should be noted that the proposed approach does not use an 8 kg load plate made of steel (as specified in the standard) because it would influence the electromagnetic field of the mechanical actuator [19]. Alternatively, heavier electrodynamic actuators or other transduction types such as piezoelectric ones could be used following a very similar measurement procedure [15]. Nevertheless, given that the standard is mainly intended to be used for comparing production samples of similar materials for loadings between 0.4 kPa and 4 kPa and that our study uses samples 0.2 × 0.2 m2 and a total loading mass of 3.45 kg, the resulting prestatic load (above 0.845 kPa) still lies in a valid range of analysis. In fact, the standard states that the differences between dynamic stiffness values measured with a static load of 2 kPa in accordance with this part of IS0 9052 and those measured with a very low preload are of the order of 10% to 20%.
Regarding the applications of the proposed approach, some examples can be the evaluation of the long-term sound reduction performance of resilient materials used in floating floor systems by monitoring their dynamic stiffness [24] or the experimental analysis of the dynamic stiffness in industrial robots [25]. Even though further research would be necessary to make the proposed approach extensible to these applications, the preliminary results are encouraging and set a good starting point for its future development.
5. Conclusions
This work proposes a simplified approach to determine the dynamic stiffness of resilient materials from the measurement of the input electrical impedance of an electrodynamic actuator excited by a random noise signal when coupled to another mass–spring system composed of a loading slab and the sample under test. In doing so, the resonance frequencies of the resulting two-degree-of-freedom system can be identified in the electrical impedance spectrum and the dynamic stiffness calculated by using simple formulas. The results showed good agreement when compared to those obtained following the ISO 9052-1 and encouraged the use of the proposed approach for the characterization of these materials.
Author Contributions
Conceptualization, J.C.; methodology, J.C., P.P. and E.S.; investigation, J.C., P.P., E.S., A.P., L.R.-M., J.D.P. and J.R.; resources, J.R.; writing—original draft preparation, J.C.; writing—review and editing, P.P. and A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rindel, J.H. Sound Insulation in Buildings; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Schiavi, A.; Pavoni, A.; Russo, F. Estimation of the acoustical performance of floating floors from dynamic stiffness of resilient layers. Build. Acoust. 2005, 12, 99–113. [Google Scholar] [CrossRef]
- ISO 9052-1; Acoustics. Determination of Dynamic Stiffness. Part 1: Materials Used under Floating Floors in Dwellings. International Organization for Standardization: Geneva, Switzerland, 1989.
- Schiavi, A.; Pavoni, A.; Corallo, M.; Russo, F. Acoustical performance characterization of resilient materials used under floating floors dwellings. Acta Acust. United Acust. 2007, 93, 477–485. [Google Scholar]
- Cremer, L.; Heckl, M.; Petersson, B.A.T. Structure Borne Sound; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Urban, D.; Zat’ko, P.; Roozen, N.B.; Muellner, H.; Glorieux, C. On the uncertainty of dynamic stiffness measurements. J. Acoust. Soc. Am. 2017, 141, 3930. [Google Scholar]
- New Transducers Ltd. NXT Technology Review; New Transducers Ltd.: Cambridge, UK, 2002. [Google Scholar]
- Fuller, C.R.; Elliott, S.J.; Nelson, P.A. Active Control of Vibration; Academic Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Paulitsch, C.; Gardonio, P.; Elliott, S.J. Active vibration control using an inertial actuator with internal damping. J. Acoust. Soc. Am. 2006, 119, 2131–3140. [Google Scholar] [CrossRef]
- Boulandet, R.; Pelletier, A.; Micheau, P.; Berry, A. Active Vibration Control Using Self-Sensing Actuators: An Experimental Comparison of Piezoelectric and Electromagnetic Technologies. In Proceedings of the ASME 2014 IMECE, Montreal, QC, Canada, 14–30 November 2014. [Google Scholar]
- Robin, O.; Chazot, J.D.; Boulandet, R.; Michau, M.; Berry, A.; Atalla, N. A plane and thin panel with representative simply supported boundary conditions for laboratory vibroacoustic tests. Acta Acust. United Acust. 2016, 102, 170–182. [Google Scholar] [CrossRef]
- Carbajo, J.; Poveda, P.; Segovia, E.; Rincón, E.; Ramis, J. Determination of dynamic elastic modulus of materials under a state of simple stresses by using electrodynamic actuators in beam-type mechanical elements. Mater. Lett. 2022, 320, 132383. [Google Scholar] [CrossRef]
- Alba, J.; Arenas, J.P.; del Rey, R.; Rodríguez, J.C. An electroacoustic method for measuring airflow resistivity of porous sound-absorbing materials. Appl. Acoust. 2019, 150, 132–137. [Google Scholar] [CrossRef]
- Marmaroli, P.; Allado, M.; Boulandet, R. Towards the detection and classification of indoor events using a loudspeaker. Appl. Acoust. 2023, 202, 109161. [Google Scholar] [CrossRef]
- Li, S.; Xu, G.; Jiang, C.; Hu, H. Determination of the dynamic modulus of elasticity of pine based on the PZT Transducer. Forests 2024, 15, 459. [Google Scholar] [CrossRef]
- Guidorzi, P.; Barbaresi, L.; Garai, M. Measuring the dynamic stiffness of resilient materials using EES and MLS signals. Appl. Acoust. 2018, 138, 92–100. [Google Scholar] [CrossRef]
- Leach, W.M., Jr. Impedance compensation networks for lossy voice-coil inductance of loudspeaker drivers. J. Audio Eng. Soc. 2004, 52, 358–365. [Google Scholar]
- Fahy, F.; Gardonio, P. Sound and Structural Vibration: Radiation, Transmission and Response; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Beranek, L.L.; Mellow, T.J. Acoustics: Sound Fields and Transducers; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- ISO 7626-2; Mechanical Vibration and Shock. Experimental Determination of Mechanical Mobility. Part 2: Measurements Using Single-Point Translation Excitation with an Attached Vibration Exciter. International Organization for Standardization: Geneva, Switzerland, 2015.
- Segovia, E.; Torres, J.; Carbajo, J.; Ramis, J.; Arenas, J.P. Determination of the elastic parameters of a material from a standardized dynamic stiffness testing. J. Sound Vib. 2019, 460, 114885. [Google Scholar] [CrossRef]
- Xia, E.; Cao, Z.; Zhu, X.; Qiu, S.; Xue, Z.; He, H.; Li, L. A modified dynamic stiffness calculation method of rubber isolator considering frequency, amplitude and preload dependency and its application in transfer path analysis of vehicle bodies. Appl. Acoust. 2021, 175, 107780. [Google Scholar] [CrossRef]
- Arenas, J.P.; Sepulveda, L.F. Impact sound insulation of a lightweight laminated floor resting on a thin underlayment material above a concrete slab. J. Build Eng. 2022, 45, 103537. [Google Scholar] [CrossRef]
- Lee, J.-Y. Evaluation of the long-term sound reduction performance of resilient materials in floating floor systems. J. Sound Vib. 2016, 366, 199–210. [Google Scholar] [CrossRef]
- Wu, K.; Kuhlenkoetter, B. Experimental analysis of the dynamic stiffness in industrial robots. Appl. Sci. 2020, 10, 8332. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).