FES Control of a Finger MP Joint with a Proxy-Based Super-Twisting Algorithm
Abstract
1. Introduction
- Robustness and High Control Accuracy: Introducing the proxy-based super-twisting algorithm (PSTA) for FES control of MP joints, combining the robustness of Sliding Mode Control (SMC) and the high control accuracy of the Super-Twisting Algorithm (STA).
- Avoiding Numerical Chattering: Proposing an implicit Euler discretization method to avoid numerical chattering while maintaining high control accuracy and robustness.
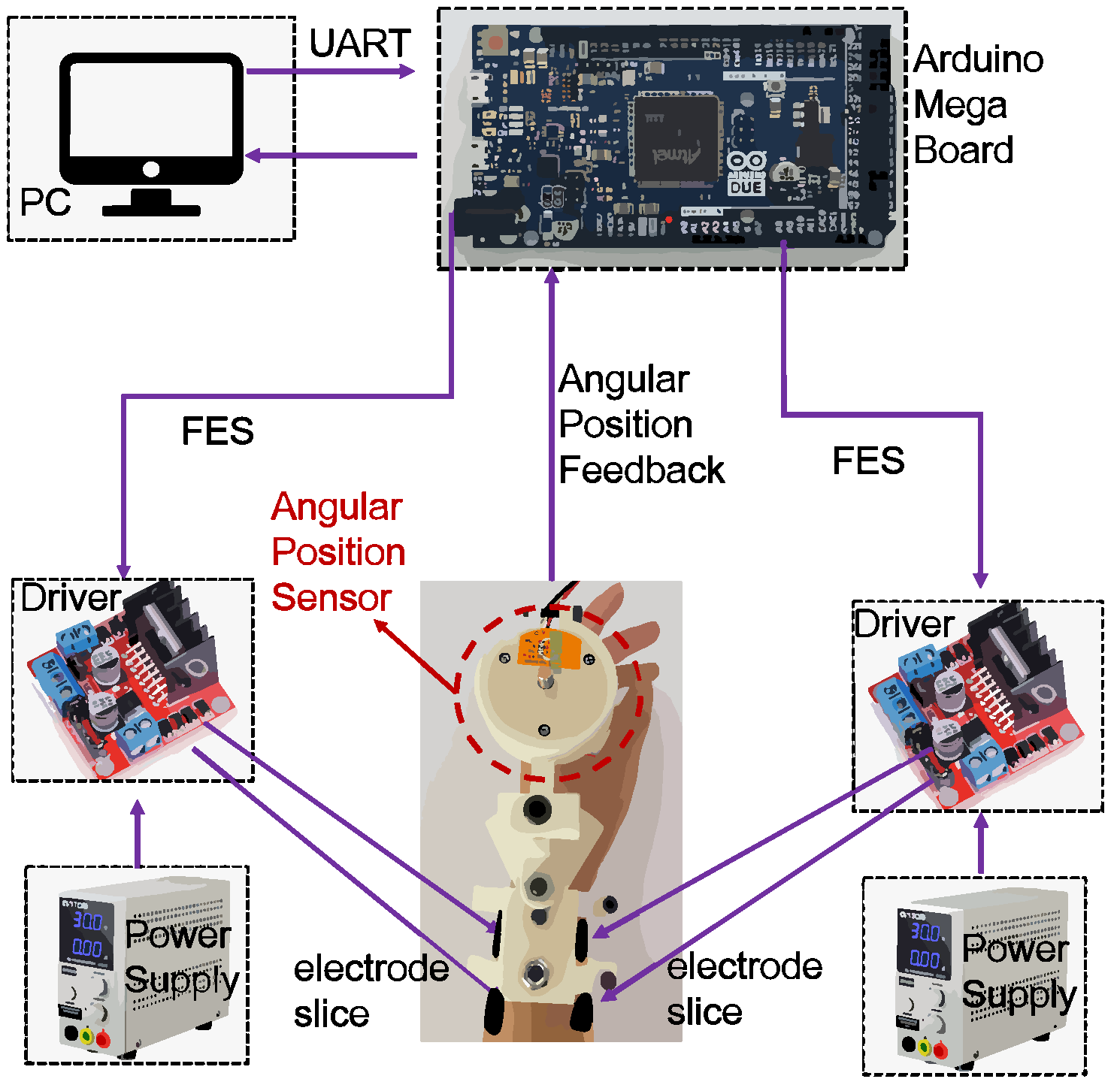
- Experimental Validation: Validating the PSTA and its implicit discretization through experiments on MP joints using FES. Achieving high accuracy on a low-cost Arduino Mega board in real-time, demonstrating robustness and low computational complexity without detailed muscle model information.
2. Problem Statement
- Without the knowledge of boundness parameters , , , and and only the actuation saturation level F, adaptive SMC methods can be designed here, while their implementations require high-frequency sampling and switching rate of actuation, which is not suitable for the embedded platform of a low computation resource and sampling rate.
- One strategy is to set the gains of the gains of terminal SMC and HOSMC strategies as large as possible such that the stability of the uncertain closed-loop systems (5) and (6) is guaranteed. The problem is that the magnitude of chattering is proportional to the size of gains and the sampling period, which deteriorates the control accuracy, especially for the embedded system with a low sampling frequency.
- Even with large gains, the implicit-Euler discretizatoins of SMC can remove the numerical chattering in the absence of noises, but the method requires the knowledge of unavailable term , making it difficult to be implemented in such cases.
3. Proposed Proxy-Based Super-Twisting Algorithm (PSTA)
Continuous-Time Expression of PSTA
4. Discretization Scheme of PSTA
5. Experiments
5.1. Experiment Setup
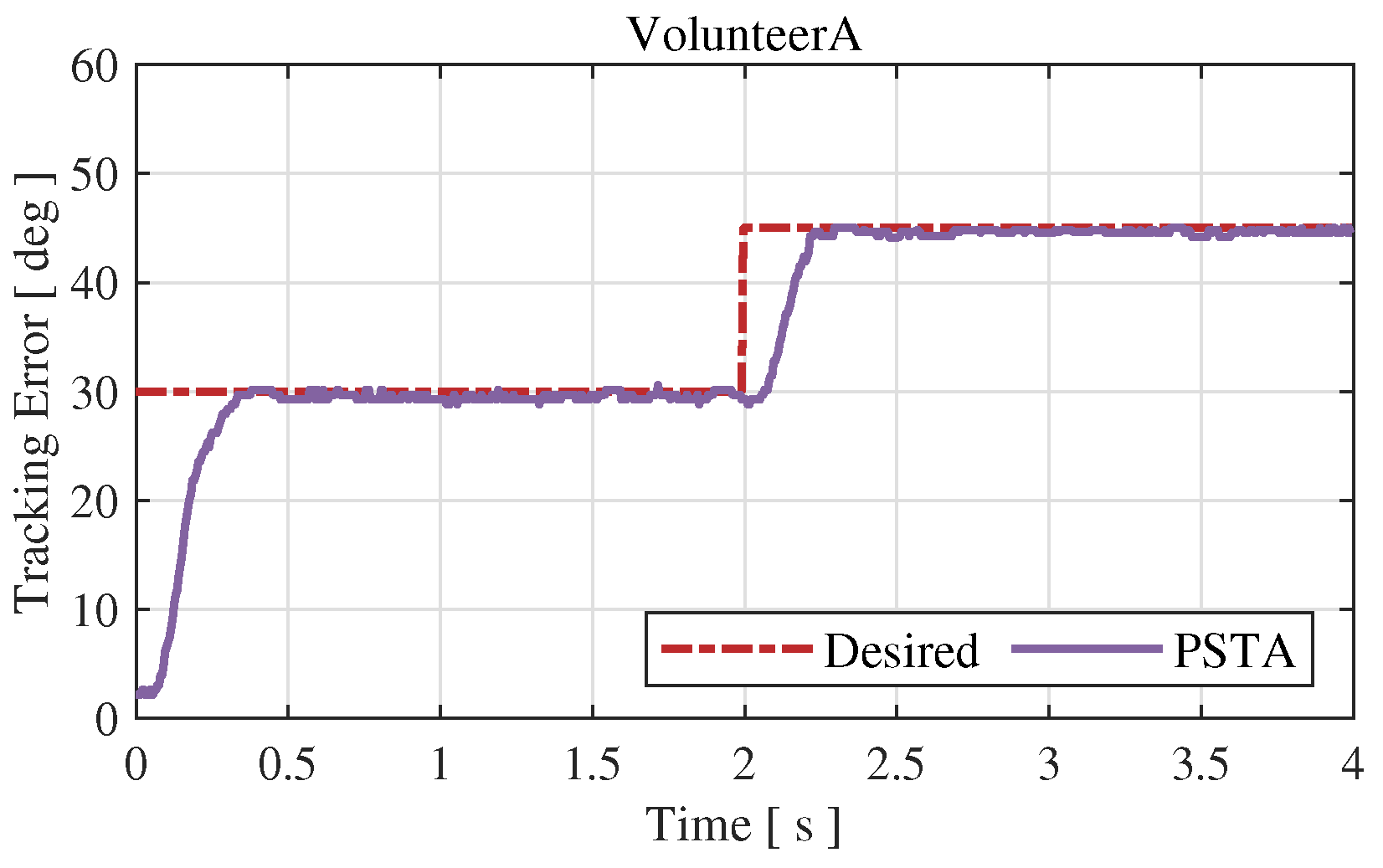
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FES | Functional electrical stimulation |
| MP joint | Finger metacarpophalangeal joint |
| SMC | Sliding mode control |
| STA | Super-twisting algorithm |
| PSTA | Proxy-based super-twisting algorithm |
References
- Furlan, J.C.; Pakosh, M.; Craven, B.C.; Popovic, M.R. Insights on the Potential Mechanisms of Action of Functional Electrical Stimulation Therapy in Combination with Task-Specific Training: A Scoping Review. Neuromodul. J. Int. Neuromodul. Soc. 2022, 25, 1280–1288. [Google Scholar] [CrossRef] [PubMed]
- Lopes, P.; Ion, A.; Baudisch, P. Impacto: Simulating Physical Impact by Combining Tactile Stimulation with Electrical Muscle Stimulation. In Proceedings of the 28th Annual ACM Symposium on User Interface Software & Technology, UIST ’15, Charlotte, NC, USA, 8–11 November 2015; ACM Digital Library: New York, NY, USA, 2015; pp. 11–19. [Google Scholar] [CrossRef]
- Remsik, A.B.; van Kan, P.L.E.; Gloe, S.; Gjini, K.; Williams, L., Jr.; Nair, V.; Caldera, K.; Williams, J.C.; Prabhakaran, V. BCI-FES With Multimodal Feedback for Motor Recovery Poststroke. Front. Hum. Neurosci. 2022, 16, 725715. [Google Scholar] [CrossRef] [PubMed]
- Ikura, I.; Katsura, S. Servo Control of Finger MP Joint by Functional Electrical Stimulation of Lumbrical and Extensor Digitorum Muscle. In Proceedings of the 2022 15th International Conference on Human System Interaction (HSI), Melbourne, Australia, 28–31 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Honda, K.; Nakashima, Y.; Hua, C.; Yamamoto, M. Influence of Combined Vibration and Electrical Stimulation on Latency of Kinesthetic Illusion. J. Robot. Mechatronics 2023, 35, 823–833. [Google Scholar] [CrossRef]
- Sharma, N.; Kirsch, N.A.; Alibeji, N.A.; Dixon, W.E. A Non-Linear Control Method to Compensate for Muscle Fatigue during Neuromuscular Electrical Stimulation. Front. Robot. 2017, 4, 68. [Google Scholar] [CrossRef]
- Bao, X.; Sheng, Z.; Dicianno, B.E.; Sharma, N. A Tube-Based Model Predictive Control Method to Regulate a Knee Joint With Functional Electrical Stimulation and Electric Motor Assist. IEEE Trans. Control. Syst. Technol. 2021, 29, 2180–2191. [Google Scholar] [CrossRef]
- Ajoudani, A.; Erfanian, A. A Neuro-Sliding-Mode Control With Adaptive Modeling of Uncertainty for Control of Movement in Paralyzed Limbs Using Functional Electrical Stimulation. IEEE Trans. Biomed. Eng. 2009, 56, 1771–1780. [Google Scholar] [CrossRef]
- Sharma, N.; Stegath, K.; Gregory, C.M.; Dixon, W.E. Nonlinear Neuromuscular Electrical Stimulation Tracking Control of a Human Limb. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 17, 576–584. [Google Scholar] [CrossRef] [PubMed]
- Kobravi, H.R.; Erfanian, A. Decentralized adaptive robust control based on sliding mode and nonlinear compensator for the control of ankle movement using functional electrical stimulation of agonist-antagonist muscles. J. Neural Eng. 2009, 6, 046007. [Google Scholar] [CrossRef] [PubMed]
- Nekoukar, V.; Erfanian, A. A Decentralized Modular Control Framework for Robust Control of FES-Activated Walker-Assisted Paraplegic Walking Using Terminal Sliding Mode and Fuzzy Logic Control. IEEE Trans. Biomed. Eng. 2012, 59, 2818–2827. [Google Scholar] [CrossRef]
- Brogliato, B.; Polyakov, A.; Efimov, D. The Implicit Discretization of the Supertwisting Sliding-Mode Control Algorithm. IEEE Trans. Autom. Control 2020, 65, 3707–3713. [Google Scholar] [CrossRef]
- Hanan, A.; Levant, A.; Jbara, A. Low-Chattering Discretization of Homogeneous Differentiators. IEEE Trans. Autom. Control 2022, 67, 2946–2956. [Google Scholar] [CrossRef]
- Hanan, A.; Jbara, A.; Levant, A. Homogeneous low-chattering sliding mode discretization. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 6–9 December 2022; pp. 4276–4281. [Google Scholar] [CrossRef]
- Sakaino, S.; Kitamura, T.; Mizukami, N.; Tsuji, T. High-Precision Control for Functional Electrical Stimulation Utilizing a High-Resolution Encoder. IEEJ J. Ind. Appl. 2021, 10, 124–133. [Google Scholar] [CrossRef]
- Wang, H.; Mi, C.; Cao, Z.; Zheng, J.; Man, Z.; Jin, X.; Tang, H. Precise Discrete-Time Steering Control for Robotic Fish Based on Data-Assisted Technique and Super-Twisting-Like Algorithm. IEEE Trans. Ind. Electron. 2020, 67, 10587–10599. [Google Scholar] [CrossRef]
- Rakhtala, S.M. Adaptive gain super twisting algorithm to control a knee exoskeleton disturbed by unknown bounds. Int. J. Dyn. Control 2021, 9, 711–726. [Google Scholar]
- Fazli, E.; Rakhtala, S.M.; Mirrashid, N.; Karimi, H.R. Real-time implementation of a super twisting control algorithm for an upper limb wearable robot. Mechatronics 2022, 84, 102808. [Google Scholar] [CrossRef]
- Tiaiba, H.; Daachi, M.E.H.; Madani, T. Real-time adaptive super twisting algorithm based on PSO algorithm: Application for an exoskeleton robot. In Robotica; Cambridge University Press: Cambridge, UK, 2024; pp. 1–26. [Google Scholar] [CrossRef]
- Rakhtala, S.M.; Ghayebi, R. Real time control and fabrication of a soft robotic glove by two parallel sensors with MBD approach. Med. Eng. Phys. 2022, 100, 103743. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, M.; Du, F. Robust Finite-Time Command-Filtered Backstepping Control for Flexible-Joint Robots with Only Position Measurements. IEEE Trans. Syst. Man. Cybern. Syst. 2024, 54, 1263–1275. [Google Scholar] [CrossRef]
- Zhang, M.; Jing, X.; Zhou, Z.; Sun, M. Rapid and restricted swing control via adaptive output feedback for 5-DOF tower crane systems. Mech. Syst. Signal Process. 2024, 212, 111283. [Google Scholar] [CrossRef]
- Qian, Y.; Zhang, H.; Hu, D. Finite-time neural network-based hierarchical sliding mode antiswing control for underactuated dual ship-mounted cranes with unmatched sea wave disturbances suppression. IEEE Trans. Neural Netw. Learn. Syst. 2023; in press. [Google Scholar]
- Kikuuwe, R.; Yasukouchi, S.; Fujimoto, H.; Yamamoto, M. Proxy-based sliding mode control: A safer extension of PID position control. IEEE Trans. Robot. 2010, 26, 670–683. [Google Scholar] [CrossRef]
- Kikuuwe, R. Sliding motion accuracy of proxy-based sliding mode control subjected to measurement noise and disturbance. Eur. J. Control 2021, 58, 114–122. [Google Scholar] [CrossRef]
- Acary, V.; Brogliato, B.; Orlov, Y.V. Chattering-Free Digital Sliding-Mode Control with State Observer and Disturbance Rejection. IEEE Trans. Autom. Control 2012, 57, 1087–1101. [Google Scholar] [CrossRef]
- Acary, V.; Brogliato, B. Implicit Euler numerical scheme and chattering-free implementation of sliding mode systems. Syst. Control Lett. 2010, 59, 284–293. [Google Scholar] [CrossRef]
- Jin, S.; Kikuuwe, R.; Yamamoto, M. Improving Velocity Feedback for Position Control by Using a Discrete-Time Sliding Mode Filtering with Adaptive Windowing. Adv. Robot. 2014, 28, 943–953. [Google Scholar] [CrossRef]
- Haeufle, D.; Günther, M.; Bayer, A.; Schmitt, S. Hill-type muscle model with serial damping and eccentric force–velocity relation. J. Biomech. 2014, 47, 1531–1536. [Google Scholar] [CrossRef] [PubMed]
- Ferrarin, M.; Pedotti, A. The relationship between electrical stimulus and joint torque: A dynamic model. IEEE Trans. Rehabil. Eng. 2000, 8, 342–352. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Xiong, X.; Chen, G.; Lou, Y.; Huang, R.; Kamal, S. Discrete-Time Implementation of Super-Twisting Control With Semi-Implicit Euler Method. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 99–103. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. Strict Lyapunov Functions for the Super-Twisting Algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Moreno, J.A. On strict Lyapunov Functions for some non-homogeneous super-Twisting algorithms. J. Frankl. Inst. 2014, 351, 1902–1919. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, W.X.; Ding, S. An Adaptive SOSM Controller Design by Using a Sliding-Mode-Based Filter and its Application to Buck Converter. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 2409–2418. [Google Scholar] [CrossRef]
- Seeber, R.; Reichhartinger, M. Conditioned Super-Twisting Algorithm for systems with saturated control action. Automatica 2020, 116, 108921. [Google Scholar] [CrossRef]
- Seeber, R.; Horn, M. Stability proof for a well-established super-twisting parameter setting. Automatica 2017, 84, 241–243. [Google Scholar] [CrossRef]
- Xiong, X.; Bai, Y.; Shi, R.; Kamal, S.; Wang, Y.; Lou, Y. Discrete-Time Twisting Algorithm Implementation with Implicit–Euler ZOH Discretization Method. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3435–3439. [Google Scholar] [CrossRef]
- Levant, A. Quasi-continuous high-order sliding-mode controllers. IEEE Trans. Autom. Control 2005, 50, 1812–1816. [Google Scholar] [CrossRef]
- Koch, S.; Reichhartinger, M. Discrete-time equivalents of the super-twisting algorithm. Automatica 2019, 107, 190–199. [Google Scholar] [CrossRef]
- Xiong, X.; Liu, Z.; Kamal, S.; Jin, S. Discrete-Time Super-Twisting Observer with Implicit Euler Method. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 1288–1292. [Google Scholar] [CrossRef]
- Hua, C.; Nakashima, Y.; Yamamoto, M. On a Precise Control for MP Joint of Human Index Finger Using Functional Electrical Stimulation—Basic Characteristics of the Joint Movement. In Proceedings of the 2020 IEEE/SICE International Symposium on System Integration (SII), Honolulu, HI, USA, 12–15 January 2020; pp. 1324–1327. [Google Scholar] [CrossRef]
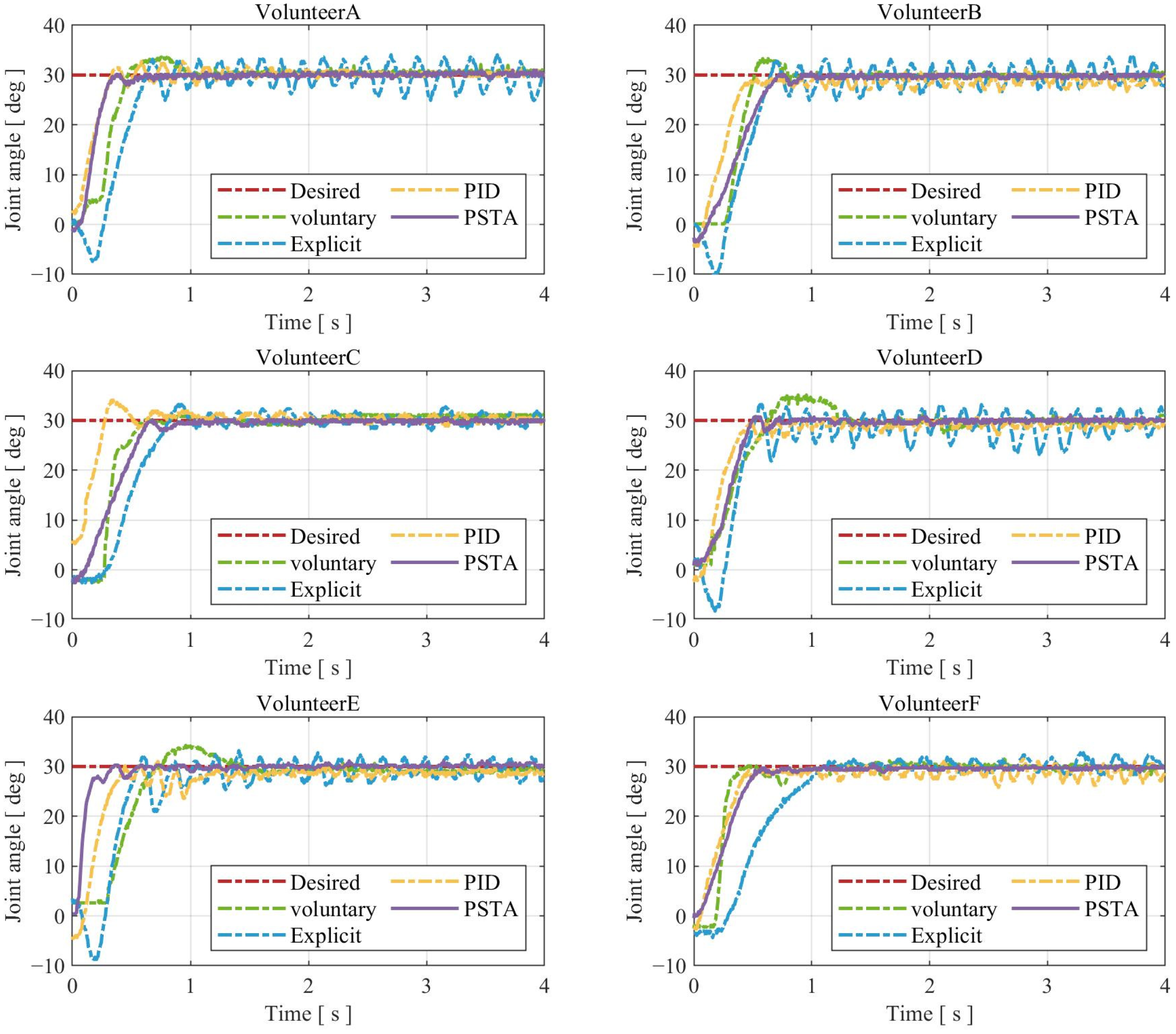
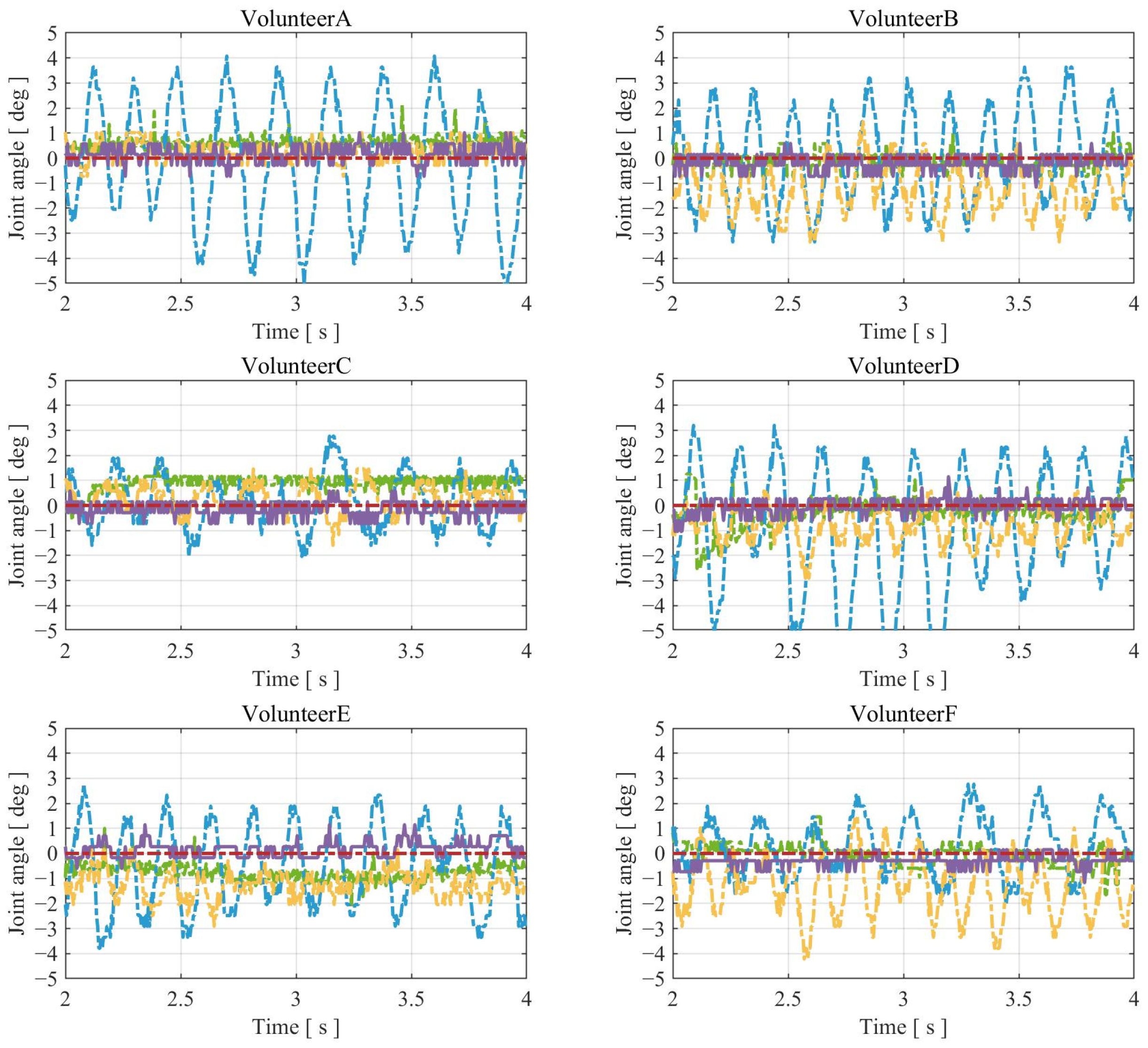
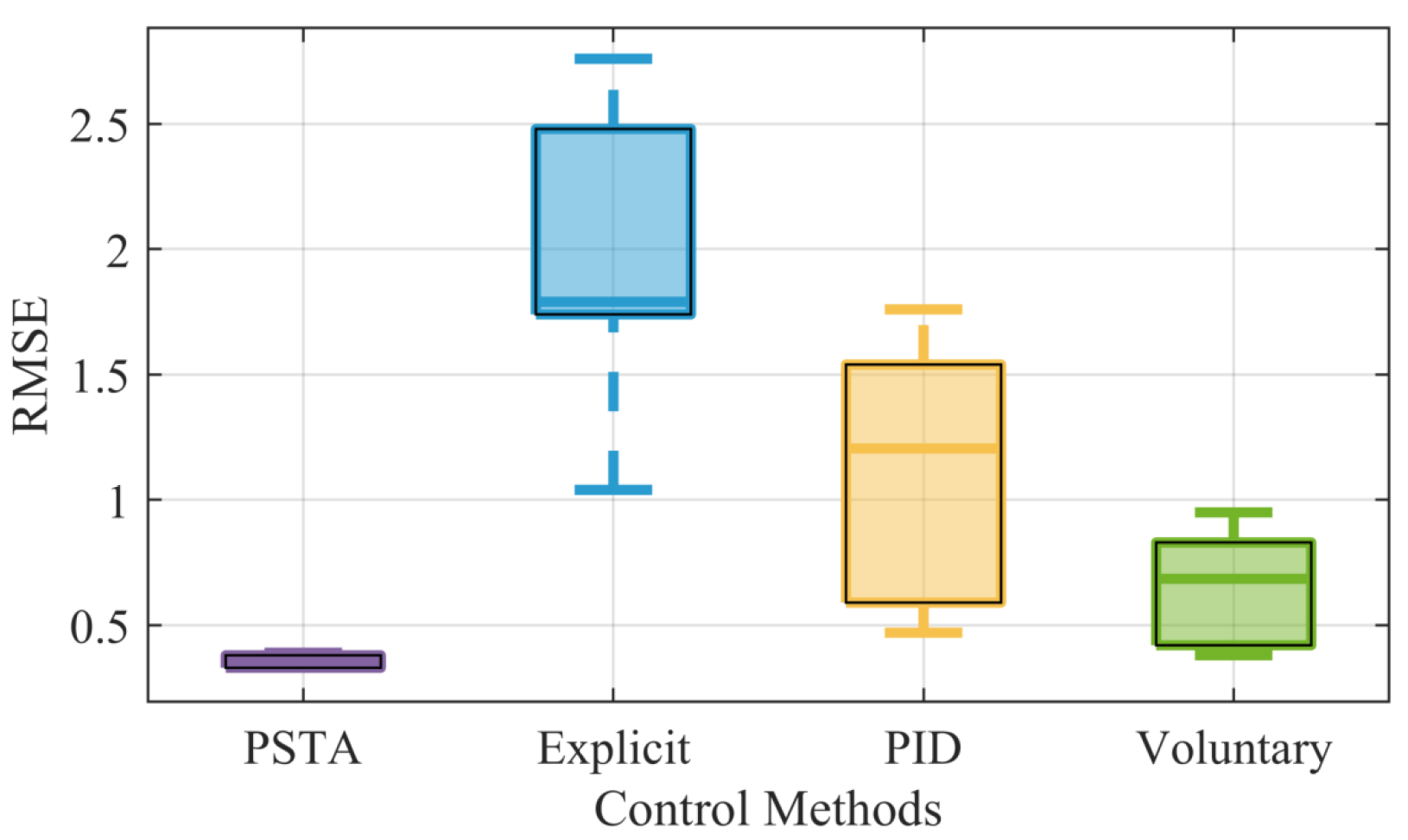
| Volunteer | Metric | PSTA | Explicit | PID | Voluntary |
|---|---|---|---|---|---|
| A | RMSE | 0.39 | 2.48 | 0.47 | 0.67 |
| SSE | 0.33 | 0.33 | 0.33 | 0.67 | |
| B | RMSE | 0.35 | 1.84 | 1.54 | 0.38 |
| SSE | 0.02 | 4.16 | 0.02 | 0.02 | |
| C | RMSE | 0.33 | 1.04 | 0.59 | 0.95 |
| SSE | 0.08 | 0.02 | 0.08 | 1.34 | |
| D | RMSE | 0.33 | 2.76 | 1.06 | 0.70 |
| SSE | 0.02 | 1.04 | 0.08 | 1.04 | |
| E | RMSE | 0.35 | 1.74 | 1.35 | 0.83 |
| SSE | 0.02 | 8.46 | 1.36 | 0.44 | |
| F | RMSE | 0.38 | 1.74 | 1.76 | 0.42 |
| SSE | 0.08 | 0.08 | 0.08 | 0.08 |
| PSTA | Explicit | PID | |
|---|---|---|---|
| Average value [] | 420 | 199 | 265 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Xiong, X.; Honda, K.; Okunami, S.; Yamamoto, M. FES Control of a Finger MP Joint with a Proxy-Based Super-Twisting Algorithm. Appl. Sci. 2024, 14, 4905. https://doi.org/10.3390/app14114905
Chen H, Xiong X, Honda K, Okunami S, Yamamoto M. FES Control of a Finger MP Joint with a Proxy-Based Super-Twisting Algorithm. Applied Sciences. 2024; 14(11):4905. https://doi.org/10.3390/app14114905
Chicago/Turabian StyleChen, Hua, Xiaogang Xiong, Koki Honda, Shouta Okunami, and Motoji Yamamoto. 2024. "FES Control of a Finger MP Joint with a Proxy-Based Super-Twisting Algorithm" Applied Sciences 14, no. 11: 4905. https://doi.org/10.3390/app14114905
APA StyleChen, H., Xiong, X., Honda, K., Okunami, S., & Yamamoto, M. (2024). FES Control of a Finger MP Joint with a Proxy-Based Super-Twisting Algorithm. Applied Sciences, 14(11), 4905. https://doi.org/10.3390/app14114905






