Prediction of Tooth Profile Deviation for WEDM Rigid Gears Based on ISSA-LSSVM
Abstract
1. Introduction
2. Methodology
2.1. LSSVM Model
2.2. Sparrow Search Algorithm
2.3. Improved Sparrow Search Algorithm
2.3.1. Improved Tent Chaotic Mapping
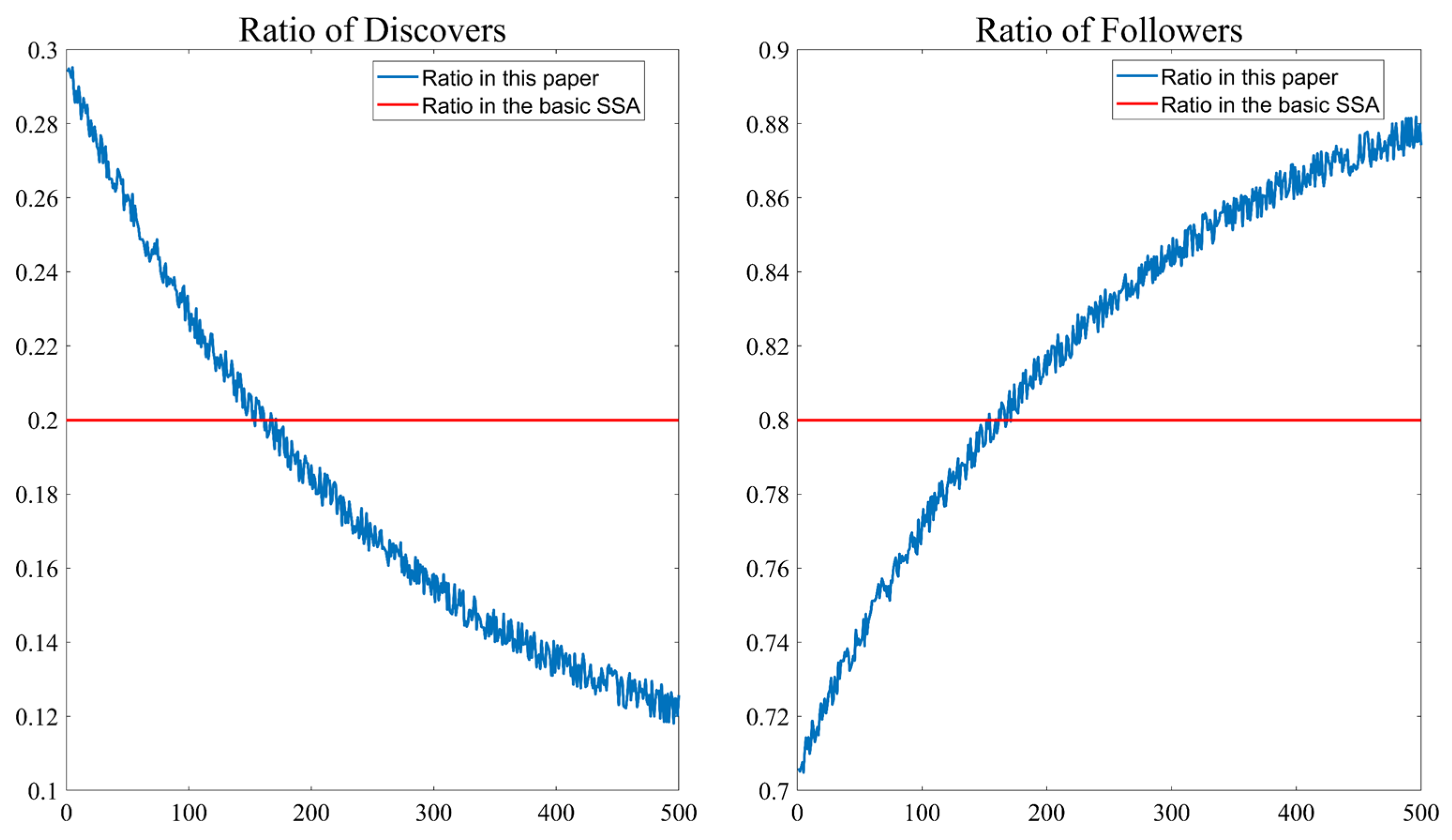
2.3.2. Adaptive Adjustment Strategy
2.3.3. Dynamic Inertia Weights
2.3.4. Grey Wolf Hierarchy Strategy
2.4. Performance Test of ISSA
3. Experimental Section and Methods
3.1. Experimental Conditions
3.2. Orthogonal Test Scheme
3.3. Total Tooth Profile Deviation Measurement
4. Tooth Profile Deviation Prediction Model Based on ISSA-LSSVM
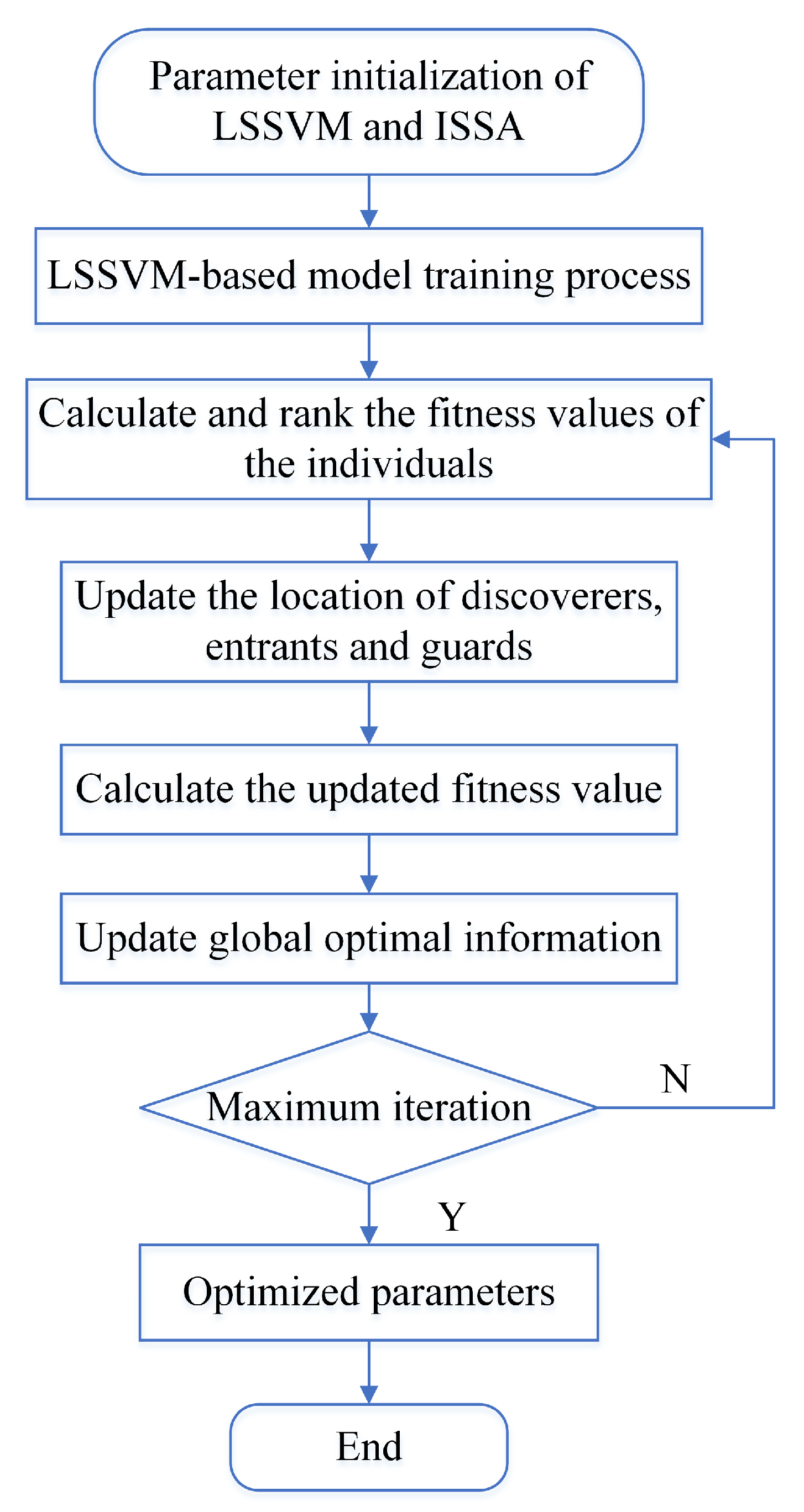
4.1. Model Construction
4.2. Model Setup and Indicators’ Selection
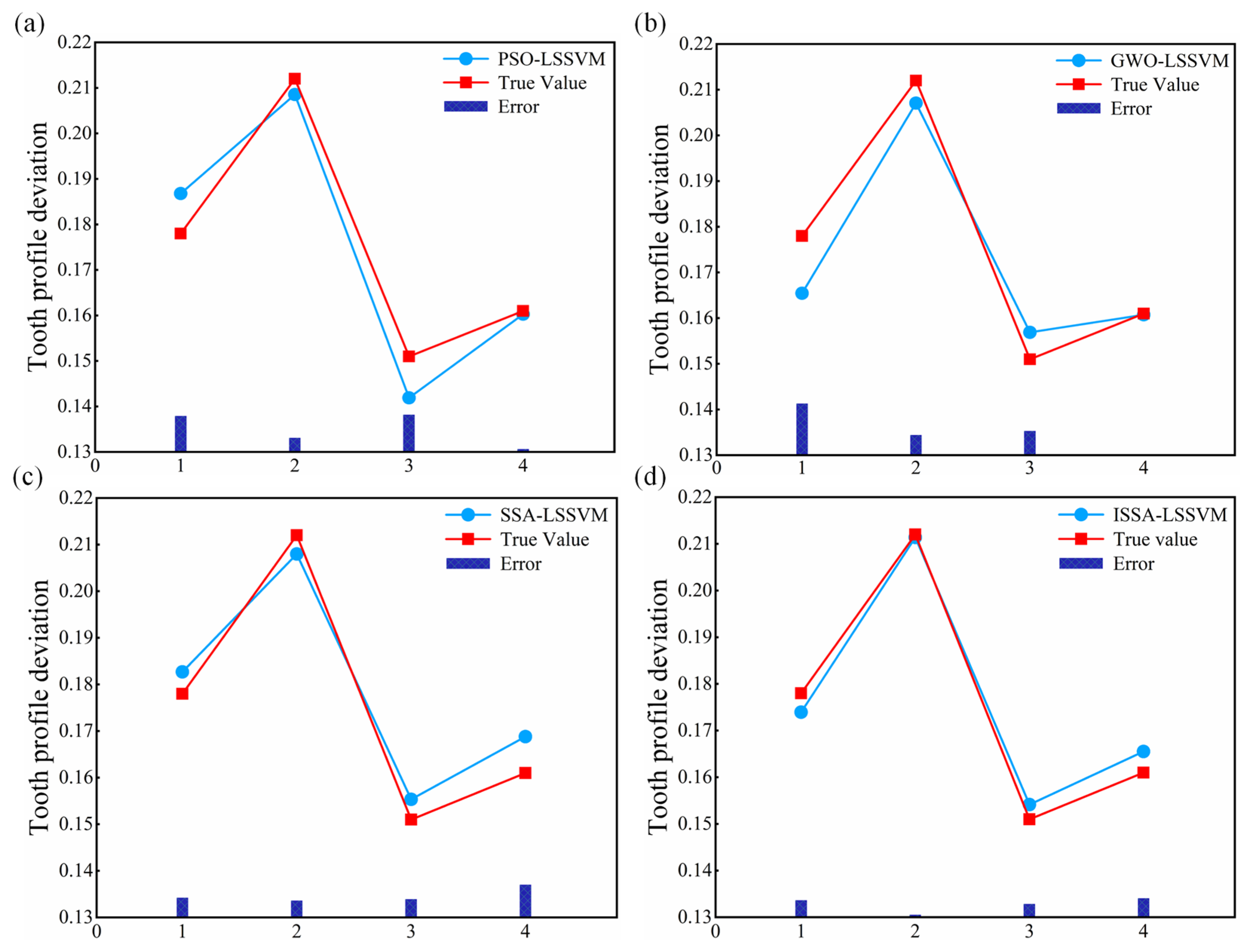
4.3. Model Validation
5. Conclusions
- The standard SSA is improved by introducing Tent chaotic mapping, adaptive adjustment strategy, dynamic inertia weights, and grey wolf hierarchy strategy, which significantly improve the effectiveness and robustness of the algorithm. The improved ISSA is verified to have better convergence speed and global optimization capability than PSO, GWO, and SSA by four different types of benchmark test functions.
- The prediction results and errors of the ISSA-LSSVM tooth profile deviation prediction model were compared with those of the PSO-LSSVM, GWO-LSSVM, and SSA-LSSVM prediction models on different datasets. The results show that the ISSA-LSSVM prediction model has a higher prediction accuracy and faster convergence speed (ISSA-LSSVM model: R2 = 0.9828, RMSE = 0.0029, MAPE = 0.0156).
- The developed ISSA-LSSVM model exhibits superior prediction capability and can provide reliable theoretical guidance for predicting the tooth profile deviation of rigid gears.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Li, C.; Luo, Y.; Cui, L. Simulation of meshing characteristics of harmonic reducer and experimental verification. Adv. Mech. Eng. 2018, 10, 1687814018767494. [Google Scholar] [CrossRef]
- Song, C.; Li, X.; Yang, Y.; Sun, J. Parameter design of double-circular-arc tooth profile and its influence on meshing characteristics of harmonic drive. Mech. Mach. Theory 2022, 167, 104567. [Google Scholar] [CrossRef]
- Guo, Z.; Mao, S.; Li, X.; Ren, Z. Research on the theoretical tooth profile errors of gears machined by skiving. Mech. Mach. Theory 2016, 97, 1–11. [Google Scholar] [CrossRef]
- Yuan, B.; Han, J.; Tian, X.; Xia, L. Optimization and active control of internal gearing power honing process parameters for better gear precision. Mech. Sci. 2022, 13, 449–458. [Google Scholar] [CrossRef]
- Shilong, W.; Shouli, S.U.N.; Jie, Z.; Ling, K.; Cheng, C. Research on Mapping Rules of Hob Geometric Errors and Gear Geometric Precision. J. Mech. Eng. 2013, 49, 119–125. [Google Scholar]
- Sun, S.; Wang, S.; Wang, Y.; Lim, T.; Yang, Y. Prediction and optimization of hobbing gear geometric deviations. Mech. Mach. Theory 2018, 120, 288–301. [Google Scholar] [CrossRef]
- Peng, B.; Luo, Y.; Wang, H.; Niu, T.; Wang, Y. Investigation on the effects of tooth profile deviation in gear rolling process. Int. J. Adv. Manuf. Technol. 2023, 126, 1877–1887. [Google Scholar] [CrossRef]
- Yusron, R.M.; Prasetyo, T.; Pramudia, M. Investigation of Involute Profile Error on Spur Gear Processed using Wire EDM. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1125, 012119. [Google Scholar] [CrossRef]
- Kharka, V.; Jain, N.K.; Gupta, K. Influence of MQL and hobbing parameters on microgeometry deviations and flank roughness of spur gears manufactured by MQL assisted hobbing. J. Mater. Res. Technol. 2020, 9, 9646–9656. [Google Scholar] [CrossRef]
- Mo, S.; Li, Y.; Luo, B.; Wang, L.; Bao, H.; Cen, G.; Huang, Y. Research on the meshing characteristics of asymmetric gears considering the tooth profile deviation. Mech. Mach. Theory 2022, 175, 104926. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Z.; Zhai, W.; Wang, K. Improved analytical calculation model of spur gear mesh excitations with tooth profile deviations. Mech. Mach. Theory 2020, 149, 103838. [Google Scholar] [CrossRef]
- Tsai, C. Simple mathematical approach for analyzing gear tooth profile errors of different gears cut using same power-skiving tool. Mech. Mach. Theory 2022, 177, 105042. [Google Scholar] [CrossRef]
- Chaudhari, R.; Vora, J.J.; Patel, V.; Lacalle, L.N.L.D.; Parikh, D.M. Effect of WEDM Process Parameters on Surface Morphology of Nitinol Shape Memory Alloy. Materials 2020, 13, 4943. [Google Scholar] [CrossRef]
- Sliusarenko, O.; Escudero, G.G.; González, H.; Calleja, A.; Bartoň, M.; Ortega, N.; de Lacalle, L.N.L. Constant probe orientation for fast contact-based inspection of 3D free-form surfaces using (3+2)-axis inspection machines. Precis. Eng. 2023, 84, 37–44. [Google Scholar] [CrossRef]
- Escudero, G.G.; Bo, P.; González-Barrio, H.; Calleja-Ochoa, A.; Bartoň, M.; de Lacalle, L.N.L. 5-axis double-flank CNC machining of spiral bevel gears via custom-shaped tools—Part II: Physical validations and experiments. Int. J. Adv. Manuf. Technol. 2022, 119, 1647–1658. [Google Scholar] [CrossRef]
- Gupta, K.; Jain, N.K. On Micro-Geometry of Miniature Gears Manufactured by Wire Electrical Discharge Machining. Mater. Manuf. Process. 2013, 28, 1153–1159. [Google Scholar] [CrossRef]
- Nain, S.S.; Garg, D.; Kumar, S. Evaluation and analysis of cutting speed, wire wear ratio, and dimensional deviation of wire electric discharge machining of super alloy Udimet-L605 using support vector machine and grey relational analysis. Adv. Manuf. 2018, 6, 225–246. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Zhang, H.; Huang, D.; Zhang, L. The prediction of contact force networks in granular materials based on graph neural networks. J. Chem. Phys. 2023, 158, 054905. [Google Scholar] [CrossRef]
- Zhu, C.; Li, G.; Luis, N.V.J.; Dong, W.; Wang, L. Optimization of RF to alloy elastic modulus prediction based on cuckoo algorithm. Comput. Mater. Sci. 2024, 231, 112515. [Google Scholar] [CrossRef]
- He, J.; Cu, S.; Xia, H.; Sun, Y.; Xiao, W.; Ren, Y. High accuracy roll forming springback prediction model of SVR based on SA-PSO optimization. J. Intell. Manuf. 2023, 1–17. [Google Scholar] [CrossRef]
- Shi, M.; Tan, P.; Qin, L.; Huang, Z. Research on Valve Life Prediction Based on PCA-PSO-LSSVM. Processes 2023, 11, 1396. [Google Scholar] [CrossRef]
- Feng, Y.; Hong, Z.; Gao, Y.; Lu, R.; Wang, Y.; Tan, J. Optimization of variable blank holder force in deep drawing based on support vector regression model and trust region. Int. J. Adv. Manuf. Technol. 2019, 105, 4265–4278. [Google Scholar] [CrossRef]
- Li, S.; Li, S.; Liu, Z.; Vladimirovich, P.A. Roughness prediction model of milling noise-vibration-surface texture multi-dimensional feature fusion for N6 nickel metal. J. Manuf. Process. 2022, 79, 166–176. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, K.; Chen, Y.; Dai, Y.; Liu, Z.; Zhao, K.; Wang, H.; Peng, Z. An Ultra-Fast Power Prediction Method Based on Simplified LSSVM Hyperparameters Optimization for PV Power Smoothing. Energies 2021, 14, 5752. [Google Scholar] [CrossRef]
- Wan, P.; Zou, H.; Wang, K.; Zhao, Z. Hot deformation characterization of Ti–Nb alloy based on GA-LSSVM and 3D processing map. J. Mater. Res. Technol. 2021, 13, 1083–1097. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Ge, Y.; Zhang, J.; Song, G.; Zhu, K. An effective LSSVM-based approach for milling tool wear prediction. Int. J. Adv. Manuf. Technol. 2023, 126, 4555–4571. [Google Scholar] [CrossRef]
- Yu, C.; Xi, Z.; Lu, Y.; Tao, K.; Yi, Z. LSSVM-based color prediction for cotton fabrics with reactive pad-dry-pad-steam dyeing. Chemometr. Intell. Lab. 2020, 199, 103956. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Ouyang, C.; Qiu, Y.; Zhu, D. Adaptive Spiral Flying Sparrow Search Algorithm. Sci. Program. 2021, 2021, 6505253. [Google Scholar] [CrossRef]
- Qiu, S.; Li, A. Application of Chaos Mutation Adaptive Sparrow Search Algorithm in Edge Data Compression. Sensors 2022, 22, 5425. [Google Scholar] [CrossRef] [PubMed]
- Sharma, P.; Raju, S. Metaheuristic optimization algorithms: A comprehensive overview and classification of benchmark test functions. Soft Comput. 2023, 28, 3123–3186. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Q.; Wang, Y.; Wu, D.; Zhang, L.; Shen, B. Research on the Tooth Surface Integrity of Non-Circular Gear WEDM Based on HPSO Optimization SVR. Appl. Sci. 2022, 12, 12858. [Google Scholar] [CrossRef]
- Erkoçak, Y.; Kayır, Y. Analyzing the Impacts of Cutting Parameters on Cutting Forces in the Taguchi Method for Boring High-Alloy White Cast Irons with CBN Inserts. Arab. J. Sci. Eng. 2023, 48, 12569–12585. [Google Scholar] [CrossRef]
- Luo, M.; Zhong, S. Non-Contact Measurement of Small-Module Gears Using Optical Coherence Tomography. Appl. Sci. 2018, 8, 2490. [Google Scholar] [CrossRef]




| Function | Dimension | Range | Fmin |
|---|---|---|---|
| 30 | [−30,30] | 0 | |
| 30 | [−30,30] | 0 | |
| 30 | [−600,600] | 0 | |
| 30 | [−5.12,5.12] | 0 |
| F | Parameters | Optimization Algorithm | |||
|---|---|---|---|---|---|
| ISSA | SSA | GWO | PSO | ||
| F1 | Average value | 6.86 × 10−291 | 6.62 × 10−221 | 0.00218 | 6.08 × 103 |
| Standard deviation | 0 | 0 | 0.00306 | 2.28 × 103 | |
| F2 | Average value | 3.17 × 10−6 | 1.33 × 10−4 | 26.75 | 2.78 × 102 |
| Standard deviation | 5.83 × 10−6 | 2.40 × 10−4 | 0.77846 | 1.48 × 102 | |
| F3 | Average value | 0 | 0 | 6.99 | 27.20 |
| Standard deviation | 0 | 0 | 5.08 | 7.43 | |
| F4 | Average value | 0 | 0 | 0.00297 | 4.07 × 102 |
| Standard deviation | 0 | 0 | 0.00685 | 32.34 | |
| Module (mm) | Pressure Angle (°) | Number of Teeth | Tooth Width (mm) | Tip Diameter (mm) | Root Diameter (mm) |
|---|---|---|---|---|---|
| 0.416 | 20 | 102 | 13 | 42.13 | 43.07 |
| Composition | Si | C | Mn | Cu | Cr | Ni | Fe |
|---|---|---|---|---|---|---|---|
| (%) | 0.17–0.37 | 0.42–0.50 | 0.50–0.80 | ≤0.25 | ≤0.25 | ≤0.25 | balance |
| Level | Peak Current/(A) | Pulse Width/(μs) | Pulse Interval/(µs) | Tracking/ (Hz/s) |
|---|---|---|---|---|
| 1 | 1 | 8 | 6 | 100 |
| 2 | 1.5 | 16 | 7 | 150 |
| 3 | 2 | 24 | 8 | 200 |
| 4 | 2.5 | 32 | 9 | 250 |
| Test Number | Peak Current (A) | Pulse Width (μs) | Pulse Interval (µs) | Tracking (Hz/s) | Fα (mm) |
|---|---|---|---|---|---|
| 1 | 1 | 8 | 6 | 100 | 0.151 |
| 2 | 1 | 16 | 7 | 150 | 0.149 |
| 3 | 1 | 24 | 8 | 200 | 0.154 |
| 4 | 1 | 32 | 9 | 250 | 0.157 |
| 5 | 1.5 | 8 | 7 | 200 | 0.146 |
| 6 | 1.5 | 16 | 6 | 250 | 0.155 |
| 7 | 1.5 | 24 | 9 | 100 | 0.161 |
| 8 | 1.5 | 32 | 8 | 150 | 0.173 |
| 9 | 2 | 8 | 8 | 250 | 0.156 |
| 10 | 2 | 16 | 9 | 200 | 0.165 |
| 11 | 2 | 24 | 6 | 150 | 0.178 |
| 12 | 2 | 32 | 7 | 100 | 0.185 |
| 13 | 2.5 | 8 | 9 | 150 | 0.158 |
| 14 | 2.5 | 16 | 8 | 100 | 0.171 |
| 15 | 2.5 | 24 | 7 | 250 | 0.212 |
| 16 | 2.5 | 32 | 6 | 200 | 0.223 |
| Model | R2 | RMSE | MAPE |
|---|---|---|---|
| PSO-LSSVM | 0.9307 | 0.0056 | 0.0327 |
| GWO-LSSVM | 0.9205 | 0.0071 | 0.0357 |
| SSA-LSSVM | 0.9439 | 0.0038 | 0.0226 |
| ISSA-LSSVM | 0.9828 | 0.0029 | 0.0156 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, Z.; Wang, G.; Xu, H. Prediction of Tooth Profile Deviation for WEDM Rigid Gears Based on ISSA-LSSVM. Appl. Sci. 2024, 14, 4596. https://doi.org/10.3390/app14114596
Wang Y, Wang Z, Wang G, Xu H. Prediction of Tooth Profile Deviation for WEDM Rigid Gears Based on ISSA-LSSVM. Applied Sciences. 2024; 14(11):4596. https://doi.org/10.3390/app14114596
Chicago/Turabian StyleWang, Yazhou, Zhen Wang, Gang Wang, and Huike Xu. 2024. "Prediction of Tooth Profile Deviation for WEDM Rigid Gears Based on ISSA-LSSVM" Applied Sciences 14, no. 11: 4596. https://doi.org/10.3390/app14114596
APA StyleWang, Y., Wang, Z., Wang, G., & Xu, H. (2024). Prediction of Tooth Profile Deviation for WEDM Rigid Gears Based on ISSA-LSSVM. Applied Sciences, 14(11), 4596. https://doi.org/10.3390/app14114596




