Integrated Extended Kalman Filter and Deep Learning Platform for Electric Vehicle Battery Health Prediction

Abstract

As the demand for electric vehicles (EVs) rises globally, ensuring the safety and reliability of EV battery systems becomes paramount. Accurately predicting the state of health (SoH) and state of charge (SoC) of EV batteries is crucial for maintaining their safe and consistent operation. This paper introduces a novel approach leveraging deep learning methodologies to predict battery SoH, focusing on implementing a system prototype for real-world applications. The proposed system integrates an extended Kalman filter (EKF) with a deep learning framework, forming a system prototype known as FELL, aimed at EV battery diagnosis and prediction. We devise an algorithm utilizing the EKF to estimate the SoH of the battery. We present a detailed overview of the system architecture and implementation, showcasing its predictive capabilities. Experimental results demonstrate the effectiveness of the system in accurately estimating battery SoH with notable improvements in prediction accuracy. Additionally, the FELL system provides users with real-time predictions and comparative analysis across multiple prediction models, offering valuable insights for EV battery management.

1. Introduction

As the global demand for electric vehicles continues to grow, ensuring the safety and reliability of electric vehicle (EV) battery systems is critical. As EVs become more prevalent, the performance and longevity of their batteries become crucial factors affecting vehicle efficiency and operating costs [1,2,3]. Accurately predicting the State of Health (SoH) and State of Charge (SoC) of EV batteries is essential for maintaining their safe and consistent operation. SoH refers to the overall condition and remaining capacity of the battery, while SoC indicates the current level of charge stored in the battery [4,5]. Developing precise and dependable models for predicting SoH and SoC is a significant research challenge in the automotive industry [6,7]. These models must account for various factors such as battery chemistry, temperature, charging cycles, and usage patterns to provide accurate assessments of battery health and charge status. As the automotive industry moves towards electrification, addressing these challenges is crucial for ensuring the sustainable and reliable advancement of EVs as a viable mode of transportation for the future. By overcoming these hurdles, manufacturers can enhance the safety, performance, and longevity of EV batteries, thereby accelerating the adoption of electric vehicles on a global scale.

There is an urgent imperative to foster the development of accurate and dependable predictive models to address the SoH and SoC of EV batteries [8,9]. In this context, leveraging deep learning methodologies emerges as a promising avenue. The deployment of deep learning techniques has demonstrated considerable success across diverse prediction tasks, holding the potential to revolutionize SoH and SoC prediction. While numerous studies delve into utilizing machine learning and deep learning technologies for forecasting electric vehicle battery health [10,11,12], the predominant focus remains on designing algorithmic models, lacking the implementation of system prototypes.

This study aims to introduce a novel research method and implement a system prototype to address this research gap. This research work is expected to assist the electric vehicle industry in addressing challenges related to the predictive diagnosis of battery failures. The significant research contributions of this study are summarized as follows:

(1)

We designed a system model and an algorithm for predicting the SoH of electric vehicle batteries based on the extended Kalman filter (EKF) and implemented it on the network platform.

(2)

Utilizing software engineering principles, we designed and implemented FELL, an electric vehicle battery diagnosis and prediction system based on machine learning. We provide a detailed description of the design approach.

(3)

We implemented five representative deep learning prediction models on the FELL system and demonstrated the results of the system prototype implementation. The outcomes of system testing and experiments also validate the functionality and effectiveness of the model and system prototype developed in this study.

The rest of this paper is organized as follows: In Section 2, we review significant research on predicting the SoH and SoC of EV batteries. Section 3 outlines the mathematical model based on the EKF to predict the battery status of electric vehicles. An EKF-SoH algorithm is presented in this section. Section 4 demonstrates the system design approach. Section 5 presents the implementation results of the system prototype. Section 6 showcases the results of system testing and experiments. Finally, we conclude this study in Section 7.

2. Related Work

In the burgeoning field of EV battery health prediction, a multitude of research endeavors have delved into the efficacy of diverse deep learning (DL) methodologies [13,14]. He et al. [15] systematically review DL methods for lithium battery management, focusing on predicting the remaining useful life (RUL), SoH, and thermal management. DL techniques like RNN, LSTM, CNN, GRU, DBN, DNN, and GAN are evaluated, highlighting their performance and limitations. The study emphasizes DL’s superiority over traditional methods while acknowledging challenges like computational complexity and data acquisition, suggesting future research directions. Kim et al. [16] introduced a deep-learning-based method for forecasting the SoH and RUL of lithium-ion batteries (LIBs), addressing diverse operating conditions and electrochemical properties. Their approach utilizes transfer learning to predict across battery types, minimizing data collection efforts and accurately forecasting SoH, even for in-use batteries. This pioneering study showcases transfer learning’s efficacy in RUL prediction, promising practical battery management system advancements. The study [17] introduces a hybrid attention and deep learning approach for predicting the SoH of lithium-ion batteries. This method integrates temperature difference curves and health features from charging data, incorporating CNN, GRU RNN, and attention mechanisms. Comparative analysis against eleven methods shows superior prediction performance, with estimation errors consistently below 1.3%. The approach is robust to battery variations, ensuring accurate SoH estimation across diverse cells, thus enhancing electric vehicle reliability. In a related contribution, Maleki et al. [18] propose a data-driven framework for lithium-ion battery SoH estimation and forecasting. Their approach combines a DNN model, knowledge transfer, and ARIMA, achieving an impressive approximately 96% accuracy in SoH estimation using only 25% of the training dataset, marking a notable 10% improvement over prior methodologies.

Weddle et al. [19] present a framework for in-operando using fast-rate voltage charge/ discharge responses of Li-ion battery SoH during fast cycling, aiming to mitigate aging variability. Their approach integrates a pseudo-2D model, deep learning, and physical interpretation to diagnose SoH. By simulating electrochemical impacts and utilizing synthetic data for training, they achieve accurate real-time SoH identification during high-rate charge/discharge cycles. Validation against standard analyses underscores the benefits of physics-based model synthesis for deep learning training. Wang et al. [20] propose a method for the accurate prediction of lithium-ion battery RUL, addressing complex degradation mechanisms and operational noise. Their approach combines complete ensemble empirical mode decomposition with adaptive noise and a Transformer-based network to separately handle short-term fluctuations and long-term residuals. Validated on public datasets, their method surpasses advanced approaches in prediction accuracy and training time, demonstrating its effectiveness and superiority. Yu et al. [21] introduced a physics-informed ensemble deep learning (PIEDL) framework to enhance SoC estimation in lithium-ion batteries. They integrate physical information extracted from a simplified electrochemical model (SEM) into the DL model, forming the physics-informed deep learning (PIDL) component. The ensemble deep learning (EDL) component combines DL models enhanced by various techniques, demonstrating superior SoC estimation compared to individual models in rigorous evaluations. In another contribution, the paper [22] presents a comprehensive review of recent advancements in deep learning for lithium-ion battery SoC estimation. It outlines challenges, introduces a general deep learning framework, and reviews prevalent deep neural networks such as fully connected, recurrent, and convolutional networks for SoC estimation. The study underscores deep learning’s potential in bridging battery big data, and traditional SoC estimation methods, providing insights into future opportunities and challenges.

While numerous studies have focused on designing various deep learning models to predict the RUL and SoH of EV batteries, there remains a dearth of research on system prototypes that implement predictive models. To address this gap, our study not only devises a system model for predicting battery SoH but also implements a corresponding system prototype.

3. System Modeling and Mathematical Formulation

EKF technology stands out as a compelling option for estimating EV battery SoH owing to several inherent advantages. Firstly, EKF, rooted in Bayesian estimation principles, can assimilate prior knowledge of battery behavior and dynamics into the estimation process. This renders EKF particularly adept at modeling nonlinear and time-varying systems, traits commonly encountered in the degradation processes of EV batteries. Through the utilization of a mathematical battery behavior model, EKF effectively monitors changes in battery health over time, thus enhancing accuracy and reliability.

Moreover, EKF offers computational efficiency, making it suitable for real-time applications such as onboard battery health monitoring in EVs. Unlike ML and DL techniques, which often demand substantial data volumes for training and complex computational resources, EKF can operate efficiently even with limited computational resources. This characteristic renders it an appealing choice for embedded systems in EVs, where computational constraints may be prevalent. In contrast to data-driven ML and DL approaches that heavily rely on training data to generalize patterns, EKF employs a deterministic model of battery behavior to estimate SoH. This can prove advantageous in scenarios with limited historical data availability or when acquiring accurate ground truth labels for training ML/DL models proves challenging. Additionally, the transparency and interpretability of the mathematical model employed in EKF foster a deeper understanding of the underlying physical processes governing battery degradation. This, in turn, aids in the development of more robust and interpretable battery health estimation algorithms.

This study presents a method and mathematical model for estimating the SoH of electric vehicle batteries using EKF technology. Within the EKF framework’s state space representation, we define a state vector, denoted by $\mathbf{x}$, which represents the battery’s relevant characteristics. The state vector $\mathbf{x}$ is formally expressed as Equation (1), where V is the terminal voltage of the battery, $I_x$ is the current flowing through the battery which represents the system’s internal state at a given time, T is the temperature of the battery, $SoC$ is the state of charge of the battery, representing the remaining capacity of the battery relative to its fully charged state, and C is the capacity of the battery, reflecting its ability to store and deliver charge effectively over time.

$$\mathbf{x}={[V,I_x,T,SoC,C]}^T$$

(1)

The input vector $\mathbf{u}$ comprises factors that influence battery behavior. In the context of estimating the SoH of electric vehicle batteries, typical factors affecting battery behavior include charging/discharging current (I), representing the current flowing into or out of the battery during charging or discharging processes, and temperature (T), which denotes the temperature of the battery itself. Temperature significantly impacts battery performance and degradation. Therefore, the input vector $\mathbf{u}$ can be defined as follows (Equation (2)):

$$\mathbf{u}={[I,T]}^T$$

(2)

Let $\mathbf{z}$ represent a measurement vector that includes observed battery parameters such as voltage ($V_{observed}$), current ($I_{observed}$), and temperature ($T_{observed}$). Then, $\mathbf{z}$ is defined as follows (Equation (3)):

$$\mathbf{z}={[V_{observed},I_{observed},T_{observed}]}^T$$

(3)

Then, we establish a measurement model that correlates the observed measurements to the battery’s internal state, which can be defined as Equation (4), where $h\left(X\right)$ is the measurement model function and V denotes measurement noise. The measurement model function, $h\left(\mathbf{x}\right)$, relates the battery’s internal state vector, $\mathbf{x}$, to the observed measurements. In the context of electric vehicle battery SoH estimation, this function relates the battery’s internal state, such as voltage, current, and temperature, to the observed measurements. $h\left(\mathbf{x}\right)$ can be described as a mapping from the battery’s internal state vector $\mathbf{x}$ to the observed measurements $\mathbf{z}$. This mapping considers the relationship between the battery’s internal state and the measurements obtained from sensors. The specific mathematical expression for $h\left(\mathbf{x}\right)$ is given by Equation (5):

$$\mathbf{z}=h\left(\mathbf{x}\right)+\mathbf{v}$$

(4)

$$\mathbf{z}=\left[\begin{array}{c}{V}_{\mathrm{observed}}\\ I_{\mathrm{observed}}\\ T_{\mathrm{observed}}\end{array}\right]=h\left(\mathbf{x}\right)+\mathbf{v}=\left[\begin{array}{c}V\\ I\\ T\end{array}\right]+\mathbf{v}$$

(5)

We define a dynamic model function $f(x,u)$ to forecast the evolution of battery characteristics over time based on system dynamics, as shown in Equation (6). Here, ${\mathbf{x}}^{\prime }$ represents the derivative of the state vector with respect to time, $\mathbf{u}$ is the control input vector, and $\mathbf{w}$ represents the process noise. The dynamic model elucidates the battery’s voltage, current, and temperature response during charge and discharge cycles. The dynamic model function, based on system dynamics, incorporates the effects of charge and discharge current, as well as temperature, to forecast the evolution of battery characteristics over time, as described in Equation (7), where $I_u$ denotes the current that is used as a control input (e.g., during charging or discharging operations).

$${\mathbf{x}}^{\prime }=f(\mathbf{x},\mathbf{u})+\mathbf{w}$$

(6)

$$\frac{d}{dt}\left[\begin{array}{c}V\\ I_u\\ T\\ SoC\\ C\end{array}\right]=f\left(\left[\begin{array}{c}V\\ I_u\\ T\\ SoC\\ C\end{array}\right]\right),\left[\begin{array}{c}I\\ T\end{array}\right]+\mathbf{w}$$

(7)

In the state prediction steps, our proposed EKF employs a dynamic model to predict the battery’s internal state at the next time step based on the preceding state and system dynamics. It adjusts the state covariance matrix $\mathbf{P}$ to accommodate uncertainty in the prediction. The prediction process is represented by Equations (8) and (9), where $\mathbf{F}$ denotes the Jacobian matrix of the dynamic model, and $\mathbf{Q}$ denotes the covariance matrix of the process noise.

$$\widehat{\mathbf{x}}(k+1)=\mathbf{f}(\widehat{\mathbf{x}}\left(k\right),\mathbf{u}\left(k\right))$$

(8)

$$\mathbf{P}(k+1)=\mathbf{F}\mathbf{P}\left(k\right){\mathbf{F}}^T+\mathbf{Q}$$

(9)

In the subsequent measurement update step, the EKF computes the Kalman gain using Equation (10) and revises the predicted state and covariance matrix based on the difference between the predicted and observed measurements, as outlined in Equations (11) and (12). Here, $\mathbf{H}$ represents the Jacobian matrix of the measurement model, and $\mathbf{R}$ denotes the covariance matrix of the measurement noise.

$$\mathbf{K}(k+1)=\mathbf{P}(k+1){\mathbf{H}}^T{\left(\mathbf{H}\mathbf{P}(k+1){\mathbf{H}}^T+\mathbf{R}\right)}^{-1}$$

(10)

$$\widehat{\mathbf{x}}(k+1)=\widehat{\mathbf{x}}(k+1)+\mathbf{K}(k+1)(\mathbf{z}(k+1)-\mathbf{h}\left(\widehat{\mathbf{x}}(k+1)\right))$$

(11)

$$\mathbf{P}(k+1)=(I-\mathbf{K}(k+1\left)\mathbf{H}\right)\mathbf{P}(k+1)$$

(12)

$$SoH=\frac{C}{C_i}$$

(13)

To calculate the SoH based on the estimated parameters obtained from the EKF, we further define a degradation model that reflects the relationship between the battery’s internal state and its health status. The parameters are estimated utilizing the EKF framework. The process and measurement models are iteratively employed in the prediction and update steps of the EKF algorithm to estimate the internal state of the battery. The sampling rate represents the time interval between consecutive measurements of the battery’s characteristics (voltage, current, temperature) during the estimation process. In this study, we set the sampling rate to 1 h, a commonly used interval for data collection in battery monitoring systems. The SoC is a critical parameter in battery management systems, indicating the remaining capacity of the battery relative to its fully charged state. SoC is defined as the ratio of the remaining capacity to the battery capacity, typically expressed as a percentage ranging from 0 to 1 or 0 to 100%. Here, 0 represents a fully discharged battery, while 1 represents a fully charged battery. During each iteration of the data collection process, SoC is calculated using the current capacity estimated by the EKF and the battery’s initial capacity.

SoH is commonly associated with the capacity or ability of the battery to store and deliver charge effectively over time. We select a degradation model that best represents the aging process of the battery. Let X represent the state vector estimated by the EKF, with one of its components denoting the battery capacity, labeled as C. Denoting the initial capacity by $C_i$, we express a capacity fade degradation model as Equation (13), where C is the estimated current capacity of the battery, $C_i$ is its initial capacity when new, and SoH represents the state of health of the battery. In this model, as the battery capacity C diminishes over time due to aging, the SoH value will decrease accordingly. When $C=C_i$, SoH will be 1, indicating the battery is in perfect health. As C decreases over time, SoH will also decrease accordingly. The SoH model update rate refers to how frequently the SoH estimation is conducted. In our model, SoH is estimated at regular intervals corresponding to the data collection frequency. The SoH model can be evaluated at different SoC levels to assess its performance under various operating conditions.

This study introduces a novel approach to EV battery SoH prediction through the integration of EKF and DL models. Our research stands out for developing a comprehensive system that harmonizes the strengths of EKF’s deterministic modeling with the data-driven capabilities of deep learning techniques. This integration facilitates more precise and dependable predictions of EV battery SoH by capitalizing on the prior knowledge of battery behavior embedded in the EKF framework and the deep learning models’ ability to discern complex patterns from data. We devised an algorithm utilizing the EKF to estimate the SoH of the EV battery, named the EKF-SoH algorithm. The symbols and definitions in the algorithm are presented in

Table 1. Symbols and definitions in the EKF-SoH algorithm.

Symbols	Descriptions
$C_i$	Initial capacity of the battery
$V_{max}$	Maximum voltage of the battery
$V_{min}$	Minimum voltage of the battery
$I_{max}$	Maximum discharge current
$T_{max}$	Maximum operating temperature of the battery
$C_d$	Depth of discharge during cycling
Q	Process noise covariance matrix
R	Measurement noise covariance matrix
$n_c$	Number of charge–discharge cycles
$n_{tc}$	Number of steps per cycle
$T_s$	Time step in days
X	Initial state of the battery (voltage, current, temperature)
P	Initial covariance matrix for EKF
f	Dynamic model function to simulate battery dynamics
z	Measurement model function to model battery measurements
EKF	Class implementing EKF
$L_t$	List to store time values
$L_{SoH}$	List to store SoH values

. The pseudocode of the EKF-SoH algorithm is shown in Algorithm 1.

By leveraging EKF’s Bayesian estimation principles, our system adeptly integrates prior knowledge of battery dynamics and nonlinear behaviors into the prediction process. This ensures resilience and adaptability to diverse operational conditions and degradation patterns inherent in real-world EV applications. Prior knowledge of battery dynamics utilized in the prediction process involves understanding the relationship between battery internal states (such as voltage, current, temperature, and state of charge) and the observed measurements. This knowledge is integrated into the dynamic and measurement models employed in the EKF. The battery dynamics were modeled at a specific time scale, which may vary depending on the application. Specifically, the battery dynamics were modeled at the sampling rate scale, representing the time interval between consecutive measurements of the battery’s characteristics during the estimation process. Additionally, the incorporation of deep learning models augments the system’s capacity to capture intricate relationships and subtleties in battery health data, thereby enhancing prediction accuracy and generalization performance.

The fusion of EKF and deep learning models in our system represents a significant advancement in EV battery SoH prediction methodologies. It offers a holistic approach that melds the strengths of deterministic and data-driven modeling paradigms, resulting in a versatile and efficient predictive system. This original research contribution holds promise for advancing EV battery management systems, with potential applications in optimizing battery performance, prolonging battery lifespan, and bolstering overall EV reliability and sustainability.

Algorithm 1 EKF-SoH: estimate the SoH of electric vehicle batteries using EKF

Input: $C_i$, $V_{max}$, $V_{min}$, $I_{max}$, $T_{max}$, $C_d$, Q, R, $n_c$, $n_{tc}$, $T_s$, X, P, z

Output: $L_t,L_{SoH}$ 1: Initialize parameters and classes of ekf 2: Initialize initial state, initial covariance, Q, and R 3: Establish a measurement model with Equation (4) 4: EKF forecasts the evolution of battery characteristics over time with Equation (6) 5: $F=$ Identity matrix (linear dynamic model) 6: $Covariance=F·Covariance·F^T+\mathbf{Q}$ 7: Predict the battery’s internal state at the next time step with Equations (8) and (9) 8: $H=$ Identity matrix (linear measurement model) 9: $K=Covariance·H^T·{(H·Covariance·H^T+\mathbf{R})}^{-1}$ 10: Computes the Kalman Gain with Equation (10) 11: $Innovation=Measurement-measurement\_model(current\_state)$ 12: $Current\_state=Current\_state+K·Innovation$ 13: $Covariance=(Identitymatrix-K·H)·Covariance$ 14: update the predicted state and covariance matrix with Equations (11) and (12) 15: for $cycle$ from 1 to $n_c$ do 16:       for $step$ from 1 to $n_{tc}$ do 17:             $t=(cycle-1)*n_{tc}+step$ 18:             $control\_input=T_c$ 19:             $voltage=initial\_state\left[0\right]*(initial\_capacity/100)*C_d$ 20:             $current=I_{max}*sin(t/100)$ 21:             $temperature=T_{max}*sin(t/50)$ 22:             $measurement=[voltage,current,temperature]$ 23:             $predicted\_state=ekf.predict(control\_input,dynamic\_model)$ 24:             $ekf.update(measurement,measurement\_model)$ 25:             $estimated\_capacity=ekf.state\left[0\right]/V_{max}*100$ 26:             $SoH=initial\_SoH\_function\left(t\right)$ 27:             append t to $L_t$ 28:             append $SoH$ to $L_{SoH}$ 29:       end for 30: end for 31: Output: $L_t,L_{SoH}$

4. System Design Based on Software Engineering

To furnish users with a dependable electric vehicle battery prediction and management system, this study devised FELL (fusion of extended Kalman filter learning and deep learning models), a battery health diagnosis and prediction platform integrating the EKF and DL models.

4.1. System Architecture

Figure 1 depicts the FELL system architecture diagram. The system architecture encompasses the essential components requisite for predicting the health of electric vehicle batteries. The presentation layer incorporates the user interfaces module, serving as the front-facing component of the system. This layer comprises web pages or user-friendly graphical user interfaces (GUIs) through which users interact with the system. Its focus lies in providing intuitive and user-friendly interfaces for users to input data, view predictions, and access system functionalities pertinent to EV battery health analysis.

The business logic layer and data access layer comprises two main modules: the authentication module and the core business function module. The authentication module manages user authentication and authorization processes, ensuring that only authorized users can access the system and its functionalities. It implements secure authentication mechanisms such as OAuth, JWT (JSON Web Tokens), or other industry-standard protocols to enhance security. The core business function module serves as the central processing unit of the FELL system, handling requests from the presentation layer, processing data, conducting data analyses, and interacting with the database layer. This module hosts the business logic responsible for predicting battery health indicators such as SoC and SoH. The business logic layer and data access kayer ensures that the system’s backend is scalable, reliable, and efficient in handling varying loads and data processing requirements. The data storage layer houses the database module, responsible for storing and managing the system’s data. It is designed to accommodate structured data related to electric vehicle batteries, including historical battery performance data, sensor readings, user profiles, and analysis results.

The data analysis component entails the processing and analysis of battery-related data collected from electric vehicles. It employs techniques such as statistical analysis, machine learning algorithms, and data visualization to derive insights and patterns. Big data analytic technologies ensure the robustness, scalability, and efficient handling of large volumes of data within this component. The predicting battery SoC component focuses on estimating the current charge level of electric vehicle batteries based on historical data, usage patterns, environmental factors, and other relevant parameters. It involves the use of algorithms such as Kalman filtering, neural networks, or regression models to accurately predict battery SoC. The predicting battery SoH component aims to forecast the overall health condition of electric vehicle batteries over time. It considers factors like battery degradation, cycle life, internal resistance, and capacity fade to assess long-term viability and performance. Utilizing predictive modeling techniques and diagnostic algorithms, it evaluates battery SoH and offers actionable insights for maintenance and replacement strategies.

4.2. Class Diagram

The incorporation of object-oriented programming (OOP) methods is imperative in both the design and implementation phases of the FELL system, aimed at forecasting the health status of electric vehicle batteries. OOP provides a structured and modular framework for system development, facilitating the organization of data and functionality into discrete objects capable of interacting seamlessly. 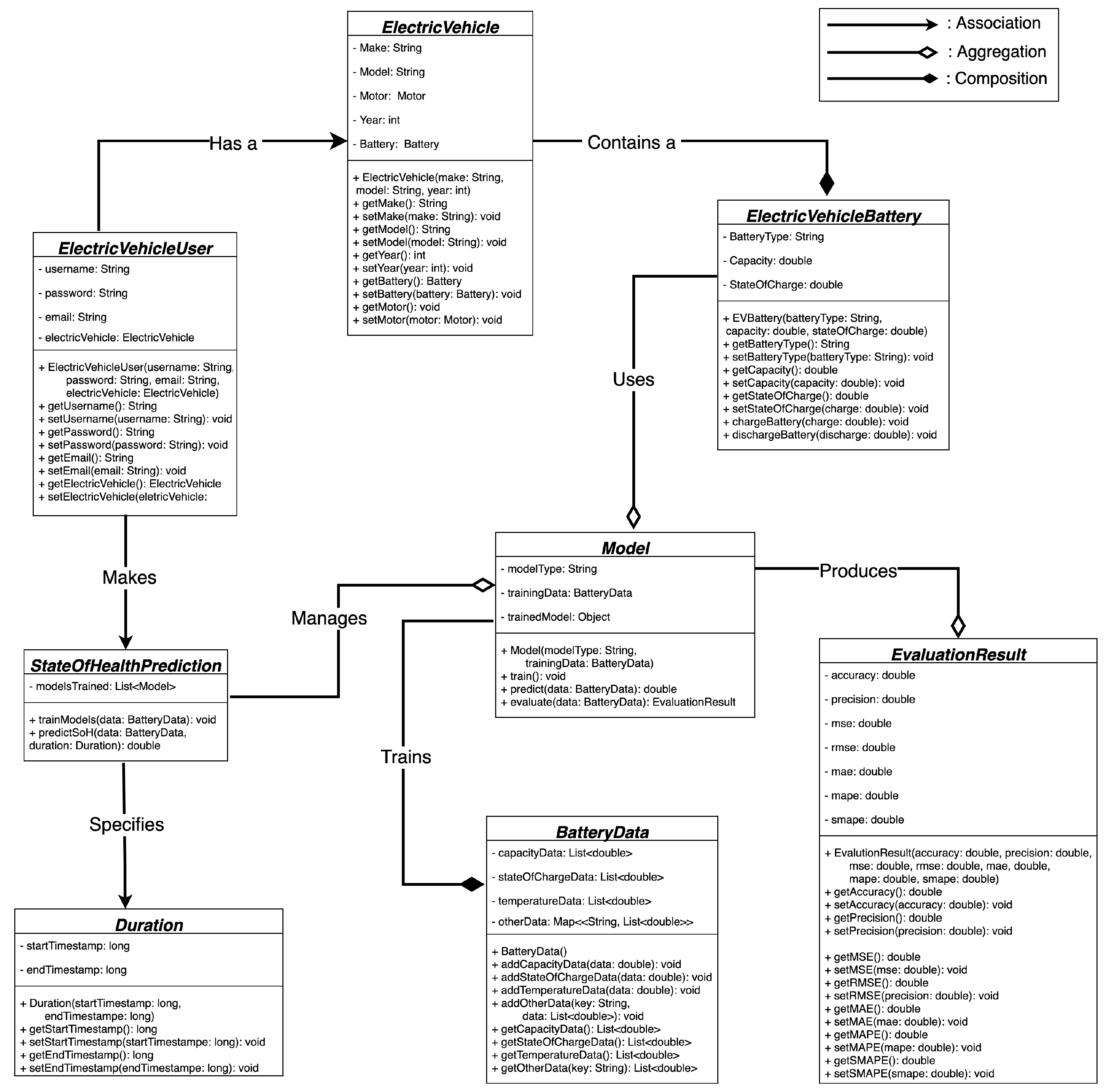As illustrated in Figure 2, the class diagram of the FELL system underscores the pivotal role of OOP principles in orchestrating and managing system components. Through the delineation of entities such as ElectricVehicle, ElectricVehicleBattery, and Model as distinct classes interconnected via composition and aggregation relationships, OOP enables the representation of real-world entities and their interactions in a lucid and intuitive manner. Furthermore, OOP fosters code reuse, scalability, and maintainability, essential attributes in the evolution of intricate systems like FELL. The strategic adoption of object-oriented programming ensures the coherence, flexibility, and extensibility of the FELL system, establishing a robust foundation for the integration of extended Kalman Filter and deep learning models to augment electric vehicle battery health prediction capabilities.

Figure 2 depicts a class diagram of the FELL system, structured upon principles of object-oriented programming. This diagram encompasses eight distinct categories: ElectricVehicle, ElectricVehicleUser, ElectricVehicleBattery, BatteryData, Duration, StateOfHealthPrediction, Model, and EvaluationResult. Notably, ElectricVehicle exhibits a composition relationship with ElectricVehicleBattery, signifying that an ElectricVehicle encompasses an ElectricVehicleBattery within its structure. Additionally, ElectricVehicleUser is linked with ElectricVehicle, illustrating the potential ownership of an electric vehicle by a user. Furthermore, StateOfHealthPrediction is depicted with an aggregation relationship to Model, indicating its role in managing a collection of prediction models. Similarly, Model is portrayed with a composition relationship to BatteryData, suggesting that each model is intricately linked with specific battery data utilized for training and prediction purposes. Moreover, StateOfHealthPrediction is associated with Duration, detailing the time duration specified for SoH prediction. Lastly, Model is shown to possess an aggregation relationship with EvaluationResult, implying the generation of an evaluation result during the process of assessing the model’s performance.

4.3. Interaction Models

We present the sequence model diagram of a use case where electric vehicle users utilize the FELL platform to predict the SoH of their batteries. The use case involves electric vehicle users accessing the FELL platform to predict the SoH of their batteries. Users input various parameters such as usage days, state of charge, battery voltage, current, temperature, and average usage time per day. They then select the desired prediction duration (short, medium, or long-term) and initiate the prediction process. The FELL platform invokes the SoH Prediction Module, which processes the input parameters and predicts the battery’s health status. The predicted SoH result is returned to the platform and displayed to the user, who can take appropriate actions based on the prediction.

Figure 3 is the sequence model diagram illustrating the interactions between the electric vehicle user, the FELL platform, and the SoH prediction module during the prediction process. It consists of a series of steps depicting the flow of control and data between the entities involved. The user interacts with the FELL platform to predict the SoH of their battery. The FELL platform facilitates the prediction process by collecting user input, invoking the SoH prediction module, and displaying the predicted SoH result. The SoH prediction module processes the input parameters, predicts the battery’s health status, and returns the predicted SoH result to the FELL platform. Once the prediction is completed, the FELL platform retrieves the predicted SoH result and displays it to the user. If the prediction fails due to incorrect input parameters or other reasons, the FELL platform will also return an error message to the user and remind the user of the reason for the failed prediction.

5. System Implementation

This study utilizes an open dataset [23] of electric vehicle batteries and employs a specifically designed method based on the EKF to estimate the SoH of the battery, thus exploring its feasibility. We implemented the FELL system using software engineering methods. Figure 4a depicts the homepage of the FELL system website platform implemented in this study. As illustrated, the FELL platform offers users three significant system functions: data analysis, SoH test, and SoC prediction. Figure 4b represents the user interface furnished by the FELL system, facilitating electric vehicle users in inputting fundamental details concerning electric vehicles and batteries. The data supplied by users undergoes secure storage within the system’s backend database, facilitating subsequent processes such as data analysis, algorithmic computations, and training of prediction models.

Figure 5 displays the web page featuring the user interface for the implemented data analysis function (UI 1). As depicted, the FELL website employs a box-and-whisker plot to present users with pertinent statistical analysis results concerning the utilization of electric vehicle batteries. These results encompass battery operating temperature, voltage, electric vehicle mileage, current, and other relevant metrics. Moreover, below each data analysis graph, users can find data analysis conclusions and insights aimed at facilitating their timely understanding of the critical performance aspects of electric vehicle batteries.

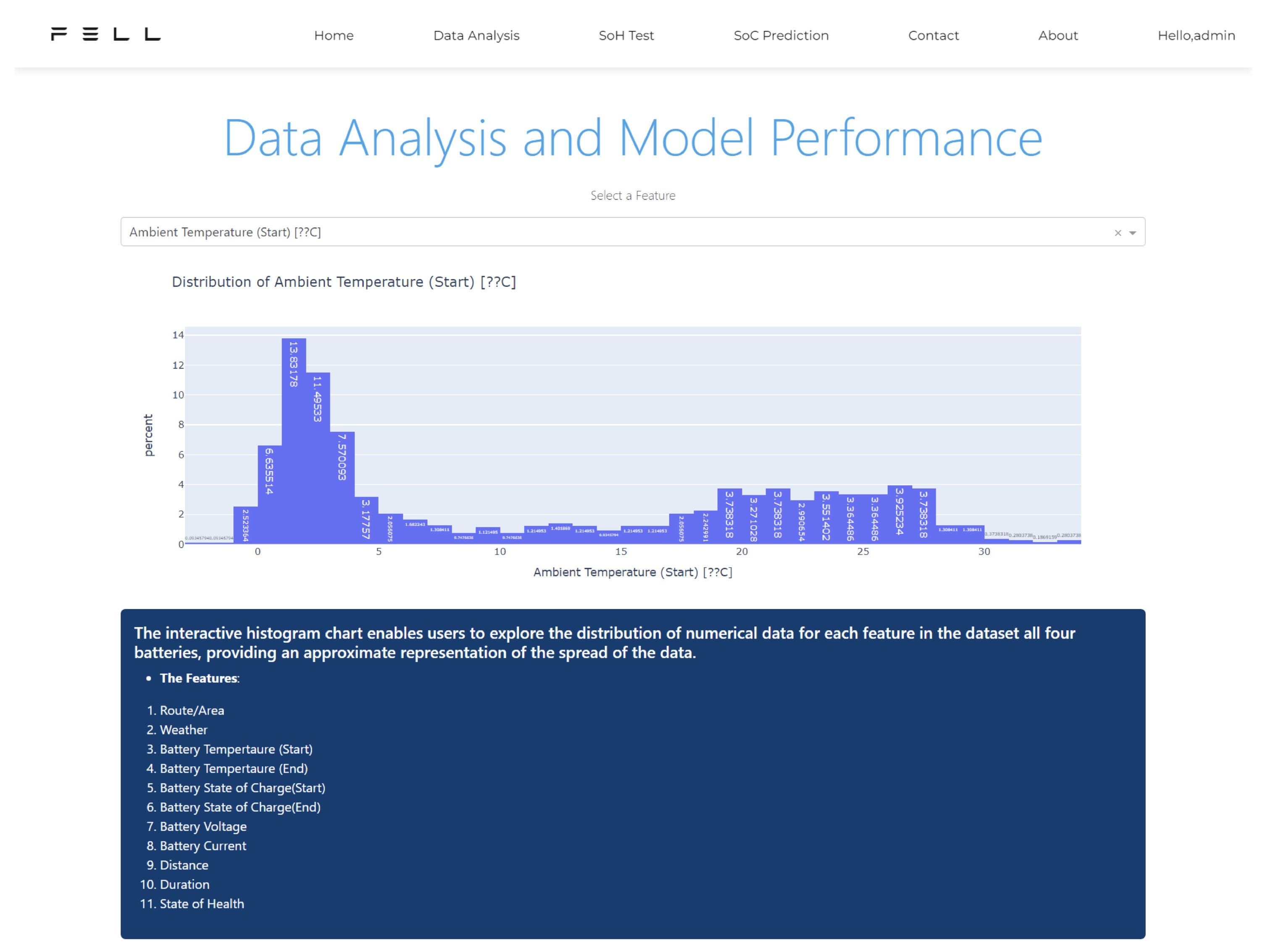
Figure 6 depicts another implemented data analysis function user interface web page. As illustrated, the FELL website employs an interactive histogram, enabling users to select from 11 data analysis options related to electric vehicle batteries. Subsequently, the web page dynamically presents corresponding data analysis results to the user in a timely manner, facilitating their comprehension of battery usage patterns. Moreover, users can utilize the outcomes of data analysis as input values for the predictive battery health function (SoH test) on the FELL website.

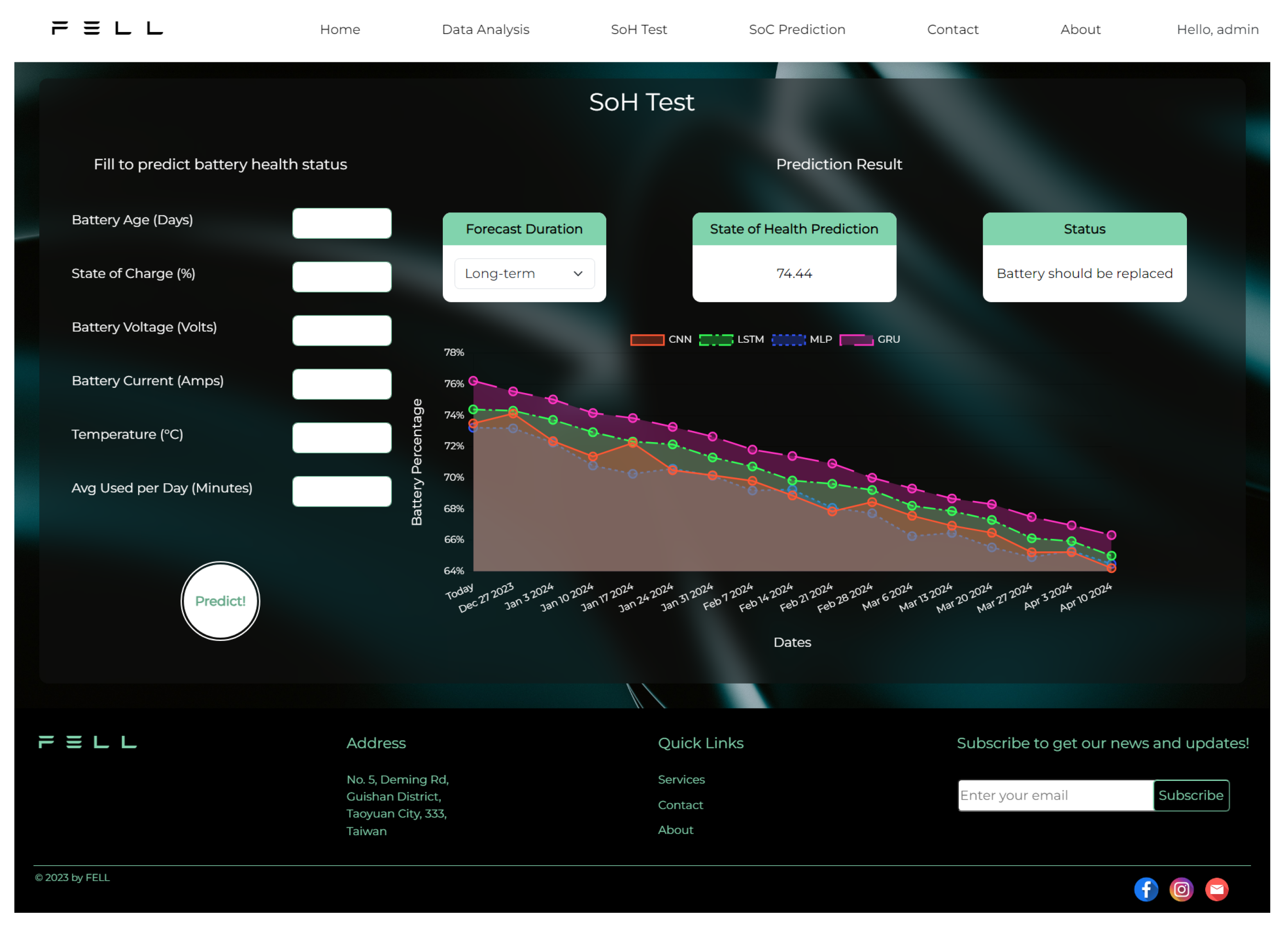
Figure 7 displays the implemented SoH test function user interface web page. Users of the website can input parameters related to electric vehicle batteries, including battery usage days, state of charge, battery voltage, battery current, battery temperature, and the average usage time (in minutes) of electric vehicles per day. Upon clicking the prediction button, the API of the SoH prediction module of the website platform’s back-end system will be invoked, returning the predicted health status of the electric vehicle battery. Users can choose between short, medium, and long-term predictions, and the web page will exhibit the results of electric vehicle battery health predictions based on the user’s selections.

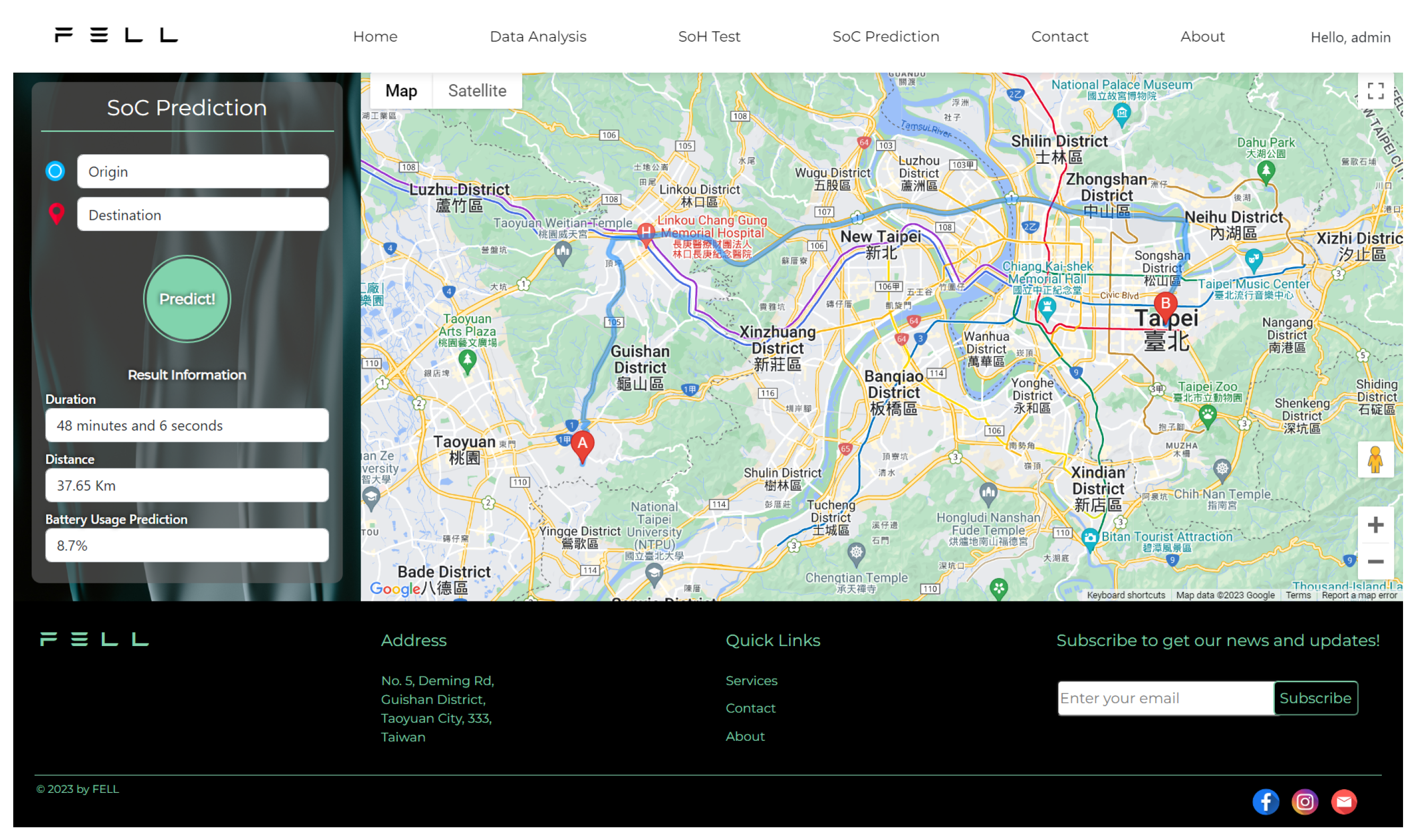
Figure 8 illustrates the user interface webpage of the implemented SoC prediction function. Users can utilize this webpage to forecast electric vehicle battery consumption and plan charging in advance before traveling. Users input the start and destination locations of their trip and click the Predict button. The system invokes the back-end map API and SoC prediction function API, displaying the calculation results on the webpage. This provides the user with the estimated driving distance, driving time, and electric vehicle battery consumption. Importantly, the website system conducts real-time analysis and calculations based on the user’s historical data on electric vehicle battery usage, thereby offering users real-time SoC prediction results.

The motivation for designing the FELL system’s dashboard arises from the imperative to furnish users with an intuitive and comprehensive tool for effectively managing electric vehicle battery health. Given the pivotal transition towards sustainable transportation embodied by electric vehicles, the longevity and performance of their batteries are fundamental to their viability. By providing a centralized hub for monitoring battery health metrics, historical usage patterns, and actionable insights gleaned from sophisticated data analysis techniques, the dashboard aims to empower users with the requisite knowledge to make informed decisions pertaining to maintenance, repair, and optimization strategies. This proactive approach not only enhances the reliability and efficiency of electric vehicle operations but also contributes to the overarching objective of advancing sustainable mobility solutions. Figure 9 depicts the dashboard management interface extended to users by the FELL platform. This dashboard empowers users to swiftly grasp the holistic health status of electric vehicle batteries, incorporating details such as battery usage history, insights derived from data analysis, and the outcomes of model predictions. Furthermore, users retain the autonomy to strategize repair and maintenance actions for electric vehicle batteries, guided by the visualized results presented through diverse graphical representations on the dashboard.

6. System Evaluation and Model Prediction Performance

To assess the efficacy of the proposed functions within the FELL platform, this study employed five prominent deep neural network models to predict the SoH of electric vehicle batteries. Additionally, we conducted an analysis comparing the prediction accuracies of these models. The models utilized encompassed multi-layer perceptron (MLP), convolutional neural network (CNN), long short-term memory (LSTM), gated recurrent unit (GRU), and multi-head self-attention transformer architectures. Evaluation metrics employed to gauge prediction performance consisted of mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and symmetric mean absolute percentage error (SMAPE). The electric vehicle battery usage dataset [23] comprises 38,222 samples. The training dataset constitutes 70% of the total dataset, approximately 26,755 samples. The validation dataset and test dataset each represent 15% of the total dataset, consisting of approximately 5733 samples each.

6.1. EKF Model Effectiveness Evaluation

The experiment conducted in this study aimed to evaluate the effectiveness of the EKF model in estimating the SoH of electric vehicle batteries. Using an 60 Ah lithium battery installed in a BMW i3 electric vehicle (German Marque, Shah Alam, Malaysia) as the subject, we applied the EKF to generate a SoH change curve over time, as illustrated as Figure 10. The x axis of the graph denotes the duration of battery usage in days, while the y axis represents the SoH of the battery. The graph reveals fluctuations in SoH, indicating that, under normal operating conditions, the EKF predicts a decline in the battery’s SoH to 80% after 7810 days of usage. Subsequently, when the SoH falls below 80%, the degradation accelerates, with the SoH plummeting to below 30% after approximately 12,300 days. The SoH of the battery exhibits a rapid decrease from 91% to 80% within the initial period, possibly due to factors such as aggressive driving, extreme temperatures, or fast charging. Subsequently, from day 7810 until day 12,300, the SoH shows an exponential downward trend, decreasing by less than 30%, which could be attributed to aging effects and prolonged usage. Potential causes for the abrupt change in SoH observed in Figure 10 include unexpected high discharge rates or deep discharges beyond typical operational parameters, both of which can lead to significant and sudden capacity degradation. Furthermore, sensor inaccuracies or calibration issues might result in sudden drops in the measured SoH.

Figure 11a,b illustrate the application of EKF simulation to estimate the state of health (SoH) change distribution across 20 lithium batteries used in electric vehicles. Figure 11a presents the distribution map of SoH, while Figure 11b displays the kernel density estimation (KDE) of SoH. The simulation outcomes reveal that the EKF, as proposed in this study, predominantly estimates SoH values above 90% for electric vehicle lithium batteries, with additional values clustered within the range of 20–85%. These results align with the anticipated performance characteristics of the majority of batteries employed in electric vehicles. Our observations indicate that the model and method proposed in this study effectively estimate the SoH of electric vehicle batteries.

6.2. Models Prediction Performance

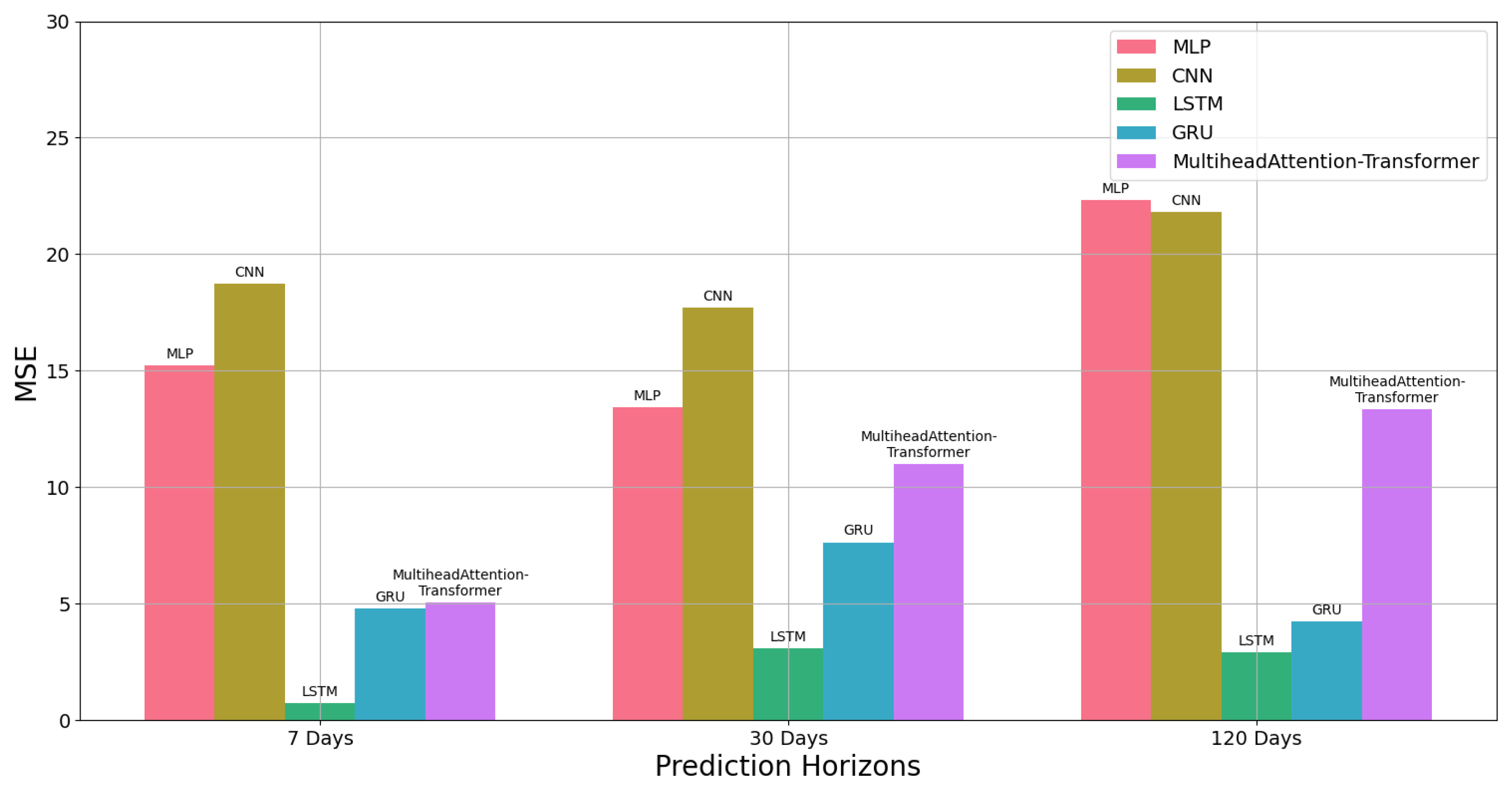
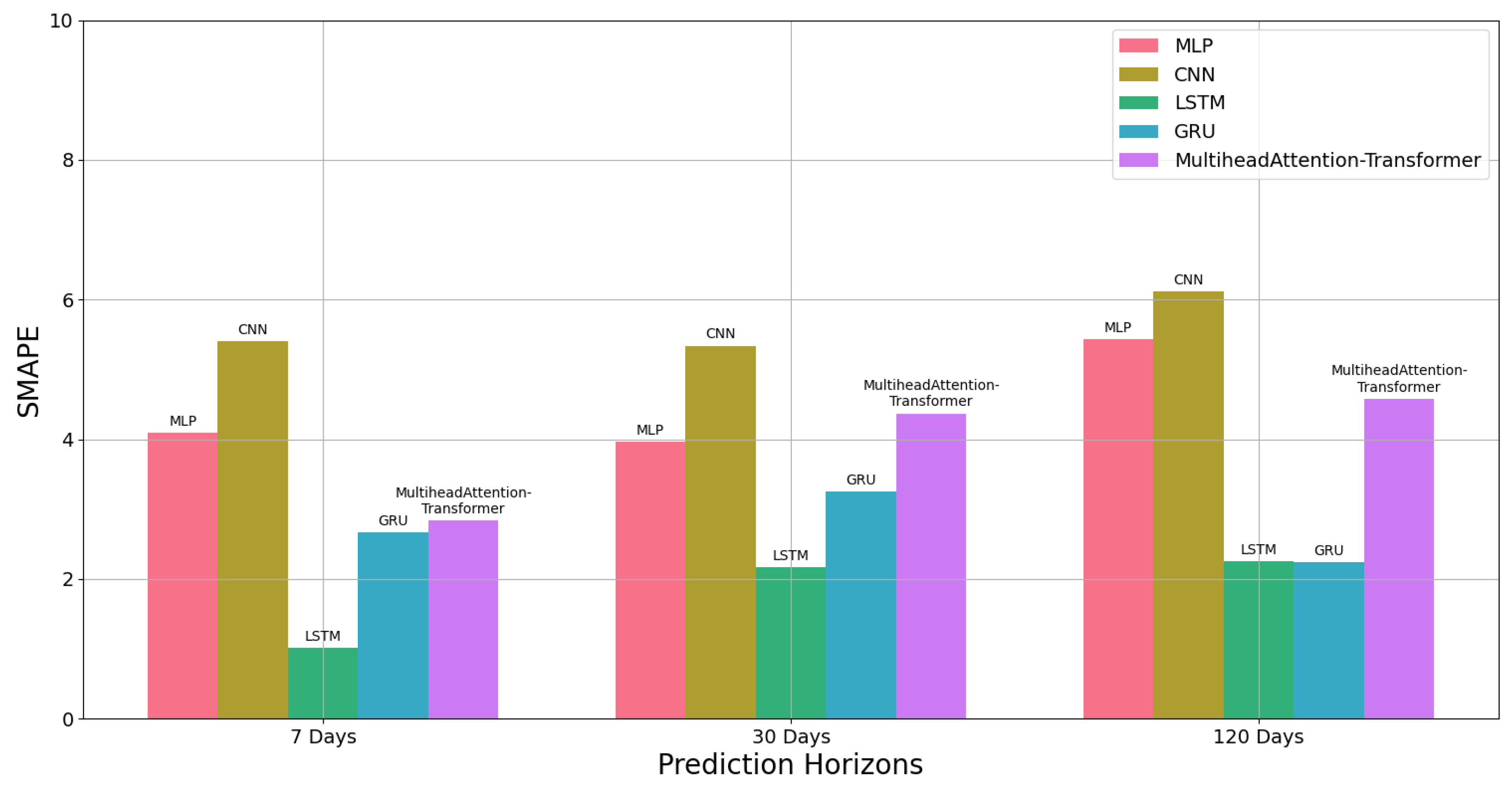
Table 2. Prediction performance results of five distinct models trained on the FELL platform to forecast the SoH of electric vehicle batteries over the subsequent 7 days.

Models	Forecast Steps = 7 Days
	MSE	RMSE	MAE	MAPE	SMAPE
MLP	15.21	3.90	3.17	3.99	4.09
CNN	18.75	4.33	3.70	5.50	5.40
LSTM	0.73	0.85	0.74	1.02	1.01
GRU	4.79	2.19	1.96	2.71	2.66
Multi-head Attention Transformer	5.05	2.25	1.91	2.87	2.84

presents the performance results of five distinct models trained on the FELL platform to forecast the SoH of electric vehicle batteries over the subsequent 7 days. Among these models, the LSTM model achieved the lowest MSE of 0.73, indicating superior predictive accuracy compared to the others. Correspondingly, LSTM demonstrated the lowest RMSE of 0.85, emphasizing its superior ability to capture the variability of SoH values. Furthermore, LSTM yielded the lowest MAE of 0.74, highlighting its effectiveness in minimizing prediction errors. In terms of percentage-based metrics, LSTM attained the lowest MAPE of 1.02% and the lowest SMAPE of 1.01%, further accentuating its superior performance in accurately predicting SoH values. Conversely, the MLP model exhibited the highest values for MSE, RMSE, MAE, MAPE, and SMAPE among the models, indicating relatively poorer predictive performance. Overall, the LSTM model emerges as the most effective in forecasting the SoH of electric vehicle batteries over the next 7 days, closely followed by the GRU and multi-head attention transformer models, while the MLP and CNN models demonstrate lower predictive accuracy.

Table 3. Prediction performance results of five distinct models trained on the FELL platform to forecast the SoH of electric vehicle batteries over the subsequent 120 days.

Models	Forecast Steps = 120 Days
	MSE	RMSE	MAE	MAPE	SMAPE
MLP	22.33	4.73	4.01	5.27	5.43
CNN	21.82	4.67	3.98	6.31	6.11
LSTM	2.91	1.70	1.50	2.29	2.26
GRU	4.23	2.06	1.41	2.18	2.24
Multi-head attention transformer	13.33	3.65	3.11	4.62	4.58

depicts the performance results of five models trained on the FELL platform to predict the SoH of electric vehicle batteries over the next 120 days. Among these models, the LSTM architecture achieved the lowest MSE of 2.91, signifying its superior predictive accuracy compared to the other models. Furthermore, LSTM demonstrated the lowest RMSE of 1.70, indicating its capability in effectively capturing the variability of SoH values throughout the 120-day forecast period. Additionally, LSTM yielded the lowest MAE of 1.50, emphasizing its proficiency in minimizing prediction errors. In terms of percentage-based metrics, LSTM also attained the lowest MAPE of 2.29% and the lowest SMAPE of 2.26%, further illustrating its superior performance in accurately predicting SoH values over the extended forecast period. Conversely, the MLP model exhibited the highest MSE, RMSE, MAE, MAPE, and SMAPE values among the models, indicating its relatively poorer predictive performance. Overall, the LSTM model emerges as the most effective in forecasting the SoH of electric vehicle batteries over the subsequent 120 days, closely followed by the GRU model, while the MLP, CNN, and Multi-head Attention Transformer models display lower predictive accuracy.

The structure of the model predicting electric vehicle battery SoH over the next 120 days is outlined as follows: the MLP model consists of an input layer with 128 neurons, followed by two hidden layers with 64 and 32 neurons, and an output layer with 120 neurons, resulting in a total of 15,064 trainable parameters. The LSTM model comprises an LSTM layer with 128 units, followed by two LSTM layers with 64 and 32 units, and a fully connected dense layer with 16 units, resulting in a total of 130,952 trainable parameters. The CNN model is composed of a 1D convolutional layer with 64 filters, followed by a MaxPooling layer, a dropout layer, and a fully connected dense layer, amounting to a total of 6296 trainable parameters. The GRU model includes a GRU layer with 128 units, followed by two GRU layers with 64 and 32 units, and a fully connected dense layer with 16 units, totaling 99,528 trainable parameters. Finally, the multi-head attention transformer model comprises a multi-head attention layer, followed by fully connected dense layers, a reshape layer, and a TimeDistributed layer, resulting in a total of 192,763 trainable parameters.

Figure 12 illustrates a comparison of the MSE of the five models in predicting the SoH of the user’s electric vehicle battery over varying time horizons: 7 days, 30 days, and 120 days. Figure 13 provides a SMAPE comparison of models predicting battery SoH for the next 7 days, 30 days, and 120 days. The experimental results validate the functionality and effectiveness of the prediction model implemented by the FELL platform. Notably, the FELL system not only furnishes users with predictive outcomes regarding the electric vehicle battery status but also offers a comparative analysis of the prediction performance across multiple models for users’ reference.

Figure 14 offers a comprehensive comparison of the accuracy demonstrated by the five models in predicting short, medium, and long-term battery SoH. Through a thorough examination of the performance indicators across the five prediction models, FELL users can readily discern which model can provide the most accurate prediction results. It is evident that LSTM achieves the highest prediction accuracy, followed by the GRU model, and subsequently, the multi-head attention transformer model. 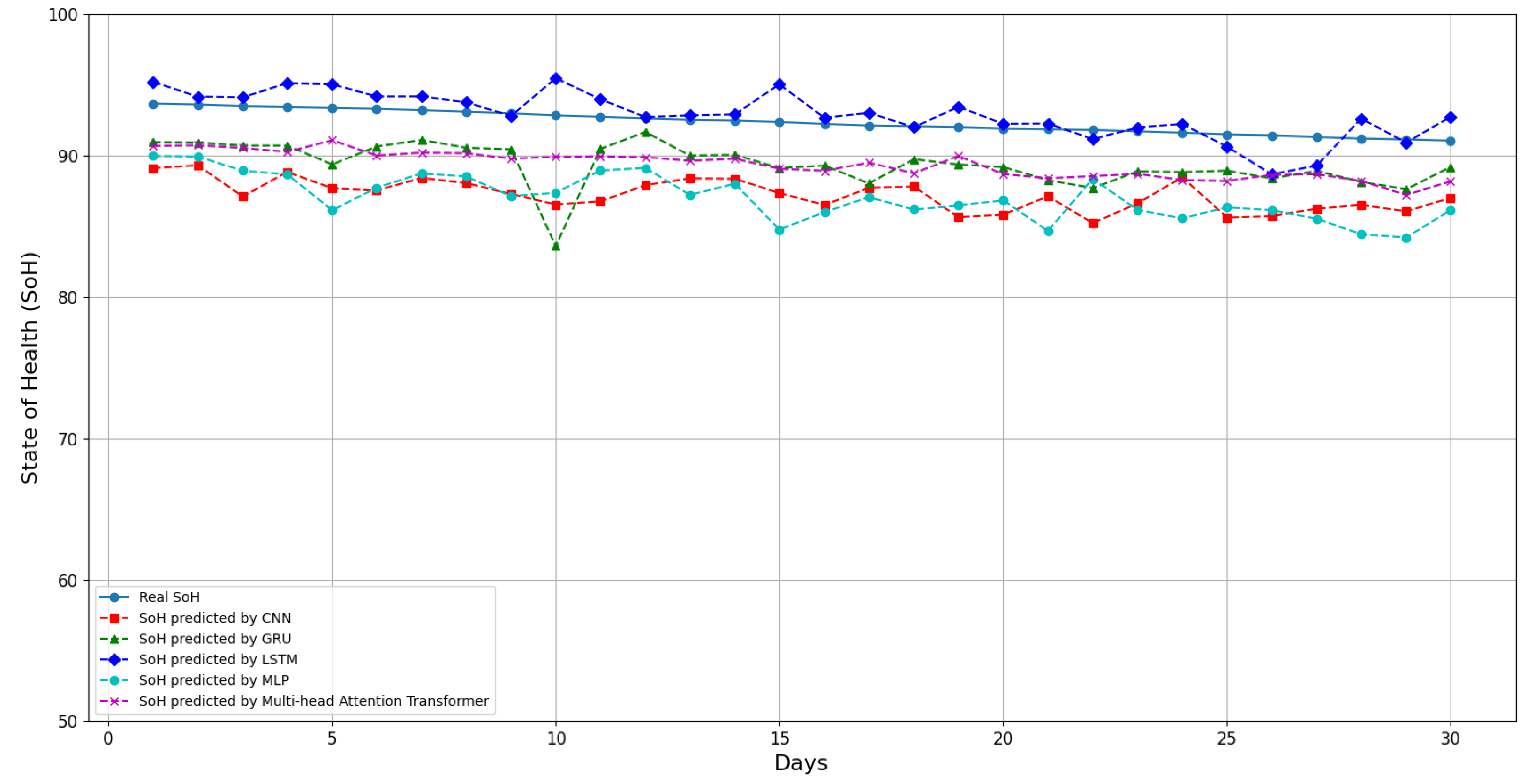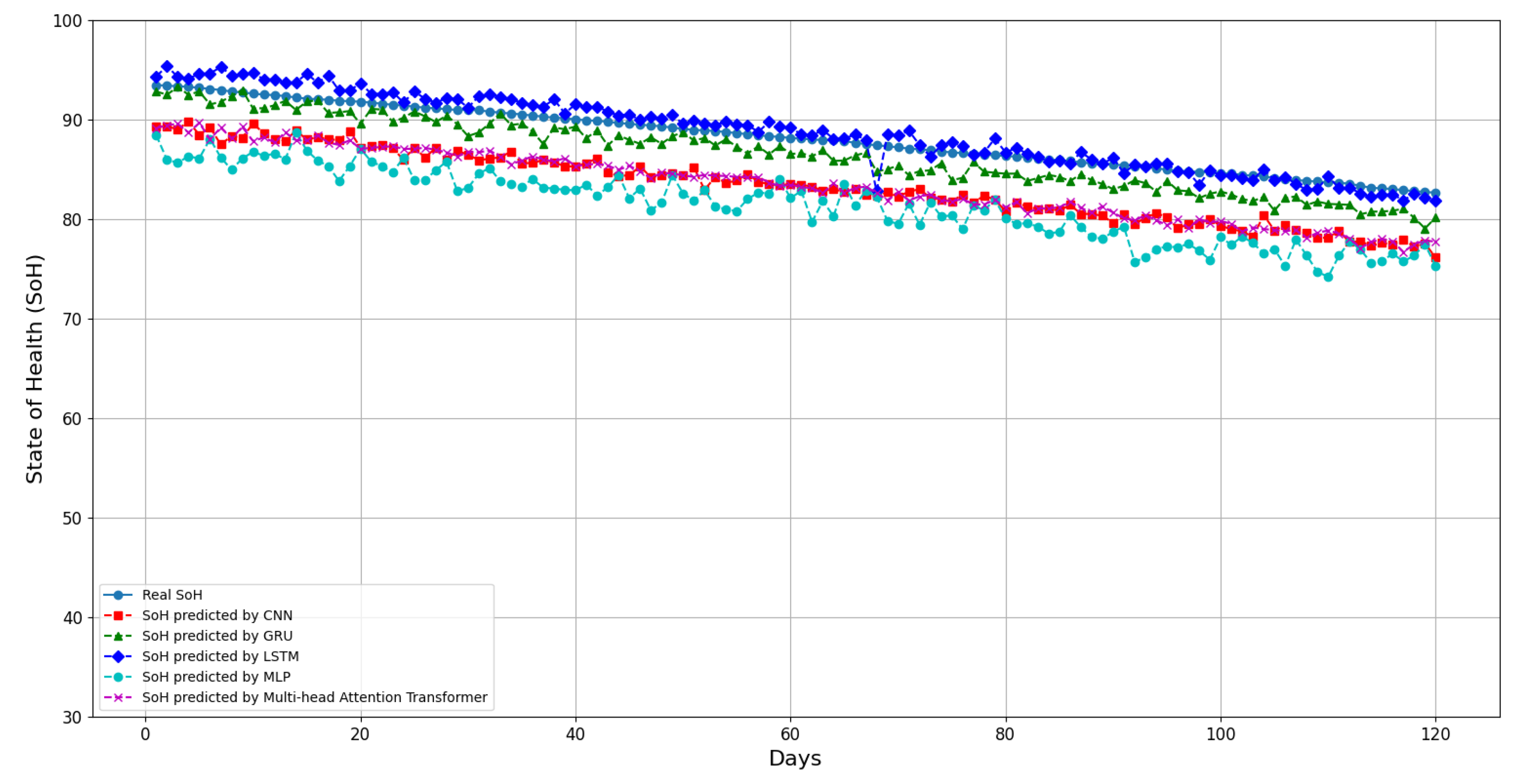Figure 15 and Figure 16 depict the comparison results of the five prediction models implemented on the FELL platform for forecasting the SoH of electric vehicle batteries over the next 30 days and 120 days, respectively. Notably, these experimental findings align with the performance analysis results presented in Table 2 and Table 3. Figure 16 shows a dramatic degradation of the EV battery, with more than a 10% capacity fade over four months. This rapid degradation may be attributed to factors such as extreme driving conditions, frequent fast charging, high temperatures, and other environmental factors that can accelerate battery degradation.

In our study, we employed a two-step approach to estimate the SoH of electric vehicle batteries. Initially, we applied the EKF to estimate the SoH based on relevant battery characteristics, including voltage, current, temperature, and other states. Subsequently, we utilized the estimated SoH, along with other battery-related states and temporal features, as input fields to train time-series deep learning models. These deep learning models were specifically developed to predict the short-, medium-, and long-term SoH of electric vehicle batteries. By combining the EKF with deep learning models, our study achieved more accurate and reliable SoH predictions across various time horizons. The outcomes of the experiment validate the efficacy of integrating EKF and DL technologies into the FELL platform, enabling the effective prediction of electric vehicle battery health and offering diverse short-, medium-, and long-term prediction results.

7. Conclusions

In this study, we introduced a novel approach to address the critical challenges in predicting the SoH of electric vehicle batteries. By combining an extended Kalman filter with a deep learning framework, our proposed system prototype, FELL, offers a robust solution for EV battery diagnosis and prediction. Through extensive experimentation and analysis, we demonstrated the effectiveness of our approach in accurately estimating battery SoH, surpassing traditional methods in prediction accuracy. Our research makes several significant contributions to the field. Firstly, we designed and implemented a comprehensive system prototype, FELL, which integrates advanced predictive modeling techniques with user-friendly interfaces for real-world application. Secondly, we introduced a novel method for predicting battery SoH by leveraging the strengths of both EKF and deep learning, addressing the limitations of individual approaches. Finally, we conducted thorough experimentation and validation, showcasing the functionality and effectiveness of our proposed system in predicting battery health. As future work, we aim to further refine and optimize our system prototype and explore additional avenues for improving battery health prediction accuracy.