Application Cluster Analysis as a Support form Modelling and Digitalizing the Logistics Processes in Warehousing
Abstract
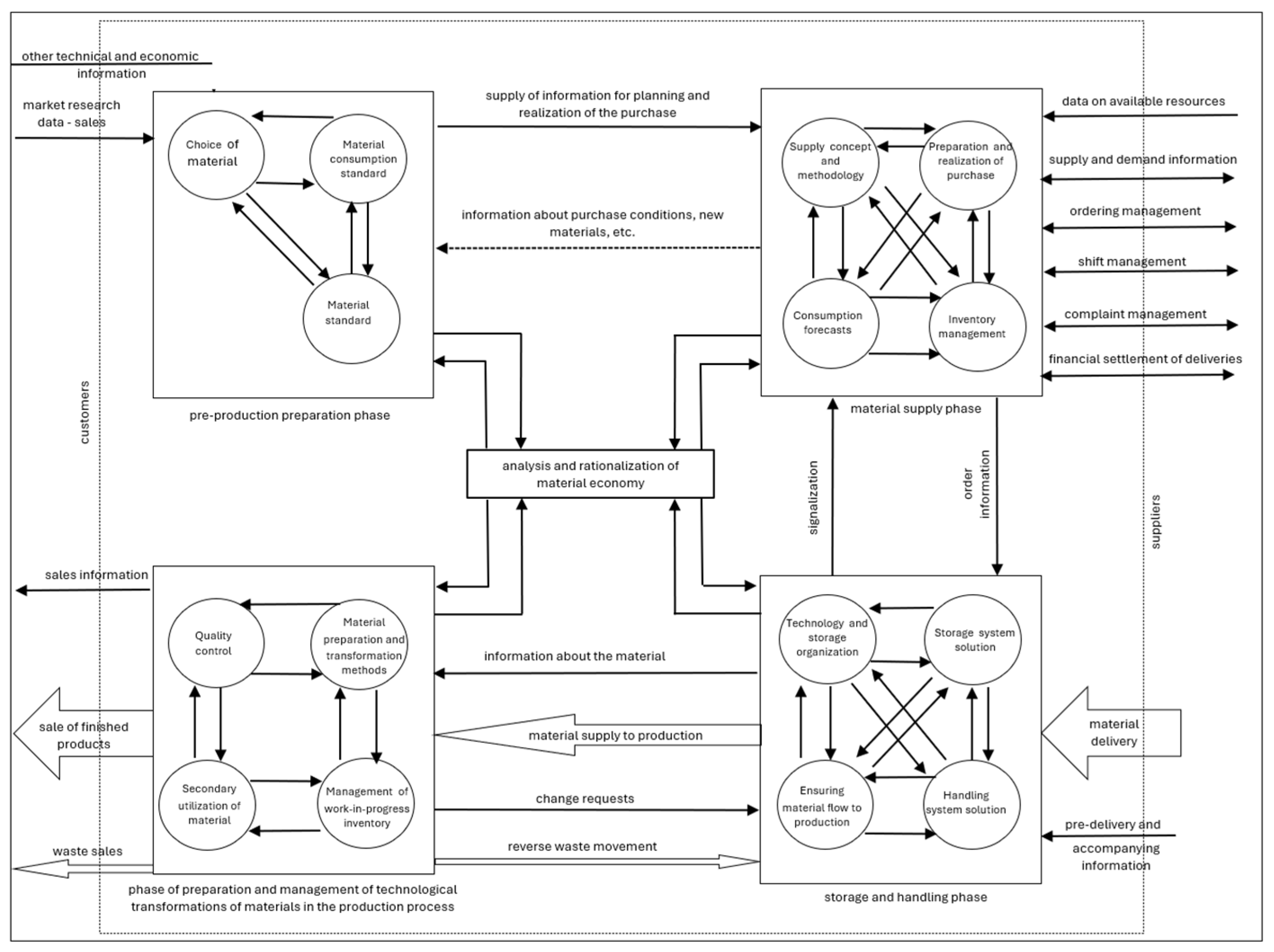
1. Introduction
Inefficiency in Storage
- the excessive handling and underutilization of the storage space;
- the low utilization of the storage area and space;
- excessive maintenance costs and outages due to outdated equipment;
- outdated methods of receipt and dispatch of goods;
- outdated methods of computerized processing of routine transactions.
- Analyzing the efficiency and productivity of the work in warehouses, with a focus on cost reduction and optimization. Implementing automation in warehouse operations emerges as the optimal solution.
- Analyzing the performance of the supplier-to-customer link in the supply chain to select an appropriate storage system and integrate it seamlessly into the material flow.
2. Materials and Methods
- hierarchical algorithms—the assignment of subjects to individual groups is stable and does not change during the algorithm;
- non-hierarchical (partitioning) algorithms—assignment of subjects to individual groups can change during the algorithm.
- hard clustering methods—each object belongs to a cluster or not;
- fuzzy clustering—each object belongs to each cluster to a certain degree.
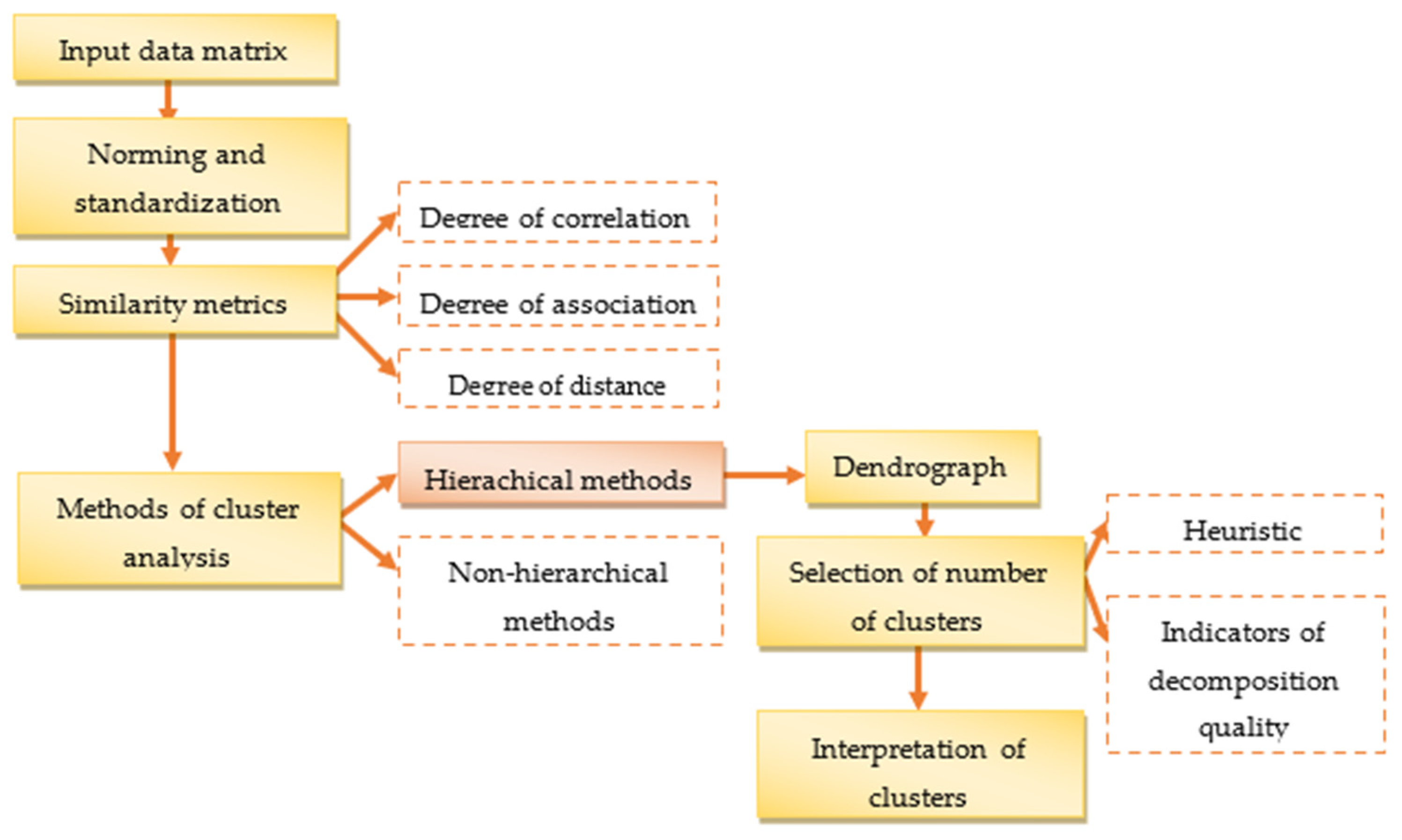
- The distance matrix E1 is compiled from the input data matrix E0 according to the squared Euclidean distance dES.
- The smallest distance is searched in the distance matrix E1, which generates the first cluster.
- All remaining objects are then connected to the first cluster, and a new distance matrix E2 is recalculated. This distance matrix is calculated using individual cluster analysis methods. Any missing values in matrix E2 are filled from the input distance matrix E1.
- The smallest distance is once again selected from matrix E2, generating the second cluster. The remaining objects or clusters are then connected to it, and a new distance matrix E3 is recalculated.
- Once again, the smallest distance is selected from distance matrix E3, representing another cluster.
- This procedure is repeated until all objects or clusters have been assigned.
- The output of hierarchical cluster analysis method is a dendrogram.
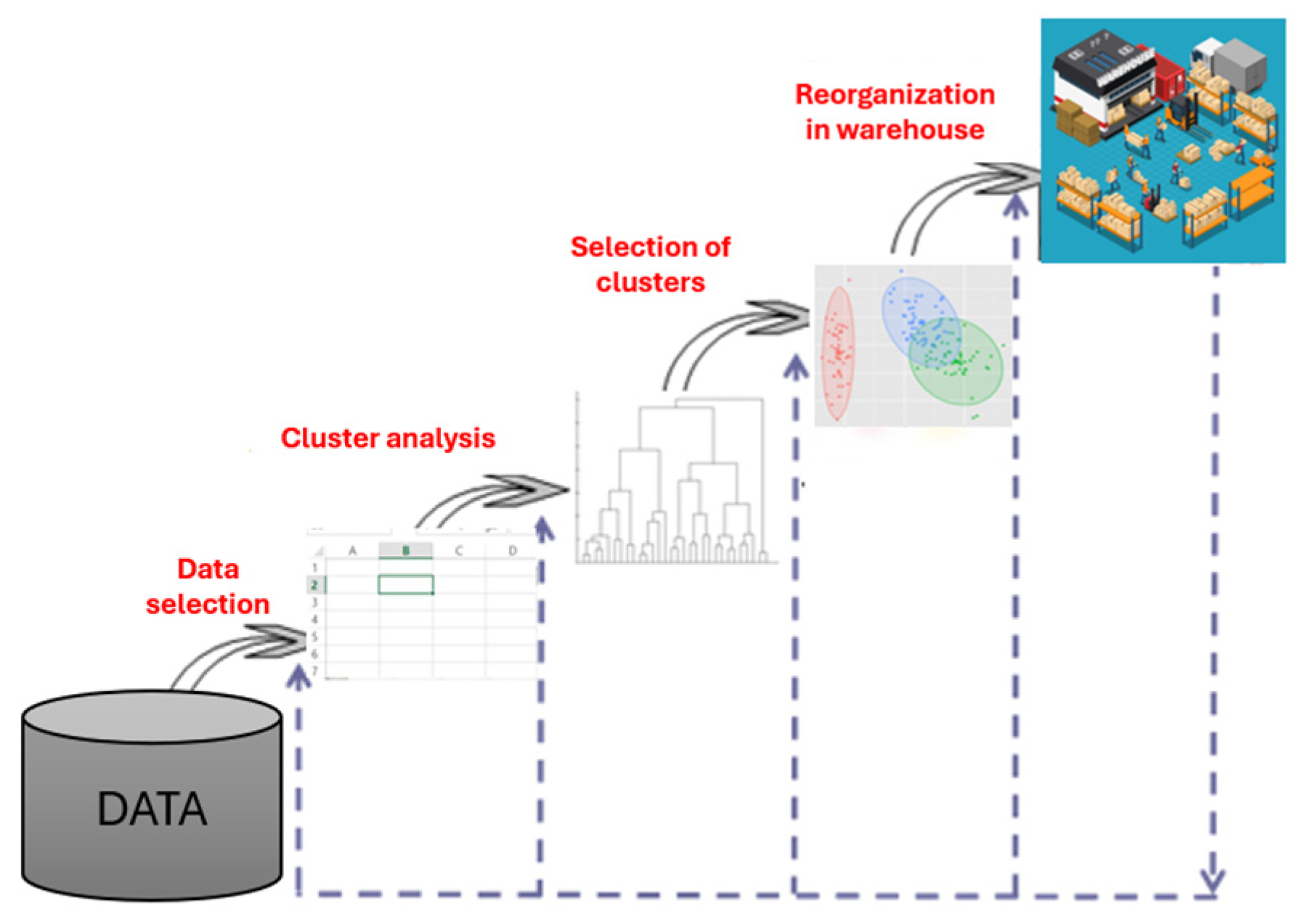
- Stage—preparation;
- Stage—implementation and cluster analysis;
- Stage—evaluation and proposal.
3. Results
4. Discussion
- the optimization of the company’s inventory in terms of structure and quantity;
- the selection of rational methods of material supply and their technical and economic justification;
- limiting the creation of over-standard and unnecessary stocks, identifying methods for their most effective use since excess stocks lead to significant losses of funds tied up in these stocks, and also increasing the costs associated with storage and care as there is a risk of loss, damage, obsolescence of stocks, and their gradual depreciation;
- a method for the control and regulation of production stocks.
5. Conclusions
- the regularity of deliveries, determined by the frequency and size of deliveries;
- the delivery speed, depending on the type of transport, the distance of the transport method, and the degree of mechanization of the loading and unloading processes;
- the degree of certainty that the supplier delivers according to the required quality, quantity, price, and time.
- the size of the consumption, which should be under the production program (production consumption);
- the production consumption, which is determined by the conditions of the production process;
- the consumption standards, which are converted to specific final products in connection with the production technology used.
- the incorporation of the proposed algorithm of the application of cluster analysis methods in storage into software designed for modeling and simulating the processes of manufacturing enterprises (e.g., Siemens Tecnomatix);
- the creation of integrated statistical software for performing cluster analysis and simulation software;
- the expansion of the algorithm by the detailed elements and restrictions resulting from real production conditions in the search for an optimal solution for the arrangement of warehouse stocks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hnilica, R.; Jankovsky, M.; Dado, M.; Messingerova, V.; Schwarz, M.; Veverkova, D. Use of the analytic hierarchy process for complex assessment of the work environment. Qual. Quant. 2017, 51, 93–101. [Google Scholar] [CrossRef]
- Knapcikova, L.; Behunova, A.; Behun, M. Using a discrete event simulation as an effective method applied in the production of recycled material. Adv. Prod. Eng. Manag. 2020, 15, 431–440. [Google Scholar] [CrossRef]
- Rosová, A.; Malindžaková, M. Material flow—Starting point for recovery of inputs in the production: Company. In Proceedings of the 14th International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management, SGEM, Albena, Bulgaria, 16–26 June 2014. [Google Scholar]
- Gregor, M.; Hodon, R.; Grznar, P.; Mozol, Š. Design of a System for Verification of Automatic Guided Vehicle Routes Using Computer Emulation. Appl. Sci. 2022, 12, 3397. [Google Scholar] [CrossRef]
- Straka, M.; Sofranko, M.; Glova, J.; Vegsoová, O.; Kovalcik, J. Simulation of homogeneous production processes. Int. J. Simul. Model. 2022, 21, 214–225. [Google Scholar] [CrossRef]
- Fedorko, G.; Molnár, V.; Honus, S.; Neradilova, H.; Kampf, R. The application of simulation model of a milk run to identify the occurrence of failures. Int. J. Simul. Model. 2018, 17, 444–457. [Google Scholar] [CrossRef] [PubMed]
- Grznár, P.; Krajčovič, M.; Gola, A.; Dulina, Ľ.; Furmannová, B.; Mozol, Š.; Plinta, D.; Burganová, N.; Danilczuk, W.; Svitek, R. The Use of a Genetic Algorithm for Sorting Warehouse Optimisation. Processes 2021, 9, 1197. [Google Scholar] [CrossRef]
- Meloun, M.; Militký, J. [Statistická Analýza Experimentálních Dat] Statistical Analysis of Experimental Data, 2nd ed.; Academia: Praha, Czech Republic, 2004; p. 953. [Google Scholar]
- Edl, M.; Lehrer, T.; Rosi, B. Energy efficiency model for the mini-load automated storage and retrieval systems. Int. J. Adv. Manuf. Technol. 2014, 70, 97–115. [Google Scholar]
- Moravec, M.; Badida, M.; Mikusova, N.; Sobotova, L.; Svajlenka, J.; Dzuro, T. Proposed Options for Noise Reduction from a Wastewater Treatment Plant: Case Study. Sustainability 2021, 13, 2409. [Google Scholar] [CrossRef]
- Chiang, T.-A.; Che, Z.-H.; Lee, C.-H.; Liang, W.-C. Applying Clustering Methods to Develop an Optimal Storage Location Planning-Based Consolidated Picking Methodology for Driving the Smart Manufacturing of Wireless Modules. Appl. Sci. 2021, 11, 9895. [Google Scholar] [CrossRef]
- Mirzaei, M.; Zaerpour, N.; de Koster, R. The impact of integrated cluster-based storage allocation on parts-to-picker warehouse performance. Transp. Res. Part E Logist. Transp. Rev. 2021, 146, 102207. [Google Scholar] [CrossRef]
- Anuşlu, M.D.; Fırat, S.Ü. Clustering analysis application on Industry 4.0-driven global indexes. Procedia Comput. Sci. 2019, 158, 145–152. [Google Scholar] [CrossRef]
- Tschuchnig, P.; Müller, J.M. Clustering and Classification of Manufacturing Enterprises Regarding Their Industry 4.0 Reshoring Incentives. Procedia Comput. Sci. 2021, 180, 696–705. [Google Scholar]
- Das, J.N.; Tiwari, M.K.; Sinha, A.K.; Khanzode, V. Integrated warehouse assignment and carton configuration optimization using deep clustering-based evolutionary algorithms. Expert Syst. Appl. 2023, 212, 118680. [Google Scholar] [CrossRef]
- Griffin, E.C.; Burcu, B.; Keskin, B.B.; Allaway, A.W. Clustering retail stores for inventory transshipment. Eur. J. Oper. Res. 2023, 311, 690–707. [Google Scholar] [CrossRef]
- Rezankova, H.; Husek, D.; Snasel, V. Shluková Analyza Dat. Cluster Analysis of Data, 2nd ed.; Professional Publishing: Praha, Czech Republic, 2009; p. 218. [Google Scholar]
- Abonay, J.; Feil, B. Cluster Analysis for Data Mining and System Identification, 1st ed.; Springer Science & Business Media: Berlin, Germany, 2007; p. 319. [Google Scholar]
- Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. Multivariate Analyse Methoden; Springer: Munich, Germany, 2006; p. 831. [Google Scholar]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, 5th ed.; Wiley: London, UK, 2011; p. 348. [Google Scholar]
- Hebak, P. [Vicerozmerne Statisticke Metody s Aplikacemi] Multivariate Statistical Methods with Applications; SNTL/ALFA: Praha, Czech Republic, 1987; p. 456. [Google Scholar]
- Pekarcikova, M.; Trebuna, P.; Kral, S.; Duda, R. [Logistika pre Priemyselne Inzinierstvo] Logistics for Industrial Engineering, 1st ed.; TUKE: Košice, Slovakia, 2021; p. 333. [Google Scholar]
- Glova, J.; Mrazkova, S.; Dancakova, D. Measurement of intangibles and knowledge: Empirical evidence. AD Alta-J. Interdiscip. Res. 2018, 8, 76–80. [Google Scholar]
- Buckova, M.; Krajčovič, M.; Edl, M.; Bujnak, J.; Guagliano, M. Computer simulation and optimization of transport distances of order picking processes. In Proceedings of the 12th International Scientific Conference of Young Scientists on Sustainable, Modern and Safe Transport, High Tatras, Slovakia, 31 May–2 June 2017; Volume 192, pp. 69–74. [Google Scholar]
- Straka, M.; Saderová, J.; Bindzar, P.; Malkus, T.; Lis, M. Computer simulation as a means of efficiency of transport processes of raw materials in relation to a cargo rail terminal: A case study. Acta Montan. Slovaca 2020, 24, 307–317. [Google Scholar]
- Soo Jin, C.; Shah Amirul, A.; Md Taib, F. Tracking Hidden Quality Costs in a Manufacturing Company: An Action Research. Int. J. Qual. Reliab. Manag. 2011, 28, 405–442. [Google Scholar]




| Statistics | Months | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Mean | 67.00 | 66.84 | 67.16 | 66.72 | 66.48 | 65.28 | 65.80 | 66.04 | 66.56 | 67.00 | 66.84 | 67.16 |
| Standard deviation | 68.50 | 68.69 | 68.66 | 68.96 | 69.10 | 70.22 | 69.41 | 69.50 | 68.50 | 68.69 | 68.66 | 68.96 |
| Sum | 1675 | 1671 | 1679 | 1668 | 1662 | 1632 | 1645 | 1675 | 1671 | 1679 | 1668 | 1662 |
| Products | Months | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Σ | ||
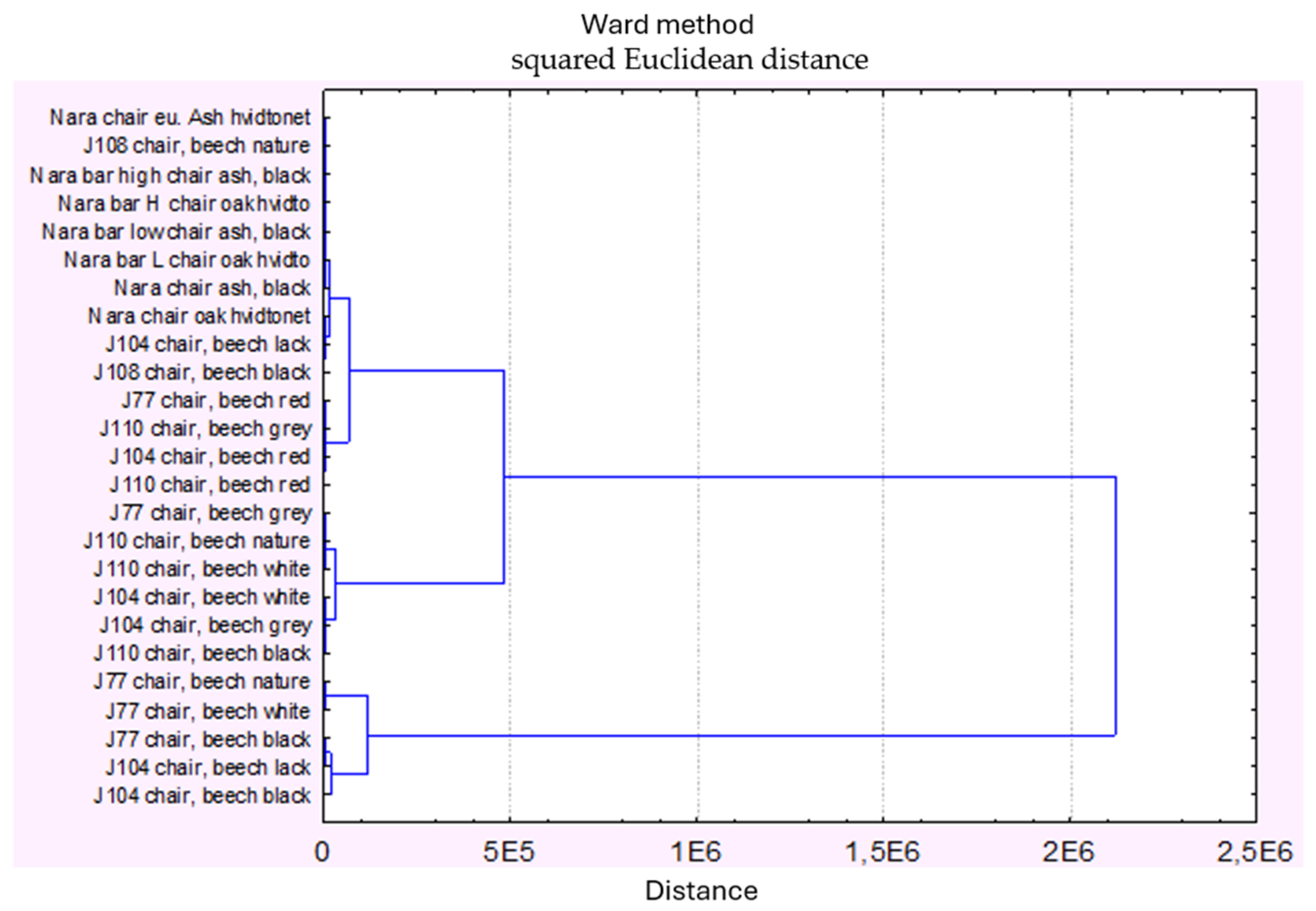
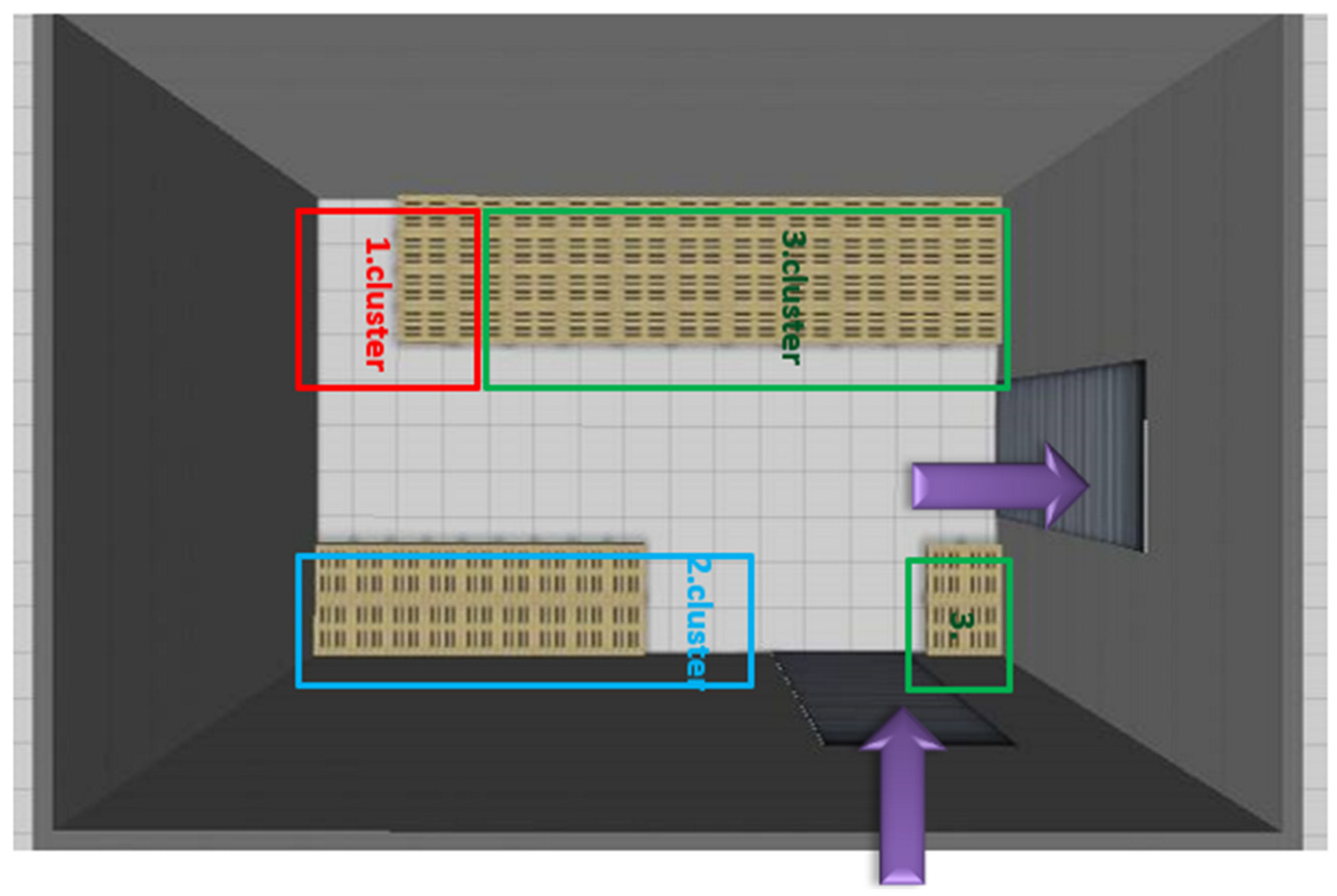
| 1. cluster | Nara chair eu. Ash hvidtonet | 0 | 0 | 0 | 12 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2657 |
| J108 chair, beech nature | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | ||
| Nara bar high chair ash, black | 0 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Nara bar H chair oak hvidto | 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Nara bar low chair ash, black | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 17 | ||
| Nara bar L chair oak hvidto | 0 | 0 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Nara chair ash, black | 0 | 0 | 0 | 0 | 0 | 0 | 22 | 23 | 23 | 22 | 0 | 0 | ||
| Nara chair oak hvidtonet | 34 | 29 | 28 | 30 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| J104 chair, beech lack | 19 | 19 | 19 | 20 | 19 | 20 | 19 | 19 | 20 | 19 | 20 | 19 | ||
| J108 chair, beech black | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | ||
| J77 chair, beech red | 48 | 47 | 48 | 47 | 47 | 47 | 48 | 47 | 48 | 47 | 48 | 47 | ||
| J110 chair, beech grey | 40 | 40 | 40 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 40 | ||
| J104 chair, beech red | 31 | 31 | 32 | 31 | 33 | 33 | 32 | 31 | 33 | 31 | 34 | 31 | ||
| J110 chair, beech red | 32 | 32 | 33 | 32 | 32 | 33 | 32 | 34 | 32 | 33 | 32 | 32 | ||
| 2. cluster | J77 chair, beech grey | 77 | 78 | 77 | 77 | 78 | 77 | 77 | 78 | 77 | 77 | 78 | 77 | 6111 |
| J110 chair, beech nature | 71 | 72 | 71 | 72 | 71 | 72 | 71 | 72 | 71 | 72 | 71 | 72 | ||
| J110 chair, beech white | 63 | 63 | 61 | 63 | 63 | 63 | 62 | 63 | 63 | 62 | 63 | 63 | ||
| J104 chair, beech white | 112 | 112 | 112 | 112 | 112 | 112 | 112 | 112 | 112 | 112 | 112 | 112 | ||
| J104 chair, beech grey | 98 | 98 | 98 | 98 | 98 | 99 | 98 | 98 | 99 | 98 | 98 | 98 | ||
| J110 chair, beech black | 87 | 87 | 89 | 87 | 87 | 90 | 87 | 87 | 89 | 87 | 87 | 87 | ||
| 3. cluster | J77 chair, beech nature | 138 | 139 | 139 | 138 | 139 | 138 | 139 | 139 | 138 | 138 | 139 | 139 | 11,109 |
| J77 chair, beech white | 155 | 155 | 155 | 156 | 155 | 155 | 155 | 156 | 155 | 155 | 155 | 155 | ||
| J77 chair, beech black | 229 | 229 | 229 | 229 | 229 | 230 | 229 | 229 | 229 | 229 | 229 | 229 | ||
| J104 chair, beech lack | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | ||
| J104 chair, beech black | 187 | 187 | 189 | 189 | 189 | 188 | 187 | 188 | 188 | 188 | 187 | 188 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kronova, J.; Izarikova, G.; Trebuna, P.; Pekarcikova, M.; Filo, M. Application Cluster Analysis as a Support form Modelling and Digitalizing the Logistics Processes in Warehousing. Appl. Sci. 2024, 14, 4343. https://doi.org/10.3390/app14114343
Kronova J, Izarikova G, Trebuna P, Pekarcikova M, Filo M. Application Cluster Analysis as a Support form Modelling and Digitalizing the Logistics Processes in Warehousing. Applied Sciences. 2024; 14(11):4343. https://doi.org/10.3390/app14114343
Chicago/Turabian StyleKronova, Jana, Gabriela Izarikova, Peter Trebuna, Miriam Pekarcikova, and Milan Filo. 2024. "Application Cluster Analysis as a Support form Modelling and Digitalizing the Logistics Processes in Warehousing" Applied Sciences 14, no. 11: 4343. https://doi.org/10.3390/app14114343
APA StyleKronova, J., Izarikova, G., Trebuna, P., Pekarcikova, M., & Filo, M. (2024). Application Cluster Analysis as a Support form Modelling and Digitalizing the Logistics Processes in Warehousing. Applied Sciences, 14(11), 4343. https://doi.org/10.3390/app14114343








