1. Introduction
Quantum key distribution (QKD) is the most mature quantum technology [
1,
2,
3,
4,
5,
6,
7,
8]. Different QKD systems by various vendors are available on the market, and national and international initiatives aim to test the integration of the available QKD systems into existing communication infrastructures, as well their operation in various use cases under realistic conditions.
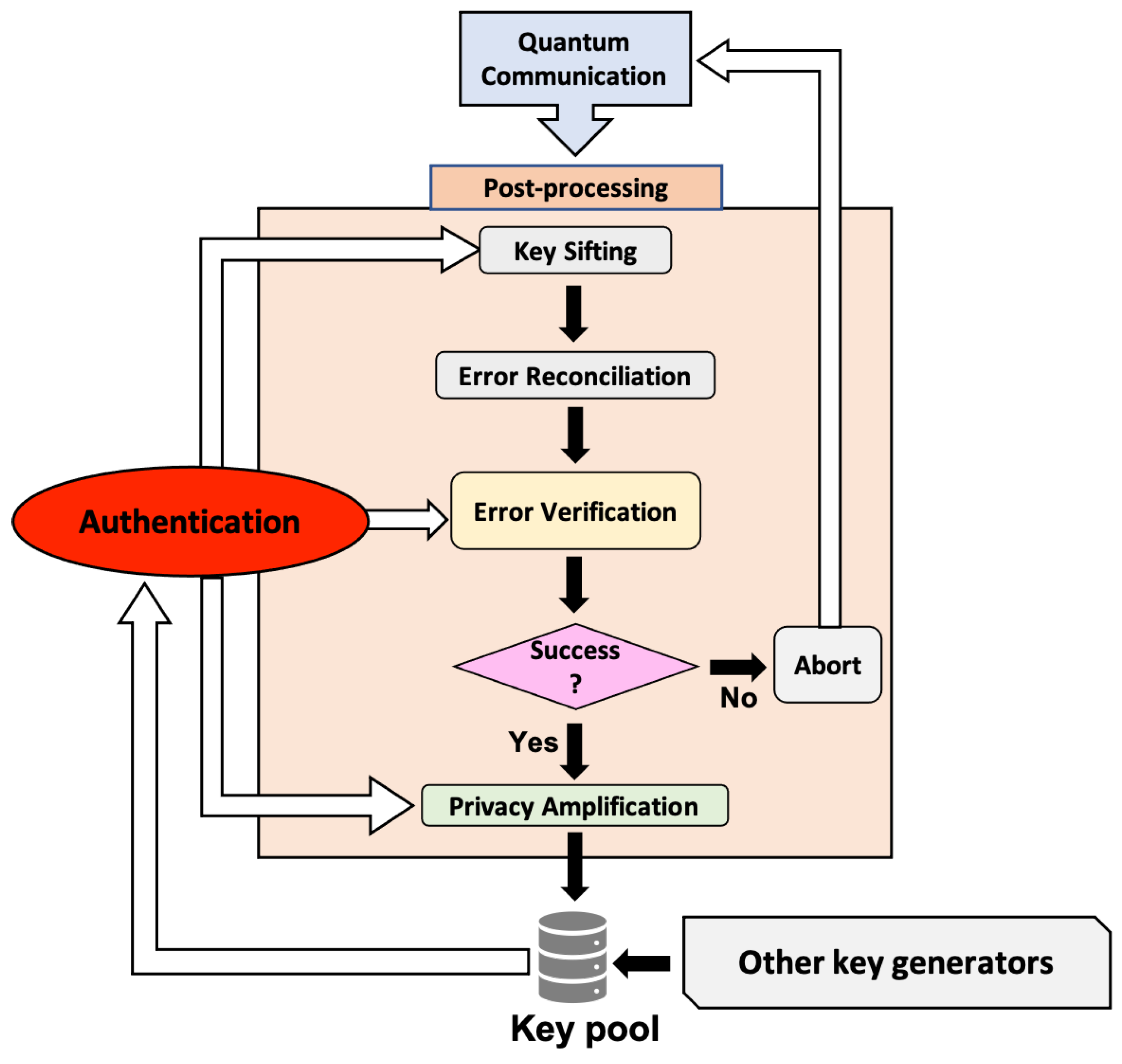
Typically, the establishment of a secret key between two honest users (Alice and Bob) pertains to a quantum communication and a post-processing stage (see
Figure 1). In the first stage, Alice encodes random bits on non-orthogonal photonic states, which are sent to Bob over a quantum channel. Bob measures each received signal and records the outcomes. Subsequently, the two users publicly post-process their classical data in order to obtain a final information-theoretically secure secret key. The main steps involved in the post-processing stage are key sifting, error reconciliation, error verification, and privacy amplification. A successful implementation of all of these steps, without any detected failure, is expected to lead to a final secret key. However, for any of these steps, there is always a probability of undetected failure, in which case the security of the protocol is compromised.
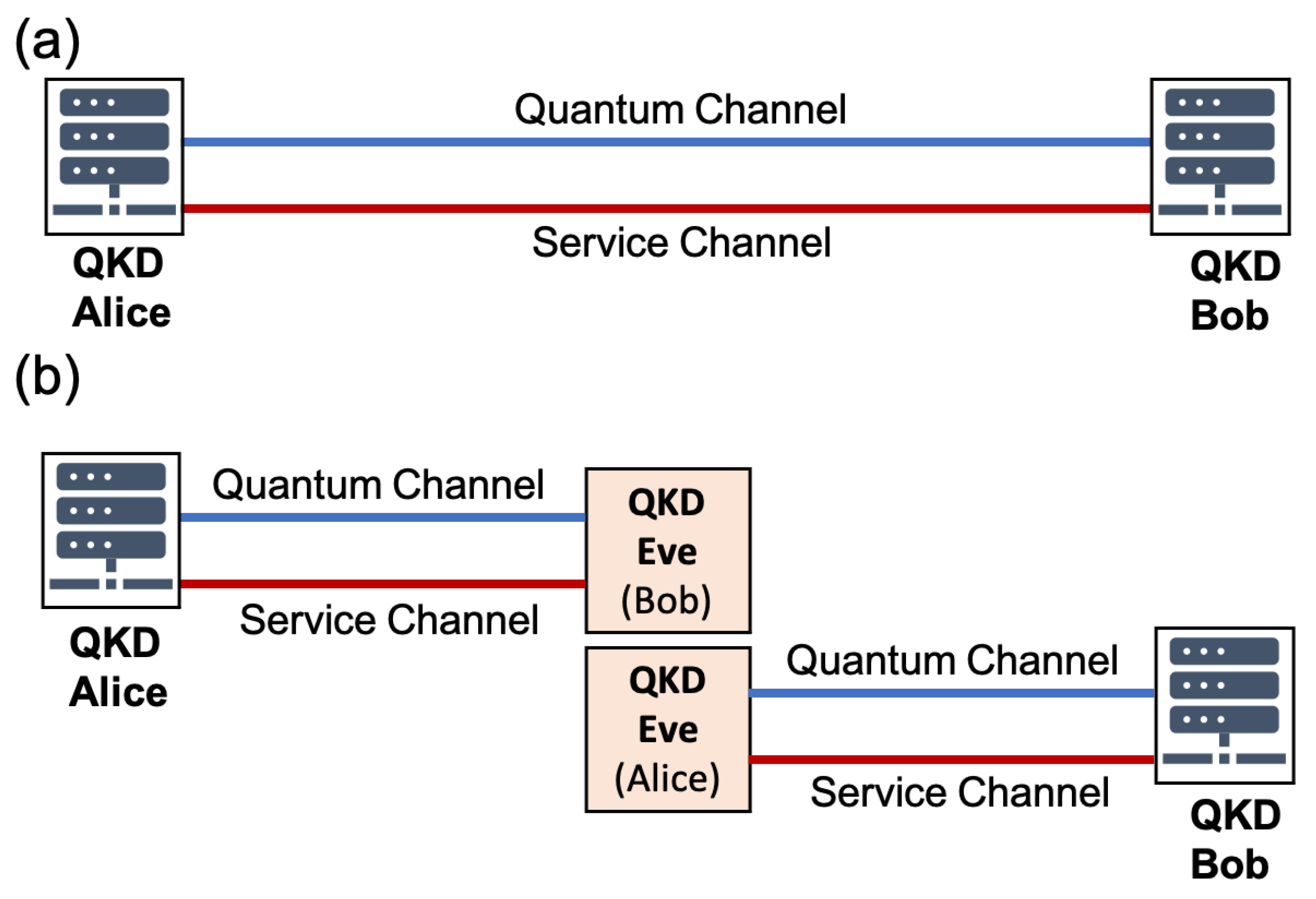
While processing their data, the two users have to verify the origin of the exchanged messages, otherwise the protocol is prone to a man-in-the-middle attack outlined in
Figure 2. In this rather simple attack, an adversary (Eve) cuts the quantum and classical service channels that connect Alice and Bob. She connects her QKD devices to the loose ends of the channels and pretends to be Bob to Alice and Alice to Bob. In this way, she can establish two secret keys, one with Alice and one with Bob, which allow her, e.g., to decrypt and modify any message sent from Alice to Bob (or vice versa). Such an attack can be prevented only by authenticating the service channel, and given that QKD protocols promise information-theoretically secure (ITS) distribution of random keys, authentication by means of ITS message authentication protocols is the natural choice for QKD [
9,
10,
11]. Standard ITS message authentication codes (MACs) [
12,
13,
14,
15,
16,
17,
18], however, require that the two users share a secret truly random key before they run their QKD system for the first time (see also
Appendix A).
For this reason, a typical commercially available pair (sender–receiver) of QKD devices comes with a pre-shared secret key, or the users who purchase the system have to generate the key by some means and transfer it to their devices. Among other tasks, this key is used for authentication in the first QKD session until a sufficient amount of fresh secret key material has been produced. From that point on, message authentication for the subsequent QKD sessions is expected to consume part of the existing secret key that has been generated through QKD. Clearly, a QKD protocol is meaningful only if key consumption is smaller than the generation of fresh key in a session. For large distances and/or lossy channels, however, the generation of fresh secret bits may become very costly in terms of the amount of the pre-shared key information required for their production. Another problem is that the need for a pre-shared secret key considerably complicates the design of large full-mesh QKD networks. These drawbacks, together with the strong dependence of QKD on ITS MACs, have made individuals as well as public authorities and organizations question the usefulness of QKD protocols and hold a negative position with respect to further proliferation of the technology.
The complications caused by the necessity for authentication and the management of pre-shared secret keys have not gone unnoticed by the community. When a pre-shared key is stored or distributed in plaintext, one cannot guarantee that a malicious third party will not obtain access to it and launch a successful man-in-the-middle attack in the first QKD session, which will compromise the security of the next sessions as well. The problem is not solved by encrypting the pre-shared key or by storing it in a password-protected electronic device, but rather it is transferred to the management and the distribution of an additional key (or password), which is needed in order to ensure the secrecy of the pre-shared key.
There have been efforts in the past to decrease the length of the pre-shared key in existing QKD protocols, as well as to facilitate the distribution and management of pre-shared keys. Peev et al. [
19] proposed an authentication scheme which relies on a two-step hash function evaluation and involves two-step non-ITS hashing, resulting in low key consumption. Later, it was shown that the proposed scheme is not secure [
20,
21]. More recently, Pan and co-workers [
22,
23] experimentally studied the performance of QKD when the authentication relied on a post-quantum cryptographic (PQC) protocol [
24]. Although this hybrid protocol has efficient key management and new users can be easily added to the QKD network, it is not ITS, because the adopted PQC is computationally and not information-theoretically secure. In fact, the key that is distributed by means of the hybrid protocol is secure provided that the underlying PQC has not been broken during the execution of the protocol, which can be guaranteed only in the framework of computational security. Unless the adversary is present during the execution, they cannot later obtain the distributed key, even if they have unlimited resources.
In the present work, our aim is to propose a scheme for the generation, distribution, and management of pre-shared keys that relies on physical unclonable functions (PUFs). In contrast to post-quantum public-key cryptosystems, the judicious integration of PUFs in existing QKD systems promises ITS QKD under limited assumptions pertaining mainly to the performance of the PUF under consideration. Furthermore, our scheme allows for the real-time authentication of the QKD devices that are connected to the network.
PUFs were proposed by Pappu et al. [
25] as a means to generate random numerical keys from the laser speckle that is produced from a multiple-scattering optical medium. The optical medium plays the role of a token, which is technologically hard to clone and it can produce a large number of independent, almost truly random keys, each one associated with different parameters of the input laser light (e.g., wavelength, power, wavefront, angle of incidence, etc.). Following the work of Pappu et al., PUFs have attracted considerable attention over the last two decades or so, and the related literature is rather rich [
26,
27,
28,
29,
30,
31,
32,
33]. Currently, there are different types of PUFs, including optical (non-silicon) PUFs, time-delay-based silicon PUFs, intrinsic silicon PUFs, magnetic PUFs, etc. Their main applications are in entity authentication, and in the development of anti-counterfeiting methods, and there is also a number of companies commercializing PUF products [
27]. For our purposes, it is sufficient to know the basic operation of a PUF, which is the generation of random keys, leaving aside details that go beyond the scope of the present work. An interested reader may refer to the related review articles [
26,
27,
28,
29,
30,
31,
32,
33], and the references therein.
In a nutshell, as shown in
Figure 3, a PUF is a mathematical function that refers to the behaviour of a physical object or device (to be referred to hereafter as the PUF token or tag). The PUF tag is characterized by internal random disorder, which plays the role of a fingerprint, and it is technologically hard to clone. A PUF operates as a pseudo-random number generator (PRNG) in the sense that it produces a random numerical key as a response to an input stimulus (to be referred to hereafter as a challenge). The nature of the challenge depends on the PUF under consideration, while the response to a given challenge depends strongly on the internal disorder of the device. The raw noisy response is classically processed by means of a fuzzy extractor to yield a nearly perfect robust binary key. The fuzzy extractor typically involves two separate processes: reconciliation and hashing. The former aims at a reconciled key that is not affected by environmental variations and ageing of the token, whereas the latter compresses the reconciled key further, so that the final key is nearly uniformly distributed. A useful PUF is robust, easy to evaluate, difficult to replicate, unique (highly unlikely for two independent devices to return the same key for the same challenge), and unpredictable (very difficult or impossible to predict the response to a given challenge). Many of the PUFs that have been discussed in the literature satisfy these requirements. The main advantage of PUFs is that they remove the necessity of secret key storage, as the key is essentially physically stored in the disordered token and can be recovered on demand when the appropriate challenge is given. The only requirement is that the user has access to the token.
The strength of a PUF is generally determined by the number of supported challenge–response pairs (CRPs), or to be more precise, by the way the number of potential CRPs scales with the increasing token size. In general, a PUF for which the number of supported CRPs grows exponentially with the size of the token is considered to be strong, while linear or polynomial growth typically refers to weak PUFs. Given that weak PUFs support a relatively small number of CRPs, an attacker can obtain the responses to all possible challenges, provided they have access to the PUF for a sufficiently long period of time. Hence, they can emulate a particular PUF in any cryptographic protocol without having an actual clone of the token. By contrast, strong PUFs support a much larger set of CRPs and an attacker must have access to the PUF for a time period that is considerably longer than the one required for the readout of a weak PUF. Ring-oscillator and SRAM PUFs are considered to be weak, whereas optical and arbiter PUFs (a type of delay-based silicon PUF) are considered to be strong [
26,
27,
28,
29,
30,
31,
32,
33].
2. Results and Discussion
We discuss now how PUFs can be integrated in existing QKD systems, facilitating the generation and distribution of the necessary pre-shared key between Alice and Bob.
2.1. Integration of PUFs in Point-to-Point QKD Links
The manufacturer of the QKD devices associates a PUF with each of the QKD boxes (sender or receiver). For instance, a PUF tag is attached to each QKD box in a fashion similar to the barcodes or QR codes that accompany various products on the market. In contrast to these codes, however, as mentioned above, the PUF tags are technologically hard to copy, and they serve as unique fingerprints for the boxes they are attached to. Alternatively, we can assume that the PUF token associated with a QKD device is given to the owner of the device, e.g., in the form of a smart card [
34].
We will first consider a point-to-point communication scenario, with a pair of QKD boxes intended for Alice (sender) and Bob (receiver). A pair PUF tokens/tags is associated with them. Each token is interrogated by a number of challenges
, and the corresponding keys
are recorded, where
is the label of the user. One of the honest users, say Alice, keeps a database of the challenge–response pairs (CRPs) in the following form [
34,
35]
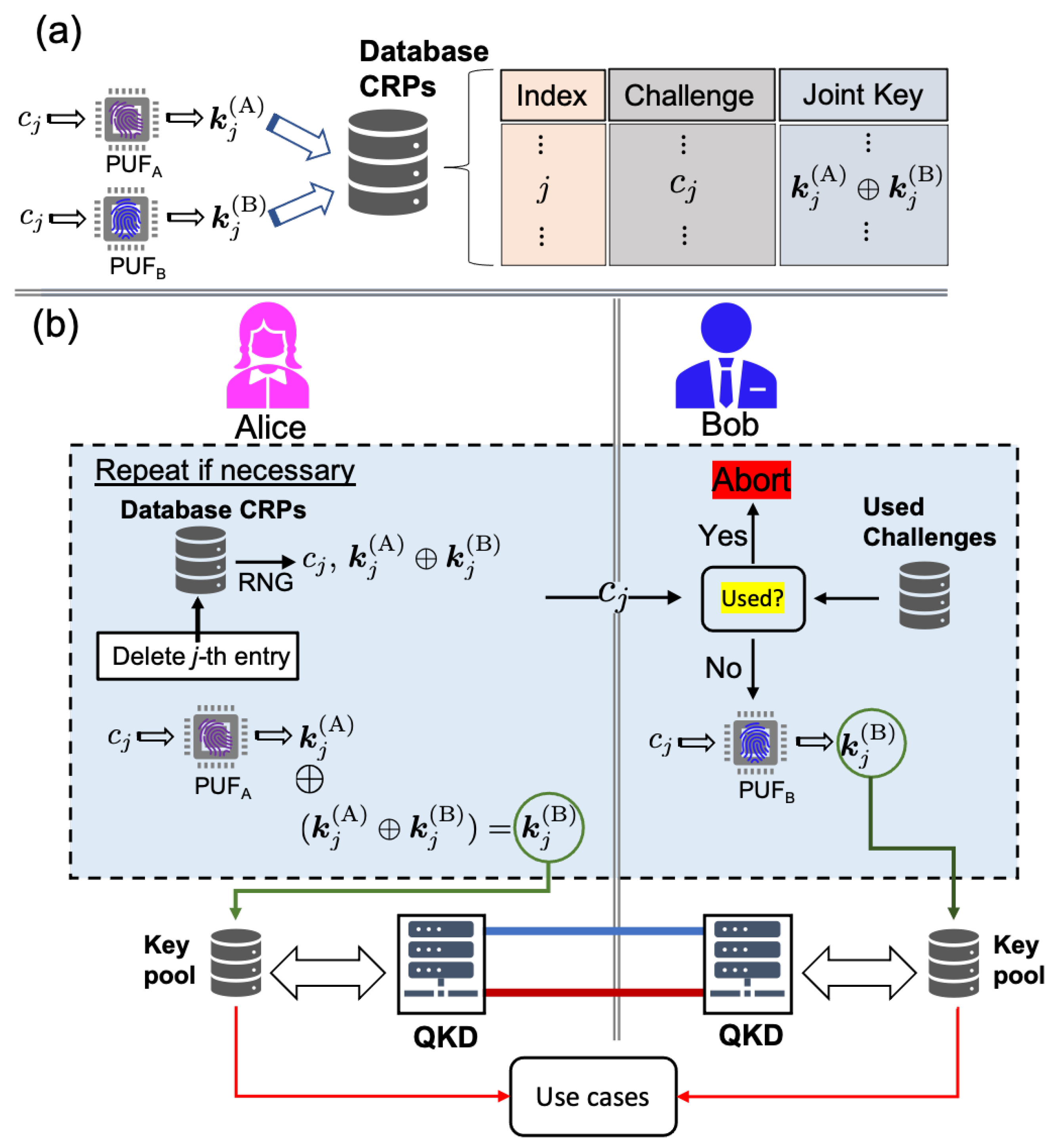
A schematic representation of the process is shown in
Figure 4a. As will be discussed in detail below, the particular form of storage protects the individual keys against an adversary who obtains undetected access to the database.
A question arises here: who creates and who has access to this database? There are two options. One possibility is that the manufacturer creates the database and gives it to either of the two honest users during the delivery of the QKD boxes. Alternatively, one of the honest users (say Alice), has access to both boxes (and thus to both PUFs) simultaneously, and she creates the database before she gives one of the boxes to Bob. In both of these scenarios, only trusted parties are involved, in the sense that by definition Alice, Bob, and the manufacturer of the QKD devices are honest. In
Figure 4, we assume that Alice possesses the database and hence there is no need for including an additional trusted third party. As will be discussed in the next subsection, however, the inclusion of a third party is inevitable in the case of larger QKD networks.
As discussed in the introduction, before Alice and Bob operate their QKD boxes for the first time, they must generate a common secret key, which will be used for post-processing purposes until a sufficiently large number of secret bits has been generated from the QKD sessions. To this end, Alice chooses at random one of the available challenges in the database, say the
jth one, and sends it to Bob (see
Figure 4b) over a classical channel which may not be authenticated (see related discussion in
Section 2.4). The two users run their PUFs independently in order to recover their individual keys
and
. Alice adds her key to the joint key
in order to recover Bob’s key which will seed the first QKD session. The corresponding entry is permanently deleted from the database, while Bob also keeps a blacklist of the used challenges so that they are not used again for the particular PUFs.
Under normal conditions, the key material in the corresponding pools of Alice and Bob will grow through the operation of QKD sessions, and there will be no need for the users to execute the above procedure again. However, if for any reason, at any time, QKD alone cannot support the needs for keys and additional key material is needed, the procedure can be repeated again.
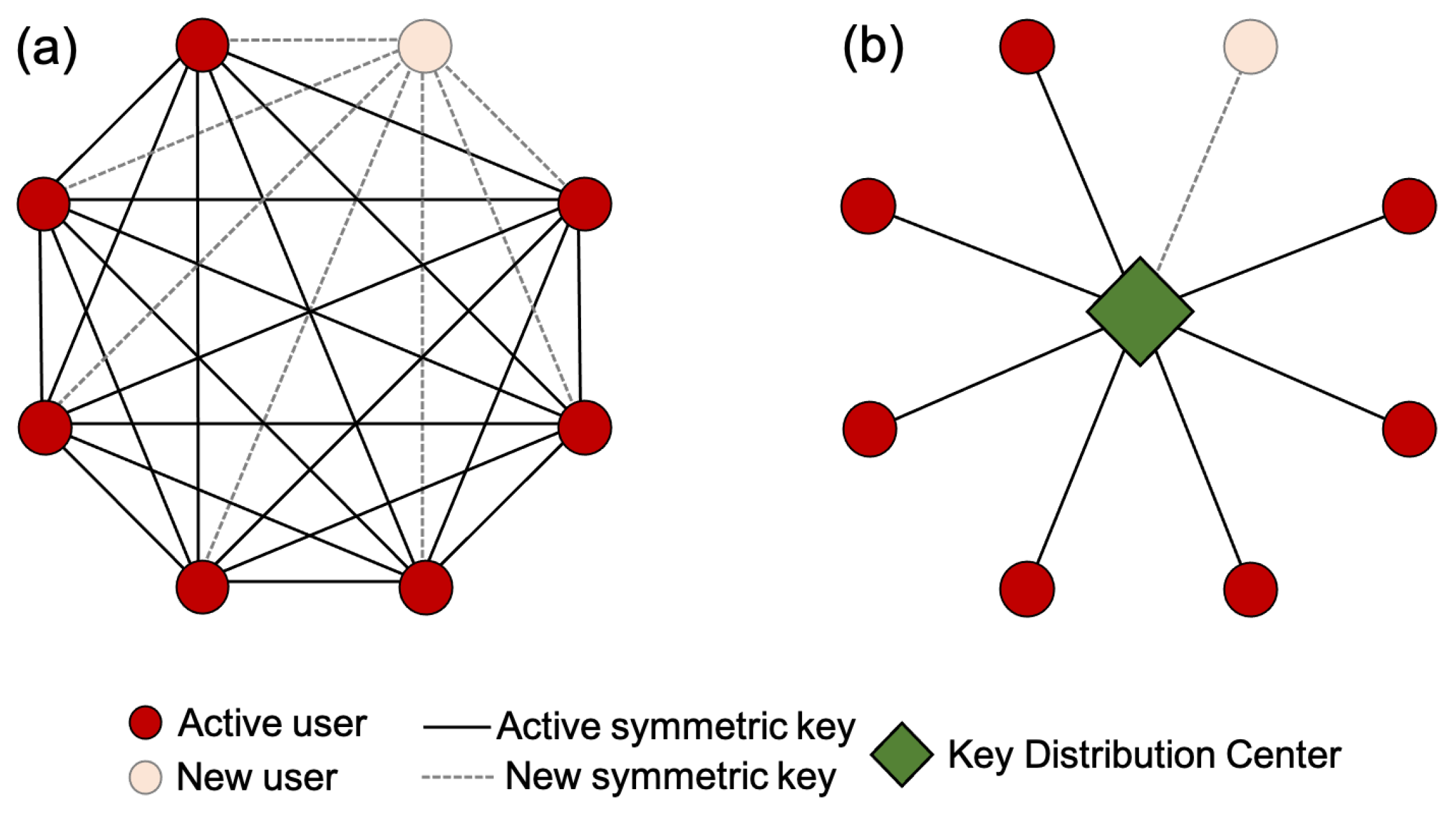
2.2. Large QKD Networks
The previous subsection focuses on a typical point-to-point QKD scenario, where only two honest parties are involved and a single pre-shared key is required for the seeding of the first QKD session. The design of large full-mesh QKD networks with
n users, however, requires
pre-shared keys (see
Figure 5a). For large
n, there is a large amount of key material that has to be distributed in a secure manner among the users in order for the first pairwise QKD sessions to be implemented. Moreover, it is very hard to add a new user to the network. Indeed, as soon as a new user (let us say Charlie) receives his QKD device, this should come with a list of keys pertaining to each one of the other users with whom Charlie may want to establish a QKD link. Each one of these users has to be informed about Charlie joining the network, and he/she should receive a copy of the corresponding symmetric key to be used for the implementation of the first QKD session with him. Overall, the addition of a new user in a network with
n users should be accompanied by the generation and the distribution of
n additional symmetric secret keys, a rather tedious task.
One solution to this problem is the use of a trusted centre, which shares a secret key with each one of the
n users, thereby significantly reducing the number of pairwise shared secret keys (see
Figure 5b). In this case, it is relatively easy for Charlie to join the existing network, as he has to obtain, together with his QKD device, only one secret key which is known to the key-distribution centre (KDC). The establishment of a QKD link with any other user can be achieved through the KDC, which can help the users to agree on a common secret key required for the post-processing in the first QKD session. The second solution to the aforementioned problems relies on the use of classical or quantum asymmetric cryptosystems, where each user holds a pair of keys (a private key and a public key). Standard widely used asymmetric cryptosystems rely on the difficulty of certain mathematical problems, and thus they offer computational security only [
12,
13,
14,
15,
22,
24,
36,
37]. On the other hand, a small number of ITS quantum public-key cryptosystems have been proposed in the literature, but their implementation is beyond reach of current technology [
38,
39,
40].
As long as we are interested in preserving the ITS character of QKD protocols, the only currently available route towards the realization of large QKD networks involves, in one way or another, the use of a trusted authority, such as a KDC, which is trusted by all the parties participating in the network. This solution is by no means optimal, because the functionality and the security of the entire QKD network depends strongly on the KDC, which automatically becomes the main target of potential adversaries. Given the current status of quantum technologies, however, the presence of a KDC in large networks facilitates and guarantees the generation and the distribution of pre-shared keys between users, which are essential for the establishment of the first secure pairwise QKD sessions. In the literature of QKD, the inclusion of a KDC is also considered essential for one more reason, namely, it can operate as a relay, thereby allowing two users that are separated by a distance well beyond the reach of current QKD systems to establish a secret key [
6].
The ideas discussed in the previous subsection can be generalized in the context of large QKD networks if we assume that the KDC holds all the databases of CRPs, as shown in
Figure 6. The manufacturer assigns a PUF tag to each QKD device (sender or receiver), and a separate database of CRPs is created along the lines discussed in the previous subsection. For the sake of simplicity, let us assume that the manufacturer of the QKD devices also controls the KDC, while the manager of the KDC has one PUF for each database, i.e., for each user. So, the KDC manages as many databases and PUFs as the user devices in the QKD network. For the sake of concreteness, let us consider the database for the QKD device C, intended for Charlie, who will join the QKD network. Let PUF
denote the PUF used by the KDC for the encryption of the entries in Charlie’s database of the CRPs. The
jth entry in the database involves the challenge
and the joint key
, where
and
denote the keys associated with the responses of PUF
and PUF
to challenge
, respectively. As soon as Charlie is ready to join the network, his first task is to establish a common secret key with the KDC, following the steps discussed in the previous subsection. The procedure is recapitulated in
Figure 6b, with the necessary changes in the labels.
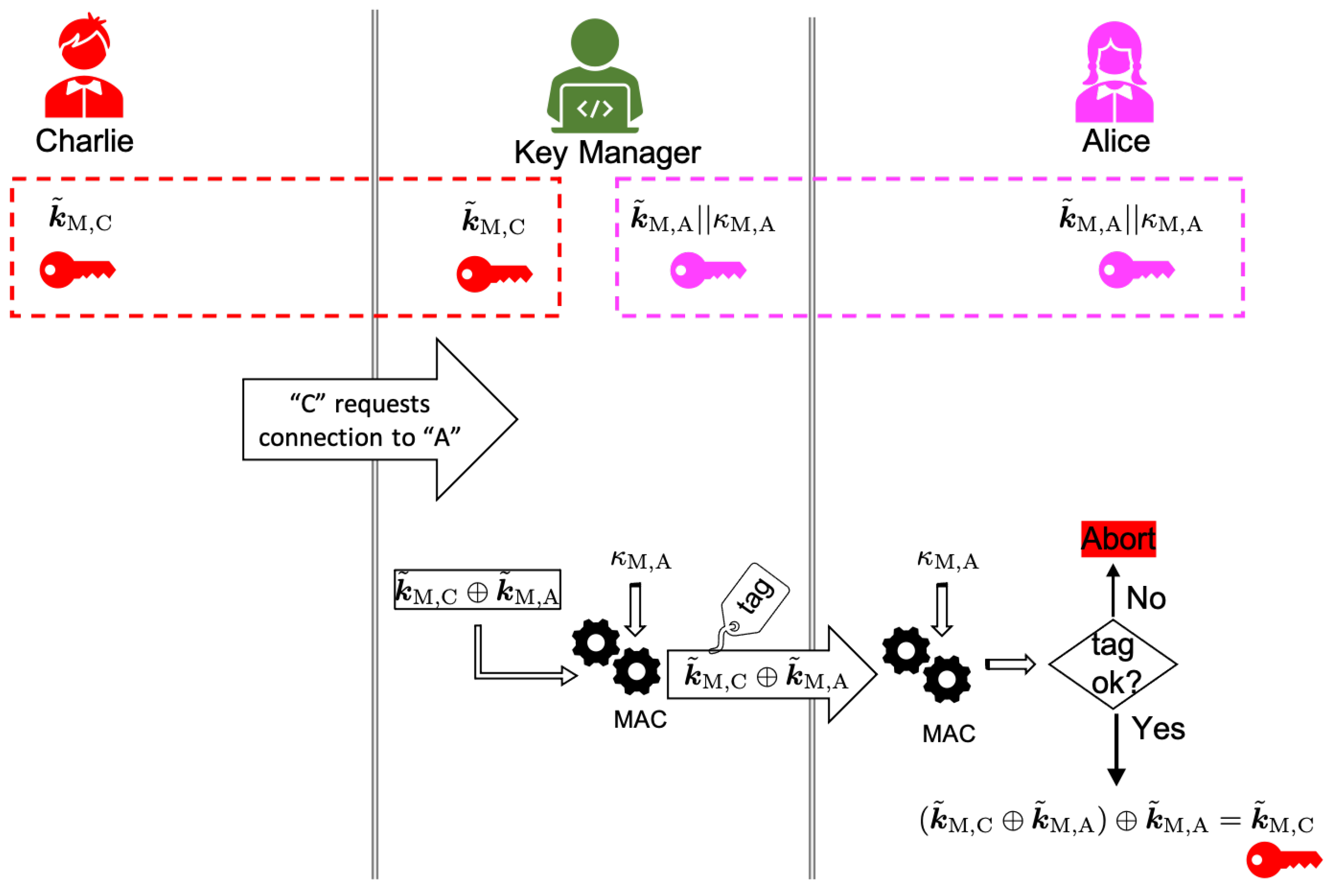
Having established a common secret key with the KDC, Charlie can establish a common secret key with any other existing user in the network, which will allow them to run the post-processing in the first QKD sessions until a sufficiently large number of fresh secret random bits has been generated through the QKD. The procedure is outlined in
Figure 7 and it is as follows. The key manager of the KDC shares a common secret key
with Charlie and another key with Alice, a user who is already in the network and with whom Charlie wants to communicate. For the sake of clarity, we write the latter key as a concatenation of two smaller keys, i.e.,
. Charlie contacts the KDC and requests connection with Alice, who is already in the network. The key manager calculates
and sends it to Alic over a classical channel. The message is authenticated with the key
. Upon receipt of the message, Alice confirms its origin, and she adds her key to the received message to obtain
. Hence, Alice and Charlie share a common secret key, which can be expanded through QKD.
It is worth emphasizing here that the realization of the ideas we have just presented does not require a QKD link between each user and the KDC. As shown in
Figure 6, the manager and the user can agree on a common secret key by means of classical communication and local operations on their PUFs. The only requirement is for the manager to communicate a randomly chosen challenge to Charlie over a public channel. This allows a lot of flexibility with respect to the physical topology of the network, in the sense that there are no limitations associated with the transmission of quantum signals on the spatial separation between a user and the KDC. In the absence of QKD links between the KDC and the users, all the key material is provided only by the PUFs, and thus it is limited by the number of challenge–response pairs that can be supported by the PUFs under consideration. In this context, strong PUFs are preferable. However, even though a QKD link between Charlie and the KDC imposes limitations on the distance, at the same time it allows for the expansion of an initial key that has been obtained through PUFs. In this case, the network may become self-sustainable, with respect to the generation and the consumption of key material, and its operation is not expected to depend strongly on the type of used PUFs.
2.3. QKD Device Authentication
Message authentication is what prevents a man-in-the-middle attack against QKD systems, and the ideas discussed in the previous subsections facilitate the generation and the distribution of pre-shared secret keys to this end. Entity authentication (also known as identification) is a different and very important cryptographic task, which allows the identity of a user or device to be confirmed [
12,
13,
14,
15]. By means of entity authentication, one can control which users or devices have access to certain physical or virtual resources. Entity authentication should not be confused with message authentication. They are different cryptographic tasks with distinct goals, and one cannot replace the other. A fundamental difference between the two is that an identification scheme provides real-time evidence about the identity of a user or a device, whereas MACs (and signature schemes) allow data origin authentication, which can be performed any time after the relevant message has been tagged or signed.
The integration of PUFs in QKD networks allows the KDC to confirm the identity of the QKD devices that are connected to the network at any time, thereby preventing the connection of counterfeit or unauthorized devices through which an attacker may try to connect to the KDC or to other users in the network in order to access databases or to sabotage the operation of the network. Moreover, an honest user can confirm the authenticity of a purchased QKD device. A PUF tag that is attached to a QKD device serves as a unique fingerprint and protects against counterfeiting.
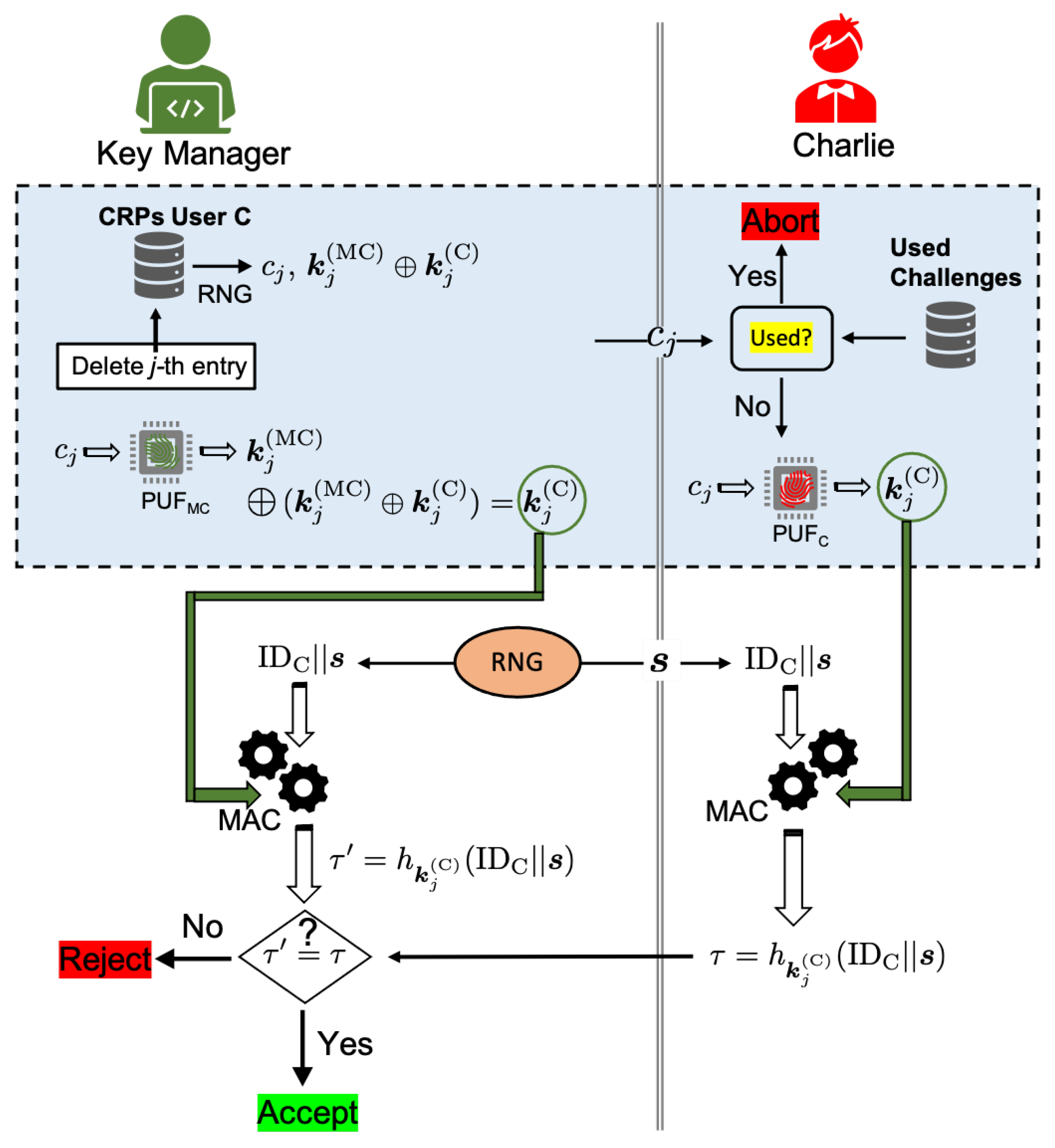
Let us consider a scenario where a new user, Charlie, joins the network, and that the KDC wants to authenticate his QKD device. The procedure is outlined in
Figure 8. As in the previous subsections, we will assume that Charlie’s QKD device is associated with PUF
. The related database of CRPs is generated by the manufacturer, and it is available to the KDC. Moreover, we will assume that each user (or QKD device) is uniquely identified by a binary string (a serial number). Given that Charlie is a new user who does not share a secret key with the KDC, the key manager randomly chooses one of the available challenges from the database of CRPs associated with PUF
. Moreover, the manager generates a random bit string
, and they send it to Charlie together with a challenge chosen at random
. Charlie obtains the response
of PUF
to challenge
, whereas the manager recovers the same response after they add the response of PUF
to the same challenge to the joint key. Charlie passes the concatenation of his identification string
with
through a MAC with key
, and the resulting tag,
, is sent to the KDC. The key manager computes the tag for the same message and they accept the QKD device as authentic only if this agrees with the tag received from Charlie.
In the protocol outlined in
Figure 8, we have assumed that the user does not share a common secret key with the KDC and it has to be generated locally through their PUFs. If the user shares a secret key with the KDC, then the procedure in the shaded region of
Figure 8 can be omitted, and the entity authentication can rely on the existing key material. Moreover, the protocol can be easily extended to mutual entity authentication by adding a second round of authentication, where the user chooses at random another binary string, which is sent to the KDC [
12,
14].
2.4. Security Considerations
The Wegman–Carter authentication (WCA) scheme [
17] that is usually employed in standard QKD systems is ITS only if the pre-shared secret key is truly random, or at least very close to perfect. In particular, it has been shown that a WCA scheme that is executed with an
perfect key, is indistinguishable from the ideal scenario, with a probability of
, where
refers to the security of the ideal scheme [
16,
41]. The protocols outlined in
Figure 4,
Figure 6, and
Figure 7, can provide two honest users with the secret key that is necessary for ITS post-processing in the first QKD session if the following conditions are satisfied:
- (C1)
The numerical keys produced by the PUFs under consideration are close to truly random.
- (C2)
The legitimate users never make their PUF tokens/tags available to other parties.
- (C3)
Each entry in the database of challenge–response pairs is used only once.
- (C4)
The MAC that is used for the distribution of the key in
Figure 7 is ITS.
For various PUFs that have been discussed in the literature, the generated keys have been shown to successfully pass widely accepted tests of random sequence certification, such as the ones provided by the NIST suite [
25,
31,
35,
42]. For all practical purposes, such a key can be considered to be close to truly random, and there are no correlations between different elements or parts of the key. Moreover, keys that have been generated from different PUFs or from the same PUF but for different challenges can be considered as uniformly distributed independent random strings. As a result, the entries in a database of CRPs are ITS, because the extraction of the individual keys
and
from the joint key
is impossible by virtue of a one-time-pad (OTP) encryption, unless the attacker has also access to at least one of the PUFs. Furthermore, an attacker cannot launch a machine learning attack [
27] in order to create a model of either of the two PUFs. This is because machine learning requires direct access to a set of CRPs
, whereas in our case, the individual keys are not accessible and they are stored encrypted in a secure manner.
For the sake of simplicity, in
Figure 4 and
Figure 6 we have assumed that one challenge suffices for the seeding of the first QKD session. This may not be always the case. A typical QKD system requires at least a 256-bit key (e.g., see
Appendix A), while the length of the key that can be generated from a PUF for a single challenge ranges from a few hundred to a few thousand bits. The precise length depends on the type of the PUF under consideration as well as on the details of the fuzzy extractor. If a single challenge cannot provide a key of an appropriate length for seeding the first QKD session, then one can concatenate two or more keys pertaining to different challenges. Indeed, as long as different challenges yield independent nearly perfect keys, the resulting longer key is also close to truly random.
Let us turn now to the entity authentication protocol in
Figure 8. One can readily show that it is information-theoretically secure if an
l-time
-secure MAC is used [
12,
14,
43] with
(see also
Appendix). In particular, the probability that the KDC uses the same random string
in the
ith session is
. Hence, the probability for a repeat in any of the
l sessions is
. The same result can be obtained through the birthday bound for
. On the other hand, there is a probability of at most
for an adversary to construct the correct tag. Hence, the overall probability for an adversary to deceive the KDC is at most
. Of course, one should not forget here that unconditionally secure
l-time
-secure MACs require a uniform truly random key. Hence, from the previous discussion, the quality of the keys that are produced from PUFs and the security of the databases also affect the security of the entity authentication protocol in
Figure 8.
Another issue that deserves our attention is the communication of the randomly chosen challenge
in the procedures outlined in
Figure 4b,
Figure 6b, and
Figure 8. The challenge is sent in plain text over a public, possibly unauthenticated channel. An adversary who learns the challenge and does not have access to the PUF of the sender or the receiver cannot use it to their advantage, because, as previously discussed, the PUFs operate as PRNGs, and their output to a given challenge cannot be predicted with a probability much better than random guessing. Even if the adversary has access to the database of CRPs, they cannot deduce the individual keys from the joint key by virtue of the OTP encryption. Finally, given that the entry pertaining to the communicated challenge is deleted from the database of CRPs and is added to a blacklist, an adversary cannot repeat it so as to fool either of the two users. The adversary can launch a type of DoS attack by changing the challenge. In this case, the two users will essentially not share the same key, as required for successful realization of a QKD session, and it is almost certain that the different keys will make the QKD protocol abort, and the users will have to start all over again. We have a similar situation in
Figure 7, where Charlie’s request for communication with Alice is also sent in plain text, and its origin is not verified by the receiver. In principle, an attacker can send multiple such requests to the KDC, thereby enforcing the manager to consume keys without reason and depleting the relevant databases and key pools. In all of these scenarios, the attacks are possible because the classical communication is not authenticated. However, none of these attacks threaten the security of the QKD network; rather, they target the resources of the QKD network. For this reason, there is no need for ITS message authentication, and they can be prevented by means of computationally secure MACs [
12,
13,
14,
15,
44] or public key cryptosystems [
12,
15,
36,
37].
Finally, throughout this work we have assumed that the manager of the KDC uses a different PUF for each user participating in the network, namely, PUF, PUF, PUF, etc. In this way, we have added an additional level of security in the sense that if, for any reason, a database of CRPs is compromised, the security of the other databases is not affected, as long as different PUFs produce independent random keys. In particular, the jth entry in the databases of CRPs for two different users, say A and B, pertains to the joint keys and , where all of the individual keys refer to the same challenge but to different independent PUFs, namely, PUF, PUF, PUF and PUF. By virtue of the OTP encryption, even if user A is malicious, they cannot deduce either or from and PUF, provided that conditions (C1) and (C2) are satisfied for the PUFs under consideration.
Perhaps one way to avoid the use of different PUFs for each user is to consider the use of PUF duplicates in the spirit of the recent work by Marakis et al. [
45]. In this preprint, the authors demonstrate for a particular type of PUF, that the original PUF manufacturer (which is a trusted authority in our case), can fabricate multiple identical structures (tokens) that possess essentially the same optical scattering behaviour (i.e., the same challenge–response pairs), but at the same time, they remain unclonable for external adversaries who do not know their internal features and inner construction plan. The use of PUF duplicates deserves a thorough analysis, which goes beyond the scope of the present work because it may open up new security loopholes which are not present at the moment.
3. Conclusions
We have considered the distribution of a common secret key between two honest users of a QKD network, which is necessary for authentication and encryption purposes during the post-processing stage in the first pairwise QKD session. Such a key (usually referred to as a pre-shared key in the QKD literature), is necessary for any QKD system because it prevents a man-in-the-middle attack.
We have discussed the generation and the distribution of pre-shared keys by means of PUFs. Each QKD device (sender or receiver) is associated with a disordered token/tag, which plays the role of a unique fingerprint and allows the users to generate nearly perfect random keys as well as to authenticate their devices. Two users can generate a common secret random key by locally interrogating their tokens with the same randomly chosen challenge. The main advantages offered by the proposed scheme are the following: (i) It does not require quantum communication. (ii) In contrast to PQC protocols, the distributed pre-shared keys are information-theoretically secure, which ensures the ITS character of the entire QKD session (see also related discussion in
Section 1). (iii) There is no need for distributing additional secret keys or passwords to Alice and Bob to ensure the secrecy of the pre-shared key. (iv) There is no need to keep the database of CRPs private. Even if an adversary obtains access to the database, they cannot deduce the possible pre-shared keys, as discussed in
Section 3. (v) By definition, a PUF is hard to clone, even if one has access to it, because its response to a particular challenge is very sensitive to the internal randomness of the token (tag), which also depends on the conditions of fabrication. (vi) There is no need to ensure the authenticity of the randomly chosen challenge that is used for the establishment of the pre-shared key, unless one wishes to prevent a DoS attack (see the related discussion in
Section 3). All of these features make our scheme more attractive than other currently used methods, such as the inclusion of the pre-shared key in the software that accompanies the QKD boxes, its storage in password-protected devices, the use of a trusted courier, or the distribution by means of PQC.
For two users, a single CRP suffices for establishing the necessary pre-shared key for the first QKD session, provided that the length of the key that can be generated from the PUF under consideration is at least equal to the length of the pre-shared key required by the used QKD system (see also the related discussion in
Section 3). In other words, by employing the right type of PUF, the present protocol does not require more pre-shared keys (or equivalently challenges) than the number required by the current QKD systems. Of course, having more CRPs available in the database, in case something goes wrong, is an additional feature which is provided by our protocol and, to the best of our knowledge, it is not an option in the QKD systems that are available on the market today. Extending this reasoning to a case of
n users with a trusted KDC, one can easily see that the number of challenges (entries) required by the present protocol are as many as the number of pre-shared keys required in the QKD network without PUFs. The additional entries that are provided by a PUF is a benefit that can be exploited by the users if needed.
As discussed above, the inclusion of a trusted KDC is essential in large QKD networks (many users) in order to preserve the ITS character of QKD systems. Moreover, even for two users, a trusted intermediate node may operate as a relay, which allows the distribution of a secret key beyond the distances that can be covered by a direct QKD link. In other words, the trusted KDC is not a requirement that originates from our protocol, but rather it is a necessity which originates from the point-to-point character of QKD links, the limitations of the available QKD systems, and the absence of quantum repeaters. If one is willing to accept a computationally secure system, PUFs can be combined with standard public key cryptosystems in order to generate and distribute keys between users. In particular, the key that is generated from a PUF device may serve as a private key, or it can be used as a random seed for the generation of a private key. Subsequently, building upon the private key, the corresponding public key is generated, which becomes publicly available through a trusted public key server. An advantage of such an asymmetric cryptosystem is that it allows for the implementation of various cryptographic tasks beyond the generation and the distribution of a key, including digital signatures. At the same time, the pair of private–public keys is bound to the PUF device.
Throughout this work, we have adopted a rather general theoretical framework, which is not restricted to a particular type of PUF. The present results pave the way for the integration of PUFs in currently used QKD systems, but there are many practical issues that deserve further investigation in order to identify which type of PUF better serves the needs of QKD networks. To this end, one has to take into account various facts including the required key lengths, the size of the network, the robustness of the PUF in the presence of environmental fluctuations, etc. Optical PUFs may be a very promising candidate because they are considered to be among the strong PUFs, and they can typically support long keys (thousand of bits) [
25,
35,
42]. Moreover, they are compatible with QKD infrastructure and, in principle, they are amenable to remote quantum readout [
46]. Remote quantum readout of optical PUFs is very attractive if one is interested in saving classical resources, at the cost of introducing limitations in the spatial separation between the users and the KDC. However, all the known quantum readout schemes [
47,
48,
49] are currently limited to very short distances (of the order of 1 km), and there is a need for their extension to distances comparable to the ones that can be covered by standard QKD systems. Only experimental research may shed light on the integration of PUFs in operational QKD networks and provide answers to many of these questions.