Numerical Simulation and Experimental Research on Heat Transfer Characteristics Based on Internal Meshing Screw
Abstract
:1. Introduction
2. The Working Principle and Process of an Internal Meshing Screw Mixer
3. Material and Methods
3.1. Experimental Equipment and Dimensions
3.2. Experimental Plan and Experimental Equipment
3.3. Material Properties
3.4. Steps of the Experiment
- (1)
- Experiment equipment setup: The experimental setup involved the application of a heating element to the surface of the internal meshing screw mixing section, followed by the envelopment of the heating element with glass insulation cotton to ensure compliance with overall temperature requirements.
- (2)
- Preparation of experiment materials: The test materials were meticulously prepared by adhering to a 5:1 ratio of corn syrup to distilled water. This mixture was subsequently placed within a temperature-controlled water bath set to 25 °C, allowing it to stabilize for a duration of 40 min.
- (3)
- Experimental procedure: The prepared test material was gently introduced into the internal meshing screw device. The inlet was sealed with an oil plug, and the temperature measuring instrument’s probe was inserted through the oil plug to attain the designated position.
- (4)
- Experimental execution: The heating plate temperature was methodically adjusted to reach a steady state at 50 °C. Subsequently, the equipment was initiated, with the rotation speed calibrated to 60 rpm. Temperature variations were recorded by the temperature-measuring instrument within a time frame of 1–4 s.
- (5)
- Post-experiment protocol: Following the completion of the experiment, the equipment was meticulously cleaned, and the test bench was maintained in a pristine condition. Finally, the power supply was switched off.
4. Numerical Simulation Model
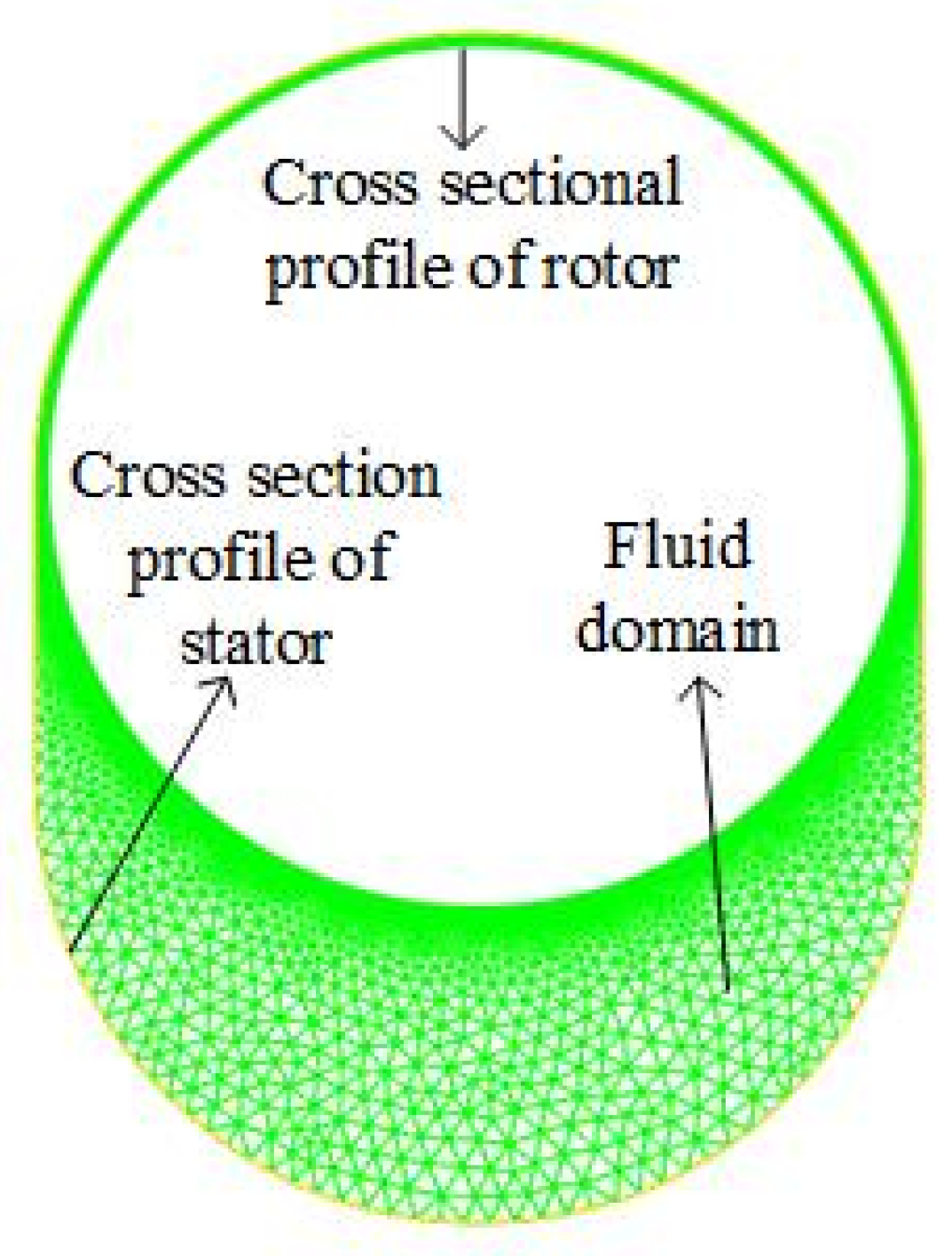
4.1. Geometric Model
4.2. Mathematical Model
4.3. Grid and Calculation
4.4. Grid Independence Verification
5. Heat Transfer Analysis of Internal Meshing Screw Mixer
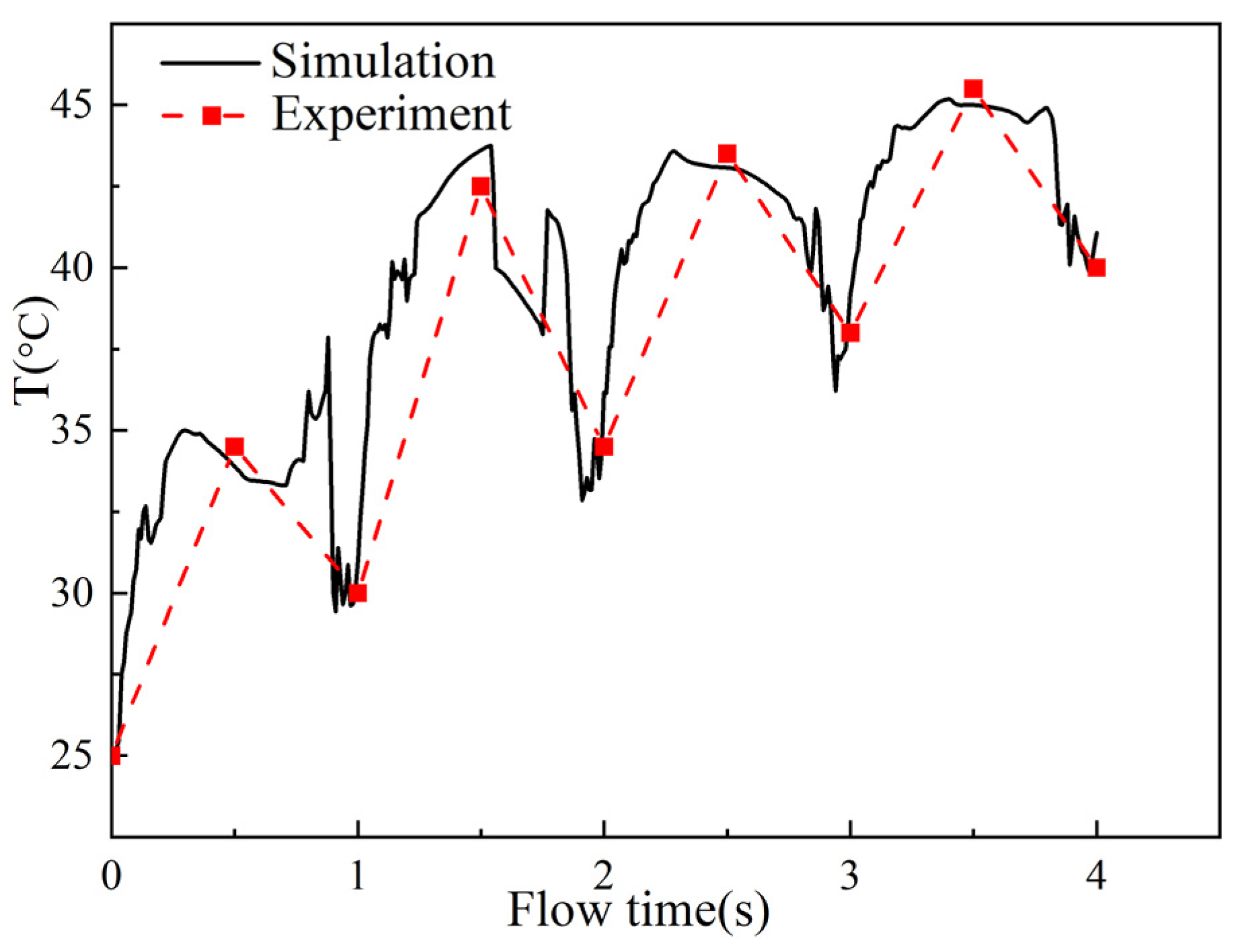
5.1. Comparisons of CFD Simulations and Experiment
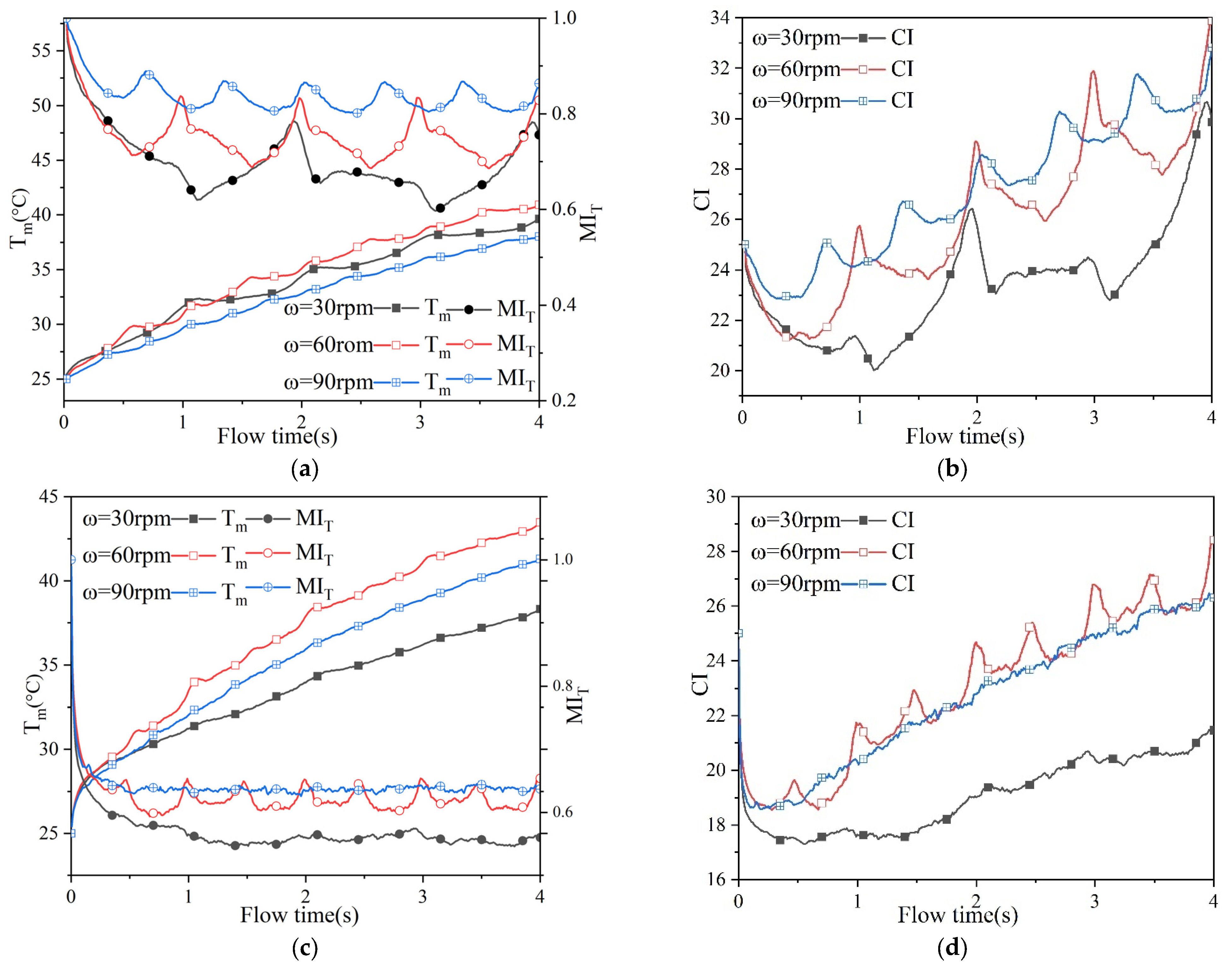
5.2. Comprehensive Index of Heat Transfer
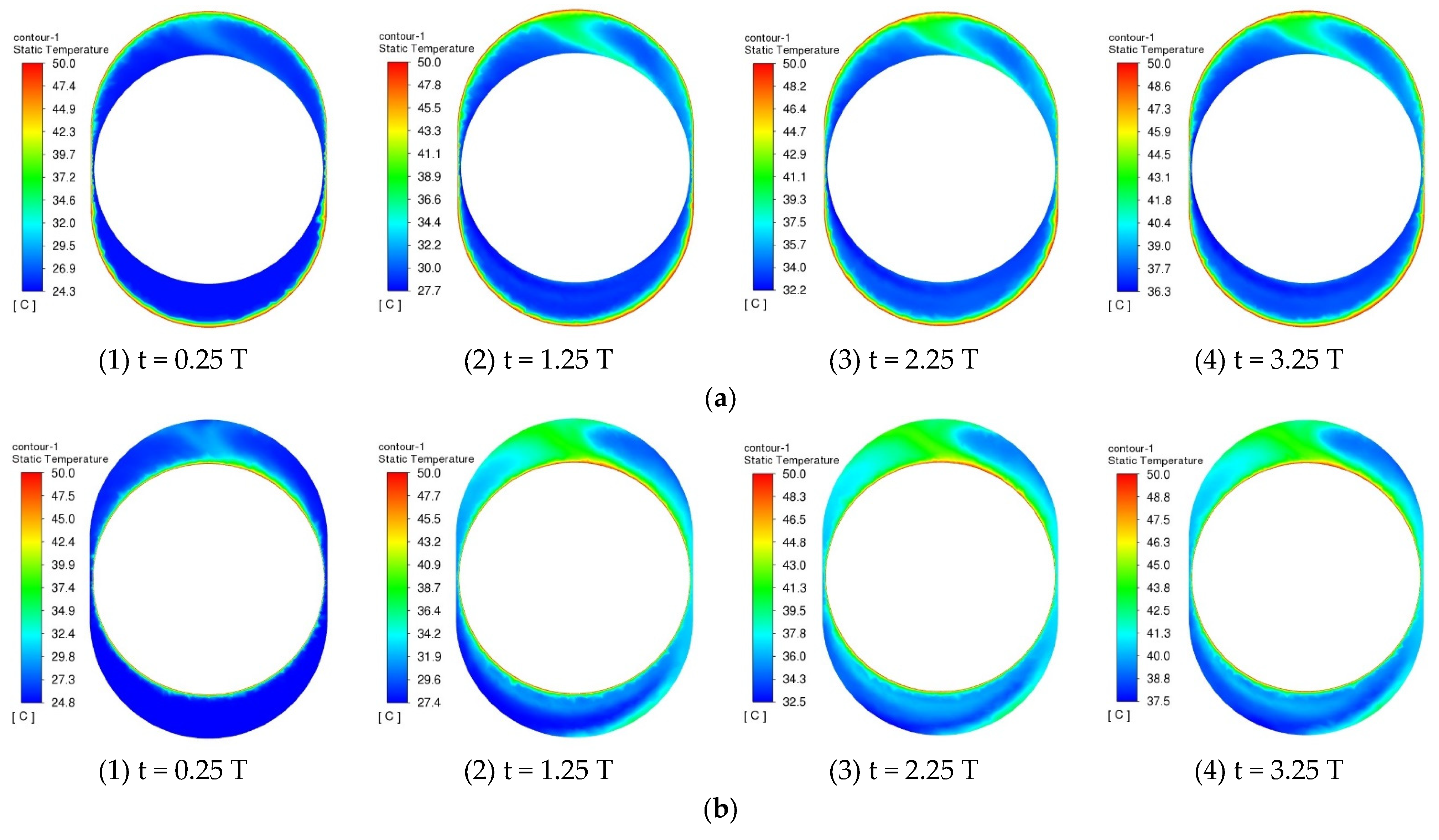
5.3. Heat Transfer Mechanism in Two Models
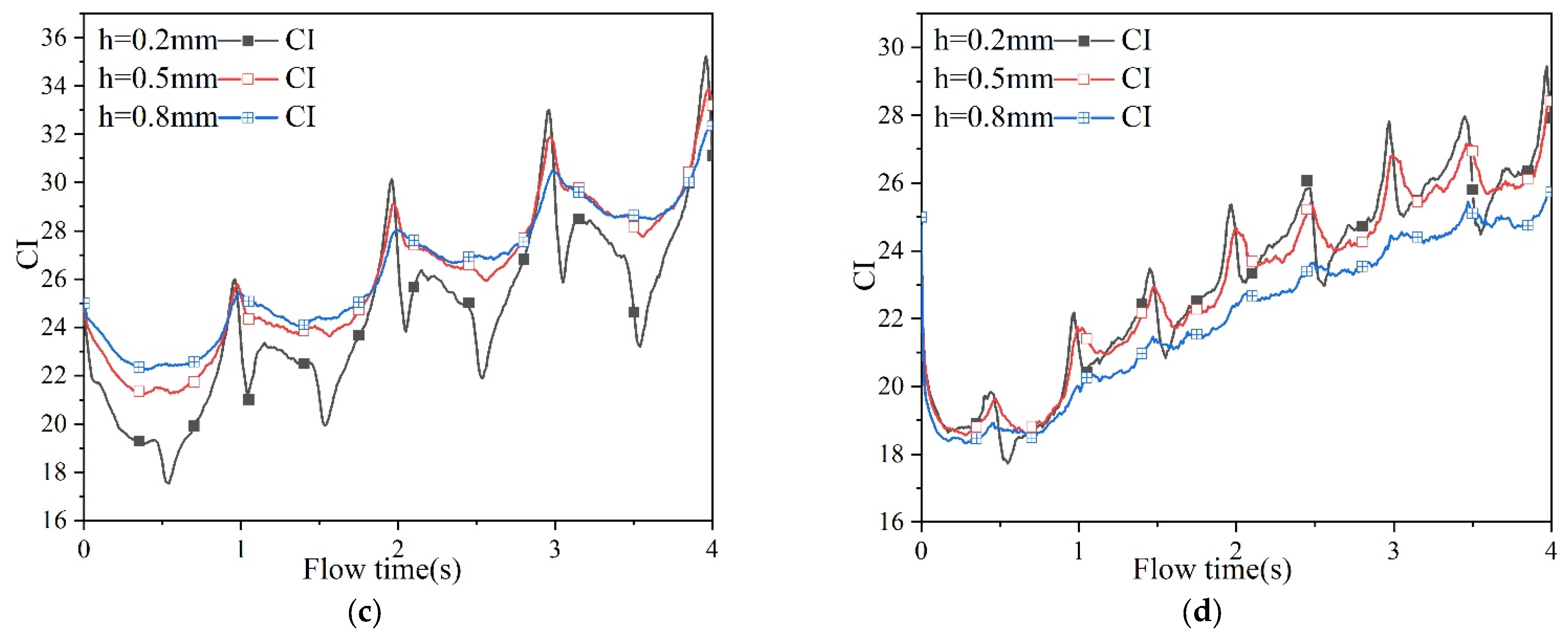
5.4. Effect of Process Parameters on Heat Transfer
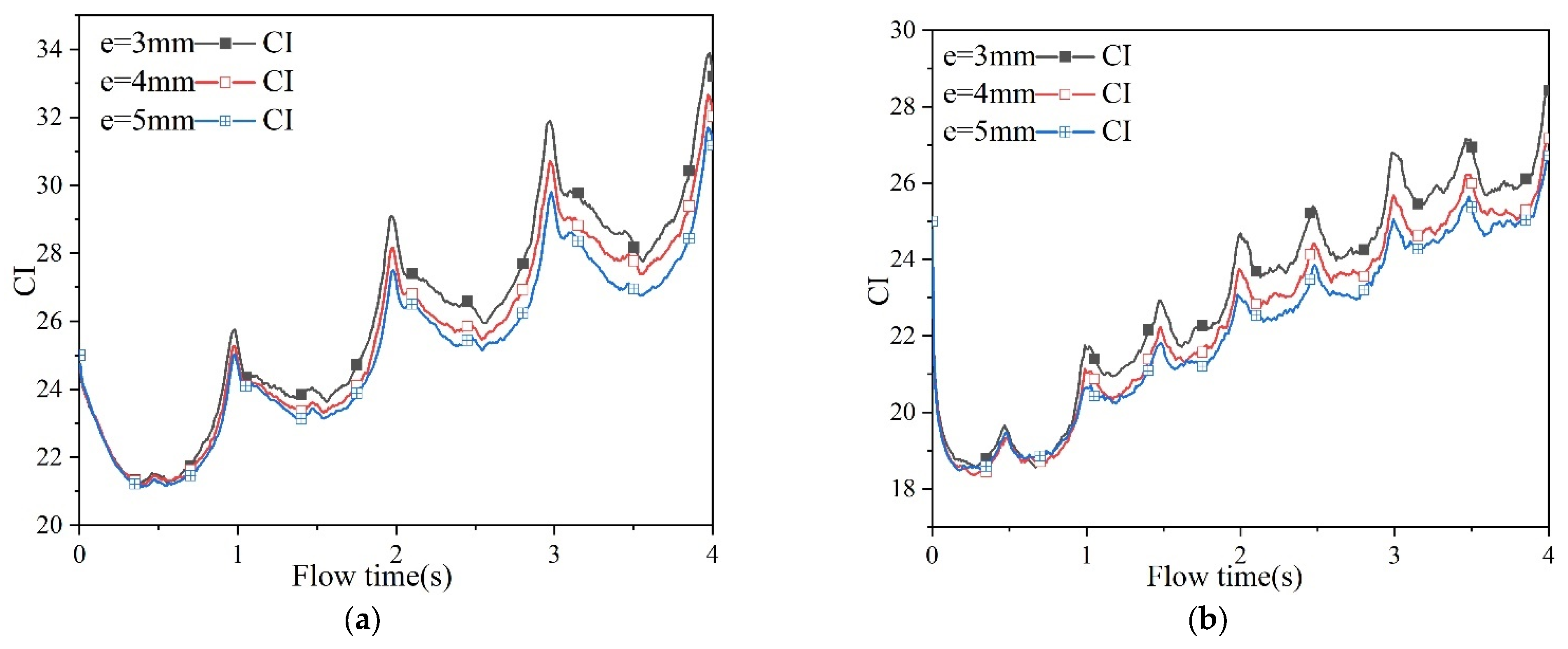
5.5. Effect of Structural Parameters on Heat Transfer
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tofail, S.A.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; Lisa, O.D.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. [Google Scholar] [CrossRef]
- Arun, K.S.; Bhandari, R.; Aherwar, A.; Rimašauskienė, R.; Camelia, P. A study of advancement in application opportunities of aluminum metal matrix composites. Mater. Today Proc. 2020, 26, 2419–2424. [Google Scholar]
- Evode, N.; Qamar, S.A.; Bilal, M.; Barceló, D.; Iqbal, H.N. Plastic waste and its management strategies for environmental sustainability. Case Stud. Chem. Environ. Eng. 2021, 4, 100142. [Google Scholar] [CrossRef]
- Karkala, S.; Ramachandran, R. Investigating the effects of material properties on the mixing dynamics of cohesive particles in a twin screw mixer using a discrete element method approach. Powder Technol. 2022, 409, 117762. [Google Scholar] [CrossRef]
- Ren, A.; Koleng, J.J.; Costello, M.; Spahn, J.E.; Smyth, H.D.; Zhang, F. Twin-Screw Continuous Mixing Can Produce Dry Powder Inhalation Mixtures for Pulmonary Delivery. J. Pharm. Sci. 2023, 112, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Kotamarthy, L.; Ramachandran, R. Mechanistic understanding of the effects of process and design parameters on the mixing dynamics in continuous twin-screw granulation. Powder Technol. 2021, 390, 73–85. [Google Scholar] [CrossRef]
- Qu, J.P.; Chen, J.J.; Liu, H.Y.; Zhang, G.Z.; Ying, X.C.; He, H.Z. Recent Advances in Volume Stretching Deformation Processing and Forming Methods. Polym. Bull. 2013, 9, 9–17. [Google Scholar]
- Gupta, S.; Vanapalli, S. Microfluidic shear rheology and wall-slip of viscoelastic fluids using holography-based flow kinematics. Phys. Fluids 2020, 32, 012006. [Google Scholar] [CrossRef]
- Venerus, D.C. A novel and noninvasive approach to study the shear rheology of complex fluid interfaces. J. Rheol. 2023, 67, 923–933. [Google Scholar] [CrossRef]
- Matsumiya, Y.; Watanabe, H. Non-Universal Features in Uniaxially Extensional Rheology of Linear Polymer Melts and Concentrated Solutions: A Review. Prog. Polym. Sci. 2021, 112, 101325. [Google Scholar] [CrossRef]
- Gamonpilas, C.; Kongjaroen, A.; Methacanon, P. The importance of shear and extensional rheology and tribology as the design tools for developing food thickeners for dysphagia management. Food Hydrocolloids 2023, 140, 108603. [Google Scholar] [CrossRef]
- Sefiane, K.; Koşar, A. Prospects of heat transfer approaches to dissipate high heat fluxes: Opportunities and challenges. Appl. Therm. Eng. 2022, 215, 118990. [Google Scholar] [CrossRef]
- Stehlík, P.; Jegla, Z.; Kilkovský, B. Possibilities of intensifying heat transfer through finned surfaces in heat exchangers for high temperature applications. Appl. Therm. Eng. 2014, 70, 1283–1287. [Google Scholar] [CrossRef]
- Ali, S.A. Design and dynamic simulation of a photovoltaic thermal-organic Rankine cycle considering heat transfer between components. Energy Convers. Manag. 2020, 225, 113435. [Google Scholar]
- Natesan, K.; Karinka, S. A comprehensive review of heat transfer enhancement of heat exchanger, heat pipe and electronic components using graphene. Case Stud. Therm. Eng. 2023, 45, 102874. [Google Scholar] [CrossRef]
- Dović, D.; Horvat, I.; Filipović, P. Impact of velocities and geometry on flow components and heat transfer in plate heat exchangers. Case Stud. Therm. Eng. 2021, 197, 117371. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K. Modeling of Twin Screw Extrusion of Polymeric Materials. Polymers 2022, 14, 274. [Google Scholar] [CrossRef] [PubMed]
- Estrada, O.; Ortiz, J.C.; Hernández, A.; López, I.; Chejne, F.; María, D.N. Experimental study of energy performance of grooved feed and grooved plasticating single screw extrusion processes in terms of SEC, theoretical maximum energy efficiency and relative energy efficiency. Energy 2020, 194, 116879. [Google Scholar] [CrossRef]
- Marschik, C.; Roland, W.; Osswald, T.A. Melt Conveying in Single-Screw Extruders: Modeling and Simulation. Polymers 2022, 14, 875. [Google Scholar] [CrossRef]
- Eitzlmayr, A.; Koscher, G.; Reynolds, G.; Huang, Z.Y.; Booth, J.; Shering, P.; Khinast, J. Mechanistic modeling of modular co-rotating twin-screw extruders. Int. J. Pharm. 2014, 474, 157–176. [Google Scholar] [CrossRef]
- Andrea, L.G.; Fiorio, R.; Erkoç, M.; Cardon, L.; D’hooge, D.R. Theoretical Evaluation of the Melting Efficiency for the Single-Screw Micro-Extrusion Process: The Case of 3D Printing of ABS. Processes 2020, 8, 1522. [Google Scholar]
- Chang, Y. Study on Visualization Twin-Screw Extrusion and Plasticizing Quality of Simulation Material for Energetic Materials; BUCT: Beijing, China, 2023; p. 001338. [Google Scholar]
- García-León, R.A.; Afanador-García, N.; Gómez-Camperos, J.A. Numerical Study of Heat Transfer and Speed Air Flow on Performance of an Auto-Ventilated Disc Brake. Fluids 2021, 6, 160. [Google Scholar] [CrossRef]
- Zeng, X.X.; Yu, H.; Hw, T.B.; Mao, N. A Numerical Study on Heat Transfer Characteristics of a Novel Rectangular Grooved Microchannel with Al2O3/Water Nanofluids. Energies 2022, 15, 7187. [Google Scholar] [CrossRef]
- Kim, M.H.; Pettersen, J.; Bullard, C.W. Fundamental process and system design issues in CO2 vapor compression systems. Prog. Energy Combust. Sci. 2004, 30, 119–174. [Google Scholar] [CrossRef]
- Barr, R.A. Extruder screw with improved energy efficient melting. US Patent 2003, 7, 29. [Google Scholar]
- Fei, T.; Yin, L.; Xin, C.L.; He, Y.D. Heat Transfer Model of Cooling Single-Screw Polymer Melt. J. Beijing Univ. Chem. Technol. 2021, 48, 50–58. [Google Scholar]
- Jian, R.R.; Xie, P.Y.; Ding, Y.M.; Yang, W.M. Application of Field Synergy Theory in Polymer Processing. Plastics 2019, 48, 8–11. [Google Scholar]
- Rauwendaal, C. Heat transfer in twin screw compounding extruders. AIP Conf. Proc. AIP Publ. 2016, 1779, 030014. [Google Scholar]
- Liu, P.; Peng, X.B.; Song, Y.T. Subcooled water flow boiling heat transfer in screw cooling tubes under one-sided heating conditions. Appl. Therm. Eng. 2017, 113, 621–631. [Google Scholar] [CrossRef]
- Kamal, S.D.; Fazilati, M.A.; Hajatzadeh, A. Surface Scraped Heat Exchanger for cooling Newtonian fluids and enhancing its heat transfer characteristics, a review and a numerical approach. Appl. Therm. Eng. 2015, 87, 56–65. [Google Scholar]
- Wen, Q.Y.; Zhi, R.P.; Wu, Y.T.; Lei, B.; Liu, S.W.; Shen, L.L. Performance optimization of a heat pump integrated with a single-screw refrigeration compressor with liquid refrigerant injection. Energy 2020, 207, 118197. [Google Scholar] [CrossRef]
- Kang, B.H. Study on the Solid Conveying Process and Characteristics of a Single-Screw Eccentric Rotating Extruder; SCUT: Guangzhou, China, 2020; p. 000248. [Google Scholar]
- Zhang, H.H. Preparation and Structural Properties Study of PVDF-Based Composite Materials under Volume Stretching Rheological Action; SCUT: Guangzhou, China, 2021; p. 004999. [Google Scholar]
- Peng, J.G.; Shao, S.S.; Shao, S.A.; Shi, L.; Huang, Q.M. Inertial Force Analysis of a Four-Cylinder Gasoline Engine Designed Based on the Epitrochoid Principle. Small Intern. Combust Engines Veh. Technol. 2023, 52, 18–23+27. [Google Scholar]
- Fan, D.J. Numerical Simulation and Experimental Study on the Flow Field and Mixing Performance of an Eccentric Rotating Extruder; SCUT: Guangzhou, China, 2019; p. 003079. [Google Scholar]
- Qu, J.P.; Wu, T. Innovation in Materials Development with Volume Stretch Rheological Plasticization and Transport Technology. Sci. Technol. Rev. 2020, 8, 54–62. [Google Scholar]
- Qu, J.P.; Wu, T. Research Progress in Technological Innovation of Polymer Product Batch Manufacturing and Forming. Mech. Electr. Eng. Technol. 2018, 47, 1–6. [Google Scholar]
- Tong, Y.R. Study on the Mechanism of CPVC and PVC Twin-Screw Eccentric Rotational Plasticizing Extruder; SCUT: Guangzhou, China, 2021; p. 001099. [Google Scholar]
- Kamal, E.O.; Yves, L.G. Alternate rotating walls for thermal chaotic mixing. Int. J. Heat Mass Transfer. 2010, 53, 123–134. [Google Scholar]
- Jaluria, Y. Chapter One–Heat and Mass Transfer in Materials Processing and Manufacturing. Adv. Heat Transfer. 2016, 48, 1–94. [Google Scholar]
- Xie, P.Y.; Zhang, X.B. Study on the influence of periodic contraction and expansion flow disturbance on convection heat transfer. Int. Commun. Heat Mass Transfer. 2022, 138, 106384. [Google Scholar] [CrossRef]
- Zontul, H.; Şahin, B. Experimental investigation of convective heat transfer performance and hydrodynamics of pulsating flow through the rectangular grooved channel. Exp. Therm. Fluid Sci. 2023, 141, 110796. [Google Scholar] [CrossRef]
- Gao, J.; Hu, Z.H.; Yang, Q.G.; Liang, X.; Wu, H.W. Fluid flow and heat transfer in microchannel heat sinks: Modelling review and recent progress. Therm. Sci. Eng. Prog. 2022, 29, 101203. [Google Scholar] [CrossRef]






| Experimental Instrument Name | Model | Effect |
|---|---|---|
| Silicone rubber heating plate | 130 mm × 280 mm external digital display | Provide stable heat source |
| Unilid contact thermometer | U T320D | Continuously detect temperature changes at the temperature measurement point |
| High-density fiberglass insulation cotton | 0.5 m × 1 m | Make the outer wall of the stator an insulating wall |
| Lichen digital display rotational viscometer | N DJ-8S | Test the viscosity of experimental materials |
| Point | Parameter Value | Trajectory Equation | Velocity Equation | ||
|---|---|---|---|---|---|
| O1 | -- | (3) | (7) | ||
| (4) | (8) | ||||
| O2 | LAB = e | (5) | (9) | ||
| O | LBC = e | (6) | (10) | ||
| Grid | Number of Grids | Grid Quality Range | Minimum Grid Size | Local Encryption Size | Operation Hours |
|---|---|---|---|---|---|
| coarse mesh | 10,289 | 0.67, 0.98 | 1 mm | 0.1 mm | 12 h |
| medium grid | 23,867 | 0.68, 0.98 | 0.5 mm | 0.05 mm | 16 h |
| fine mesh | 196,515 | 0.54, 0.97 | 0.1 mm | 0.01 mm | 24 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Y.; Guo, F.; Wu, G.; Hou, Z.; Li, N.; Liu, G.; Cui, X.; Meng, D.; Li, Y.; Li, X. Numerical Simulation and Experimental Research on Heat Transfer Characteristics Based on Internal Meshing Screw. Appl. Sci. 2024, 14, 220. https://doi.org/10.3390/app14010220
Hao Y, Guo F, Wu G, Hou Z, Li N, Liu G, Cui X, Meng D, Li Y, Li X. Numerical Simulation and Experimental Research on Heat Transfer Characteristics Based on Internal Meshing Screw. Applied Sciences. 2024; 14(1):220. https://doi.org/10.3390/app14010220
Chicago/Turabian StyleHao, Yinghai, Fang Guo, Guifang Wu, Zhanfeng Hou, Na Li, Genhao Liu, Xiafan Cui, Dezhao Meng, Yuanyuan Li, and Xiwen Li. 2024. "Numerical Simulation and Experimental Research on Heat Transfer Characteristics Based on Internal Meshing Screw" Applied Sciences 14, no. 1: 220. https://doi.org/10.3390/app14010220
APA StyleHao, Y., Guo, F., Wu, G., Hou, Z., Li, N., Liu, G., Cui, X., Meng, D., Li, Y., & Li, X. (2024). Numerical Simulation and Experimental Research on Heat Transfer Characteristics Based on Internal Meshing Screw. Applied Sciences, 14(1), 220. https://doi.org/10.3390/app14010220







