Gaussian-Linearized Transformer with Tranquilized Time-Series Decomposition Methods for Fault Diagnosis and Forecasting of Methane Gas Sensor Arrays
Abstract
:1. Introduction
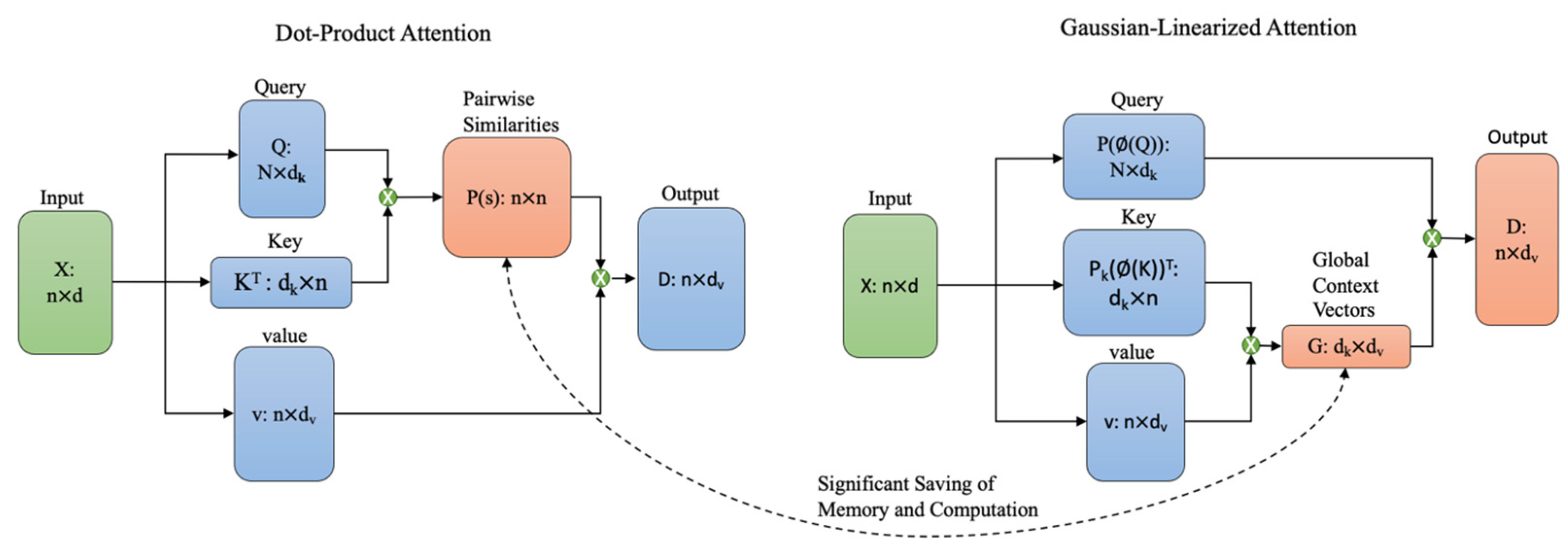
- The traditional self-attention mechanism was changed to reduce the time complexity to O (L). Firstly, Q and K were mapped to the Gelu function to obtain a Gaussian distribution, which was inspired by the kernel method. Secondly, in contrast to the traditional softmax calculation, we performed a softmax operation on Gelu (Q) and Gelu (K), and then multiplied the product of softmax (Gelu (K)) and V with Gelu (Q) to complete the calculation of the Gaussian-linearized attention. Finally, the time complexity of the model was reduced to O (L);
- The traditional embedding block was changed into a tranquilized time-series decomposition block in the fault forecasting task. After the decomposition block, we obtained multivariate time-series sequences and transformed them into the Gaussian-linearized transformer model with improved accuracy of fault forecast data;
- The complex fault environment was taken into account in the actual use of the methane sensor array. In practice, the number of sensor array faults occurs randomly and the fault models may be different at the same time. Therefore, combined with the above actual situation, the data were made closer to the actual situation.
2. Theoretical Fundamentals
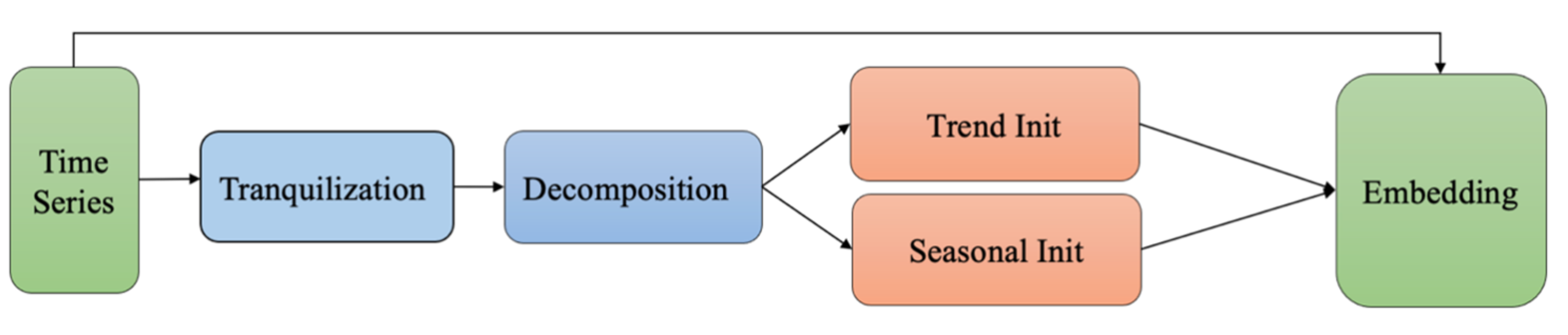
2.1. Tranquilized Time-Series-Decomposition Embedding
| Algorithm 1 Algorithm of continuous sequence decomposition embedding. | ||
| function | embedding(Xi) | |
| | | Xtql ←Tranquilized our raw time series sequence Xi | Equation (1) |
| | | Xt = [], Xs = [] | |
| | | for j from 1 to K do | |
| | | | Xj ← , m = K + 1 | Equation (3) |
| | | | xt += Xj | |
| | | | xs += XTql -Xt | Equation (2) |
| | | Xt.append(xt), Xs.append(xs) | |
| | | end | |
| | | return Xembedding ← [Xtql, Xt, Xs] | Equation (4) |
| end | ||
2.2. Gaussian-Linearized Attention
| Algorithm 2 Gaussian-linearized attention. | ||
| function | Attention(Xembedding) | |
| | | Q, K, V ← Xembedding | |
| | | ← Gelu(x) | Equation (10) |
| | | for i from 1 to N do | |
| | | | for j from 1 to N do | |
| | | | | ← · | Equation (12) |
| | | | end | |
| | | end | |
| | | return | Equation (14) |
| end | ||
2.3. Encoder Stacks
3. Experiment and Validation of the Proposed Method
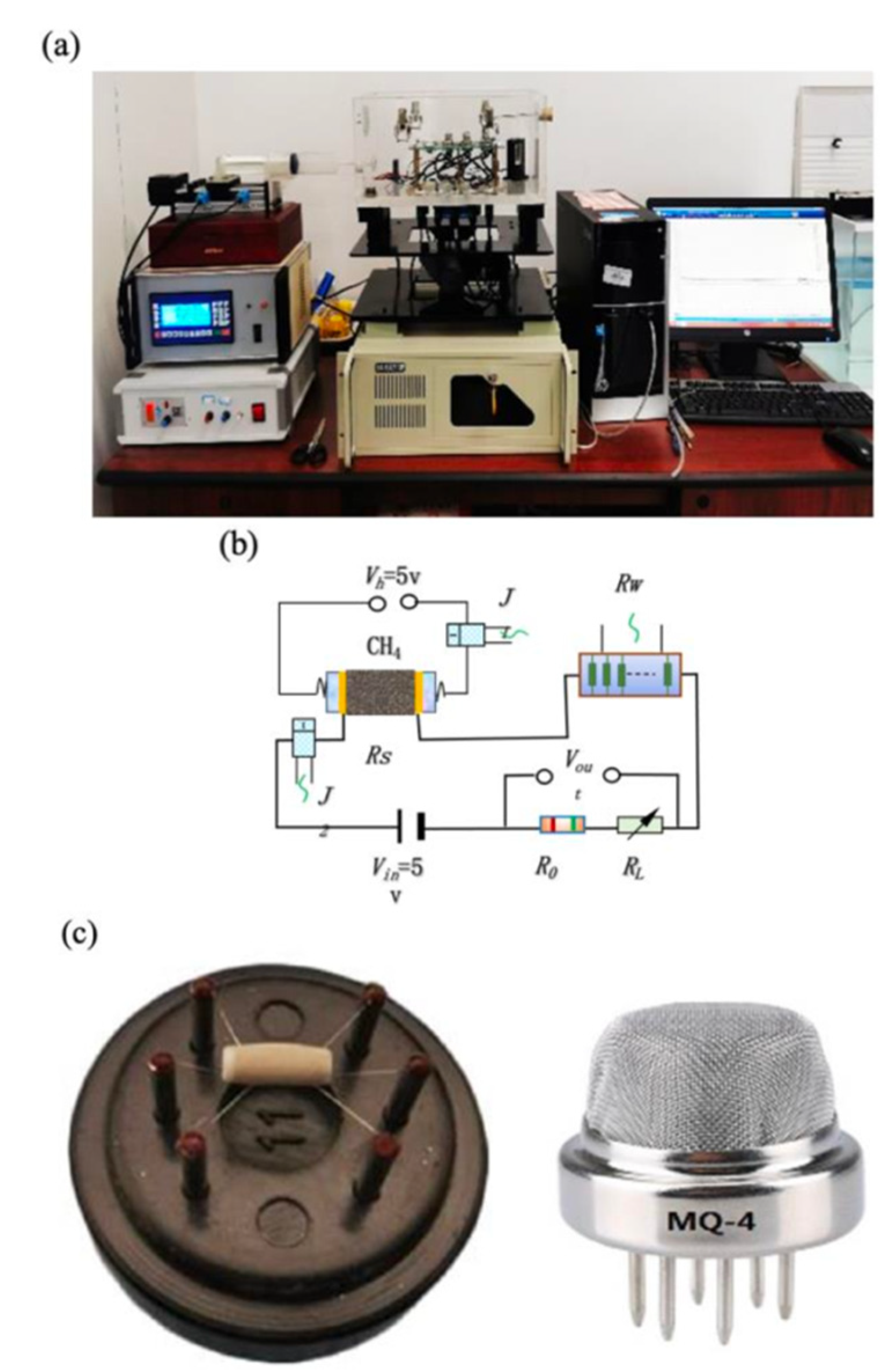
3.1. Experiment Setup
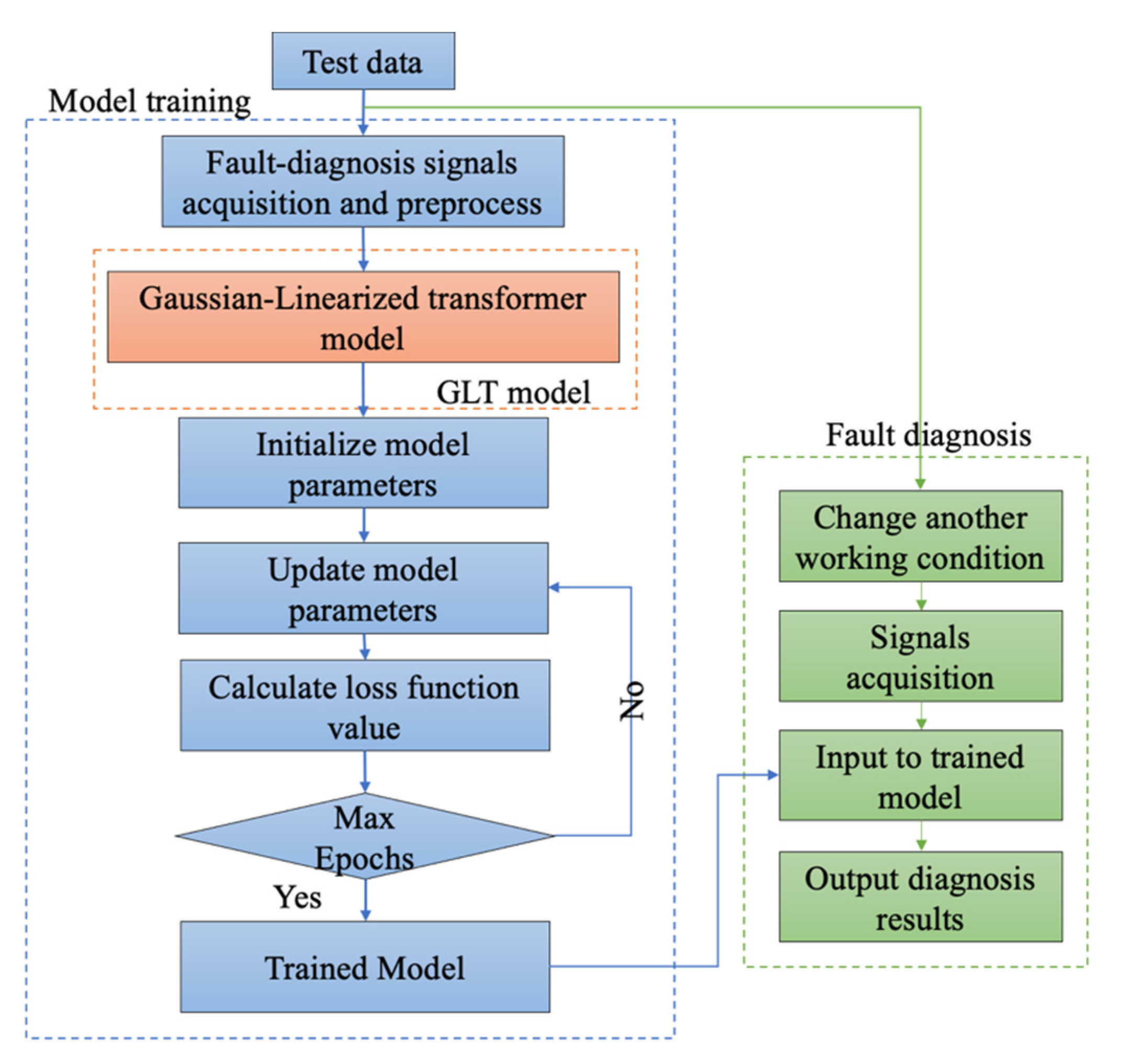
3.2. The Flowchart of the Fault Diagnosis Process
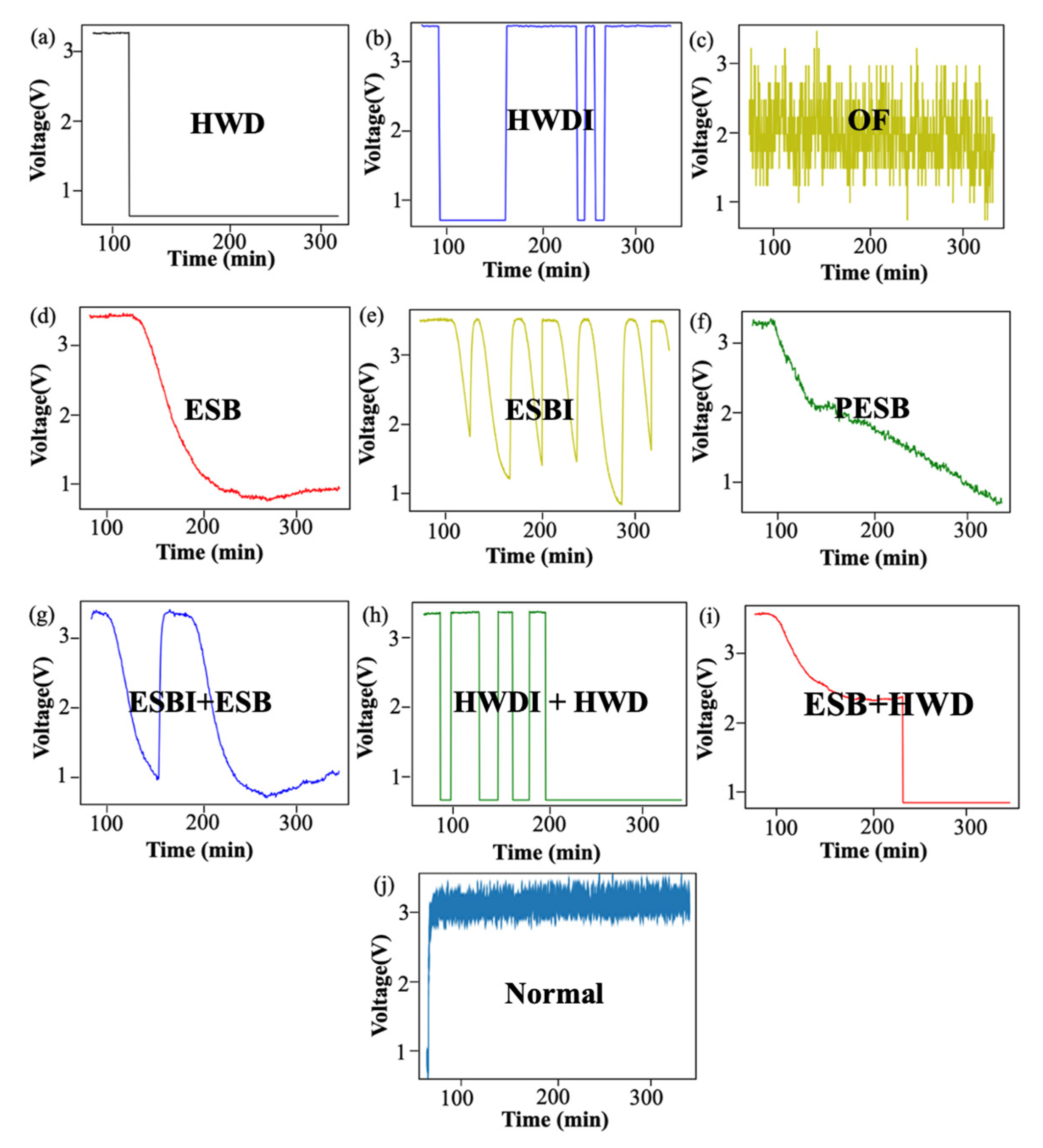
3.3. Validation of Fault Diagnosis Method and Inference
3.4. Fault Diagnosis Task Results by Confusion Matrix
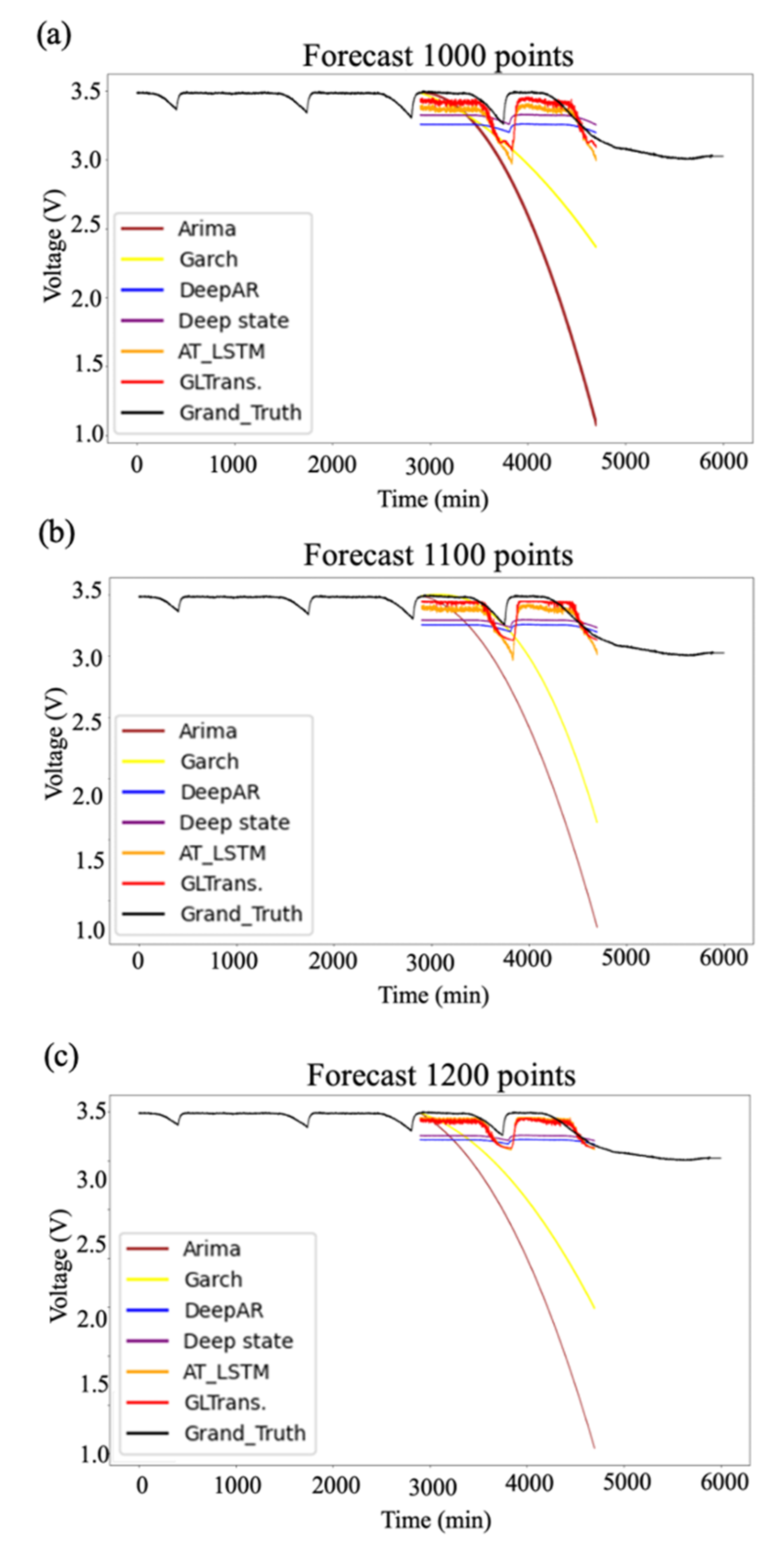
3.5. Validation of Fault Forecast Method and Inference
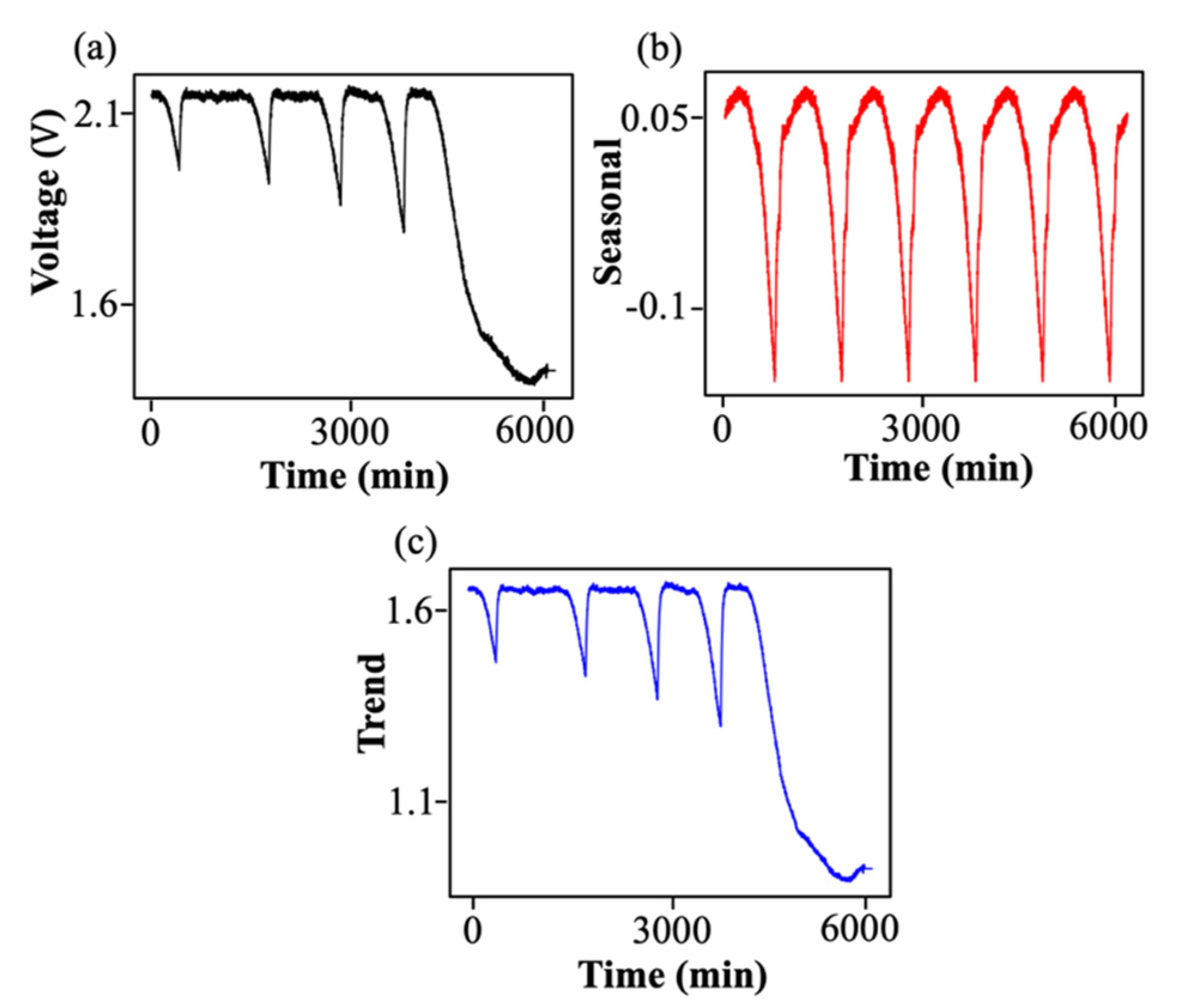
3.6. Visualization of Fault Forecast Task Results
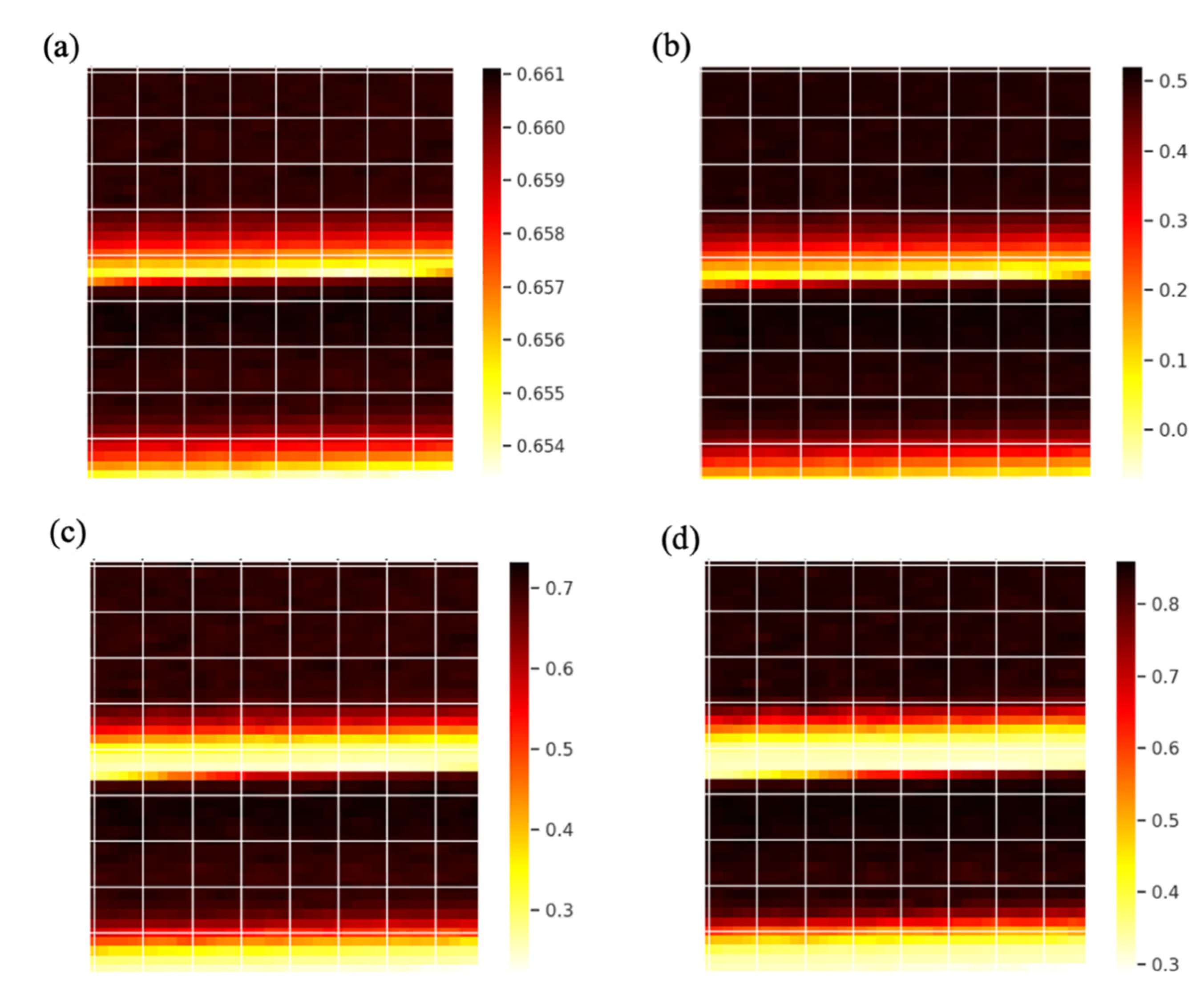
3.7. Attention Visualization for Fault Forecast Task Training Process
3.8. Contrast of Memory Cost with Different Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hyo, L.; Jong, S.; Sang, B. Alternative risk assessment for dangerous chemicals in Republic of Korea regulation: Comparing three modeling programs. Int. J. Environ. Res. Public Health 2018, 15, 1600. [Google Scholar]
- George, F.; Ludmila, O.; Nelly, M. Semiconductor gas sensors based on Pd/SnO2 nanomaterials for methane detection in air. Nanosc. Res. Lett. 2017, 12, 329. [Google Scholar]
- Cedric, B.; Matthew, M.; Douglas, P. A novel low-cost high performance dissolved methane sensor for aqueous environments. Opt. Express 2008, 16, 12607–12617. [Google Scholar]
- Fukasawa, T.; Hozumi, S. Dissolved methane sensor for methane leakage monitoring in methane hydrate production. In OCEANS 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 15, pp. 1–6. [Google Scholar]
- Boulart, C.; Connelly, D.P.; Mowlem, M.C. Sensors and technologies for in situ dissolved methane measurements and their evaluation using technology readiness levels. Trac Trends Anal. Chem. 2010, 29, 186–195. [Google Scholar] [CrossRef]
- Lamontagne, A.; Rose, S. Response of METs Sensor to Methane Concentrations Found on the Texas-Louisiana Shelf in the Gulf of Mexico; Naval Research Laboratory: Washington, DC, USA, 2001; Volume 15, pp. 1–10. [Google Scholar]
- Ke, W.; Svartaas, T.M.; Chen, D. A review of gas hydrate nucleation theories and growth models. J. Nat. Gas Sci. Eng. 2019, 61, 169–196. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, H. In-situ detection of ocean floor seawater and gas hydrate exploration of the South China Sea. Earth Sci. Front. 2017, 24, 225–241. [Google Scholar]
- Li-fu, Z.; Kang, Q. The development of in situ detection technology and device for dissolved methane and carbon dioxide in deep sea. Mar. Geol. Front. 2022, 38, 1–18. [Google Scholar]
- Xijie, Y.; Huaiyang, Z. The evidence for the existence of methane seepages in the northern South China Sea: Abnormal high methane concentration in bottom water. Acta Oceanol. Sin. 2008, 30, 69–75. [Google Scholar]
- Jia-ye, Z.; Xian-qin, W. The dissolved methane in seawater of estuaries, distribution features and formation. J. Oceanogr. Huanghai Bohai Seas 1997, 15, 20–29. [Google Scholar]
- Chen, Y.S.; Xu, Y.H. Fault detection, isolation, and diagnosis of status self-validating gas sensor arrays. Rev. Sci. Instrum. 2010, 87, 045001. [Google Scholar] [CrossRef]
- Sana, J.; Young, L.; Jungpil, S. Sensor fault classification based on support vector machine and statistical time-domain features. IEEE Access 2017, 5, 8682–8690. [Google Scholar]
- Yang, J.; Chen, Y. An efficient approach for fault detection, isolation, and data recovery of self-validating multifunctional sensors. IEEE Trans. Instrum. Meas. 2017, 66, 543–558. [Google Scholar] [CrossRef]
- Zhi-wei, G.; Carlo, C. A survey of fault diagnosis and fault tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar]
- Lu, J.; Huang, J.; Lu, F. Sensor fault diagnosis for aero engine based on online sequential extreme learning machine with memory principle. Energies 2017, 10, 39. [Google Scholar] [CrossRef]
- Fang, D.; Su, G.; Rui, Z. Sensor multi-fault diagnosis with improved support vector machines. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1053–1063. [Google Scholar]
- Li, H.; Meng, Q. Fault identification of hydroelectric sets based on time-frequency diagram and convolutional neural network. In Proceedings of the 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), Xi’an, China, 21–24 October 2019. [Google Scholar]
- Qing, L.; Huang, H. Comparative study of probabilistic neural network and back propagation network for fault diagnosis of refrigeration systems. Sci. Technol. Built Environ. 2018, 24, 448–457. [Google Scholar]
- Shao, H.; Jiang, H.; Zhang, X.; Niu, M. Rolling bearing fault diagnosis using an optimization deep belief network. Meas. Sci. Technol. 2015, 26, 115002. [Google Scholar] [CrossRef]
- Long, W.; Liang, G. A new deep transfer learning based on sparse auto-encoder for fault diagnosis. IEEE Trans. Syst Man. Cybern. Syst. 2019, 49, 136–144. [Google Scholar]
- He, W.; Qiao, P.L. A new belief-rule-based method for fault diagnosis of wireless sensor network. IEEE Access 2018, 6, 9404–9419. [Google Scholar] [CrossRef]
- Ma, S.; Chu, F. Ensemble deep learning-based fault diagnosis of rotor bearing systems. Comput. Ind. 2019, 105, 143–152. [Google Scholar] [CrossRef]
- Zhan, Z.; Hua, H. Novel application of multi-model ensemble learning for fault diagnosis in refrigeration systems. Appl. Thermal Eng. 2020, 164, 114–516. [Google Scholar]
- Wang, T.; Li, Q. Transformer fault diagnosis method based on incomplete data and TPE-XGBoost. Appl. Sci. 2023, 13, 7539. [Google Scholar] [CrossRef]
- Shi, L.; Su, S.; Wang, W.; Gao, S.; Chu, C. Bearing fault diagnosis method based on deep learning and health state division. Appl. Sci. 2023, 13, 7424. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A new convolutional neural network- based data-driven fault diagnosis method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, H. A new convolutional neural network with random forest method for hydrogen sensor fault diagnosis. IEEE Access 2020, 8, 85421–85430. [Google Scholar] [CrossRef]
- Ashish, V.; Noam, S.; Niki, P.; Jakob, U. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Bahdanau, D.; Cho, K. Neural machine translation by jointly learning to align and translate. arXiv 2016, arXiv:1409.0473. [Google Scholar]
- Lin-hao, D.; Shuang, X.; Bo, X. Speech-transformer: A norecurrence sequence-to-sequence model for speech recognition. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 5884–5888. [Google Scholar]
- Tom, B.; Benjamin, M. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Ze, L.; Yu-tong, L. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Rami, A.; Dokook, C.; Noah, C. Character-level language modeling with deeper self-attention. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, p. 011920. [Google Scholar]
- Zi, D.; Zhi, Y. Transformer-XL: Language modeling with longer-term dependency. In Proceedings of the ICLR, New Orleans, LO, USA, 6–9 May 2019. [Google Scholar]
- Parmar, N.; Vaswani, A. Image transformer. Proc. Mach. Learn. Res. 2018, 80, 4055–4064. [Google Scholar]
- Wilson, A.G.; Hu, Z. Deep kernel learning. Proc. Mach. Learn. Res. 2021, 51, 370–378. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. In Proceedings of the NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Wang, S.; Li, B. Linformer: Self-attention with linear complexity. arXiv 2020, arXiv:2006.04768. [Google Scholar]
- Xiong, Y.; Zeng, Z. Nystromformer: A nystrom-based algorithm for approximating self-attention. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, p. 16. [Google Scholar]
- Yi, T.; Mostafa, D. Efficient transformer: A Survey. ACM J. 2020, 55, 6. [Google Scholar]
- Yi, T.; Mostafa, D. Long Range Arena: A Benchmark for Efficient Transformers. ICLR 2021, 23, 1022–1032. [Google Scholar]
- Dai, Z.; Yang, Z.; Yang, Y.; Carbonell, J.; Le, Q.V.; Salakhutdinov, R. Transformer-XL: Attentive language models beyond a fixed-length context. arXiv 2019, arXiv:1901.02860. [Google Scholar]
- Child, R.; Gray, S.; Radford, A.; Sutskever, I. Generating long sequences with sparse transformers. arXiv 2019, arXiv:1904.10509. [Google Scholar]
- Nikita, K.; Lukasz, K.; Anselm, L. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar]

| Model | Training Time (s) | Accuracy | Recall | Precision | F1 Score (0, 1) | Testing Time (s) |
|---|---|---|---|---|---|---|
| CNN+RF | 600 | 96% | 96% | 96.84% | 96.45% | 0.02 |
| Transformer_En | 600 | 98% | 98% | 98.76% | 98.56% | 0.02 |
| GLTrans. | 480 | 99.75% | 99.75% | 99.99% | 99.86% | 0.01 |
| Prediction Period I | Loss | {2900, 4700} | {3000, 4800} | {3100, 4900} |
|---|---|---|---|---|
| Prediction Length O | 1000 | 1100 | 1200 | |
| ARIMA | MSE | 3.75 | 4.96 | 8.8 |
| MAE | 1.56 | 1.89 | 2.36 | |
| Garch | MSE | 0.85 | 1.48 | 2.66 |
| MAE | 1.03 | 1.21 | 1.31 | |
| DeepAR | MSE | 0.09 | 0.14 | 0.18 |
| MAE | 0.21 | 0.28 | 0.3 | |
| DeepState | MSE | 0.08 | 0.1 | 0.13 |
| MAE | 0.21 | 0.25 | 0.27 | |
| AT-LSTM | MSE | 0.07 | 0.09 | 0.11 |
| MAE | 0.2 | 0.23 | 0.26 | |
| GLTrans. | MSE | 0.04 | 0.08 | 0.10 |
| MAE | 0.15 | 0.2 | 0.25 |
| Models | Complexity | Decode | Class |
|---|---|---|---|
| Trans.-XL (Dai et al., 2019) [43] | O (n2) | RC | |
| Sparse Trans. (Child et al., 2019) [44] | O (n ) | FP | |
| Reformer (Kitaev et al., 2020) [45] | O (n log n) | LP | |
| GLTrans. | O (n) | KR+LR |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Ning, W.; Zhu, Y.; Li, Z.; Wang, T.; Jiang, W.; Zeng, M.; Yang, Z. Gaussian-Linearized Transformer with Tranquilized Time-Series Decomposition Methods for Fault Diagnosis and Forecasting of Methane Gas Sensor Arrays. Appl. Sci. 2024, 14, 218. https://doi.org/10.3390/app14010218
Zhang K, Ning W, Zhu Y, Li Z, Wang T, Jiang W, Zeng M, Yang Z. Gaussian-Linearized Transformer with Tranquilized Time-Series Decomposition Methods for Fault Diagnosis and Forecasting of Methane Gas Sensor Arrays. Applied Sciences. 2024; 14(1):218. https://doi.org/10.3390/app14010218
Chicago/Turabian StyleZhang, Kai, Wangze Ning, Yudi Zhu, Zhuoheng Li, Tao Wang, Wenkai Jiang, Min Zeng, and Zhi Yang. 2024. "Gaussian-Linearized Transformer with Tranquilized Time-Series Decomposition Methods for Fault Diagnosis and Forecasting of Methane Gas Sensor Arrays" Applied Sciences 14, no. 1: 218. https://doi.org/10.3390/app14010218
APA StyleZhang, K., Ning, W., Zhu, Y., Li, Z., Wang, T., Jiang, W., Zeng, M., & Yang, Z. (2024). Gaussian-Linearized Transformer with Tranquilized Time-Series Decomposition Methods for Fault Diagnosis and Forecasting of Methane Gas Sensor Arrays. Applied Sciences, 14(1), 218. https://doi.org/10.3390/app14010218








