Synthetic Biology and Control Theory: Designing Synthetic Biomolecular Controllers by Exploiting Dynamic Covalent Modification Cycle with Positive Autoregulation Properties
Abstract
1. Introduction
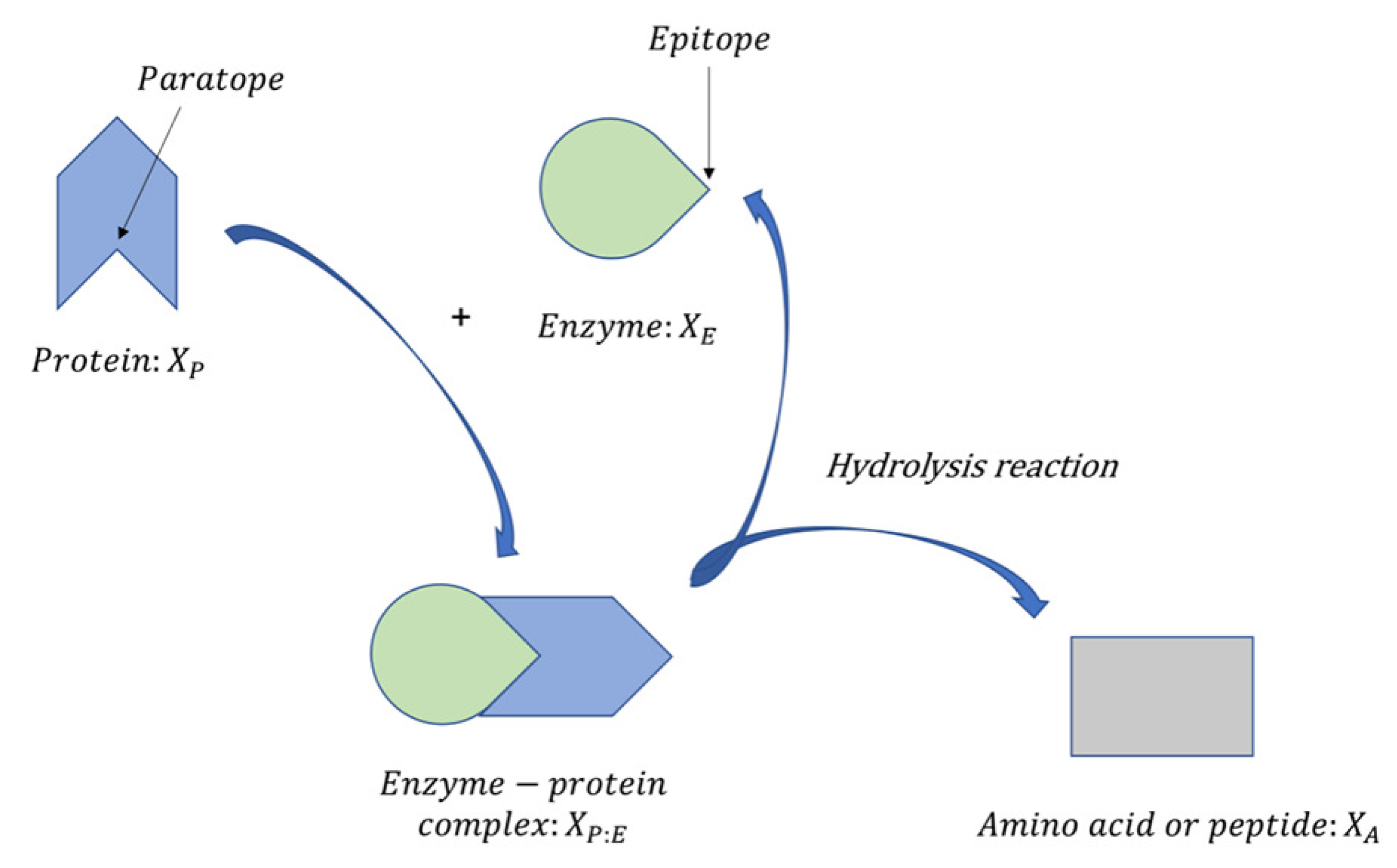
2. An Enzymatic Protein Hydrolysis Model
3. Methodology
3.1. Covalent Modification Cycle and Brink Controller (BC)
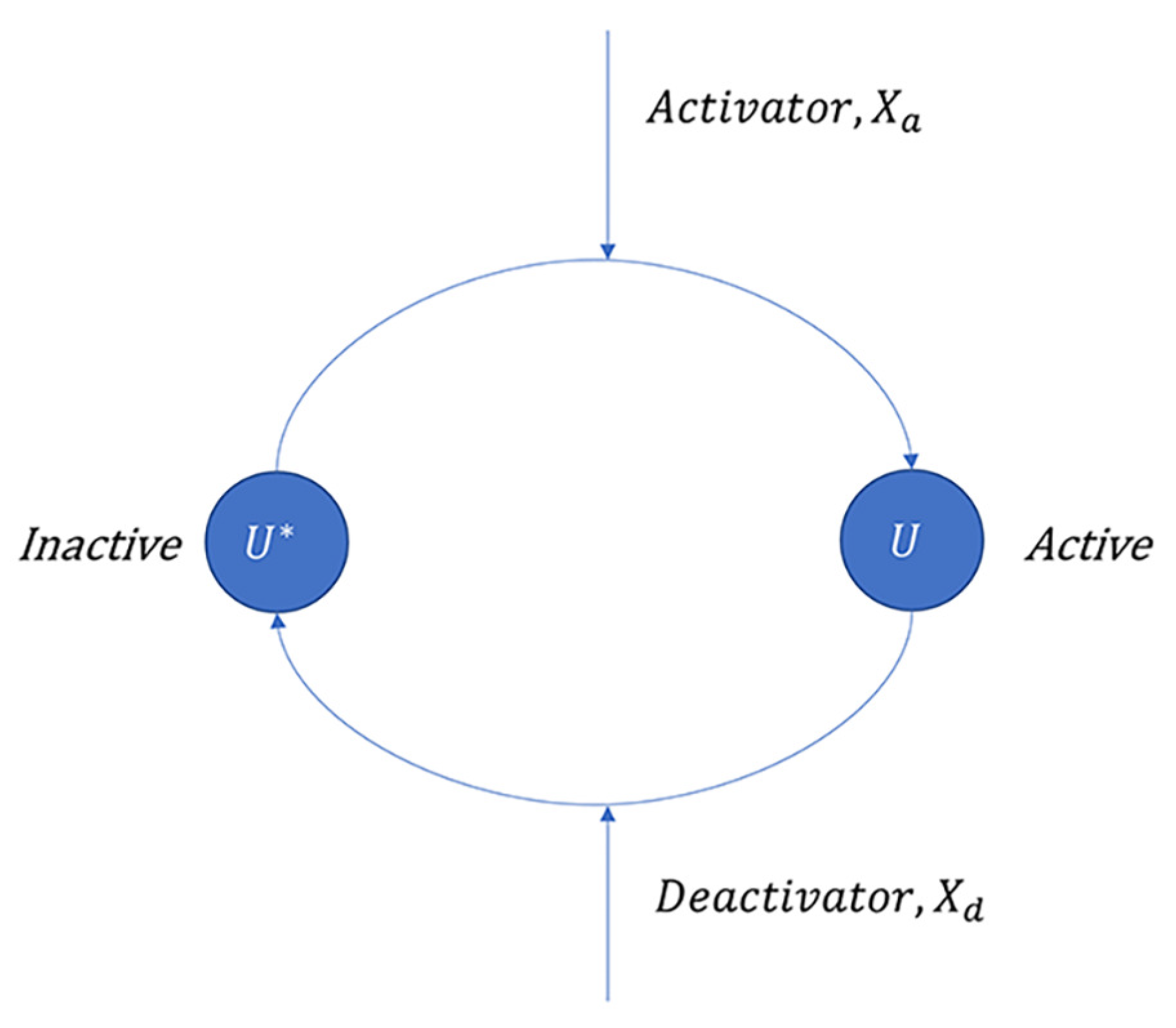
3.1.1. Covalent Modification Cycle (CMC)
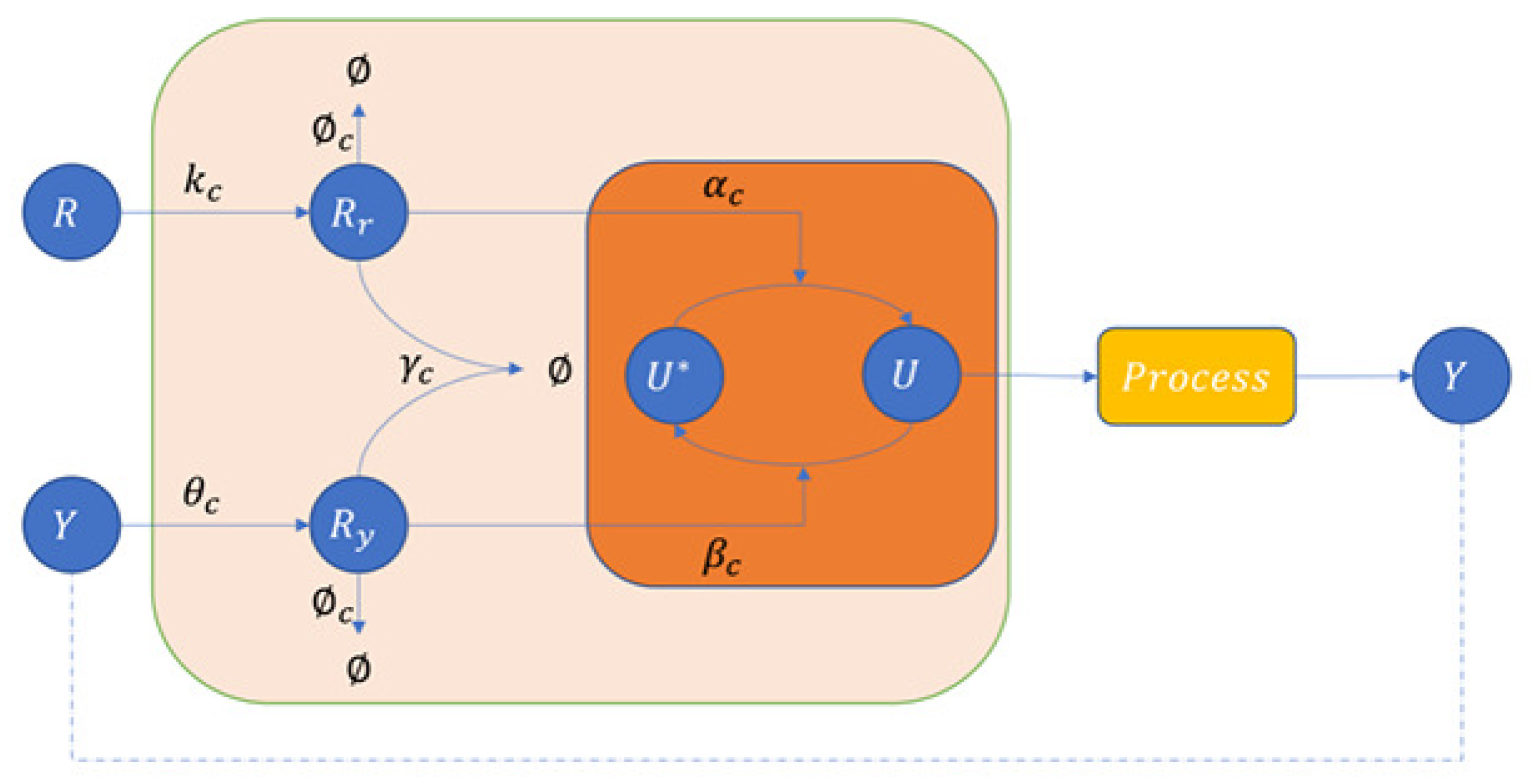
3.1.2. An Application of the Covalent Modification Cycle—Brink Controller (BC)
3.2. Covalent Modification Cycle with Direct Positive Autoregulation and a Novel Controller BC-DPAR
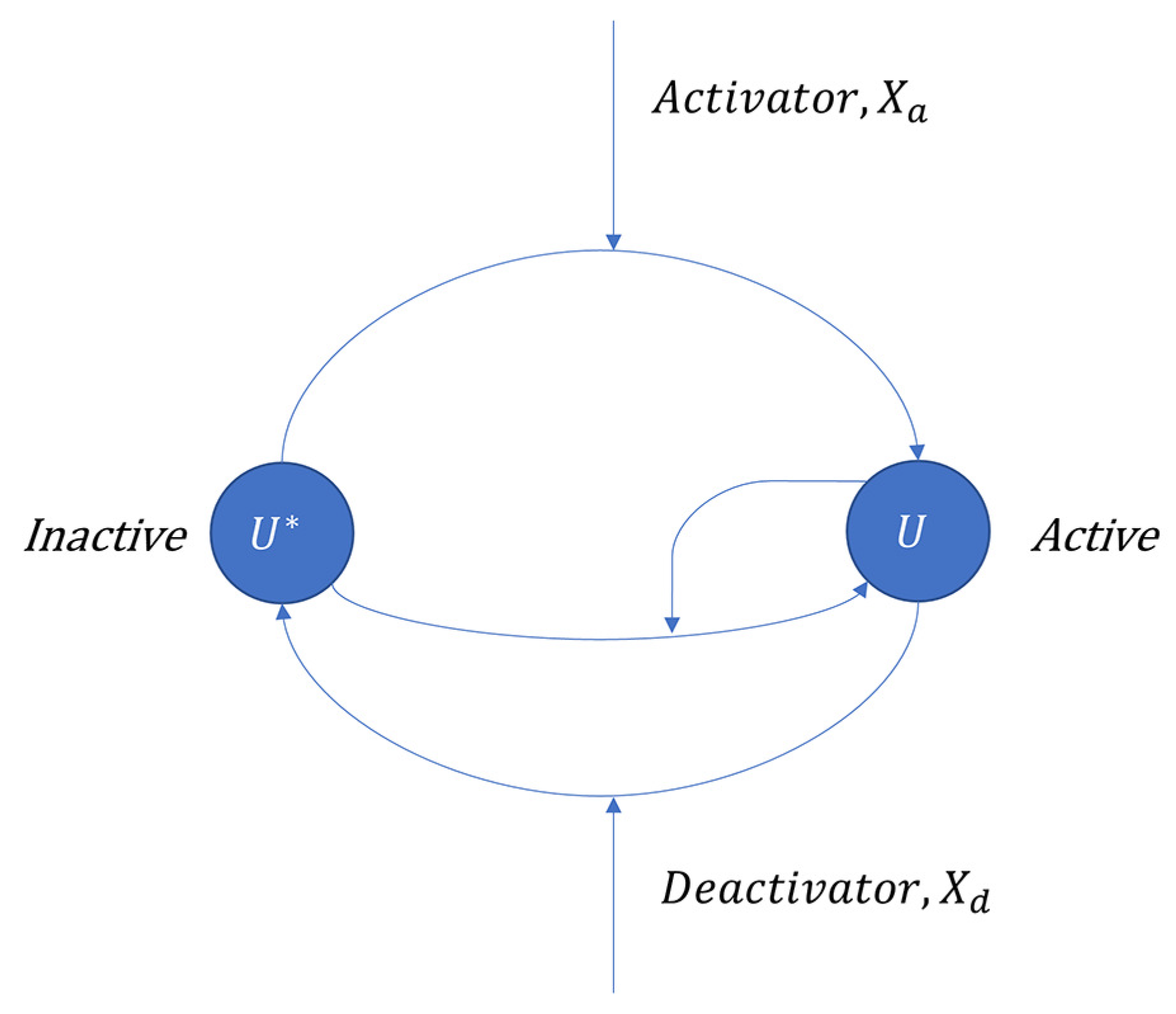
3.2.1. Covalent Modification Cycle with Direct Positive Autoregulation (CMC-D)
3.2.2. Proposed an Application of the Covalent Modification Cycle with Direct Positive Autoregulation—BC-DPAR
3.3. Covalent Modification Cycle with Indirect Positive Autoregulation and a Novel Controller BC-IPAR
3.3.1. Covalent Modification Cycle with Indirect Positive Autoregulation (CMC-I)
3.3.2. Proposed an Application of the Covalent Modification Cycle with Indirect Positive Autoregulation—BC-IPAR
4. Implementations with DSD Reaction Networks
4.1. The Enzymatic Protein Hydrolysis Model
4.2. Brink Controller (BC)
4.3. Brink Controller with Direct PAR (BC-DPAR)
4.4. Brink Controller with Indirect PAR (BC-IPAR)
4.5. Results
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CRNs | Chemical reaction networks |
| DCRNs | Dual chemical reaction networks |
| BC | Brink controller |
| PAR | Positive autoregulation |
| BC-DPAR | Brink controller (BC) with direct positive autoregulation (PAR) |
| BC-IPAR | Brink controller (BC) with indirect positive autoregulation (PAR) |
| PI | Proportional integral |
| QSM | Quasi sliding mode |
| PID | Proportional integral derivative |
| 2DOF | Two-degree-of-freedom |
| DSD | DNA strand displacement |
| CMC | Covalent modification cycle |
| CMC-I | Covalent modification cycle with indirect PAR |
| CMC-D | Covalent modification cycle with direct PAR |
| ODEs | Ordinary differential equations |
| RPA | Robust perfect adaptation |
References
- Filo, M.; Kumar, S.; Khammash, M. A hierarchy of biomolecular proportional-integral-derivative feedback controllers for robust perfect adaptation and dynamic performance. Nat. Commun. 2022, 13, 2119. [Google Scholar] [CrossRef] [PubMed]
- Busseniers, E.; Veloz, T.; Heylighen, F. Goal directedness, chemical organizations, and cybernetic mechanisms. Entropy 2021, 23, 1039. [Google Scholar] [CrossRef] [PubMed]
- Chevalier, M.; Gómez-Schiavon, M.; El-Samad, H. Design and analysis of a proportional-integral-derivative controller with biological molecules. Cell Syst. 2019, 9, 338–353. [Google Scholar] [CrossRef] [PubMed]
- Tamba, M.; Murayama, K.; Asanuma, H.; Nakakuki, T. Renewable DNA proportional-integral controller with photoresponsive molecules. Micromachines 2022, 13, 193. [Google Scholar] [CrossRef]
- Foo, M.; Akman, O.E.; Bates, D.G. Restoring circadian gene profiles in clock networks using synthetic feedback control. NPJ Syst. Biol. Appl. 2022, 8, 7. [Google Scholar] [CrossRef]
- Kim, J.; Enciso, J. Absolutely robust controllers for chemical reaction networks. J. R. Soc. Interface 2020, 17, 20200031. [Google Scholar] [CrossRef]
- Paulino, N.M.G.; Foo, M.; Kim, J.; Bates, D.G. On the stability of nucleic acid feedback control systems. Automatica 2020, 119, 109103. [Google Scholar] [CrossRef]
- Oishi, K.; Klavins, E. Biomolecular implementation of linear I/O systems. IET Syst. Biol. 2011, 5, 252–260. [Google Scholar] [CrossRef]
- Yordanov, B.; Kim, J.; Petersen, R.L.; Shudy, A.; Kulkarni, V.V.; Phillips, A. Computational design of nucleic acid feedback control circuits. ACS Synth. Biol. 2014, 3, 600–616. [Google Scholar] [CrossRef]
- Rong, P.; Nakakuki, T. Analysis of finite-time regulation property of biomolecular PI controller. Control Theory Technol. 2020, 18, 135–142. [Google Scholar] [CrossRef]
- Sawlekar, R.; Montefusco, F.; Kulkarni, V.V.; Bates, D.G. Implementing nonlinear feedback controllers using DNA strand displacement reactions. IEEE Trans. NanoBiosci. 2016, 15, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Paulino, N.M.G.; Foo, M.; Kim, J.; Bates, D.G. PID and state feedback controllers using DNA strand displacement reactions. IEEE Control Syst. Lett. 2019, 3, 805–810. [Google Scholar] [CrossRef]
- Whitby, M.; Cardelli, L.; Kwiatkowska, M.; Laurenti, L.; Tribastone, M.; Tschaikowski, M. PID control of biochemical reaction networks. IEEE Trans. Autom. Control 2021, 67, 1023–1030. [Google Scholar] [CrossRef]
- Yuan, Y.; Lv, H.; Zhang, Q. DNA strand displacement reactions to accomplish a two-degree-of-freedom PID controller and its application in subtraction gate. IEEE Trans. NanoBiosci. 2021, 20, 554–564. [Google Scholar] [CrossRef]
- Gorecki, J. Information Processing Using Networks of Chemical Oscillators. Entropy 2022, 24, 1054. [Google Scholar] [CrossRef]
- Qian, H.; Bishop, L.M. The chemical master equation approach to nonequilibrium steady-state of open biochemical systems: Linear single-molecule enzyme kinetics and nonlinear biochemical reaction networks. Int. J. Mol. Sci. 2010, 11, 3472–3500. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.S.; Wu, W.S.; Wang, Y.C.; Li, W.H. On the robust circuit design schemes of biochemical networks: Steady-state approach. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 91–104. [Google Scholar] [CrossRef]
- Wang, Y.; Mao, T.; Sun, J.; Liu, P. Exponential function computation based on DNA strand displacement circuits. IEEE Trans. Biomed. Circuits Syst. 2022, 16, 479–488. [Google Scholar] [CrossRef]
- Zou, C.; Wei, X.; Zhang, Q. Visual synchronization of two 3-variable lotka–volterra oscillators based on DNA strand displacement. RSC Adv. 2018, 8, 20941–20951. [Google Scholar] [CrossRef]
- Xing, C.; Zheng, X.; Zhang, Q. Constructing DNA logic circuits based on the toehold preemption mechanism. RSC Adv. 2022, 12, 338–345. [Google Scholar] [CrossRef]
- Paulino, N.M.G.; Foo, M.; Kim, J.; Bates, D.G. Robustness analysis of a nucleic acid controller for a dynamic biomolecular process using the structured singular value. J. Process Control 2019, 78, 34–44. [Google Scholar] [CrossRef]
- Yuan, Y.; Lv, H.; Zhang, Q. Molecular device design based on chemical reaction networks: State feedback controller, static pre-filter, addition gate control system and full-dimensional state observer. J. Math. Chem. 2022, 60, 915–935. [Google Scholar] [CrossRef]
- Cosentino, C.; Ambrosino, R.; Ariola, M.; Bilotta, M.; Pironti, A.; Amato, F. On the realization of an embedded subtractor module for the control of chemical reaction networks. IEEE Trans. Autom. Control 2016, 61, 3638–3643. [Google Scholar] [CrossRef]
- Foo, M.; Kim, J.; Kim, J.; Bates, D.G. Proportional–integral degradation control allows accurate tracking of biomolecular concentrations with fewer chemical reactions. IEEE Life Sci. Lett. 2016, 2, 55–58. [Google Scholar] [CrossRef]
- Goldbeter, A.; Koshland, D.E., Jr. An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA 1981, 78, 6840–6844. [Google Scholar] [CrossRef]
- Gomez-Uribe, C.; Verghese, G.C.; Mirny, L.A. Operating regimes of signaling cycles: Statics, dynamics, and noise filtering. PLoS Comput. Biol. 2007, 3, e246. [Google Scholar] [CrossRef]
- Jeynes-Smith, C.; Araujo, R.P. Ultrasensitivity and bistability in covalent-modification cycles with positive autoregulation. Proc. R. Soc. A 2021, 477, 20210069. [Google Scholar] [CrossRef]
- Jones, R.D.; Qian, Y.; Ilia, K.; Wang, B.; Laub, M.T.; Vecchio, D.D.; Weiss, R. Robust and tunable signal processing in mammalian cells via engineered covalent modification cycles. Nat. Commun. 2022, 13, 1720. [Google Scholar] [CrossRef]
- Foo, M.; Sawlekar, R.; Bates, D.G. Exploiting the dynamic properties of covalent modification cycle for the design of synthetic analog biomolecular circuitry. J. Biol. Eng. 2016, 10, 15. [Google Scholar] [CrossRef]
- Samaniego, C.C.; Franco, E. Ultrasensitive molecular controllers for quasi-integral feedback. Cell Syst. 2021, 12, 272–288. [Google Scholar] [CrossRef]
- Wang, D.; Yan, L.; Ma, X.; Wang, W.; Zou, M.; Zhong, J.; Ding, T.; Ye, X.; Liu, D. Ultrasound promotes enzymatic reactions by acting on different targets: Enzymes, substrates and enzymatic reaction systems. Int. J. Biol. Macromol. 2018, 119, 453–461. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Narlikar, G.J.; Kutateladze, T.G. Enzymatic reactions inside biological condensates. J. Mol. Biol. 2021, 433, 166624. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.J.; Chen, J.; Wang, Y.Q.; Zhu, N.; Fang, Z.; Xu, J.H.; Guo, K. Biocatalysts used for multi-step reactions in continuous flow. Chem. Eng. J. 2022, 135400. [Google Scholar] [CrossRef]
- Márquez, M.; Vázquez, M. Modeling of enzymatic protein hydrolysis. Process Biochem. 1999, 35, 111–117. [Google Scholar] [CrossRef]
- Valencia, P.; Espinoza, K.; Ceballos, A.; Pinto, M.; Almonacid, S. Novel modeling methodology for the characterization of enzymatic hydrolysis of proteins. Process Biochem. 2015, 50, 589–597. [Google Scholar] [CrossRef]
- Butré, C.I.; Sforza, S.; Gruppen, H.; Wierenga, P.A. Introducing enzyme selectivity: A quantitative parameter to describe enzymatic protein hydrolysis. Anal. Bioanal. Chem. 2014, 406, 5827–5841. [Google Scholar] [CrossRef] [PubMed]
- Araujo, R.P.; Liotta, L.A. The topological requirements for robust perfect adaptation in networks of any size. Nat. Commun. 2018, 9, 1757. [Google Scholar] [CrossRef]
- Araujo, R.P.; Liotta, L.A. Design principles underlying robust adaptation of complex biochemical networks. In Computational Modeling of Signaling Networks; Humana: New York, NY, USA, 2023; pp. 3–32. [Google Scholar]
- Becskei, A.; Serrano, L. Engineering stability in gene networks by autoregulation. Nature 2000, 405, 590–593. [Google Scholar] [CrossRef]
- Tiwari, A.; Igoshin, O.A. Coupling between feedback loops in autoregulatory networks affects bistability range, open-loop gain and switching times. Phys. Biol. 2012, 9, 055003. [Google Scholar] [CrossRef]
- Chen, Z.; Kibler, R.D.; Hunt, A.; Busch, F.; Pearl, J.; Jia, M.; VanAernum, Z.L.; Wicky, B.I.; Dods, G.; Liao, H. De novo design of protein logic gates. Science 2020, 368, 78–84. [Google Scholar] [CrossRef]
- Lehr, F.X.; Hanst, M.; Vogel, M.; Kremer, J.; Pearl, J.; Göringer, H.U.; Suess, B.; Koeppl, H. Cell-free prototyping of and-logic gates based on heterogeneous rna activators. ACS Synth. Biol. 2019, 8, 2163–2173. [Google Scholar] [CrossRef] [PubMed]

| Parameters | Descriptions | Nominal Values |
|---|---|---|
| Catalytic reaction rate | ||
| Catalytic reaction rate | ||
| Binding rate | ||
| Degradation reaction rate | ||
| Catalytic reaction rate | ||
| Binding rate | ||
| (BC-DPAR) | Catalytic reaction rate | |
| (BC-IPAR) | Catalytic reaction rate | |
| Total amount of |
| Parameters | Descriptions | Nominal Values |
|---|---|---|
| Binding rate | ||
| Unbinding rate | ||
| Degradation reaction rate | ||
| Total amount of |
| Controllers | BC | BC-IPAR | BC-DPAR |
|---|---|---|---|
| Setting time t | |||
| Setting time t |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Lv, H.; Wang, X. Synthetic Biology and Control Theory: Designing Synthetic Biomolecular Controllers by Exploiting Dynamic Covalent Modification Cycle with Positive Autoregulation Properties. Appl. Sci. 2023, 13, 5786. https://doi.org/10.3390/app13095786
Xiao Y, Lv H, Wang X. Synthetic Biology and Control Theory: Designing Synthetic Biomolecular Controllers by Exploiting Dynamic Covalent Modification Cycle with Positive Autoregulation Properties. Applied Sciences. 2023; 13(9):5786. https://doi.org/10.3390/app13095786
Chicago/Turabian StyleXiao, Yijun, Hui Lv, and Xing’an Wang. 2023. "Synthetic Biology and Control Theory: Designing Synthetic Biomolecular Controllers by Exploiting Dynamic Covalent Modification Cycle with Positive Autoregulation Properties" Applied Sciences 13, no. 9: 5786. https://doi.org/10.3390/app13095786
APA StyleXiao, Y., Lv, H., & Wang, X. (2023). Synthetic Biology and Control Theory: Designing Synthetic Biomolecular Controllers by Exploiting Dynamic Covalent Modification Cycle with Positive Autoregulation Properties. Applied Sciences, 13(9), 5786. https://doi.org/10.3390/app13095786






