Research on Effective Design Methods of Core Beam of Full Bridge Aeroelastic Model
Abstract
:1. Introduction
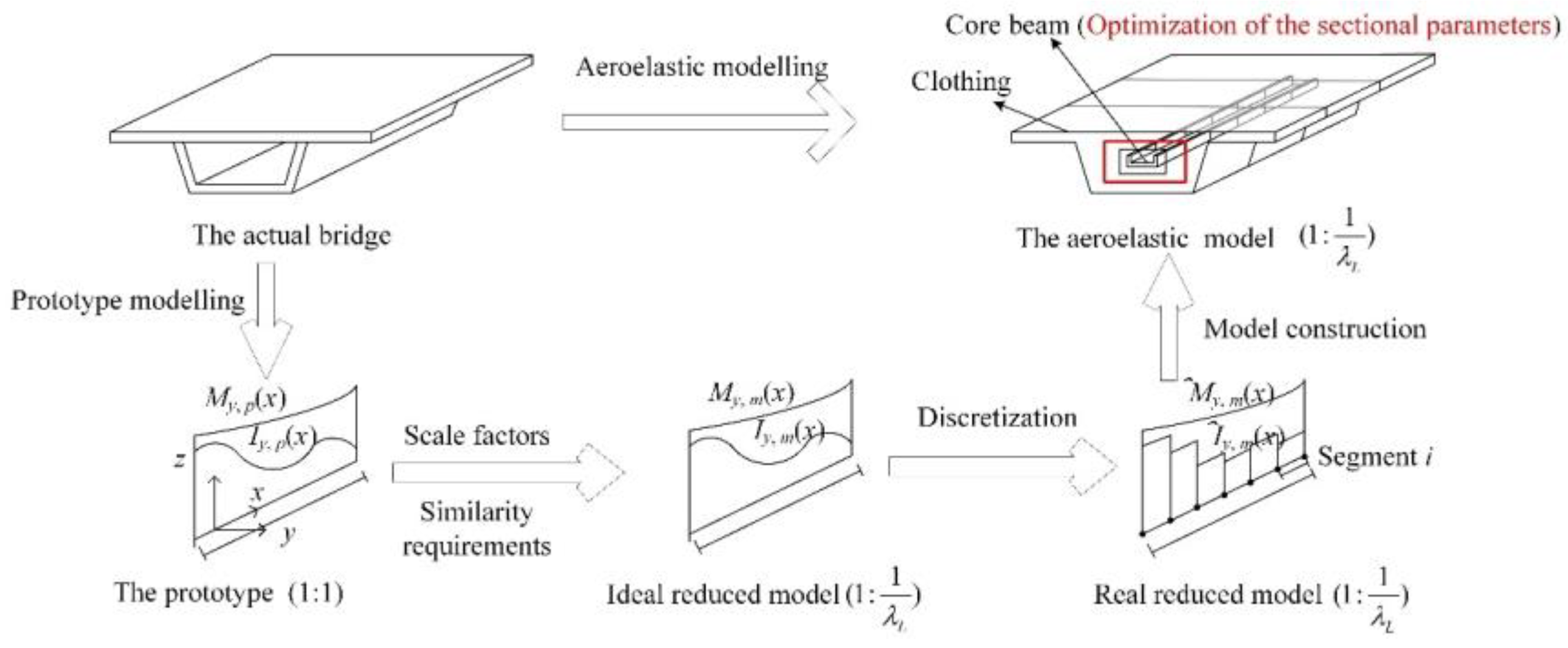
2. Design of Reduced-Scale Aeroelastic Models
3. Numerical Solution of Torsion Constant
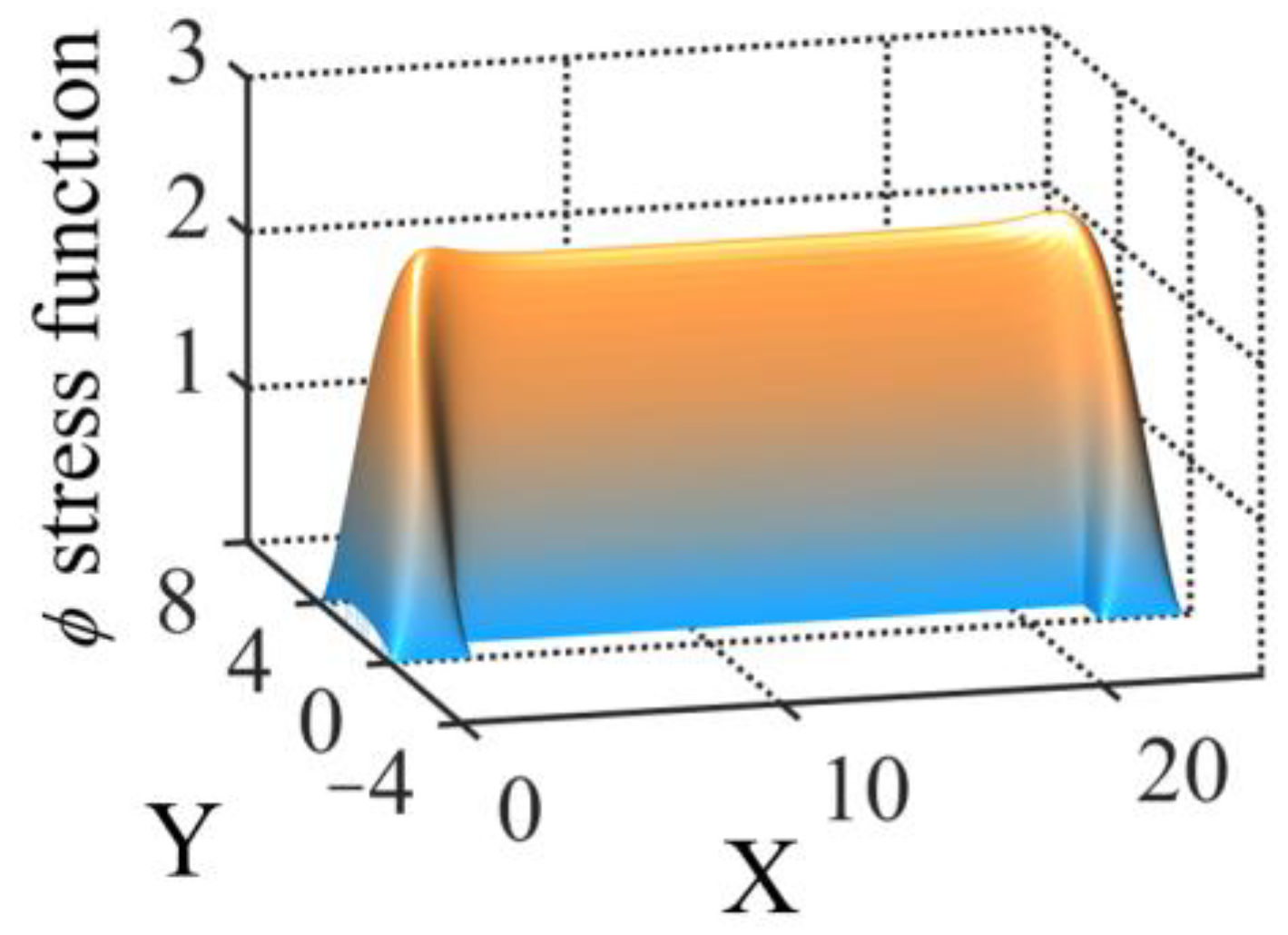
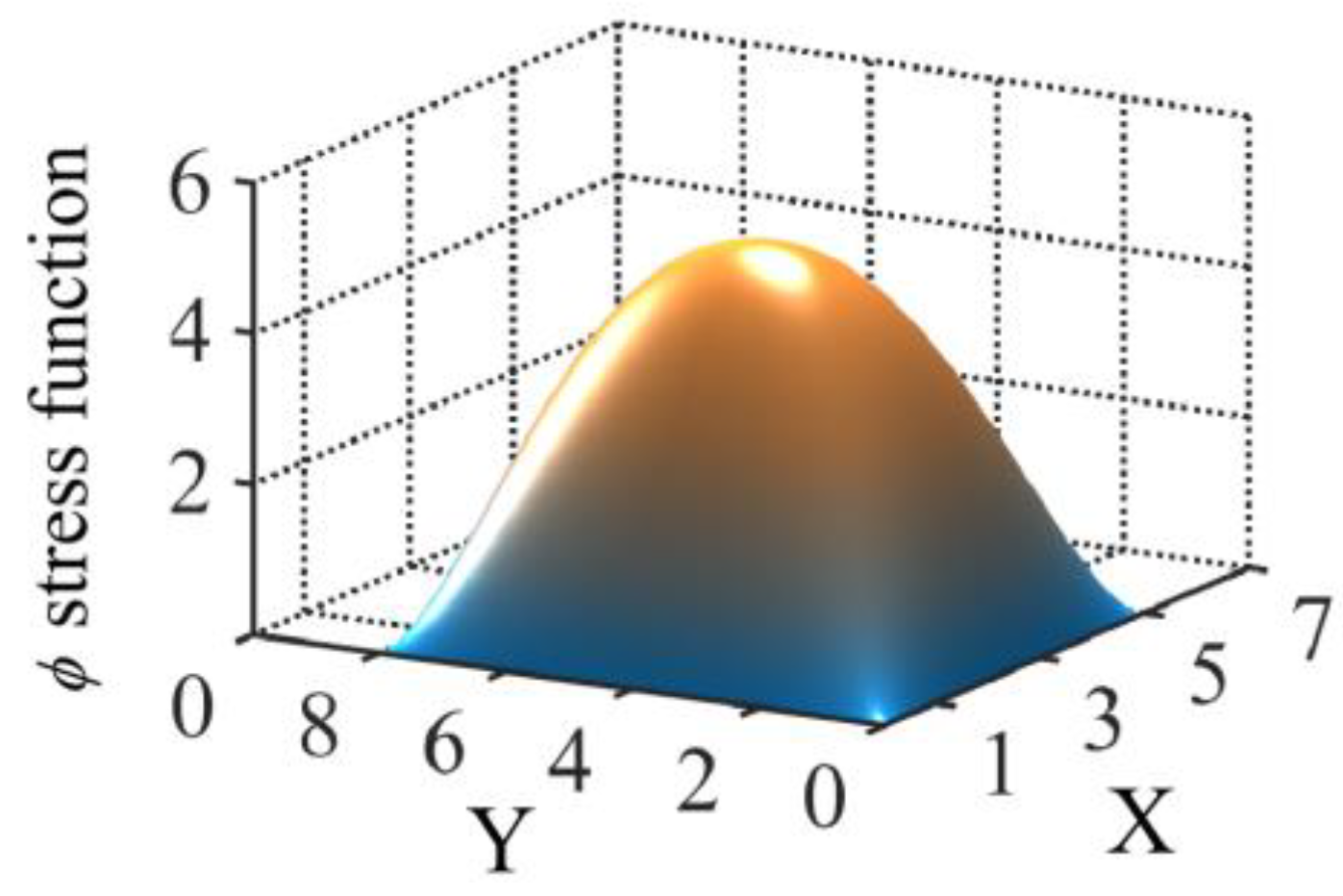
3.1. Basic Theory
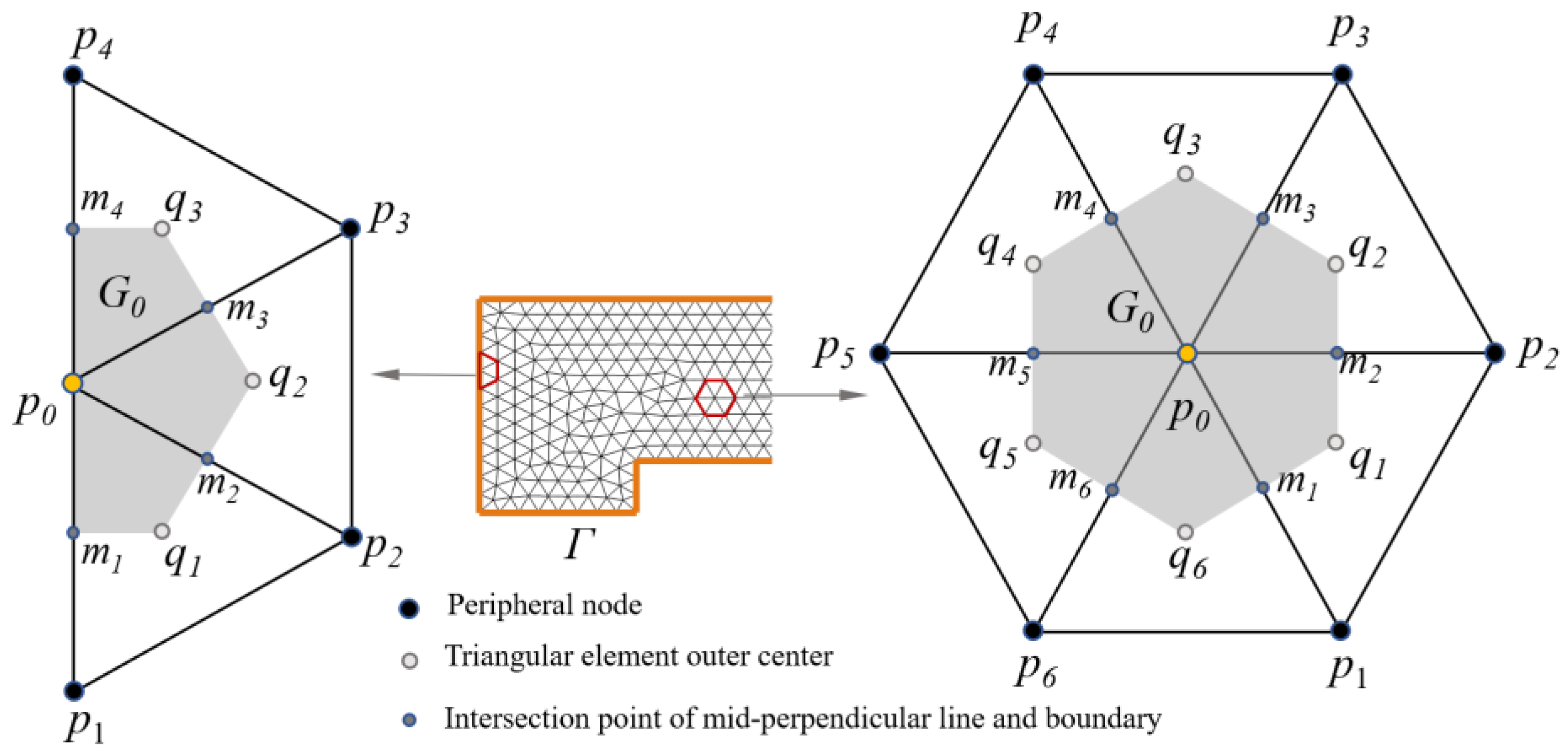
3.2. Generalized Difference Method
3.3. Finite Element Method
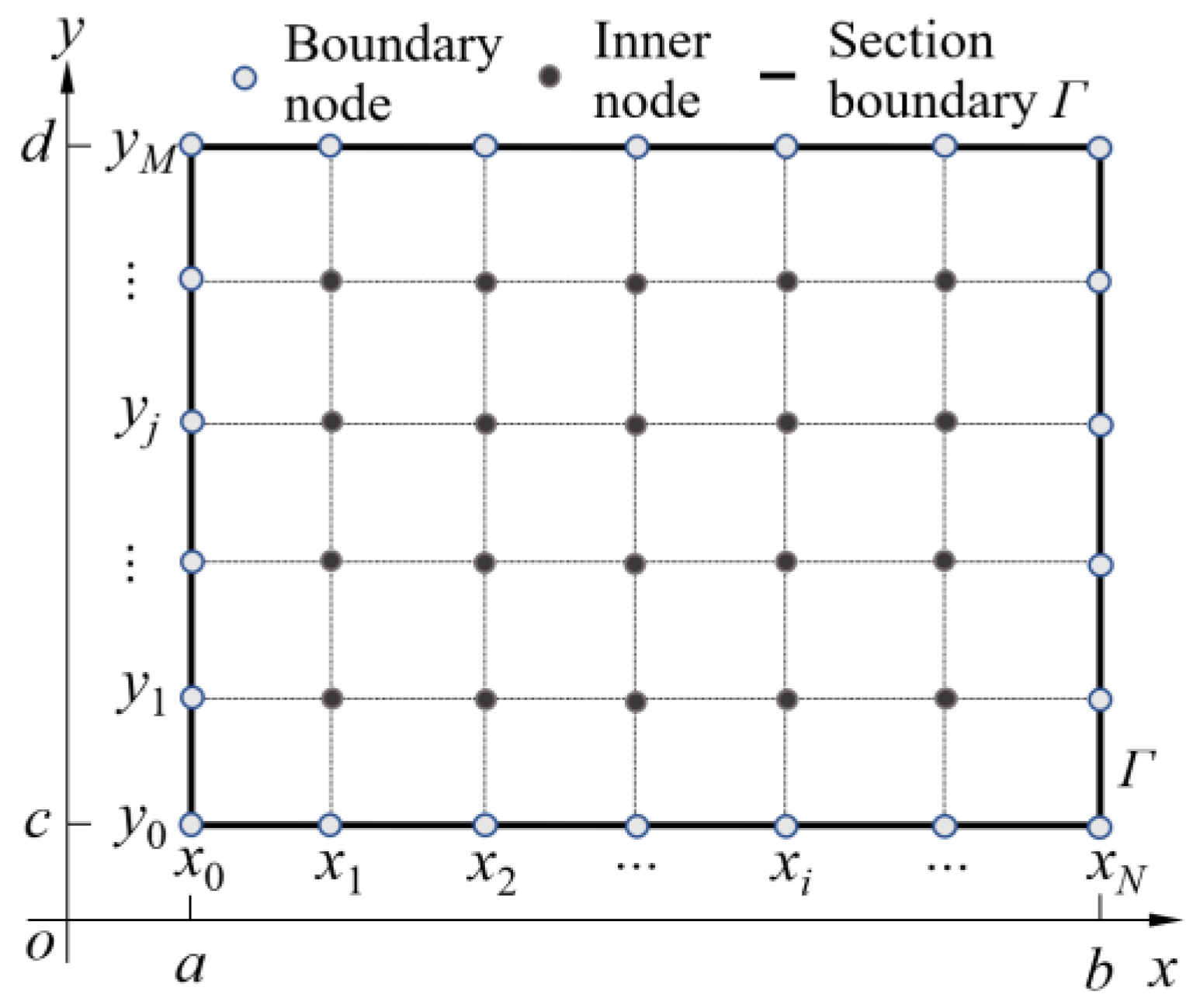
3.4. Five-Point Difference Method
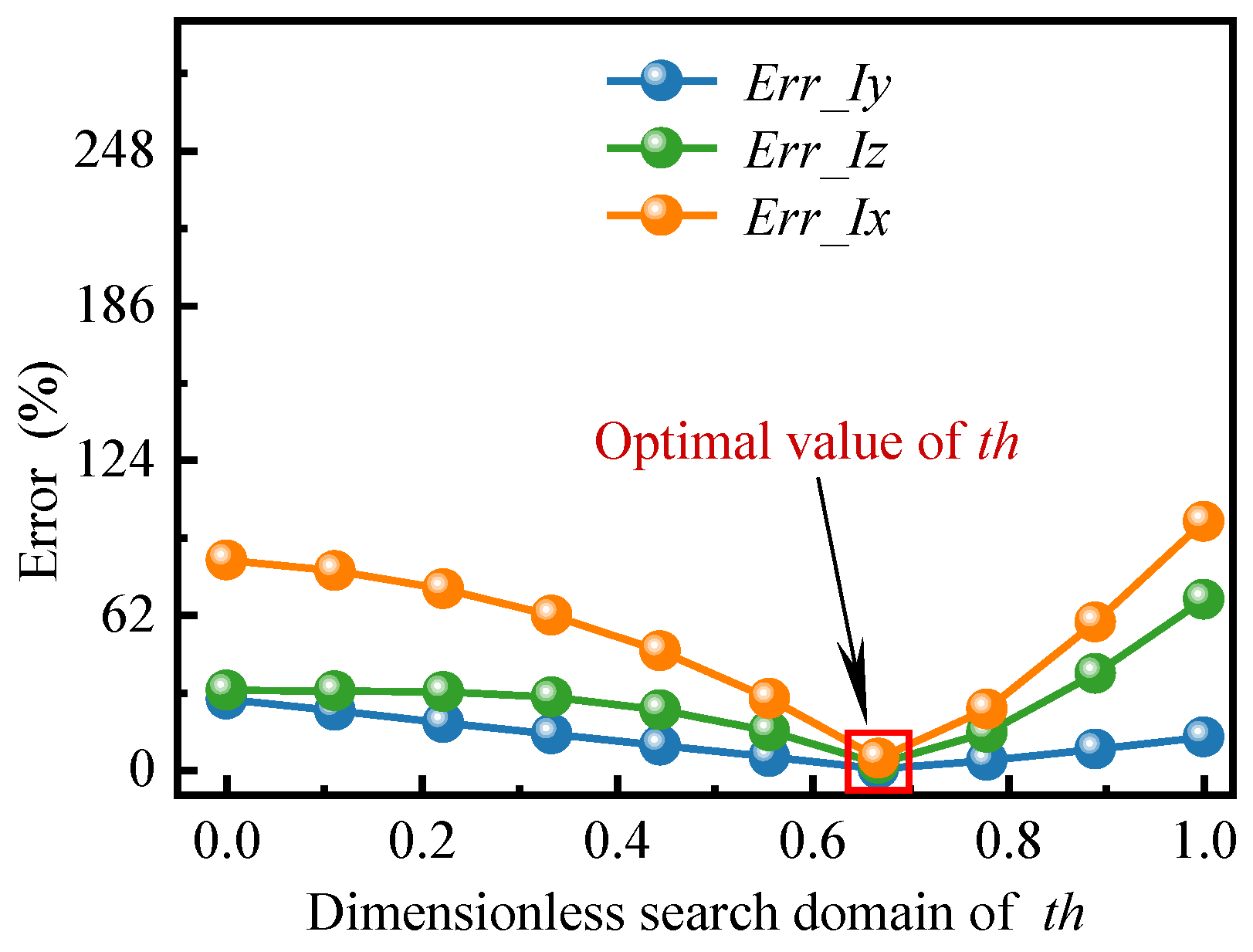
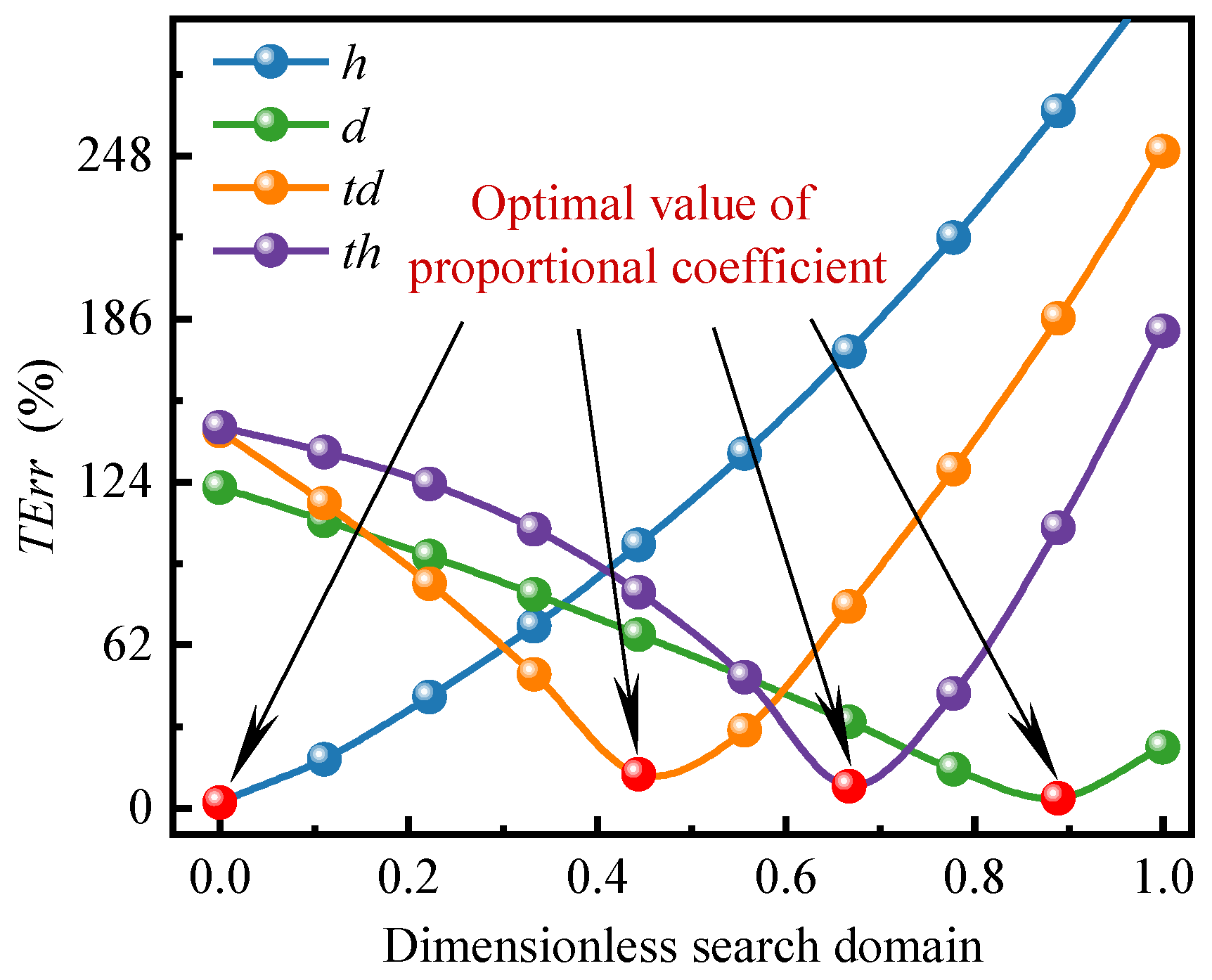
4. Geometric Parameters Searching
4.1. Optimization Method by ANSYS
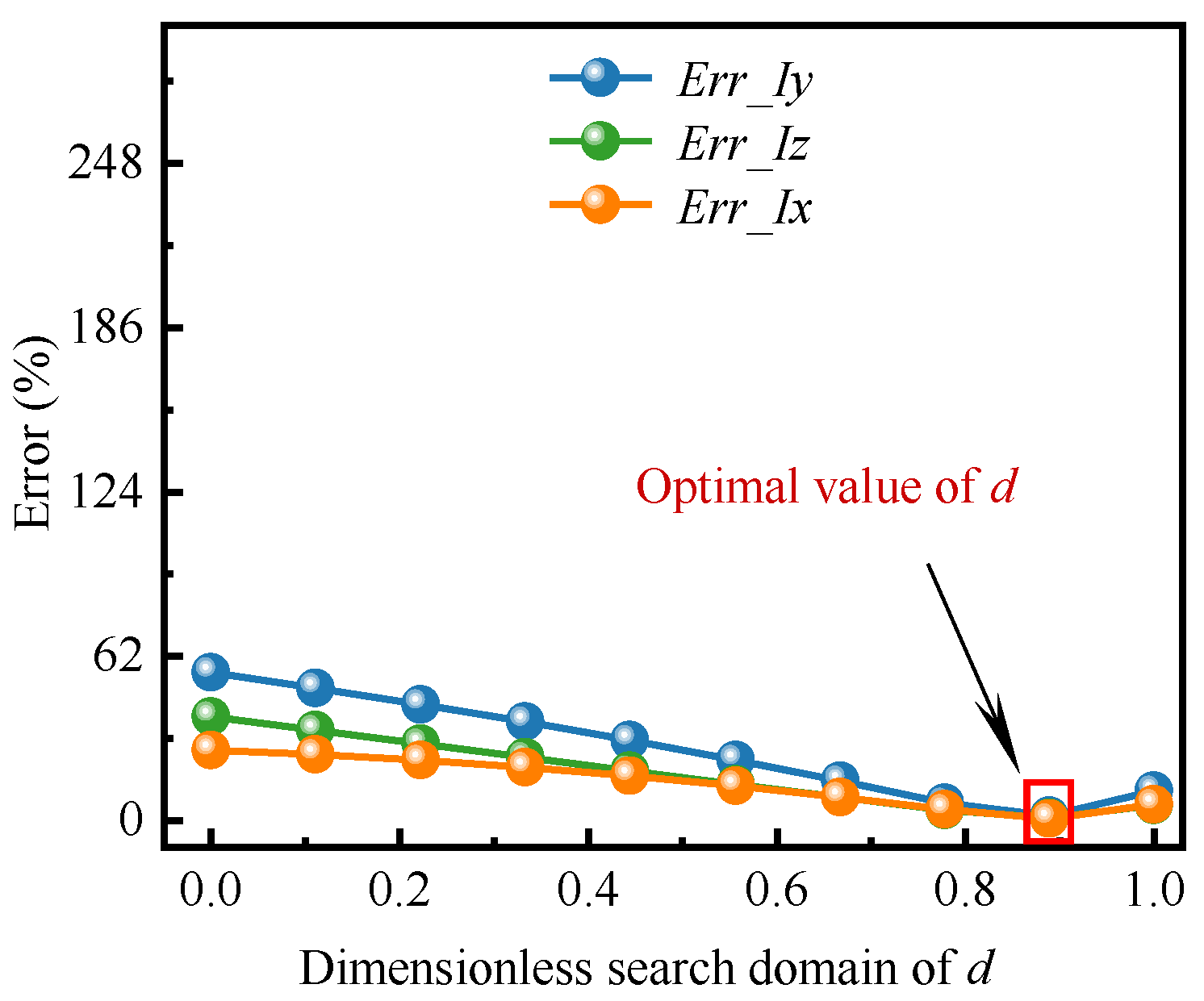
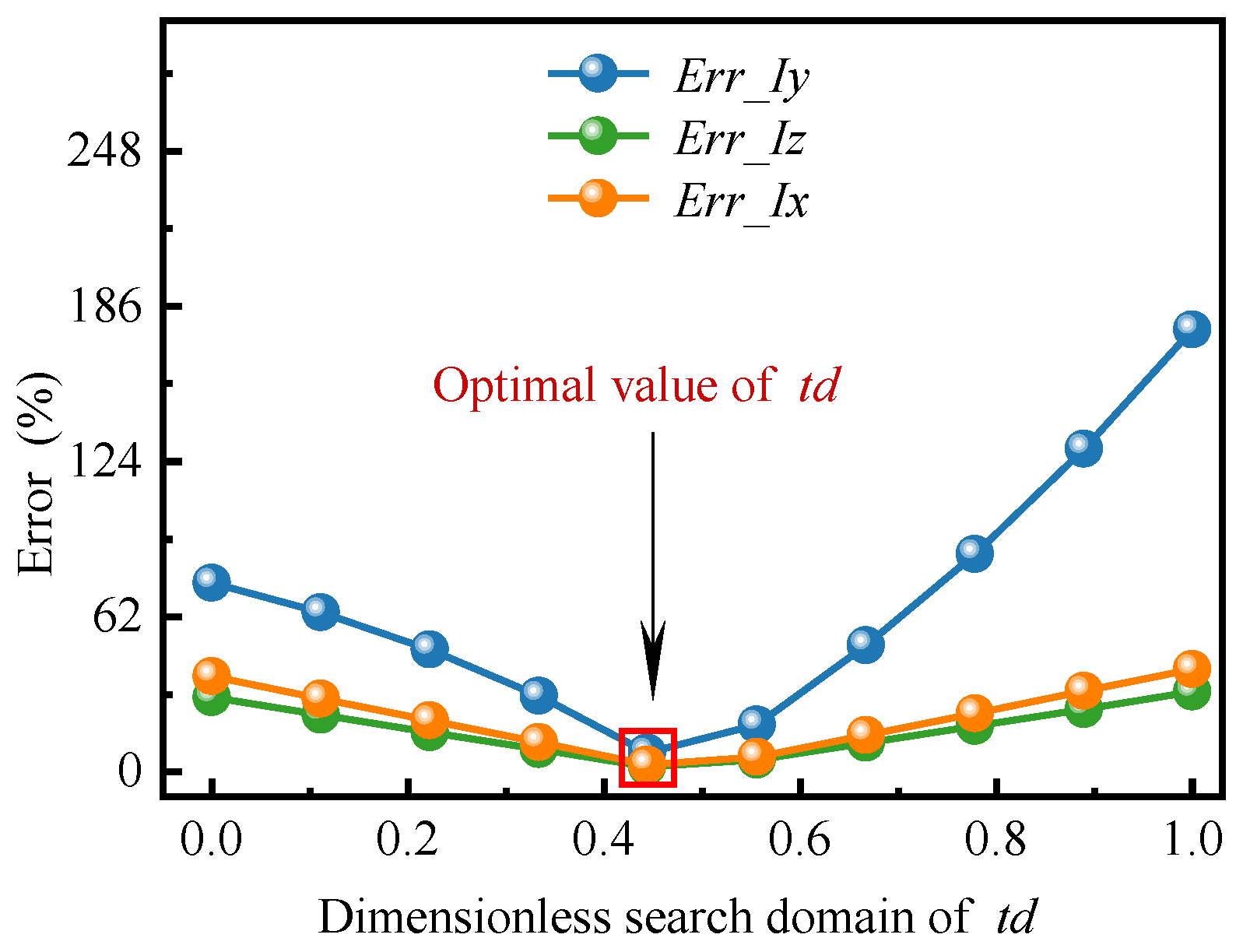
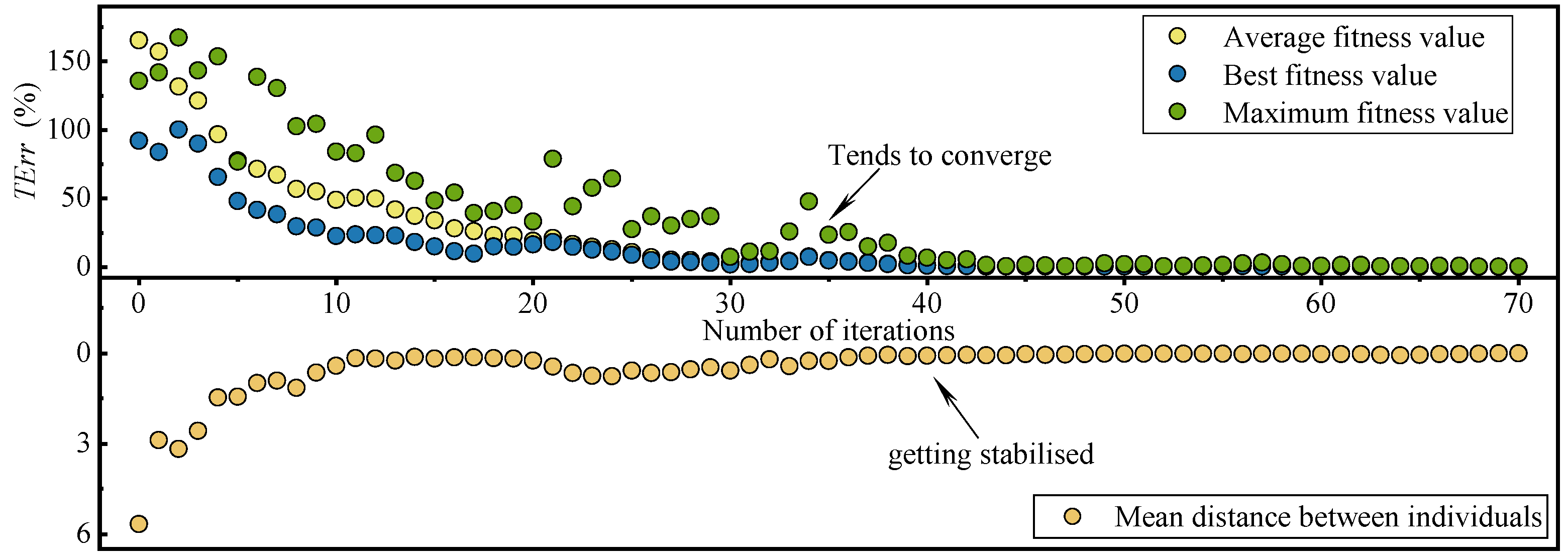
4.2. Genetic Algorithm
5. Practical Application
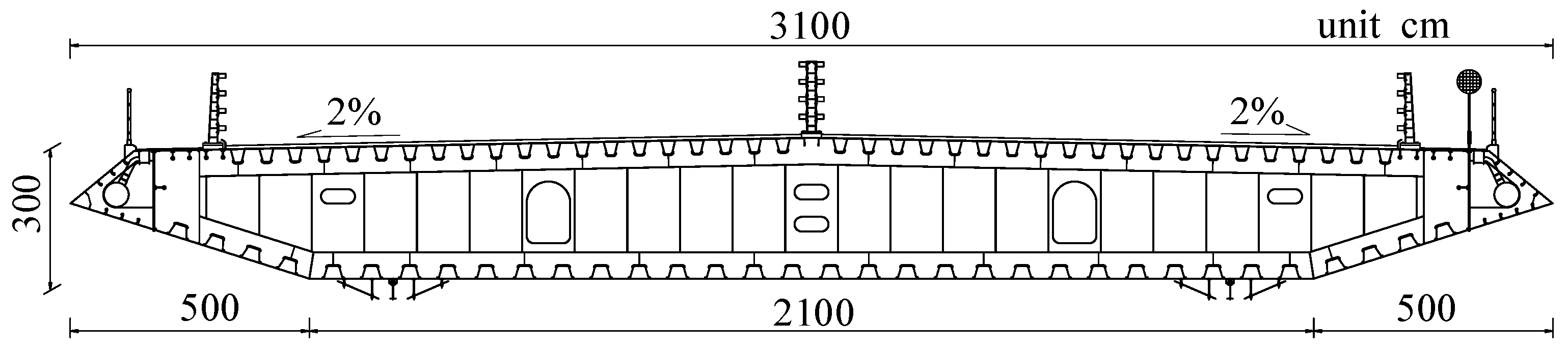
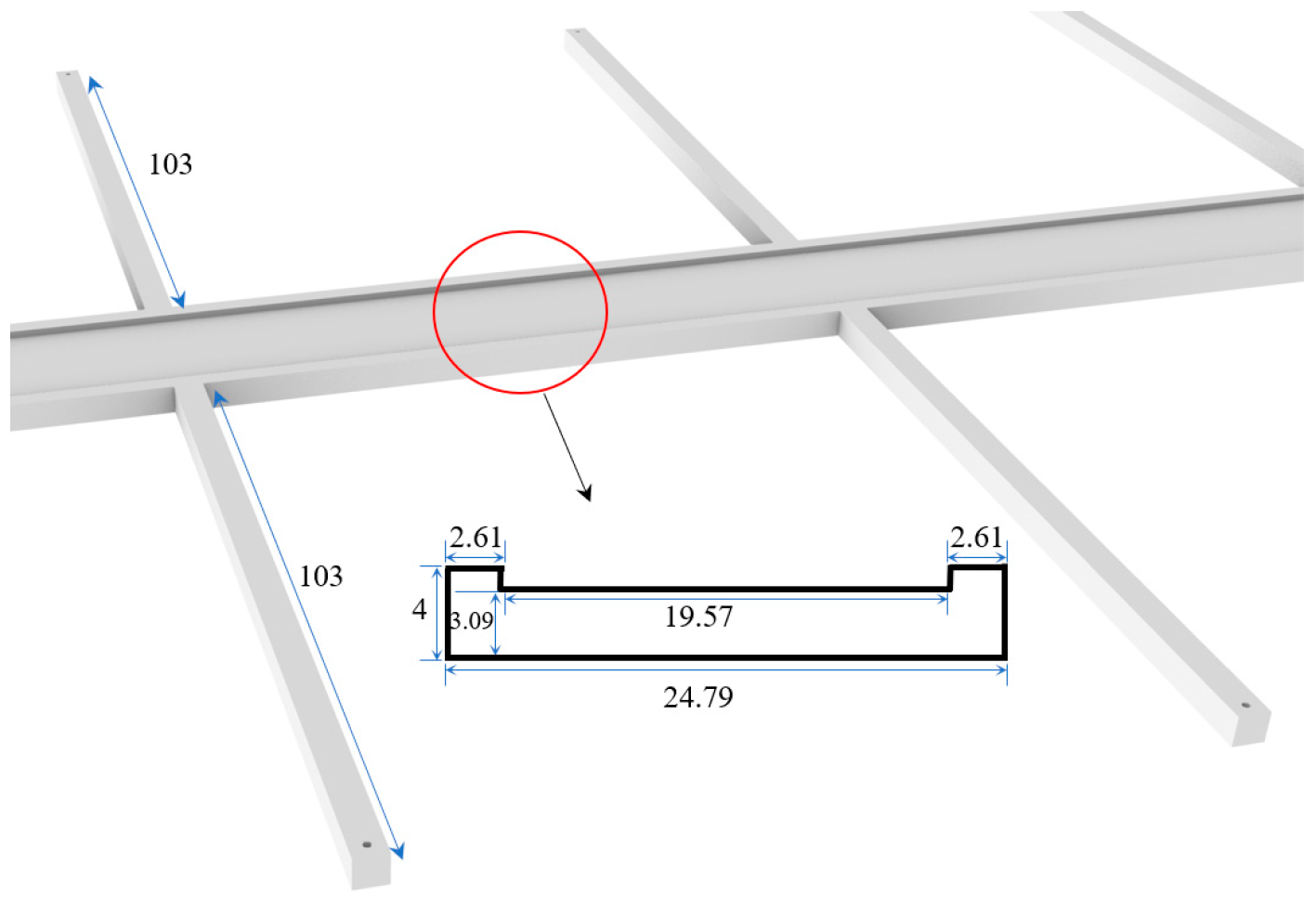
5.1. Core Beam Design of the Deck Girder
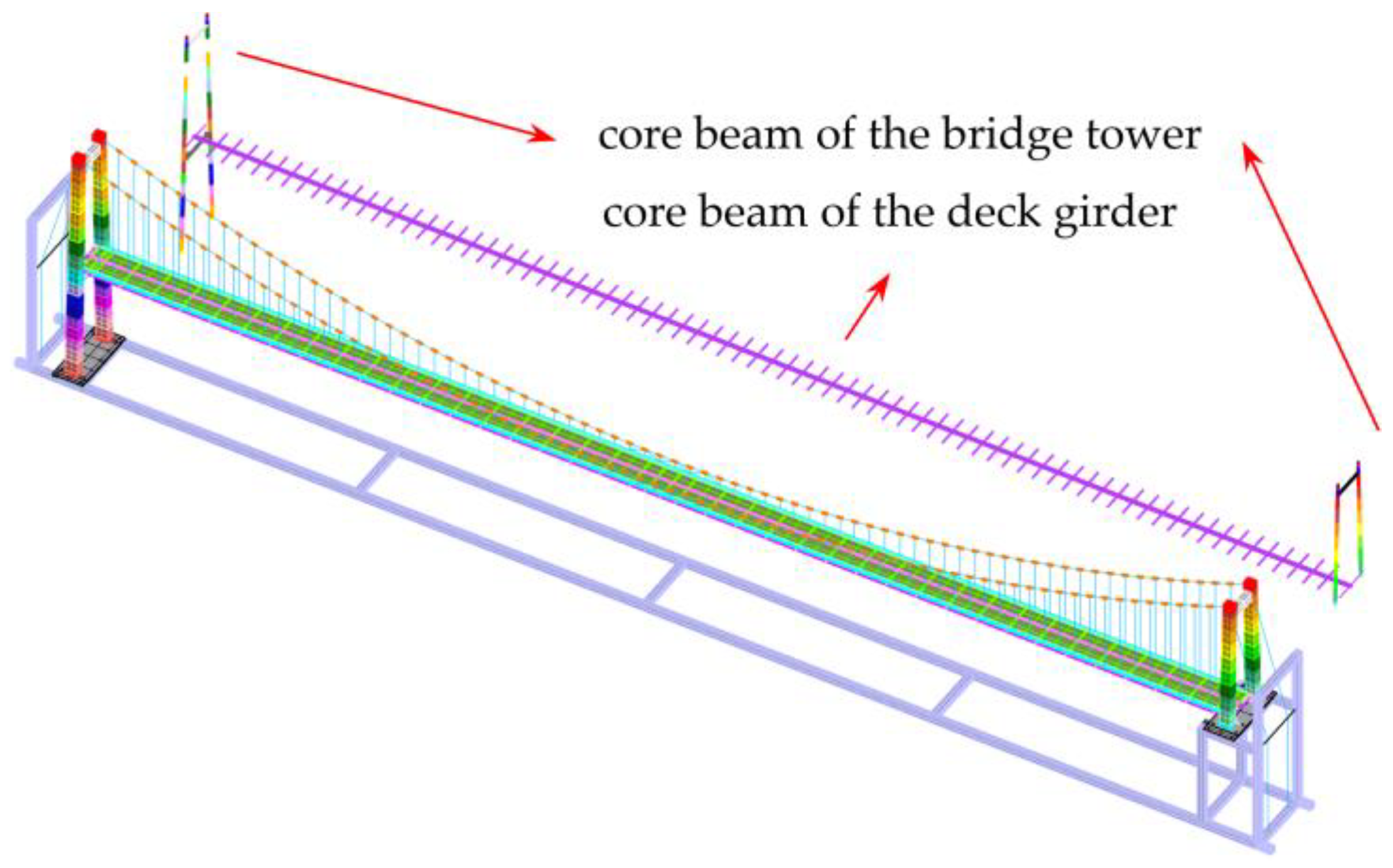
5.2. Core Beam Design of the Bridge Tower
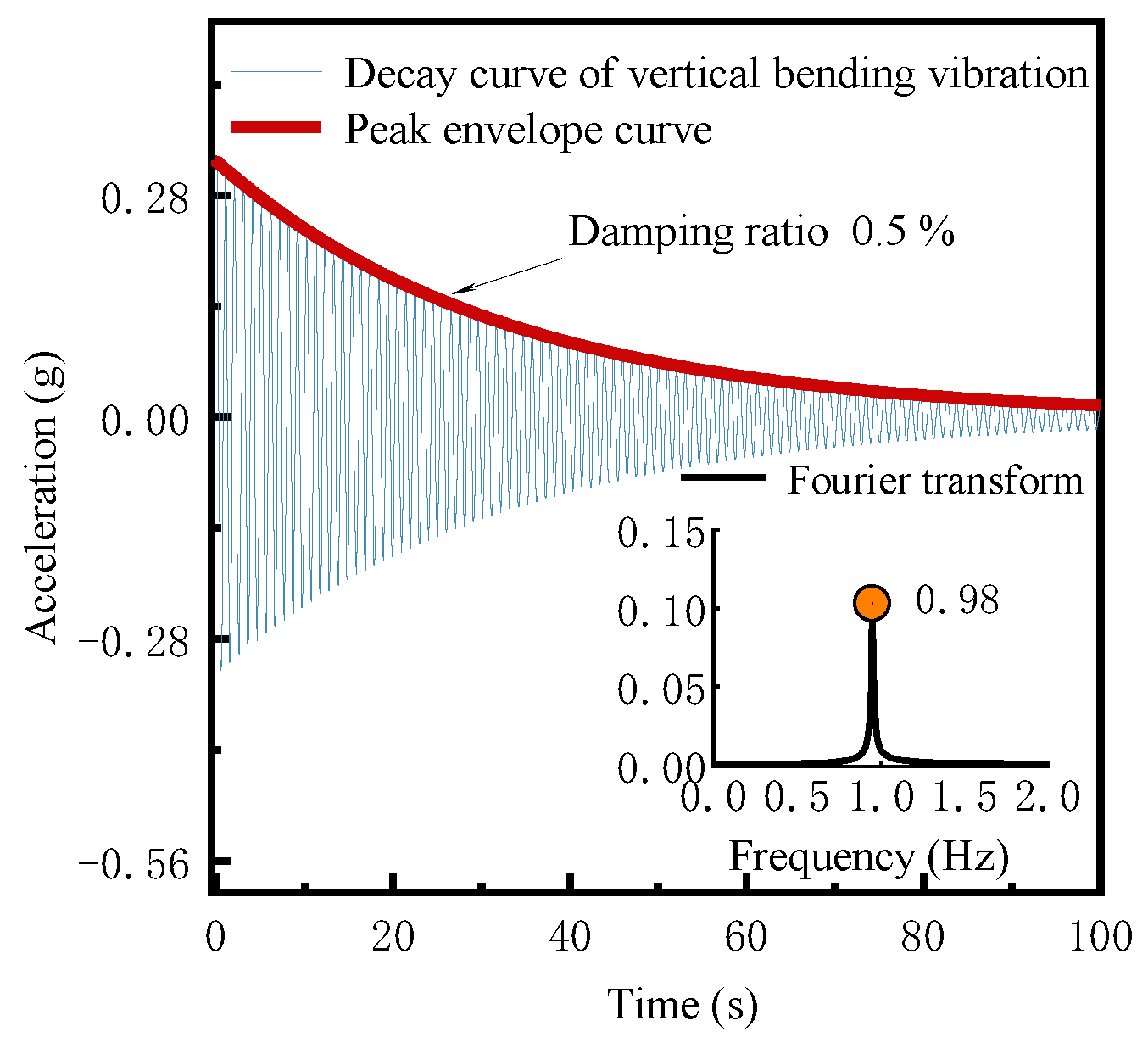
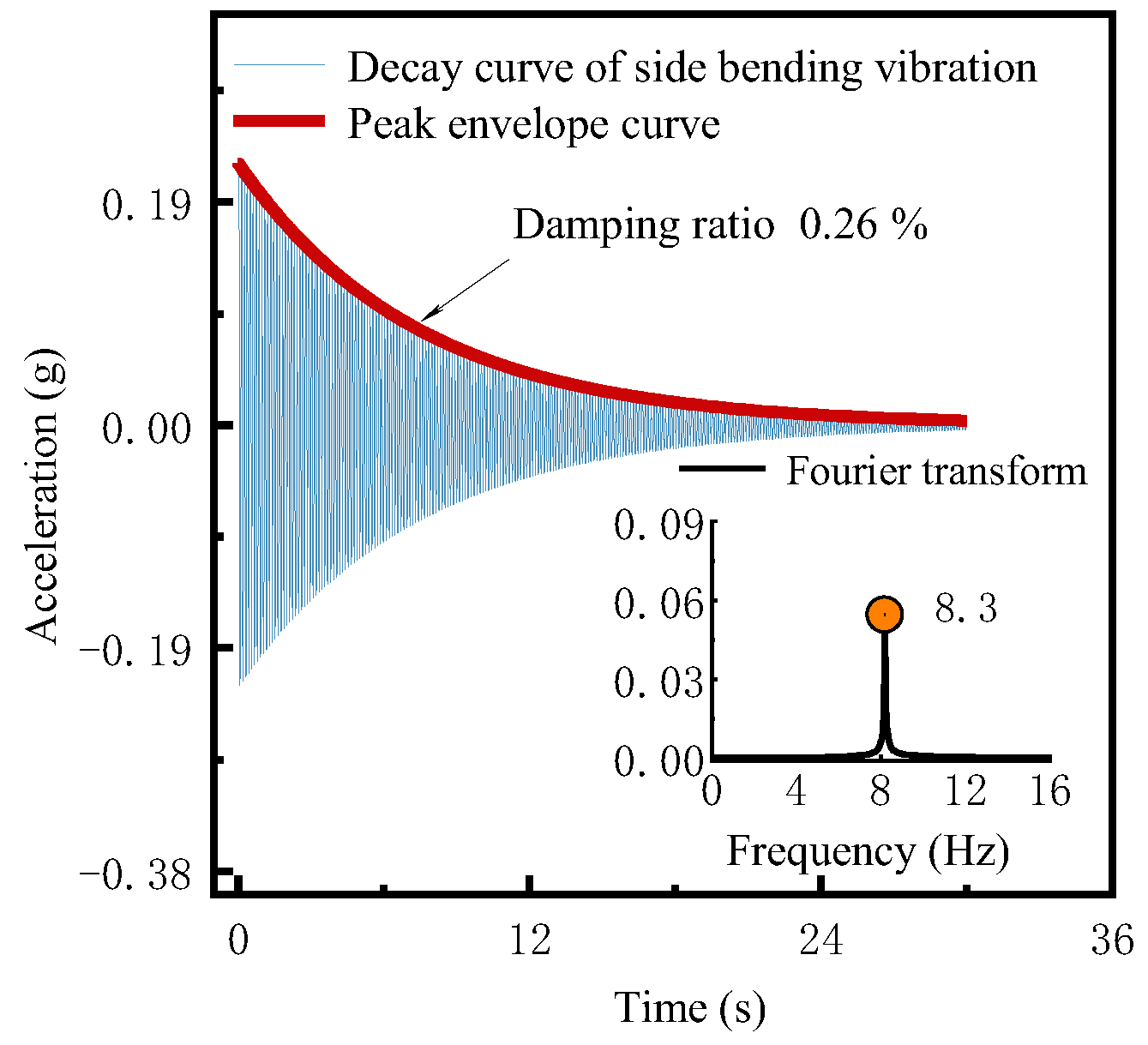
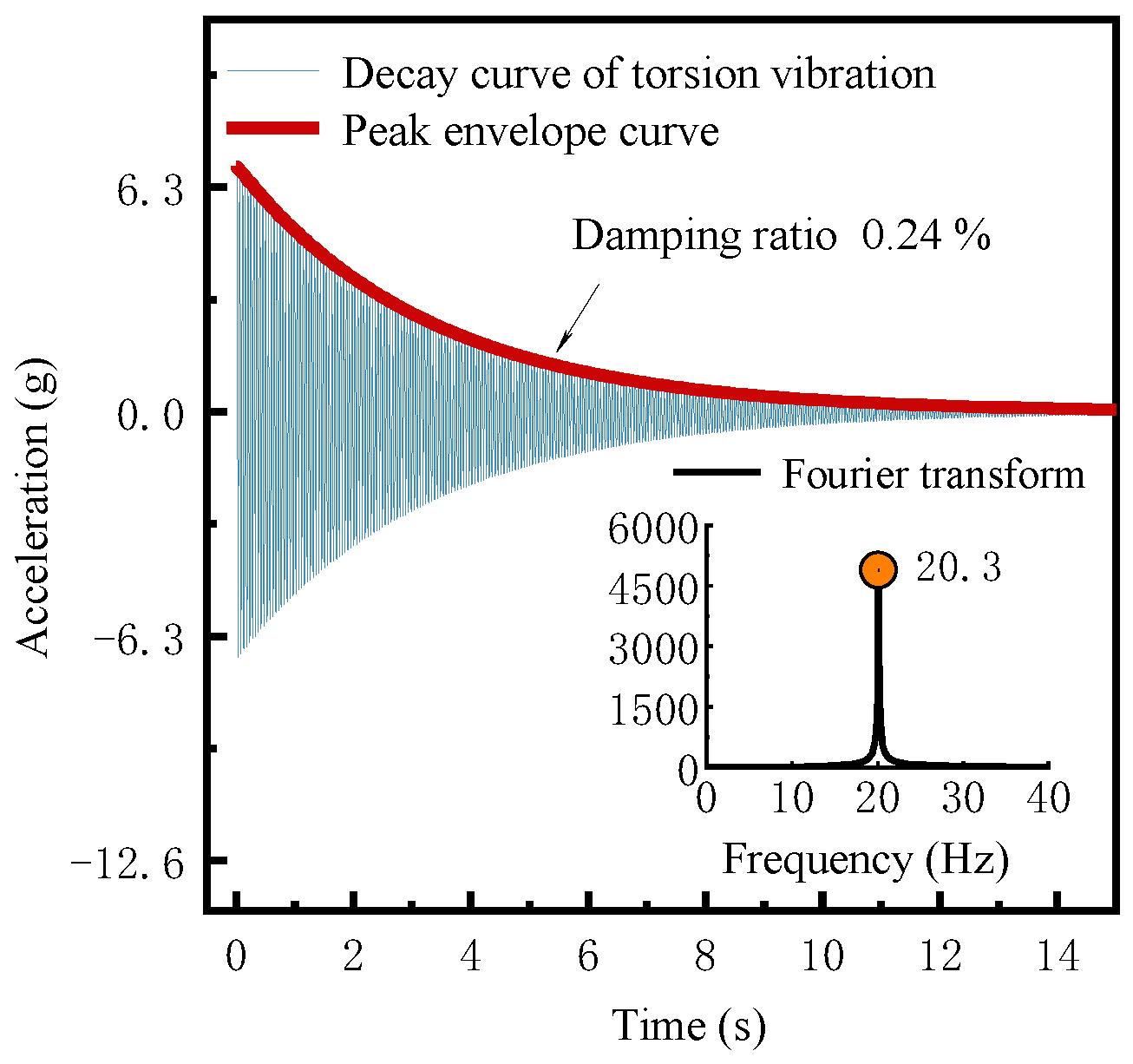
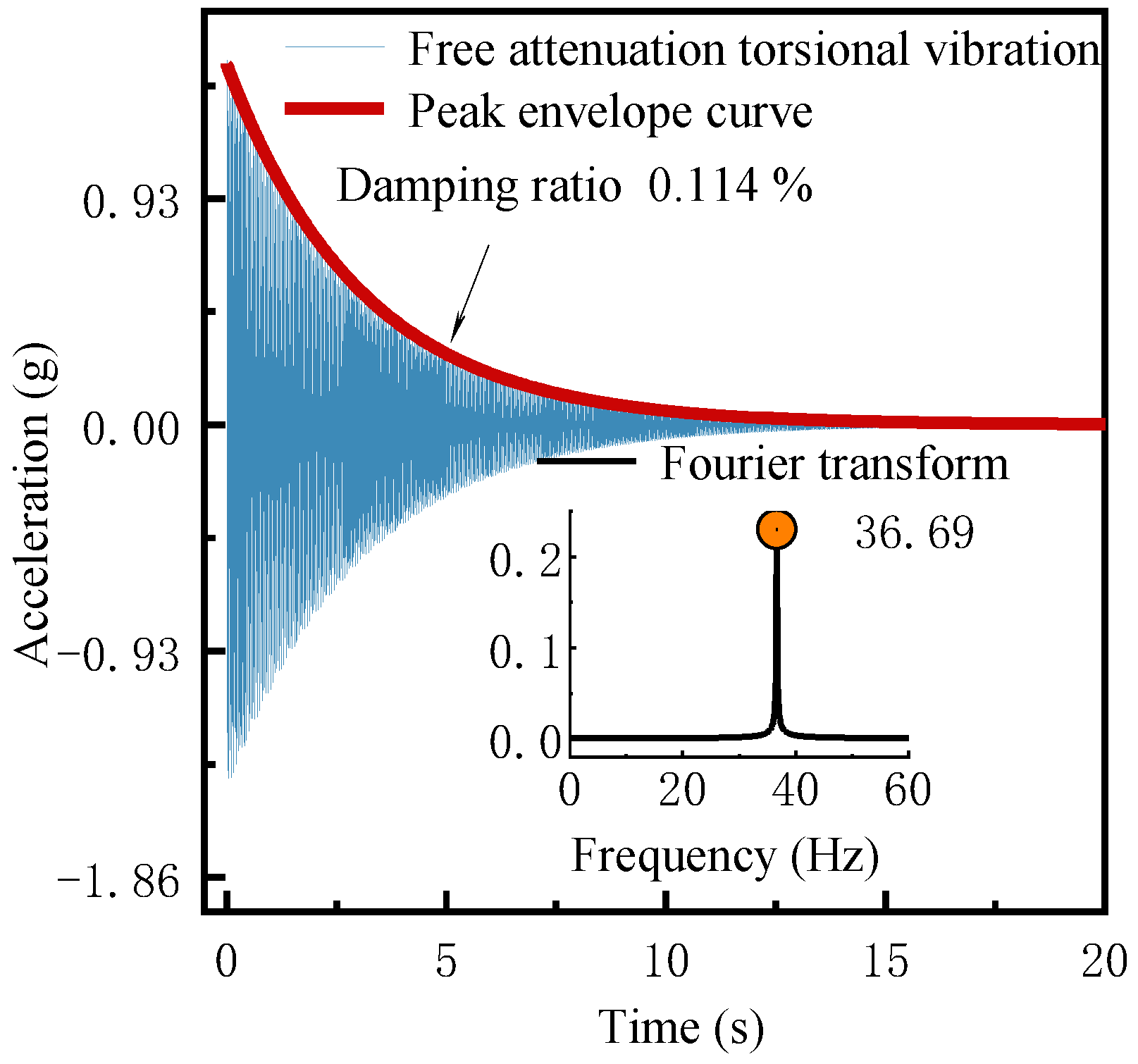
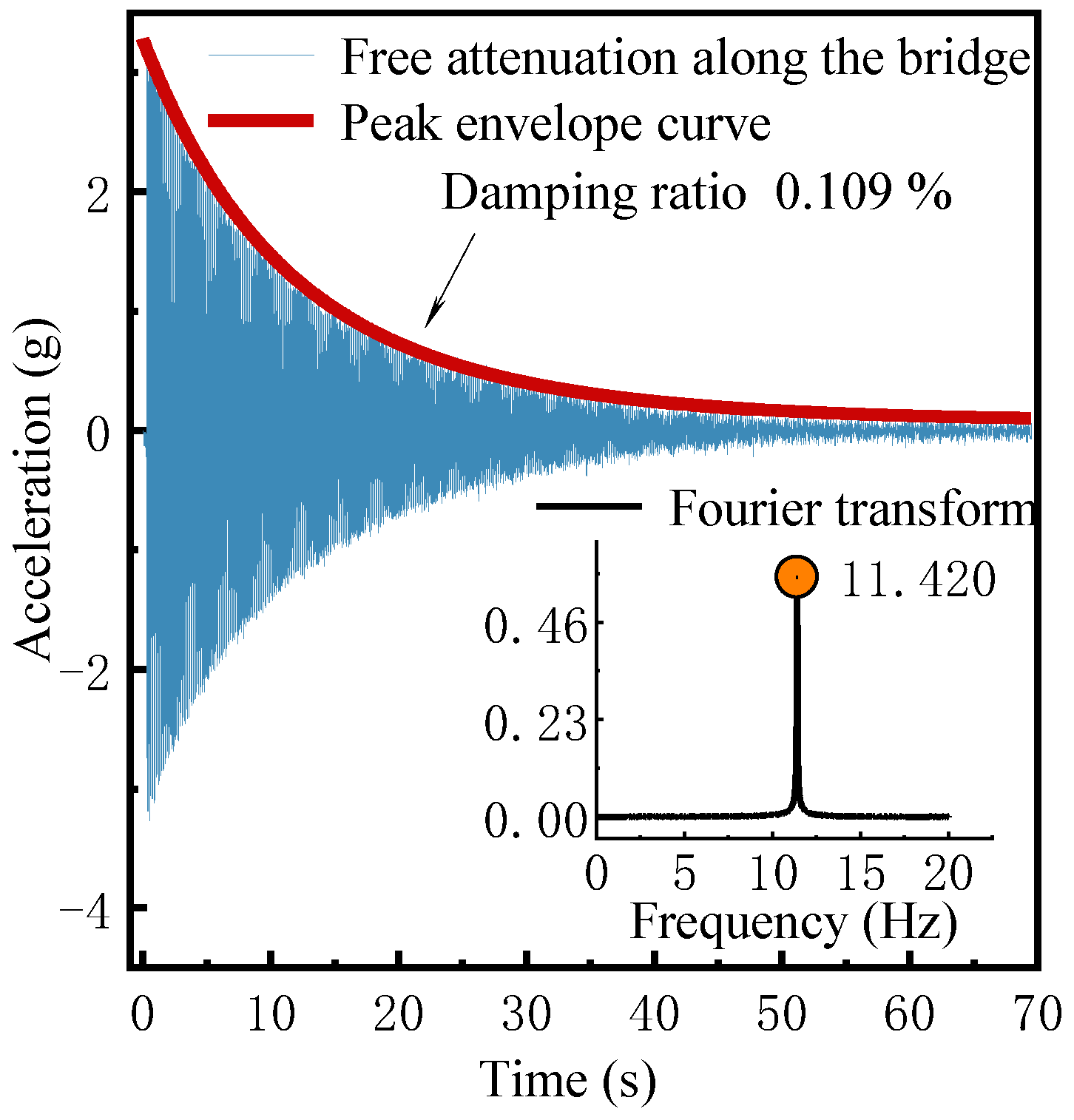
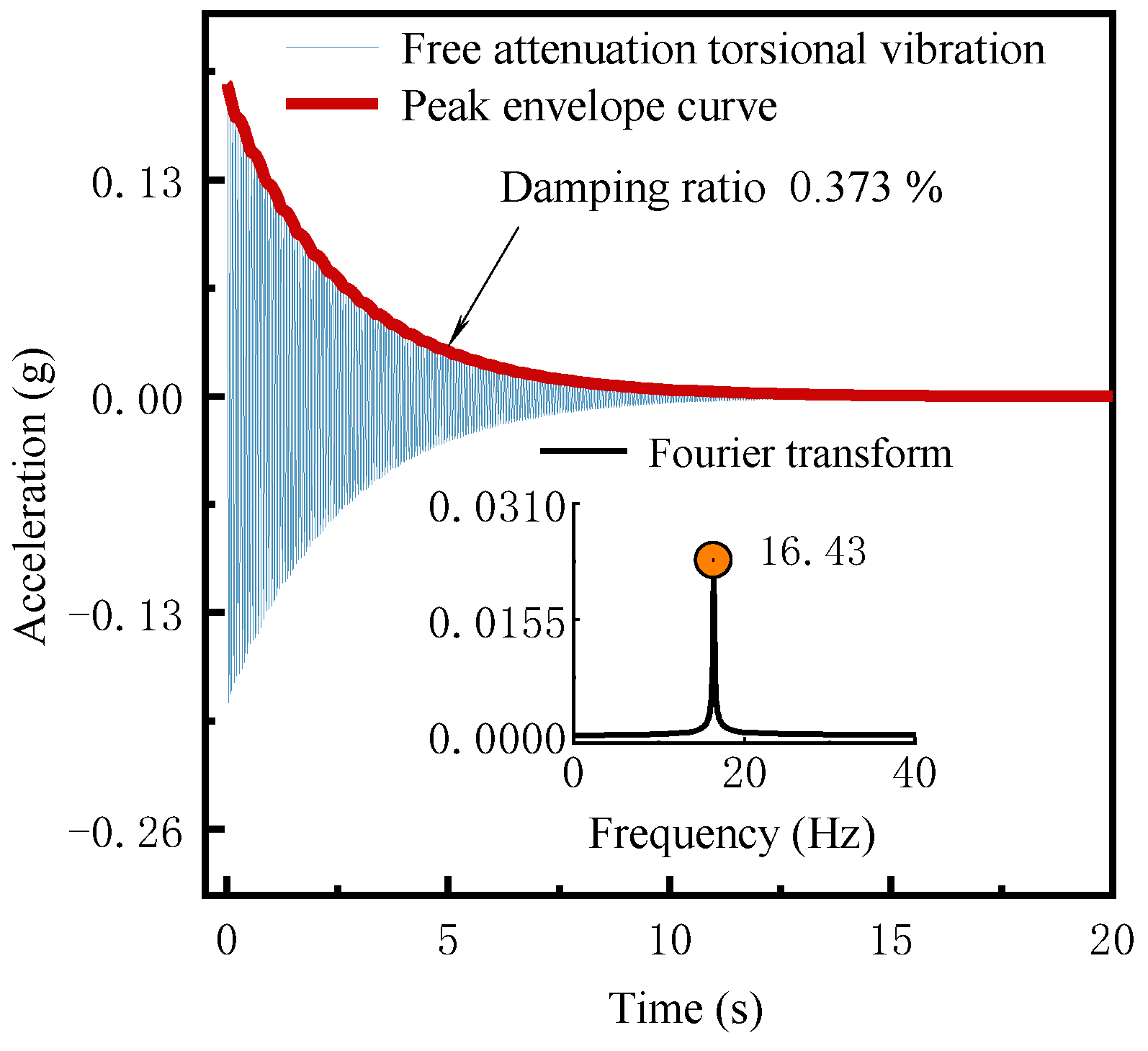
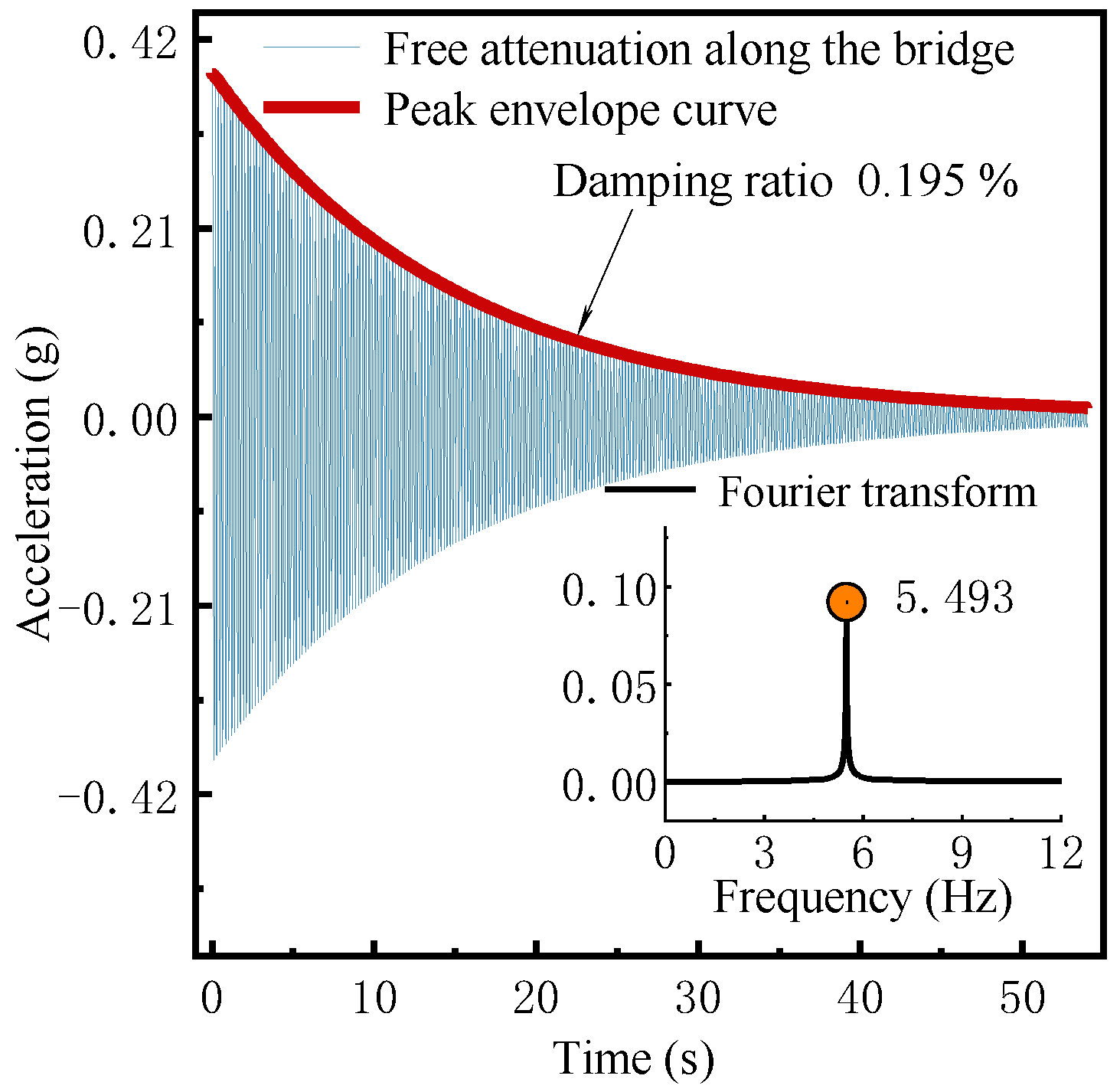
5.3. The Dynamic Characteristics Testing of the Aeroelastic Model
6. Conclusions
- (1)
- For simple simply connected sections, such as rectangular sections, the simple five-point difference method is recommended to determine the torsion constant. For complex simply connected sections, such as U-shaped cross sections, the generalized difference method and finite element method can be used to determine the torsion constant.
- (2)
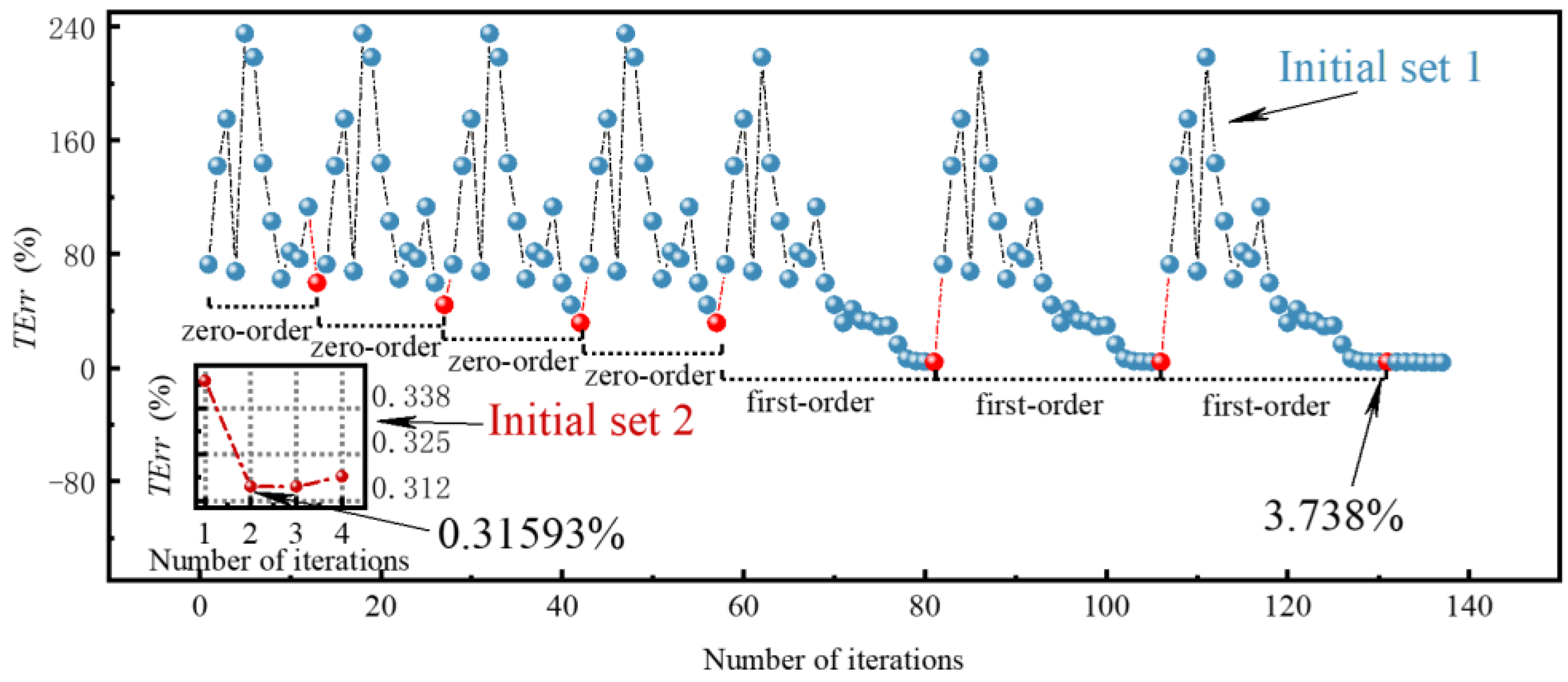
- For the ANSYS optimization method, the initial values of the section parameters of the core beams are required. If the initial values are not well-designed, the ANSYS optimization method is prone to fall into a local optimal solution. This study derives the numerical solution method for the torsion constant of rectangular and U-shaped sections commonly used in aeroelastic models, and proposes the genetic algorithm in the form of the total error of the section parameters. Through the optimization process, it is found that the genetic algorithm is easy to find out with the global optimization solution. It not only converges at a fast speed, but also leads to results of high quality and reliability. Since the investigated concerns can deal with any reduced-scale model, the proposed solution is of general validity and can be extended to many other different cases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khamprapai, W.; Tsai, C.-F.; Wang, P. Analyzing the Performance of the Multiple-Searching Genetic Algorithm to Generate Test Cases. Appl. Sci. 2020, 10, 7264. [Google Scholar] [CrossRef]
- Astiz, M.A. Flutter Stability of Very Long Suspension Bridges. J. Bridge Eng. 1998, 3, 132–139. [Google Scholar] [CrossRef]
- Ito, M. Cable-stayed Bridges: Recent Developments and Their Future. In Proceedings of the Seminar, Yokohama, Japan, 10–11 December 1991. [Google Scholar]
- Nagai, M.; Fujino, Y.; Yamaguchi, H.; Iwasaki, E. Feasibility of a 1400 m Span Steel Cable-Stayed Bridge. J. Bridge Eng. 2004, 9, 444–452. [Google Scholar] [CrossRef]
- Xu, Y.-L. Wind Effects on Cable-Supported Bridges; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Scanlan, R. The action of flexible bridges under wind, I: Flutter theory. J. Sound Vib. 1978, 60, 187–199. [Google Scholar] [CrossRef]
- Scanlan, R. The action of flexible bridges under wind, II: Buffeting theory. J. Sound Vib. 1978, 60, 201–211. [Google Scholar] [CrossRef]
- Bernuzzi, C.; Crespi, P.; Montuori, R.; Nastri, E.; Simoncelli, M.; Stochino, F.; Zucca, M. Resonance of steel wind turbines: Problems and solutions. Structures 2021, 32, 65–75. [Google Scholar] [CrossRef]
- Cochran, L.; Derickson, R. A physical modeler’s view of computational wind engineering. J. Wind Eng. Ind. Aerodyn. 2011, 99, 139–153. [Google Scholar] [CrossRef]
- Nieto, F.; Owen, J.S.; Hargreaves, D.M.; Hernández, S. Bridge deck flutter deriv-atives: Efficient numerical evaluation exploiting their interdependence. J. Wind Eng. Ind. Aerodyn. 2015, 136, 138–150. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Kareem, A. Bridge aerodynamics and aeroelasticity: A comparison of modeling schemes. J. Fluids Struct. 2013, 43, 347–370. [Google Scholar] [CrossRef]
- Kareem, A.; Wu, T. Wind-induced effects on bluff bodies in turbulent flows: Nonstationary, non-Gaussian and nonlinear features. J. Wind Eng. Ind. Aerodyn. 2013, 122, 21–37. [Google Scholar] [CrossRef]
- Diana, G.; Resta, F.; Zasso, A.; Belloli, M.; Rocchi, D. Forced motion and free motion aeroelastic tests on a new concept dynamometric section model of the Messina suspension bridge. J. Wind Eng. Ind. Aerodyn. 2004, 92, 441–462. [Google Scholar] [CrossRef]
- Diana, G.; Rocchi, D.; Argentini, T. An experimental validation of a band superposition model of the aerodynamic forces acting on multi-box deck sections. J. Wind Eng. Ind. Aerodyn. 2013, 113, 40–58. [Google Scholar] [CrossRef]
- LaRose, G.; Davenport, A.; King, J. Wind effects on long span bridges: Consistency of wind tunnel results. J. Wind Eng. Ind. Aerodyn. 1992, 42, 1191–1202. [Google Scholar] [CrossRef]
- Diana, G.; Falco, M.; Bruni, S.; Cigada, A.; Larose, G.; Darnsgaard, A.; Collina, A. Comparisons between wind tunnel tests on a full aeroelastic model of the proposed bridge over Stretto di Messina and numerical results. J. Wind Eng. Ind. Aerodyn. 1995, 54–55, 101–113. [Google Scholar] [CrossRef]
- Zasso, A.; Cigada, A.; Negri, S. Flutter derivatives identification through full bridge aeroelastic model transfer function analysis. J. Wind Eng. Ind. Aerodyn. 1996, 60, 17–33. [Google Scholar] [CrossRef]
- Hui, M.C.; Larsen, A.; Falbe-Hansen, K. Full aeroelastic model tests for Stonecutters bridge. In IABSE Symposium Report; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 2004; pp. 72–77. [Google Scholar]
- Saeed, A.T.; Liang, Z.L.; Yun, Y.Z.; Zoubi, F.A.; Salih, O.A. Full Model Wind Tunnel Study on the Xia-Zhang Bridge Under Operation Stage. Am. J. Eng. Appl. Sci. 2010, 3, 390–395. [Google Scholar] [CrossRef] [Green Version]
- Fujino, Y.; Ito, M.; Shino, I.; Iwamoto, M.; Hikami, Y.-I.; Tatsumi, M.; Miyata, T. Wind tunnel study of long-span suspension bridge under smooth and turbulent flow. J. Wind Eng. Ind. Aerodyn. 1990, 33, 313–322. [Google Scholar] [CrossRef]
- Xiang, H.; Chen, A.; Song, J. On wind resistant properties of Tiger Gate suspension bridge. Wind Struct. 1998, 1, 67–75. [Google Scholar] [CrossRef]
- Gu, M.; Chen, W.; Zhu, L.; Song, J.; Xiang, H. Flutter and buffeting responses of the Shantou Bay Bridge. Wind Struct. 2001, 4, 505–518. [Google Scholar] [CrossRef]
- Irwin, P.A.; Stoyanoff, S.; Xie, J.; Hunter, M. Tacoma Narrows 50 years later—Wind engineering investigations for parallel bridges. Bridge Struct. 2005, 1, 3–17. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, M.; Wang, D.; Guo, Z.; Cao, F. Flutter and buffeting performances of Third Nanjing Bridge over Yangtze River under yaw wind via aeroelastic model test. J. Wind Eng. Ind. Aerodyn. 2007, 95, 1579–1606. [Google Scholar] [CrossRef]
- Argentini, T.; Diana, G.; Rocchi, D.; Somaschini, C. A case-study of double multi-modal bridge flutter: Experimental result and numerical analysis. J. Wind Eng. Ind. Aerodyn. 2016, 151, 25–36. [Google Scholar] [CrossRef]
- Davenport, A.; King, J. The influence of topography on the dynamic wind loading of long span bridges. J. Wind Eng. Ind. Aerodyn. 1990, 36, 1373–1382. [Google Scholar] [CrossRef]
- Irwin, P.A. Bluff body aerodynamics in wind engineering. J. Wind Eng. Ind. Aerodyn. 2008, 96, 701–712. [Google Scholar] [CrossRef]
- Schewe, G.; Allan, L. Reynolds Number Effects in the Flow around a Bluff Bridge Deck Cross Section. J. Wind Eng. Ind. Aerodyn. 1998, 74–76, 829–838. [Google Scholar] [CrossRef]
- Mannini, C.; Šoda, A.; Voß, R.; Schewe, G. Unsteady RANS simulations of flow around a bridge section. J. Wind Eng. Ind. Aerodyn. 2010, 98, 742–753. [Google Scholar] [CrossRef] [Green Version]
- Montoya, M.C.; King, J.; Kong, L.; Nieto, F.; Hernández, S. A method for improving the dynamic response of full bridge reduced-scale models in aeroelastic wind tunnel tests by using optimization algorithms. J. Wind Eng. Ind. Aerodyn. 2017, 167, 198–216. [Google Scholar] [CrossRef]
- Ge, Y.; Xia, J.; Zhao, L.; Zhao, S. Full Aeroelastic Model Testing for Examining Wind-Induced Vibration of a 5,000 m Spanned Suspension Bridge. Front. Built Environ. 2018, 4, 20. [Google Scholar] [CrossRef] [Green Version]
- Diana, G.; Rocchi, D.; Argentini, T. Buffeting response of long span bridges: Numerical-experimental validation of fluid-structure interaction models. In Proceedings of the IABSE Conference: Structural Engineering: Providing Solutions to Global Challenges, Geneva, Switzerland, 23–25 September 2015. [Google Scholar]
- Li, G.H.; Wang, W.J.; Ma, X.C.; Zuo, L.B.; Wang, F.B.; Li, T.Z. Wind Tunnel Test Study on Pipeline Suspension Bridge via Aeroelastic Model with π Connection. J. Pipeline Syst. Eng. Pract. 2019, 10, 04018025. [Google Scholar] [CrossRef]
- Conti, E.; Grillaud, G.; Jacob, J.; Cohen, N. Wind effects on the Normandie cable-stayed bridge: Comparison between full aeroelastic model tests and quasi-steady analytical approach. J. Wind Eng. Ind. Aerodyn. 1996, 65, 189–201. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodierwrited, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill Book Company: New York, NY, USA, 1970. [Google Scholar]
- Li, R. A survey on the generalized defference method and its application. Acta Sci. Nat. Univ. Jilinensis 1995, 1, 14–22. (In Chinese) [Google Scholar]
- Zhang, X. Matlab Efficient Solution of Differential Equations: Principle and Realization of Spectral Method; China Machine Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Holland, J.H. Adaptation in Natural and Articial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Yang, Z.N.; Wu, Z.W.; Lei, T.A. A comparision between ANSYS optimization and GA in the truss structure. Tech. Autom. Appl. 2004, 7, 4–6+12. (In Chinese) [Google Scholar]
- Deb, K.; Sundar, J. Reference Point Based Multi-Objective Optimization Using Evolutionary Algorithms. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, GECCO ′06, Seattle, WA, USA, 8–12 July 2006; ACM: New York, NY, USA, 2006. [Google Scholar]









| Target_Iz (mm4) | Target_Iy (mm4) | Target_Ix (mm4) |
|---|---|---|
| 79.04 | 4518.74 | 241.44 |
| h (mm) | d (mm) | th (mm) | td (mm) | |
|---|---|---|---|---|
| Initial set 1 | 5.038 | 3.612 | 3.0579 | 19.585 |
| Initial set 2 | 4.138 | 2.712 | 3.06 | 19.6 |
| Searching domain | 4.0~7.0 | 0.1~3.0 | 1.0~3.99 | 10.0~30.0 |
| Initial set 1 | 5.038 | 3.612 | 3.0579 | 19.585 |
| Initial Set 2 + First-Order | |||
|---|---|---|---|
| h (mm) | d (mm) | th (mm) | td (mm) |
| 4.0378 | 2.6119 | 3.0574 | 19.582 |
| Err_Iz | Err_Iy | Err_Ix | TErr |
| 0.083% | 0.003% | 0.229% | 0.315% |
| Moment of Inertia | Target Values (mm4) | Optimized (mm4) | Error (%) | Final geometric sizes (mm) | h | 4 |
| Iz | 79.05 | 79.34 | 0.37 | d | 2.62 | |
| Iy | 4518.74 | 4518.70 | 0.09 | th | 3.09 | |
| Ix | 241.44 | 241.42 | 0.01 | td | 19.57 |
| Parameter | Unit | Similarity Ratio |
|---|---|---|
| Length | m | 1:121 |
| Wind Speed | m/s | 1:11 |
| Frequency | Hz | 11: 1 |
| Time | s | 1:11 |
| Mass per unit length | Kg/m | 1:1212 |
| Moment of inertia per unit mass | Kg·m2/m | 1:1214 |
| Bending stiffness | N·m2 | 1:1215 |
| Torsional stiffness | N·m2 | 1:1215 |
| Axial stiffness | N | 1:1213 |
| Moment of Inertia | Prototype (m4) | Model (mm4) | Error (%) | Section sizes (mm) | h | 4.00 | |
| Required | Realized | ||||||
| Iz | 2.05 | 79.05 | 79.34 | 0.37 | d | 2.61 | |
| Iy | 117.20 | 4518.74 | 4518.70 | 0.09 | th | 3.09 | |
| Ix | 6.26 | 241.44 | 241.42 | 0.01 | td | 19.57 | |
| core beam of the deck girder | Mode | Targeted (Hz) | Measured (Hz) | Error (%) |
| 1st-Vertical bending | 1.00 | 0.98 | −1.93 | |
| 1st-Side bending | 8.47 | 8.3 | −2.04 | |
| 1st-Torsional | 20.49 | 20.3 | −0.93 |
| Segment | Moment of Inertia | Core Beam | Error (%) | |||||
|---|---|---|---|---|---|---|---|---|
| Prototype (m4) | Model (mm4) | Section (mm) | ||||||
| Iz | Ix | Iz | Ix | Width | Height | Iz | Ix | |
| B-top | 135.35 | 203.95 | 571.72 | 954.86 | 9.15 | 8.95 | 0.14 | 0.03 |
| B-C | 144.89 | 212.61 | 848.96 | 1426.5 | 10.09 | 9.93 | 0.20 | 0.35 |
| C-D | 154.83 | 221.31 | 907.98 | 1486.0 | 10.34 | 9.86 | 0.03 | 0.30 |
| D-E | 165.18 | 230.05 | 969.42 | 1545.7 | 10.56 | 9.89 | 0.05 | 0.32 |
| E-F | 175.93 | 238.83 | 1033.3 | 1605.7 | 10.80 | 9.84 | 0.01 | 0.08 |
| F-G | 187.10 | 247.65 | 1099.7 | 1666.0 | 11.02 | 9.84 | 0.37 | 0.08 |
| G-H | 198.69 | 256.49 | 1168.7 | 1726.4 | 11.27 | 9.81 | 0.01 | 0.01 |
| H-I | 210.71 | 265.36 | 1240.2 | 1787.1 | 11.49 | 9.80 | 0.03 | 0.14 |
| I-J | 223.17 | 274.27 | 1314.4 | 1848.0 | 11.77 | 9.73 | 0.51 | 0.51 |
| J-K | 226.43 | 276.55 | 1362.0 | 1886.3 | 11.88 | 9.75 | 0.03 | 0.33 |
| L | 84.29 | 145.63 | 510. 7 | 997.42 | 8.55 | 9.80 | 0.04 | 0.35 |
| Segment | Prototype (kg) | Required for the Model (g) | Core Beam (g) | Total Mass of Thin Lead Sheets and Clothing (g) |
|---|---|---|---|---|
| B-top | 278,150.32 | 157.01 | 58.14 | 98.87 |
| B-C | 670,724.55 | 378.61 | 76.58 | 302.03 |
| C-D | 681,692.03 | 384.80 | 77.94 | 306.85 |
| D-E | 692,659.52 | 390.99 | 79.77 | 311.21 |
| E-F | 703,627.00 | 397.18 | 81.23 | 315.95 |
| F-G | 714,594.48 | 403.37 | 82.81 | 320.56 |
| G-H | 725,561.97 | 409.56 | 84.46 | 325.11 |
| H-I | 736,529.45 | 415.75 | 86.11 | 329.64 |
| I-J | 747,496.93 | 421.94 | 87.50 | 334.45 |
| J-K | 192,097.71 | 108.43 | 22.54 | 85.89 |
| L | 1,249,633.13 | 705.39 | 151.53 | 553.85 |
| Mode | Targeted (Hz) | Measured (Hz) | Error (%) | |
|---|---|---|---|---|
| A-core beam | 1st-Vertical bending | 4.226 | 4.321 | 2.25 |
| A-core beam | 1st-Torsional | 19.82 | 20.117 | 1.48 |
| B-core beam | 1st-Vertical bending | 11.551 | 11.42 | 1.13 |
| B-core beam | 1st-Torsional | 36.66 | 36.69 | 0.08 |
| A-bridge tower | 1st-Vertical bending | 1.913 | 1.953 | 2.11 |
| A-bridge tower | 1st-Torsional | 8.678 | 8.789 | 1.28 |
| B-bridge tower | 1st-Vertical bending | 5.405 | 5.493 | 1.63 |
| B-bridge tower | 1st-Torsional | 16.529 | 16.43 | 0.60 |
| Mode | Targeted (Hz) | Measured (Hz) | Error (%) |
|---|---|---|---|
| 1st-Positive symmetrical vertical bending | 1.859 | 1.818 | −2.234 |
| 1st-Antisymmetric vertical bending | 1.280 | 1.270 | −0.795 |
| 1st-Positive symmetrical torsional | 4.582 | 4.430 | −3.323 |
| 1st-Positive symmetrical lateral bending | 6.302 | / | / |
| 1st-Positive symmetrical lateral bending | 0.874 | 0.879 | 0.4801 |
| 1st-Antisymmetric lateral bending | 2.804 | 2.734 | −2.483 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qie, K.; Zhang, Z.; Li, S.; Wang, Y. Research on Effective Design Methods of Core Beam of Full Bridge Aeroelastic Model. Appl. Sci. 2023, 13, 5593. https://doi.org/10.3390/app13095593
Qie K, Zhang Z, Li S, Wang Y. Research on Effective Design Methods of Core Beam of Full Bridge Aeroelastic Model. Applied Sciences. 2023; 13(9):5593. https://doi.org/10.3390/app13095593
Chicago/Turabian StyleQie, Kai, Zhitian Zhang, Shouying Li, and Yuanyuan Wang. 2023. "Research on Effective Design Methods of Core Beam of Full Bridge Aeroelastic Model" Applied Sciences 13, no. 9: 5593. https://doi.org/10.3390/app13095593
APA StyleQie, K., Zhang, Z., Li, S., & Wang, Y. (2023). Research on Effective Design Methods of Core Beam of Full Bridge Aeroelastic Model. Applied Sciences, 13(9), 5593. https://doi.org/10.3390/app13095593








