Abstract
The optical axis angle fluctuation due to thermal deformation of the satellite bus between the laser communication load and the star sensor must be constrained to within 0.16 mrad to meet the rapid acquisition needs of the laser communication satellite. This paper analyzes the satellite’s in-orbit temperature field distribution, which is then used as the input boundary condition for the thermal deformation analysis. The optical axis angle fluctuation is reduced by the common reference optimization design. Then, adaptable isolation between the satellite bus structure and the reference support structure reduces the thermal deformation coupling. As a result, there will be less optical axis angle fluctuation caused by thermal deformation. The thermal deformation between the optimized laser communication load and the star sensor installation angle is decreased to 14.25″ according to the entire satellite simulation analysis of the modified structure. The maximum angle variation induced by temperature change dropped from 117.74″ to 10.72″ through the ground temperature deviation and prism calibration tests. The on-orbit alignment test confirms that the required capture time of 30 s is met. The aforementioned work minimizes the uncertain region of laser communication load, lessens the in-orbit acquisition time, and satisfies the demand for speedy acquisition.
1. Introduction
FSO communication is a technology for unimpeded free space optical communication that can be utilized in inter-satellite, satellite-ground, and ground communication [1,2,3]. The intersatellite laser communication transmission techniques employed in this satellite project are one of the FSO communication technology application possibilities.
High transmission speed, no special application for the communication frequency band, smaller size and weight, convenient layout design, a narrow communication beam, difficulty in being captured and monitored, and more secure communication are all advantages of laser communication over conventional high-power radio frequency communication [4]. In light of the fact that the pace of communication satellite constellation construction is accelerating, the bandwidth needed for communication is expanding, and frequency coordination is becoming more and more challenging, laser communication, a crucial form of space communication, has a wide range of potential applications. More than 12,000 satellites will make up the Space X Company’s Starlink constellation [5]. According to the article [6], each satellite has four laser communication loads deployed, which are used to implement inter-satellite communication between satellites in orbits with various inclination degrees. Miniaturization of laser communication loads is another developing trend that is used in CubeSats [7]. The wide application of laser communication loads is better suited to the development direction of downsizing. The field of satellite-to-satellite communication, as well as satellite-to-earth communication, can both utilize laser communication technology [8], and there is new progress in the study of atmospheric turbulence [9].
According to earlier research, the reduction of the in-orbit capture time of the laser communication payload is primarily carried out through the design optimization of the payload itself [10,11]. The design of a communication satellite is a systematic project. The factors affecting the acquisition time of a laser communication load include not only the factors related to the load itself but also the orbit prediction error of the satellite bus, the attitude measurement error of the satellite, and the dynamic deformation error of the satellite [12].
The orbital state of the satellite, the load’s operating mode, and the thermal design state must all be examined in order to determine the thermal deformation magnitude of the satellite [13,14]. When the thermal analysis model has been established, the relevant thermal deformation situation is next examined in order to determine whether the thermal deformation’s influence magnitude can meet the requirements of the laser communication load acquisition time. The degree of thermal deformation between the star sensor and laser communication load implemented in a honeycomb sandwich structure is discovered to be significantly greater than what is necessary for index allocation in this work. To control the angle variation between the laser communication load and the star sensor optical axis, it is important to optimize the thermal deformation.
The goal of the optimization design is to establish a stable thermal deformation connection between the star sensor and laser communication load. This common reference optimization design idea is often used in remote sensing satellites [15], but it is rarely used in communication satellites. Second, it uses flexible isolation with the satellite bus to lessen the impact of the entire satellite’s temperature variation on the support’s temperature swings as well as the impact of the entire satellite’s thermal deformation on the ambiguous zone of laser communication alignment. The flexible isolator used in this paper is usually used to reduce the effect of micro-vibration in orbit [16]. Finally, satellite load isolation was used to reduce the thermal control challenge, precisely manage the temperature of the isolated physical reference support, and lessen the impact of the physical reference support’s temperature fluctuation.
The topology optimization method adopted in this paper, as a structure optimization design concept, has been rapidly developed in weight optimization design in recent years [17,18,19]. Topology optimization is used to determine the relative placement of the star sensor and the laser communication load while taking other engineering considerations into account. The reference bracket adopts an I-section design based on the structural topological relationship found through topological optimization, and size optimization establishes the critical dimensions. The thermal deformation between the optimized laser communication load and the star sensor installation angle decreased to 14.25″ according to the entire satellite simulation analysis of the modified structure. By comparing the optimized design scheme with the unoptimized design scheme, the maximum angle variation induced by temperature change fell from 117.73″ to 10.73″ during the ground temperature deviation test and prism calibration test. The on-orbit alignment test confirms that the required capture time of 30 s following the entire test is met. The in-orbit acquisition time test results show that the satellite’s uncertain region satisfies design requirements and that the thermal deformation stability between the satellite’s laser communication load and star sensor satisfies requirements.
2. The Impact of Satellite Bus Thermal Deformation on the Laser Communication Load Acquisition Time
In general, the energy of the laser beam has a significant impact on the transmission bandwidth of the laser communication load. The beam of the laser communication load is typically constructed at a smaller angle to improve the gain of the laser beam for communication [4]. In light of the relatively narrow laser beam, it is generally necessary to design a more complex acquisition, tracking, and pointing (ATP) system for laser communication loads because errors in attitude measurement accuracy, attitude pointing accuracy, orbit measurement error, and other aspects of communication satellites in orbit will make alignment of the laser difficult [12].
The reduction of the acquisition time of the laser communication payload in orbit has significant economic implications for satellite communication. The topological relationship between the relative positions of satellites will be impacted by the continually changing orbit characteristics, particularly for large communication satellite constellations, leading to repeated disconnection and reconnection of laser communication lines. One can only reduce, rather than completely eliminate, the time required for laser chain formation and reconnection. The effective communication duration can be increased by shortening each chain’s building time, increasing the overall working efficiency of the communication satellite [10,20]. Topology optimization can increase the effectiveness of link establishment over the entire constellation after the communication satellite has finished networking [21]. Reduced connection establishment times are crucial since this constellation’s topology optimization method necessitates frequent link switching.
The low-orbit communication test satellite 03/04’s laser communication load installation directional thermal stability optimization design is the basis for this work. On 20 May 2022, the low-orbit communication test satellite 03/04 was launched. In Figure 1, one of the satellites is depicted.

Figure 1.
Low-orbit communication test satellite.
The two satellites were in a circular orbit with an eccentricity of zero, an inclination angle of 86 degrees, and an altitude of 880 km. In order to complete the laser communication task verification between two satellites in the same orbit as well as two satellites in a future adjacent orbit, an inter-satellite laser communication payload is configured in the flight direction and the flight opposite direction of the satellite, respectively. Figure 2 displays the schematic diagram of the laser communication chain. Low-orbit communication test satellite inter-satellite communication calls for link switching between the same orbit and the different orbit, as well as re-capitulation of the broken link. Reduced alignment intervals are important for the laser communication satellite.
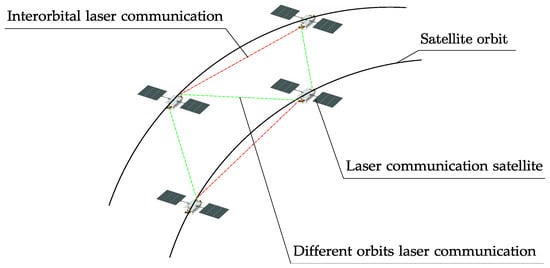
Figure 2.
Schematic diagram of the laser link in the same orbit and the different orbit.
The laser communication load used in this project is shown in Figure 3. Its appearance is shown in Figure 3a. The surface is a thermal control coating material. Its composition and principles are shown in Figure 3b. The laser communication load consists of an optical telescope, a relay optical path transmitting system, a beacon transmitting optical system, and an electronic unit. The two-dimensional turntable of the optical telescope realizes the coarse pointing function of the laser communication load of the target satellite. The precise tracking is located in the relay optical path, and the piezoelectric fast-pointing mirror is used as the actuator. Precision tracking control can realize the control function of higher frequency characteristics and the correction of small angle deviation, which is mainly used to reduce the influence of satellite high-frequency vibration sources such as flywheels and SADA on laser communication. For the satellite bus, the micro-vibration level of the whole satellite needs to be controlled within the control ability of the piezoelectric fast-pointing mirror to ensure that the satellite laser communication will not cause a code error or communication link break [22]. However, this is a fine operation after the completion of coarse tracking, which will not influence the acquisition time of the laser communication load. Because the signal optical band of 1550 nm is far away from the beacon optical band of 808 nm, the large array detector commonly used in the capture and tracking system is not sensitive to signal light, and the signal light is not convenient to be used as a beacon light. An independent optical laser beacon is configured at both ends.
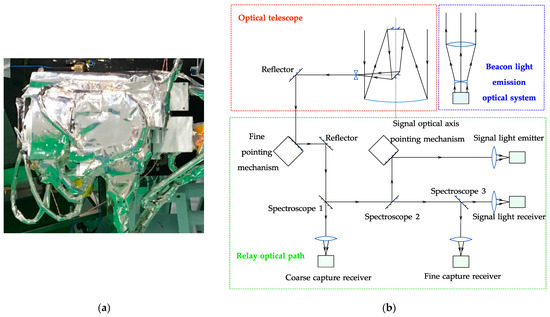
Figure 3.
Laser communication load system composition: (a) appearance; (b) system composition.
Table 1 displays a few laser communication load metrics. There are two common configurations for transmission rate when the communication distance is less than 5000 km and less than 3000 km for the satellite, which is now in the experimental stage.

Table 1.
Parameters of the laser communication load.
The scanning mode, resident duration, unclear area size, and other aspects affect the laser communication load acquisition time. Common beacon light scanning techniques include rosette scanning, Lisaru scanning, compound scanning, spiral scanning, rectangular spiral scanning, and others. Each scanning mode has its advantages in terms of difficulty of realization, scanning time, scanning probability, and so on [23]. The paper by Xin Li [24] suggests a method for figuring out the capture time and determines the connection between the capture time and the uncertain region. Rectangular scanning provides clear advantages in terms of effective coverage and is reasonably straightforward to implement in terms of algorithm, software, and hardware, but the scanning time is quite long. The longest scanning time is estimated using this scanning technique. The capture time of a rectangular scan was calculated by Formula (1).
where is the overlap coefficient. Considering that the beacon light pointing error will cause the uncertain region to miss scanning in the scanning process, the beam scanning step should take into account the overlapping of adjacent scanning areas to reduce the probability of missing scanning. It is necessary to consider the satellite attitude stability, the stepping error of the pointing mirror, and the optic axis jitter caused by satellite vibration on the pointing mirror to determine the overlap coefficient. The overlap coefficient is set to . is the residence time. The resident time is set to . is the beacon light emission angle. The beacon light with a divergent angle is used for scanning. is the uncertain region after calibration.
According to Formula (1), if the acquisition time of the satellite laser communication payload is less than 30 s, should be less than 1.53 mrad.
To eliminate unrecoverable errors caused by factors such as vibration during satellite transportation and launch, gravity release after orbit, etc., star calibration, inter-satellite calibration, and satellite landmark calibration will be adopted. The error eliminated in the calibration process can be considered a fixed system error, and the influence on the acquisition time can be ignored. On-orbit calibration cannot completely eliminate all undetected system faults. For example, orbit prediction error, attitude measurement error, satellite dynamic deformation error introduced by the satellite bus, open-loop control error of the pointing mirror, coarse tracking residual error, and laser solution accuracy error introduced by the laser communication load itself. These errors are independent and irrelevant. The distribution of this part of the error is listed in Table 2. The uncertainty error is calculated by the conservative method of absolute sum, and the formula is shown in (2).

Table 2.
Uncertainty analysis after inter-satellites calibration.
The satellite attitude measurement error in Table 2 is affected by the star sensor attitude error, the star sensor temperature drift error, the thermal deformation error of the satellite bus, and other factors. The thermal deformation error of the satellite bus plays a dominant role. When the thermal deformation error is controlled within 0.16 mrad, the attitude measurement error of the satellite can meet the index requirement of 0.35 mrad.
It is challenging to regulate the thermal deformation error of the honeycomb sandwich communication satellite bus within 0.16 mrad due to a number of reasons. First off, because communication loads come in a variety of forms, operate in a variety of ways, and consume a lot of power, there is a significant disparity between the peak power and steady power of communication satellites. In order to lower the cost of launch, the thermal design of the satellite must take into account both the volume and weight of the entire satellite as well as an adequate cooling area to fulfill the peak cooling power requirement. The temperature variation of the satellite bus between normal power working mode and peak power working mode is caused by the difference between normal power and peak power as well as the difference in external heat flow while the satellite is at different points in orbit. Finding a steady satellite temperature distribution state to use as the temperature reference for the thermal deformation input is therefore challenging. The honeycomb sandwich structure’s characteristics make it challenging for communication satellites to locate a stable thermal reference for the installation of high-precision attitude measurement components such as star sensors and laser communication loads. The aforementioned two points have the effect of altering the uncertain region where the laser communication load points by causing the angle variation between the laser communication load and the star sensor to fluctuate significantly in the classic design mode of laser communication satellites.
In Section 4, it is discovered through ground tests that when the star sensor and laser communication load are installed conventionally on the satellite structural plate, the angle variation between the two equipment’s prisms caused by the thermal deformation of the satellite bus will reach 117.74″ and the corresponding synthetic uncertainty will reach 0.57 mrad, much higher than the required 0.16 mrad. The capture time increased by 65.16% to 46.55 s, despite the uncertainty area expanding by 27.3%. This was due to a quadratic positive correlation between the capture time and the uncertainty area. The thermal deformation management of the satellite bus must be optimized in order to achieve the design requirement of laser communication load capture time within 30 s. Controlling the uncertain region of the laser communication load is crucial for quickly acquiring and building the link in the business mode of the laser communication satellite.
3. Control of Thermal Deformation Optimization Strategy
The following concepts guide the optimization design process: Initially, it is essential to analyze the satellite’s orbital temperature distribution. The satellite bus’s thermal deformation is estimated using the temperature distribution as an input. The needed method is produced through optimization using the amount of orbital deformation as the boundary condition. Finally, simulation calculations are used to confirm the optimization effect.
3.1. Orbital Temperature Distribution
3.1.1. Heat Dissipation Surface Analysis
The low-orbit communication test satellite weighs 490 kg and has an orbital lifetime of 5 years. It can perform multi-functional technology verification and on-orbit service, including satellite-earth broadband communication, inter-satellite communication, and network working. It is outfitted with a laser and Ka-band microwave inter-satellite chain, a Ka-band satellite-earth link, and an integrated on-satellite processing load. Very strict requirements for the thermal control system are presented by the high power density, several working modes, power consumption variations across modes, and other characteristics.
The satellite’s external heat flow analysis is necessary in order to calculate the dimensions of the heat dissipation surface in each direction. The angle between the satellite orbit plane and the sunlight vector is known as the β-angle. The exterior heat flow of a satellite at various β-angles varies due to the action of sunlight. The analysis of the time fluctuation of the β-angle of the low-orbit communication test satellites is shown in Figure 4 as the results. The low-orbit communication test satellite’s β-angle fluctuates from −89° to +88° and changes by 1.423° every 24 h in its near-polar circular orbit. The variation in the β-angle and the amount of external heat flow at various times are both significant.
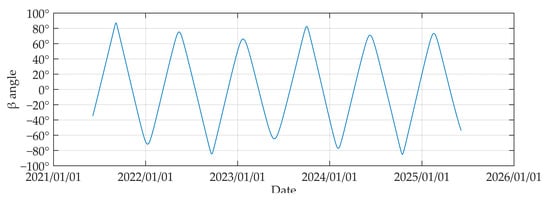
Figure 4.
Change of the β-angle in orbit.
After entering orbit, the satellite + Z-axis are oriented toward the ground, and the three axes are stable to maintain the load of the phased array antenna pointed at the ground in order to carry out data transmission activities between the satellite and the ground. To accomplish the energy balance of a single circle in any orbit state and working mode if a fixed solar panel is used, a large solar panel area is required. This is not the best design approach for increasing the precision of satellite control in orbit, decreasing the launch weight into orbit, and enhancing the economics. In this project, an A/B dual-axis SADA drive is used to monitor the solar panel’s solar capture and ensure that the satellite’s energy balance is maintained in a single circle beneath the tiny solar panel area. The solar panel’s axis A, which is located close to the satellite bus, is used to regulate the solar panel’s continuous rotation along the satellite’s Y-axis (pitch axis) within a 360° range. The solar panel development satellite’s B axis, which is located adjacent to the solar panel, is used to regulate the precession rotation of the X axis (rolling axis) within a range of 42°. The thermal deformation of the solar panel and the coupling of the satellite bus can be disregarded because the A/B axis of the solar panel is connected by thin rods. The mathematical model for thermal deformation simplifies the concept of a solar panel. Yet, the shielding of the solar wing’s intricate motion route will affect the heat flow outside the satellite’s Y planes, and this influence on the satellite’s temperature cannot be disregarded.
A simulation model of the satellite’s thermal properties was created; each surface was separated into a number of sections, and the heat flow to the satellite’s surface was measured, as seen in Figure 5. The heat flow to the exterior of each surface was determined by weighing and averaging the final statistical data, as shown in Figure 6.
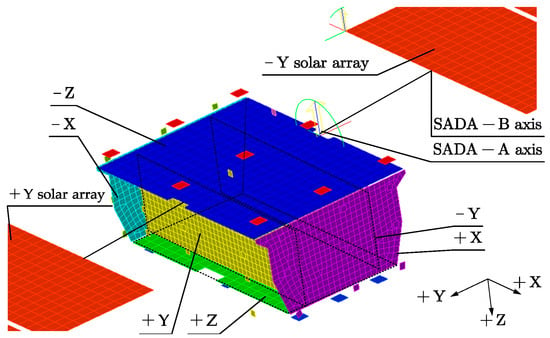
Figure 5.
Finite element model for thermal analysis.
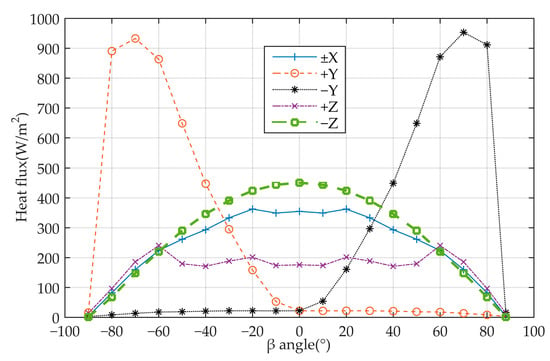
Figure 6.
Satellite surface heat flux.
The infrared heat flow from the Earth that is incident directly on the outside surface of every single board has little change since the satellite has been in a state of orientation to the ground for a long period, as indicated in Table 3. The solar radiation heat flow that is immediately incident on each surface of the satellite changes noticeably under the impact of the β-angle fluctuation. The infrared heat flux from the satellite to the ground (+Z plane) is greater but smaller from the perspective of infrared radiation heat flux straight into the earth. The satellite +Y/−Y plane is significantly impacted by the alternating external heat flux from the direct incoming solar radiation heat flux (including the earth’s albedo heat flux).

Table 3.
Earth Infrared Incident Heat Flux on a Honeycomb Plate.
The satellite’s +Z-plane changes the least during its whole life cycle because of its orientation to the earth, while the satellite’s −Z, +X, and −X planes also shift dramatically when the β-angle changes.
The satellite’s Y and Z opposing planes obtain direct solar radiation. The OSR cerium glass secondary surface mirrors are firmly mounted to lessen the impact of solar irradiation on the entire satellite (low solar absorption and slow degradation in orbit). According to the terminal properties of the heat dissipation surface, OSR_EOL (α/ε = 0.13/0.79), the thermal control white paint with small solar absorption and large hemisphere emissivity, brand KS-ZA, is used because X and +Z surfaces are primarily affected by the earth’s albedo, whose magnitude is much smaller than the direct solar irradiation surface. Figure 7 depicts the heat dissipation capability of each surface of the KS-ZA EOL (α/ε = 0.22/0.92) and the relationship with the β-angle.
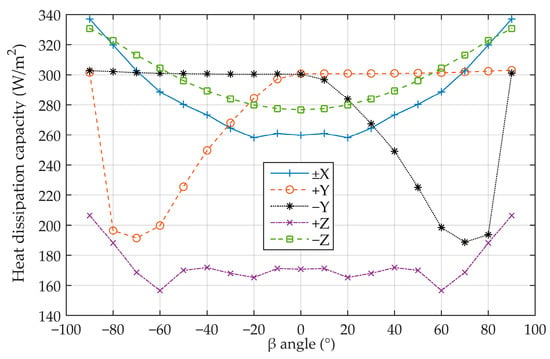
Figure 7.
Each panel’s heat dissipation.
The β-angle has a significant impact on the ability of Y planes to dissipate heat. The satellite’s ability to dissipate heat is stable and powerful while it is in a shadowy area. When the Y planes were in an area that was sunny, the ability to dissipate heat gradually reduced as the β-angle (0° + 70°, 0° − 70°) increased. The heat dissipation ability increases gradually as the Y-angle increases (from −70° to −90°, from +70° to +90°), primarily because the solar panels’ rotation in relation to the sun blocks the Y planes; at 90°, the Y planes are completely blocked, which is equivalent to the Y planes being in the shadow area and represents the maximum heat dissipation capacity of the entire satellite; The heat dissipation capability of the +Z plane is the smallest and weakest of all planes because of the significant infrared heat flow to the ground. OSR absorbs little sunlight at various angles, and the variation in its ability to dissipate heat is negligible. The capacity of the X plane to dissipate heat remains constant.
According to the above analysis results, Table 4 shows the unit heat dissipation capacity of the heat dissipation surface in orbital space.

Table 4.
Average heat dissipation capacity of each surface.
Honeycomb sandwich construction is often utilized in the main bearing force of spacecraft, which has the features of light weight and many performance parameters that may be designed [25]. The communication test confirms that the satellite uses a honeycomb panel with an aluminum skin honeycomb sandwich structure as the cooling surface of the satellite, and the honeycomb structure is also the main bearing structure of the entire satellite because aluminum skin and aluminum honeycomb have good heat conduction characteristics. Table 5 displays the design criteria for each honeycomb panel. The heat of the satellite is transferred through the heat pipe network implanted in each honeycomb plate, allowing the heat to dissipate more quickly into space. Figure 8 shows the satellite bus’s primary structure.

Table 5.
Honeycomb panel parameters.

Figure 8.
The satellite bus’s primary structure.
3.1.2. Analysis of Temperature Distribution
This section uses thermal control design and FEM simulation to determine the temperature field distribution of the satellite, which is then used as the input condition for thermal deformation optimization design. A proven technique for obtaining temperature field distribution is FEM simulation, which is used in the CubeSat design simulation [26,27].
The influence of the temperature field on the deformation of the satellite structural body under varied working situations must be taken into account given the diversified load of the satellite and the complex task combination. The model’s construction and simulation, however, are too challenging. We select the variance between the high and low temperature conditions in orbit as the measurement of the thermal deformation scale to simplify the work requirements. Some working situations have a thermal environment that fluctuates between high and low temperatures. Since linear materials can approximate the thermal expansion coefficient of satellite materials, it can be assumed that the satellite’s thermal deformation varies between high-temperature and low-temperature situations.
The position of the internal heat source and the external heat flow largely determine the setting of the high and low temperature conditions. The temperature of the satellite will increase as the strength of the internal heat source increases and as the spacecraft’s ability to dissipate heat decreases. For now, it is set to a high temperature condition, and the opposite is true for a low temperature condition. Table 6 displays summary data on internal heat source power.

Table 6.
Summary statistics of internal heat source power.
The electric pusher module is only initiated in orbit control mode, not business mode, so the influence of electric propulsion is not taken into account when establishing the high and low temperature conditions. Terahertz was utilized as a payload for technical validation and is not activated in business mode; hence, in both hot and low temperature situations, there is no power usage. All on-board equipment, with the exception of terahertz, electric propulsion, and backup equipment, functions at its maximum power consumption under the high temperature condition, which replicates the maximum power consumption of all equipment in the on-orbit business mode. In the low temperature condition, the load on the satellite is shut down, the equipment of the satellite bus maintains the lowest energy consumption state, and the laser communication load is turned on to carry out the intersatellite alignment capture. In this condition, heating belts should be used for temperature compensation to keep the temperature of the equipment on the satellite higher than the lower limit of its temperature requirement, so as to ensure the safety of the satellite. According to statistics, the power consumption of the satellite is 2039.2 W under high temperature conditions and 887.6 W under low temperature conditions.
As can be seen from Table 6, the Ka-band phased array antenna, as the main load of the whole satellite, has high power consumption. When three phased array antennas work at the same time, the heat dissipation capacity of the antenna mounting surface is insufficient to meet the heat dissipation requirements of phased array antennas. Phased array antennas are easy to overheat when working in high temperatures. It needs to be coupled with ±Y planes to dissipate heat generated by the high-power operation of phased array antennas. With the phased array antenna as the reference feature point, the minimum heat dissipation capacity of +Z and ±Y cooperative honeycomb planes was defined as the high temperature condition.
Figure 9 shows the corresponding heat dissipation capabilities of the +Z and ±Y planes. When the β angle is ±60°, the heat dissipation capacity of the +Z and ±Y planes is the lowest. Therefore, the external heat flow condition is selected as the analysis input for the high temperature condition when the β angle is ±60°.
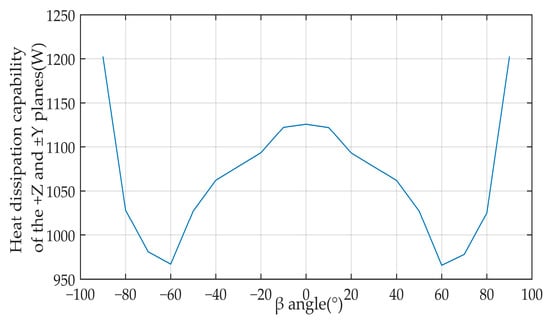
Figure 9.
Heat dissipation capability of the +Z and ±Y planes.
Figure 10 shows the heat dissipation capacity of the satellite at different β angles. In the range of β angle −60~+60°, the heat dissipation capacity of the satellite is stable. When β angle is greater than ±60°, the heat dissipation capacity of the satellite is continuously enhanced due to the solar panel blocking the external heat flow of the sun. According to the β angle simulation, when the β angle is ±90°, the heat dissipation capacity of the satellite is the strongest, so define that condition as the low temperature condition.
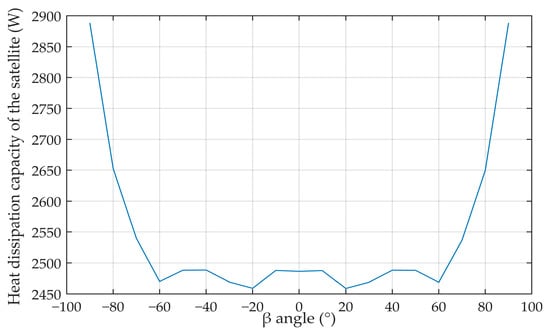
Figure 10.
The heat dissipation capacity of the satellite.
The temperature distribution under high- and low-temperature conditions is shown in Figure 11.
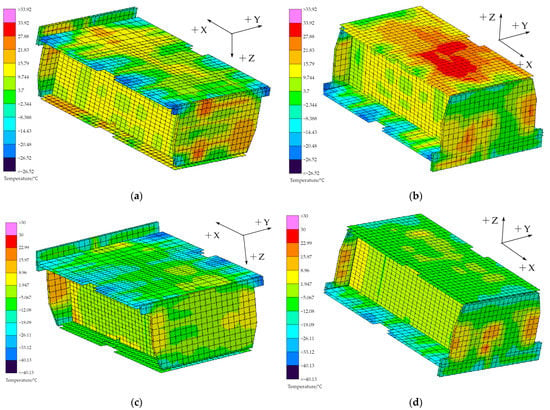
Figure 11.
Temperature distribution under high-temperature and low-temperature conditions: (a) −X\−Y\−Z structural plate at high-temperature condition; (b) +X\−Y\+Z structural plate at high-temperature condition; (c) −X\−Y\−Z structural plate at low-temperature condition; (d) +X\−Y\+Z structural plate at low-temperature condition.
3.2. Thermal Deformation of Satellite Bus
Typically, the satellite’s structure is placed with the communication load and the star sensor load separately. Using this design strategy, we compute the impact of the satellite’s thermal deformation on the angle variation between the laser and the star sensor load.
With the maximum temperature difference obtained by simulation in high and low temperature conditions as input, the satellite finite element simulation model is used to calculate the thermal deformation of the satellite, as shown in Figure 12. The maximum displacement of the satellite during low- and high-temperature fluctuations is 0.689 mm. Both the laser communication load and the star sensor are directly mounted on the +X honeycomb structure. The flatness of the +X honeycomb structure will change under the coupling effect of the whole satellite thermal deformation, and the normal vector of the mounting surface will change due to the change in the flatness of the +X honeycomb structure, resulting in changes in the laser communication load and the pointing of the star sensor.
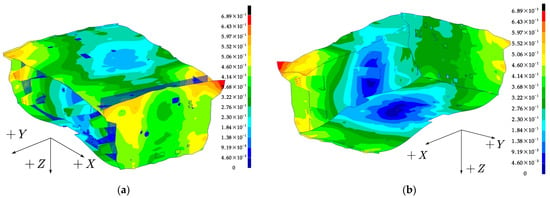
Figure 12.
Calculation results of the maximum thermal deformation of the main structure of the satellite in orbit (a) +X, +Y, −Z plane; (b) −X, −Y, +Z plane.
The coordinates of the laser communication load and star sensor installation point after deformation are extracted from the finite element model. The plane corresponding to the point coordinates fitted by the least square method is the loading surface of the star sensor and laser communication. The included angle variation between the fitted plane vectors is the one between the star sensor and the laser communication load caused by temperature change. The variation of the normal vector angle variation between the star sensor and the laser communication load mounting surface obtained by fitting here is 113.58″.
3.3. Multi-Objective Optimization Design
3.3.1. The Overall Optimized Design Idea
Through the above simulation calculation, we can see that the angle change between the laser communication load and the star sensor is greatly affected by the thermal deformation of the satellite, so it is necessary to control the thermal deformation of the satellite. The most effective thermal deformation control method is to precisely control the temperature variation range of the whole satellite structure. However, the characteristics of high heat consumption of communication satellites make all the masks of satellite bodies need to be designed as cooling surfaces. This design method can meet the temperature balance of the whole satellite under high-temperature conditions, but the satellite has a variety of different power consumption scenarios, such as automatic standby mode after the main load is out of the range of the monitoring and control station, orbit maintenance mode, etc. The change in internal heat source power and the constant heat dissipation area make it difficult for the satellite to maintain the same temperature environment. At the same time, different external heat flow conditions will also affect the temperature of the satellite. The above reasons cause the temperature distribution of satellite bodies to change greatly. The resources for satellite active temperature control and temperature measurement are limited, and the cost of accurately controlling the temperature change of satellite body structure is high.
Based on the above analysis, a local accurate thermal deformation control method based on the design of a flexible isolation common physical reference is proposed in this study to reduce the influence of the whole satellite temperature variation on the laser communication load alignment uncertainty region and acquisition time.
In this method, the star sensor and laser communication are connected and installed through the same physical reference bracket with stable thermal deformation. The support material uses 55% SiC/Al with a large elastic modulus, high thermal conductivity, and a small linear expansion coefficient. A large elastic modulus is beneficial to improve its adaptability to dynamic characteristics and reduce weight. A smaller linear expansion coefficient is conducive to reducing the thermal deformation of the support. High thermal conductivity is conducive to the uniform temperature design of the support, reducing the temperature fluctuation of the support and thus reducing the thermal deformation of the support.
Secondly, it provides flexible isolation with the satellite bus to reduce the influence of the temperature fluctuation of the whole satellite on the temperature fluctuation of the support and reduce the influence of the thermal deformation of the whole satellite on the uncertain region of laser communication alignment. The material for flexible isolation is a flexible isolation device made of silicone rubber material commonly used in aerospace to isolate the influence of thermal deformation of the satellite bus on laser and satellite sensitivity. The appearance of the isolation material is shown in Figure 13.

Figure 13.
Flexible isolation device.
Finally, satellite load isolation was adopted to narrow the thermal control area, reduce the difficulty of thermal control, accurately control the temperature of the isolated physical reference support, and reduce the influence of the temperature change of the physical reference support.
3.3.2. Multi-Objective Optimization Design of Reference Support
The design of the reference bracket is restricted by many factors, and how to balance the selection of all factors needs to be carried out according to the results of topology optimization.
The first factor to consider is mass constraints. Aerospace products strive to meet the design requirements with a smaller structural mass. In this paper, the density method is adopted for topology optimization, and the minimum total volume is set as the optimization objective.
The displacement of the reference bracket caused by the whole satellite temperature field is taken as the displacement input of the reference bracket.
The precise temperature control of the reference bracket can be achieved within the fluctuation range of ±1 °C. According to the temperature fluctuation range as the temperature data, the thermal deformation caused by the temperature fluctuation of the bracket is calculated, and the deformation caused by the bracket itself is taken as the constraint to constrain the changes in the optical axis angle of the star-sensor and laser communication load.
The above constraints can be used to optimize the design of the reference bracket when determining the location of the star sensor and laser communication load on the satellite bus. The current topology optimization design method is often used to optimize the design of spacecraft weight reduction, which can deal with this kind of problem well [17,28]. The relative position relationship between the star sensor and the laser communication load on the satellite is also one of the variables affecting the design result. In this paper, the installation location of the star sensor is also taken as an optimization objective. Laser communication load turntables usually have a universal frame structure, a single reflector structure, and a latent structure. The laser communication load in this system adopts the latent configuration, as shown in Figure 14. During the layout of the satellite, the installation position of the star sensor and the avoidance of the rotation range of the rotating laser communication load turntable should be considered. In this paper, the range above the rotating area of the rotating table of the rotating laser communication load is set as the area where the star sensor can be laid out. With as the optimization variable, topology optimization iterations are carried out for different positions. The mathematical relationship expression is shown below.
where the represents the above equation represents the total volume, represents the displacement constraint, represents the fundamental frequency constraint, and represents the upper and lower limits of the design objectives and design variables.
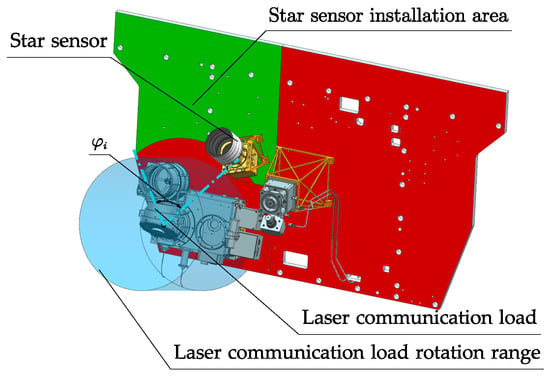
Figure 14.
Area where a star sensor can be installed.
Figure 15 shows the principle of optimization iteration. The optimization of the position determined by the star sensor is transformed into a routine topology optimization process. In addition to the topology optimization process, we add a loop about the optimization variable.
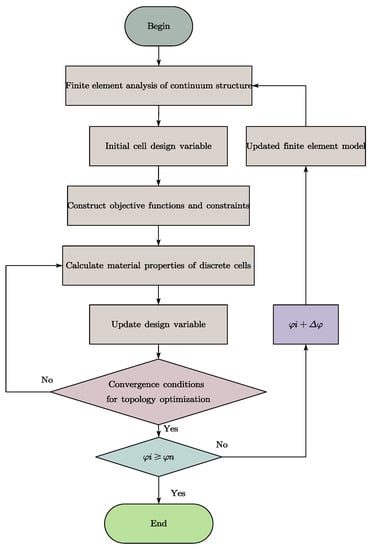
Figure 15.
Optimization process.
The is traversed with a certain step size, and the topology optimization results of each position are compared, judged, and selected. The optimization analysis results are shown in Figure 16, and density distributions under different conditions are obtained.

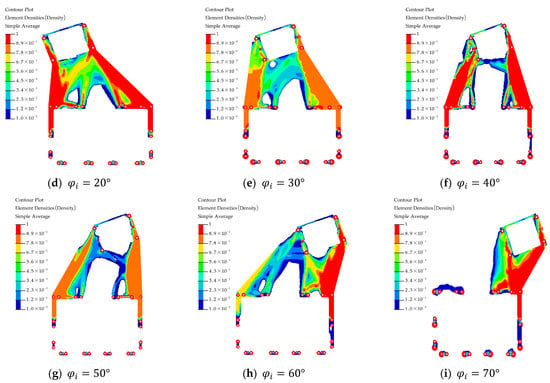
Figure 16.
Cloud image of the topology optimization results.
The total volume results of topology optimization were extracted and shown in Figure 17. With the change in angle, the total volume has a trend of first rising and then falling. When or , the total volume is the smallest. However, in the process of practical engineering application, not only the mathematical optimization results but also other engineering constraints that are not easy to quantify should be considered. When approaches 70°, the distance between the star sensor and the thruster is relatively close, and the high-energy substances ejected by the thruster may affect the normal operation of the star sensor. Therefore, optimization results in the range of 50~70° are not selected for actual use. In the range of 0° to 20°, the overall volume tends to rise. However, since the satellite mounting surface is suspended at 0°, the dynamic response of the whole satellite launching process will be harsh. Considering the compromise, the support is designed under the condition that .
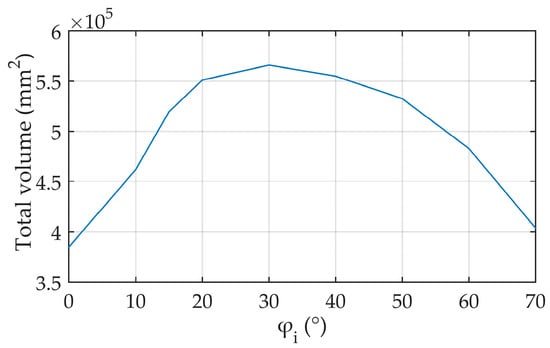
Figure 17.
Total volume change.
It can be seen from the schematic diagram of topology optimization results at that the area with high unit density presents a sandwich shape with high density on two sides and low density in the middle. According to this feature, an I-beam was adopted to design the section in the process of designing the support, and the layout of the stretching position was carried out according to the optimized cloud map. The size selection of the I-beam section is further carried out by size optimization. The size optimization model is shown in Figure 18. Three optimized areas, A, B, and C, are set in the model, corresponding to the blue, green, and red areas, respectively. One-dimensional pbarl elements are used to calculate the three regions, and the parameter definition of the element section is shown in Figure 18.
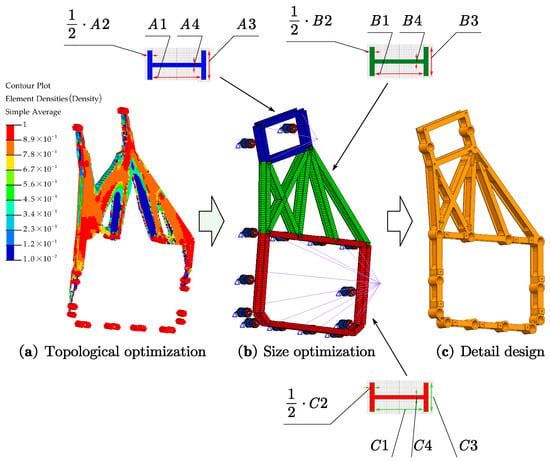
Figure 18.
Optimal design process for thermal deformation control support.
To facilitate the realization of processing technology, the total thickness of the three areas is set to be consistent, namely , .
The size optimization problem can be expressed by the following mathematical expression:
Table 7 presents the optimization results for the 12 variables and the results for volume, first-order mode, and maximum displacement sensitivity. Through Table 7, we can see the degree of contribution of each size to the optimization goal. According to the optimization results obtained, a detailed design can be carried out.

Table 7.
Size optimization results and sensitivity.
3.4. Thermal Deformation Analysis after Optimization
3.4.1. Support Temperature Control Design
The temperature fluctuation of the reference support is controlled by precise temperature control.
The design of the two heating circuits is shown in Figure 19a. The heating belts H1~H9 form a heating circuit in series, with a total resistance of 293.9 Ω, and the heating belts H10~H23 form another heating circuit in series, with a total resistance of 244.8 Ω. The heating belts are set on the web plate of the I-beam by means of adhesive. The size and resistance of the heating belt are shown in Table 8. The 28 V satellite bus voltage powers the two heating circuits. The closed-loop control of temperature is realized by setting up two temperature measuring circuits. The temperature sensor is pasted at T1 and T2 in Figure 19a. In order to maintain temperature stability, the reference bracket is coated with 20 units of multi-layer insulation components, the outermost layer being F46. The completion state of thermal control is shown in Figure 19b.
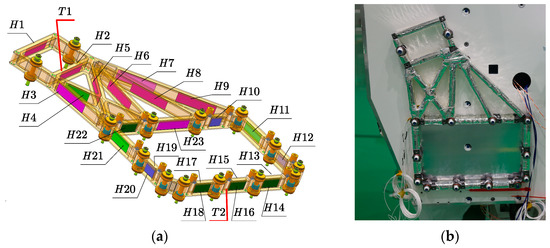
Figure 19.
Reference support for thermal control design and implementation status: (a) active temperature control design; (b) completion state of thermal control.

Table 8.
Heating belt design parameters.
The simulation of the temperature control effect is shown in Figure 20, and the temperature of the support can fluctuate between 19.86 °C and 22.18 °C. The temperature is used as the input condition for the calculation of the pointing variation of both the star sensor and the laser communication load in the whole satellite model.
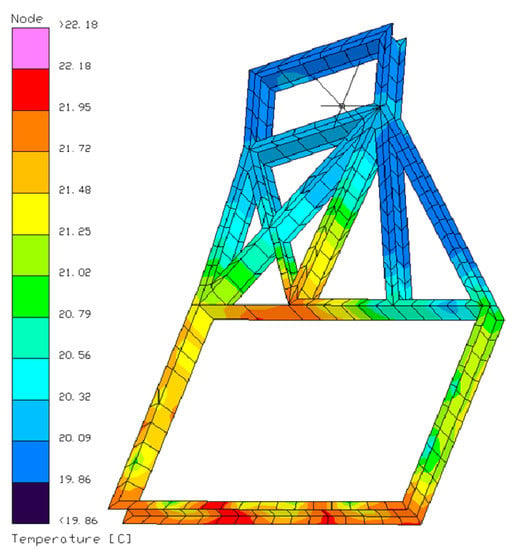
Figure 20.
Temperature cloud map of deformation control support.
3.4.2. Thermal Deformation Analysis Results
According to the temperature of every single machine and plate as input, the angle variation of the laser communication load caused by thermal deformation and the star sensor in the full satellite simulation model is calculated. The full satellite simulation model is shown in Figure 21. The cloud map of thermal deformation is shown in Figure 22.
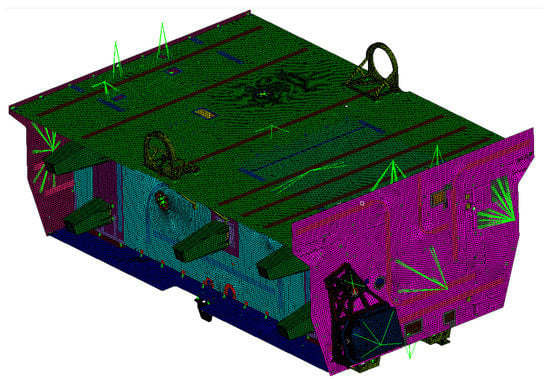
Figure 21.
Full satellite simulation model.
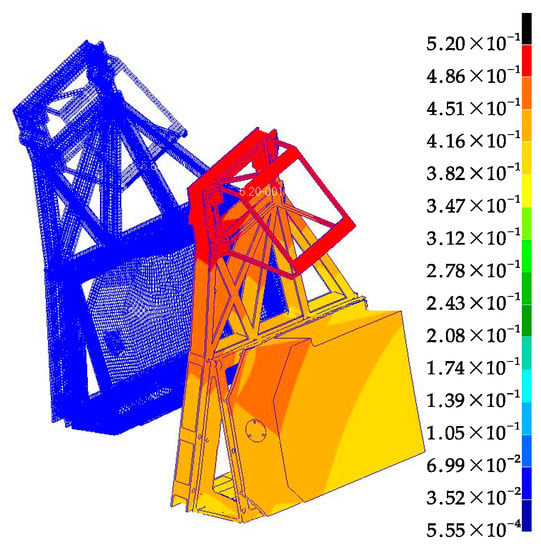
Figure 22.
Simulation results of thermal deformation.
The coordinate values after thermal deformation of the installation points of the star sensor and laser communication loads extracted after calculation are shown in Table 9. ID indicates the number of the installation plane point.

Table 9.
Coordinates after thermal deformation of the installation points of the star sensor and laser communication load.
The least square method was used to fit the expressions of two device installation planes, as shown in (5).
The , , and parameters of the two planes are shown in Table 10.

Table 10.
Fitting parameters of the installation plane.
The included angle variation between the two plane normal vectors fitted after thermal deformation can be calculated as 14.25″. The calculation results show that the optimization scheme has an obvious effect.
4. Tests
4.1. Ground Tests
To ensure the accuracy of the results of the optimized design, the low-orbit communication test satellite underwent a thermal deformation test. Theodolite calibration is used to measure the angle shift between the laser communication load prisms and the star sensor. It is challenging to implement real-time regulation and protection of theodolite equipment in a vacuum tank due to testing conditions. Hence, by heating the satellite temperature hauled up under the ambient temperature of 20 °C in the ground atmosphere backdrop, the effect of thermal deformation on prism angle fluctuation between the star sensor and laser communication burden is determined. The results can still be utilized to assess the effectiveness of design and optimization even though the distribution of the temperature field in the ground environment differs from that of the satellite in orbit.
We set up three ground-test schemes to judge the effectiveness of the optimized design. In test scheme 1, no optimized support was used. The laser communication load and star sensor were directly installed on the honeycomb panel of the satellite structure. The on-board equipment was opened according to the high temperature conditions in orbit, and the temperature of the satellite structure was increased by this temperature pull-up method. In test scheme 2, optimized support is adopted, and the laser communication load and star sensor are directly installed on the optimized support. A flexible isolation device is used to connect the optimized support and satellite, and the heating mode is the same as that of test scheme 1. The installation mode of test scheme 3 is the same as that of test scheme 2. In addition to the heating mode adopting the same working mode of equipment under high temperature conditions as that of schemes 1 and 2, all heating belts on the satellite are also turned on to maximum pull-up satellite structure temperature and test the ultimate capacity of the optimization effect of the satellite support. The purpose of setting test scheme 3 is mainly because the temperature distribution in the ground test is quite different from the actual distribution in orbit. Therefore, the problem of insufficient verification in the ground test is solved by the maximum pulling up of the satellite temperature field.
Table 11 shows the temperature telemetry data of some equipment in the three ground test schemes. The temperature of test scheme 1 and test scheme 2 is similar, so it can be considered that the difference between them is caused by the support optimization scheme.

Table 11.
Temperature data in the 3 ground test schemes.
The calibration site is shown in Figure 23. Theodolites A and B are used to target the star-sensor prism, and theodolites C and D are used to target the laser communication payload prism.

Figure 23.
Calibration site of low-orbit communication test satellite.
Table 12 shows the calibration results of the prism. In test scheme 1, the star-sensor and laser communication loads are respectively installed on the satellite structure plate. The maximum angle variation of the prism before and after the temperature pull-up test is 117.74″, which appears on the X-axis of the star sensor. In test scheme 2, the maximum angle variation is 10.72″ when the on-board equipment is turned on in high temperature conditions, which appears on the Z-axis of the star sensor. The comparison between scheme 1 and scheme 2 shows that the optimal design obviously reduces the influence of the thermal deformation of the satellite on the angle variation between the prism of the star-sensitive bracket and the laser communication load. Scheme 3 shows that under the condition of maximum temperature pull-up during the ground test, the maximum angle variation between prisms appears on the star-sensor’s Y-axis, with a maximum value of 31.6″. When converted into radians, the result is 0.1532 mrad. Under such extremely strict temperature test conditions, the results are close to the requirement of 0.16 mrad assigned in Section 2, which further proves the effectiveness of the optimized design.

Table 12.
Prism angle calibration results.
4.2. In-Orbit Tests
On 20 May 2022, the low-orbit communications test satellite 03/04 was put into orbit. On 20 July, the first chain was started, and on 21 July, the first error-free transmission was finished. A 145-min period of stable and error-free connection was accomplished on 27 July. By 27 July, 14 bidirectional captures had been completed after the first chain establishment, with 10 of those taking place in under 30 s (71.4%). The four capture times that were longer than 30 s all occurred early in the test, and after the test’s full completion on 23 July, all capture times were within the required range of 30 s. Table 13 displays statistics regarding capture times. The satellite bus’s thermal deformation control optimization design was shown to be successful by the on-orbit acquisition time.

Table 13.
Statistical table of capture time in orbit.
5. Conclusions
This paper analyzes and assigns various factors affecting the uncertain region of satellite laser communication loads in orbit in order to meet the requirements of rapid acquisition and chain construction in the business mode of laser communication satellites, reduce the acquisition time of laser communication loads between satellites, and narrow the orientation of laser communication loads to the uncertain region of the optical axis. As a result of the thermal deformation of the satellite bus, the angle variation between the laser communication load and star sensor should be limited to 0.16 mrad.
The satellite’s temperature field in orbit under high- and low-temperature situations is obtained by simulation analysis. As the input boundary conditions for satellite thermal deformation analysis, it is found that the influence of thermal deformation on the angle variation between the laser communication load and the star sensor installed on the honeycomb sandwich structure does not conform to the requirement of index allocation. It is necessary to optimize the thermal deformation control of the angle variation between the laser communication load and the star-sensor optical axis.
A local accurate thermal deformation control method based on the design of a flexible isolation common physical reference is proposed in this study to reduce the influence of the whole satellite temperature variation on the laser communication load alignment uncertainty region and acquisition time. The goal of the optimization design is to connect the laser communication load and the star-sensor load using the same physical reference bracket and stable thermal deformation with 55% SiC/Al material. Second, it uses flexible isolation with the satellite bus to lessen the impact of the entire satellite’s temperature variation on the support’s temperature swings as well as the impact of the entire satellite’s thermal deformation on the uncertain region of laser communication alignment. Finally, satellite load isolation was used to reduce the thermal control challenge, precisely manage the temperature of the isolated physical reference support, and lessen the impact of the physical reference support’s temperature fluctuation.
Topology optimization is used to determine the relative placement of the star sensor and the laser communication load and is the best result we select while taking into account the mass of the structure, the radius of rotation, and other engineering considerations. The reference bracket adopts an I-section design based on the structural topological relationship found through topological optimization, and size optimization establishes the critical dimensions. The combination of active and passive temperature control is adopted to control the temperature within the range between 19.86 °C and 22.18 °C so as to reduce the deformation of the reference structure itself. The thermal deformation between the optimized laser communication load and the star sensor angle variation is decreased to 14.25″ according to the entire satellite simulation analysis of the modified structure.
After completing the optimized design, we carried out ground and space test validations. Compare the schemes after and before optimization; the maximum angle variation induced by temperature change dropped from 117.74″ to 10.72″ through the ground temperature deviation and prism calibration test by heating the satellite temperature hauled up under the ambient temperature of 20 °C in the ground atmosphere backdrop. Under the condition of maximum temperature pull-up, the maximum angle variation is 0.1532 mrad, close to the requirement of 0.16 mrad, which further proves the effectiveness of the optimized design. The on-orbit alignment test confirms that the required capture time of 30 s is met. After launch, by 27 July, 14 bidirectional captures had been completed after the first chain establishment, with 10 of those taking place in under 30 s (71.4%). The four capture times that were longer than 30 s all occurred early in the test, and after the test’s full completion on 23 July all capture times were within the required range of 30 s. The in-orbit acquisition time test results demonstrate that the uncertain region of the satellite satisfies the design specifications and that the thermal deformation stability between the satellite star sensor and laser communication load satisfies the specifications.
Author Contributions
Conceptualization, Y.S. and S.C.; methodology, Y.S. and Y.W.; software, Y.S. and M.Y.; validation, Y.S.; formal analysis, Y.S.; investigation, Y.S.; resources, S.C.; data curation, Y.S. and M.Y.; writing—original draft preparation, Y.S.; writing—review and editing, S.C. and J.Y.; visualization, Y.S.; supervision, S.C. and L.Z.; project administration, L.Z.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Jilin Province Science and Technology Development Plan Project of China, Grant No.20210509052RQ.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Garlinska, M.; Pregowska, A.; Masztalerz, K.; Osial, M. From Mirrors to Free-Space Optical Communication—Historical Aspects in Data Transmission. Future Internet 2020, 12, 179. [Google Scholar] [CrossRef]
- Sinha, S.; Kumar, C.; Armghan, A.; Singh, M.; Alsharari, M.; Aliqab, K. Capacity Enhancement Analysis of an OAM-OFDM-SMM Multiplexed Free Space Communication System in Atmospheric Turbulence. Appl. Sci. 2023, 13, 3897. [Google Scholar] [CrossRef]
- Garlinska, M.; Pregowska, A.; Gutowska, I.; Osial, M.; Szczepanski, J. Experimental Study of the Free Space Optics Communication System Operating in the 8–12 Μm Spectral Range. Electronics 2021, 10, 875. [Google Scholar] [CrossRef]
- Demers, F.; Yanikomeroglu, H.; St-Hilaire, M. A Survey of Opportunities for Free Space Optics in next Generation Cellular Networks. In Proceedings of the 2011 9th Annual Communication Networks and Services Research Conference, CNSR 2011, Ottawa, ON, Canada, 2–5 May 2011; pp. 210–216. [Google Scholar]
- Chaudhry, A.U.; Yanikomeroglu, H. Laser Intersatellite Links in a Starlink Constellation: A Classification and Analysis. IEEE Veh. Technol. Mag. 2021, 16, 48–56. [Google Scholar] [CrossRef]
- Chaudhry, A.U.; Yanikomeroglu, H. Free Space Optics for Next-Generation Satellite Networks. IEEE Consum. Electron. Mag. 2021, 10, 21–31. [Google Scholar] [CrossRef]
- Carrasco-Casado, A.; Shiratama, K.; Kolev, D.; Trinh, P.V.; Ishola, F.; Fuse, T.; Toyoshima, M. Development and Space-Qualification of a Miniaturized CubeSat’s 2-W EDFA for Space Laser Communications. Electronics 2022, 11, 2468. [Google Scholar] [CrossRef]
- Toyoshima, M.; Takayama, Y.; Takahashi, T.; Suzuki, K.; Kimura, S.; Takizawa, K.; Kuri, T.; Klaus, W.; Toyoda, M.; Kunimori, H.; et al. Ground-To-Satellite Laser Communication Experiments. IEEE Aerosp. Electron. Syst. Mag. 2008, 23, 10–18. [Google Scholar] [CrossRef]
- Naghshvarianjahromi, M.; Kumar, S.; Deen, M.J. Free Space Ground to Satellite Optical Communications Using Kramers–Kronig Transceiver in the Presence of Atmospheric Turbulence. Sensors 2022, 22, 3435. [Google Scholar] [CrossRef]
- Wang, J.; Lv, J.; Zhao, G.; Wang, G. Free-Space Laser Communication System with Rapid Acquisition Based on Astronomical Telescopes. Opt. Express 2015, 23, 20655. [Google Scholar] [CrossRef]
- Wang, J.; Kahn, J.M.; Lau, K.Y. Minimization of Acquisition Time in Short-Range Free-Space Optical Communication. Appl. Opt. 2002, 41, 7592–7602. [Google Scholar] [CrossRef]
- Nielsen, T.T. Pointing, Acquisition and Tracking System for the Free Space Laser Communication System, SILEX. In Proceedings of the Free-Space Laser Communication Technologies VII. SPIE: Bellingham, WA, USA, 1995; Volume 2381, pp. 194–205. [Google Scholar]
- Bradford, W.H.; Delliponti, A.; Formel, R. Utilizing Additive Manufacturing of Semi-Crystalline Thermoplastics and Topology Optimized Generative Designs for Complex Small Satellite Bus Geometries. In Proceedings of the 36th Annual Small Satellite Conference, Logan, UT, USA, 6–11 August 2022. [Google Scholar]
- Ibrahim, S.A.; Yamaguchi, E. Thermally Induced Dynamics of Deployable Solar Panels of Nanosatellite. Aircr. Eng. Aerosp. Technol. 2019, 91, 1039–1050. [Google Scholar] [CrossRef]
- Lu, Q.; Xu, Q.; Yin, Y.; Luo, W.; Qian, Z.; Bai, G. Design and Verification of GF-7 Satellite Configuration Based on Common Reference Payload. Spacecr. Eng. 2020, 29, 31–36. [Google Scholar]
- Safarabadi, M.; Izi, H.; Haghshenas, J.; Kelardeh, H.K. Design of Micro-Vibration Isolation System for a Remote-Sensing Satellite Payload Using Viscoelastic Materials. Eng. Solid Mech. 2020, 8, 69–76. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, H.; Wang, C.; Zhou, L.; Yuan, S.; Zhang, W. A Review of Topology Optimization for Additive Manufacturing: Status and Challenges. Chin. J. Aeronaut. 2021, 34, 91–110. [Google Scholar] [CrossRef]
- Wu, J.; Sigmund, O.; Groen, J.P. Topology Optimization of Multi-Scale Structures: A Review. Struct. Multidiscip. Optim. 2021, 63, 1455–1480. [Google Scholar]
- Zhu, B.; Zhang, X.; Zhang, H.; Liang, J.; Zang, H.; Li, H.; Wang, R. Design of Compliant Mechanisms Using Continuum Topology Optimization: A Review. Mech. Mach. Theory 2020, 143, 103622. [Google Scholar]
- Marbel, R.; Yozevitch, R.; Grinshpoun, T.; Ben-Moshe, B. Dynamic Network Formation for FSO Satellite Communication. Appl. Sci. 2022, 12, 738. [Google Scholar] [CrossRef]
- Jin, J.; Tian, F.; Yang, Z.; Di, H.; Li, G. A Disruption Tolerant Distributed Routing Algorithm in LEO Satellite Networks. Appl. Sci. 2022, 12, 3802. [Google Scholar] [CrossRef]
- Yu, J.; Guan, Y.; Zhang, D.; Chen, S.; Zhao, C.; Zhang, L. Simulation and Experimental Research on the Disturbance Behavior of a Sun-Tracking Solar Array Driven by a Stepping Motor. Appl. Sci. 2021, 11, 9076. [Google Scholar] [CrossRef]
- Scheinfeild, M.; Kopeika, N.S.; Shlomi, A. Acquisition Time Calculation and Influence of Vibrations for Micro Satellite Laser Communication in Space. In Proceedings of the Acquisition, Tracking, and Pointing XV; SPIE: Bellingham, WA, USA, 2001; Volume 4365. [Google Scholar]
- Li, X.; Yu, S.; Ma, J.; Tan, L. Analytical Expression and Optimization of Spatial Acquisition for Intersatellite Optical Communications. Opt. Express 2011, 19, 2381–2390. [Google Scholar] [CrossRef]
- Bianchi, G.; Aglietti, G.S.; Richardson, G. Development of Efficient and Cost-Effective Spacecraft Structures Based on Honeycomb Panel Assemblies. In Proceedings of the 2010 IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2010. [Google Scholar]
- Mason, J.P.; Lamprecht, B.; Woods, T.N.; Downs, C. CubeSat On-Orbit Temperature Comparison to Thermal-Balance-Tuned-Model Predictions. J. Thermophys. Heat Transf. 2018, 32, 237–255. [Google Scholar] [CrossRef]
- Escobar, E.; Diaz, M.; Zagal, J.C. Evolutionary Design of a Satellite Thermal Control System: Real Experiments for a CubeSat Mission. Appl. Eng. 2016, 105, 490–500. [Google Scholar] [CrossRef]
- Zhao, J.; Yoon, H.; Youn, B.D. An Efficient Concurrent Topology Optimization Approach for Frequency Response Problems. Comput Methods Appl. Mech. Eng. 2019, 347, 700–734. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).