Abstract
The objective of this research was to assess the profitability of the housing development project located in Bangkok, and the perimeter areas are Nonthaburi, Samut Prakan, and Pathum Thani, which are the result of good construction management. Moreover, the researchers’ previous data were used to predict the profit for construction planning, using stepwise multiple regression analysis. Then, we found the profit equation of the housing development project and applied it to the optimization model to clarify the model by the case study. The case study has 427 units, dividing the house into three types, with an optimization performed using the GAMS tool. In the same way, according to this optimization, it can be divided into two scenarios: scenario one found the maximized profit of the project to be 1053.91 MB, and scenario two was the result of making a sensitive analysis of scenario one and found the maximized profit of the project to be 1054.18 MB, which is the best scenario for the maximized profit of the project, and so it is the best choice for construction planning. The research contribution in this model can be applied to other projects that are suitable for large or densely populated cities, such as Beijing, New Delhi, and others. In the Conclusion section, we offer recommendations and detail future work that the researchers have discussed and described for the benefit of future research in housing development projects.
1. Introduction
In Thailand, most housing development projects are located in large cities, such as Bangkok, Nonthaburi, Samut Prakan, and Pathum Thani. Moreover, they are highly competitive and complicated businesses that require large investments. There are various problems for housing development projects, i.e., for a new housing development project in general. There will be a chance of making profit mistakes due to inadequate construction planning. As a project owner, it is necessary to manage the housing development project to maximize profit and set the number of houses in each style, especially in the big projects that require tons of capital in terms of construction costs and land costs and other costs. In this case, there will be many relevant factors, such as the number of houses in the whole project, that determine the suitable number of houses to be built in each type, as well as the appropriate land size of each house type. These factors will affect the profit of the project. With this concern, the main objective of this research is to maximize the project’s profit by optimizing the construction quantity of each house type. This research employed a multiple regression analysis technique to determine the relationship between project profits and costs on various aspects of the project, among other variables. The data were collected by interviewing the owners or project managers, who are key factors that affect the project’s profit. Multiple linear regression analysis was used to determine the factors affecting the profit of housing development projects.
There have been studies employing multiple linear regression analysis for various purposes. A multiple linear regression analysis was used to investigate the housing unit price for one-bedroom and two-bedroom house units and compared it to the existing data for 15.5 years [1]. In addition, this approach was used to seek the relationship equation between the sale price of a house and house attributes [2]. Moreover, a multiple linear regression analysis was also employed to develop a model for predicting cost and duration based on the historical data of fifty-one old buildings. The multiple linear regression analysis effectively predicts cost, duration, or profit based on relevant variables of the particular issue [3]. After we obtained the results from the multiple linear regression analysis, we used the optimization model for the housing development project in Thailand. In this case, one project was selected as a case to investigate the maximum profit of the project and determine the number of houses of each type.
In the same way, previous research has shown the use of an optimization approach in construction business and housing development projects. The research with the purpose of the optimization model is to provide an answer to the condition of whether the housing development project is suitable for the Anugrah Dian Regency for market needs. Then, according to infrastructures, this location has the potential for housing development projects of Anugrah Dian Regency. Furthermore, the infrastructures can be easily accessed in the meantime for twenty minutes, such as office buildings, educational facilities, shopping centers, and airports, and finally, it can be included with the housing development project position of Anugerah Dian Regency as a suitable location for the housing development [4]. The study aimed at developing a multi-objective optimization method for design and building renovation and then was used in the actual renovation of an apartment building in Denmark that focused on increasing the efficiency of insulated roofs and exterior walls, as well as windows [5]. Pandit applied linear programming to find the maximized profit of house construction companies and shopping malls in the development area of a housing society [6]. This research aimed to decide on support in selecting the optimal contractor by using the analytic hierarchy process (AHP) with the PROMETHEE method for minimizing uncertainty and achieving the best possible project performance in construction projects under limited resources. Moreover, the emphasis is focused on these details: (1) prequalification and (2) evaluation of tenderers influencing the achievement of the optimal solution [7]. Laokhongthavorn and U-tapao applied operation research on solid waste disposal, for which there are two objective functions: to reduce operating costs and predict the expected net carbon dioxide equivalent (CDE) emissions and the uncertainty of solid waste or electricity that considers with the management of solid waste, such as landfill, incineration, composting, and recycling. Similarly, composting and landfilling are effective alternatives to Bangkok’s solid waste management system, where plant operators can implement the proposed optimization model under the uncertainty of waste disposal selection. Therefore, the most suitable waste, the operational costs, and the net CDE emissions will be lowered if the municipal solid waste can be reduced [8].
Another work was presented by Baldominos et al. [9] in 2018, who developed a machine learning application that identifies real estate opportunities and focused on real estate assets located in the Salamanca District in Madrid (Spain) by implementing a regression problem that tries to estimate the market price of a house. Ahmed applied the linear programming technique or the simplex method to find the maximized profit within the limited budget of the construction project [10]. The research aims to develop a model to describe both the role of the property manager and the role of the owner on net profit and net operating income, respectively. Moreover, it is capable of solving problems. Similarly, according to owners, revenue optimization is achieved by the increase in rent, which is the basis of net income. For the property managers, the collected rent is their source of income, and the net profit is optimized at an optimal number of locations [11]. Utiarahman and Rauf optimized the land based on the type of houses for the maximized profit of the project located in Gorontalo City, using linear programming and QM as tools, because this population has rapidly grown by [12].
The research contribution is derived from the statement of problems of housing development projects, i.e., for a new housing development project in general. Moreover, there is a chance for profit mistakes caused by inadequate construction planning. Therefore, this research contributes to assessing the profitability of a housing development project by using data collections with many house types and projects and by interviewing developers. Thus, it is difficult to collect data because it should take a long time to obtain them before applying multiple regression by stepwise multiple regression to find a representative of the data or the profit equation. After that, it can be applied to the optimization model by using a case study at a large city in Thailand to clarify the model. Finally, it will gain the final result as the maximized profit of the project, and this research gives importance to the housing development project business in Thailand and other countries, especially for this model to be applied to other projects in densely populated areas such as Beijing and New Delhi, making them likely to gain the most reasonable result.
The objectives of this research were as follows:
- To assess the profitability of the housing development project located in Bangkok and perimeter in Thailand.
- This model can be applied with construction management and resource allocation with the budget of project for the maximized profit of the project.
- This model can be applied to the other projects suitably for the large cities or densely populated cities which are similar to Bangkok and perimeter in Thailand.
2. Materials and Methods
This research aimed to assess the profit of a housing development project located in Bangkok and the perimeter areas Nonthaburi, Samut Prakan, and Pathum Thani, which is the result of good construction management. Moreover, the researcher used the previous data to predict profit for construction planning, using the multiple linear regression analysis technique. Then, the researcher found the profit equation of the housing development project and applied it to the optimization model to verify the model by the case study. The research process is explained in Figure 1.
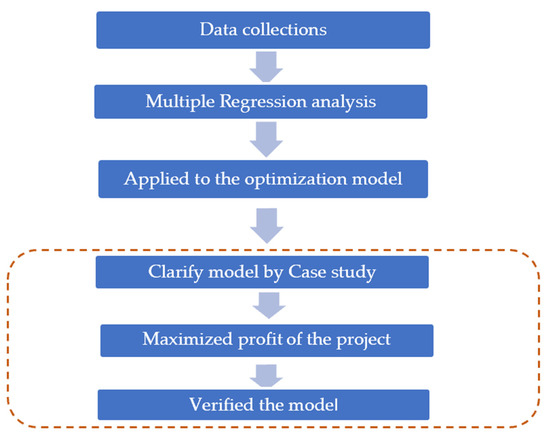
Figure 1.
Research procedure.
2.1. Data Collections
The data collected from the interviews with the owners or the senior executives with many units or many projects for the housing development located in large cities are from Bangkok, Nonthaburi, Samut Prakan, and Pathum Thani. The data that are difficult to access; therefore, it takes quite a long time to request a meeting for direct interviewing, and we obtained the data with a total of 1649 units divided into 15 types from many projects in Bangkok and the perimeter in Thailand, as shown in Table 1.

Table 1.
Summary statistics of the housing development project situated in Bangkok and the perimeter.
To specify the number of house units as a sample size, the reference information of the population was collected from Real Estate Information Center, REIC [13]. The statistical data are shown in Figure 2.
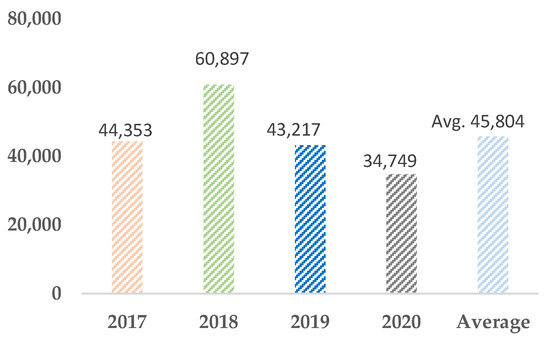
Figure 2.
Statistic of new houses for sale in Bangkok and perimeter of Thailand/years (units).
According to Figure 2, the average number of new houses for sale between 2017 and 2020 was 45,804 units. In order to determine the sample size, we used Yamane’s formular [14], which is presented in Equation (1).
where n = sample size required, N = number of people in the population, and E = allowable error %.
It reveals that the acceptable sample size was 397 units. However, the data collected for this study were 1649 units from many projects that are located in Bangkok, and perimeter areas are shown in Table 1.
Table 1 shows the data of the housing development project located in Bangkok and perimeters (Nonthaburi, Samut Prakan, and Pathum Thani) that were obtained from an interview with the owner of 1649 units from 15 types. Then, we used the data of variables used in the study of each house type from Table 1 by using these data for multiple regression analysis models in the next step.
2.2. Multiple Regression Analysis
The data were used for multiple regression by stepwise multiple regression to find a representation of the data, which is the profit equation.
A stepwise multiple regression analysis was carried out to investigate the relationship between independent variables and the dependent variable and use the regression tool in SPSS software to fit the sample data, and the values of coefficients of regression equations were computed. In the next step, the results obtained from the multiple regression analysis were applied to the optimization model for clarifying the model by the case study.
Therefore, this model can be applied to other projects, which may have conditions for use: the model is suitable for large or densely populated cities, such as Beijing, New Delhi, and others. Multiple regression analysis is used to forecast the relationship between independent and dependent variables in linear form, as shown in Equation (2) [15,16,17,18,19].
where = dependent variable, = independent variable, = intercept point, = regression coefficient of independent variables, and = random error.
Hypothesis testing used to determine whether the model is adequate for estimating dependent variable was developed. Null hypothesis (H0): β1 = β2 =…= βk = 0 (no model). Alternative hypothesis (H1): At least one βk ≠ 0 (model exist).
2.2.1. Application of Multiple Regression Analysis
Figure 3 shows that the dependent variable is profit/type and the independent variables used in this study consisted of seven variables.
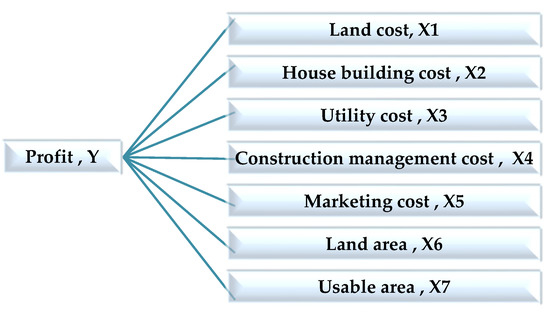
Figure 3.
Dependent variable code and independent variables code of multiple regression analysis in research.
Table 2 shows that the multiple regression is 0.968, which shows that the correlation between the independent and dependent variables is positive, which is usually that the value R2 range will be 0 < R2 < 1. The coefficient of determination from regression result is 0.937. This means that the combined influence of seven independent variables can explain 93.7% of profit variations.

Table 2.
Model summary.
Table 3 shows the results from the multiple linear regression by displaying the results of the coefficients from each independent variable, where the intercept value is −384,364.26. Then, it represents the value of Y when the values of all independent variables are zero. Moreover, according to hypothesis testing, this study was assigned a 95% confidence level, which means that the p-value output of variables will not exceed 0.005. As shown in Table 3, there are two variables with a p-value < 0.005, which are land cost and house building cost. They are variables that yield significant value in this multiple linear regression analysis. As a result, land cost has the highest influence on profit or the dependent variable, followed by the house building cost. In Table 3, the multiple regression equation for the profit of each type of house is elaborated. Then, Equation (3) was obtained, and the researchers applied this equation in the next step of research, which is the optimization model.

Table 3.
Summary of model variables.
Profit/type = −384,364.26 + 1.486 × (Land cost/type) + 0.919 × (House building cost/type)
2.2.2. A Graph Comparing the Predicted Profit/Type Values from the Regression Models with the Actual Profit/Type Values
Figure 4 shows the comparison between actual data and the result of the predicted equation from the multiple linear regression analysis. Moreover, it was found that the prediction equation can predict the result of profit/type quite accurately, with 93.73%, or the coefficient of determination (R2) = 0.9373.
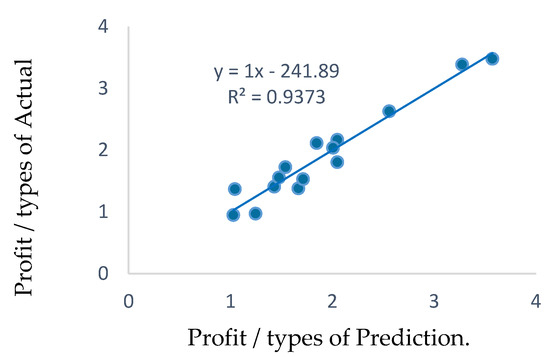
Figure 4.
The accuracy of prediction equation for profit/type.
2.3. Optimization Approach
Optimization involves solving mathematical problems to achieve the optimal result of a set of variables that will allow the objective function to be maximum or minimum [15,16,19,20,21]. Generally, the purpose of optimization is to find the maximum value or the minimum value of a given objective function which has the following components:
- Designed Variable
The designed variable refers to the variable that is the answer to a problem solved, and the designed variables are defined to clearly describe the nature of the engineering system, such as size, weight, and quantity.
- 2.
- Objective Function
The objective function is a function in which we want to find the minimum or maximum value by defining the objective function in the form of mathematical equations. Therefore, we can write the objective function in the form of a mathematical equation as Z = f(x), where X = x1, x2, …, xm.
- 3.
- Constraints
Constraints are conditions or constraints of an objective function relating to variables selected in the objective. The objective function must correspond to given constraints, and it can be classified according to two types of signs: equality constraints (=) and inequality constraints (≤, ≥).
- 4.
- Sign Restrictions
The sign restriction is associated with each variable; each variable must be non-negative.
Linear Programming
Linear programming is an optimization technique that is used for problems with objective functions and constraints as linear functions, where the equations of constraints are in the form of equality constraints or inequality constraints [15,16,19,20,21].
The objective function is defined as the maximization problem, which has the standard form of Equation (4):
3. Case Study
This research’s main objective was to determine the maximized profit of housing development projects, as this is the most important issue in the housing development project business. Therefore, the optimization method in resource allocation is required to determine the amount of house construction in each house type to achieve the main objective, which is to maximize the project’s profit.
This model was implemented by the case study, which is the housing development project located in Bangkok, Thailand, and the data were collected from the interview. The owner of the project, who has 427 units, was recruited.
This model uses the results of the multiple regression analysis from the previous stage that was applied to the model and implemented. Moreover, the model used by the case study is used to clarify the model, and the main purpose is to assess the profitability of the housing development project located in Bangkok and perimeter in Thailand. In addition, the result of this model is the maximized profit of the project from the determination of the house type under the appropriate budget in each aspect of the project. In this case, the model consists of three main parts: (1) decision variables, (2) constraints functions, and (3) objectives functions. Therefore, all three main parts are explained, with the details being offered in Section 3.1–3.4, and the model results are presented in Section 4.
The houses were divided into three house constructions: type one, type two, and type three. The information on each house type is shown in Table 4.

Table 4.
Data collection of house types.
3.1. Decision Variables
For , j is the set of house types; is the number of house-type one; is the number of house-type two, and is the number of house-type three.
3.2. Coefficients of the Decision Variables
The coefficients of decision variables code for this research as shown in Figure 5.
Figure 5.
Chart of coefficients of decision variables code for house types.
3.3. Constraint Functions, or Limiting Functions
Constraint Functions, or limiting functions, are included in the costs of the house type and the land area of the house type; all units in the whole project consist of 427 units.
Equation (5) is a constraint equation, which limits the functions of this project budget, and Figure 5 shows a chart of coefficients of decision variables’ codes for house types.
The budget of each constraint or the right-hand side of the equation is listed below, in Equations (6)–(17).
where aij is the coefficients of constraint for cost type i of house type j, is the number of house-type one, is the number of house-type two, and is the number of house-type three.
3.4. Objective Function
The objective function in this research was to find out the maximized profit of the project by using the multiple linear regression results and applying them to the optimization model to investigate the maximized profit of the project, which is derived from determining the number of houses of each type to be constructed, as shown in Equation (18):
where the is set of house-type j, (j = 1, 2, …, n); and : is set for cost type i of house-type j, (i = 1, 2, …, m).
4. Results and Discussion
Figure 6 shows the results of the optimal solution from the analysis by using the GAMS software under all constraints. The maximized profit to be obtained is THB 1053.91 million. Then, it must construct each type of house as follows: 211 units of house-type one, 100 units of house-type two, and 116 units of house-type three, respectively.
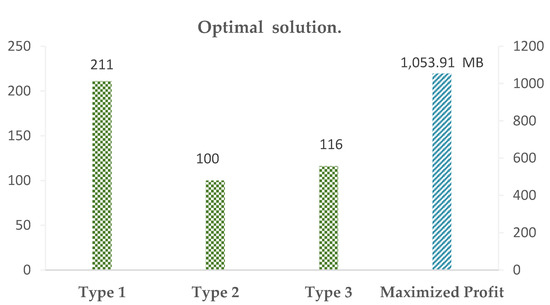
Figure 6.
Optimal solutions.
4.1. Verification of the Optimization Model
The validity of the optimization model is an important process for the model performance measures. The percentage error (PE), as shown in Equation (19), was used to verify the result of the comparison between the profit of optimal solution and actual data [22,23].
Figure 7 represents the number of houses for each type of actual data and the optimal solution or results of the optimization model. Then, as presented in Table 5, the profit/type data from the actual data (Table 4) were calculated with the number of houses for each type of the results from the optimization model, which is 211 for type one, 100 for type two, and 116 for type three. Therefore, the profit of the project was 967.36 MB, and that was very close to the project’s profit of the actual data (963.97 MB). When verifying the model, it was found that the percentage error accounted for 0.35%, as shown in Table 5.
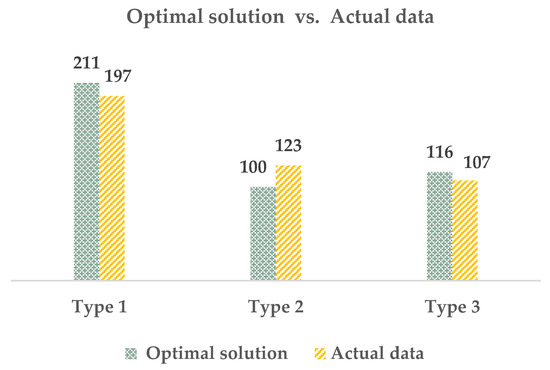
Figure 7.
Comparison of number house types between optimal solution with actual data.

Table 5.
The percentage error of the project’s profit between actual data with optimal solution.
Table 5 shows that the percentage error of the optimization model was 0.35%. The number is acceptable since it is within +/−10% [24].
4.2. Sensitivity Analysis
The sensitivity analysis of the project was used to demonstrate how parameters should be changed for better results [15,16,19,20,21] since the researchers aimed to determine the maximized profit of the project. Therefore, the sensitivity analysis was employed to increase the objective function value. The two project planning scenarios were introduced, as shown in Table 6.

Table 6.
Sensitivity analysis results and scenarios’ applications of the model.
4.2.1. Scenario One
If the maximized profit of the project is required to be 1053.91 MB, the required house-type one must be 211 units, house-type two is 100 units, and house-type three is 116 units.
4.2.2. Scenario Two
If the maximized profit of the project is required to be 1054.18 MB, the required house-type one must be 214 units, while house-type two must be 96 units and house-type three must be 117 units. Table 6 shows the sensitivity analysis results that are expected to be beneficial for the owner or decision maker in planning a construction project, as shown in this table, and it depends on the constraints of the owner with the question, what is the difference in the demand for planning the numbers of houses in each type and which direction will affect the maximum profit of the project?
According to the final result of this research, we found the maximized profit of the housing development project where the model was clarified by using a case study located in Bangkok and the perimeter in Thailand, as mentioned, and we verified the model for gaining satisfied answers. Then, it is extremely important and beneficial to the housing development of both the project in Thailand and other projects in the world that the model can be used for large and densely populated cities to obtain the most suitable answer.
Thus, it is useful for construction planning and is especially significant for business in the present and future research, because this model will help reduce errors in the construction management of each project, which will affect the profits.
5. Conclusions
This paper used a multiple regression model to predict the dependent variable, which is the profit of each house type, and the result is based on the relationship of independent variables with the two most influential variables, land cost and house-building cost, respectively. The prediction equation of profit/type from the multiple regression analysis results can predict results with high accuracy when compared to the actual data.
This paper aimed to assess the profit of a housing development project located in Bangkok and the perimeter areas Nonthaburi, Samut Prakan, and Pathum Thani, which is the result of good construction management. The final product of the research was the maximized profit obtained from determining each house type of the project from the optimization model, and we clarified the model by the case study.
The model can be applied to other projects that are suitable for large or densely populated cities, such as Beijing, New Delhi, and others, to gain the most reasonable result.
The constraint function, which is an important part of the optimization model for the program user, can be classified into two main types:
- For the default constraint or the fixed constraint, it was found that constraints are needed in every project with to find out the objective function value that is called the maximized profit of the housing development project, namely Constraint No. 1, or the land cost limitation; Constraint No. 2, or the house building cost limitation; Constraint No. 3, or the utility cost limitation; Constraint No. 4, or the construction management cost limitation; and Constraint No. 5 or the marketing cost limitation. Moreover, all of them are the resource constraints of housing development projects. Thus, the default constraint represents the total resource required for decision variables, or x1, x2, and x3 for this study. As a result, this constraint will be used depending on the product per unit.
- Various constraints or user constraints depend on the users to define their own requirement or determining the owner’s plan. Then, the constraints can be set according to the project’s budget in the project planning stage, and each project will be different. There are other constraints, namely Constraint No. 6, or the land area limitation; Constraint No. 7, or usable area limitation; Constraint No. 8, or total houses in the project limitation; Constraint No. 9, or a minimum of x1; Constraint No. 10, or a minimum of x2; and Constraint No. 11, or a minimum of x3. A varying constraint is the control of the budget of the project that should be determined by the program user. However, it also depends on each program user, while varying constraints should be compatible with default constraints to gain the best objective function value or a quite reliable and effective objective function value.
- The optimal solution showed how to determine the maximized profit for all houses in the case study of the project under resource constraints, such as the land cost limitation, the building cost limitation, the utility cost limitation, and the number of houses for each type in the project.
This paper used a sensitivity analysis to investigate the maximized profit of the project from the optimal solution or scenario one by defining the number of houses in each type. According to the results shown in scenario two, it is the best scenario for the project owner to define a plan for the construction of each house type for maximized profit. Most real estate business problems require allocating scarce resources, such as land, which is the greatest influencer affecting the profit of the house type. In this case, land is an important variable for future research in housing development projects.
The optimization method is a highly effective method for problem-solving, and the resource allocations can be applied to use in the construction management plan of housing development projects, as the most important goal is the maximum profit of the project, and using this model for owners of housing development projects will be the best solution based on the construction cost aspect.
Author Contributions
Conceptualization, S.K. and C.U.-t.; methodology, S.K. and C.U.-t.; software, S.K. and C.U.-t.; validation, S.K. and C.U.-t.; formal analysis, S.K. and C.U.-t.; investigation, S.K. and C.U.-t.; resources, S.K.; data curation, S.K.; writing—original draft preparation, S.K.; writing—review and editing, S.K. and C.U.-t.; visualization, S.K. and C.U.-t.; supervision, S.K. and C.U.-t.; project administration, S.K. and C.U.-t. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
The authors acknowledge and thank the real estate companies in Thailand for supporting the data and knowledge in this research study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boye, P.; Mireku-Gyimah, D.; Okpoti, D. Multiple Linear Regression Model for Estimating the Price of a Housing Unit. Ghana Min. J. 2017, 17, 66–77. [Google Scholar] [CrossRef]
- Chaphalkar, N.; Dhatunde, M. Real property valuation using sales comparison method and multiple regression analysis. Int. J. Mod. Trends Eng. Res. 2015, 2, 305–315. [Google Scholar]
- Thomas, N.; Thomas, A. Regression Modelling for Prediction of Construction Cost and Duration. Appl. Mech. Mater. 2016, 857, 195–199. [Google Scholar] [CrossRef]
- Rasyadan, F.; Hapsari, I.R. Housing Development Optimizition (Case Study: Anugerah Dian Regency In Kabupaten Banjar). Am. J. Eng. Res. 2020, 9, 55–59. [Google Scholar]
- Montana, F.; Kanafani, K.; Wittchen, K.B.; Birgisdottir, H.; Longo, S.; Cellura, M.; Riva Sanseverino, E. Multi-Objective Optimization of Building Life Cycle Performance. A Housing Renovation Case Study in Northern Europe. Sustainability 2020, 12, 7807. [Google Scholar] [CrossRef]
- Pandit, A. Application of Linear programming for Profit maximization of a Housing construction company: Case study of Urbanization of Millennials. Int. J. Eng. Appl. Sci. Technol. 2020, 5, 578–581. [Google Scholar] [CrossRef]
- Marović, I.; Perić, M.; Hanak, T. A Multi-Criteria Decision Support Concept for Selecting the Optimal Contractor. Appl. Sci. 2021, 11, 1660. [Google Scholar] [CrossRef]
- Laokhongthavorn, L.; U-tapao, C. A Multi-Objective Optimization Model for Solid Waste Disposal Under Uncertainty: A Case Study of Bangkok, Thailand. Int. J. Civ. Eng. 2017, 15, 205–212. [Google Scholar] [CrossRef]
- Baldominos, A.; Blanco, I.; Moreno, A.J.; Iturrarte, R.; Bernárdez, Ó.; Afonso, C. Identifying Real Estate Opportunities Using Machine Learning. Appl. Sci. 2018, 8, 2321. [Google Scholar] [CrossRef]
- Ahmed, S. An Approach to Maximize profit of a constructing project within Limited Budget by using Simplex Method. Int. J. Sci. Eng. Res. 2015, 6, 786–791. [Google Scholar]
- Klingenberg, B.; Brown, R.J. Optimization of residential property management. Prop. Manag. 2006, 24, 397–414. [Google Scholar] [CrossRef]
- Arfan Utiarahman, A.S.R. Case Study of Housing Development with Optimization of Housing Land Utilization by Using Linear Programs. Int. J. Innov. Sci. Res. Technol. 2018, 3, 307–313. [Google Scholar]
- Real Estate Information Center. Real Estate Situation Bangkok-Perimeter. 2004. Available online: www.reic.or.th (accessed on 25 August 2004).
- Yamane, T. Statistics, an Introductory Analysis, 2nd ed.; Harper: New York, NY, USA, 1967. [Google Scholar]
- Sarker, R.A.; Newton, C.S. Optimization Modelling a Practical Approach; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Winston, W.L. Operations Research Applications and Algorithms, 4th ed.; Thomson Brooks/Cole: Belmont, CA, USA, 2004. [Google Scholar]
- Balakrishnan, N.; Stair, R.M.; Render, B. Managerial Decision Modeling with Spreadsheets; Pearson Education Ltd.: New York, NY, USA, 2013. [Google Scholar]
- Render, B.; Stair, R.M., Jr.; Hanna, M.E.; Hale, T.S. Quantitative Analysis for Management, 12th ed.; Pearson Education Ltd.: New York, NY, USA, 2015. [Google Scholar]
- Taylor, B.W. Introduction to Management Science; Pearson Education Ltd.: New York, NY, USA, 2019. [Google Scholar]
- Wisniewski, M.; Dacre, T. Mathematical Programming: Optimization Models for Business and Management Decision-Making; McGRAW-HILL Book Company Ltd.: Maidenhead, Berkshire, UK, 1990. [Google Scholar]
- Meredith, J.R.; Shafer, S.M.; Turban, E. Quantitative Business Modeling; South-Western/Thomson Learning: Mason, OH, USA, 2002. [Google Scholar]
- Chan, D.W.M.; Kumaraswamy, M.M. Modelling and predicting construction durations in Hong Kong public housing. Constr. Manag. Econ. 1999, 17, 351–362. [Google Scholar] [CrossRef]
- Chan, A.P.C.; Chan, D.W.M. Developing a benchmark model for project construction time performance in Hong Kong. Build. Environ. 2004, 39, 339–349. [Google Scholar] [CrossRef]
- Le-Hoai, L.; Lee, Y.D.; Nguyen, A.T. Estimating time performance for building construction projects in Vietnam. KSCE J. Civ. Eng. 2013, 17, 1–8. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).