Abstract
Object tracking requires heterogeneous images that are well registered in advance, with cross-modal image registration used to transform images of the same scene generated by different sensors into the same coordinate system. Infrared and visible light sensors are the most widely used in environmental perception; however, misaligned pixel coordinates in cross-modal images remain a challenge in practical applications of the object tracking task. Traditional feature-based approaches can only be applied in single-mode scenarios, and cannot be well extended to cross-modal scenarios. Recent deep learning technology employs neural networks with large parameter scales for prediction of feature points for image registration. However, supervised learning methods require numerous manually aligned images for model training, leading to the scalability and adaptivity problems. The Unsupervised Deep Homography Network (UDHN) applies Mean Absolute Error (MAE) metrics for cost function computation without labelled images; however, it is currently inapplicable for cross-modal image registration. In this paper, we propose aligning infrared and visible images using a rasterized parameter prediction algorithm with similarity measurement evaluation. Specifically, we use Cost Volume (CV) to predict registration parameters from coarse-grained to fine-grained layers with a raster constraint for multimodal feature fusion. In addition, motivated by the utilization of mutual information in contrastive learning, we apply a cross-modal similarity measurement algorithm for semi-supervised image registration. Our proposed method achieves state-of-the-art performance on the MS-COCO and FLIR datasets.
1. Introduction
Cross-modal image registration is used to align the pixels of two or more images of the same scene generated by different sensors and describe them in a consistent coordinate system [1,2]. In object tracking, infrared and visible light are the most widely used in environmental perception, and are of great importance for many applications, such as medical imaging [3,4,5], remote sensing [6,7], panoramic vision [8,9,10], autonomous vehicles [11,12,13,14], and more. Visible light cameras are similar to the human visual system in that they have a wide range of perception, are affected by changes in light intensity, and lack night vision capabilities. Infrared cameras can enhance perception in low-light and poor weather conditions by sensing thermal radiation [1,15]. However, due to their complicated detection scenario with large geometric changes and significant difference in contrast, infrared and visible image registration remains a challenging task.
Conventional feature-based image registration methods use multi-scale transforms [5], sparse representations [16], and saliency-based algorithms [17] to extract features from original image for matching and obtain resolved coordinate mapping parameters between image pairs based on mutual relation of image features. Although these algorithms achieve excellent results in single-mode scenarios [18,19,20], they cannot be well extended to multimodal scenarios, as the appearance and texture of images in different modalities are quite disparate.
Deep learning-based methods design diverse neural networks to predict the offsets of pixel points and use labelled data to train neural networks for homography prediction, such as the DenseFuse [21], FusionGAN [22], SDNet [23], and other models [24], which have been reported to have better adaptability, fault tolerance, and noise resistance for image registration study [25]. These supervised learning methods require a large number of manually aligned images as labels for model training, which is time-consuming and labor-intensive. Nguyen et al. (2018) [26] proposed an Unsupervised Deep Homography Network (UDHN) which applies Mean Absolute Error (MAE) metrics for cost function computation without labelled images; however, it is not yet applicable for multimodal image registration.
To solve this problem, we first propose a rasterized registration parameter prediction method for image registration that uses Cost Volume (CV) [27] to fuse multimodal features and estimate registration parameters from coarse-grained to fine-grained layers. CV is a commonly used multi-scale feature matching method in computer vision, and is often used to find corresponding points between two images. To address the boundary discontinuity problem in rasterized parameter prediction, we use a position-dependent weight matrix as a raster constraint to make the inside pixels more significant and the intersection points more equal. Additionally, motivated by the utilization of mutual information in contrastive learning, we propose a cross-modal similarity measurement algorithm for semi-supervised image registration.
In this paper, we propose a cross-modal image registration algorithm to solve the problem of pixel coordinate misalignment between visible-light and infrared images. The proposed model contains four modules. The first is a Feature Extraction Module (FEM) that uses the VGG convolutional neural network [28] to encode feature pyramids for a reference image (visible light) and a moving image (infrared). The second module is the Registration Parameter Prediction Module (RPPM), which predicts a homography matrix for each raster in all layers of the feature pyramids and outputs a homography matrix group for both images in order to fuse multimodal images and enhance the representation of high-resolution images. The third module is the Image Transformation Module (ITM), which transforms the homography matrix groups into a kind of transform image representation via sampling point transformation and bilinear sampling for image alignment. The last module is the Similarity Measurement Module (SMM); it first pre-trains two encoders to generate the similarity representation of images, then uses the similarity scores as the cost function for training an image registration model.
We conducted experiments on the MS-COCO and FLIR datasets, and the experimental results show that our method achieves state-of-the-art performance on most metrics. Our main contributions cn be summarized as follows:
- We propose a cross-modal image registration method that solves the problem of pixel coordinate misalignment between visible-light and infrared images.
- We propose a deep learning-based multi-modality and multi-scale feature transformation parameter prediction method.
- We introduce a contrastive learning-based cross-modal similarity measurement model for semi-supervised image alignment.
2. Related Work
2.1. Area-Based Image Registration
Image registration is used to geometrically align images from different sources, with the key goal being to align the pixel coordinates. Conventional area-based methods use template matching to search the transformation function of moving image in a reference image in order to maximize the similarity score [29,30,31,32]. For example, Lu et al. [31] employed Mutual Information (MI) as a similarity measurement for multimodal image registration. Chen and Varshney [30] used mutual information-based techniques and a generalized partial volume model for CT and MR brain images registration. Gao et al. [32] used mutual information-based techniques for registering monomodal images. However, computing all the grayscale information in an image is quite computationally intensive.
2.2. Feature Extraction-Based Image Registration
Conventional image registration methods extract sparse features from a raw image, then implement image registration at the feature layer. The coordinate mapping parameters between image pairs are obtained by solving the relationship between feature pairs, such as the Scale-Invariant Feature Transform (SIFT) feature point detection algorithm [33,34] and Random Sample Consensus (RANSAC) outlier removal algorithm [35,36,37]. The SIFT algorithm [33] extracts feature points by constructing an image pyramid, computing the dominant orientation, and computing descriptor vectors. The RANSAC algorithm [35] uses hypothesis testing to obtain the minimal subset without outliers by resampling, minimizing the proportion of incorrectly matched samples in feature pairs and improving the estimation accuracy of the pixel coordinate mapping relationship.
Several researches [18,19,20,38] have proposed combining the SIFT class feature extraction algorithm [33] and RANSAC abnormal value deletion algorithm [35] for image registration. The SIFT algorithm constructs image pyramids to compute the main direction and description vectors for feature points extraction, which is scale- and rotation-invariant. The RANSAC algorithm uses the hypothesis testing method to resample a potential smallest subset without abnormal values for reduction of incorrectly matching samples and improved pixel coordinate mapping estimating accuracy. As the transformation between multimodal images is nonlinear and grayscale, researchers have proposed enhancing the feature operators description capability [39,40,41,42,43]. For example, Tang et al. [39] employed the Speeded-Up Robust Features (SURF) algorithm for local feature extraction, then used the shape represented by boundaries as global features to describe the appearance of differences. Jiang et al. [40] used an edge detection operator to extract the contour maps of infrared-visible image pairs as matching features, which were then used to process the spatial gradient differences between multimodal image pixels.
In addition, other researchers have proposed enhancing the processing of feature matching and image transformation for infrared–visible light image registration [41,42]. For example, Min et al. [41] constructed an enhanced model by combining affine and polynomial transformation. Their approach uses the edge point features of an infrared–visible light image pair for transformation parameter estimation, leading to the description of non-rigid and global deformation modes. Liu et al. [42] extracted similar structural features through multi-directional phase coherence and saliency ranking. Then, the feature points were tracked using the kernel correlation filtering method and matched by incorporating the RANSAC algorithm.
2.3. Deep Learning-Based Image Registration
Deep learning-based methods design diverse neural networks to predict the offsets of pixel points and compute the L2 norm between predictions and truth labels as the cost function used to train the model; examples include the Deep Homography Network (DHN) [44], Quicksilver deep encoder–decoder network [45], and others [46,47,48,49]. For example, Yi et al. [46] proposed a DHN-based method for learning good corresponding points between two images and compared it with other methods to demonstrate its superiority in image registration. Daniel et al. [44] introduced a deep convolutional neural network [50] to predict the feature point correspondence between unregistered images. However, these supervised learning methods require a large number of manually aligned images as labels for model training, which is time-consuming and labor-intensive.
Unsupervised learning methods apply mean absolute error metrics to compute cost function without labelled images for image registration. For example, Nguyen et al. [26] proposed an Unsupervised Deep Homography Network to apply the Direct Linear Transform (DLT) [51] for homography matrix resolution. Then, their model uses a spatial transformation layer to obtain the corrected transformed image and compute the L1 norm between the transformed image and reference image as the loss function for use in network optimization. Kalluri et al. [52] proposed an unsupervised domain adaptation method based on UDHN for image registration. By introducing a new loss function, their model can learn more discriminative feature representations, improving its generalization ability across different datasets.
The method proposed in the present paper is a deep neural network model that employs a similarity measurement algorithm for semi-supervised cross-modal image registration.
3. Methodology
Figure 1 illustrates the framework of our proposed image registration method, including the FEM, RPPM, ITM, and SMM.
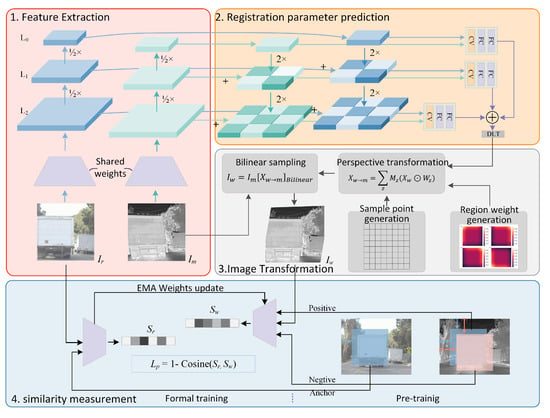
Figure 1.
The framework of our image registration model, including the FEM, RPPM, ITM, and SMM. First, the FEM encodes feature pyramids for a reference image (visible light) and a moving image (infrared). Then, the RPPM predicts a homography matrix for each raster of the feature pyramid layers. Next, the ITM conducts perspective transformation for the homography matrix group of the moving image. Finally, the SMM computes the similarity scores of the two images for image registration.
- The FEM uses a VGG convolutional neural network to encode reference image (visible light) and moving image (infrared) feature pyramids.
- The RPPM predicts a homography matrix for each raster of the feature pyramid layers and outputs homography matrix groups for each image.
- The ITM conducts perspective transformation for the homography matrix group of the moving images.
- The SMM computes the similarity scores of the two images as a cost function for image registration model training.
3.1. Feature Extraction
We first use the VGG convolutional neural network [28] to extract image features, as illustrated in the top left part of Figure 1. The VGG convolutional neural network was proposed by the Visual Geometry Group at Oxford University (https://www.robots.ox.ac.uk/vgg/, accessed on 1 September 2022), and uses stacked convolutional kernels for image feature extraction. We use two VGG networks with shared training parameters to extract the respective features of the reference image and moving image and then further construct their feature pyramids, which are subsequently used in registration parameter prediction.
3.2. Registration Parameter Prediction
The rasterized registration parameter prediction schema is provided in Algorithm 1. After feature extraction, a group of homography matrices is predicted for the feature pyramids in each layer, as illustrated in the top right part of Figure 1. We first predict a coarse-grained global homography matrix in the layer, which is divided into an raster for the layer. Next, we predict a group of fine-grained local homography matrices in the layer. Iteratively, we then predict a more fine-grained group of local homography matrices in the layer.
| Algorithm 1 The registration parameter prediction algorithm |
| Input: |
| Output: |
| Hyperparameter: |
|
Specifically, as illustrated in Figure 2, assuming that the corner coordinate set of the reference image and moving image are X and Y, respectively, the matching response of dual-way features are fed into some fully-connected layers to predict the offsets of the four corner points between the moving image and reference image . Then, the feature point pair is obtained and used to resolve homography matrices H using the Direct Linear Transform [51].

Figure 2.
The process of registration parameter prediction; the matching response of dual-way features is fed into the full-connected layers to predict the offsets of the four corner points between the moving image and reference image. Then, obtain the feature point pair is obtained to resolve the respective homography matrices.
Multi-modal fusion: To fuse the features of the reference image and moving image , the Cost Volume [27] is computed for stereo matching of each pixel feature vector between the two input images, as follows:
where is the feature map of the reference image and moving image, respectively, in one layer of the feature pyramid, and represents the pixel coordinates of images and , respectively. After multi-modal fusion, we obtain a matching response .
Multi-scale prediction: To enhance the matching effect of high-resolution images, we propose a Rasterized Feature Pyramid Network (RFPN) for multi-scale feature construction and further estimate the registration parameters from a coarse-grained resolution to a fine-grained resolution in a top-down manner.
Specifically, we first use the feature pyramid network to predict the base offset of the top layer, which is then used to predict a residual offset for the lower layers. next, we sum up all the prediction offsets in each layer as the final offset , where L is the number of layers.
Rasterized homography estimation: As multi-modal CV computation is an outer product operation in the spatial dimension, it requires significant computing and storage resources; moreover, its efficiency is very low on low-level feature maps with large spatial dimensions. In this paper, we propose a rasterized local homography estimation method that divides the low-level feature maps into multiple rasters, then performs homography estimation on the rasterized feature maps.
3.3. Image Transformation
A homography matrix describes the transformation relations between the moving image and reference image . Here, we use to represent the homogeneous coordinates of one sampling point in the moving image ; after transformation, this is represented as in the coordinate system of the reference image . Based on this transformation relation, we can use bilinear sampling and sampling point transformation for image registration between the moving image and reference image to obtain a transformation image , which has a grayscale space that is coherent with and pixel coordinates aligned with .
Specifically, we first generate a sampling point matrix according to the resolution of the transformation image , in which each column vector represents the homogeneous coordinates of each pixel in . The corresponding pixel coordinates of the sampling point for transformation image in moving image are represented as
where is the inverse matrix of homography matrix H, indicating the transformation relation from the coordinate of to the coordinate of . We note that the sampling point transformation is performed in each raster region using its own homography matrix in accordance with the rasterized local homography matrix estimation method of our registration parameter prediction network. In this case, the final sampled transformation image has serious boundary discontinuity problems when the homography matrices of adjacent raters are quite different, as shown by the example in Figure 3a.
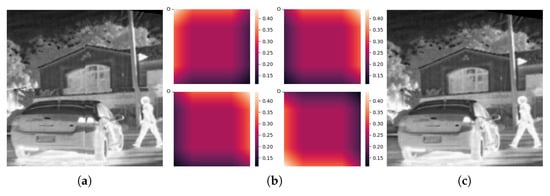
Figure 3.
Illustration of weighted raster image transformation to address boundary discontinuity problems, showing (a) example image with discontinuous boundary issue, (b) the raster region weights, and (c) the weighted transformed image.
In this paper, we propose a position-dependent weight matrix for the homography matrix constraint in each raster region. The weight matrix is used to enhance the transformation effect of the homography matrix on the pixels inside the raster area while equalizing the effect on the raster junctions. Specifically, a vector w is generated in accordance with the ratio of the weights’ full action region length to the raster action length a and the ratio of the transition action region b, where the weight of full action region is 1 and the weights of the transition regions on the left and right sides are linearly distributed from 1 to 0.
Next, we take an outer product on the vector w to obtain the weight matrix of a single raster, then translate it according to each raster’s center point to obtain the final weight matrix W. The complete sampling point transformation can be expressed as follows:
3.4. Similarity Measurement
Similarity measurement aims to quantify the alignment effect between the reference image and transformation image by computing a similarity score as the input of a cost function. Motivated by contrastive learning, in this paper we propose a mutual information learning method for similarity measurement.
Specifically, we use the MoCo siamese network framework [53] with the VGG-16 encoding model. In pre-training, we first randomly crop the aligned image at the same spatial position and obtain an infrared–visible light image pair as a positive sample. The image pairs at different spatial positions are used as a negative sample, including pairs from the same image and different images. We then set a negative sample sequence which has much more samples than the training samples to ensure a sufficient number of indistinguishable samples in the sequence. In model training, the similarity encoder employs pre-trained parameters to compute two similarity vectors, and , for the input images and , respectively.
3.5. Image Registration
We define the following cost function for model training:
where is the balance factor and is the transformation mask obtained by the perspective transformation of an all-one matrix, which has a same size as the transformation image. We compute the difference degree of the similarity vectors and output by similarity measurement as the pixel match loss , as follows:
We define the transformation mask loss as a regular term for the mask size, as follows:
where H and W are the height and width of the transformation image. The constraint ensures that the transformed image has as much overlap with the reference image as possible.
4. Experiment Settings
4.1. Datasets and Parameter Settings
All of our experiments a = were conducted on two datasets: the Microsoft Common Objects in Context (MS-COCO) dataset (https://cocodataset.org/ accessed on 1 September 2022) and the FREE Teledyne FLIR Thermal dataset (https://www.flir.com/ accessed on 1 September 2022).
MS-COCO is a large-scale visible-light image dataset provided by Microsoft; it contains more than 200,000 images, and covers a variety of real-life scenarios [54]. FLIR is a multimodal image dataset provided by the Teledyne FLIR Company; it contains more than 8000 infrared-visible image pairs, which mainly focus on cars and driving scenes [55]. All the samples in these two datasets are taken by on-board cameras while driving.
Following the data generation method in UDHN [26], we set the corner offset interval as [−32 pixel, 32 pixel] for our image registration experimental dataset generation with a size of , including 4000 training images and 800 test images. In addition, we set the learning rate to 1e-5 and the training epoch to 200. All experiments were implemented in the PaddlePaddle framework developed by the Baidu company (https://www.paddlepaddle.org.cn/ accessed on 1 September 2022), and were run with CUDA on NVIDIA GTX 3080 Ti GPUs.
4.2. Competitors
We compared our image registration method with the following advanced models:
- MI (2008) [31], which uses mutual information for image similarity measurement.
- UDHN+CSM (2009) [56], which combines UDHN with a real-time correlative scan matching algorithm.
- SIFT+RANSAC (2015) [20], which combines SIFT feature extraction with the RANSAC outlier removal algorithm.
- UDHN (2018) [26], which uses a convolutional neural network to predict feature point pairs and applies mean absolute error metrics for cost function computation.
- VFIS (2020) [27], which applies Cost Volume for multimodal image feature fusion.
4.3. Evaluation Metric
For image registration evaluation, we computed the Root Mean Squared Error (RMSE) of the corner point coordinates, which indicates the matching degree between transformation image and reference image, as follows:
In addition, various conventional image quality metrics can be used to evaluate the effect of image registration in different views, including the following:
- Correlation Coefficient (CC): describes the linear correlation between images; a larger correlation coefficient between the target and reference images indicates higher similarity between the two, i.e., a better registration result, and is calculated as follows:
- Structural Similarity Index Measure (SSIM): constructs the quality loss and distortion of images, including the correlation loss, grayscale distortion, and contrast distortion; a larger SSIM indicates that the quality of the target image is closer to that of the reference image. SSIM is calculated as follows:
- Peak Signal-to-Noise Ratio (PSNR): computes the ratio of peak energy to noise energy for measurement of distortion in the image registration process; the larger the PSNR value, the closer the target image is to the reference image. PSNR is calculated as follows:
- Mutual Information (MI): describes the mutual information contained in each image. The higher the similarity or overlap between two images, the higher their correlation, and the smaller their joint entropy, which means that the mutual information is greater. MI is calculated as follows:
5. Results and Analysis
5.1. Overall Results
Table 1 shows a comparison of the overall performance between our image registration method and competing methods. We implemented image registration experiments on the MS-COCO visible light image dataset and the FLIR infrared–visible light image dataset with both labelled and unlabelled images. Note that all the annotated labels were used for performance evaluation only, and were not used in model training. It can be observed from these results that our proposed image registration method outperforms competing methods in terms of all the evaluation metrics on both the MS-COCO and FLIR datasets.

Table 1.
Overall results of model comparison for image registration on the MS-COCO and FLIR datasets. MS-COCO is a large-scale visible light image dataset provided by Microsoft that contains more than 200,000 images and covers a variety of real-life scenarios [54]. MS FLIR is a multimodal image dataset provided by the Teledyne FLIR Company; it contains more than 8000 infrared-visible image pairs, which mainly focus on cars and driving scenes [55].
Specifically, we first observe that the VFIS model improves the RMSE of the UDHN model by 1.8% on the MS-COCO visible light image dataset. This might be attributed to the use of cost volume computation in the VFIS, which performs stereoscopic matching of the pixel feature vectors of two images. Our proposed method improves the RMSE of the VFIS model by 10.5%, validating our proposed design for registration parameter estimation.
The second observation is that the experimental results of the SIFT+RANSAC model on the FLIR infrared–visible light multimodal dataset (RMSE 17.8542) decline sharply compared to the results on the MS-COCO visible light dataset (RMSE 859.4847). However, this is not unexpected. The SIFT algorithm cannot extract consistent features from infrared and visible light images for registration parameter estimation, resulting in a large number of matching failures. On the other hand, the experimental results show that the UDHN model with similarity measure enhancement is successfully applied in infrared–visible light cross-modal image matching (RMSE 24.7125), indicating that the similarity measurement algorithm can improve the spatial offset resolution of the Mean Absolute Error (MAE) metrics in multimodal image registration.
Finally, our proposed method achieves state-of-the-art results on the FLIR infrared–visible light multimodal dataset (RMSE 15.9170), validating our proposed design for transformation parameter estimation. In addition, our proposed model achieves state-of-the-art results on the unlabelled FLIR infrared–visible light multimodal dataset. This suggests that our proposed model has excellent generalization performance on the infrared–visible light multimodal image registration task.
5.2. Visualization
Figure 4a,b illustrates the cumulative error distribution of the RMSE corner offsets on the MS-COCO and FLIR datasets, respectively. It can first be observed that SIFT has excellent performance on the MS-COCO single-mode visible light image dataset, as shown in Figure 4a. However, SIFT is seriously affected by abnormal values, meaning that the average RMSE score remains large. On the other hand, the conventional MI algorithm is affected by abnormal samples as well, as illustrated in Figure 4b. Finally, our proposed image registration method has smaller RMSE corner offsets than either the UHDN or VFIS models.
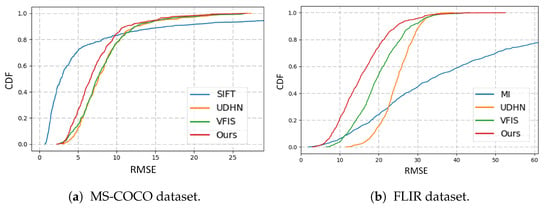
Figure 4.
RMSE cumulative error distribution.
We next provide a visualization of the image registration effects with different algorithms in Figure 5 for comparison. The size of the overlapping shadow regions around scene in each image represents the registration effects. It can be observed that the overlapping shadow regions obtained by our algorithm are the smallest. This suggests that our image registration method is able to achieve the best performance.

Figure 5.
Visualization of image registration effects obtained by different algorithms. The first row shows transformation images, while the second row shows enhanced reference images that replace the R channel in the reference image with the pixel intensity of the corresponding transformation image. The first column shows test images, while the other columns show registration images obtained with UDHN, VFIS, and our proposed algorithm, respectively.
5.3. Discussion
Our proposed method for image registration outperforms competing methods in terms of all the evaluation metrics on both the MS-COCO and FLIR datasets. For single-mode visible light image registration, we use cost volume computation to estimate registration parameters, effectively improving on the performance of the VFIS model by stereoscopically matching the pixel feature vectors of the two images. Furthermore, for infrared–visible light multimodal image registration, we successfully use a similarity measure-enhanced version of UDHN to address the spatial offset resolution problem of MAE metrics. Compared to the competing methods, our algorithm produces the smallest overlapping shadow region in the output image.
6. Conclusions
In this paper, we present a design for a rasterized registration parameter prediction algorithm that fuses multimodal images for enhanced representation. In addition, we propose a cross-modal similarity measurement algorithm for semi-supervised image registration. Our proposed method consists of an FEM module to encode feature pyramids for both a visible light and an infrared image, an RPPM module to predict the homography matrices from the feature pyramid layers for fusion of multimodal images, a ITM module to transform the homography matrix groups into transform representations for image alignment, and an SMM module to generate similarity representations of images for semi-supervised image registration. Experiments on the MS-COCO visible light image dataset and the FLIR multi-modal image dataset validate our design objectives for cross-modal image registration between infrared and visible light images.
While the present paper has realized infrared and visible light image registration, we additionally intend to integrate the multi-modal image registration task in our future work. On the one hand, there is no need to design complicated timing synchronization for real-time online scenarios; on the other hand, however, it can reduce the information redundancy of multiple feature extraction modules, resulting in reduced computational cost and improved speed.
Author Contributions
Conceptualization, Q.Z. and W.X.; Methodology, Q.Z.; Investigation, Q.Z. and W.X.; Writing—original draft, Q.Z.; Writing—review & editing, W.X.; Supervision, W.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Open Research Fund for Research on Knowledge Graph on Water Conservancy in Yangtze River Basin from Hubei Key Laboratory of Intelligent Yangtze and Hydroelectric Science, China Yangtze Power Co., Ltd., with grant number ZH2102000101.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
Author Qing Zhang was employed by the company Hubei Key Laboratory of Intelligent Yangtze and Hydroelectric Science, China Yangtze Power Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The authors declare that this study received funding from Hubei Key Laboratory of Intelligent Yangtze and Hydroelectric Science, China Yangtze Power Co., Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
References
- Ma, J.; Ma, Y.; Li, C. Infrared and visible image fusion methods and applications: A survey. Inf. Fusion 2019, 45, 153–178. [Google Scholar] [CrossRef]
- Zhang, X.; Ye, P.; Leung, H.; Gong, K.; Xiao, G. Object fusion tracking based on visible and infrared images: A comprehensive review. Inf. Fusion 2020, 63, 166–187. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, W.; Zhang, R.; Wang, R.; Robbins, D. Dual-channel cascade pose estimation network trained on infrared thermal image and groundtruth annotation for real-time gait measurement. Med. Image Anal. 2022, 79, 102435. [Google Scholar] [CrossRef] [PubMed]
- Hazra, S.; Roy, P.; Nandy, A.; Scherer, R. A Pilot Study for Investigating Gait Signatures in Multi-Scenario Applications. In Proceedings of the 2020 International Joint Conference on Neural Networks, Glasgow, UK, 19–24 July 2020; pp. 1–10. [Google Scholar]
- Du, J.; Li, W.; Xiao, B.; Nawaz, Q. Union Laplacian pyramid with multiple features for medical image fusion. Neurocomputing 2016, 194, 326–339. [Google Scholar] [CrossRef]
- Li, X.; He, Y.S.; Zhan, X.; Liu, F.Y. A rapid fusion Algorithm of infrared and the visible images based on Directionlet transform. Appl. Mech. Mater. 2010, 20, 45–51. [Google Scholar] [CrossRef]
- Deng, M.; Kang, J.; Li, Y. The Fusion Algorithm of Infrared and Visible Images Based on Computer Vision. Adv. Mater. Res. 2014, 945, 1851–1855. [Google Scholar] [CrossRef]
- Kudinov, I.; Nikiforov, M.; Kholopov, I. Camera and auxiliary sensor calibration for a multispectral panoramic vision system with a distributed aperture. J. Phys. Conf. Ser. 2019, 1368, 032009. [Google Scholar] [CrossRef]
- Rhee, J.H.; Seo, J. Low-Cost Curb Detection and Localization System Using Multiple Ultrasonic Sensors. Sensors 2019, 19, 1389. [Google Scholar] [CrossRef]
- Valkov, V.; Kuzin, A.; Kazantsev, A. Calibration of digital non-metric cameras for measuring works. J. Phys. Conf. Ser. 2018, 1118, 012044. [Google Scholar] [CrossRef]
- Badue, C.; Guidolini, R.; Carneiro, R.V.; Azevedo, P.; Cardoso, V.B.; Forechi, A.; Jesus, L.F.R.; Berriel, R.F.; Paixão, T.M.; Mutz, F.W.; et al. Self-driving cars: A survey. Expert Syst. Appl. 2021, 165, 113816. [Google Scholar] [CrossRef]
- Drew, S.; Andersen, H.; Du, X.; Shen, X.; Meghjani, M.; Eng, Y.H.; Rus, D.; Ang, M.H. Perception, Planning, Control, and Coordination for Autonomous Vehicles. Machines 2017, 5, 6. [Google Scholar]
- Campbell, M.; Egerstedt, M.; How, J.P.; Murray, R.M. Autonomous driving in urban environments: Approaches, lessons and challenges. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 4649–4672. [Google Scholar] [CrossRef] [PubMed]
- Susilo, J.; Febriani, A.; Rahmalisa, U.; Irawan, Y. Car parking distance controller using ultrasonic sensors based on arduino uno. J. Robot. Control (JRC) 2021, 2, 353–356. [Google Scholar] [CrossRef]
- Takumi, K.; Watanabe, K.; Ha, Q.; Tejero-De-Pablos, A.; Ushiku, Y.; Harada, T. Multispectral object detection for autonomous vehicles. In Proceedings of the on Thematic Workshops of ACM Multimedia, Mountain View, CA, USA, 23–27 October 2017; pp. 35–43. [Google Scholar]
- Li, H.; Wu, X.J.; Kittler, J. MDLatLRR: A novel decomposition method for infrared and visible image fusion. IEEE Trans. Image Process. 2020, 29, 4733–4746. [Google Scholar] [CrossRef]
- Bavirisetti, D.P.; Dhuli, R. Two-scale image fusion of visible and infrared images using saliency detection. Infrared Phys. Technol. 2016, 76, 52–64. [Google Scholar] [CrossRef]
- Gao, J.; Kim, S.J.; Brown, M.S. Constructing image panoramas using dual-homography warping. In Proceedings of the 24th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Springs, CO, USA, 20–25 June 2011; pp. 49–56. [Google Scholar]
- Zaragoza, J.; Chin, T.; Brown, M.S.; Suter, D. As-Projective-As-Possible Image Stitching with Moving DLT. In Proceedings of the 26th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 2339–2346. [Google Scholar]
- Lin, C.; Pankanti, S.; Ramamurthy, K.N.; Aravkin, A.Y. Adaptive as-natural-as-possible image stitching. In Proceedings of the 28th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1155–1163. [Google Scholar]
- Li, H.; Wu, X.J. DenseFuse: A fusion approach to infrared and visible images. IEEE Trans. Image Process. 2018, 28, 2614–2623. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Liang, P.; Yu, W.; Chen, C.; Guo, X.; Wu, J.; Jiang, J. Infrared and visible image fusion via detail preserving adversarial learning. Inf. Fusion 2020, 54, 85–98. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, J. SDNet: A versatile squeeze-and-decomposition network for real-time image fusion. Int. J. Comput. Vis. 2021, 129, 2761–2785. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Jiang, H.; Tian, Y. Fuzzy image fusion based on modified Self-Generating Neural Network. Expert Syst. Appl. 2011, 38, 8515–8523. [Google Scholar] [CrossRef]
- Nguyen, T.; Chen, S.W.; Shivakumar, S.S.; Taylor, C.J.; Kumar, V. Unsupervised Deep Homography: A Fast and Robust Homography Estimation Model. IEEE Robot. Autom. Lett. 2018, 3, 2346–2353. [Google Scholar] [CrossRef]
- Nie, L.; Lin, C.; Liao, K.; Liu, M.; Zhao, Y. A view-free image stitching network based on global homography. J. Vis. Commun. Image Represent. 2020, 73, 102950. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- Zitová, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Chen, H.; Varshney, P.K. Mutual information-based CT-MR brain image registration using generalized partial volume joint histogram estimation. IEEE Trans. Med. Imaging 2003, 22, 1111–1119. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Zhang, S.; Su, H.; Chen, Y. Mutual information-based multimodal image registration using a novel joint histogram estimation. Comput. Med. Imaging Graph. 2008, 32, 202–209. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Gu, B.; Lin, J. Monomodal image registration using mutual information based methods. Image Vis. Comput. 2008, 26, 164–173. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. SURF: Speeded Up Robust Features. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Torr, P.H.S.; Zisserman, A. MLESAC: A New Robust Estimator with Application to Estimating Image Geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]
- Krig, S. Interest Point Detector and Feature Descriptor Survey. In Computer Vision Metrics: Textbook Edition; Springer International Publishing: Cham, Switzerland, 2016; pp. 187–246. [Google Scholar]
- Zhang, G.; He, Y.; Chen, W.; Jia, J.; Bao, H. Multi-viewpoint panorama construction with wide-baseline images. IEEE Trans. Image Process. 2016, 25, 3099–3111. [Google Scholar] [CrossRef]
- Tang, C.; Tian, G.Y.; Chen, X.; Wu, J.; Li, K.; Meng, H. Infrared and visible images registration with adaptable local-global feature integration for rail inspection. Infrared Phys. Technol. 2017, 87, 31–39. [Google Scholar] [CrossRef]
- Jiang, Q.; Liu, Y.; Yan, Y.; Deng, J.; Fang, J.; Li, Z.; Jiang, X. A Contour Angle Orientation for Power Equipment Infrared and Visible Image Registration. IEEE Trans. Power Deliv. 2021, 36, 2559–2569. [Google Scholar] [CrossRef]
- Min, C.; Gu, Y.; Li, Y.; Yang, F. Non-rigid infrared and visible image registration by enhanced affine transformation. Pattern Recognit. 2020, 106, 107377. [Google Scholar] [CrossRef]
- Liu, X.; Ai, Y.; Tian, B.; Cao, D. Robust and Fast Registration of Infrared and Visible Images for Electro-Optical Pod. IEEE Trans. Ind. Electron. 2019, 66, 1335–1344. [Google Scholar] [CrossRef]
- Yang, Z.; Dan, T.; Yang, Y. Multi-temporal remote sensing image registration using deep convolutional features. IEEE Access 2018, 6, 38544–38555. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Deep Image Homography Estimation. arXiv 2016, arXiv:1606.03798. [Google Scholar]
- Yang, X.; Kwitt, R.; Styner, M.; Niethammer, M. Quicksilver: Fast predictive image registration – A deep learning approach. NeuroImage 2017, 158, 378–396. [Google Scholar] [CrossRef]
- Yi, K.M.; Trulls, E.; Ono, Y.; Lepetit, V.; Salzmann, M.; Fua, P. Learning to Find Good Correspondences. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2666–2674. [Google Scholar]
- Toldo, X.; Maracani, A.; Michieli, U.; Zanuttigh, P. Unsupervised Domain Adaptation in Semantic Segmentation: A Review. Technologies 2020, 8, 35. [Google Scholar] [CrossRef]
- Le, H.; Liu, F.; Zhang, S.; Agarwala, A. Deep homography estimation for dynamic scenes. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognitio, Seattle, WA, USA, 13–19 June 2020; pp. 7652–7661. [Google Scholar]
- Zhang, J.; Wang, C.; Liu, S.; Jia, L.; Ye, N.; Wang, J.; Zhou, J.; Sun, J. Content-aware unsupervised deep homography estimation. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 653–669. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Zaragoza, J.; Chin, T.; Tran, Q.; Brown, M.S.; Suter, D. As-Projective-As-Possible Image Stitching with Moving DLT. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1285–1298. [Google Scholar]
- Kalluri, K.; Varma, G.; Chandraker, M.; Jawahar, C.V. Universal Semi-Supervised Semantic Segmentation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5258–5269. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshic, R.B. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognitio, Seattle, WA, USA, 13–19 June 2020; pp. 9726–9735. [Google Scholar]
- Lin, T.; Maire, M.; Belongie, S.J.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Fang, Q.; Han, D.; Wang, Z. Cross-Modality Fusion Transformer for Multispectral Object Detection. arXiv 2021, arXiv:2111.00273. [Google Scholar] [CrossRef]
- Olson, E.B. Real-time correlative scan matching. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4387–4393. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).