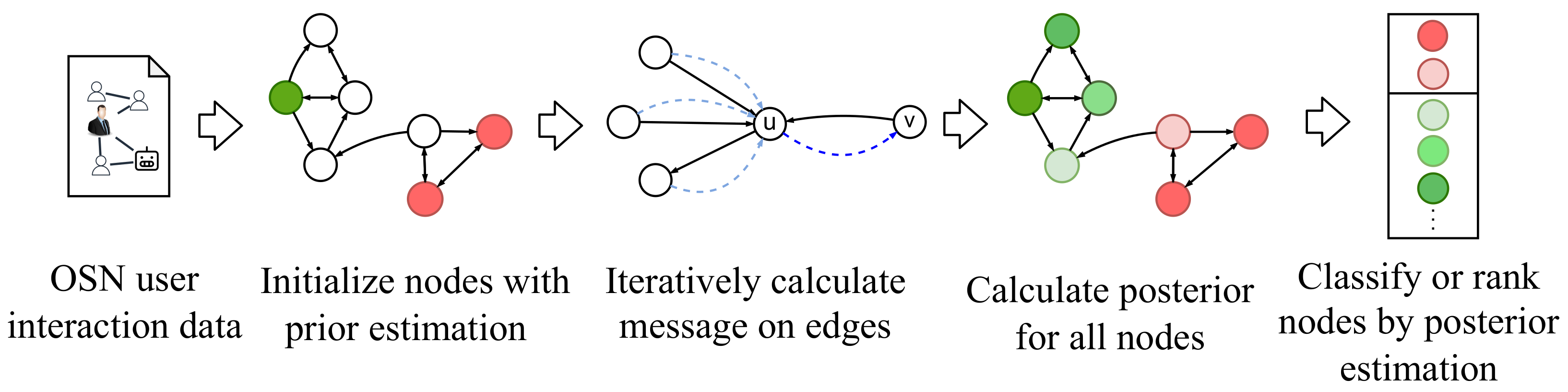
1. Introduction
While celebrities and influencers have a huge influence on OSNs, not all of their followers are authentic human beings on the other side of the screen. It was reported that 9–15% of active Twitter users were bots [
1,
2]. By creating and controlling such bots, or Sybil accounts, malicious adversaries in social networks carry out spamming, phishing scams, referral traffic, and manipulating online public opinion, thereby causing a series of security problems and a crisis of trust.
In order to counter such abuse in social networks, an increasing number of Sybil-detection methods have been proposed. According to the data used, feature-based and graph-based methods are extensively mainstreamed. Feature-based methods train supervised classifiers for detection using diverse information of Sybil and normal users, such as local connections, profiles, IP addresses, and all kinds of behaviors and content features [
3,
4,
5,
6,
7,
8].
While graph-based methods only make use of the global structure of the social graph, and detection relies on exploiting interrelations among entities (e.g., “friendship” on Facebook or “follow” on Twitter) [
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25], GNN-based methods use both node features and structural characteristics of the OSN data to train graph neural networks (GNNs) for user classification [
26,
27,
28,
29]. This paper focuses on graph-based detection methods.
Theoretically, an underlying assumption for graph-based Sybil-detection methods is that the benign community and the Sybil community are sparsely connected; therefore, the connections between nodes follow homophily, i.e., adjacent nodes tend to share the same label. Under this assumption, graph-based methods essentially use the block model [
30] to represent a network as a set of blocks and discriminate whether an unknown node belongs to a Sybil community or a benign community. Label propagation algorithms [
31,
32] are a common class of methods to achieve block segmentation.
Starting from some labeled nodes, label propagation algorithms iteratively propagate the users’ influence, trust, or reputation along the social connections between them, until sufficient information for label prediction is obtained. By means of propagation, most graph-based methods can be grouped into random walk (RW)-based [
9,
10,
11,
12,
13,
14,
15,
22] and Loopy Belief Propagation (LBP)-based [
16,
17,
20] methods. However, excluding space and time efficiency, LBP-based methods outperform RW-based methods as they can leverage both labeled benign and Sybil data, and its nonlinear nature endows robustness against label noise [
17]. However, existing LBP-based methods suffer from the following problems:
(1) They either assume a global homophily strength for all edges (e.g., GANG [
20]) or predefined edge weights as homophily strength (e.g., SybilSCAR-D uses degree-normalized homophily strength [
17]), while such an assumption ignores the local homophily difference of edges and, thus, fails to characterize the behavior pattern of nodes. A clear example is that users may have different capabilities to discern another benign user to follow; hence, their following edges should bear different homophily strengths.
(2) They are mostly designed for undirected (symmetric) social graph models, while many real-world platforms, such as Twitter, establish networks by a “follow”, “retweet”, or “thumbs up”, which are asymmetric relationships. Applying these methods directly cannot make full use of edge information. The study in [
20] adapts LBP-based methods for directed graphs; however, during two-way message-passing between a directed pair, its edge-potential function acts in the same way, which does not agree with the asymmetric trust relationship.
Our work: In order to overcome the limitations above, we propose a novel Sybil-detection method named SybilHP, a Sybil-detection method optimized for directed social networks with adaptive homophily prediction.
Overall, we use the LBP framework to estimate the posterior probability distribution of nodes for classification or ranking from a labeled subset of the social graph. SybilHP adapts to directed graphs by controlling belief propagation on directed edges with a novel edge-potential-function design, which integrates both the local preference of nodes and the directionality of edges. Specifically, our design involves an adaptive homophily strength estimator for the node’s preference that is iteratively updated along with the belief propagation. Moreover, we incorporate a direction-sensitive mechanism into our edge-potential function to better capture the asymmetric interplay between follower and followee. We extensively analyze and evaluate the performance of SybilHP under different conditions, including different parameter settings, attack sparsity, and label noise.
The experiments on synthetic social networks show that the proposed SybilHP has relatively competitive accuracy and robustness. Then, we further evaluate SybilHP and compare it with multiple state-of-the-art methods on a large Twitter dataset. The results demonstrate that the SybilHP performs substantially better than existing methods concerning classification and ranking tasks.
2. Related Work
Both random-walk-based methods and LBP-based methods start from some labeled nodes to predict the unknown labels by semi-supervised learning. The basic idea of random-walk-based methods is that random walks starting from benign nodes tend to reach other benign nodes quickly, while it is difficult for Sybil to reach a benign node in a short walk. From this intuition, SybilGuard [
10] and SybilLimit [
11] have spawned many works, including SmartWalk [
33], SybilIfer [
12], SybilRank [
9], SybilWalk [
19], and Integro [
15]. However, note that the training set for these methods should either consist of benign users or Sybil users but not both.
On another front, leveraging both labeled Sybil and benign nodes, LBP-based methods model the joint distribution over each node’s label with Markov random fields and then use the LBP algorithm to iteratively estimate posterior probability distributions for unknown labels. Stemming from the seminal SybilBelief [
16], SybilSCAR [
17] integrates LBP-based and RW-based methods into a unified framework and further simplifies the local update rule for posterior estimation, which largely enhances the detection efficiency of LBP-based methods. SybilFuse [
18] incorporates local graph attributes to better estimate the node priors by pre-trained classifiers and then uses LBP to compute the posteriors. Satoshi et al. [
24] first showed that existing graph-based Sybil-detection methods can be interpreted in a unified framework of low-pass filtering, and then they proposed SybilHeat.
However, for directed edges, the methods mentioned above either prune the one-way edges and retain those bidirectional ones, or they directly treat all edges as undirected, causing under-use of the original edge information. Worse still, “sparse connection” or “homophily assumption” requires a significant structural gap between Sybil and benign communities. However, such a structural gap in the directed social graph can be particularly obscure because the one-way linkage is much easier to achieve, and Sybils can link to benign users as many as they want. GANG [
20] adapted LBP for a directed graph by incorporating the one-way edge scenario into the edge-potential design and further derived a scalable and convergent matrix form. However, the use of a global edge weight still limits its modeling fidelity.
Based on social graph data, recent works have tended to incorporate various side information. For example, SybilHunter [
23] provides a hybrid graph-based Sybil-detection approach by aggregating user social behavior patterns. Hosseini et al. [
26] first applied graph convolutional networks to social robot detection. The use of GCN makes it possible to perform end-to-end learning using both node attribute information and node structure information. TrustGCN [
27] used a “friend request” graph and, by combining social-graph-based defenses and graph neural networks, improved the robustness of adversarial attacks.
BotRGCN [
28] and SATAR [
29] applied graph convolutional networks on a Twitter follower–followee graph with multi-modal user semantics, properties, and neighborhood information. Improved CGAN [
34] manages to extend imbalanced data sets before applying training classifiers to improve the detection accuracy of social bots. RoSGAS [
35] is a novel reinforced and self-supervised GNN architecture search framework that adaptively pinpoints the most suitable multi-hop neighborhood and the number of layers in the GNN architecture for social bot detection. However, as the neural network-based models become more complex, the cost of training and deploying the models increases, which limits their scalability and portability.
4. Methodology
Based on the motivations mentioned above, in this section, we derive finer modeling to adapt to the directed social graph, highlighting initial homophily strength parameters and adaptive homophily estimators.
4.1. Initial Homophily Strength Parameters
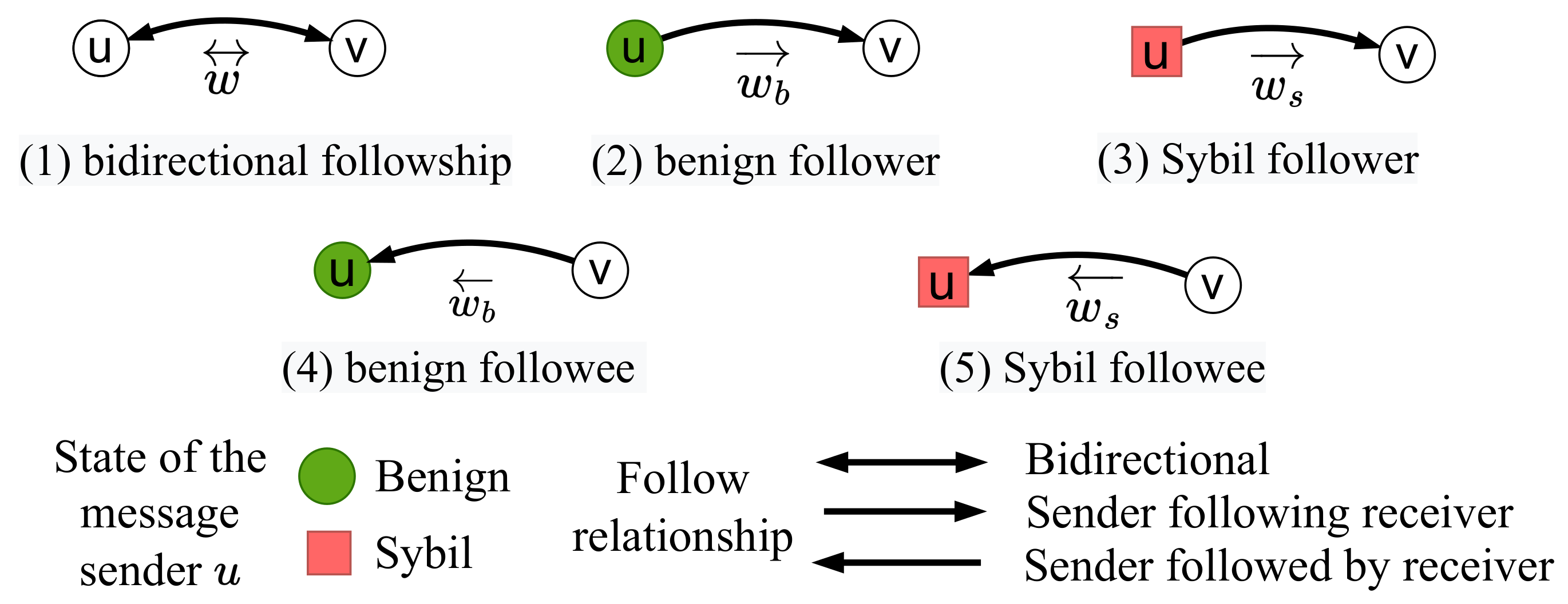
In this subsection, we present how SybilHP profiles the label coordination of a pair of nodes according to different edge types and the states of the message sender.
Note that LBP lets the variables pass messages to exchange their beliefs about each other until the message converges to a consensus [
36,
37]. Specifically, we take the message passed from
u to
v as an inference about
from
u’s standpoint [
38,
39]. However, homophily strength included in a message
sent from
u to
v should differ according to message types and the state of the message sender as shown in
Figure 3.
Therefore, we design five initial homophily strength parameters for these cases. Our design considerations are as follows.
4.1.1. The Case of Bidirectional Edge
(1) As shown in
Figure 3(1), the bidirectional edge
represents a mutual following relationship, and it naturally implies strong homophily strength between nodes. Furthermore, for this symmetric relationship, we use one parameter
representing the initial homophily strength to profile the co-occurrence probability of the pair.
For the unidirectional pair, however, we need more than one parameter to describe such an asymmetric relationship in the message sent from u to v.
4.1.2. The Case When Message Sender u Is a Follower/Tail
(2) As shown in
Figure 3(2), given a benign tail
u, from
u’s standpoint, we can assume that
v is also benign with high confidence because most human users hold an inherent discernment to follow human users. We use parameter
(“b” stands for “benign”) to represent such initial homophily strength.
(3) As shown in
Figure 3(3), if the tail
u is a Sybil, we assume Sybils are group controlled and share a similar “following” pattern [
40], that is, the probability that the head
v is also Sybil, which we denote as a homophily strength parameter
(“s” stands for “Sybil”).
4.1.3. The Case When Message Sender u Is a Followee/Head
(4) As shown in
Figure 3(4), if head
u is benign, from
u’s standpoint, we estimate that the possibility of the follower
v being benign as initial homophily strength
.
(5) As shown in
Figure 3(5), if a Sybil head
u is followed by
v, we denote the initial homophily strength from
u’s perspective as
.
4.2. Adaptive Homophily Estimator
In this subsection, we build adaptive estimators to predict the assortativity [
41,
42] for each node, i.e., the likelihood that an individual will form connections with other individuals. Here, we do not distinguish between homophily and assortativity, although the former is descriptive, and the latter is predictive. Furthermore, we call the estimators homophily estimators.
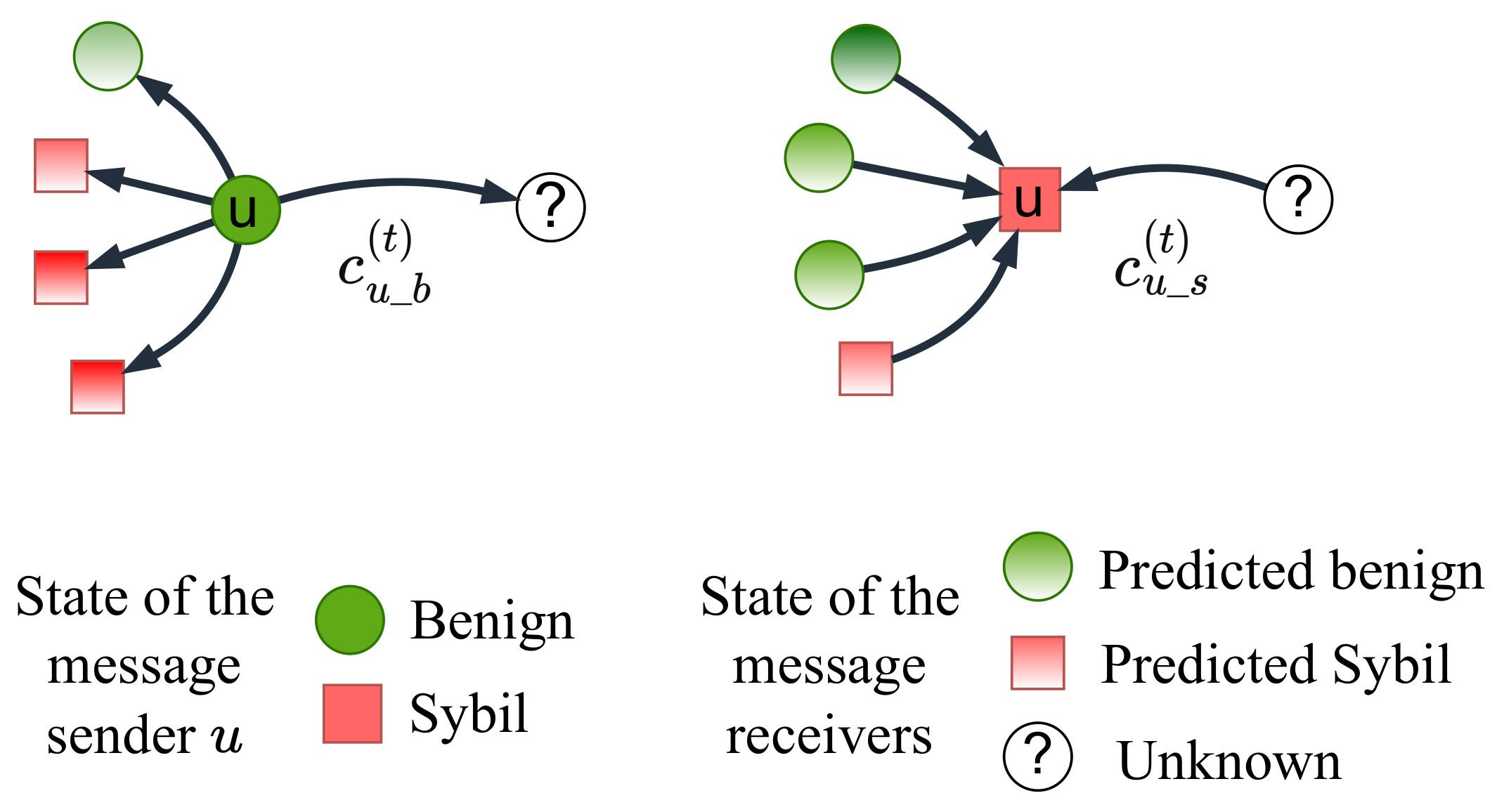
Our idea comes from an observation that it is uncommon for Sybils to be actively followed by human users, so the Sybil heads and benign tails tend to play more informative roles compared to benign heads and Sybil tails. To better capture this information, we maintain a pair of homophily estimators to measure a benign user’s capability to resist the Sybil attack, and the Sybil’s capability to make a benign user compromise. These assortative capabilities can be reflected in the statistics of the neighboring nodes’ states. Therefore, for unlabeled nodes, we take their posterior probabilities in the previous iteration as their state; thus, the estimators should be updated in each iteration.
If a benign user
u has already followed a certain number of Sybils, then it is safe to say that he/she will do it again. In other words, its discernment depends on the percentage of benign nodes among the nodes it follows as shown on the left of
Figure 4. We thus define adaptive homophily estimator
as follows:
where
is the set of outgoing neighbors of
u. Furthermore,
is the temporary posterior probability distribution at iteration
t, which is calculated by the aggregation of propagated label information at iteration
:
Similarly, a Sybil
u who has already managed to obtain many benign followers can also entice one more benign follower at a small price. In other words, its deception capability depends on the percentage of benign nodes among its followers as shown on the right of
Figure 4. We thus define adaptive homophily estimator
as follows:
where
is the set of incoming neighbors of
u.
is the label propagation from iteration
defined in Equation (
8). Note that we count the bidirectional linked neighbors in both
and
.
4.3. Redefine Potential Function
Finally, we integrate the results derived from the previous sections into our edge-potential design. For unidirectional edge , considering that message passing in the LBP algorithm goes both ways, we make our potential function direction sensitive based on the initial homophily strength parameters and then involve the adaptive homophily estimators to adapt to characteristics of nodes.
Existing work [
20,
21] assumes that a Sybil’s following behavior is unpredictable. So, from a Sybil tail
u’s standpoint, we cannot gain much effective information about the head’s state. Similarly, if a benign user is being followed, chances are slim that one could infer the follower’s state. Therefore, in these cases, we only use the initial homophily strength parameters
and
for a rough estimation of the benign head and the Sybil tail’s homophily strength as shown in
Figure 5(1,3), respectively.
Dynamic homophily estimators
and
can be applied to weaken the homophily-based inference for “dumb” benign nodes who always follow Sybils and enhance the heterogeneity-based inference for “enticing” Sybil nodes who have plenty benign followers. In each iteration, they are updated to further elaborate the initial homophily strength
and
according to the nodes’ preferences as shown in
Figure 5(2,4).
Formally, we have unidirectional edge-potential functions as follows. When sending a message from tail
u to head
v of a unidirectional edge, we have
design:
When sending a message from head
u to tail
v,
follows:
For bidirectional edges, we adopt homophily strength
with the following modification:
To sum up, we have the following direction-sensitive edge-potential design:
Integrated with the proposed edge-potential function
, the pMRF model along with the LBP algorithm forms SybilHP. Given the social graph and a training set, SybilHP returns the posterior probability of nodes being Sybil in graph
G for further classification or ranking tasks. Algorithm 1 summarizes the pseudo-code of SybilHP, from which, we can see that the time complexity of SybilHP is
. As most social networks are often sparse graphs, we have
.
| Algorithm 1 SybilHP |
Require: directed social graph , the training set , the soft probability for labeled Sybil q, initial homophily strength parameters , , , , , and the number of iterations . Ensure:
posterior probability distribution for nodes do initialize according to u, if , if , if u is unlabeled, initialize , initialize for all . end for for
do for edges do compute and per Equation ( 3), update , , and per Equations ( 7) and ( 9). end for for do update per Equation ( 8). end for end for Return for all u.
|
5. Experiment
5.1. Experiment Setup
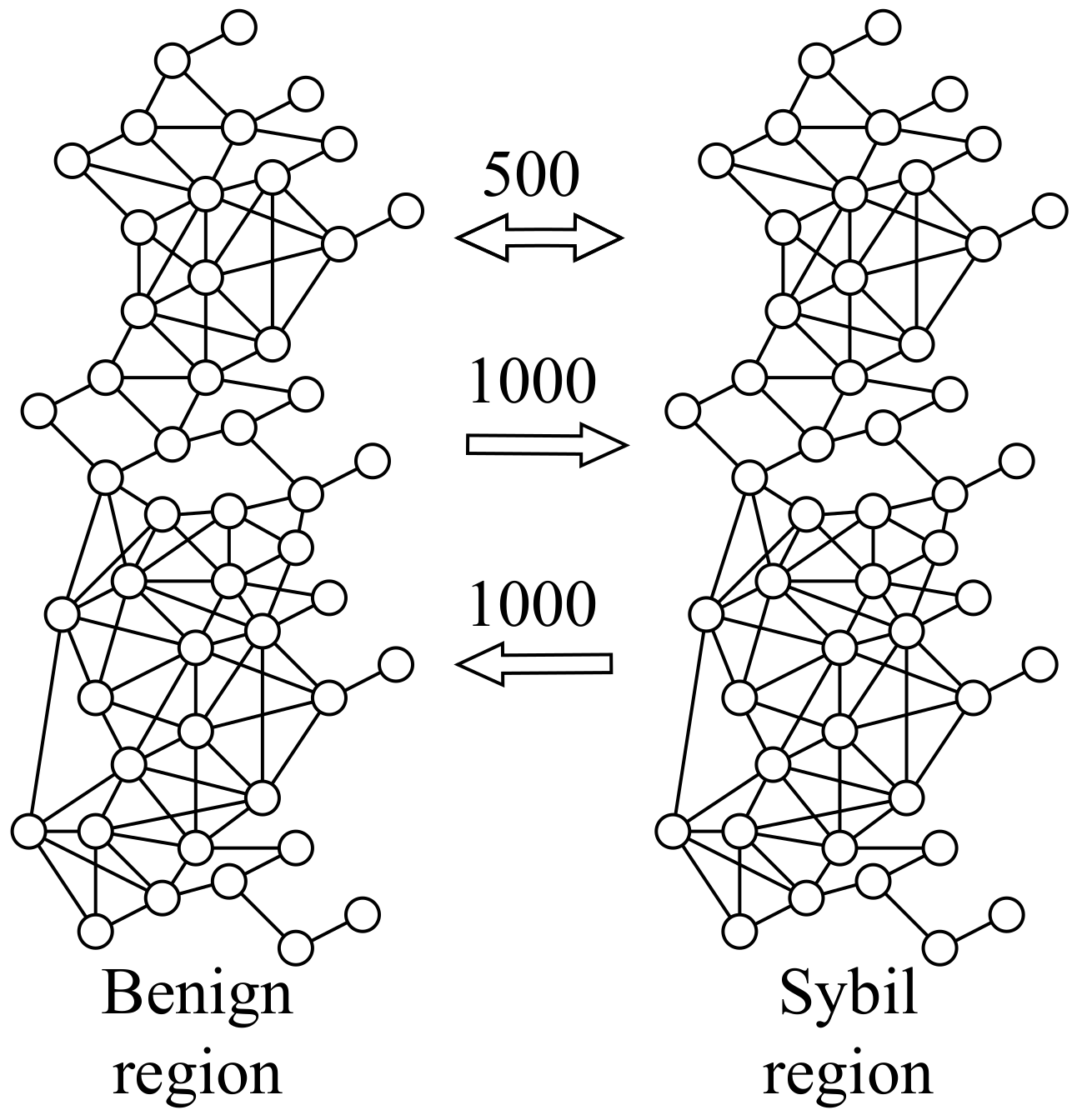
Dataset description: In this section, we first evaluate the influence of various factors including Sybil attack strength, Sybil group scale, and label noise in SybilHP. Since our experiments require social networks with various forms and patterns, we synthesize benign and Sybil regions based on a real-world social graph.
- (1)
Synthetic-directed Pokec
For the sake of fairness and comparison, we adopted this directed Pokec network [
43] from the official repository (
https://github.com/binghuiwang/sybildetection (accessed on 2 July 2022)) of for GANG [
20], SybilSCAR [
17] and SybilBelief [
16] for robustness and performance illustration. In particular, we extract a connected component that contains 10,000 nodes and 90,065 edges from Pokec as the benign region, and then we make the Sybil region a replicate of the benign region and add (bidirectional, unidirectional) attack edges between the two regions uniformly at random. If not specified, we add 500 bidirectional edges, 1000 unidirectional Sybil-to-benign attack edges, and 100 unidirectional benign-to-Sybil compromised edges as illustrated in
Figure 6. We keep 100 Sybil and 100 benign users as the training set and test on the overall social graph.
Furthermore, we compare the detection performance of the proposed method and some state-of-the-art benchmark methods on a large real Twitter dataset.
- (2)
Real-world Twitter follower–followee graph
By the means of breadth-first search (BFS) graph traversal, we sampled a Twitter follower–followee graph with 269,640 nodes and 6,818,501 edges from [
44]. The original data was crawled by Kwak in 2009 [
44]. The graph is directed and includes 41,652,230 users and 1,468,364,884 edges. However, only 10,000 Sybils and 10,000,000 benign users are labeled, which can be used as ground truth for training and testing. The remaining nodes are treated as unknown. In other words, there are less than a quarter of labeled nodes in the original dataset.
The ratio of Sybil to benign nodes is even more severely imbalanced at 1:100, which makes the discrimination of benign nodes dominate the performance evaluation results. To address the under-labeling and imbalance of the original dataset, we sampled the original dataset. The BFS starts from these labeled nodes, and we only keep those labeled neighbors until all nodes are reached. Finally, we delete those isolated nodes, and we obtain 91,263 Sybils and 178,377 benign users to form our connected and labeled social graph. We divide 9000 Sybil and 17,000 benign users (about 10%) from them as the labeled training set and test on the overall social graph.
An overview of the datasets is presented in
Table 1.
Compared methods: We compared SybilHP with directed graph-based method GANG [
20] (including a matrix version and a basic version) and other LBP-based methods SybilSCAR [
17] (SybilSCAR-D) and SybilBelief [
16]. For undirected graph-based methods, we transformed the directed graph to be undirected by only keeping those bidirectional edges (which is recommended by the original paper). Note that this can cause many nodes isolated and fail to involve in the LBP process.
Parameter setting: For SybilHP, we set the prior probability for labeled Sybil nodes
, which was also suggested by authors of GANG, SybilSCAR, and SybilBelief; We assigned initial homophily strength parameters
,
,
,
,
, and set the number of LBP iterations
. For GANG, we set
adapting to Twitter as suggested by the author. Note that we also adopt the basic version of GANG with an optimized parameter (
) for our Twitter dataset. We set the parameters of SybilSCAR and SybilBelief in the same way as introduced in [
16,
17]. An overview of the parameter settings is presented in
Table 2.
Evaluation metrics: The following indicators are adopted to evaluate the performance of Bot detection methods:
Accuracy is the fraction of instances that are correctly classified. It is a simple and intuitive metric, but it can be misleading in cases where the classes are imbalanced.
Recall is the fraction of positive instances that are correctly classified. It is a measure of how well the model is able to identify positive instances.
Precision is the fraction of predicted positive instances that are actually positive. It is a measure of how well the model is able to avoid false positives.
The area under the curve (AUC) is a measure of the overall performance of a classifier. It is calculated by plotting the true positive rate (TPR) against the false positive rate (FPR) for a range of classification thresholds. A higher AUC indicates a better-performing classifier.
We implemented SybilHP in Python 3.8. For the proper comparative experiment, we also ported the original C++ codes (from the authors) of GANG, SybilSCAR, and SybilBelief to Python.
5.2. General Robustness Evaluation
We first briefly evaluate the robustness of SybilHP under different conditions including attack edges density, Sybil community scales, and labeling with noises on the Synthesized Pokec dataset.
Impact of attack edges: We add different numbers of unidirectional attack edges and bidirectional edges (compromised edges) in a ratio of 2:1.
Table 3 shows the accuracy decay as the number of attacking edges increases. We found no distinct performance difference between these homophily-inference-based methods. As the synthesized dataset does not reflect the behavioral preferences of real-world users and Sybil users, the proposed algorithm has only a slight advantage on this dataset, which could be attributed to the additional parameters.
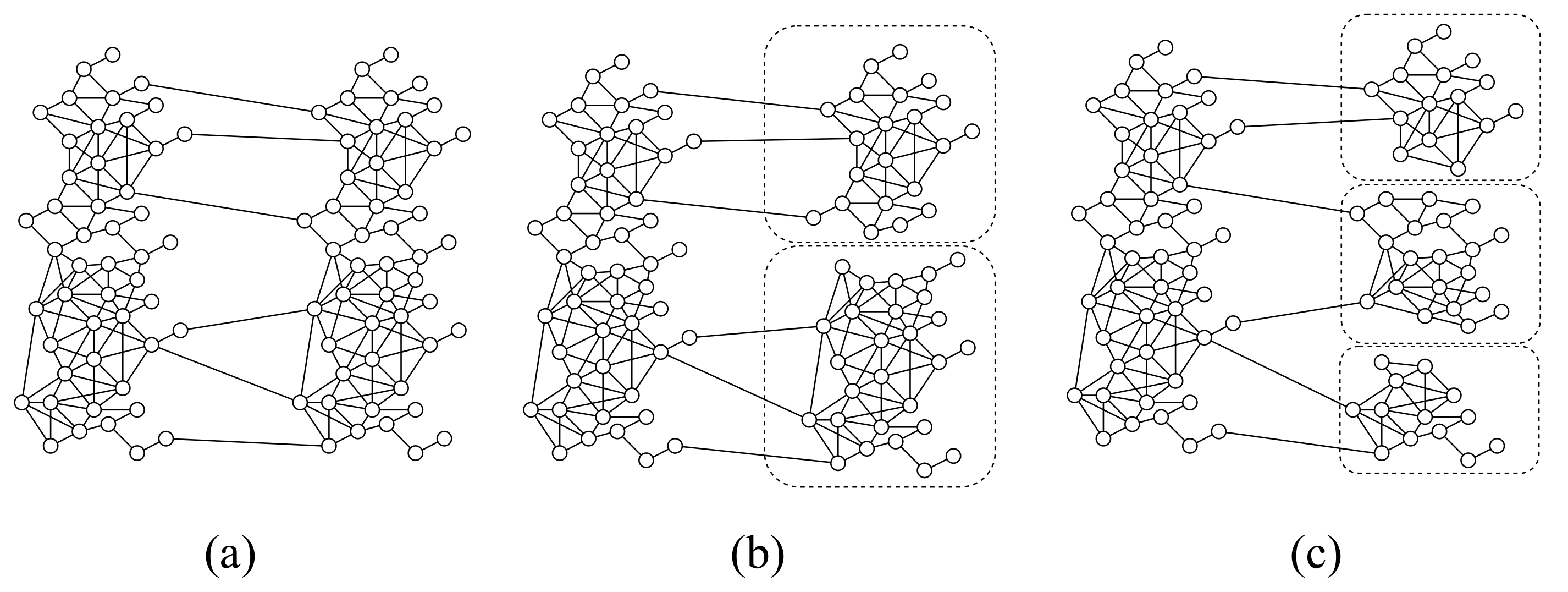
Impact of Sybil community scale: To be more realistic, we split the Sybil region to form several smaller communities to simulate the scenario when multiple Sybil clusters launch attacks on a benign user community, as shown in
Figure 7, where (a), (b), and (c) correspond to one, two, and three Sybil clusters attacking the benign region, respectively. Then, the detection performance of SybilHP is examined. Specifically, we partition the Sybil region by obtaining a certain number of neighboring nodes that constitute the community through a BFS traversal starting at a certain point.
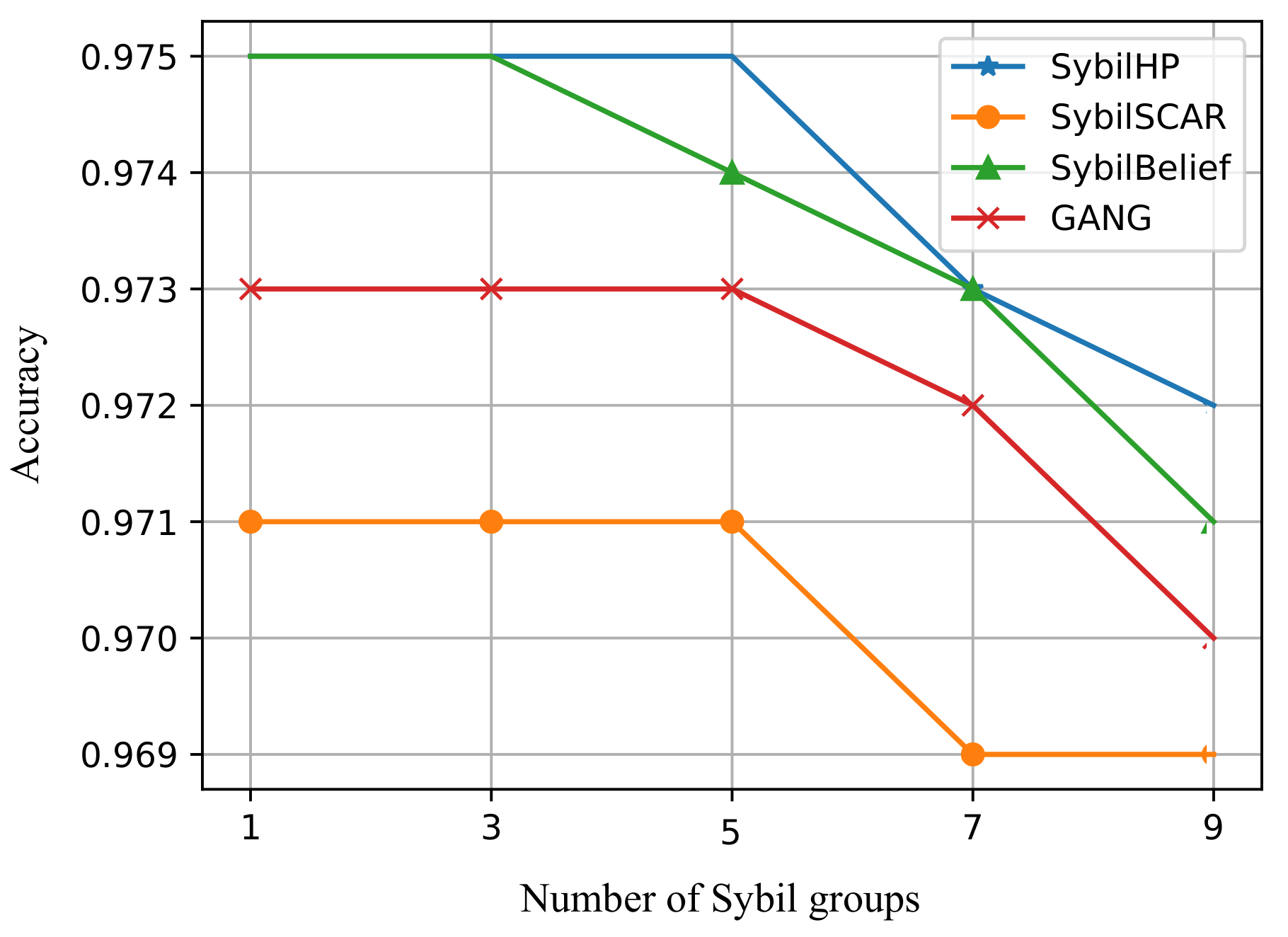
It can be seen that the total number of Sybil communities increases as the number of individual community nodes decreases, which is similar to the real-world scenario in which Sybil is controlled by different organizations and individuals. We did not change the edges between Sybil and benign regions nor the training set, and the detection performance of SybilHP is shown in
Figure 8. It can be seen that the size of the Sybil cluster has almost no impact on the performance of our method. Note, however, that this assumes that nodes in the training set are present in each Sybil cluster.
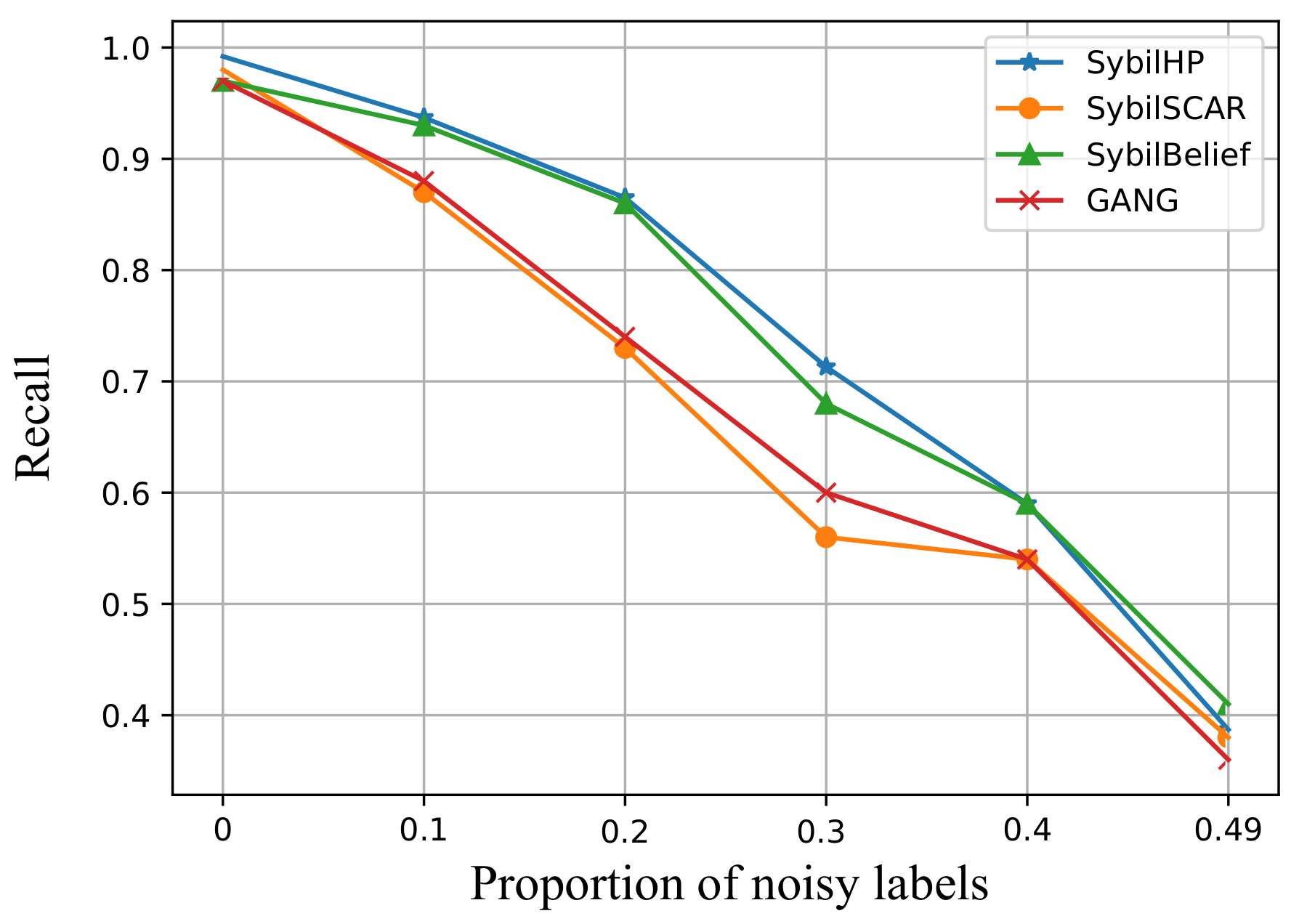
Impact of label noises:In the case of a partially mislabeled training set, LBP-based methods have inherent robustness against label noise.
Figure 9 shows the influences of different percentages of false labels on the recall rate for Sybil. We found that SybilBelief and SybilHP showed stronger robustness against label noises compared to SybilSCAR and GANG, which could be due to their nonlinearity.
5.3. Comparative Experiments on Real-World Twitter Dataset
In this section, we first focus on the model parameters’ adaptation to the real-world Twitter datasets and then give a comparison study with other LBP-based methods.
Model parameter adaptation: The initial homophily strength
for edge potential can be taken as adjustable parameters. We evaluate different configurations of these parameters by variable-controlling on the directed Twitter dataset.
Figure 10 shows the variation of detection performance when we vary one of the parameters. We observe that there are points with a good trade-off between precision and recall, and we set them as the parameters for subsequent experiments.
Overall classification and ranking performance:
Table 4 shows the overall classification performance compared with the other state-of-the-art Sybil-detection methods. SybilHP achieved the highest precision and accuracy and second highest recall. Note that the SybilHP_basic in the table does not incorporate the adaptive homophily estimator mechanism, we see that, with the ablation of the adaptive homophily estimator enhancement, SybilHP still shows superiority over other methods.
As LBP-based detection methods estimate the posterior probability for each node to be Sybil, we can rank the nodes by the posterior probabilities to produce a more thorough performance analysis. We take the Area Under the Receiver Operating Characteristic Curve (AUC) as the evaluation measure for ranking, which can be interpreted as the probability that a randomly sampled Sybil node is ranked higher than a randomly sampled benign node in the testing dataset.
Figure 11 shows the overall ranking performance by AUC, and we make the following observations.
First, we found that methods designed for directed social graphs substantially outperformed those methods for undirected graphs. To adapt to methods for undirected graphs, we only kept reciprocal edges in the original social graph (as the original papers suggest), which resulted in some isolated nodes that were unable to be involved in the computation. This is the main reason for the lower AUC performance compared with that reported in the original paper. However, even when we reevaluate these methods after excluding these isolated nodes, their performance is still limited by the loss of directed information, as SybilSCAR_re and SybilBelief_re shown in
Figure 11.
Second, we can see that complexity and more refined modeling facilitate the capturing of the characteristics of the data. SybilBelief, the basic version of GANG and SybilHP are more effective than their simplified versions because the computational efficiency can hardly be balanced with accuracy.
Finally, we observed that, without an adaptive homophily estimator mechanism, SybilHP_basic still had decent performance. Furthermore, the performance improvement brought by adaptive homophily estimators is not significant, so the balance of performance and computational cost should be properly considered in practical applications.
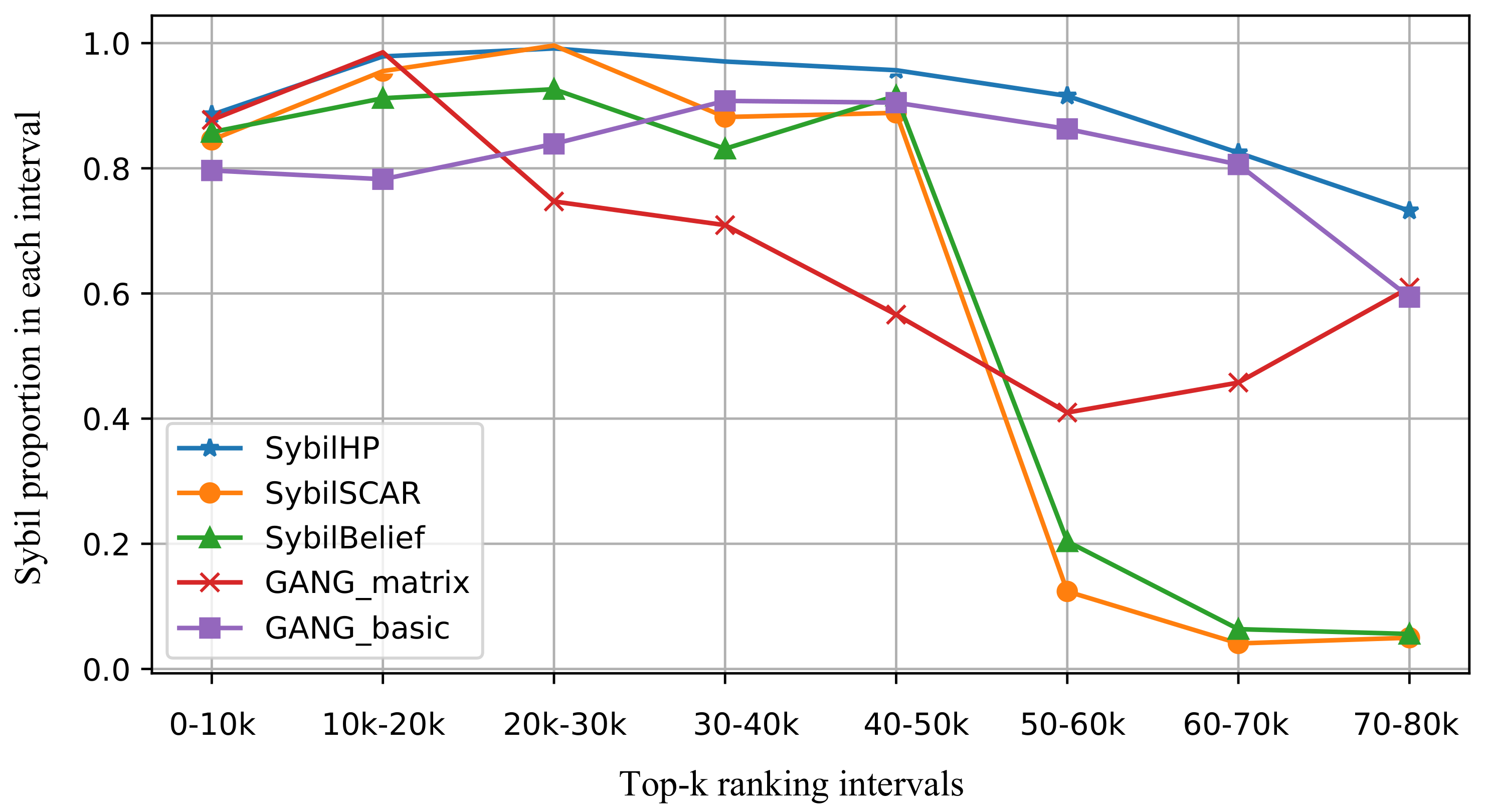
Sybil nodes in top-ranked nodes: Since the ranking of nodes can be used as a priority list to do further inspection and verification by system or humans, the accuracy in the top-ranked nodes is important because extra costs for human workers will rule out the majority of nodes. Therefore, we further compare the proportion of Sybil in different fractions of top-80,000 positive-reported nodes. Specifically, we divide top-80,000 nodes (because the dataset only contains around 90,000 Sybils) into 10 intervals and calculate the number of Sybils in each interval.
Figure 12 shows the distribution of Sybils detected in each 10,000 interval. For GANG_matrix, SybilSCAR, and SybilBelief, we can observe a clear drop at the interval 50-60k, while the proposed SybilHP proceeds with its superiority. We speculate that a group of Twitter users with a particular following pattern, “dumb benign followers” or “intriguing Sybils” could have managed to evade these detection methods. However, SybilHP has captured their pattern and discovered them.