A Deep Reinforcement Learning Approach for Efficient, Safe and Comfortable Driving †
Abstract
1. Introduction
- (i)
- We design a DRL framework that takes into account and appropriately weights the various environmental factors influencing ACC, including vehicle stability. To the best of our knowledge, we are the first to comprehensively and successfully address all relevant issues, as existing studies focusing on ACC have not focused on such a crucial issue as vehicle stability.
- (ii)
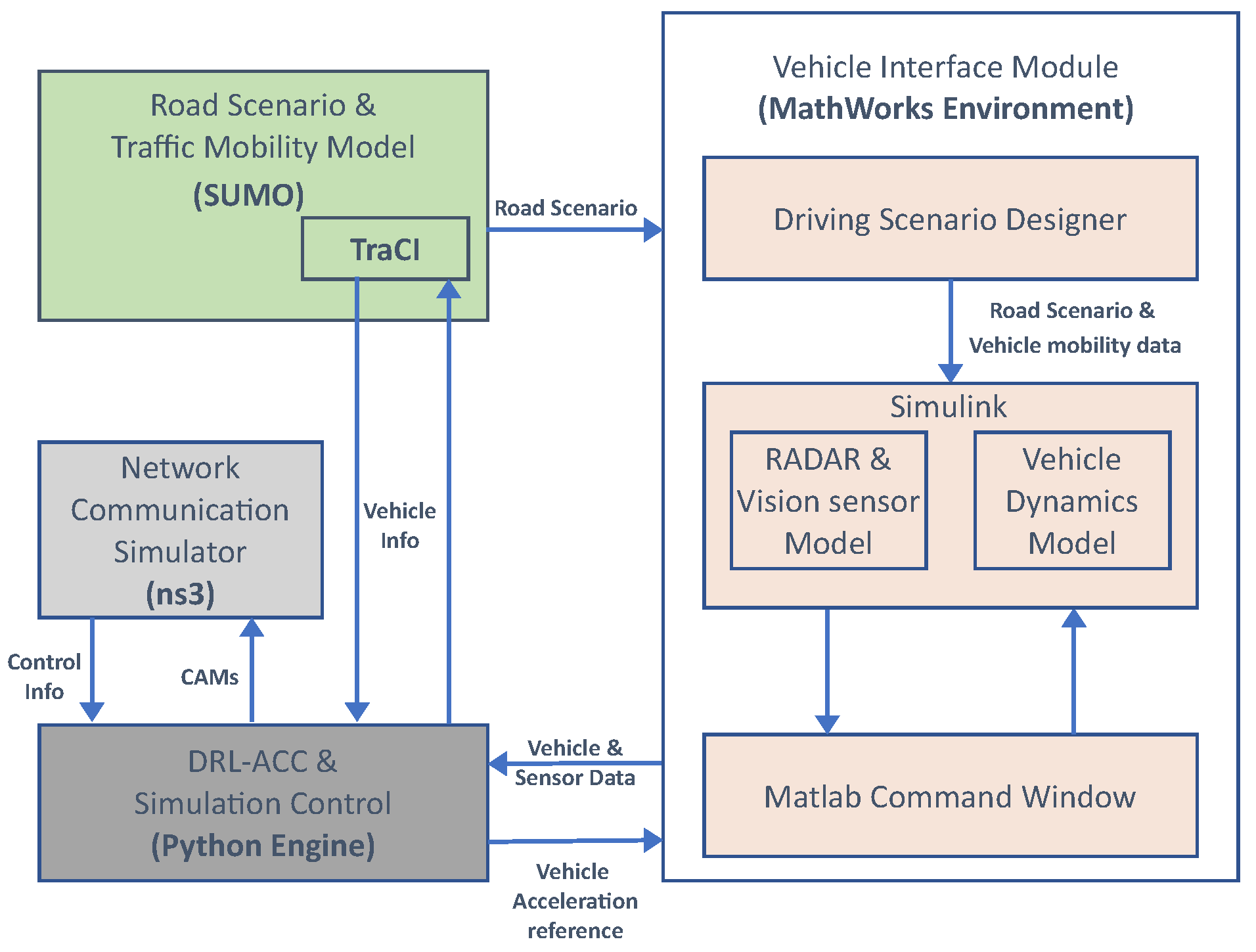
- We assess the performance of our DRL framework by incorporating it into the CoMoVe framework [12], which offers a realistic representation of traffic mobility, vehicle communication, and dynamics. By utilizing such a fully fledged simulation tool, we derive performance results regarding vehicle stability, comfort, and traffic flow efficiency under diverse traffic conditions and road circumstances.
- (iii)
- We compare the DRL framework results against traditional ACC and cooperative ACC (CACC) algorithms and demonstrate the benefits of utilizing the information obtained through V2X communications in the learning process of the DRL agent, especially concerning the algorithm convergence time.
2. Related Work
3. Design and Implementation of the DRL Framework
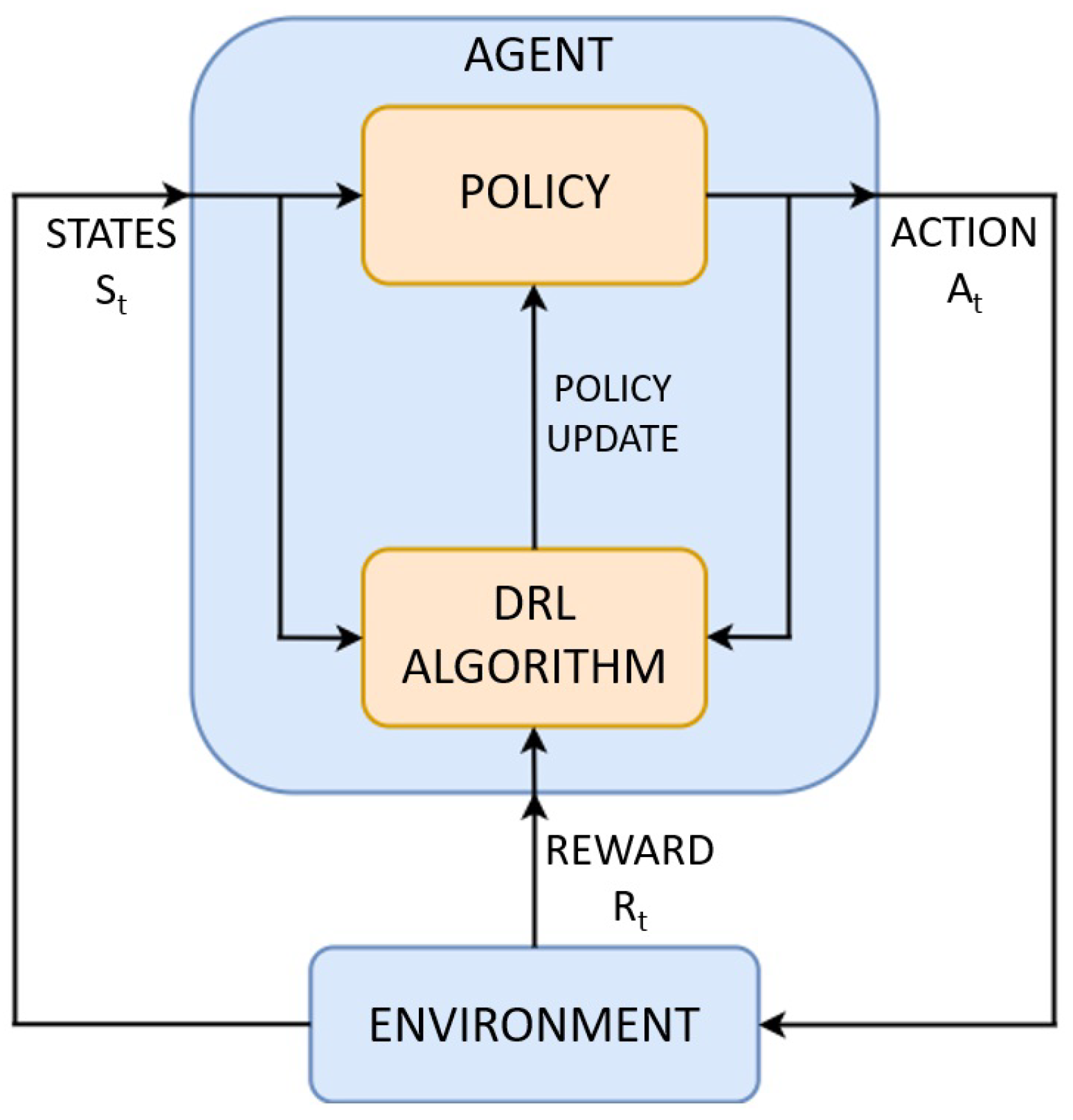
3.1. The DRL Model
3.1.1. Preliminaries
3.1.2. DRL-Based Acc Application
3.2. Integrating the Drl Model in the Comove Framework
4. Performance Results
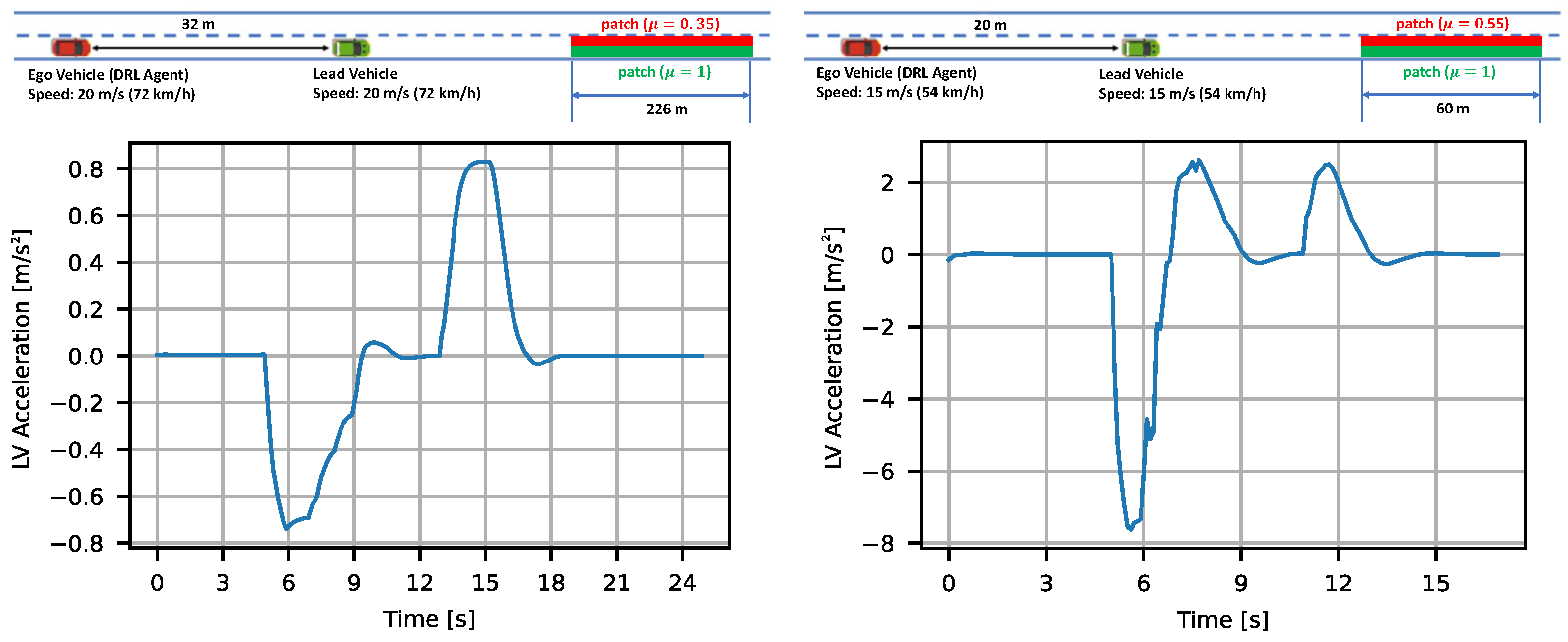
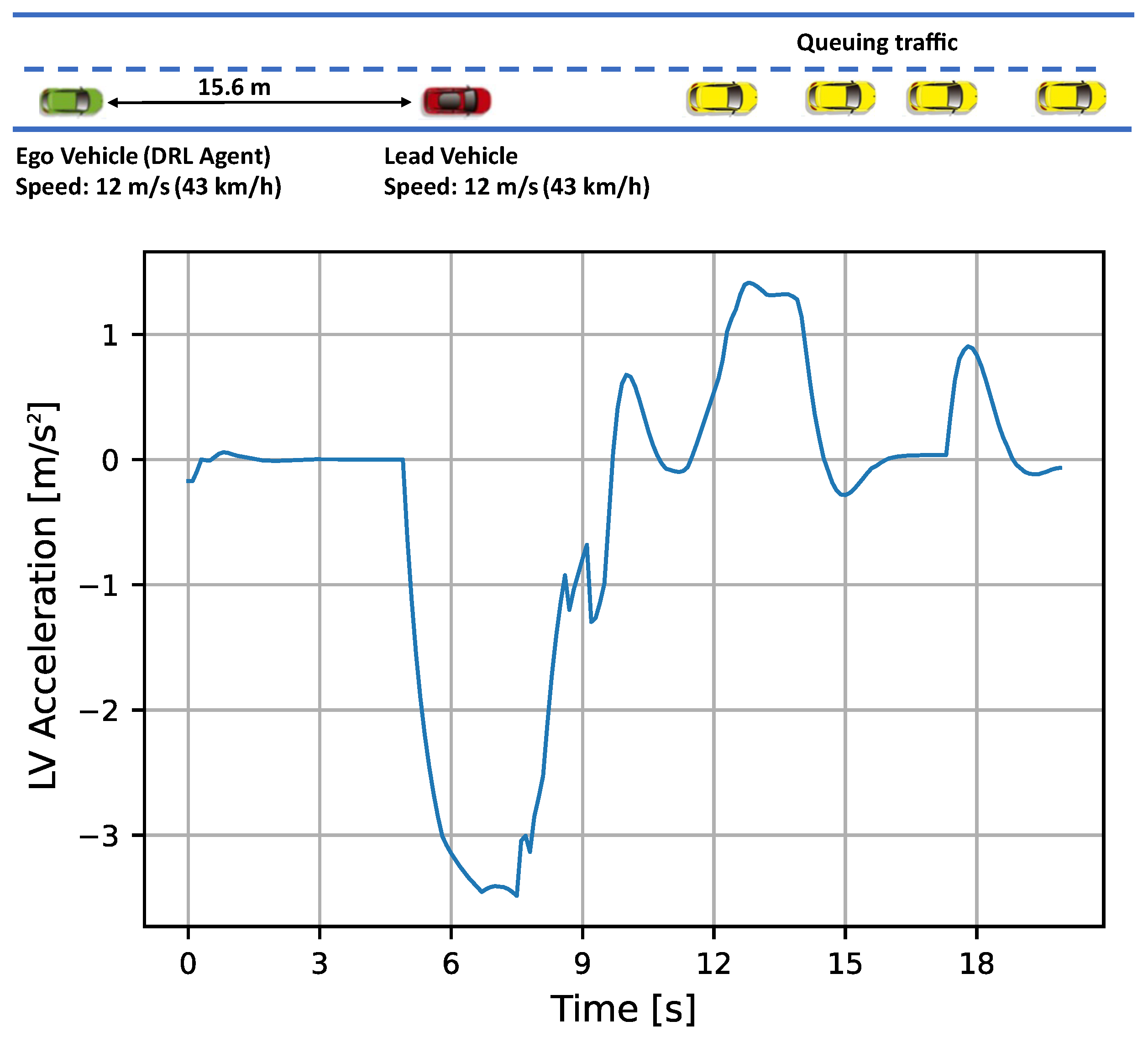
4.1. Reference Scenarios
4.2. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACC | Adaptive Cruise Control |
| DRL | Deep Reinforcement Learning |
| ML | Machine Learning |
| V2V | Vehicle-to-Vehicle Communication |
| V2X | Vehicle-to-Everything Communication |
| V2I | Vehicle-to-Infrastructure Communication |
| ADAS | Advanced Driver Assistance Systems |
| GNNS | Global navigation satellite system |
| RL | Reinforcement Learning |
| DDPG | Deep Deterministic Policy Gradient |
| CACC | Cooperative Adaptive Cruise Control |
| MPC | Model Predictive Control |
| CoMoVe | Communication, Mobility, and Vehicle dynamics |
| MDP | Markov Decision Process |
| DP | Dynamic Programming |
| TD | Temporal-Difference |
| TTC | Time-to-Collision |
| RMSE | Root Mean Square Error |
References
- World Health Organization. Global Status Report on Road Safety 2018; WHO: Geneva, Switzerland, 2018; Available online: https://www.who.int/publications/i/item/9789241565684 (accessed on 19 April 2023).
- Koglbauer, I.; Holzinger, J.; Eichberger, A.; Lex, C. Drivers’ Interaction with Adaptive Cruise Control on Dry and Snowy Roads with Various Tire-Road Grip Potentials. J. Adv. Transp. 2017, 2017, 5496837. [Google Scholar] [CrossRef]
- Das, S.; Maurya, A.K. Time Headway Analysis for Four-Lane and Two-Lane Roads. Transp. Dev. Econ. 2017, 3, 9. [Google Scholar] [CrossRef]
- Li, Y.; Lu, H.; Yu, X.; Sui, Y.G. Traffic Flow Headway Distribution and Capacity Analysis Using Urban Arterial Road Data. In Proceedings of the International Conference on Electric Technology and Civil Engineering (ICETCE), Lushan, China, 22–24 April 2011; pp. 1821–1824. [Google Scholar] [CrossRef]
- Shrivastava, A.; Li, P. Traffic Flow Stability Induced By Constant Time Headway Policy For Adaptive Cruise Control (ACC) Vehicles. In Proceedings of the 2000 American Control Conference. ACC (IEEE Cat. No.00CH36334), Chicago, IL, USA, 28–30 June 2000; Volume 3, pp. 1503–1508. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, Y.; Pu, Z.; Hu, J.; Wang, X.; Ke, R. Safe, efficient, and comfortable velocity control based on reinforcement learning for autonomous driving. Transp. Res. Part C Emerg. Technol. 2020, 117, 102662. [Google Scholar] [CrossRef]
- Desjardins, C.; Chaib-draa, B. Cooperative Adaptive Cruise Control: A Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1248–1260. [Google Scholar] [CrossRef]
- Liu, W.; Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Automated Vehicle Sideslip Angle Estimation Considering Signal Measurement Characteristic. IEEE Sens. J. 2021, 21, 21675–21687. [Google Scholar] [CrossRef]
- Gao, L.; Xiong, L.; Xia, X.; Lu, Y.; Yu, Z.; Khajepour, A. Improved Vehicle Localization Using On-Board Sensors and Vehicle Lateral Velocity. IEEE Sens. J. 2022, 22, 6818–6831. [Google Scholar] [CrossRef]
- Xia, X.; Hashemi, E.; Xiong, L.; Khajepour, A. Autonomous Vehicle Kinematics and Dynamics Synthesis for Sideslip Angle Estimation Based on Consensus Kalman Filter. IEEE Trans. Control Syst. Technol. 2023, 31, 179–192. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar] [CrossRef]
- Selvaraj, D.C.; Hegde, S.; Chiasserini, C.F.; Amati, N.; Deflorio, F.; Zennaro, G. A Full-fledge Simulation Framework for the Assessment of Connected Cars. Transp. Res. Procedia 2021, 52, 315–322. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Z.; Yang, H.; Yang, L. Artificial intelligence applications in the development of autonomous vehicles: A survey. IEEE/CAA J. Autom. Sin. 2020, 7, 315–329. [Google Scholar] [CrossRef]
- Badue, C.; Guidolini, R.; Carneiro, R.V.; Azevedo, P.; Cardoso, V.B.; Forechi, A.; Jesus, L.; Berriel, R.; Paixão, T.M.; Mutz, F.; et al. Self-driving cars: A survey. Expert Syst. Appl. 2021, 165, 113816. [Google Scholar] [CrossRef]
- Kuutti, S.; Bowden, R.; Jin, Y.; Barber, P.; Fallah, S. A Survey of Deep Learning Applications to Autonomous Vehicle Control. IEEE Trans. Intell. Transp. Syst. 2021, 22, 712–733. [Google Scholar] [CrossRef]
- Matheron, G.; Perrin, N.; Sigaud, O. Understanding Failures of Deterministic Actor-Critic with Continuous Action Spaces and Sparse Rewards. In Artificial Neural Networks and Machine Learning—ICANN 2020; Farkaš, I., Masulli, P., Wermter, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12397, pp. 308–320. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, X.; Sun, J. Automated vehicle’s behavior decision making using deep reinforcement learning and high-fidelity simulation environment. Transp. Res. Part C Emerg. Technol. 2019, 107, 155–170. [Google Scholar] [CrossRef]
- Fu, Y.; Li, C.; Yu, F.R.; Luan, T.H.; Zhang, Y. A Decision-Making Strategy for Vehicle Autonomous Braking in Emergency via Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2020, 69, 5876–5888. [Google Scholar] [CrossRef]
- Nageshrao, S.; Tseng, H.E.; Filev, D. Autonomous Highway Driving using Deep Reinforcement Learning. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 2326–2331. [Google Scholar] [CrossRef]
- Pan, F.; Bao, H. Reinforcement Learning Model with a Reward Function Based on Human Driving Characteristics. In Proceedings of the 2019 15th International Conference on Computational Intelligence and Security (CIS), Macao, Macao, 13–16 December 2019; pp. 225–229. [Google Scholar] [CrossRef]
- Dettmann, A.; Hartwich, F.; Roßner, P.; Beggiato, M.; Felbel, K.; Krems, J.; Bullinger, A.C. Comfort or Not? Automated Driving Style and User Characteristics Causing Human Discomfort in Automated Driving. Int. J. Hum.–Comput. Interact. 2021, 37, 331–339. [Google Scholar] [CrossRef]
- Amaral, J.R.; Göllinger, H.; Fiorentin, T.A. Improvement of Vehicle Stability Using Reinforcement Learning. In Proceedings of the Anais do XV Encontro Nacional de Inteligência Artificial e Computacional (ENIAC 2018), São Paulo, Brazil, 22–25 October 2018; Sociedade Brasileira de Computação—SBC: São Paulo, Brazil, 2018; pp. 240–251. [Google Scholar] [CrossRef]
- Lin, Y.; McPhee, J.; Azad, N.L. Comparison of Deep Reinforcement Learning and Model Predictive Control for Adaptive Cruise Control. IEEE Trans. Intell. Veh. 2021, 6, 221–231. [Google Scholar] [CrossRef]
- Urra, O.; Ilarri, S. MAVSIM: Testing VANET applications based on mobile agents. In Cognitive Vehicular Networks; CRC Press: Boca Raton, FL, USA, 2016; pp. 199–224. [Google Scholar] [CrossRef]
- Stevic, S.; Krunic, M.; Dragojevic, M.; Kaprocki, N. Development and Validation of ADAS Perception Application in ROS Environment Integrated with CARLA Simulator. In Proceedings of the 2019 27th Telecommunications Forum (TELFOR), Belgrade, Serbia, 26–27 November 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018; p. 526. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Mechanical Engineering Series; Springer US: Boston, MA, USA, 2012. [Google Scholar] [CrossRef]
- Bae, I.; Moon, J.; Jhung, J.; Suk, H.; Kim, T.; Park, H.; Cha, J.; Kim, J.; Kim, D.; Kim, S. Self-Driving like a Human driver instead of a Robocar: Personalized comfortable driving experience for autonomous vehicles. arXiv 2020, arXiv:2001.03908. [Google Scholar] [CrossRef]
- Makridis, M.; Mattas, K.; Ciuffo, B. Response Time and Time Headway of an Adaptive Cruise Control. An Empirical Characterization and Potential Impacts on Road Capacity. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1677–1686. [Google Scholar] [CrossRef]
- Benalie, N.; Pananurak, W.; Thanok, S.; Parnichkun, M. Improvement of adaptive cruise control system based on speed characteristics and time headway. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 2403–2408. [Google Scholar] [CrossRef]
- Houchin, A.; Dong, J.; Hawkins, N.; Knickerbocker, S. Measurement and Analysis of Heterogenous Vehicle Following Behavior on Urban Freeways: Time Headways and Standstill Distances. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 888–893. [Google Scholar] [CrossRef]
- Wong, J.Y. Theory of Ground Vehicles, 3rd ed.; John Wiley: New York, NY, USA, 2001. [Google Scholar]
- Selvaraj, D.C.; Hegde, S.; Amati, N.; Deflorio, F.; Chiasserini, C.F. An ML-Aided Reinforcement Learning Approach for Challenging Vehicle Maneuvers. IEEE Trans. Intell. Veh. 2023, 8, 1686–1698. [Google Scholar] [CrossRef]

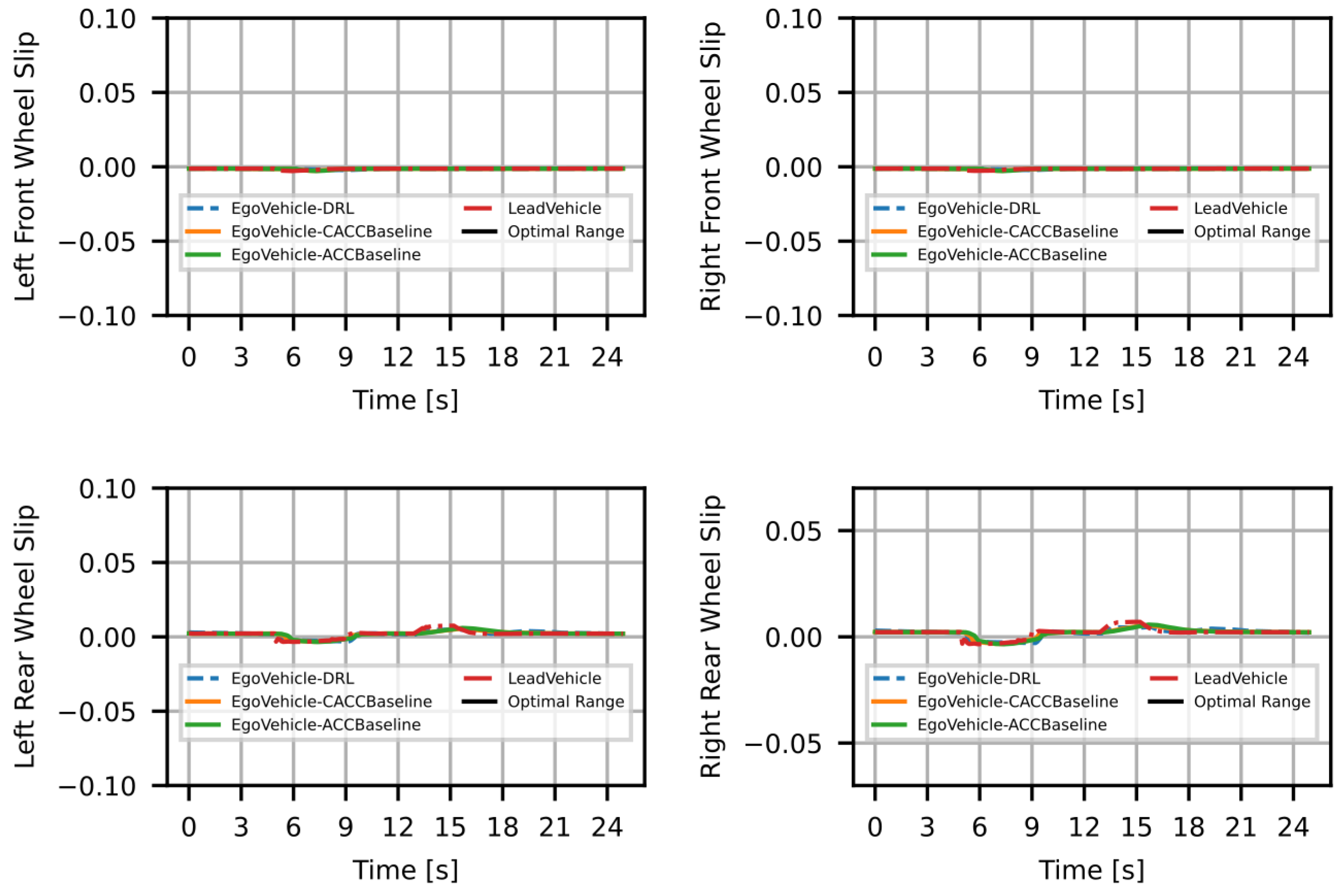
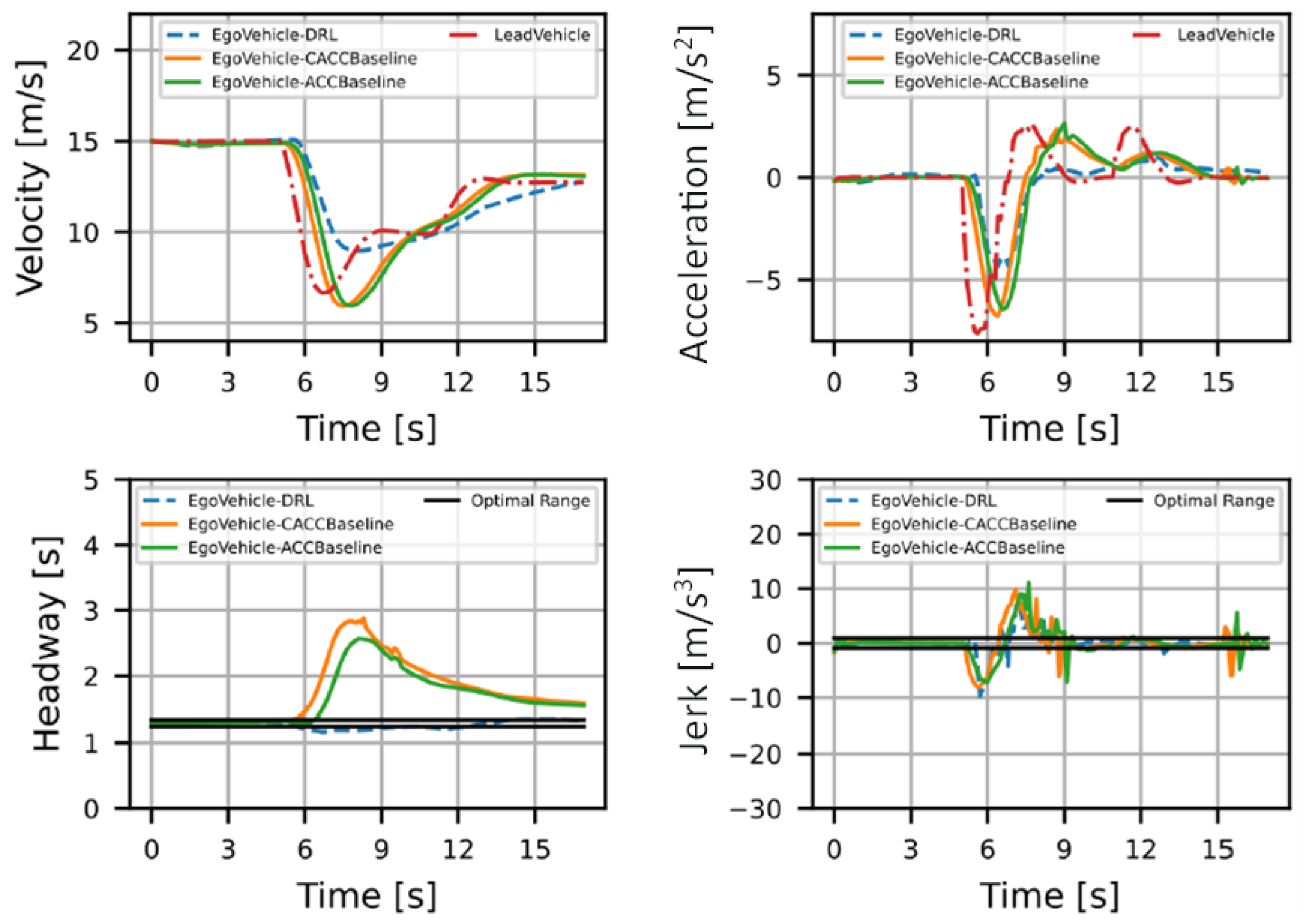
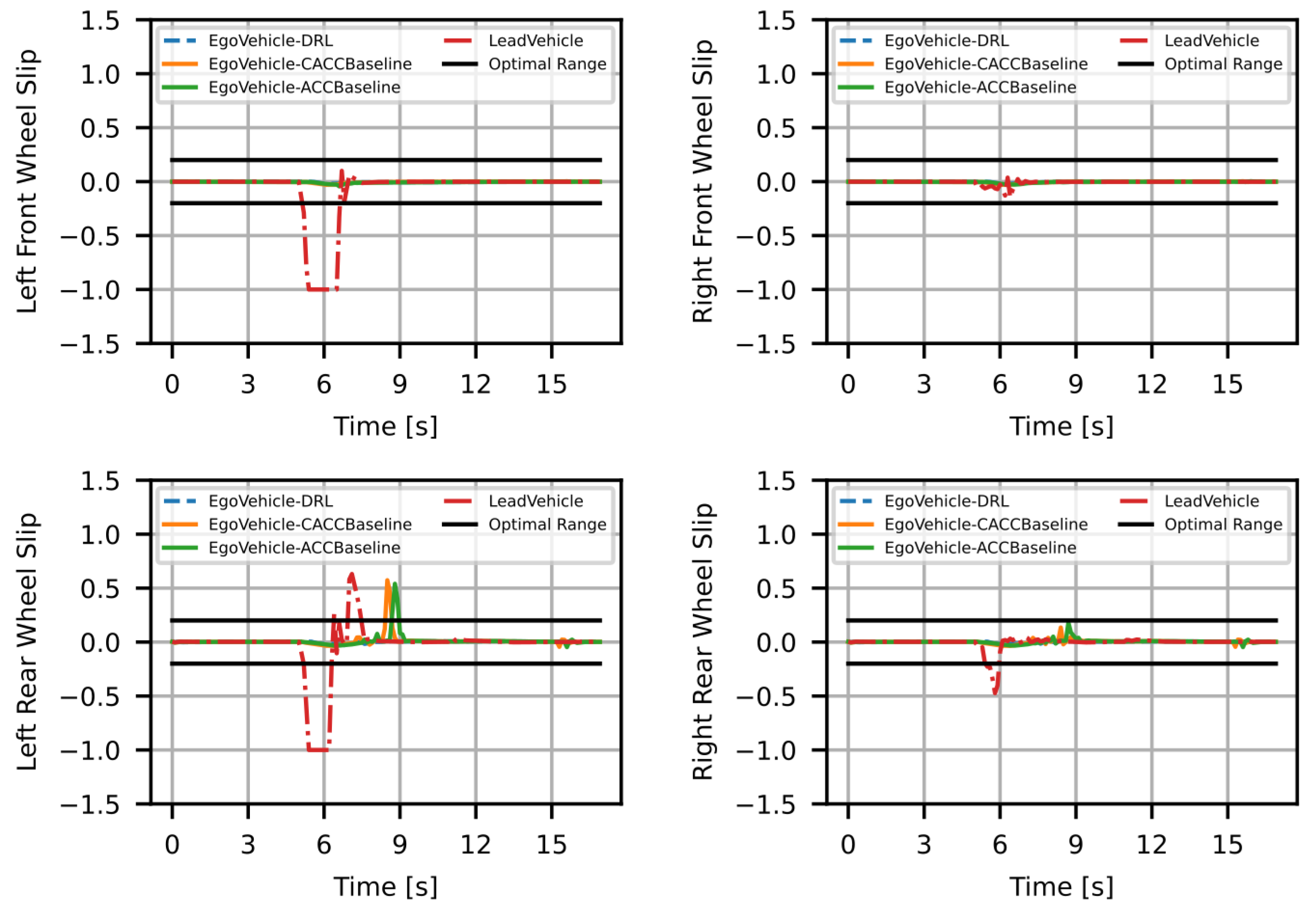
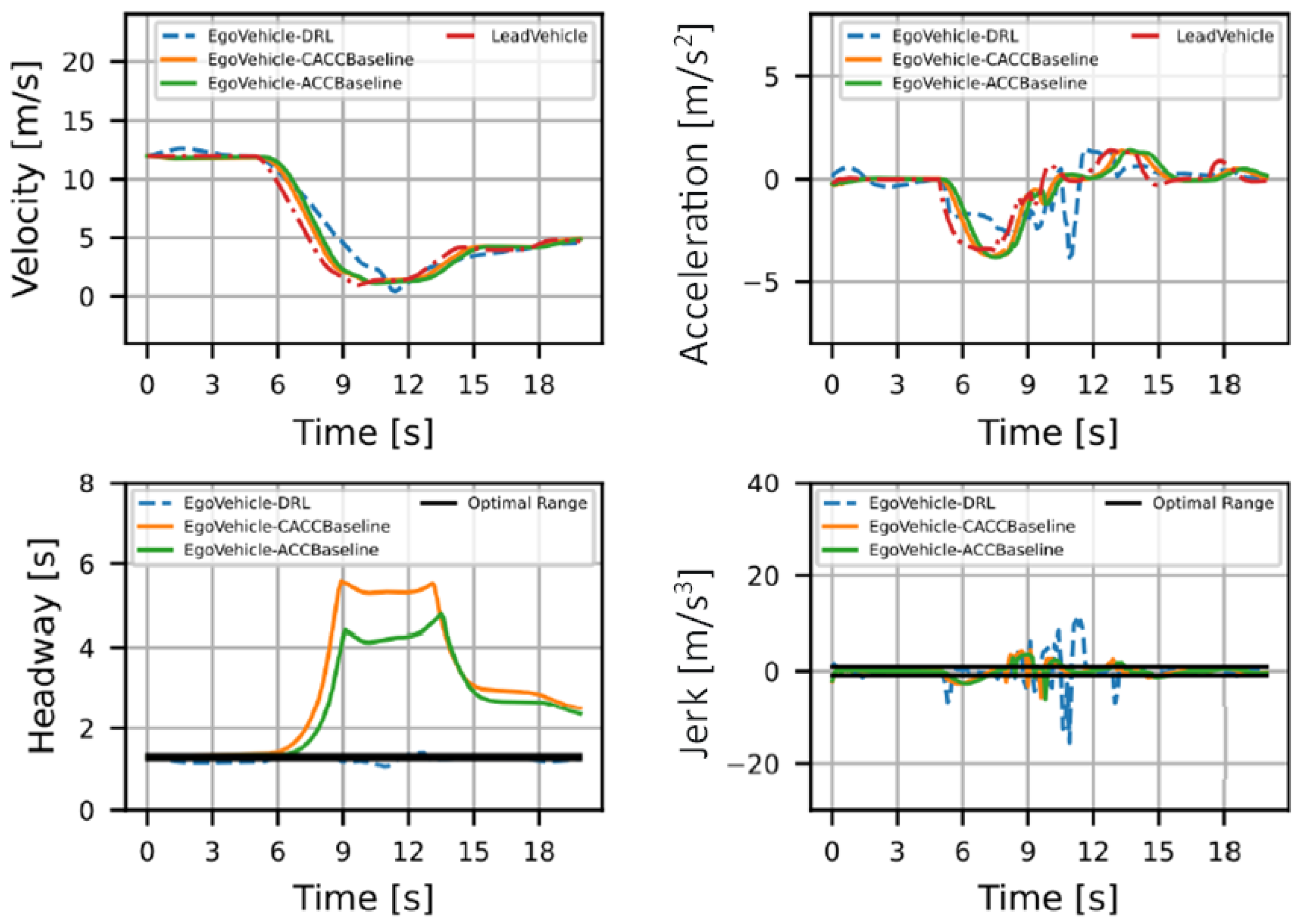
| RMSE | ||||
|---|---|---|---|---|
| Metrics | Scenarios | DRL | ACC | CACC |
| Headway (Ideal = 1.3) | Normal | 0.0278 | 0.0638 | 0.073 |
| Sharp Deceleration | 0.0629 | 0.5298 | 0.6561 | |
| Traffic queuing | 0.0839 | 1.7594 | 2.2911 | |
| Jerk (Ideal = 0) | Normal | 0.2111 | 0.1804 | 0.1693 |
| Sharp Deceleration | 1.846 | 2.471 | 2.5839 | |
| Traffic queuing | 2.8181 | 1.1773 | 1.2699 | |
| Slip (Ideal = 0) | Normal | 0.0028 | 0.0029 | 0.0028 |
| Sharp Deceleration | 0.0071 | 0.0581 | 0.0594 | |
| Traffic queuing | 0.0202 | 0.01 | 0.0115 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selvaraj, D.C.; Hegde, S.; Amati, N.; Deflorio, F.; Chiasserini, C.F. A Deep Reinforcement Learning Approach for Efficient, Safe and Comfortable Driving. Appl. Sci. 2023, 13, 5272. https://doi.org/10.3390/app13095272
Selvaraj DC, Hegde S, Amati N, Deflorio F, Chiasserini CF. A Deep Reinforcement Learning Approach for Efficient, Safe and Comfortable Driving. Applied Sciences. 2023; 13(9):5272. https://doi.org/10.3390/app13095272
Chicago/Turabian StyleSelvaraj, Dinesh Cyril, Shailesh Hegde, Nicola Amati, Francesco Deflorio, and Carla Fabiana Chiasserini. 2023. "A Deep Reinforcement Learning Approach for Efficient, Safe and Comfortable Driving" Applied Sciences 13, no. 9: 5272. https://doi.org/10.3390/app13095272
APA StyleSelvaraj, D. C., Hegde, S., Amati, N., Deflorio, F., & Chiasserini, C. F. (2023). A Deep Reinforcement Learning Approach for Efficient, Safe and Comfortable Driving. Applied Sciences, 13(9), 5272. https://doi.org/10.3390/app13095272










