Dynamic Characteristics Analysis of a Rod Fastening Rotor System Considering Contact Roughness
Abstract
1. Introduction
2. Dynamics Modeling of Rod Fastening Rotor
3. Characterization of Contact Stiffness of Joint’s Interface
- (1)
- The isotropic fractal characteristics of each grade asperity are considered.
- (2)
- The interaction between each level of asperity is ignored.
- (3)
- The material hardening phenomenon induced by contact deformation is not taken into consideration.
- (4)
- The contact behavior in the normal direction is only taken account.
3.1. Contact of Joint’s Interface
3.2. Size Distribution Function
3.3. Contact Load and Normal Contact Stiffness
4. Results and Discussion
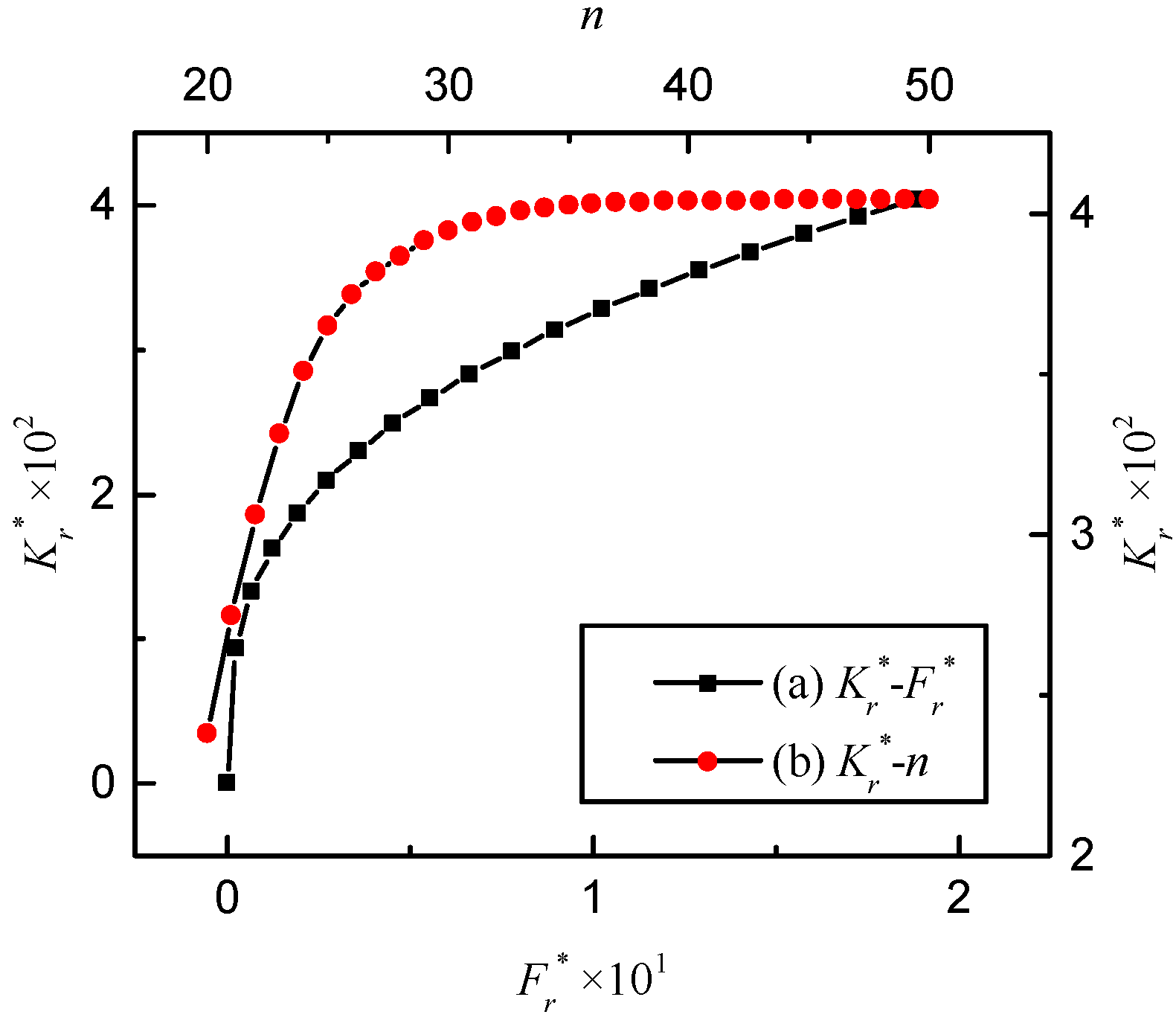
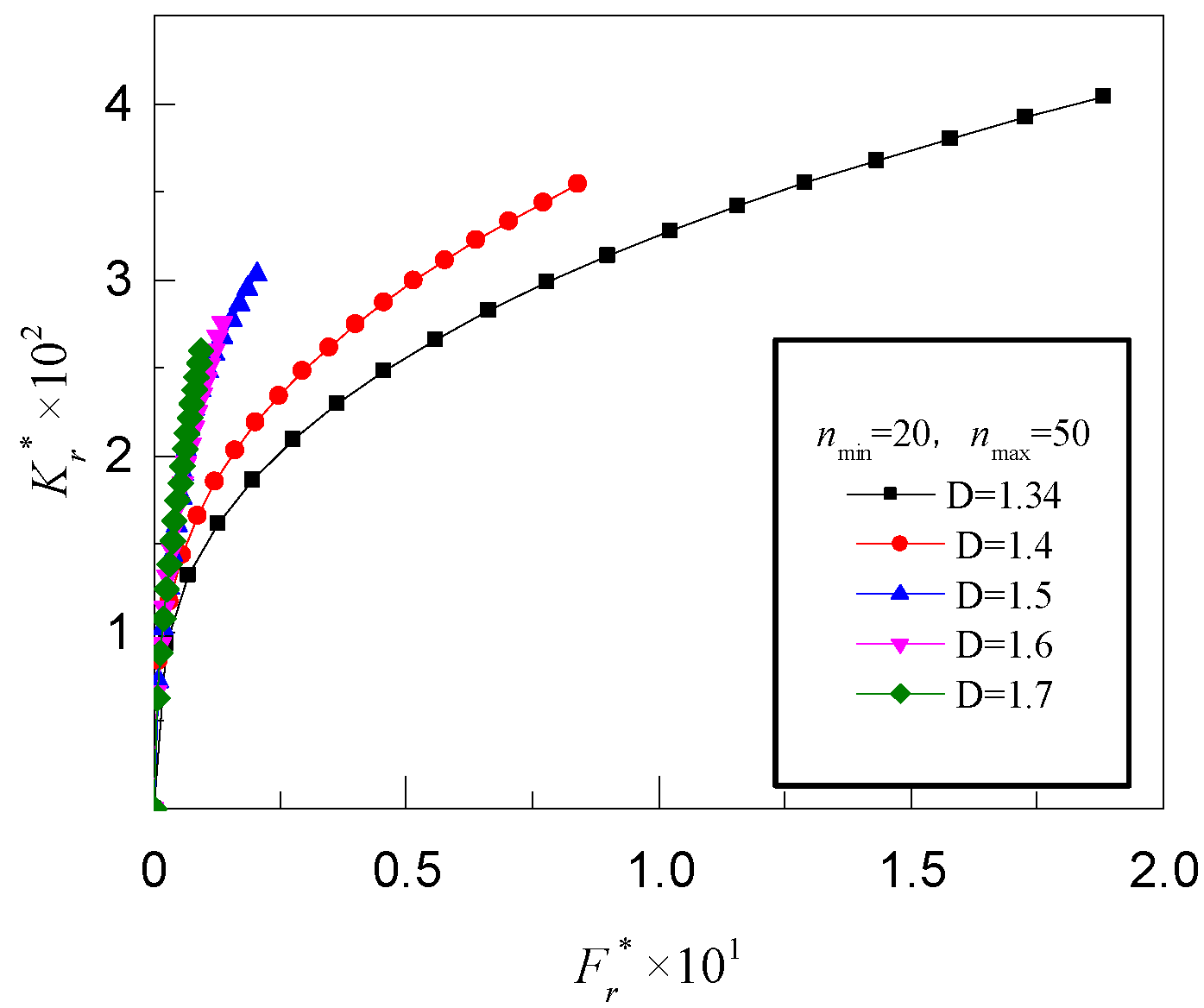
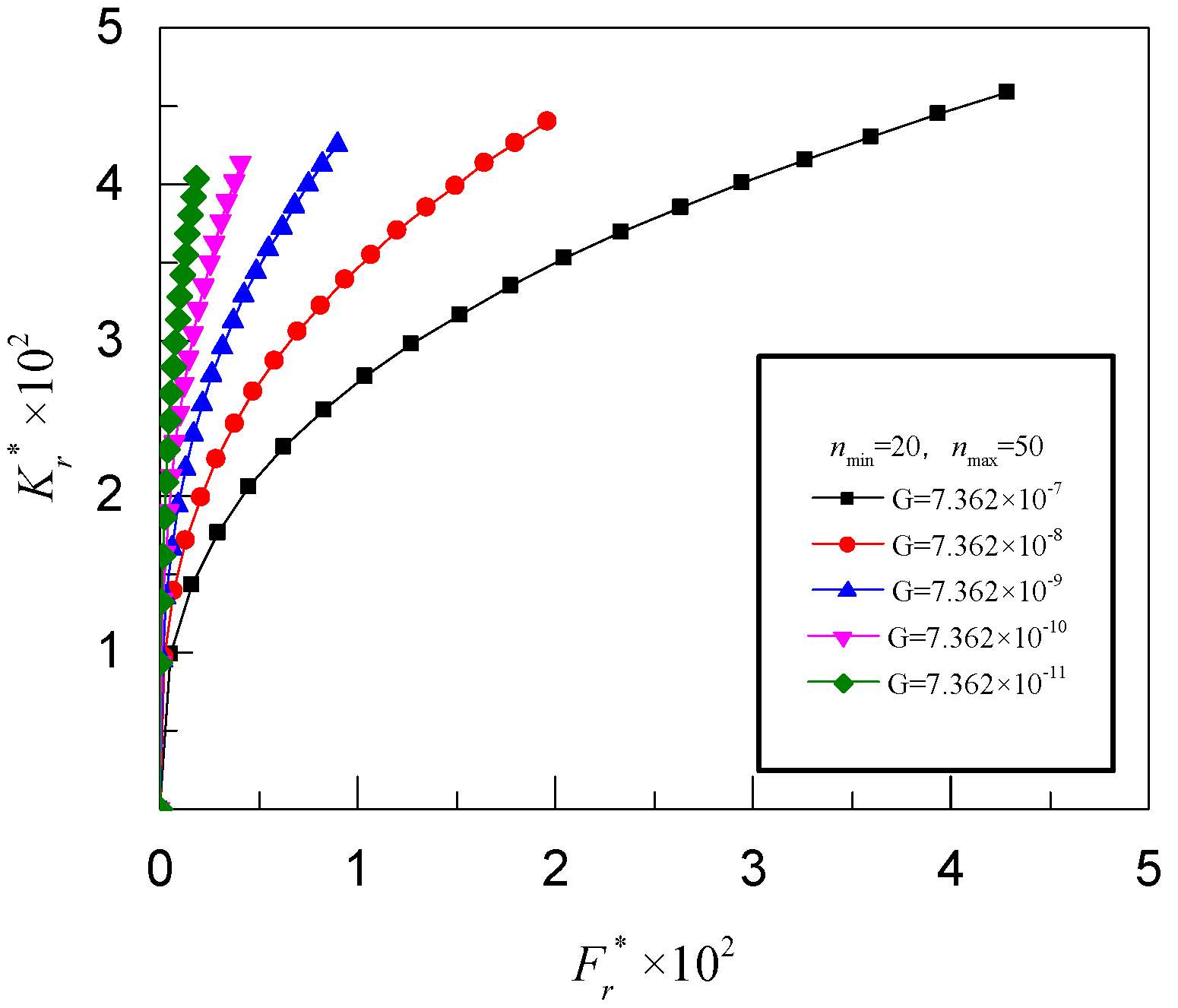
4.1. Normal Contact Stiffness of Joint’s Interface
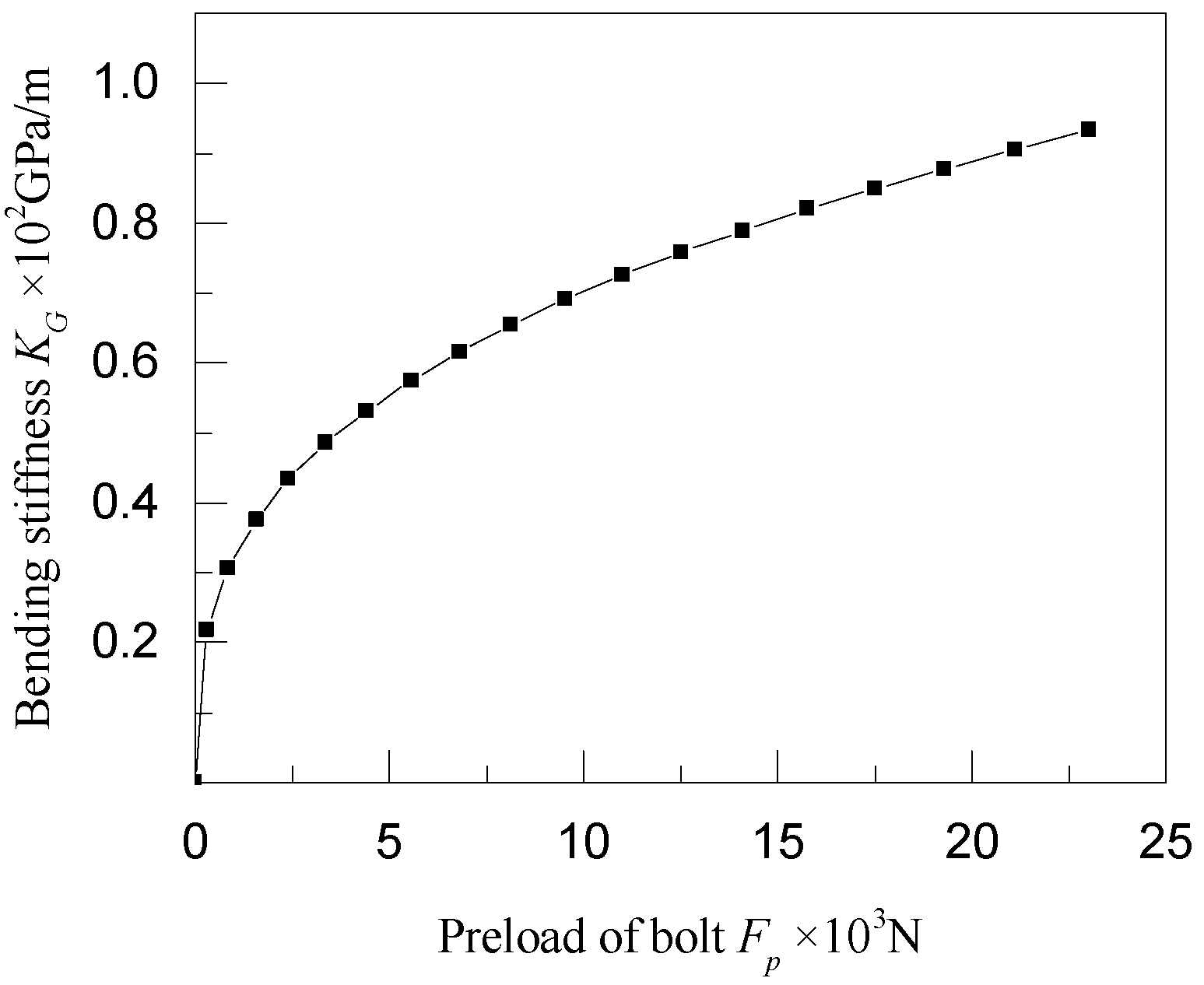
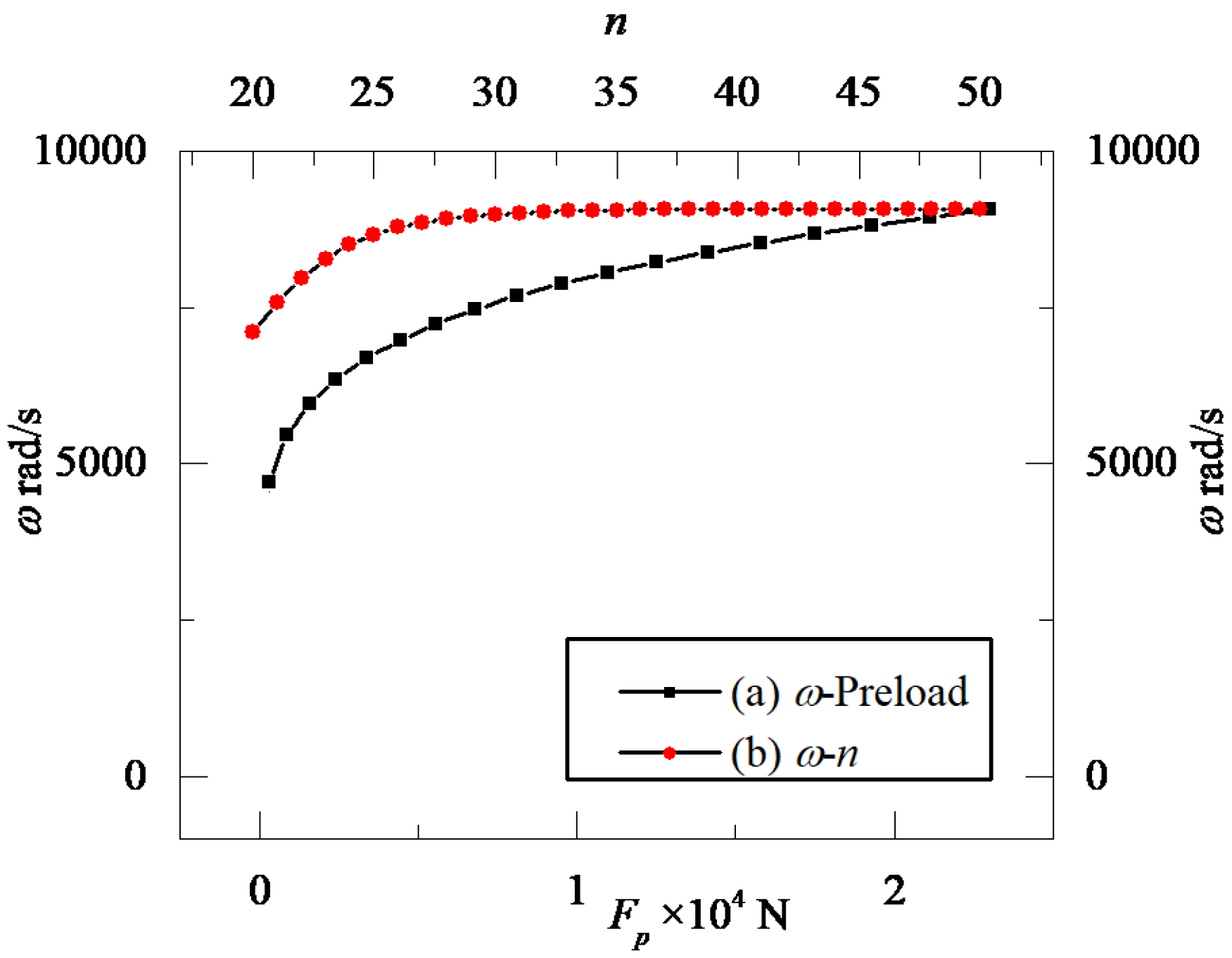
4.2. Dynamic Characteristics of Rod Fastening Rotor System
5. Conclusions
- (1)
- For the rod fastening rotor system, its dynamic characteristics are different from that of a traditional integral rotor system due to the contact effects of the joint’s interface.
- (2)
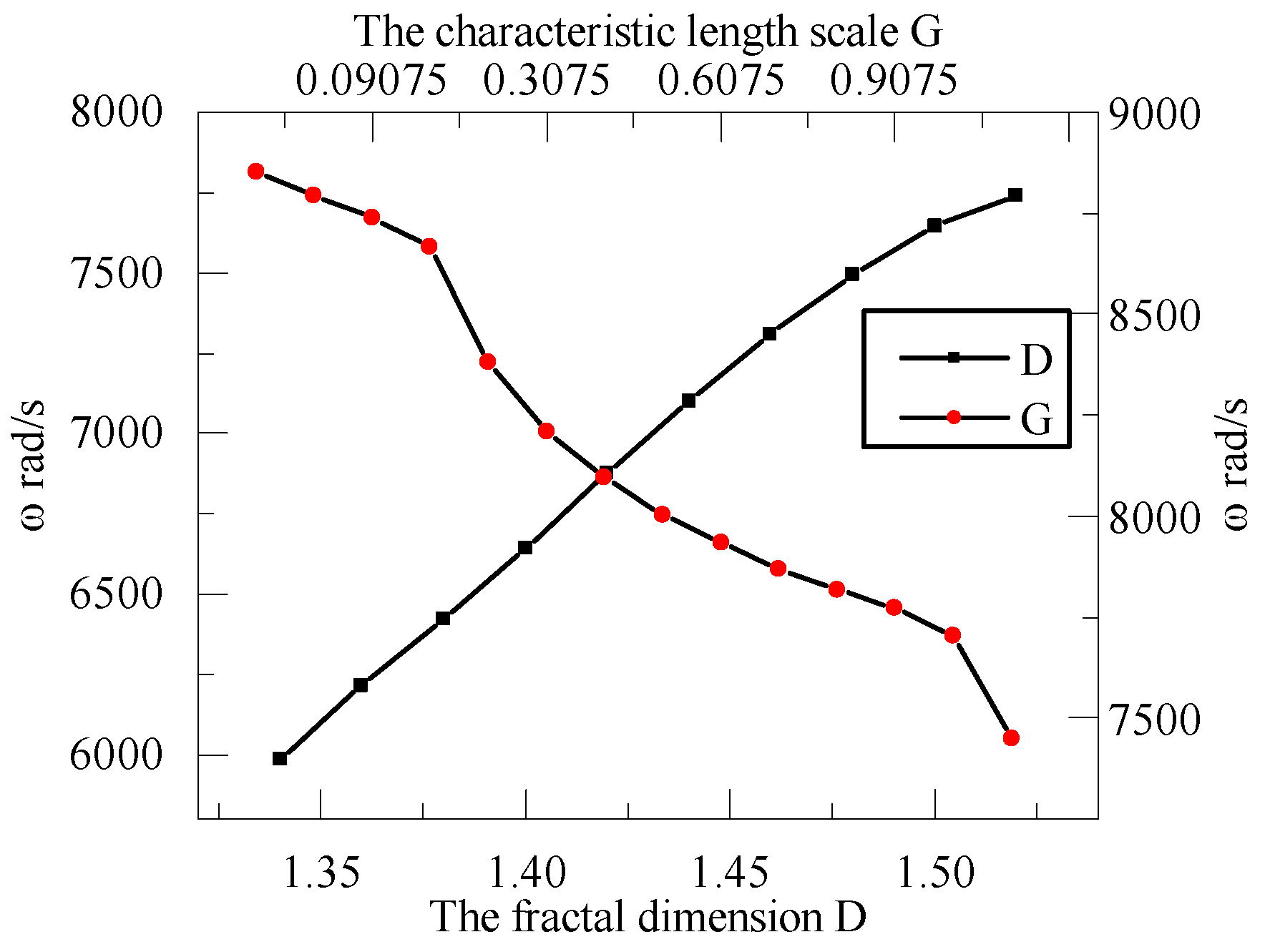
- The contact stiffness of the joint’s interface is closely related to the grade of asperities and the fractal parameters. The contact stiffness increases with an increase in the fractal dimension and a decrease in the characteristic length scale, respectively.
- (3)
- For the rod fastening rotor, the roughness of the joint’s interface can directly affect the dynamic characteristics and natural frequency of the system. Because the fractal parameters of the joint’s interface are mainly determined by the contact roughness, the natural frequencies of the system are changed accordingly.
- (4)
- During the dynamic analysis of the rod fastening rotor system, both the structural stiffness of the flexible shaft and the contact stiffness of the joint’s interface should be taken into consideration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| , | Bending stiffness of the shaft |
| , | Mass of discs 1 and 2 |
| Elastic modulus of the shaft | |
| Length of shaft | |
| Height of the surface profile | |
| Fractal dimension of surface profile | |
| Length scale of a surface | |
| Frequency spectrum of surface roughness | |
| Frequency index of surface profile | |
| Length scale of asperity | |
| Radius of asperity | |
| Deformation of single asperity | |
| Material hardness | |
| Critical elastic deformation | |
| Hardness coefficient | |
| , | Elastic modulus of hard and soft materials |
| , | Poisson’s ratio of hard and soft materials |
| Critical contact area at the elastic stage | |
| Critical contact load at the elastic stage | |
| Maximum contact area of asperities | |
| Real contact area of joint’s interface | |
| Contact load of the joint’s interface | |
| Contact load of elastic deformation | |
| Contact load of elastoplastic deformation | |
| Contact load of elastoplastic deformation | |
| Contact load of plastic deformation | |
| Critical elastoplastic contact area | |
| Critical plastic contact area | |
| Normal contact stiffness | |
| Contact stiffness of elastic deformation | |
| Contact stiffness of elastoplastic deformation | |
| Contact stiffness of elastoplastic deformation | |
| Contact stiffness of plastic deformation | |
| Dimensionless contact load | |
| Dimensionless contact stiffness | |
| Bending stiffness of interface | |
| Actual second moment of area |
References
- Peng, H.; Liu, Z.S.; Wang, G.L.; Zhang, M. Rotor dynamic analysis of tie-bolt fastened rotor based on elastic-plastic contact. In Proceedings of the ASME 2011 Turbo Expo: Technical Conference and Exposition, Vancouver, BC, Canada, 1 January 2011. [Google Scholar]
- Liu, S.G.; Ma, Y.H.; Zhang, D.Y.; Hong, J. Studies on dynamic characteristics of the joint in the aero-engine rotor system. Mech. Syst. Signal Process. 2012, 29, 120–136. [Google Scholar]
- Mayer, M.H.; Gaul, L. Segment-to-segment contact elements for modeling joint interfaces in finite element analysis. Mech. Syst. Signal Process. 2007, 21, 724–734. [Google Scholar] [CrossRef]
- Liu, H. Nonlinear dynamic analysis of a flexible rod fastening rotor bearing system. J. Eng. Mech. 2010, 46, 53. [Google Scholar] [CrossRef]
- Luan, Y.; Guan, Z.Q.; Cheng, G.D.; Liu, S. A simplified nonlinear dynamic model for the analysis of pipe structures with bolted flange joints. J. Sound Vib. 2012, 331, 3225–3344. [Google Scholar] [CrossRef]
- Meng, C.; Su, M.; Wang, S. An investigation on dynamic characteristics of a gas turbine rotor using an improved transfer matrix method. J. Eng. Gas Turb. Power 2013, 135, 122505-1–122505-12. [Google Scholar] [CrossRef]
- Hong, J.; Chen, X.Q.; Wang, Y.F.; Ma, Y.H. Optimization of dynamics of non-continuous rotor based on model of rotor stiffness. Mech. Syst. Signal Process. 2019, 131, 166–182. [Google Scholar] [CrossRef]
- Caddemi, S.; Calio, I.; Cannizzaro, F. Closed-form solutions for stepped Timoshenko beams with internal singularities and along-axis external supports. Arch. Appl. Mech. 2013, 83, 559–577. [Google Scholar] [CrossRef]
- Mackerle, J. Finite element analysis of fastening and joining: A bibliography. Int. J. Press. Vessel. Pip. 2003, 80, 253–271. [Google Scholar] [CrossRef]
- Ahmadian, H.; Mottershead, J.E.; James, S.; Friswell, M.I.; Reece, C.A. Modelling and updating of large surface-to-surface joints in the AWE-MACE structure. Mech. Syst. Signal Process. 2006, 20, 868–880. [Google Scholar] [CrossRef]
- Hartwigsen, C.J.; Song, Y.; Mcfarland, D.M.; Bergman, L.A.; Vakakis, A.F. Experimental study of non-linear effects in a typical shear lap joint configuration. J. Sound Vib. 2004, 277, 327–351. [Google Scholar] [CrossRef]
- Song, Y.; Hartwigsen, C.J.; Mcfarland, D.M.; Vakakis, A.F.; Bergman, L.A. Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements. J. Sound Vib. 2004, 273, 249–276. [Google Scholar] [CrossRef]
- Link, M.; Boeswald, M.; Laborde, S.; Weiland, M.; Calvi, A. An approach to non-linear experimental modal analysis. Nonlinear Model Appl. 2011, 2, 119–128. [Google Scholar]
- Gao, J.; Yuan, Q.; Li, P.; Feng, Z.P.; Zhang, H.T.; Lv, Z.Q. Effects of bending moments and pretightening forces on the flexural stiffness of contact interfaces in rod-fastened rotors. J. Eng. Gas Turbines Power 2012, 134, 1492–1494. [Google Scholar] [CrossRef]
- Qin, Z.Y.; Han, Q.K.; Chu, F.L. Analytical model of bolted disk-drum joints and its application to dynamic analysis of jointed rotor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 646–663. [Google Scholar] [CrossRef]
- Qin, Z.Y.; Han, Q.K.; Chu, F.L. Bolt loosening at rotating joint interface and its influence on rotor dynamics. Eng. Fail Anal. 2016, 59, 456–466. [Google Scholar] [CrossRef]
- Qin, Z.Y.; Cui, D.L.; Yan, S.Z.; Chu, F.L. Application of 2D finite element model for nonlinear dynamic analysis of clamp band joint. J. Vib. Control 2016, 23, 1480–1494. [Google Scholar] [CrossRef]
- Lu, M.J.; Sun, Y.H.; Zhou, J.; Zhao, S.Q.; Geng, H.P.; Wang, W.M. Stiffness modification and dynamic modeling of a rod fastening rotor. J. Aero Power 2016, 31, 2203–2209. (In Chinese) [Google Scholar]
- Su, Y.L.; Wang, A.L.; Li, X.P. Degradation characteristics of combined rotor for turbine considering stress relaxation of rod. Appl. Mech. Mater. 2013, 387, 168–173. [Google Scholar] [CrossRef]
- Jalali, H.; Hedayati, A.; Ahmadian, H. Modelling mechanical interfaces experiencing micro-slip/slap. Inverse Probl. Sci. Eng. 2011, 19, 751–764. [Google Scholar] [CrossRef]
- Beer, G. An isoparametric joint interface element for finite element analysis. Int. J. Numer. Methods Eng. 1985, 21, 585–600. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. A Math. Phys. Eng. Sci. 1966, 295, 300–319. [Google Scholar]
- Pohrt, R.; Popov, V.L. Normal contact stiffness of elastic solids with fractal rough surfaces. Phys. Rev. Lett. 2012, 108, 104301. [Google Scholar] [CrossRef]
- Ciavarella, M.; Murolo, G.; Demelio, G.; Barber, J.R. Elastic contact stiffness and contact resistance for the Weierstrass profile. J. Mec. Phys. Solids 2004, 52, 1247–1265. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces. J. Tribol. 1990, 112, 205. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Goerke, D.; Willner, K. Normal contact of fractal surfaces-Experimental and numerical investigations. Wear 2008, 264, 589–598. [Google Scholar] [CrossRef]
- Liu, P.; Zhao, H.; Huang, K.; Chen, Q. Research on normal stiffness of rough surface considering friction based on fractal theory. Appl. Surf. Sci. 2015, 349, 43–48. [Google Scholar] [CrossRef]
- Xu, K.; Yuan, Y.; Chen, J.J. The effects of size distribution functions on contact between fractal rough surfaces. AIP Adv. 2018, 8, 075317. [Google Scholar] [CrossRef]
- Zhuo, M.; Yang, L.H.; Yu, L. Contact stiffness calculation and effects on rotordynamic of rod fastened rotor. In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, Phoenix, AZ, USA, 11–17 November 2016. [Google Scholar]
- Jiang, S.; Zheng, Y.; Zhu, H. A contact stiffness model of machined plane joint based on fractal theory. J. Tribol. 2010, 132, 011401. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657. [Google Scholar] [CrossRef]
- Wang, S.; Komvopoulos, K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: Part I—Elastic contact and heat transfer analysis. J. Tribol. 1994, 116, 812–822. [Google Scholar] [CrossRef]
- Wang, S.; Komvopoulos, K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: Part II—Multiple domains, elastoplastic contacts and applications. J. Tribol. 1994, 116, 824–832. [Google Scholar] [CrossRef]
- Wang, G.M.; Rao, Z.S.; Xia, S.B.; Zhang, W. The analysis of mechanical model of rod fastening rotor. J. Aeronaut. 1993, 14, B420–B423. (In Chinese) [Google Scholar]
- Chen, H.X.; Dong, G.H.; Yin, Q.; Tan, F.; Yin, G.F. A normal contact stiffness model of joint surface based on the fractal theory. J. Vib. Shock 2019, 38, 218–224. (In Chinese) [Google Scholar]
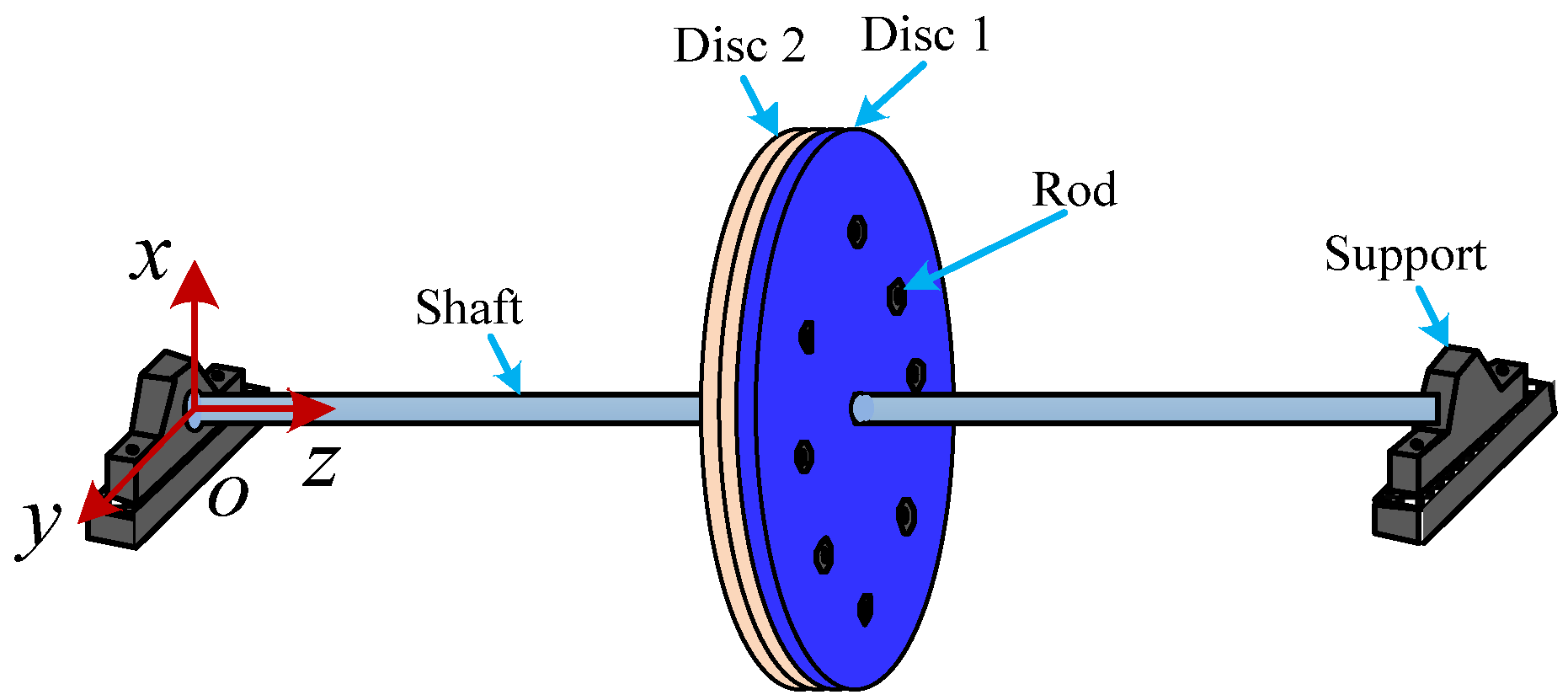
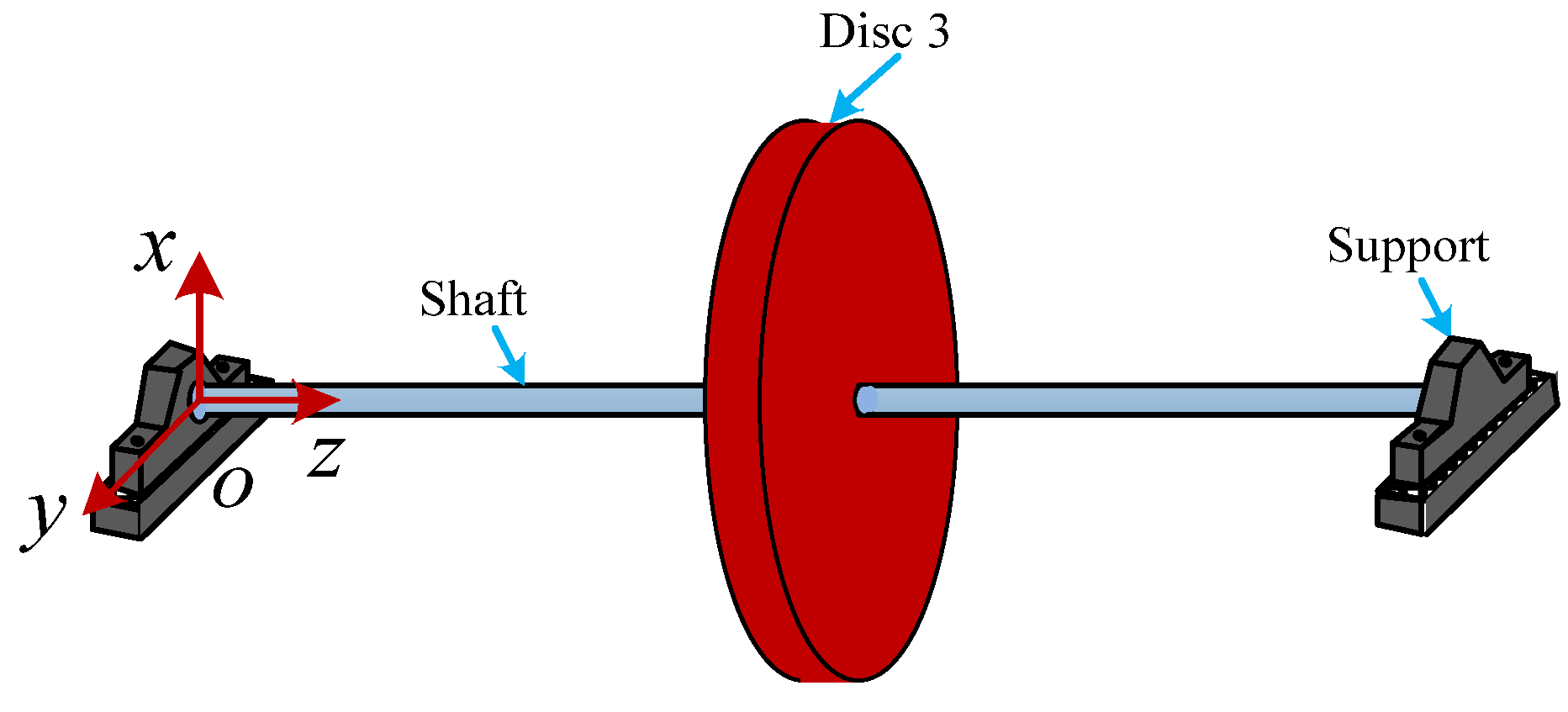
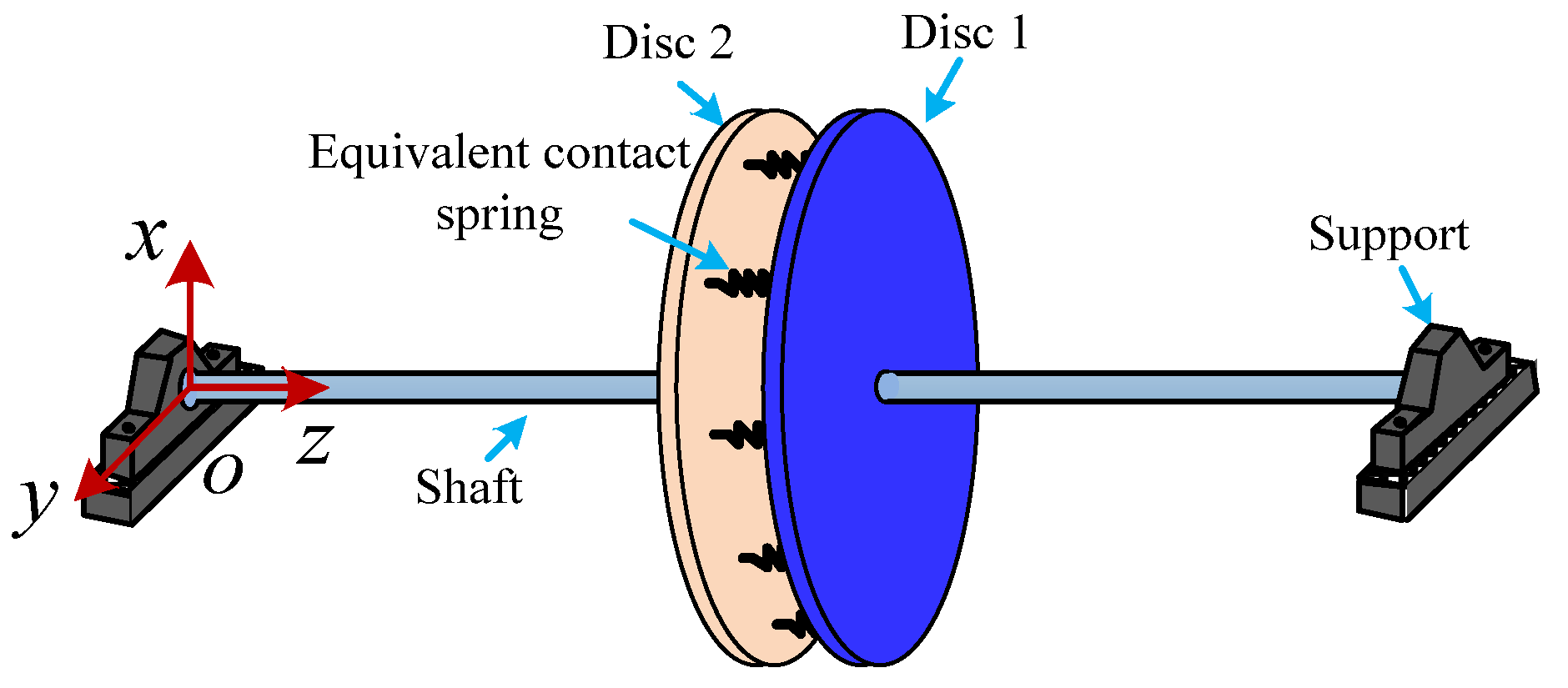

| Fractal dimension | 1.34 |
| Characteristic length scale (m) | |
| Grade of asperity | |
| Equivalent elastic modulus (GPa) | 115.4 |
| Hardness (GPa) | 6.1 |
| Poisson’s ratio | 0.3 |
| Disc mass (kg) | 29.18 |
| Disc radius (mm) | 100 |
| Shaft length (mm) | 448.8 |
| Shaft radius (mm) | 30 |
| Shaft elastic modulus (GPa) | 210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Gao, Y.; Ren, X.; Lu, K.; Yang, Y. Dynamic Characteristics Analysis of a Rod Fastening Rotor System Considering Contact Roughness. Appl. Sci. 2023, 13, 5009. https://doi.org/10.3390/app13085009
Zhao W, Gao Y, Ren X, Lu K, Yang Y. Dynamic Characteristics Analysis of a Rod Fastening Rotor System Considering Contact Roughness. Applied Sciences. 2023; 13(8):5009. https://doi.org/10.3390/app13085009
Chicago/Turabian StyleZhao, Wei, Yang Gao, Xiu Ren, Kuan Lu, and Yang Yang. 2023. "Dynamic Characteristics Analysis of a Rod Fastening Rotor System Considering Contact Roughness" Applied Sciences 13, no. 8: 5009. https://doi.org/10.3390/app13085009
APA StyleZhao, W., Gao, Y., Ren, X., Lu, K., & Yang, Y. (2023). Dynamic Characteristics Analysis of a Rod Fastening Rotor System Considering Contact Roughness. Applied Sciences, 13(8), 5009. https://doi.org/10.3390/app13085009







