Approach Draft to Evaluate the Transport System State—A Case Study Regarding the Estimation Ratio Model of Transport Supply and Demand
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Causal Loop Diagrams (CLDs)
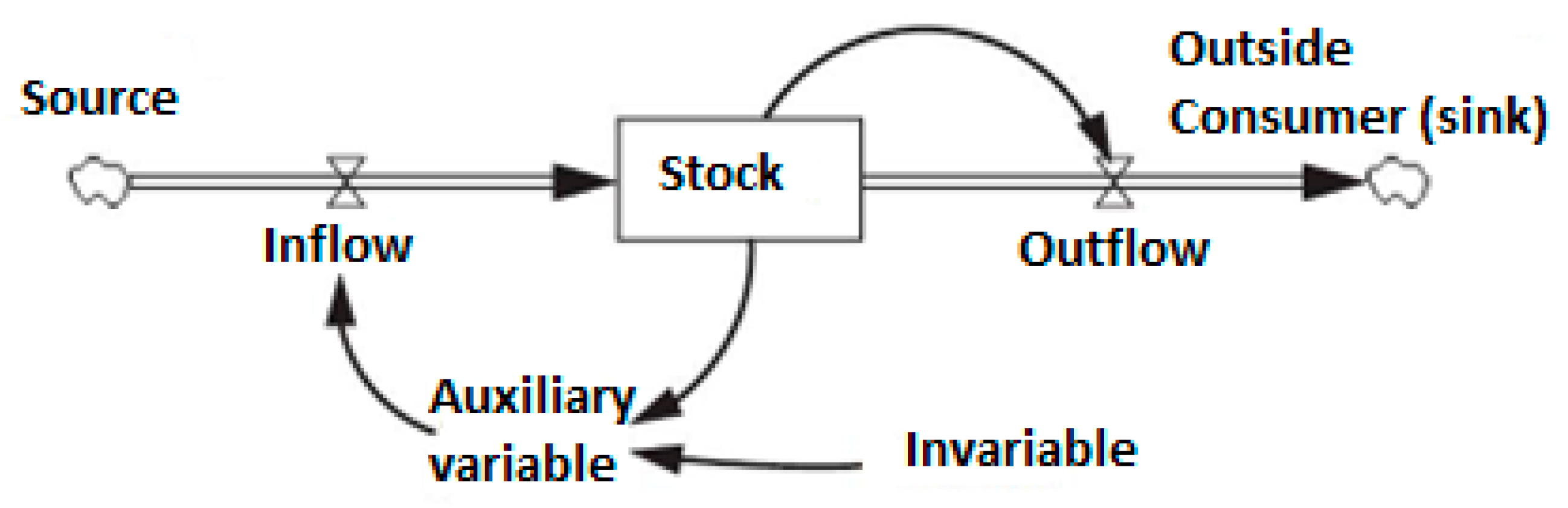
3.2. Stock and Flow Diagrams
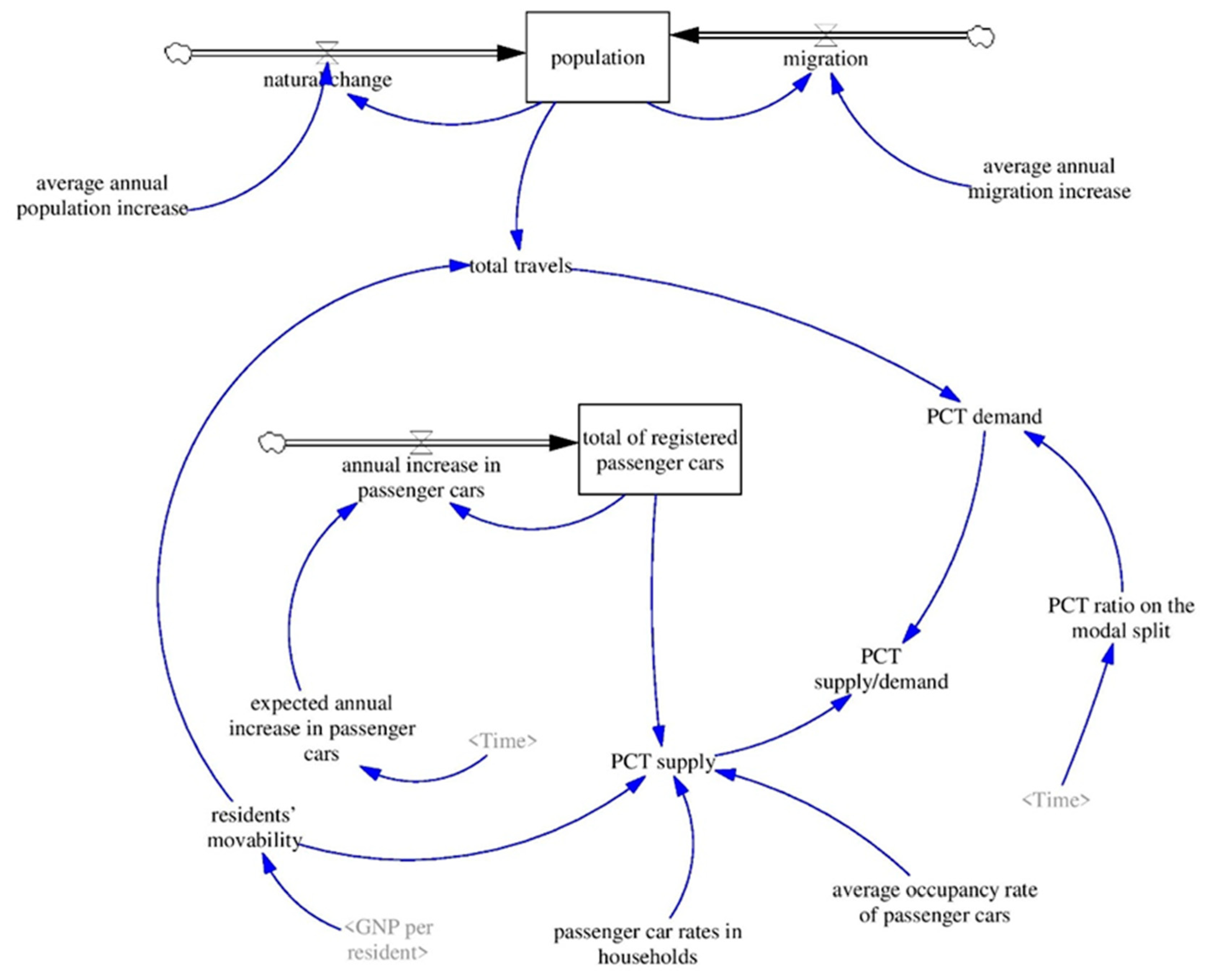
3.3. Theory of the Suggested Model
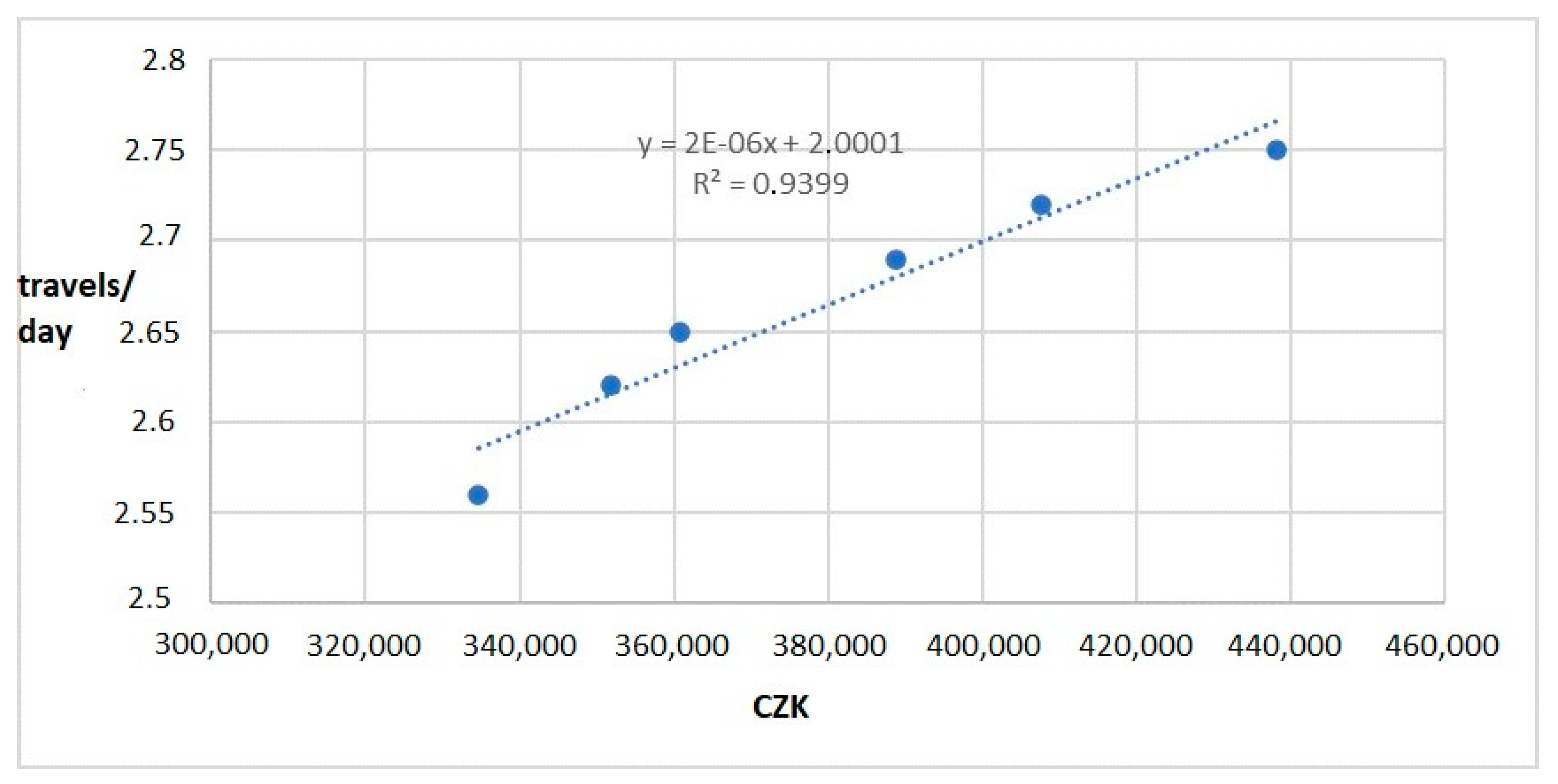
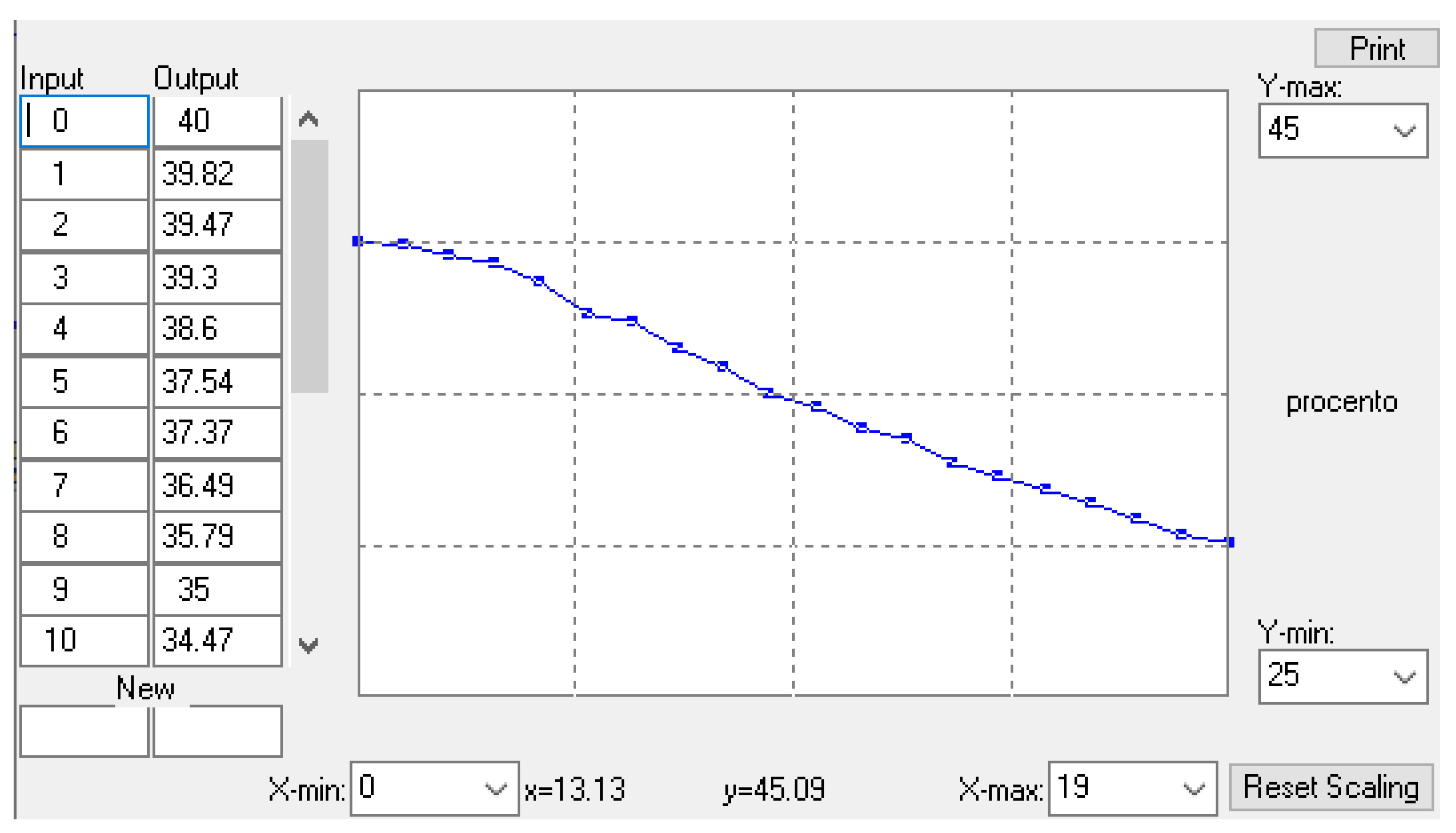
4. Results and Discussion
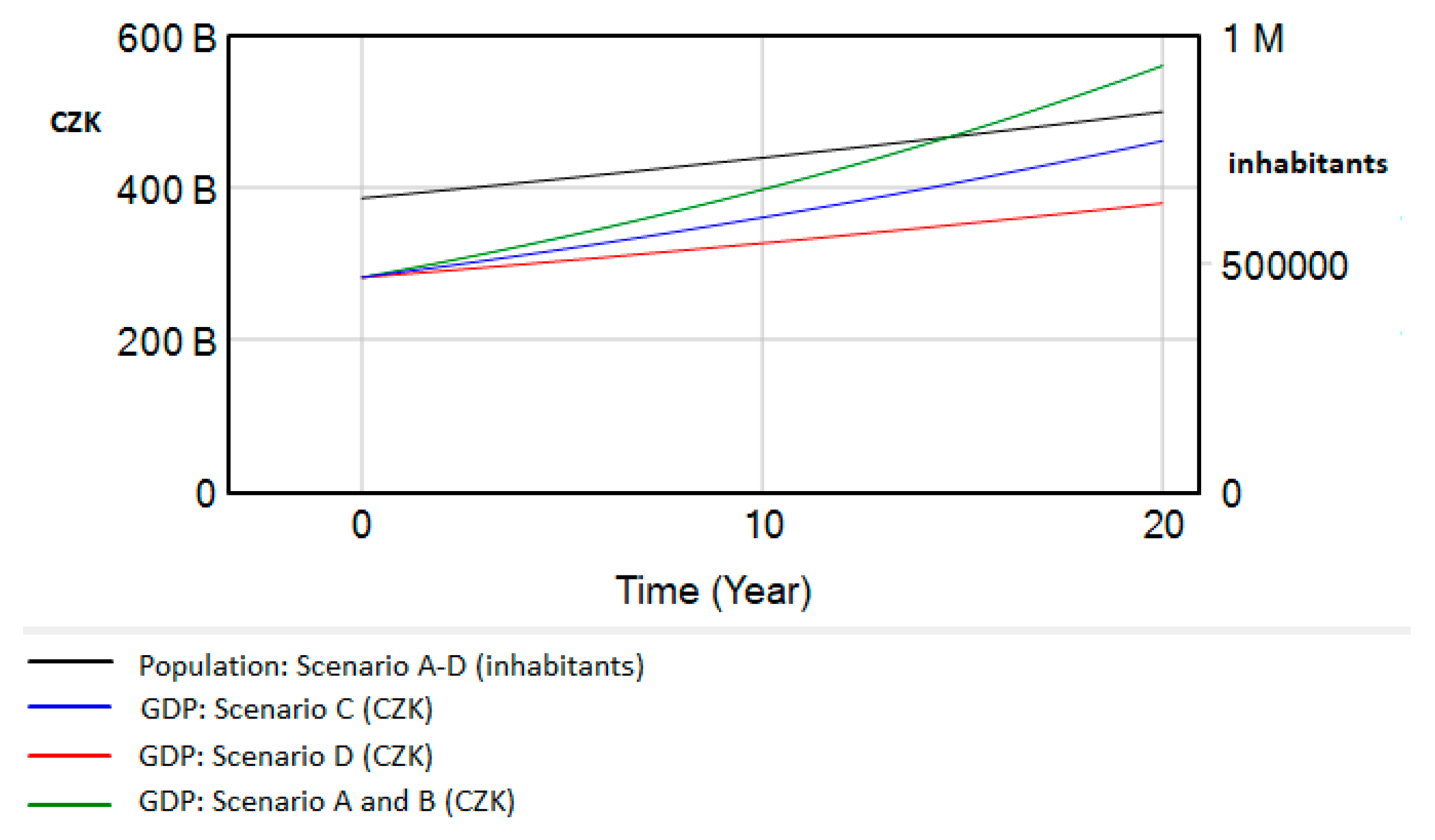
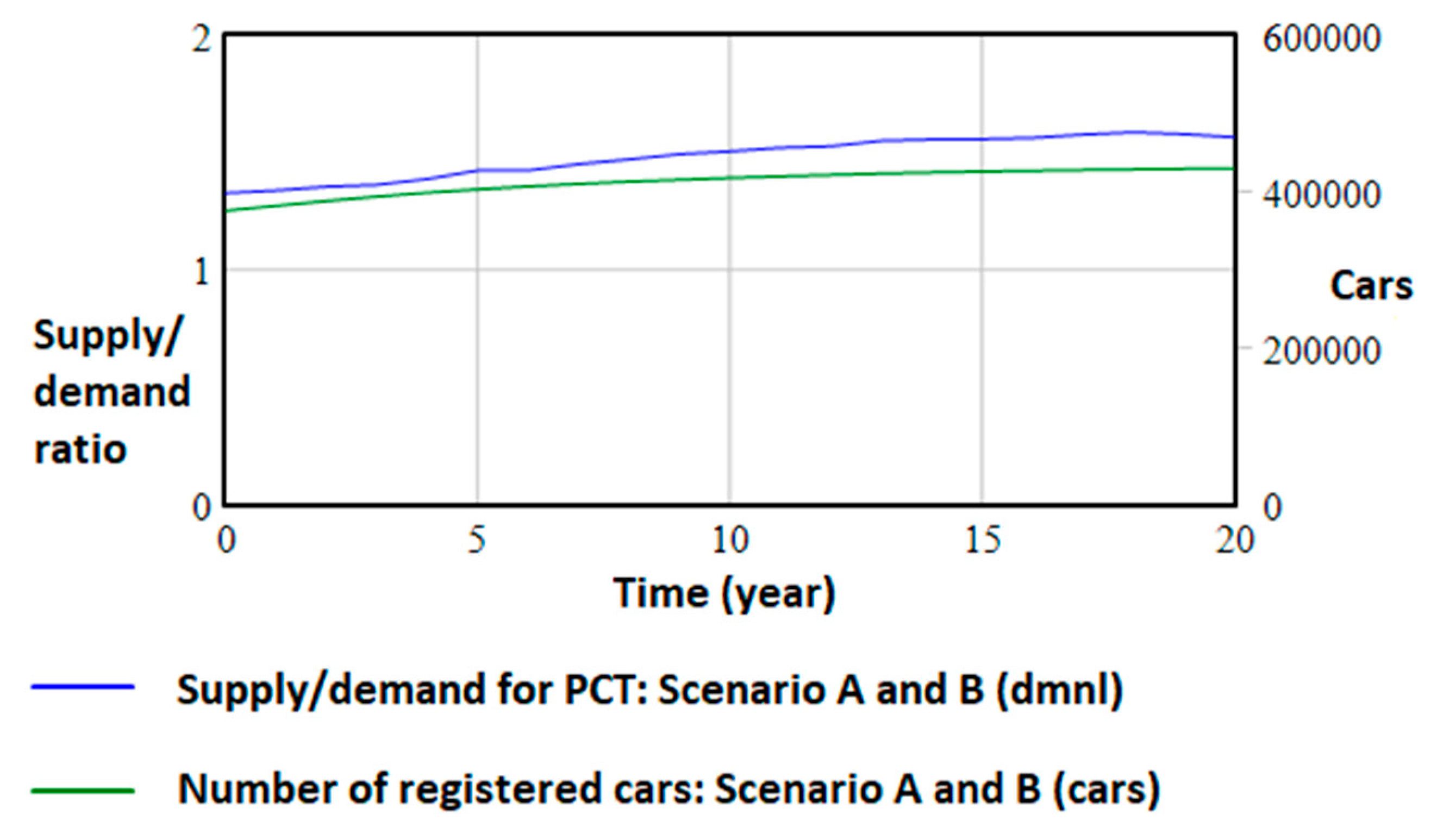
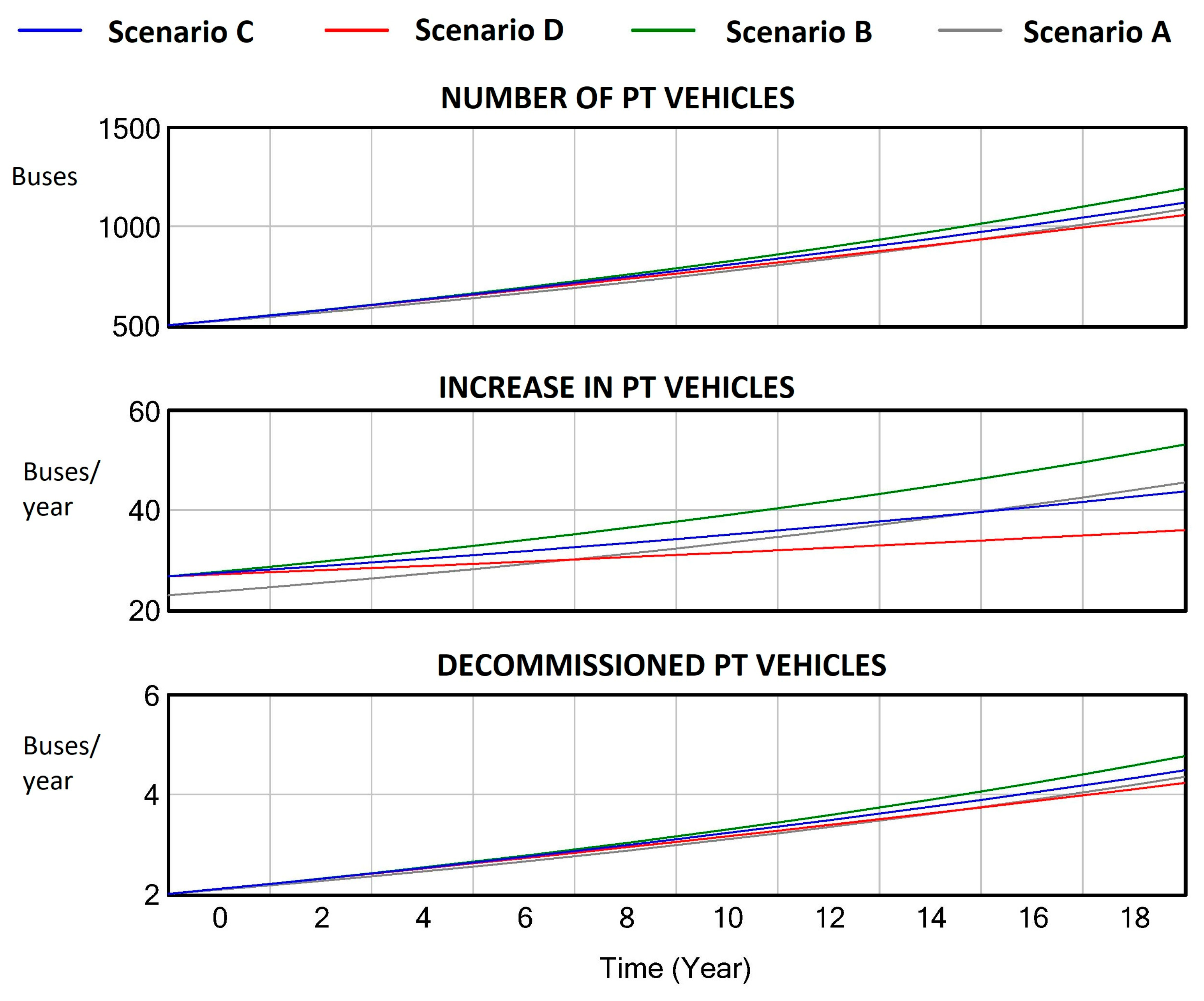
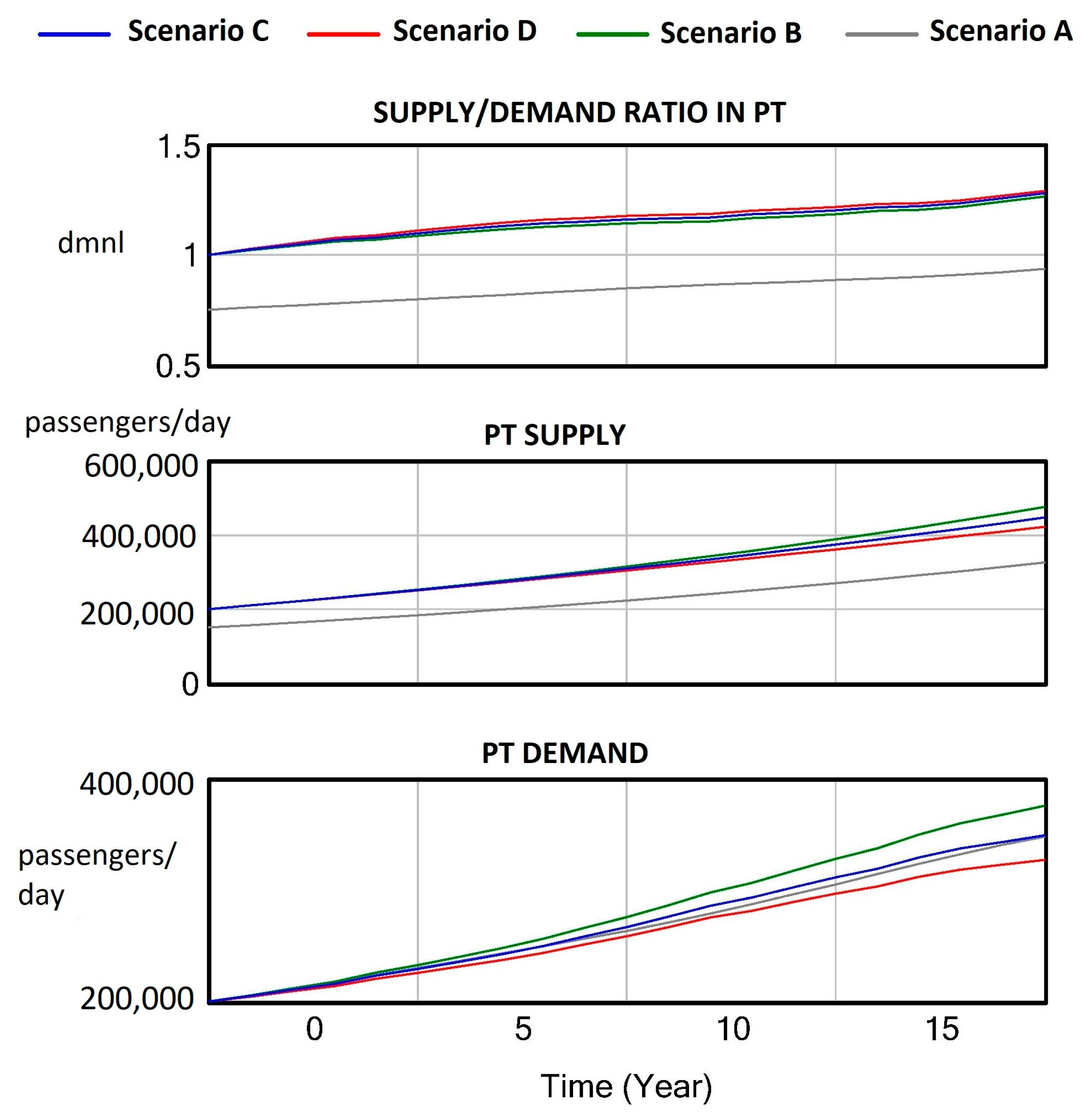
- Scenario A–The supply and demand trend in the selected modes will be the same as in previous years (reflecting current historical data of measured variables)
- Scenario B–The supply and demand trend in PT will be growing in the subsequent years, calling for a supply increase in means of transport and higher utilization rates. This enhancement involves new lines, purchasing more equipment, and so on, moving the value toward the average daily PT vehicle capacity. On the other side, PT usage rates will mount to 14.5% in 2040 to satisfy the predicted demand (see Table 2).
- Scenario C–We are considering a growing trend in PT, but with a lower value of GDP increase each year (from the current 3.5% annual growth, a drop to the growth of 2.5% on average). The rest of the variable values remain the same as in scenario B.
- Scenario D–We are considering a growing trend in PT, but with a lower value of GDP increase each year (from the current 3.5% annual growth, a drop to the growth of 1.5% on average). The rest of the variable values remain the same as in scenario B.
- quantitative and qualitative data;
- individual indicators (e.g., individual opinions within questionnaire surveys);
- ratio indicators;
- relative indicators.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, B.; Clarke, J.-P. The hidden value of air transportation infrastructure. Technol. Forecast. Soc. Chang. 2007, 74, 18–35. [Google Scholar] [CrossRef]
- Šipuš, D.; Abramović, B. The possibility of using public transport in rural area. Procedia Eng. 2017, 192, 788–793. [Google Scholar] [CrossRef]
- Rai, H.B.; Verlinde, S.; Merckx, J.; Macharis, C. Crowd logistics: An opportunity for more sustainable urban freight transport? Eur. Transp. Res. Rev. 2017, 9, 9. [Google Scholar]
- Prokudin, G.; Chupaylenko, O.; Dudnik, O.; Dudnik, A.; Omarov, D. Improvement of the methods for determining optimal characteristics of transportation networks. Eastern-Eur. J. Enterp. Technol. 2016, 6, 54–61. [Google Scholar] [CrossRef]
- Vojtek, M.; Kendra, M.; Zitrický, V.; Daniš, J. Principles of Logistics Applied to Railway Passenger Transport. MATEC Web Conf. 2017, 134, 00061. [Google Scholar] [CrossRef]
- Malhotra, S.; Khandelwal, M. Solving XpressBees Logistics Problem by Using Exact and Heuristic Method. LOGI–Sci. J. Transp. Logist. 2022, 13, 37–48. [Google Scholar] [CrossRef]
- de Langen, P.W.; Lases Figueroa, D.M.; van Donselaar, K.H.; Bozuwa, J. Intermodal connectivity in europe, an empirical exploration. Res. Transp. Bus. Manag. 2017, 23, 3–11. [Google Scholar] [CrossRef]
- Gašparík, J.; Zitrický, V. A new approach to estimating the occupation time of the railway infrastructure. Transport 2010, 25, 387–393. [Google Scholar] [CrossRef]
- Allard, R.F.; Moura, F. Effect of transport transfer quality on intercity passenger mode choice. Transp. Res. Part A Policy Pract. 2018, 109, 89–107. [Google Scholar] [CrossRef]
- Sommer, C.; Lambrecht, F. Concepts for tenant tickets for connecting habitation and transport. Transp. Res. Procedia 2016, 19, 40–48. [Google Scholar] [CrossRef]
- Nagy, E.; Csiszár, C. Analysis of delay causes in railway passenger transportation. Period. Polytech. Transp. Eng. 2015, 43, 73–80. [Google Scholar] [CrossRef]
- Nyaki, P.S.; Bwire, H.; Mushule, N.K. Travel time reliability of bus operation in heterogeneous traffic conditions of Dar es Salaam City, Tanzania. LOGI–Sci. J. Transp. Logist. 2020, 11, 44–55. [Google Scholar] [CrossRef]
- Šulyová, D.; Vodák, J.; Koman, G. Implementation smart city concepts for mobility, case study of world logistic models on the smart principles. LOGI–Sci. J. Transp. Logist. 2020, 11, 110–119. [Google Scholar] [CrossRef]
- Fonseca, J.P.; van der Hurk, E.; Roberti, R.; Larsen, A. A matheuristic for transfer synchronization through integrated timetabling and vehicle scheduling. Transp. Res. Part B Methodol. 2018, 109, 128–149. [Google Scholar] [CrossRef]
- Sekulová, J.; Nedeliaková, E. Risks assessment in railway passenger transport in relation to customers. LOGI—Sci. J. Transp. Logist. 2015, 6, 79–89. [Google Scholar]
- Oviedo, D.; Sabogal, O.; Duarte, N.V.; Chong, A.Z. Perceived liveability, transport, and mental health: A story of overlying inequalities. J. Transp. Health 2022, 27, 101513. [Google Scholar] [CrossRef]
- Patzner, J.; Rückert, R.; Müller-Hannemann, M. Passenger-Aware Real-Time Planning of Short Turns to Reduce Delays in Public Transport; Open Access Series in Informatics: Dagstuhl, Germany, 2022; Volume 106. [Google Scholar] [CrossRef]
- Kalra, G.; Chotia, V.; Goel, A. Investigating the Relationship between Transport Infrastructure and Economic Growth: The Case of India. Indian J. Econ. Dev. 2016, 12, 315. [Google Scholar] [CrossRef]
- Camacho, F.; Cárdenas, C.; Muñoz, D. Emerging technologies and research challenges for intelligent transportation systems: 5G, HetNets, and SDN. Int. J. Interact. Des. Manuf. 2018, 12, 327–335. [Google Scholar] [CrossRef]
- Rahul, T.M.; Verma, A. Socio-Demographic Variations in Mode Choice Preferences of Peri-Urban and URBAN Areas—A Case Study of Bangalore; Lecture Notes in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Siddiqui, A.; Verma, A. Influence of Connectivity of Streets on the Urban Form and Sprawl; Lecture Notes in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Forrester, J. Industrial Dynamics—A major breakthrough for decision makers. Harv. Bus. Rev. 1958, 35, 37–66. [Google Scholar]
- Sterman, J.D. Business Dynamics: Systems Thinking and Modelling for a Complex World; Irwin/McGraw-Hill: Boston, MA, USA, 2000; ISBN 0-07-231135-5. [Google Scholar]
- Pfaffenbichler, P.; Emberger, G.; Shepherd, S. A system dynamics approach to land use transport interaction modelling: The strategic model MARS and its application. Syst. Dyn. Rev. 2010, 26, 262–282. [Google Scholar] [CrossRef]
- Haghani, A.; Lee, S.Y.; Byun, J.H. A system dynamics approach to land use/transportation system performance modeling part II: Application. J. Transp. 2003, 37, 43–82. [Google Scholar] [CrossRef]
- Wang, J.; Lu, H.; Peng, H. System Dynamics Model of Urban Transportation System and Its Application. J. Transp. Syst. Eng. Inf. Technol. 2008, 8, 83–89. [Google Scholar] [CrossRef]
- Hubík, T. System Model of Corporate Management. Master’s Thesis, Charles University, Prague, Czech Republic, 2012. Available online: https://is.cuni.cz/webapps/zzp/detail/115110/?lang=en (accessed on 19 June 2022).
- Ventana Systems, Inc. [Online]. 2016. Available online: http://www.vensim.com (accessed on 10 November 2022).
- Lescaroux, F. Car ownership in relation to income distribution and consumers’ spending decisions. J. Transp. Econ. Policy 2010, 44, 207–230. [Google Scholar]
- Czech Statistical Office—Road Transport Database. 2019. Available online: http://www.czso.com (accessed on 10 November 2022).
- Krpan, L.; Hess, S.; Baričević, H. Correlation between mobility and gross domestic product at regional level: Case study of primorje-gorski kotar county, croatia. Tehnicki Vjesnik 2020, 27, 542–549. [Google Scholar] [CrossRef]
- CDV (Center for Transport Research), Results of Traffic Behavior Surveys Residents of the Czech Republic (Czech Republic on the Move). 2019. Available online: https://www.ceskovpohybu.cz/#ve (accessed on 4 May 2022).
- Brídziková, M.; Konečný, V.; Hammer, J.; Abramovic, B. Demand specifics of disabled persons and persons with reduced mobility for bus transport. Case of regional bus transport in Slovakia. Arch. Automot. Eng.–Arch. Motoryz. 2020, 87, 81–95. [Google Scholar] [CrossRef]
- Sunkur, R.; Naiko, K.; Agundhooa, A.; Jhugroo, R.; Bokhoree, C. An assessment of the underlying relationship between land transportation and climate change: Case study Mauritius. J. Air Pollut. Health 2021, 6, 79–90. [Google Scholar] [CrossRef]
- Cardell-Oliver, R.; Olaru, D. CIAM: A data-driven approach for classifying long-term engagement of public transport riders at multiple temporal scales. Transp. Res. Part A Policy Pract. 2022, 165, 321–336. [Google Scholar] [CrossRef]
- Zhang, G.S.; Shen, X.Y.; Hua, J.; Zhao, J.W.; Liu, H.X. System dynamics modelling for dynamic emergency response to accidents involving transport of dangerous goods by road. J. Adv. Transp. 2021, 2021, 2474784. [Google Scholar] [CrossRef]
- Shubenkova, K.; Zabinski, K. Machine Vision in Autonomous Vehicles: Designing and Testing the Decision Making Algorithm Based on Entity Attribute Value Model. Arch. Automot. Eng.–Arch. Motoryz. 2021, 94, 27–37. [Google Scholar] [CrossRef]
- Caban, J. The Investigation of Eco-Driving Possibilities in Passenger Car Used in Urban Traffic. In Proceedings of the 14th International Scientific Conference on Sustainable, Modern and Safe Transport, TRANSCOM 2021, High Tatras, Slovakia, 26–28 May 2021; pp. 212–219. [Google Scholar] [CrossRef]
- Orynycz, O.; Tucki, K.; Wasiak, A.; Sobótka, R.; Gola, A. Evaluation of the brake’s performance dependence upon technical condition of car tires as a factor of road safety management. Energies 2019, 13, 9. [Google Scholar] [CrossRef]
- Akbari, F.; Mahpour, A.; Ahadi, M.R. Evaluation of energy consumption and CO2 emission reduction policies for urban transport with system dynamics approach. Environ. Model. Assess. 2020, 25, 505–520. [Google Scholar] [CrossRef]



| Causal Link | Illustration | Formula |
|---|---|---|
| Positive (+) |  | ∂Y/∂X > 0 in the event of propagation |
| Negative (−) |  | ∂Y/∂X < 0 in the event of propagation |
| Variables in the SD Model | Input Value–Scenario A | Input Value–Scenario B | Input Value–Scenario C | Input Value–Scenario D | Units |
|---|---|---|---|---|---|
| population | 643,630 | 643,630 | 643,630 | 643,630 | residents |
| average annual natural population increase | 0.5 | 0.5 | 0.5 | 0.5 | % |
| average annual natural population migration increase | 0.8 | 0.8 | 0.8 | 0.8 | % |
| GDP | 281,771 × 106 | 281,771 × 106 | 281,771 × 106 | 281,771 × 106 | CZK |
| average annual GDP growth | 3.5 | 3.5 | 2.5 | 1.5 | % |
| average annual investment rates in transport per GDP | 2.3 | 2.3 | 2.3 | 2.3 | % |
| average costs of purchasing new means of transport | 3 | 3.5 | 3.5 | 3.5 | % |
| average price of a means of public transport | 8,500,000 | 8,500,000 | 8,500,000 | 8,500,000 | CZK |
| total of means of public transport | 500 | 500 | 500 | 500 | vehicles |
| average ratio of decommissioned PT vehicles | 0.5 | 0.5 | 0.5 | 0.5 | % |
| average daily capacity of means of PT | 300 | 400 | 400 | 400 | passengers/day |
| total of registered vehicles | 375,657 | 375,657 | 375,657 | 375,657 | vehicles |
| expected annual car growth | 1.71 | 1.71 | 1.71 | 1.71 | % |
| car ratio in households | 70 | 70 | 70 | 70 | % |
| average car occupancy rate | 1.3 | 1.3 | 1.3 | 1.3 | passengers/cars |
| PT rates in the division of transport work | 10.8 upward trend to 12.5 | 10.8 strong upward trend to 13.5 | 10.8 strong upward trend to 13.5 | 10.8 strong upward trend to 13.5 | % |
| PCT rates in the division of transport work | 40 | 40 | 40 | 40 | % |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartuska, L.; Stopka, O.; Luptak, V.; Masek, J. Approach Draft to Evaluate the Transport System State—A Case Study Regarding the Estimation Ratio Model of Transport Supply and Demand. Appl. Sci. 2023, 13, 4638. https://doi.org/10.3390/app13074638
Bartuska L, Stopka O, Luptak V, Masek J. Approach Draft to Evaluate the Transport System State—A Case Study Regarding the Estimation Ratio Model of Transport Supply and Demand. Applied Sciences. 2023; 13(7):4638. https://doi.org/10.3390/app13074638
Chicago/Turabian StyleBartuska, Ladislav, Ondrej Stopka, Vladimir Luptak, and Jaroslav Masek. 2023. "Approach Draft to Evaluate the Transport System State—A Case Study Regarding the Estimation Ratio Model of Transport Supply and Demand" Applied Sciences 13, no. 7: 4638. https://doi.org/10.3390/app13074638
APA StyleBartuska, L., Stopka, O., Luptak, V., & Masek, J. (2023). Approach Draft to Evaluate the Transport System State—A Case Study Regarding the Estimation Ratio Model of Transport Supply and Demand. Applied Sciences, 13(7), 4638. https://doi.org/10.3390/app13074638






