Patient–Robot Co-Navigation of Crowded Hospital Environments
Abstract
1. Introduction
2. Related Work
2.1. Robotic Walking Assistants
2.2. Crowd Navigation Using Reinforcement Learning
3. Problem Statement
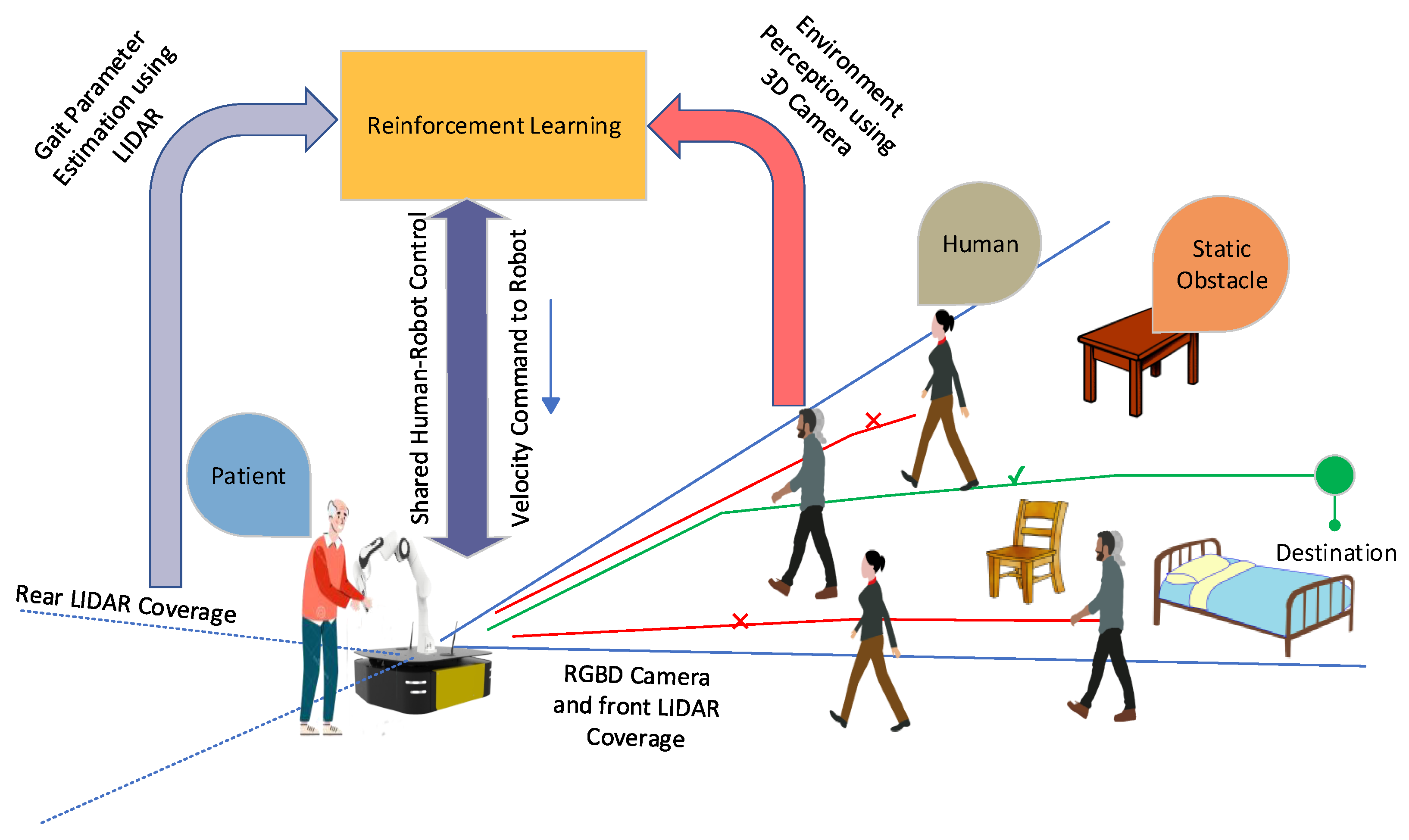
4. Proposed System for Patient–Robot Co-Navigation
4.1. Leg Detection and Gait Velocity Calculation
4.2. Shared Control in Crowded Environments Using Reinforcement Learning
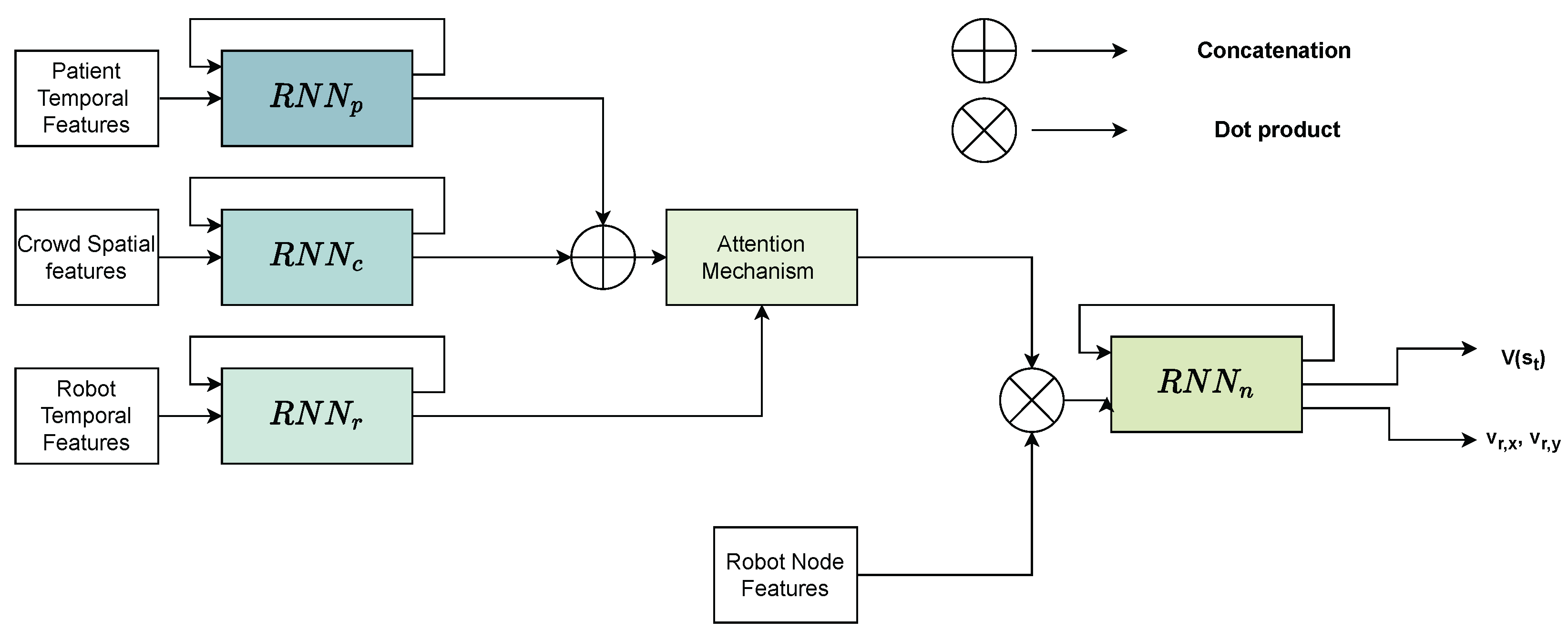
4.2.1. Shared Control Considering Only Dynamic Obstacles (Model V1)
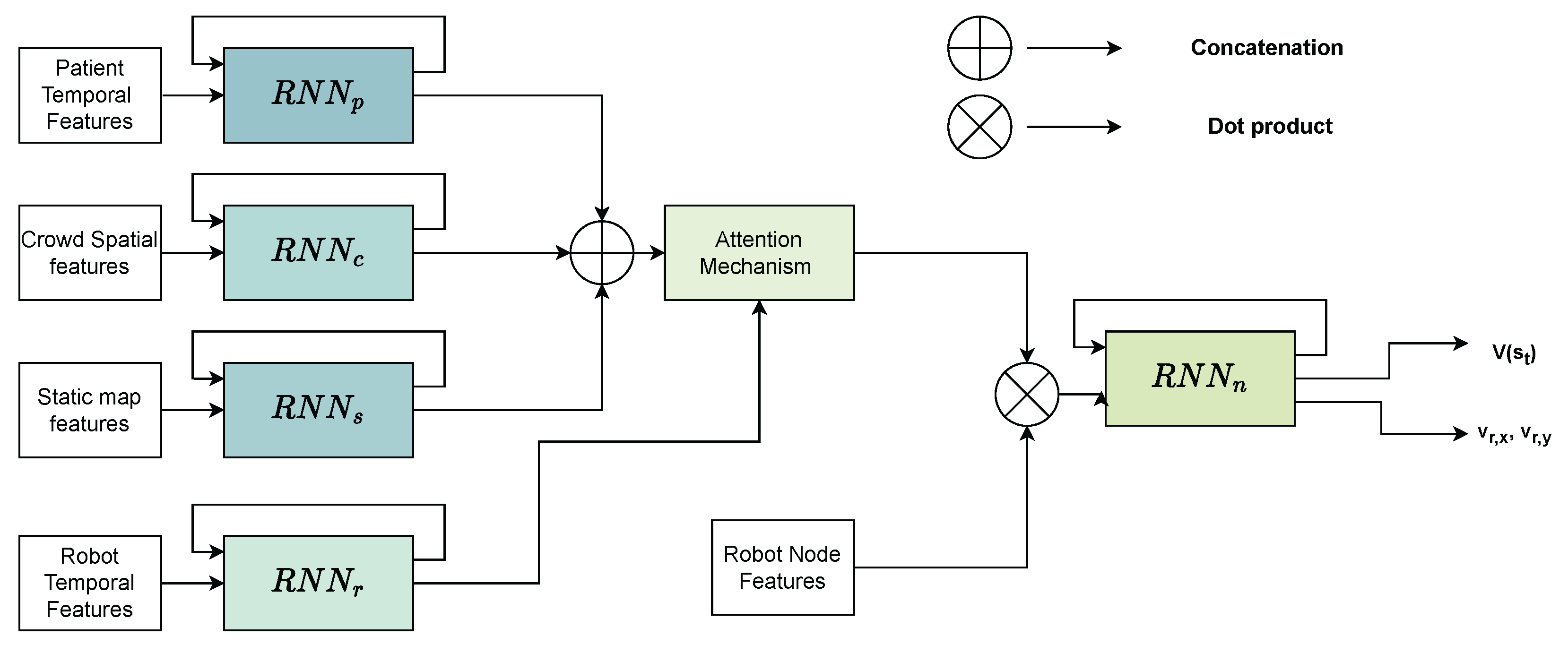
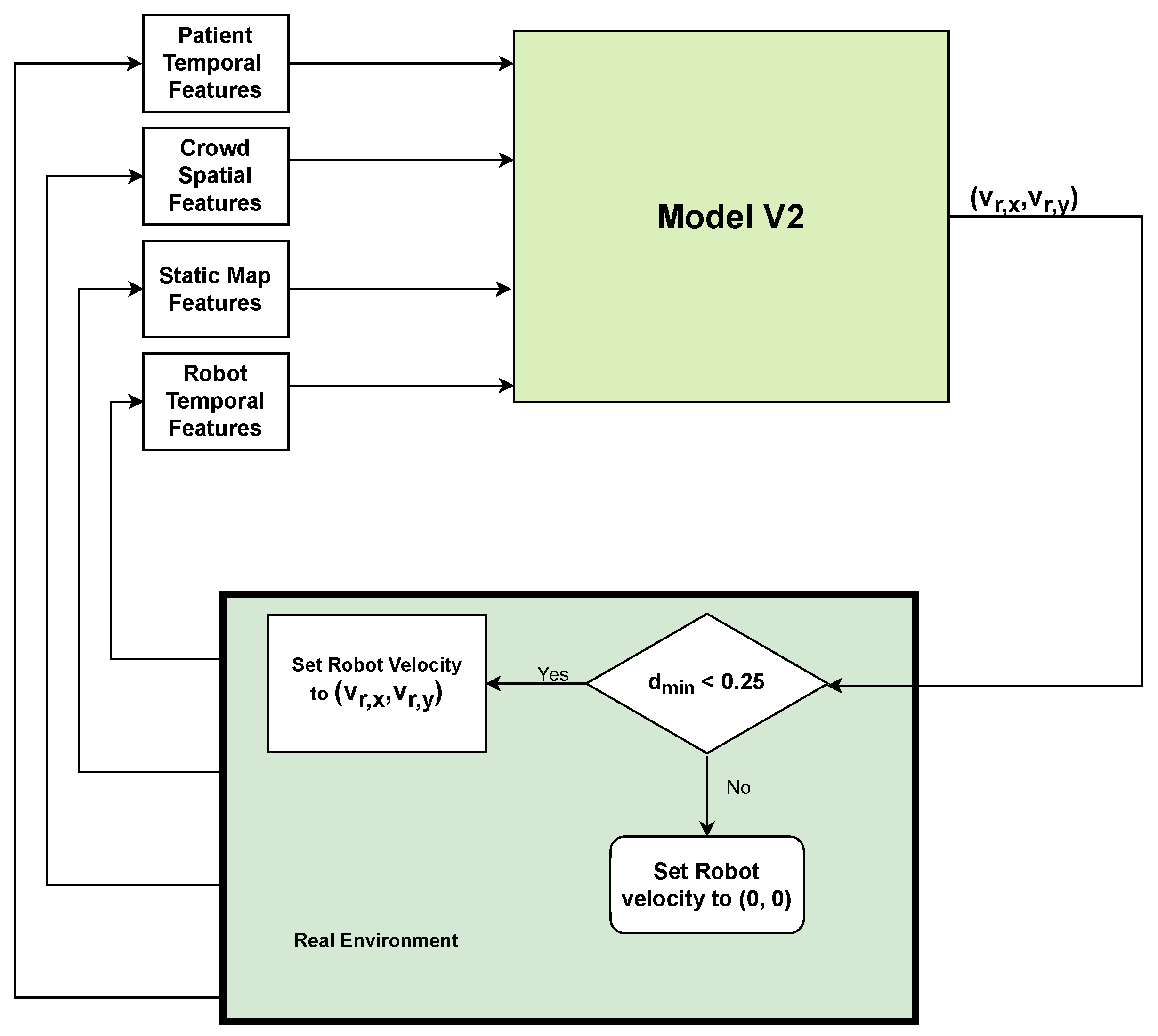
4.2.2. Shared Control Considering Dynamic and Static Obstacles (Model V2)
5. Experimental Evaluation
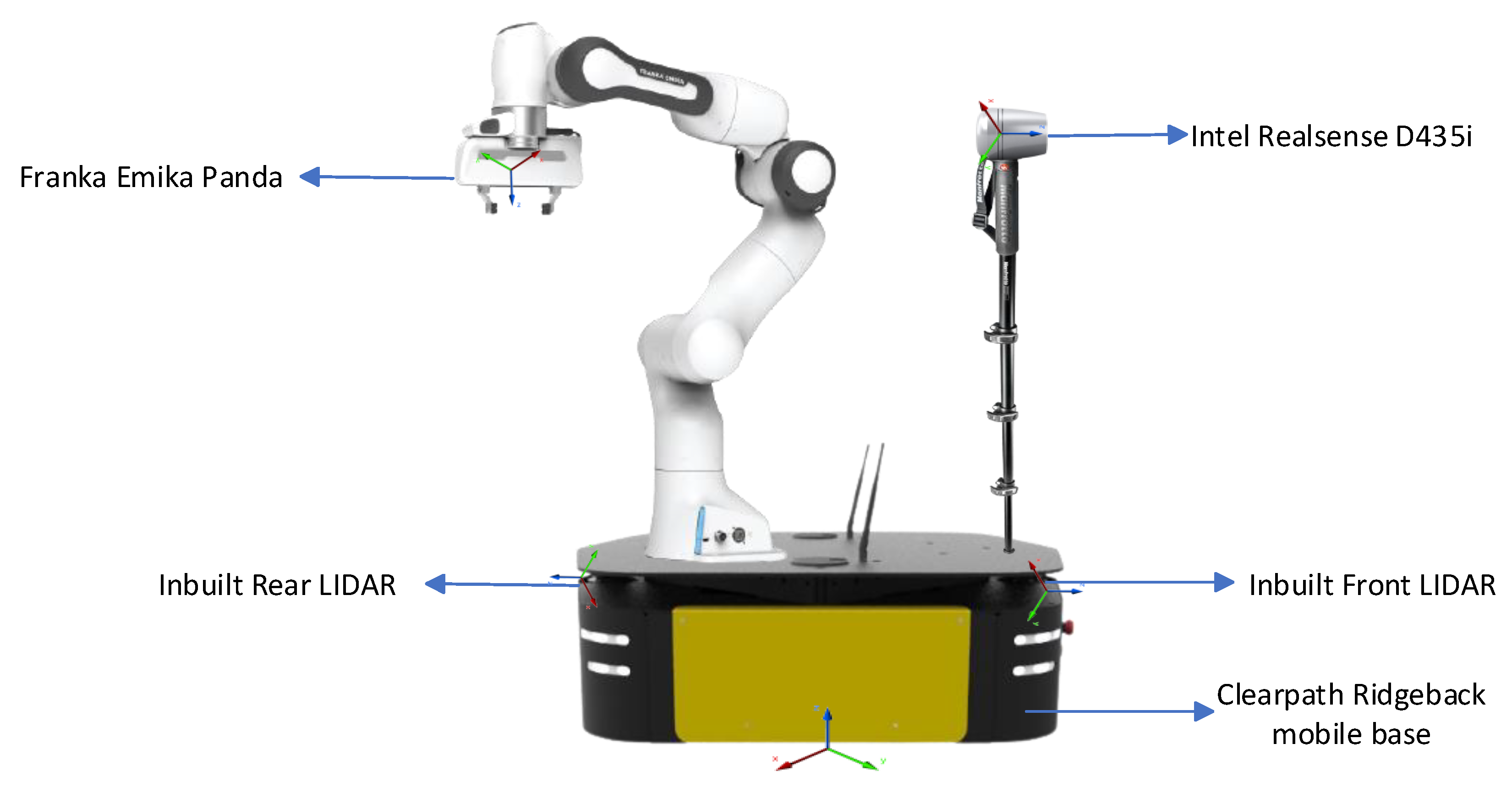
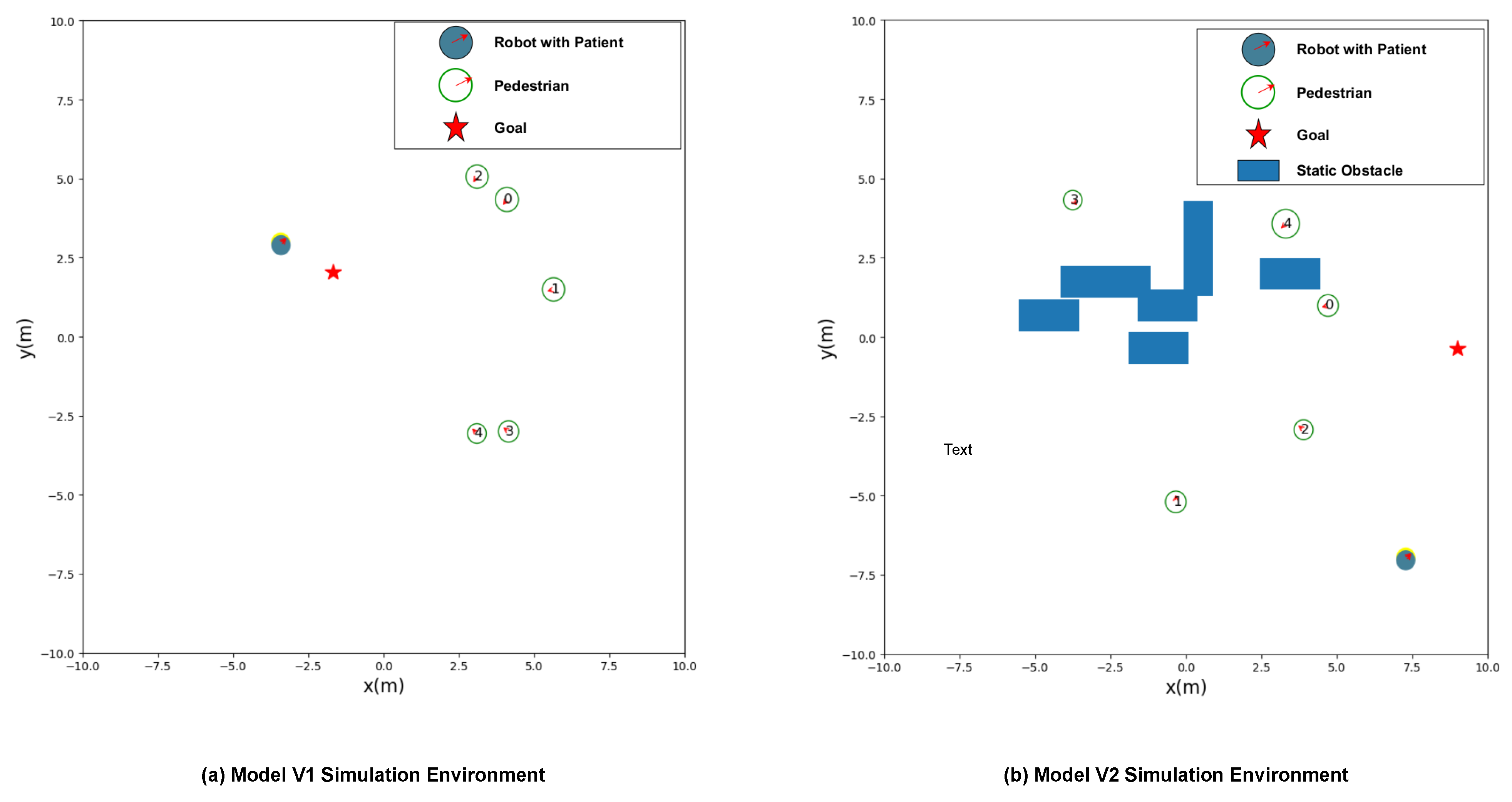
5.1. Experimental Setup
5.2. Experimental Results
5.3. Discussion
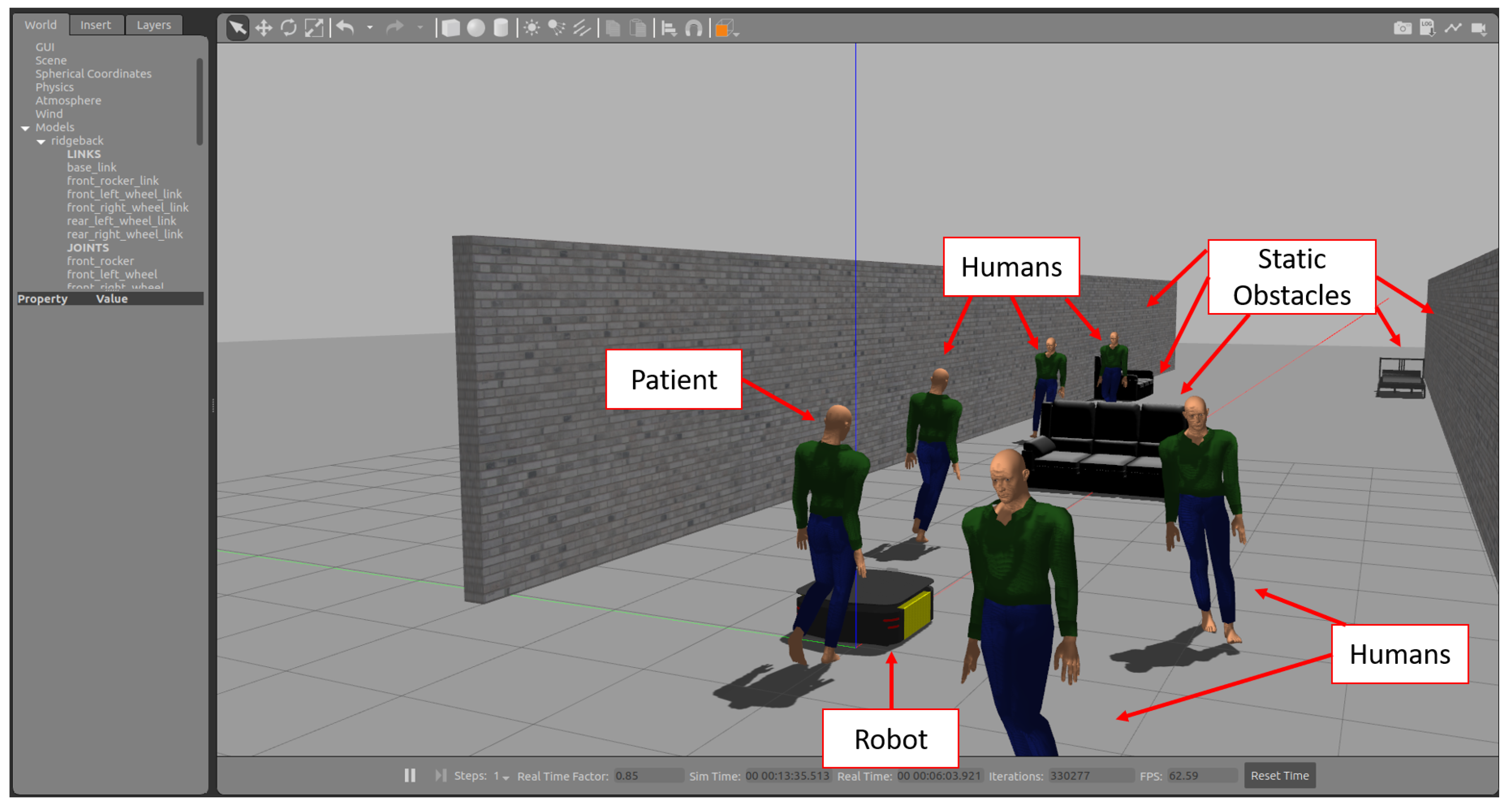
5.4. Simulation Using Gazebo
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- U.S. Bureau of Labor Statistics. Occupational Employment and Wages. Available online: https://www.bls.gov/ooh/healthcare/registered-nurses.htm (accessed on 2 February 2023).
- Hall, L.H.; Johnson, J.; Watt, I.; Tsipa, A.; O’Connor, D.B. Healthcare staff wellbeing, burnout, and patient safety: A systematic review. PLoS ONE 2016, 11, e0159015. [Google Scholar] [CrossRef] [PubMed]
- Poghosyan, L.; Clarke, S.P.; Finlayson, M.; Aiken, L.H. Nurse burnout and quality of care: Cross-national investigation in six countries. Res. Nurs. Health 2010, 33, 288–298. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Deng, L.; Zhang, L.; Lang, Q.; Liao, C.; Wang, N.; Qin, M.; Huang, H. Work stress among Chinese nurses to support Wuhan in fighting against COVID-19 epidemic. J. Nurs. Manag. 2020, 28, 1002–1009. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, M.S.; Al Mamun, S.; Mahmud, M.; Tania, M.H. Healthcare robots to combat COVID-19. In COVID-19: Prediction, Decision-Making, and Its Impacts; Springer: Berlin/Heidelberg, Germany, 2021; pp. 83–97. [Google Scholar]
- Javaid, M.; Haleem, A.; Vaish, A.; Vaishya, R.; Iyengar, K.P. Robotics applications in COVID-19: A review. J. Ind. Integr. Manag. 2020, 5, 441–451. [Google Scholar] [CrossRef]
- Kyrarini, M.; Lygerakis, F.; Rajavenkatanarayanan, A.; Sevastopoulos, C.; Nambiappan, H.R.; Chaitanya, K.K.; Babu, A.R.; Mathew, J.; Makedon, F. A Survey of Robots in Healthcare. Technologies 2021, 9, 8. [Google Scholar] [CrossRef]
- Qassim, H.M.; Wan Hasan, W. A review on upper limb rehabilitation robots. Appl. Sci. 2020, 10, 6976. [Google Scholar] [CrossRef]
- Shi, D.; Zhang, W.; Zhang, W.; Ding, X. A review on lower limb rehabilitation exoskeleton robots. Chin. J. Mech. Eng. 2019, 32, 1–11. [Google Scholar] [CrossRef]
- Nomura, T.; Kanda, T.; Yamada, S.; Suzuki, T. The effects of assistive walking robots for health care support on older persons: A preliminary field experiment in an elder care facility. Intell. Serv. Robot. 2021, 14, 25–32. [Google Scholar] [CrossRef]
- Kerr, E.; McGinnity, T.; Coleman, S.; Shepherd, A. Human vital sign determination using tactile sensing and fuzzy triage system. Expert Syst. Appl. 2021, 175, 114781. [Google Scholar] [CrossRef]
- Kim, W.; Balatti, P.; Lamon, E.; Ajoudani, A. MOCA-MAN: A MObile and reconfigurable Collaborative Robot Assistant for conjoined huMAN-robot actions. In Proceedings of the IEEE International Conference on Robotics and Automation, Paris, France, 31 May–31 August 2020; pp. 10191–10197. [Google Scholar] [CrossRef]
- Wu, Y.; Balatti, P.; Lorenzini, M.; Zhao, F.; Kim, W.; Ajoudani, A. A teleoperation interface for loco-manipulation control of mobile collaborative robotic assistant. IEEE Robot. Autom. Lett. 2019, 4, 3593–3600. [Google Scholar] [CrossRef]
- Nambiappan, H.R.; Kodur, K.C.; Kyrarini, M.; Makedon, F.; Gans, N. MINA: A Multitasking Intelligent Nurse Aid Robot. In Proceedings of the The 14th PErvasive Technologies Related to Assistive Environments Conference, Corfu, Greece, 29 June–2 July 2021; pp. 266–267. [Google Scholar]
- Kodur, K.C.; Rajpathak, K.; Rajavenkatanarayanan, A.; Kyrarini, M.; Makedon, F. Towards a Multi-purpose Robotic Nursing Assistant. arXiv 2021, arXiv:2106.03683. [Google Scholar] [CrossRef]
- Rajpathak, K.; Kodur, K.C.; Kyrarini, M.; Makedon, F. End-User Framework for Robot Control. In Proceedings of the 14th PErvasive Technologies Related to Assistive Environments Conference, Corfu, Greece, 29 June–2 July 2021; pp. 109–110. [Google Scholar]
- Nambiappan, H.R.; Arboleda, S.A.; Lundberg, C.L.; Kyrarini, M.; Makedon, F.; Gans, N. MINA: A Robotic Assistant for Hospital Fetching Tasks. Technologies 2022, 10, 41. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 19–21 May 2009; Volume 3, p. 5. [Google Scholar]
- Kuzmicheva, O.; Martinez, S.F.; Krebs, U.; Spranger, M.; Moosburner, S.; Wagner, B.; Graser, A. Overground robot based gait rehabilitation system MOPASS - Overview and first results from usability testing. Proc. IEEE Int. Conf. Robot. Autom. 2016, 2016, 3756–3763. [Google Scholar] [CrossRef]
- Tan, K.; Koyama, S.; Sakurai, H.; Teranishi, T.; Kanada, Y.; Tanabe, S. Wearable robotic exoskeleton for gait reconstruction in patients with spinal cord injury: A literature review. J. Orthop. Transl. 2021, 28, 55–64. [Google Scholar] [CrossRef]
- Matjačić, Z.; Zadravec, M.; Olenšek, A. Feasibility of robot-based perturbed-balance training during treadmill walking in a high-functioning chronic stroke subject: A case-control study. J. Neuro Eng. Rehabil. 2018, 15, 1–15. [Google Scholar] [CrossRef]
- Zheng, Q.X.; Ge, L.; Wang, C.C.; Ma, Q.S.; Liao, Y.T.; Huang, P.P.; Wang, G.D.; Xie, Q.L.; Rask, M. Robot-assisted therapy for balance function rehabilitation after stroke: A systematic review and meta-analysis. Int. J. Nurs. Stud. 2019, 95, 7–18. [Google Scholar] [CrossRef]
- Chalvatzaki, G.; Koutras, P.; Hadfield, J.; Papageorgiou, X.S.; Tzafestas, C.S.; Maragos, P. Lstm-based network for human gait stability prediction in an intelligent robotic rollator. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4225–4232. [Google Scholar]
- Van Lam, P.; Fujimoto, Y. A robotic cane for balance maintenance assistance. IEEE Trans. Ind. Inform. 2019, 15, 3998–4009. [Google Scholar] [CrossRef]
- Abubakar, S.; Das, S.K.; Robinson, C.; Saadatzi, M.N.; Cynthia Logsdon, M.; Mitchell, H.; Chlebowy, D.; Popa, D.O. ARNA, a Service robot for Nursing Assistance: System Overview and User Acceptability. IEEE Int. Conf. Autom. Sci. Eng. 2020, 2020, 1408–1414. [Google Scholar] [CrossRef]
- Ramanathan, M.; Luo, L.; Er, J.K.; Foo, M.J.; Chiam, C.H.; Li, L.; Yau, W.Y.; Ang, W.T. Visual Environment perception for obstacle detection and crossing of lower-limb exoskeletons. IEEE Int. Conf. Intell. Robot. Syst. 2022, 2022, 12267–12274. [Google Scholar] [CrossRef]
- Ruiz-Ruiz, F.J.; Giammarino, A.; Lorenzini, M.; Gandarias, J.M.; Gomez-de Gabriel, J.M.; Ajoudani, A. Improving Standing Balance Performance through the Assistance of a Mobile Collaborative Robot. arXiv 2021, arXiv:2109.12038. [Google Scholar]
- Garcia, F.; Pandey, A.K.; Fattal, C. Wait for me! Towards socially assistive walk companions. arXiv 2019, arXiv:1904.08854. [Google Scholar]
- Song, K.T.; Jiang, S.Y.; Wu, S.Y. Safe Guidance for a Walking-Assistant Robot Using Gait Estimation and Obstacle Avoidance. IEEE/ASME Trans. Mechatron. 2017, 22, 2070–2078. [Google Scholar] [CrossRef]
- Wenzel, P.; Schön, T.; Leal-Taixé, L.; Cremers, D. Vision-Based Mobile Robotics Obstacle Avoidance With Deep Reinforcement Learning. In Proceedings of the IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021; pp. 14360–14366. [Google Scholar] [CrossRef]
- Zhu, K.; Zhang, T. Deep reinforcement learning based mobile robot navigation: A review. Tsinghua Sci. Technol. 2021, 26, 674–691. [Google Scholar] [CrossRef]
- Choi, J.; Lee, G.; Lee, C. Reinforcement learning-based dynamic obstacle avoidance and integration of path planning. Intell. Serv. Robot. 2021, 14, 663–677. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. arXiv 2018, arXiv:1801.01290. [Google Scholar] [CrossRef]
- Rosmann, C.; Hoffmann, F.; Bertram, T. Timed-Elastic-Bands for time-optimal point-to-point nonlinear model predictive control. In Proceedings of the 2015 European Control Conference, ECC 2015, Linz, Austria, 15–17 July 2015; pp. 3352–3357. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Biswas, A.; Wang, A.; Silvera, G.; Steinfeld, A.; Admoni, H. SocNavBench: A Grounded Simulation Testing Framework for Evaluating Social Navigation. ACM Trans. Hum. Robot. Interact. 2020, 12, 1–24. [Google Scholar] [CrossRef]
- Lerner, A.; Chrysanthou, Y.; Lischinski, D. Crowds by Example. Comput. Graph. Forum 2007, 26, 655–664. [Google Scholar] [CrossRef]
- Pellegrini, S.; Ess, A.; Schindler, K.; Gool, L.V. You’ll never walk alone: Modeling social behavior for multi-target tracking. In Proceedings of the IEEE International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 261–268. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Y.; Kreiss, S.; Alahi, A. Crowd-Robot Interaction: Crowd-aware Robot Navigation with Attention-based Deep Reinforcement Learning. In Proceedings of the IEEE International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2018; pp. 6015–6022. [Google Scholar]
- Berg, J.V.D.; Guy, S.J.; Lin, M.; Manocha, D. Reciprocal n-Body Collision Avoidance. Springer Tracts Adv. Robot. 2011, 70, 3–19. [Google Scholar] [CrossRef]
- Liu, L.; Dugas, D.; Cesari, G.; Siegwart, R.; Dube, R. Robot navigation in crowded environments using deep reinforcement learning. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 24 October–24 January 2020; pp. 5671–5677. [Google Scholar] [CrossRef]
- Liu, S.; Chang, P.; Liang, W.; Chakraborty, N.; Driggs-Campbell, K. Decentralized Structural-RNN for Robot Crowd Navigation with Deep Reinforcement Learning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 3517–3524. [Google Scholar]
- Jain, A.; Zamir, A.R.; Savarese, S.; Saxena, A. Structural-RNN: Deep Learning on Spatio-Temporal Graphs. arXiv 2016, arXiv:1511.05298. [Google Scholar]
- Vemula, A.; Muelling, K.; Oh, J. Social Attention: Modeling Attention in Human Crowds. arXiv 2018, arXiv:1710.04689. [Google Scholar]
- Joosse, M.; Lohse, M.; Berkel, N.V.; Sardar, A.; Evers, V. Making Appearances: How Robots Should Approach People. ACM Trans. Hum. Robot Interact. 2021, 1–24. [Google Scholar] [CrossRef]
- Brett Sears. Muscle Strength Scale in Physical Therapy. Available online: https://www.verywellhealth.com/muscle-strength-measurement-2696427 (accessed on 5 March 2023).
- Shelhamer, E.; Long, J.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 640–651. [Google Scholar] [CrossRef]
- Alvarez-Aparicio, C.; Guerrero-Higueras, Á.M.; Olivera, M.C.C.; Rodríguez-Lera, F.J.; Martín, F.; Matellán, V. Benchmark dataset for evaluation of range-Based people tracker classifiers in mobile robots. Front. Neurorobot. 2018, 11, 72. [Google Scholar] [CrossRef]
- Yang, S.; Baum, M. Extended Kalman filter for extended object tracking. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017; pp. 4386–4390. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; A Bradford Book: Cambridge, MA, USA, 2018. [Google Scholar]
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)(IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Helbing, D.; Molnar, P. Social Force Model for Pedestrian Dynamics. Phys. Rev. E 1998, 51, 4282–4286. [Google Scholar] [CrossRef]
- Jocher, G.; Stoken, A.; Borovec, J.; Changyu, L.; Hogan, A. ultralytics/yolov5: V3.1—Bug Fixes and Performance Improvements. Zenodo. 2020. Available online: https://doi.org/10.5281/zenodo.4154370 (accessed on 30 March 2023). [CrossRef]
- Feil-Seifer, D.; Haring, K.S.; Rossi, S.; Wagner, A.R.; Williams, T. Where to next? The impact of COVID-19 on human-robot interaction research. ACM Trans. Hum. Robot Interact. 2020, 10, 1–7. [Google Scholar] [CrossRef]
- Poulinakis, K.; Drikakis, D.; Kokkinakis, I.W.; Spottswood, S.M. Machine-Learning Methods on Noisy and Sparse Data. Mathematics 2023, 11, 236. [Google Scholar] [CrossRef]

| Number of Humans | Dynamic Collision Rate (%) | Contact Loss Rate (%) | Timeout Rate (%) | Success Rate (%) | Navigation Time (in s) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | Proposed Model V1 | Baseline | Proposed Model V1 | Baseline | Proposed Model V1 | Baseline | Proposed Model V1 | Baseline | Proposed Model V1 | |
| 5 | 30 | 18 | NA | 18 | 0 | 0 | 70 | 82 | 12.58 | 10.13 |
| 10 | 46 | 32 | NA | 12 | 0 | 0 | 54 | 68 | 13.06 | 11.93 |
| 17 | 60 | 54 | NA | 10 | 0 | 0 | 40 | 46 | 15.05 | 12.07 |
| Number of Humans | Dynamic Object Collision Rate (%) | Static Object Collision Rate (%) | Contact Loss Rate (%) | Timeout Rate (%) | Success Rate (%) | Navigation Time (in s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | Proposed Model V2 | Baseline | Proposed Model V2 | Baseline | Proposed Model V2 | Baseline | Proposed Model V2 | Baseline | Proposed Model V2 | Baseline | Proposed Model V2 | Baseline | Proposed Model V2 |
| 2–7 | 5 | 36 | 8 | 4 | 2 | NA | 10 | 0 | 0 | 60 | 90 | NA | 11.44 |
| 2–7 | 10 | 36 | 24 | 2 | 14 | NA | 12 | 0 | 0 | 60 | 62 | NA | 19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kodur, K.; Kyrarini, M. Patient–Robot Co-Navigation of Crowded Hospital Environments. Appl. Sci. 2023, 13, 4576. https://doi.org/10.3390/app13074576
Kodur K, Kyrarini M. Patient–Robot Co-Navigation of Crowded Hospital Environments. Applied Sciences. 2023; 13(7):4576. https://doi.org/10.3390/app13074576
Chicago/Turabian StyleKodur, Krishna, and Maria Kyrarini. 2023. "Patient–Robot Co-Navigation of Crowded Hospital Environments" Applied Sciences 13, no. 7: 4576. https://doi.org/10.3390/app13074576
APA StyleKodur, K., & Kyrarini, M. (2023). Patient–Robot Co-Navigation of Crowded Hospital Environments. Applied Sciences, 13(7), 4576. https://doi.org/10.3390/app13074576








