Modeling a Typical Non-Uniform Deformation of Materials Using Physics-Informed Deep Learning: Applications to Forward and Inverse Problems
Abstract
1. Introduction
2. Basic Principles
2.1. Linear Elasticity Theory
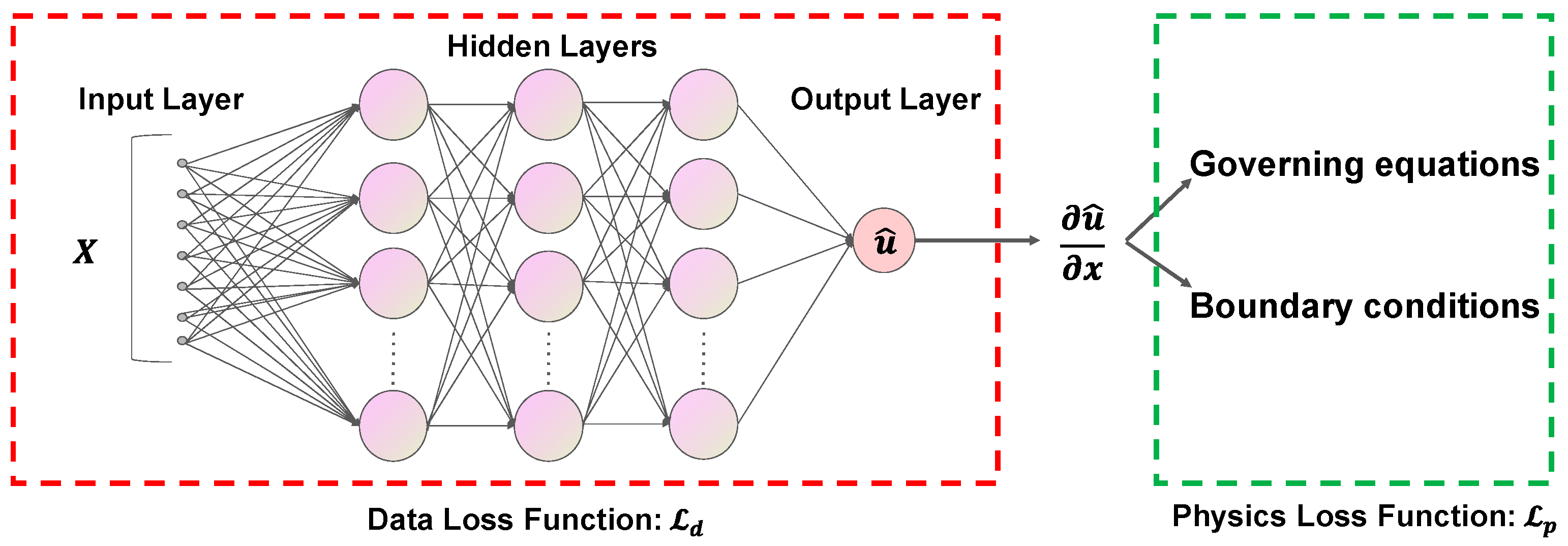
2.2. Physics-Informed Neural Network
2.3. Physics-Informed Loss Function
3. Validation Tests
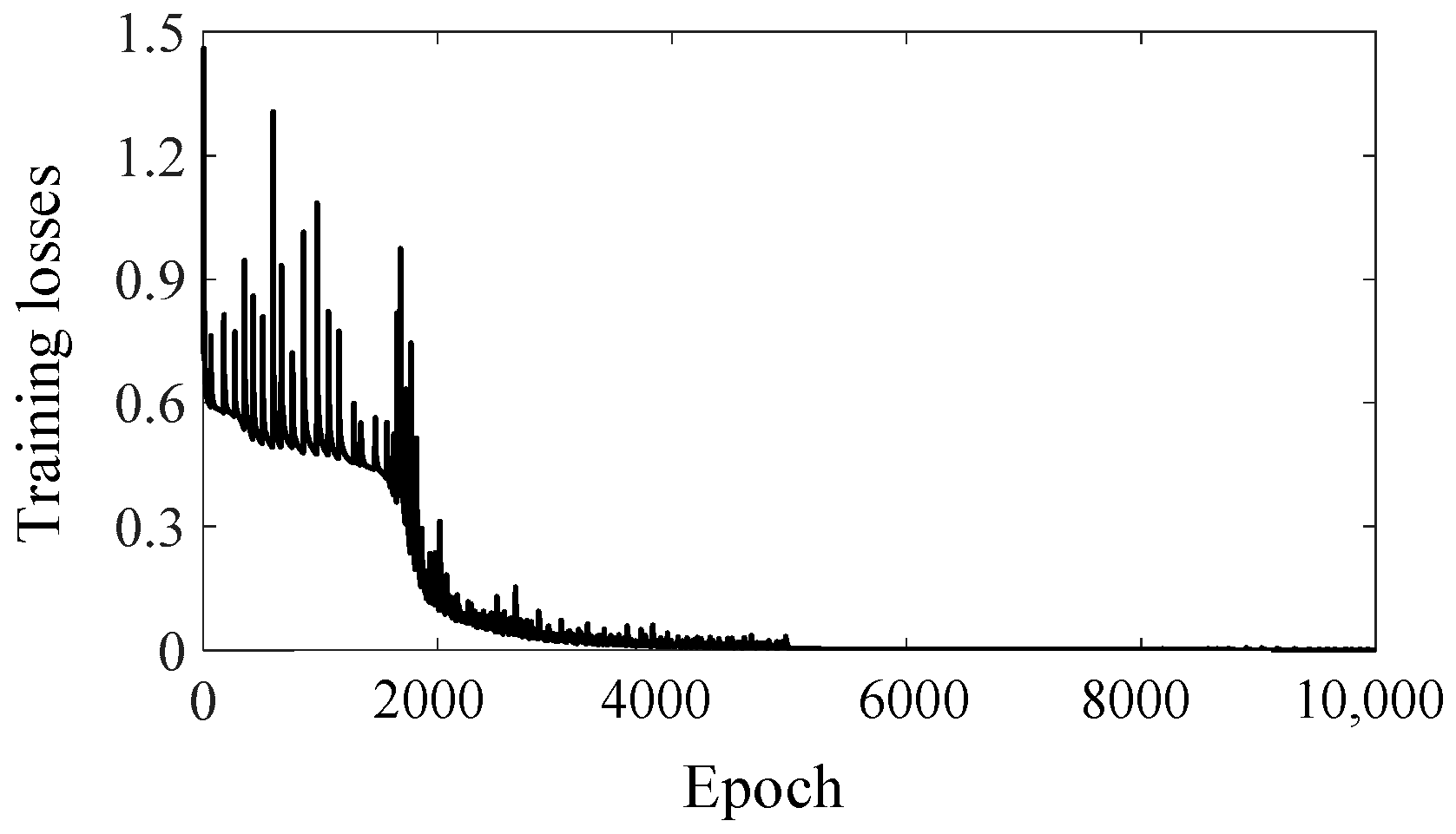
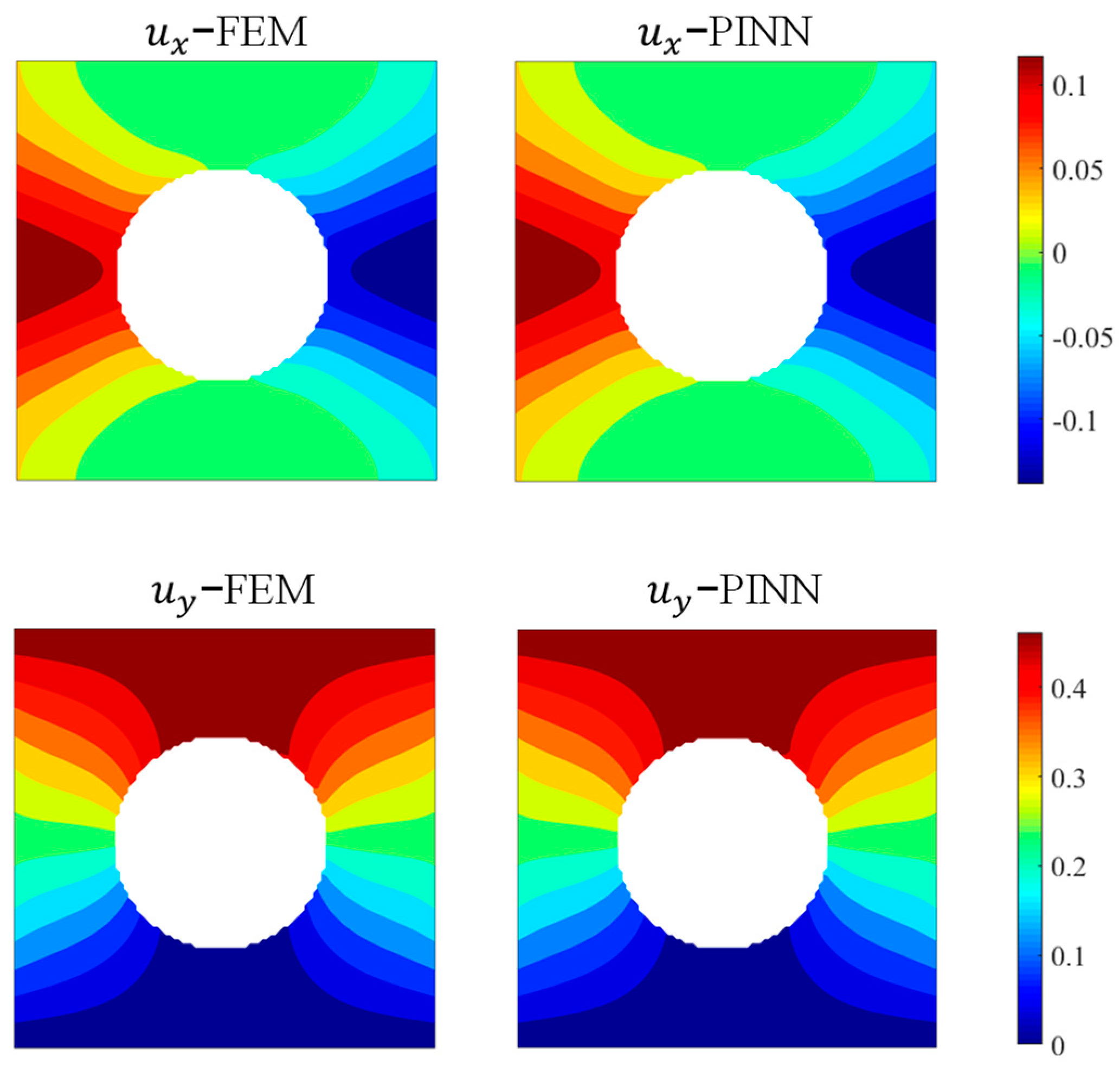
3.1. Forward Problems
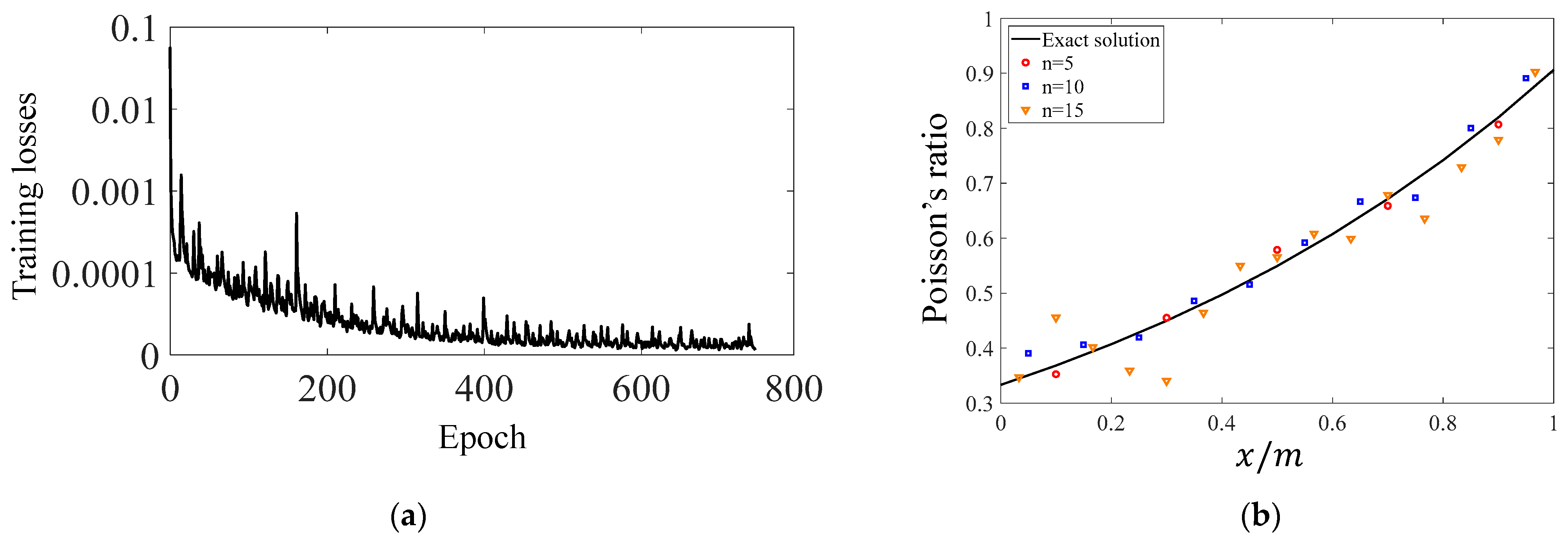
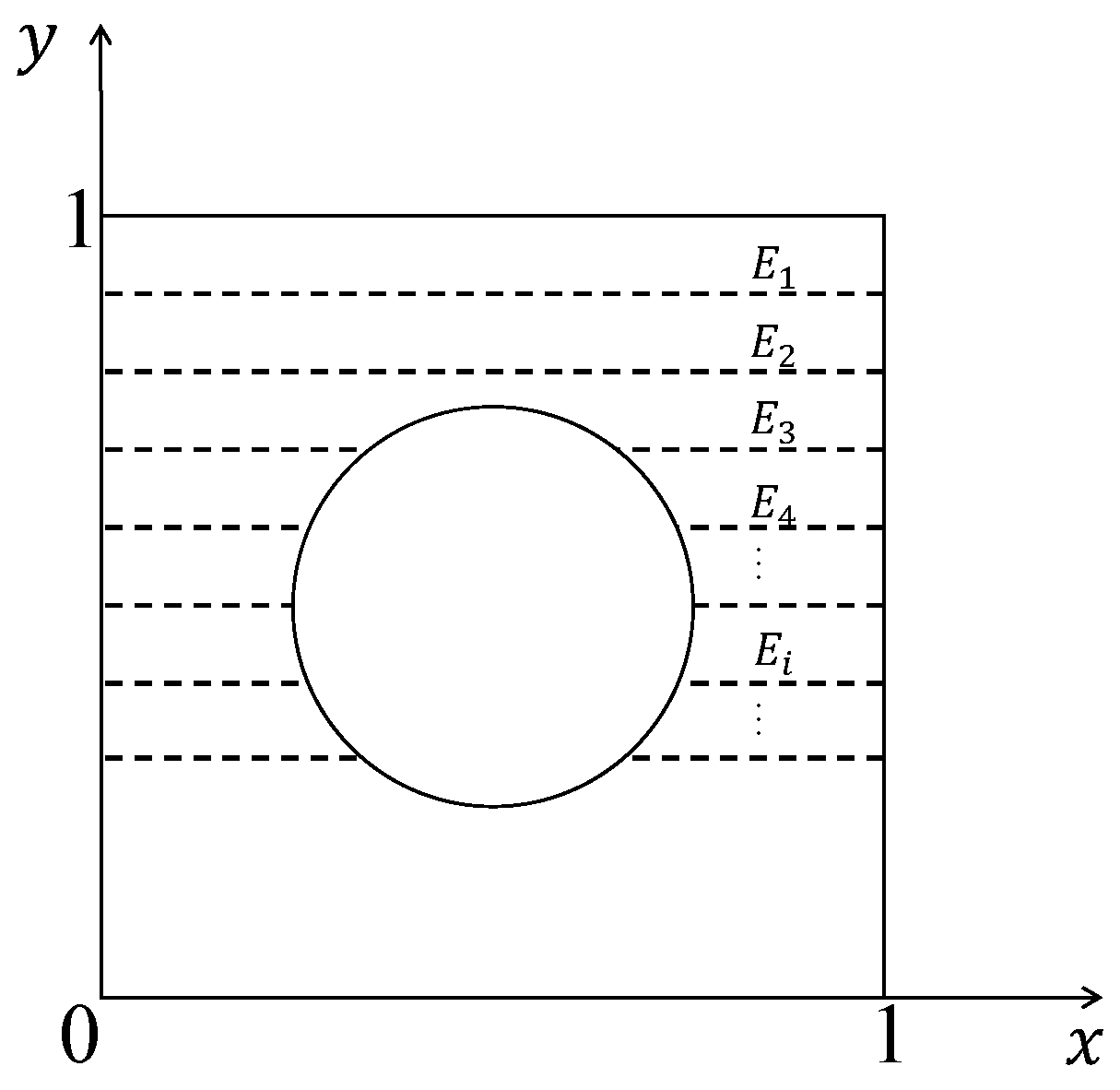
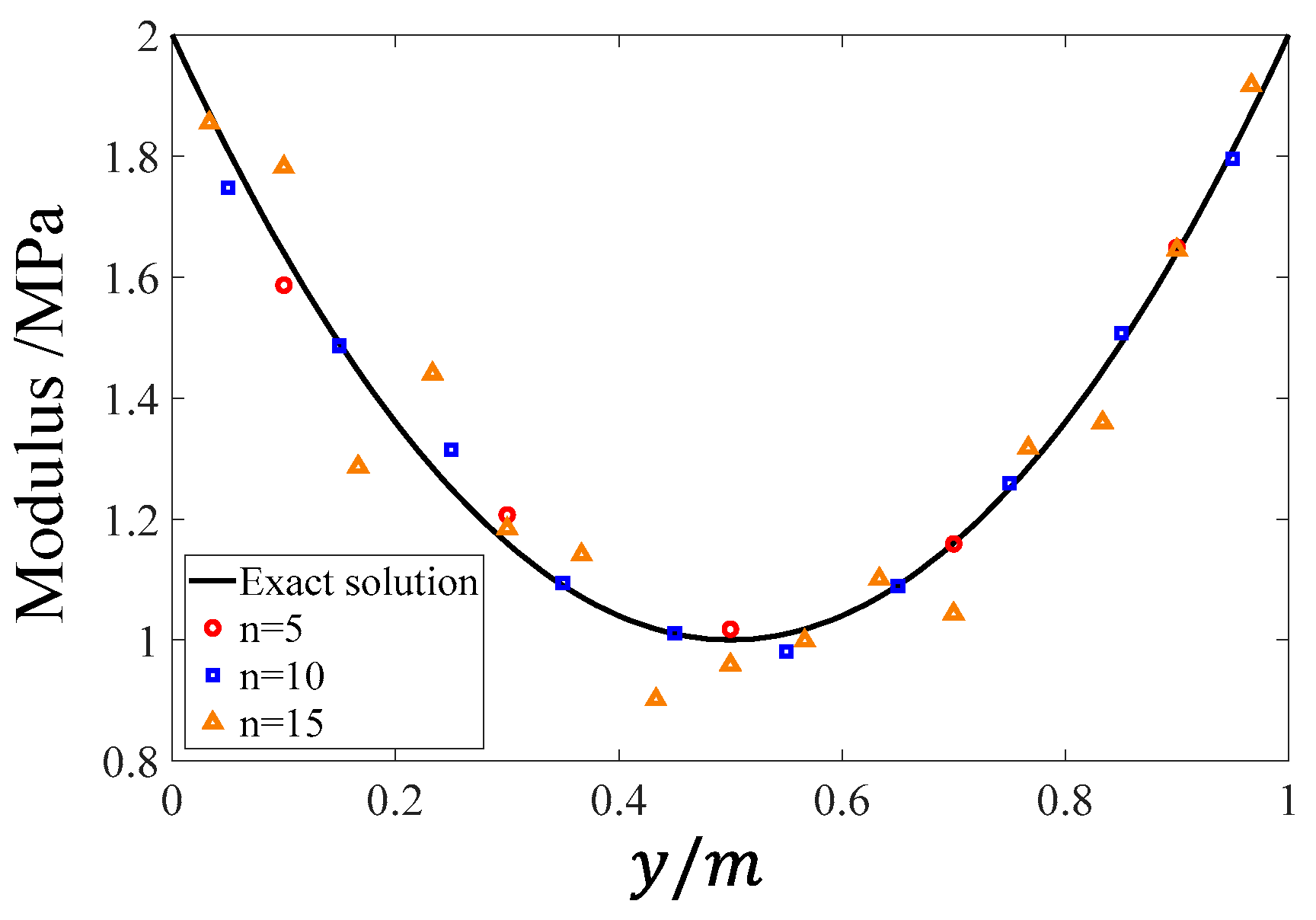
3.2. Inverse Problems
4. Conclusions
- A PINN framework comprising a simple FNN structure and a conventional physics-informed loss function can perform well in non-uniform deformation predictions and capture strain concentration well within the whole computational domain;
- The two case studies conducted to verify the effectiveness of this approach in identifying unknown physics laws show its promise and power in addressing inverse problems related to computational mechanics;
- Using the PINN method, the distribution of the unknown parameters of material can be identified via a single uniaxial test though one training session, thus avoiding the complexity of conventional uniaxial tests performed on several specimens.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Davydov, O.; Oanh, D.T.; Tuong, N.M. Improved stencil selection for meshless finite difference methods in 3D. J. Comput. Appl. Math. 2023, 425, 115031. [Google Scholar] [CrossRef]
- Xiong, Z.; Wang, X.; He, M.; Benabou, L.; Feng, Z. Investigation on thermal conductivity of silver-based porous materials by finite difference method. Mater. Today Commun. 2022, 33, 104897. [Google Scholar] [CrossRef]
- Sílvia, R.C.; Lauro, C.H.; Ana, H.; Davim, J.P. Development of FEM-based digital twins for machining difficult-to-cut materials: A roadmap for sustainability. J. Manuf. Process. 2022, 75, 739–766. [Google Scholar] [CrossRef]
- Shetty, N.; Shahabaz, S.; Sharma, S.; Shetty, S.D. A review on finite element method for machining of composite materials. Compos. Struct. 2017, 176, 790–802. [Google Scholar] [CrossRef]
- Badia, S.; Caicedo, M.A.; Martín, A.F.; Principe, J. A robust and scalable unfitted adaptive finite element framework for nonlinear solid mechanics. Comput. Methods Appl. Mech. Eng. 2021, 386, 114093. [Google Scholar] [CrossRef]
- Nouzil, I.; Eltaggaz, A.; Deiab, I.; Pervaiz, S. Numerical CFD-FEM model for machining titanium Ti-6Al-4V with nano minimum quantity lubrication: A step towards digital twin. J. Mater. Process. Technol. 2023, 312, 117867. [Google Scholar] [CrossRef]
- Wainberg, M.; Merico, D.; Delong, A.; Frey, B.J. Deep learning in biomedicine. Nat. Biotechnol. 2018, 36, 829–838. [Google Scholar] [CrossRef]
- Ching, T.; Himmelstein, D.S.; Beaulieu-Jones, B.K.; Kalinin, A.A.; Do, B.T.; Way, G.P.; Ferrero, E.; Agapow, P.-M.; Zietz, M.; Hoffman, M.M.; et al. Opportunities and obstacles for deep learning in biology and medicine. J. R. Soc. Interface 2018, 15, 20170387. [Google Scholar] [CrossRef]
- Rackauckas, C.; Ma, Y.; Martensen, J.; Warner, C.; Zubov, K.; Supekar, R.; Skinner, D.; Ramadhan, A.; Edelman, A. Universal Differential Equations for Scientific Machine Learning. arXiv 2020, arXiv:2001.04385. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Sun, L.; Gao, H.; Pan, S.; Wang, J.-X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar] [CrossRef]
- Jin, X.; Cai, S.; Li, H.; Karniadakis, G.E. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J. Comput. Phys. 2020, 426, 109951. [Google Scholar] [CrossRef]
- He, Z.; Ni, F.; Wang, W.; Zhang, J. A physics-informed deep learning method for solving direct and inverse heat conduction problems of materials. Mater. Today Commun. 2021, 28, 102719. [Google Scholar]
- Zobeiry, N.; Humfeld, K.D. A physics-informed machine learning approach for solving heat transfer equation in advanced manufacturing and engineering applications. Eng. Appl. Artif. Intell. 2021, 101, 104232. [Google Scholar] [CrossRef]
- Smith, J.D.; Azizzadenesheli, K.; Ross, Z.E. EikoNet: Solving the Eikonal Equation with Deep Neural Networks. IEEE Trans. Geosci. Remote Sens. 2020, 59, 10685–10696. [Google Scholar] [CrossRef]
- Rasht-Behesht, M.; Huber, C.; Shukla, K.; Karniadakis, G.E. Physics–Informed Neural Networks (PINNs) for Wave Propagation and Full Waveform Inversions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023120. [Google Scholar] [CrossRef]
- Song, C.; Alkhalifah, T.A. Wavefield Reconstruction Inversion via Physics-Informed Neural Networks. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Shukla, K.; Di Leoni, P.C.; Blackshire, J.; Sparkman, D.; Karniadakis, G.E. Physics-Informed Neural Network for Ultrasound Nondestructive Quantification of Surface Breaking Cracks. J. Nondestruct. Eval. 2020, 39, 1–20. [Google Scholar] [CrossRef]
- Rao, C.; Sun, H.; Liu, Y. Physics-Informed Deep Learning for Computational Elastodynamics without Labeled Data. J. Eng. Mech. 2021, 147, 04021043. [Google Scholar] [CrossRef]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Niu, S.; Zhang, E.; Bazilevs, Y.; Srivastava, V. Modeling finite-strain plasticity using physics-informed neural network and assessment of the network performance. J. Mech. Phys. Solids 2023, 172, 105177. [Google Scholar] [CrossRef]
- Kissas, G.; Yang, Y.; Hwuang, E.; Witschey, W.R.; Detre, J.A.; Perdikaris, P. Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2020, 358, 112623. [Google Scholar] [CrossRef]
- Zeng, S.; Cai, Y.; Zou, Q. Deep neural networks based temporal-difference methods for high-dimensional parabolic partial differential equations. J. Comput. Phys. 2022, 12, 111503. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Ling, J.; Jones, R.; Templeton, J. Machine learning strategies for systems with invariance properties. J. Comput. Phys. 2016, 318, 22–35. [Google Scholar] [CrossRef]
- Wang, R.; Kashinath, K.; Mustafa, M.; Albert, A.; Yu, R. Towards Physics-informed Deep Learning for Turbulent Flow Prediction. Comput. Phys. 2020, 10, 1457–1466. [Google Scholar]
- Blakseth, S.S.; Rasheed, A.; Kvamsdal, T.; San, O. Combining physics-based and data-driven techniques for reliable hybrid analysis and modeling using the corrective source term approach. Comput. Methods Appl. Mech. Eng. 2021, 379, 113759. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Yin, M.; Zhang, E.; Yu, Y.; Karniadakis, G.E. Interfacing finite elements with deep neural operators for fast multiscale modeling of mechanics problems. Comput. Methods Appl. Mech. Eng. 2022, 402, 115027. [Google Scholar] [CrossRef]
- Giuseppe, C.; Matthias, T. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602. [Google Scholar]
- Brodnik, N.R.; Muir, C.; Tulshibagwale, N.; Rossin, J.; Echlin, M.P.; Hamel, C.M.; Kramer, S.L.B.; Pollock, T.M.; Kiser, J.D.; Smith, C.; et al. Perspective: Machine learning in experimental solid mechanics. J. Mech. Phys. Solids 2023, 173, 105231. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier Neural Operator for Parametric Partial Differential Equations. arXiv 2020, arXiv:2010.08895. [Google Scholar]
- Black, N.; Najafi, A.R. Learning finite element convergence with the multi-fidelity graph neural network. Comput. Methods Appl. Mech. Eng. 2022, 397, 115120. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill Education: New York, NY, USA, 1961. [Google Scholar]
- Qu, D.; Tang, D. On control structure scheme of feedback linearization for nonlinear system based on ANN models and simulation researches. In Proceedings of the 2010 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; pp. 3645–3649. [Google Scholar] [CrossRef]
- Katageri, A.C.; Sheeparamatti, B.G. An ANN model of polymer based MEMS structures: A modal analysis approach. In Proceedings of the 2014 International Conference on Smart Structures and Systems (ICSSS), Chennai, India, 9 October 2014; pp. 112–117. [Google Scholar] [CrossRef]
- Hamel, C.M.; Long, K.N.; Kramer, S.L.B. Calibrating constitutive models with full-field data via physics informed neural networks. Strain 2022, 59, e12431. [Google Scholar] [CrossRef]
- Sun, X.; Yue, L.; Yu, L.; Shao, H.; Peng, X.; Zhou, K.; Demoly, F.; Zhao, R.; Qi, H.J. Machine Learning-Evolutionary Algorithm Enabled Design for 4D-Printed Active Composite Structures. Adv. Funct. 2021, 32, 2109805. [Google Scholar] [CrossRef]
- Chen, Q.; Xie, Y.; Ao, Y.; Li, T.; Chen, G.; Ren, S.; Wang, C.; Li, S. A deep neural network inverse solution to recover pre-crash impact data of car collisions. Transp. Res. Part C Emerg. Technol. 2021, 126, 103009. [Google Scholar] [CrossRef]
- Xie, Y.; Wu, C.T.; Li, B.; Hu, X.; Li, S. A feed-forwarded neural network-based variational Bayesian learning approach for forensic analysis of traffic accident. Comput. Methods Appl. Mech. Eng. 2022, 397, 115148. [Google Scholar] [CrossRef]
- Ye, Y.; Li, Y.; Ouyang, R.; Zhang, Z.; Tang, Y.; Bai, S. Improving machine learning based phase and hardness prediction of high-entropy alloys by using Gaussian noise augmented data. Comp. Mater. Sci. 2023, 223, 112140. [Google Scholar] [CrossRef]
- Liu, G.; Wang, L.; Yi, Y.; Sun, L.; Shi, L.; Ma, S. Inverse identification of graphite damage properties under complex stress states. Mater. Des. 2019, 183, 108135. [Google Scholar] [CrossRef]
- Liu, G.; Wang, L.; Yi, Y.; Sun, L.; Shi, L.; Jiang, H.; Ma, S. Inverse identification of tensile and compressive damage properties of graphite material based on a single four-point bending test. J. Nucl. Mater. 2018, 509, 445–453. [Google Scholar] [CrossRef]
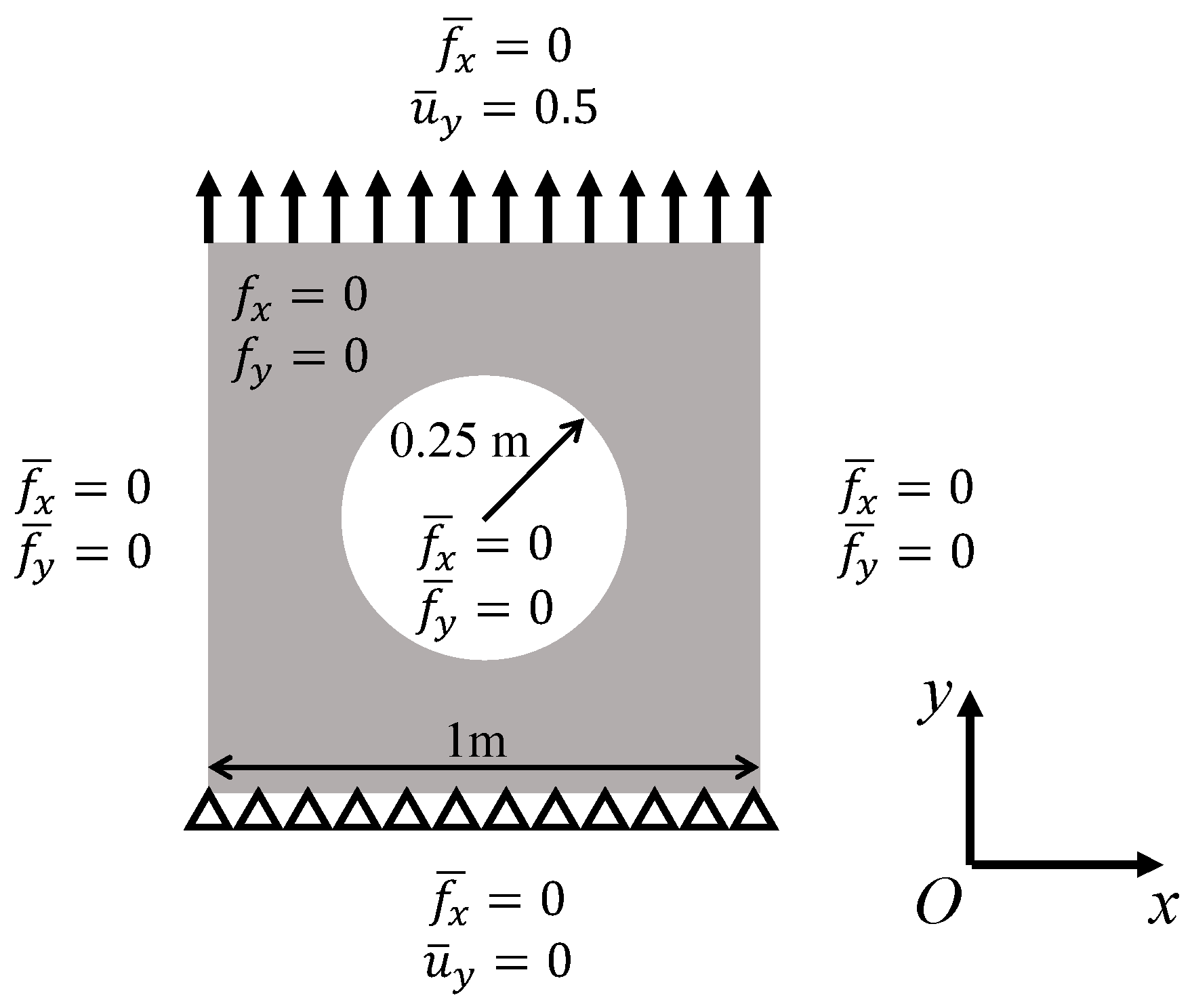


| Noise Scale | Identified | Deviation | Number of Iterations |
|---|---|---|---|
| 0.29802 | 0.00198 | 1221 | |
| 0.30758 | 0.00758 | 2523 | |
| 0.32636 | 0.02636 | 3851 |
| Example ID | FEM | PINN |
|---|---|---|
| 1 | 17 s | 14 s |
| 2 | 625 s | 63 s |
| 3 | 674 s | 66 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Chen, C.; Wang, Q.; Li, X.; Fan, Z.; Li, Y. Modeling a Typical Non-Uniform Deformation of Materials Using Physics-Informed Deep Learning: Applications to Forward and Inverse Problems. Appl. Sci. 2023, 13, 4539. https://doi.org/10.3390/app13074539
Deng Y, Chen C, Wang Q, Li X, Fan Z, Li Y. Modeling a Typical Non-Uniform Deformation of Materials Using Physics-Informed Deep Learning: Applications to Forward and Inverse Problems. Applied Sciences. 2023; 13(7):4539. https://doi.org/10.3390/app13074539
Chicago/Turabian StyleDeng, Yawen, Changchang Chen, Qingxin Wang, Xiaohe Li, Zide Fan, and Yunzi Li. 2023. "Modeling a Typical Non-Uniform Deformation of Materials Using Physics-Informed Deep Learning: Applications to Forward and Inverse Problems" Applied Sciences 13, no. 7: 4539. https://doi.org/10.3390/app13074539
APA StyleDeng, Y., Chen, C., Wang, Q., Li, X., Fan, Z., & Li, Y. (2023). Modeling a Typical Non-Uniform Deformation of Materials Using Physics-Informed Deep Learning: Applications to Forward and Inverse Problems. Applied Sciences, 13(7), 4539. https://doi.org/10.3390/app13074539





