Design and Analysis of an Inductive Coupling System for the Early Detection of Heart Failure
Abstract
1. Introduction
1.1. Literature Review
1.2. Overview of the Proposed Method
2. Methodology and the Optimization Procedure
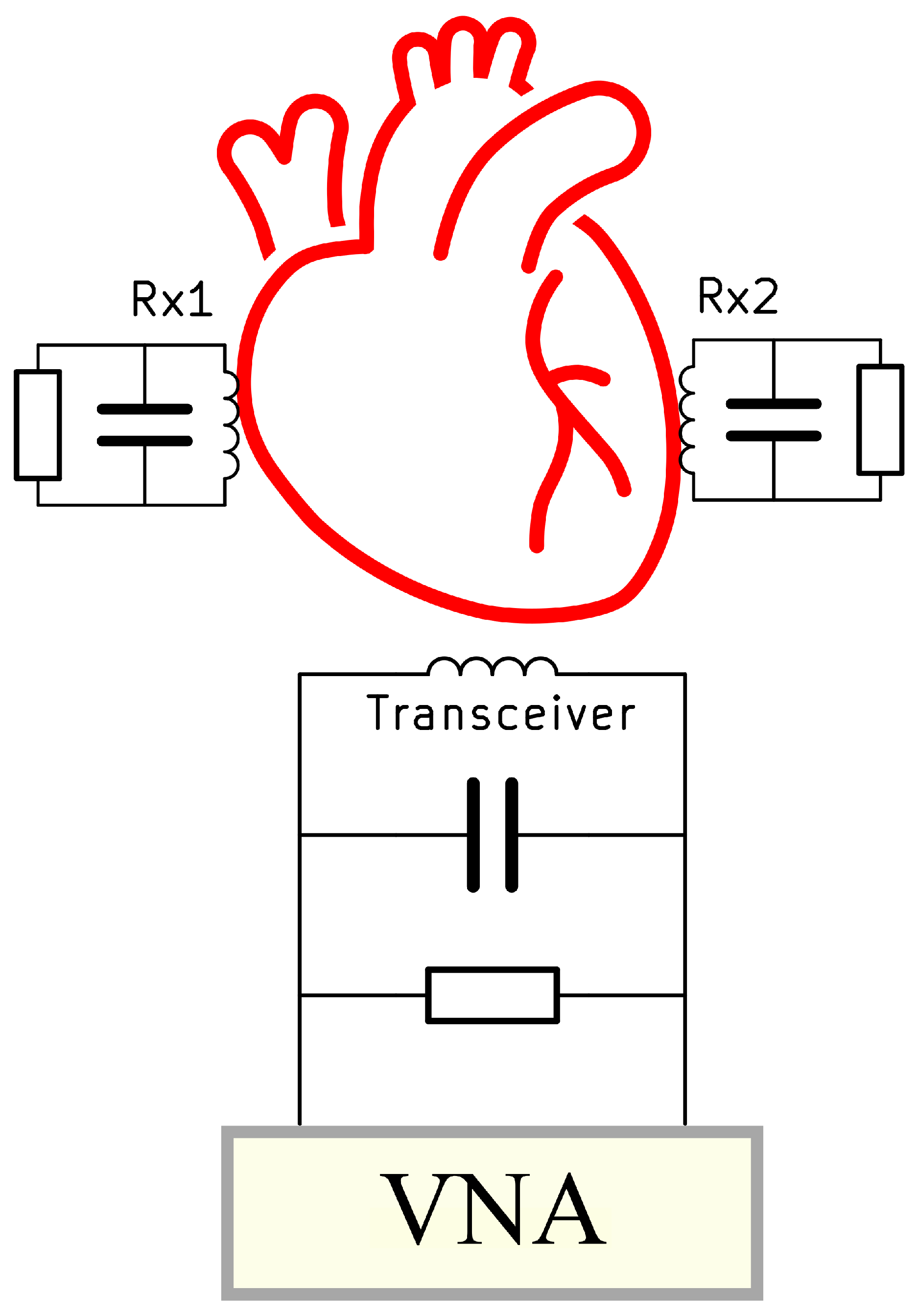
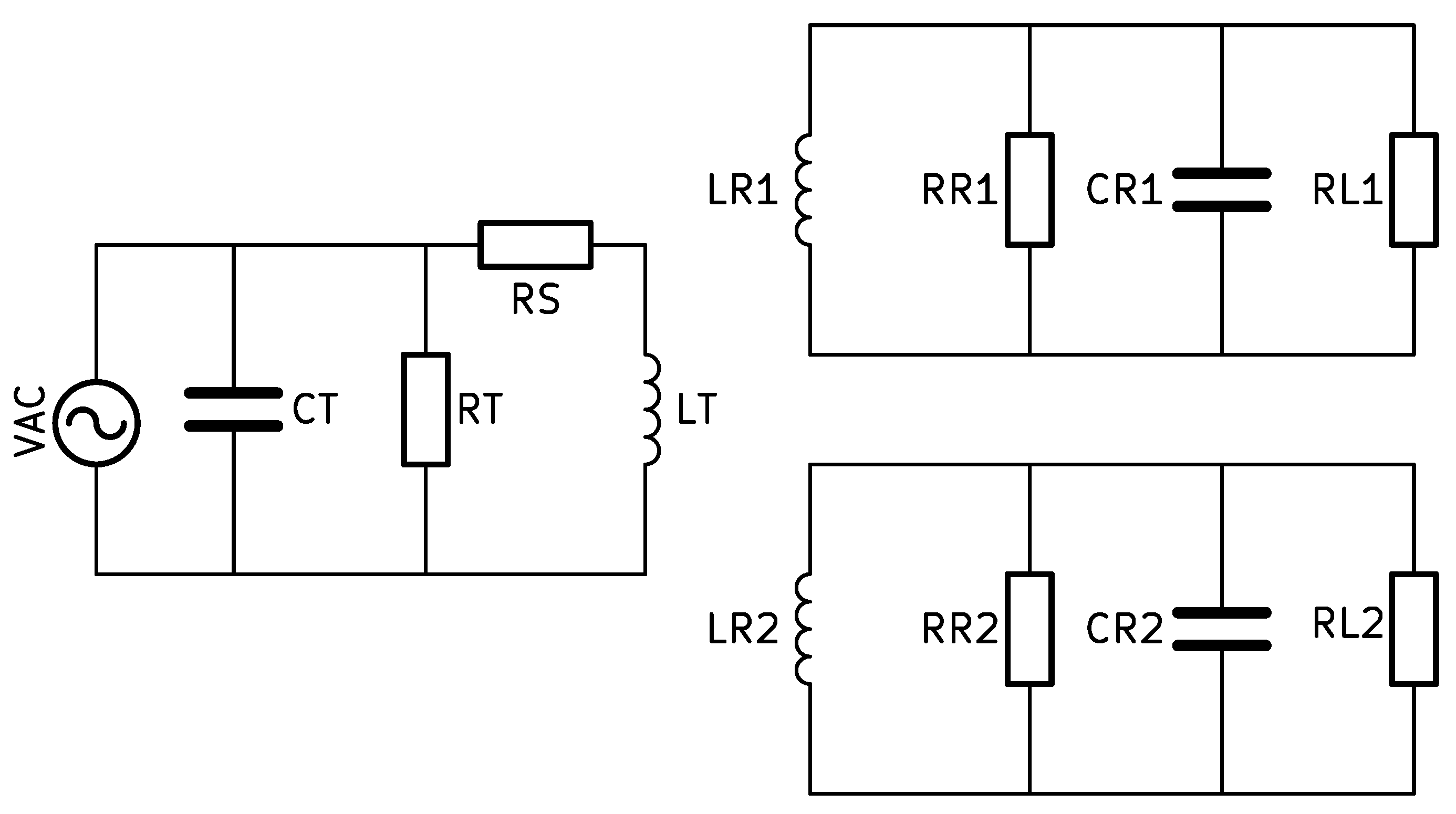
2.1. Equivalent Circuit Model of the Inductive Coupling Method
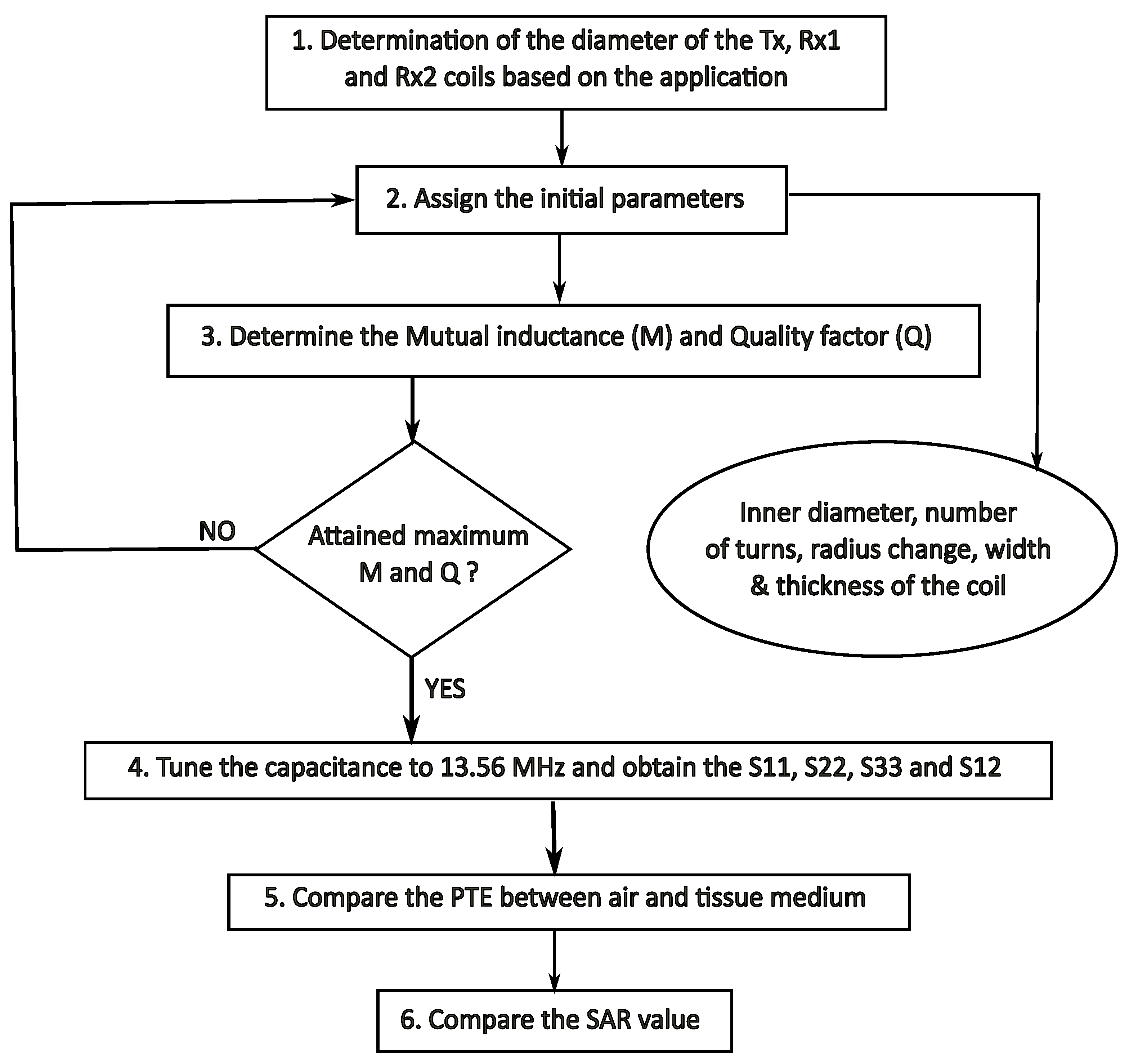
2.2. Optimization Procedure of the Proposed Method
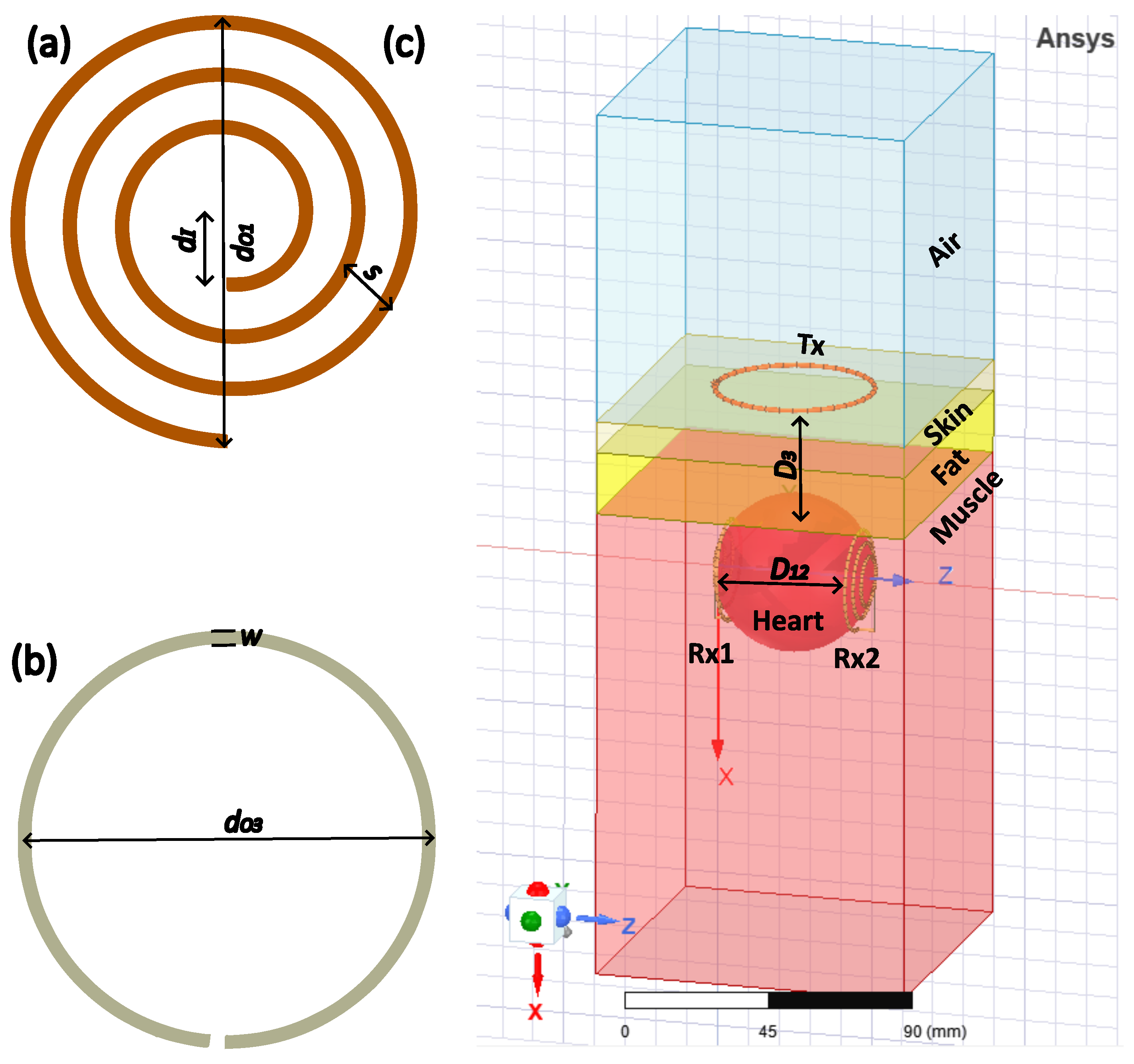
- Step 1: The design restrictions are determined in accordance with the application. There must be a determination regarding the size and shape of the coils. Taking into account the form and size of the average human heart, the spherical receiver coils are selected with a maximum diameter of 3.4 mm (we selected two spherical receiver coils). As lies on the chest, a planar circular shape is chosen to ensure comfort. The values , , and are wound with copper, and the operational frequency is 13.56 MHz.
- Step 2: In this step, the parameters of , , and are initialized. The parameters are the inner diameter of the coil (), the width of the wire (w), the number of turns (n), the distance between turns (s), and the pitch (p), respectively.
- Step 3: The mutual inductance and Q-factor between the coils are determined by performing a parametric sweep with regard to the parameters mentioned in the preceding step.
- Step 4: The procedure for optimization is performed until both Q and M have increased to their maximum values. In order to determine the transmission coefficients, the capacitance is continually adjusted to 13.56 MHz.
- Step 5: At the fifth stage, a comparison is made between the power transmission efficiency of the coils when operating in air and when operating in a tissue medium.
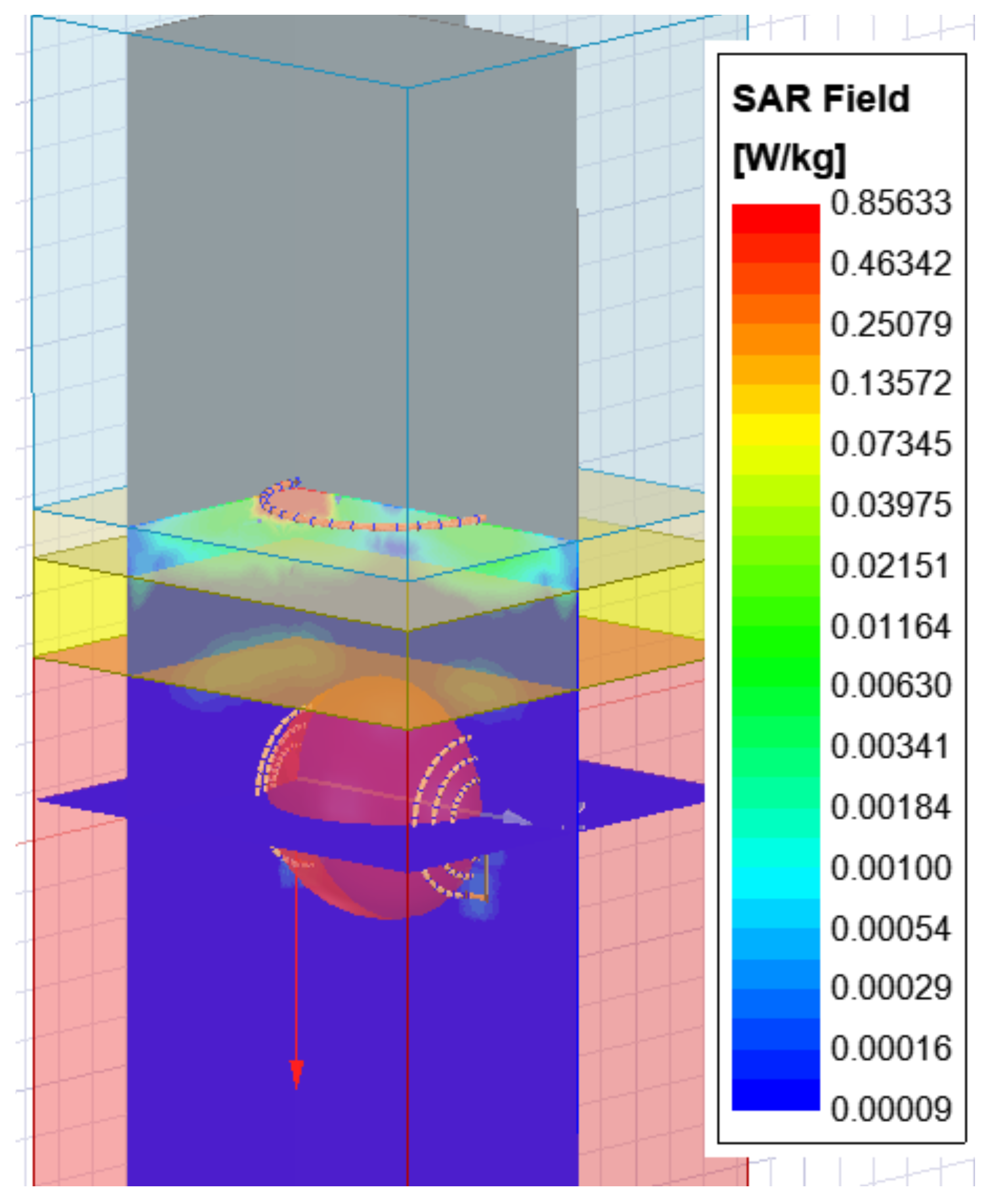
- Step 6: Finally, the specific absorption rate, often known as the SAR, is calculated to ensure that the design complies with the requirements set forth by the Federal Communications Commission (FCC).
3. Transceiver and Receiver Coil Geometries and Performance Analysis
3.1. Transceiver and Receiver Coil Geometries
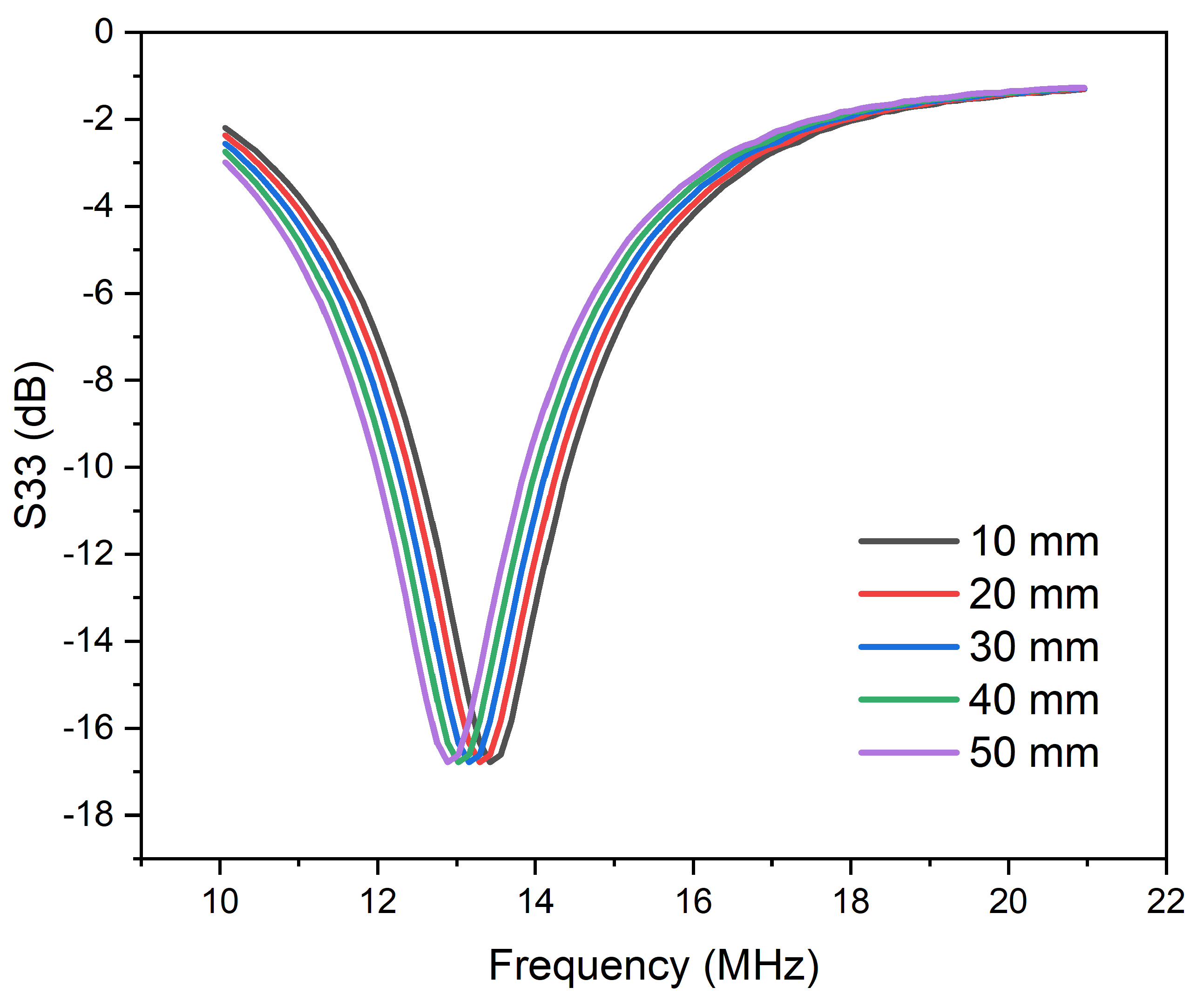
3.2. Performance Analysis in the Heterogeneous Phantom
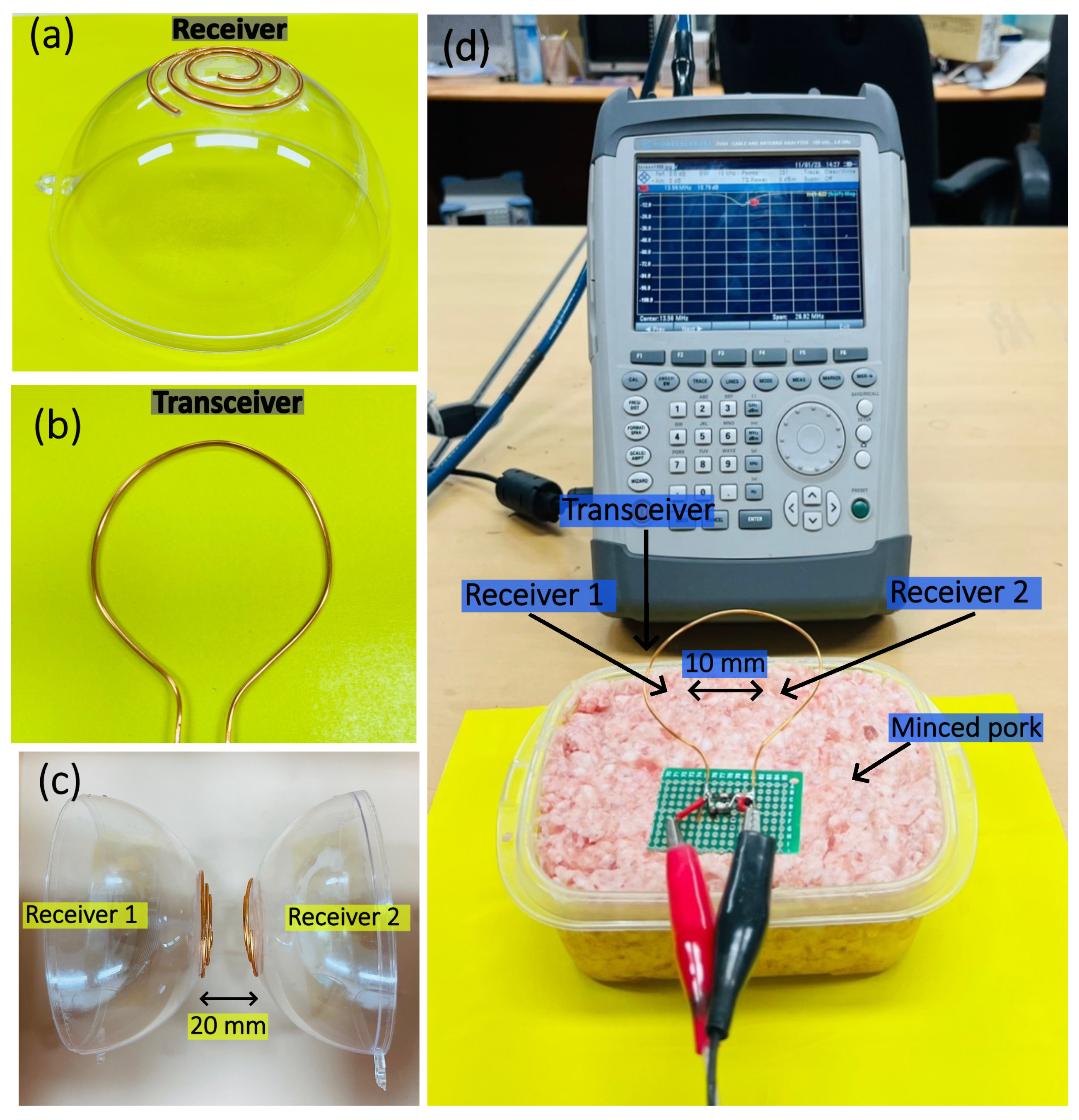
4. Experimental Measurements
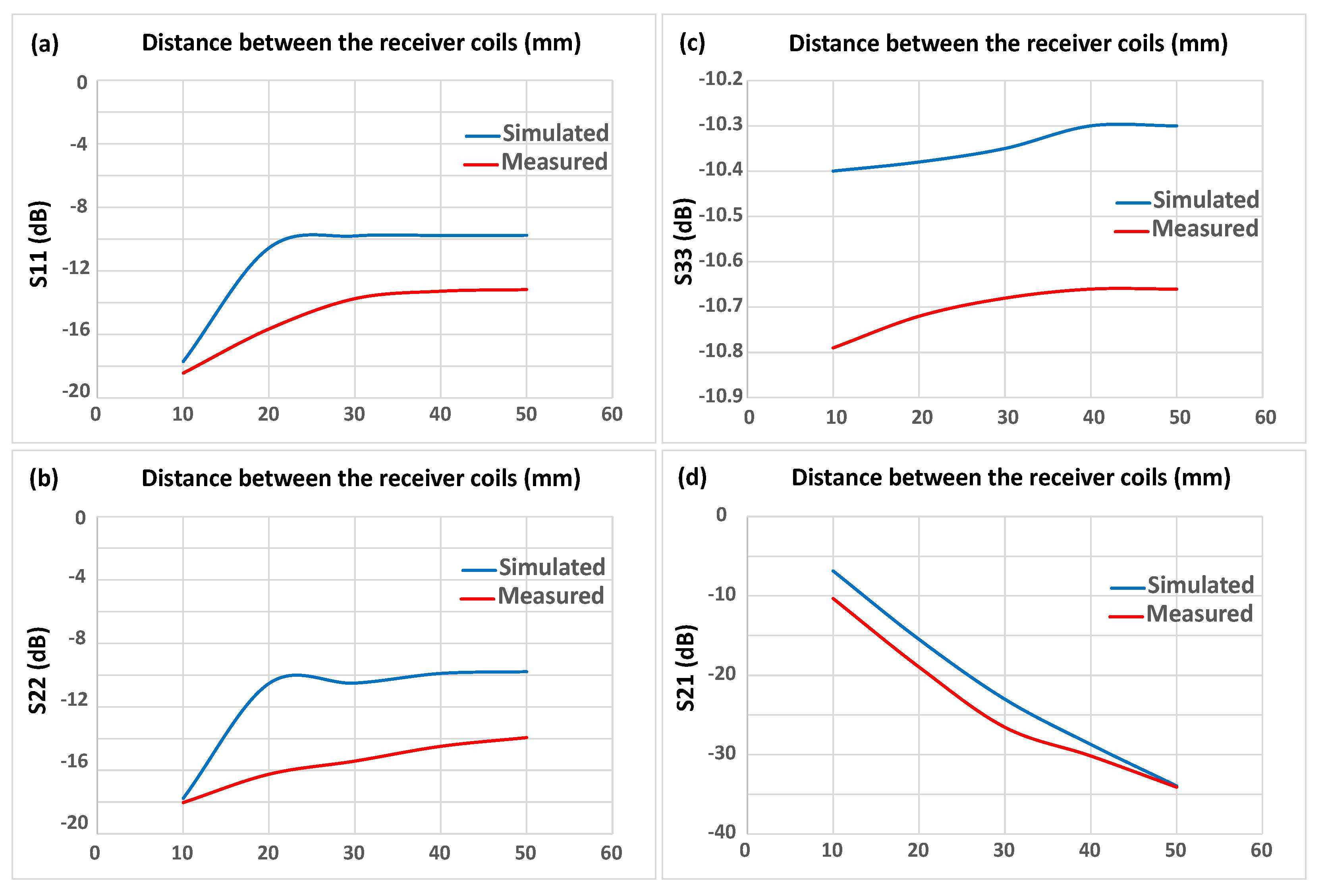
Comparison between Simulated and Measured Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hernandez Sebastian, N.; Villa Villasenor, N.; Renero-Carrillo, F.J.; Diaz Alonso, D.; Calleja Arriaga, W. Design of a fully integrated inductive coupling system: A discrete approach towards sensing ventricular pressure. Sensors 2020, 20, 1525. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Sebastián, N.; Díaz-Alonso, D.; Renero-Carrillo, F.J.; Villa-Villaseñor, N.; Calleja-Arriaga, W. Design and simulation of an integrated wireless capacitive sensors array for measuring ventricular pressure. Sensors 2018, 18, 2781. [Google Scholar] [CrossRef] [PubMed]
- Herbert, R.; Lim, H.R.; Rigo, B.; Yeo, W.H. Fully implantable wireless batteryless vascular electronics with printed soft sensors for multiplex sensing of hemodynamics. Sci. Adv. 2022, 8, eabm1175. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Bai, W.; Ouyang, W.; Liu, Y.; Wu, C.; Xu, Y.; Weng, Y.; Zang, H.; Liu, Y.; Jacobson, L.; et al. Wireless implantable optical probe for continuous monitoring of oxygen saturation in flaps and organ grafts. Nat. Commun. 2022, 13, 3009. [Google Scholar] [CrossRef] [PubMed]
- Ullah, S.; Zada, M.; Basir, A.; Yoo, H. Wireless, battery-free, and fully implantable micro-coil system for 7 T brain MRI. IEEE Trans. Biomed. Circuits Syst. 2022, 16, 430–441. [Google Scholar] [CrossRef]
- Palagani, Y.; Sorkin, E.; Bonde, R.; Bahel, P.; Bonde, P. Resonantly coupled high-efficiency sensors for assessment of ventricular chamber size for autonomous control of left ventricular assist device. ASAIO J. 2022, 69, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Haerinia, M.; Shadid, R. Wireless power transfer approaches for medical implants: A review. Signals 2020, 1, 209–229. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, C.; Huang, Y. Wireless power transfer for implanted medical application: A review. Energies 2020, 13, 2837. [Google Scholar] [CrossRef]
- Bussooa, A.; Neale, S.; Mercer, J.R. Future of smart cardiovascular implants. Sensors 2018, 18, 2008. [Google Scholar] [CrossRef]
- Nelson, B.D.; Karipott, S.S.; Wang, Y.; Ong, K.G. Wireless technologies for implantable devices. Sensors 2020, 20, 4604. [Google Scholar] [CrossRef]
- Tang, C.; Liu, Z.; Li, L. Mechanical Sensors for Cardiovascular Monitoring: From Battery-Powered to Self-Powered. Biosensors 2022, 12, 651. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.G.; Lee, S.; Park, J.U. Recent progress in wireless sensors for wearable electronics. Sensors 2019, 19, 4353. [Google Scholar] [CrossRef] [PubMed]
- Palagani, Y.; Mohanarangam, K.; Shim, J.H.; Choi, J.R. Wireless power transfer analysis of circular and spherical coils under misalignment conditions for biomedical implants. Biosens. Bioelectron. 2019, 141, 111283. [Google Scholar] [CrossRef] [PubMed]
- Alexander, C.K.; no Sadiku, M. Electric circuits. Transformation 2000, 135, 4–5. [Google Scholar]
- Daida, S.R. A Design of Inductive Coupling Wireless Power Transfer System for Electric Vehicle Applications. Master’s Thesis, Old Dominion University, Norfolk, VA, USA, 2019. [Google Scholar]
- Chopra, S.; Bauer, P. Analysis and design considerations for a contactless power transfer system. In Proceedings of the 2011 IEEE 33rd International Telecommunications Energy Conference (INTELEC), Amsterdam, The Netherlands, 9–13 October 2011; pp. 1–6. [Google Scholar]
- Mohanarangam, K.; Palagani, Y.; Cho, K.; Choi, J.R. Inductive Power Transfer Link at 13.56 MHz for Leadless Cardiac Pacemakers. Energies 2021, 14, 5436. [Google Scholar] [CrossRef]
- Braunwald, E.; Bristow, M.R. Congestive heart failure: Fifty years of progress. Circulation 2000, 102, Iv-14–Iv-23. [Google Scholar] [CrossRef]
- Rezaeieh, S.A.; Zamani, A.; Bialkowski, K.; Abbosh, A. Foam embedded wideband antenna array for early congestive heart failure detection with tests using artificial phantom with animal organs. IEEE Trans. Antennas Propag. 2015, 63, 5138–5143. [Google Scholar] [CrossRef]
- Zhong, W.; Zhang, C.; Liu, X.; Hui, S.R. A methodology for making a three-coil wireless power transfer system more energy efficient than a two-coil counterpart for extended transfer distance. IEEE Trans. Power Electron. 2014, 30, 933–942. [Google Scholar] [CrossRef]
- Mirbozorgi, S.A.; Gosselin, B.; Sawan, M. A transcutaneous power transfer interface based on a multicoil inductive link. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 1659–1662. [Google Scholar]
- Schormans, M.; Valente, V.; Demosthenous, A. Practical inductive link design for biomedical wireless power transfer: A tutorial. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 1112–1130. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; Maradei, F.; Feliziani, M. Coil design of a wireless power-transfer receiver integrated into a left ventricular assist device. Electronics 2021, 10, 874. [Google Scholar] [CrossRef]
- Masetic, Z.; Subasi, A. Congestive heart failure detection using random forest classifier. Comput. Methods Programs Biomed. 2016, 130, 54–64. [Google Scholar] [CrossRef] [PubMed]
- Betts, J.G.; Desaix, P.; Johnson, E.; Johnson, J.; Korol, O.; Kruse, D.; Poe, B.; Wise, J.; Womble, M.; Young, K. Anatomy and Physiology; OpenStax, Rice University: Houston, TX, USA, 2013. [Google Scholar]
- Available online: http://niremf.ifac.cnr.it/tissprop/htmlclie/htmlclie.php (accessed on 20 August 2022).
- Christ, A.; Douglas, M.G.; Roman, J.M.; Cooper, E.B.; Sample, A.P.; Waters, B.H.; Smith, J.R.; Kuster, N. Evaluation of wireless resonant power transfer systems with human electromagnetic exposure limits. IEEE Trans. Electromagn. Compat. 2012, 55, 265–274. [Google Scholar] [CrossRef]
- Jia, Y.; Mirbozorgi, S.A.; Wang, Z.; Hsu, C.C.; Madsen, T.E.; Rainnie, D.; Ghovanloo, M. Position and orientation insensitive wireless power transmission for EnerCage-Homecage system. IEEE Trans. Biomed. Eng. 2017, 64, 2439–2449. [Google Scholar] [CrossRef] [PubMed]
- Dutta, P.K.; Jayasree, P.V.Y.; Baba, V.S.S.N.S. SAR reduction in the modelled human head for the mobile phone using different material shields. Hum.-Centric Comput. Inf. Sci. 2016, 6, 1–22. [Google Scholar] [CrossRef]
- Available online: https://www.fcc.gov/general/specific-absorption-rate-sar-cellulartelephones (accessed on 15 April 2022).
- Han, W.; Chau, K.; Jiang, C.; Liu, W. Accurate position detection in wireless power transfer using magnetoresistive sensors for implant applications. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar]

| Parameter | Symbol | |||
|---|---|---|---|---|
| Self inductance (nH) | L | 222.0 | 222.0 | 123.2 |
| Self resistance | 0.16 | 0.16 | 0.047 | |
| Q-Factor | Q | 117.5 | 117.5 | 225.1 |
| Outer diameter (mm) | 34 | 34 | 61.5 | |
| Inner diameter (mm) | 10 | 10 | 58.5 | |
| Number of turns | n | 3 | 3 | 1 |
| Width (mm) | w | 1 | 1 | - |
| Spacing (mm) | s | 3 | 3 | - |
| Pitch (mm) | p | 1 | 1 | - |
| Weight (g) | - | 0.1 | 0.1 | - |
| Distance (mm) | = 10 to 60 | = 50 | ||
| Wire type | Copper | |||
| Frequency (MHz) | 13.56 |
| Tissue | Relative Permittivity () | Loss Tangent (tan) | Conductivity () |
|---|---|---|---|
| Air | 1.0 | 0.0 | 0.0 |
| Skin | 285 | 1.10 | 0.23 |
| Fat | 11.8 | 3.40 | 0.03 |
| Muscle | 138 | 6.01 | 0.62 |
| Heart | 239 | 2.91 | 0.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krishnamurthy Venkataramani, R.; Mohanarangam, K.; Lim, J.; Yu, K.; Gonuguntla, V.; Choi, J.R. Design and Analysis of an Inductive Coupling System for the Early Detection of Heart Failure. Appl. Sci. 2023, 13, 4381. https://doi.org/10.3390/app13074381
Krishnamurthy Venkataramani R, Mohanarangam K, Lim J, Yu K, Gonuguntla V, Choi JR. Design and Analysis of an Inductive Coupling System for the Early Detection of Heart Failure. Applied Sciences. 2023; 13(7):4381. https://doi.org/10.3390/app13074381
Chicago/Turabian StyleKrishnamurthy Venkataramani, Raghavendiran, Krithikaa Mohanarangam, Jongmin Lim, Ke Yu, Venkateswarlu Gonuguntla, and Jun Rim Choi. 2023. "Design and Analysis of an Inductive Coupling System for the Early Detection of Heart Failure" Applied Sciences 13, no. 7: 4381. https://doi.org/10.3390/app13074381
APA StyleKrishnamurthy Venkataramani, R., Mohanarangam, K., Lim, J., Yu, K., Gonuguntla, V., & Choi, J. R. (2023). Design and Analysis of an Inductive Coupling System for the Early Detection of Heart Failure. Applied Sciences, 13(7), 4381. https://doi.org/10.3390/app13074381







