A Probabilistic Forecast Algorithm of Nonconvective Turbulence over the Tibetan Plateau
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
3. Results
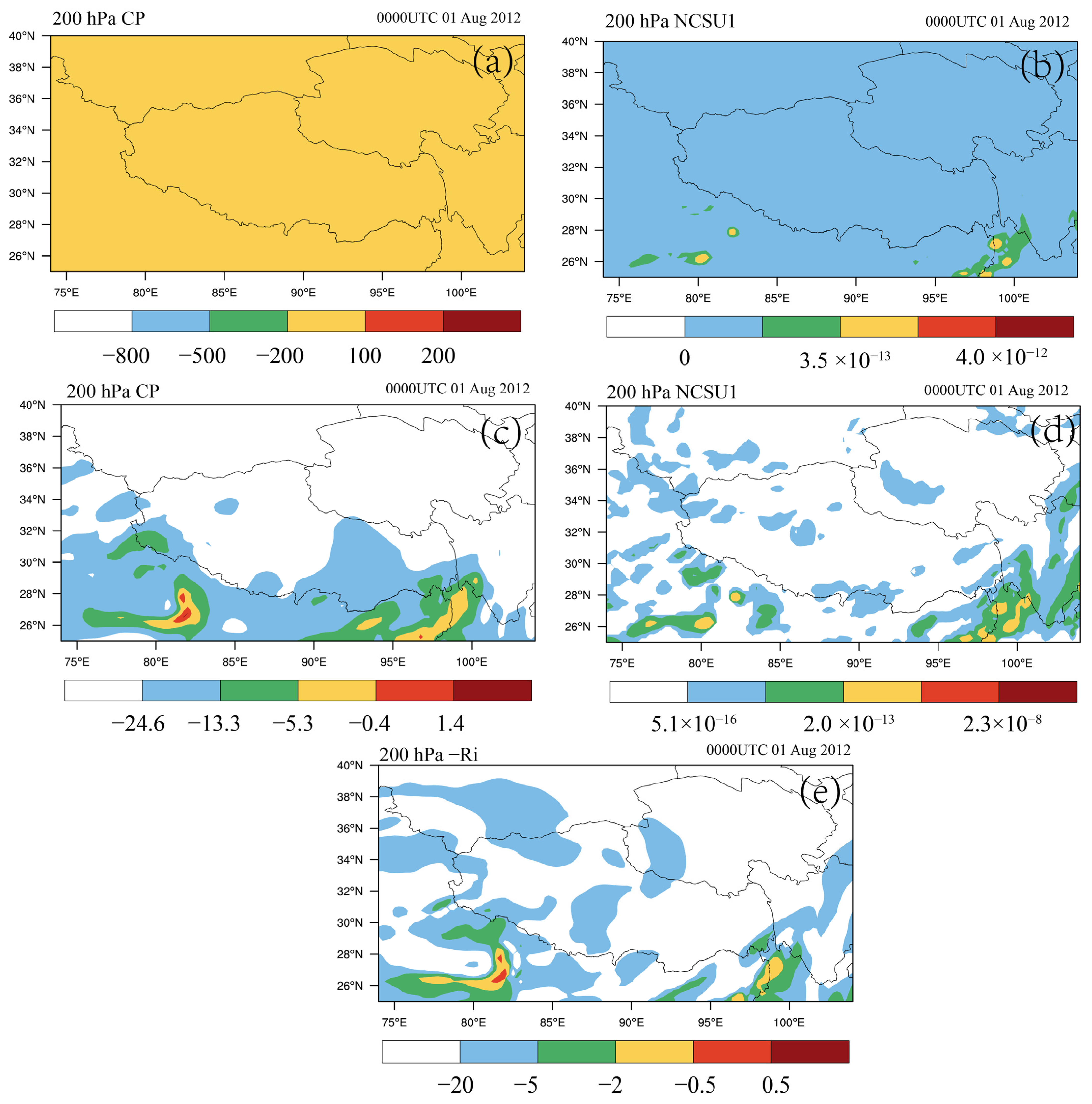
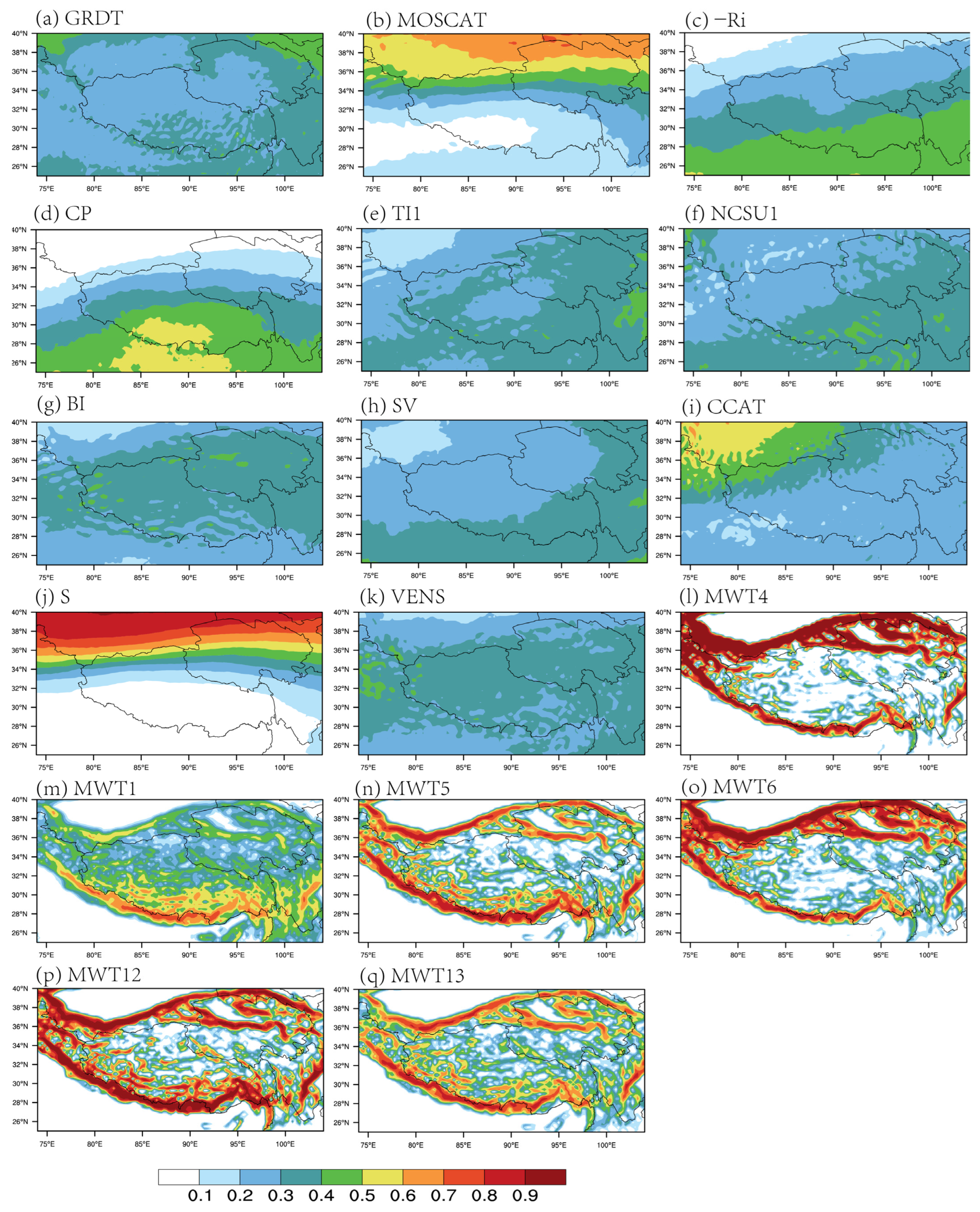
3.1. Thresholds of the Turbulence Indices
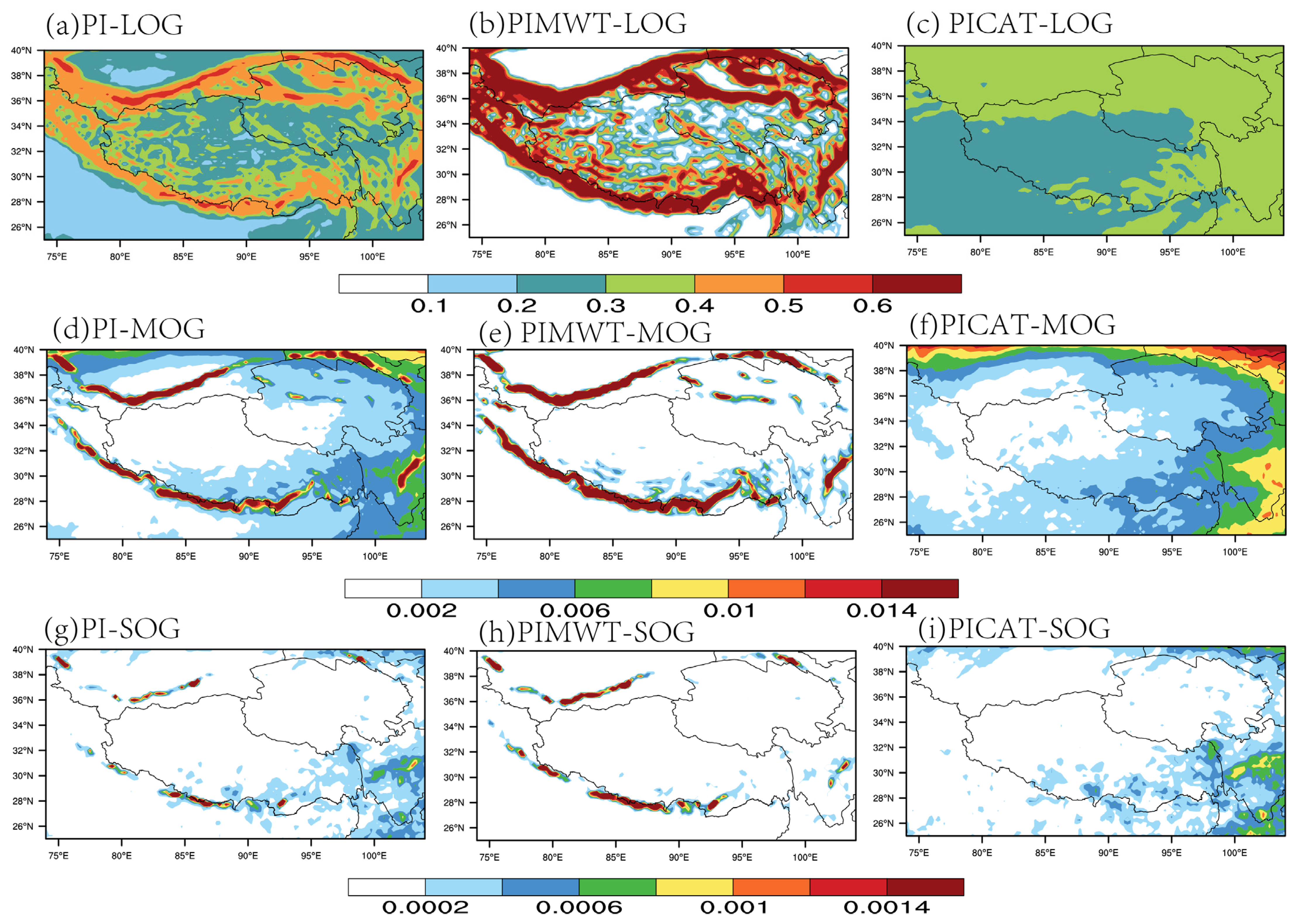
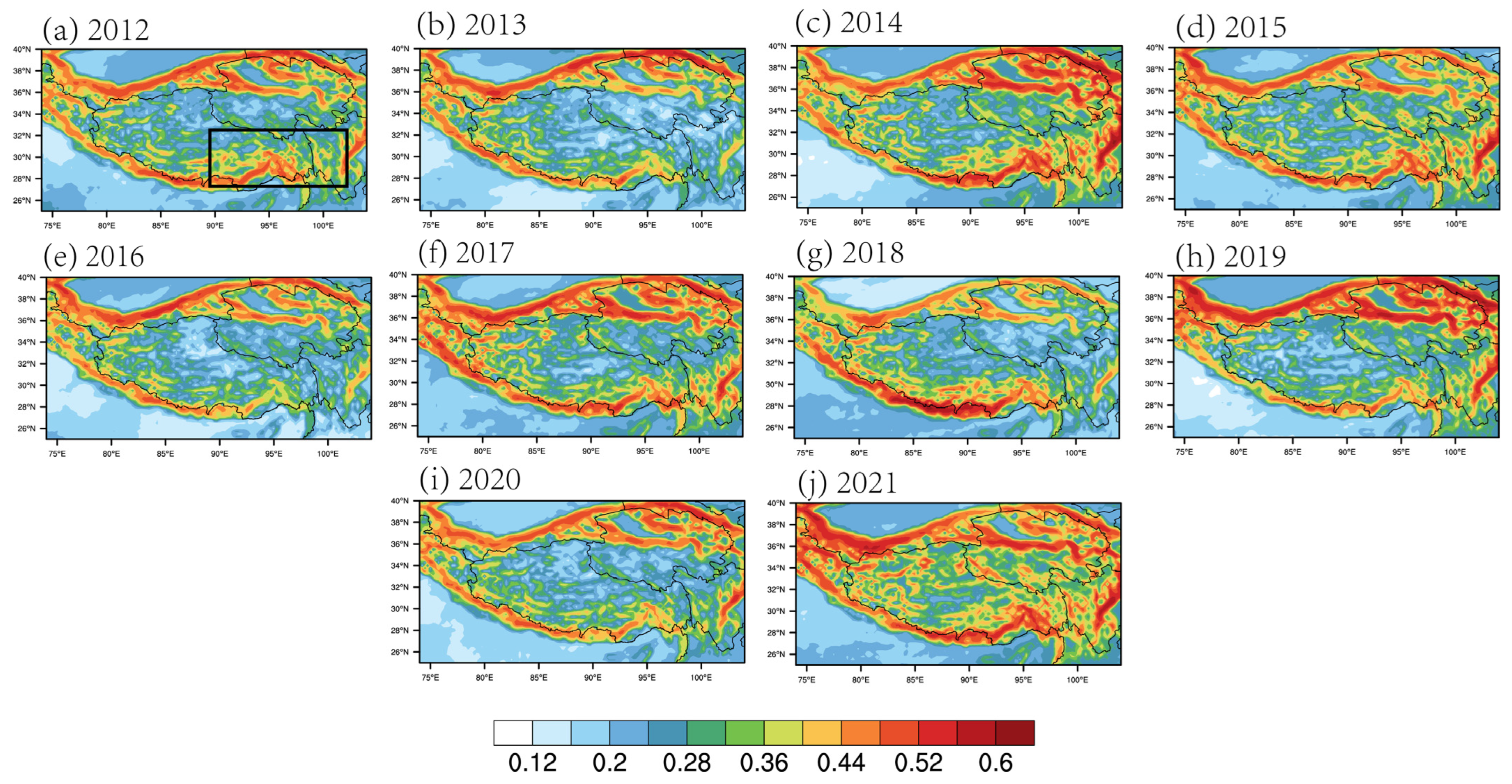
3.2. Statistical Results
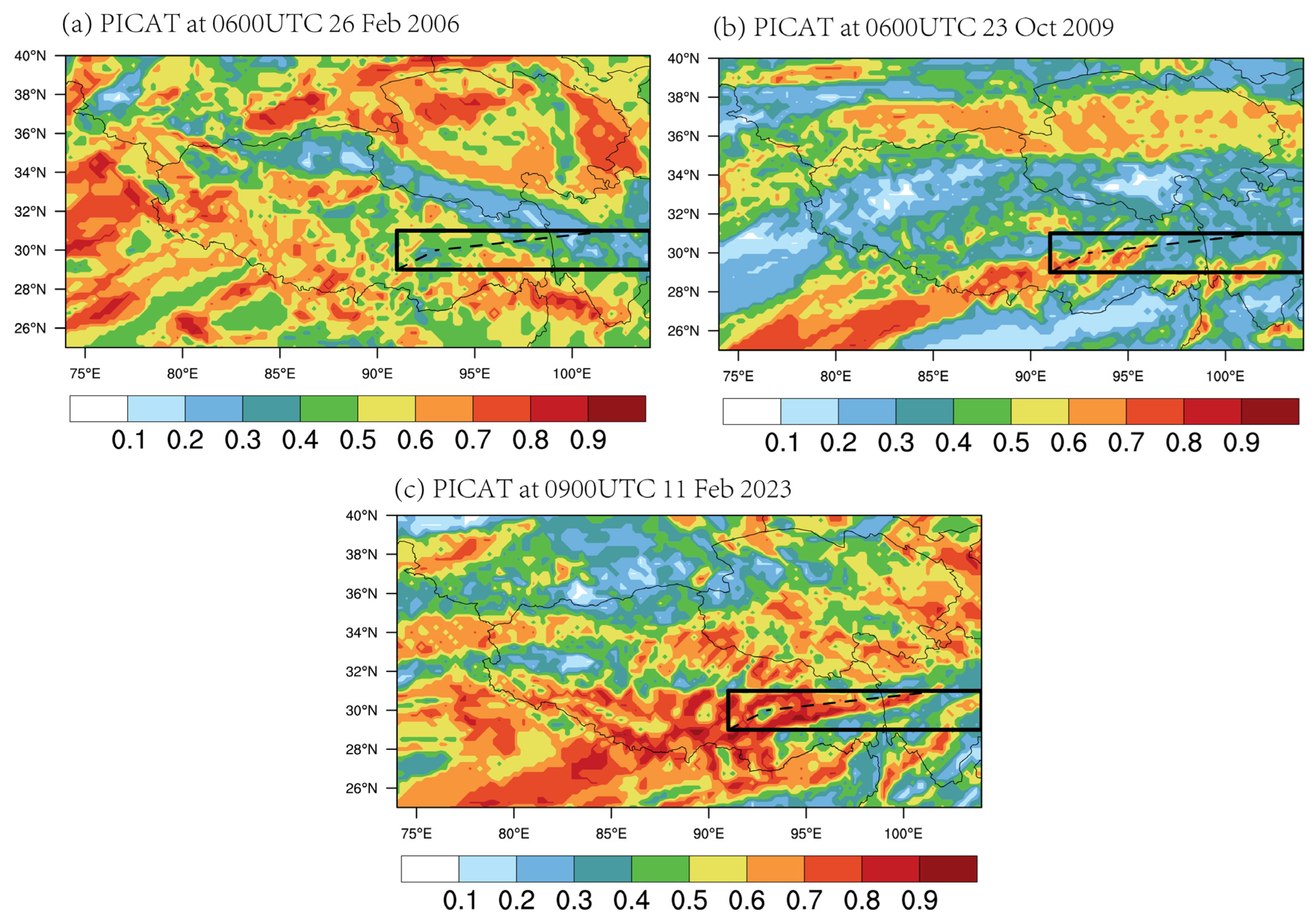
4. Turbulence Probability Index
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- -Ri: Negative Richardson number (Ref. [16])
- (2)
- CP (m2 s−2): Colson–Panofsky TKE (Ref. [7])
- (3)
- GRDT (K m−1): Horizontal temperature gradient (Ref. [16])
- (4)
- MOSCAT (m s−2): Wind speed × |deformation|(Ref. [11])
- (5)
- TI1 (s−2): Ellrod1 index (Ref. [8])
- (6)
- NCSU1 (s−3), Advection × |vorticity gradient|/Ri* (Ref. [10])
- (7)
- VENS (s−2) |Vertical vorticity|2
- (8)
- CCAT (s−2), Clark’s CAT (Ref. [33])
- (9)
- S (m s−1), Wind speed (Ref. [34])
- (10)
- SV (s−1), Vertical shear of horizontal wind (Ref. [34])
- (11)
- BI (s−1), Simplified DRi/Dt (Ref. [35])
- (1)
- MWT1 (m3 s–2): mws × Vertical velocity (w) squared/Ri
- (2)
- MWT4 (m2 s–1): mws × horizontal wind speed
- (3)
- MWT5 (m s–1): mws × |DIV|
- (4)
- MWT6 (m2 s–2): mws × MOSCAT
- (5)
- MWT12 (K): mws × |GRADT|
- (6)
- MWT13 (m s–2): mws × |Total deformation|2
References
- Storer, L.N.; Williams, P.D.; Gill, P.G. Aviation Turbulence: Dynamics, Forecasting, and Response to Climate Change. Pure Appl. Geophys. 2019, 176, 2081–2095. [Google Scholar] [CrossRef]
- Knox, J.A.; McCann, D.W.; Williams, P.D. Application of the Lighthill–Ford Theory of Spontaneous Imbalance to Clear-Air Turbulence Forecasting. J. Atmos. Sci. 2008, 65, 3292–3304. [Google Scholar] [CrossRef]
- Trier, S.B.; Sharman, R.D.; Lane, T.P. Influences of Moist Convection on a Cold-Season Outbreak of Clear-Air Turbulence (CAT). Mon. Weather Rev. 2012, 140, 2477–2496. [Google Scholar] [CrossRef]
- Trier, S.B.; Sharman, R.D. Convection-Permitting Simulations of the Environment Supporting Widespread Turbulence within the Upper-Level Outflow of a Mesoscale Convective System. Mon. Weather Rev. 2009, 137, 1972–1990. [Google Scholar] [CrossRef]
- Lane, T.P.; Sharman, R.D.; Trier, S.B.; Fovell, R.G.; Williams, J.K. Recent Advances in the Understanding of Near-Cloud Turbulence. Bull. Am. Meteorol. Soc. 2012, 93, 499–515. [Google Scholar] [CrossRef]
- Kim, J.H.; Chun, H.Y. Statistics and Possible Sources of Aviation Turbulence over South Korea. J. Appl. Meteorol. Climatol. 2011, 50, 311–324. [Google Scholar] [CrossRef]
- Colson, D.; Panofsky, H.A. An Index of Clear Air Turbulence. Q. J. R. Meteorol. Soc. 1965, 91, 507–513. [Google Scholar] [CrossRef]
- Ellrod, G.P.; Knapp, D.I. An Objective Clear-Air Turbulence Forecasting Technique: Verification and Operational Use. Weather Forecast. 1992, 7, 150–165. [Google Scholar] [CrossRef]
- Convection, B. Buoyant Convection in Geophysical Flows; Springer: Berlin/Heidelberg, Germany, 1998; ISBN 9789401061254. [Google Scholar]
- Kaplan, M.L.; Charney, J.J.; Waight, K.T.; Lux, K.M.; Cetola, J.D.; Huffman, A.W.; Riordan, A.J.; Slusser, S.D.; Kiefer, M.T.; Suffern, P.S.; et al. Characterizing the Severe Turbulence Environments Associated with Commercial Aviation Accidents. A Real-Time Turbulence Model (RTTM) Designed for the Operational Prediction of Hazardous Aviation Turbulence Environments. Meteorol. Atmos. Phys. 2006, 94, 235–270. [Google Scholar] [CrossRef]
- Reap, R.M.; SOC, A.M. Probability Forecasts of Clear-Air-Turbulence for the Contiguous US. In Proceedings of the 13th Conference on Probability and Statistics in the Atmospheric Sciences, San Francisco, CA, USA, 21–23 February 1996; pp. 66–71. [Google Scholar]
- Sharman, R.D.; Pearson, J.M. Prediction of Energy Dissipation Rates for Aviation Turbulence. Part I: Forecasting Nonconvective Turbulence. J. Appl. Meteorol. Climatol. 2017, 56, 317–337. [Google Scholar] [CrossRef]
- Kim, S.H.; Chun, H.Y.; Sharman, R.D.; Trier, S.B. Development of Near-Cloud Turbulence Diagnostics Based on a Convective Gravity Wave Drag Parameterization. J. Appl. Meteorol. Climatol. 2019, 58, 1725–1750. [Google Scholar] [CrossRef]
- Kim, S.-H.; Chun, H.-Y.; Lee, D.-B.; Kim, J.-H.; Sharman, R.D. Improving Numerical Weather Prediction-Based Near-Cloud Aviation Turbulence Forecasts by Diagnosing Convective Gravity Wave Breaking. Weather Forecast. 2021, 36, 1735–1757. [Google Scholar] [CrossRef]
- Bowler, N.E. Accounting for the Effect of Observation Errors on Verification of MOGREPS. Meteorol. Appl. 2008, 15, 199–205. [Google Scholar] [CrossRef]
- Sharman, R.; Tebaldi, C.; Wiener, G.; Wolff, J. An Integrated Approach to Mid- and Upper-Level Turbulence Forecasting. Weather Forecast. 2006, 21, 268–287. [Google Scholar] [CrossRef]
- Kim, J.-H.; Sharman, R.; Strahan, M.; Scheck, J.W.; Bartholomew, C.; Cheung, J.C.H.; Buchanan, P.; Gait, N. Improvements in Nonconvective Aviation Turbulence Prediction for the World Area Forecast System. Bull. Am. Meteorol. Soc. 2018, 99, 2295–2311. [Google Scholar] [CrossRef]
- Williams, P.D. Increased Light, Moderate, and Severe Clear-Air Turbulence in Response to Climate Change. Adv. Atmos. Sci. 2017, 34, 576–586. [Google Scholar] [CrossRef]
- Liu, X.; Chen, B. Climatic Warming in the Tibetan Plateau during Recent Decades. Int. J. Climatol. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, Y.; Wang, F.; Li, X.; Cui, S.; Zhang, Z.; Wu, X.; Weng, N.; Luo, T.; Huang, Y. Characteristics of the Vertical Structure of the Atmospheric Turbulence in the Tibetan Plateau. Science. Sci. China Earth Sci. 2022, 65, 1368–1378. (In Chinese) [Google Scholar] [CrossRef]
- Xu, J.; Wang, D.; Gong, Y.; Duan, Y. Quantitative Diagnostic and Distribution Characteristics of Aircraft Turbulence in China. J. Chengdu Univ. Inf. Technol. 2018, 33, 704–712. (In Chinese) [Google Scholar] [CrossRef]
- Li, Y.; Yang, J.; Xu, H.; Meng, Q. Numerical Simulation and Analysis of a Process of Turbulence on Lasa Airway. Plateau Mt. Meteorol. Res. 2011, 31, 56–60. (In Chinese) [Google Scholar]
- Shen, Q.; Shen, W. A New Synthesis Algorithm for Clear Air Turbulence Forecast. Meteorology And Disaster Reduction Research. Meteorol. Disaster Reduct. Res. 2009, 32, 44–49. (In Chinese) [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Zhou, L. Forecasting Results of Different Air Turbulence Environment Indexes Based on WRF Model. Equip. Environ. Eng. 2019, 16, 70–75. (In Chinese) [Google Scholar]
- Miles, J. Richardson’s Criterion for the Stability of Stratified Shear Flow. Phys. Fluids 1986, 29, 3470. [Google Scholar] [CrossRef]
- Frehlich, R.; Sharman, R. Estimates of Turbulence from Numerical Weather Prediction Model Output with Applications to Turbulence Diagnosis Data Assimilation. Mon. Weather Rev. 2004, 132, 2308–2324. [Google Scholar] [CrossRef]
- Williams, P.D.; Joshi, M.M. Intensification of Winter Transatlantic Aviation Turbulence in Response to Climate Change. Nat. Clim. Chang. 2013, 3, 644–648. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gill, P.G.; Buchanan, P. An Ensemble Based Turbulence Forecasting System. Meteorol. Appl. 2014, 21, 12–19. [Google Scholar] [CrossRef]
- Kim, J.H.; Chun, H.Y.; Sharman, R.D.; Keller, T.L. Evaluations of Upper-Level Turbulence Diagnostics Performance Using the Graphical Turbulence Guidance (GTG) System and Pilot Reports (PIREPs) over East Asia. J. Appl. Meteorol. Climatol. 2011, 50, 1936–1951. [Google Scholar] [CrossRef]
- Li, X.; A, L.; Shi, D. Statistics of Aircraft Turbulence Reports and Evaluation Analysis of the Forecasts. Air Traffic Manag. 2016, 4, 46–47. (In Chinese) [Google Scholar]
- Fang, L. Research on Charactercistics and Causes of Aircraft Turbulence on Plateau Based on Aircraft Detection Data. Master’s Thesis, Civil Aviation Flight University of China, Guanghan, China, 2021. (In Chinese). [Google Scholar]
- Vogel, G.N.; Sampson, C.R. Clear Air Turbulence Indices Derived from U.S. Navy Numerical Model Data: A Verification Study; Naval Research Lab Monterey CA Decision Aid Section: Washington, DC, USA, 1996. [Google Scholar]
- Endlich, R.M. The Mesoscale Structure of Some Regions of Clear-Air Turbulence. J. Appl. Meteorol. 1964, 3, 261–276. [Google Scholar] [CrossRef]
- Brown, R. New indexes to locate clear-air turbulence. Meteorol. Mag. 1973, 102, 347–361. [Google Scholar]
| Turbulence Intensity | Null | Light | Light–Moderate | Moderate | Moderate–Severe | Severe |
|---|---|---|---|---|---|---|
| -Ri | <−20 | −20~−5 | −5~−2 | −2~−0.5 | −0.5~0.5 | >0.5 |
| Percentile | 0–69.25 | 69.25–95.84 | 95.84–99.60 | 99.60–99.97 | 99.97–99.99 | 99.99–100 |
| Index Name | Units | T1 | T2 | T3 | T4 | T5 |
|---|---|---|---|---|---|---|
| GRDT | K m−1 | 5.3 × 10−6 | 1.1 × 10−5 | 1.9 × 10−5 | 3.2 × 10−5 | 3.8 × 10−5 |
| CP | m2 s−2 | −24.6 | −13.3 | −5.3 | −0.4 | −1.4 |
| MOSCAT | m s−2 | 1.0 × 10−3 | 2.6 × 10−3 | 4.1 × 10−3 | 5.9 × 10−3 | 6.8 × 10−3 |
| TI1 | s−2 | 5.3 × 10−8 | 1.5 × 10−7 | 3.0 × 10−7 | 5.1 × 10−7 | 6.2 × 10−7 |
| NCSU1 | s−3 | 5.1 × 10−16 | 2.3 × 10−14 | 2.0 × 10−13 | 1.5 × 10−12 | 2.3 × 10−8 |
| VENS | s−2 | 8.6 × 10−10 | 3.4 × 10−9 | 7.8 × 10−9 | 1.6 × 10−8 | 2.1 × 10−8 |
| CCAT | s−2 | 2.8 × 10−10 | 2.5 × 10−9 | 7.6 × 10−9 | 1.8 × 10−8 | 2.4 × 10−8 |
| S | m s−1 | 21.9 | 40.8 | 50.3 | 56.7 | 58.8 |
| SV | s−1 | 1.1 × 10−3 | 2.0 × 10−3 | 2.9 × 10−3 | 3.9 × 10−3 | 4.3 × 10−3 |
| BI | s−1 | 9.7 × 10−5 | 1.3 × 10−4 | 1.8 × 10−4 | 2.5 × 10−4 | 3.0 × 10−4 |
| MWT1 | m3 s–3 | 0.55 | 15.0 | 154.7 | 5335.2 | 2.62 × 107 |
| MWT4 | m2 s–2 | 4.7 × 105 | 2.2 × 106 | 4.5 × 106 | 6.5 × 106 | 7.1 × 106 |
| MWT5 | m s–2 | 0.7 | 3.2 | 8.4 | 16.4 | 20.6 |
| MWT6 | m s–2 | 21.4 | 115.7 | 285.7 | 498.5 | 598.3 |
| MWT12 | K s–1 | 0.1 | 0.5 | 1.3 | 2.4 | 3.0 |
| MWT13 | m s–2 | 7.6 × 10−5 | 4.4 × 10−4 | 1.3 × 10−3 | 3.4 × 10−3 | 4.9 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, D.; Ran, L.; Tian, L.; Zhou, K.; Tang, J. A Probabilistic Forecast Algorithm of Nonconvective Turbulence over the Tibetan Plateau. Appl. Sci. 2023, 13, 4131. https://doi.org/10.3390/app13074131
Shen D, Ran L, Tian L, Zhou K, Tang J. A Probabilistic Forecast Algorithm of Nonconvective Turbulence over the Tibetan Plateau. Applied Sciences. 2023; 13(7):4131. https://doi.org/10.3390/app13074131
Chicago/Turabian StyleShen, Dongdong, Lingkun Ran, Liqing Tian, Kuo Zhou, and Jiahui Tang. 2023. "A Probabilistic Forecast Algorithm of Nonconvective Turbulence over the Tibetan Plateau" Applied Sciences 13, no. 7: 4131. https://doi.org/10.3390/app13074131
APA StyleShen, D., Ran, L., Tian, L., Zhou, K., & Tang, J. (2023). A Probabilistic Forecast Algorithm of Nonconvective Turbulence over the Tibetan Plateau. Applied Sciences, 13(7), 4131. https://doi.org/10.3390/app13074131





