Abstract
The aim of the paper is to examine the requirements of producers in post-communist countries with lower economic level. The first requirement was how to overcome the limitations of conventional PFMEA to propose measures effectively. The second requirement solved the economic effect of failure modes. The aim of the paper was to create a new hybrid PFMEA–DEMATEL–ERPN model to manage failure modes to resolve the requirements. The DEMATEL model overcame the limitations of PFMEA. DEMATEL data were used to estimate the functionality of the proposed models. Criteria such as the occurrence of defective products and the probability of their occurrence (O and RPN) were monitored. ERPN also overcame the limitations of PFMEA. Internal and external costs arise as effects of failure modes. The costs were included in the economic evaluation of the models. We validated the models in a transfer pressing process. The estimation of models’ functionality proved to be correct. The economic evaluation refined the research results and resolved the second requirement of the manufacturers. The DEMATEL and ERPN models (compared to PFMEA) proved their validity when the use of PFMEA was limited. By using DEMATEL, we registered the lowest number of defective products and the lowest costs.
1. Introduction
Continuous improvement is an important global aspect of the growth and competitiveness of manufacturing organizations. Improving the quality of production implies the elimination of failure modes in the production process. For each single failure mode, it is important to know and research the causes of that failure [1].
FMEA (Failure Mode and Effect Analysis) is a tool used to identify failure modes of either a manufacturing process (PFMEA), design (DFMEA), system (SFMEA), or service [2]. It also has its applications in production quality and in solving the reliability of technical systems [3,4]. The goal of a process FMEA is to improve the manufacturing process, ensure the product is of the required quality, minimize downtime, and minimize defective products and scrap. The focus of the PFMEA is on the manufacturing and assembly process [5].
The risk priority number (RPN) is used to determine the risk or criticality of failure modes. The RPN is obtained by simply multiplying the risk factors such as occurrence (O), severity (S), and detection (D). The problem is that this determination of the RPN can be highly subjective and introduces many shortcomings. This invalidates its full use in practice [6].
Many authors have been devoted to solving the problems of conventional PFMEA. Authors have proposed various alternative approaches to solve this problem. Liu [2] proposed a new framework to improve the execution of the PFMEA while improving risk assessment.
The new FMEA trends offer an opportunity to refine the results of the method. However, there is still a question of how important these parameters are to the size of the RPN and the resulting threats. Several authors consider the S and O factors as the two most important risk factors [7]. The limits of PFMEA can be explained as follows: we identified three failure modes, A, B and C, which we ranked as follows: (SA = 8, OA = 5, DA = 4), (SB = 10, OB = 4, DB = 4), and (SC = 5, OC = 4, DC = 8). Although each factor is rated differently, the resulting RPN is 160 for all failure modes. This poses a problem in determining the prioritization for the measures proposed. This is a metric where equal weight is given to each of the risk factors (S, O, and D) [8].
As summarized by Liu [9] in his paper, many authors have proposed many ways to enhance the effectiveness of FMEA. The most widely used techniques are cognitive mapping [10]; mathematical programming methods such as data envelopment analysis (DEA) [11]; adaptive resonance theory [12]; linear programming [13]; fuzzy rule-base [14,15]. Often used are multi-criteria decision-making (MCDM) methods such as a technique for order preference by similarity to ideal solution (TOPSIS) [16,17,18]; grey relational analysis (GRA) [19,20]; and decision-making trial and evaluation laboratory (DEMATEL) [9,21,22]. Hybrid models have also found their use as a combination of the baseline method (PMEA) with fuzzy analytic hierarchy process (AHP) and fuzzy TOPSIS [23]; integrated approaches such as similarity measure and adaptive resonance theory [24], D numbers, and grey relational projection method [25]; extended FMEA [8]; PFDA-FMEA [26], and other methods and techniques [27,28].
The Battelle Memorial Institute developed the DEMATEL method to solve complex and interrelated problems [29,30]. The DEMATEL methodology is based on pairwise comparisons of individual factors, the definitions and descriptions of which will be available to experts to assess the interrelations between the factors (quantitatively using scales). Its strength is its ability to map all the influences and factors of a decision problem, including their representation in a clear influence map. In practice, it involves one or two rounds of questioning via a paper-based or online questionnaire. It is possible to include a larger number of experts, resulting in a map that depicts the relations among them as well as the significance of each step [31].
DEMATEL (Decision-Making Trial and Evaluation Laboratory) clarifies the complex relations between failure modes in the manufacturing process and provides solutions by comparing these failure modes in the manufacturing process. The solution uses matrices to calculate direct and indirect causal relations, influence rates, and quantify the degree of mutual influence between factors. By doing so, the FMEA process’ limitations about the same RPN should be overcome [21].
In Table 1, we can see the studies that have considered the issue of combining FMEA and DEMATEL. Most of the authors used the DEMATEL model to prioritize the failure modes.

Table 1.
Review of PFMEA and DEMATEL usage.
Nowadays, in the context of globalization and international integration, competition in the marketplace becomes more and more severe. Hence, focusing on improving the quality of a product/service with high speed and low waste production has been highly appreciated over the last few years, especially with the current prices of materials and energy. With a good quality scheme, a company can sustain its development by gaining critical competitive advantages over its competitors: high yield and low wastage [8].
ERPN is an extended risk priority number created from conventional RPN. With the identification of failure modes, costs are also incurred because of these modes. The controllable costs are related to the preventive approach and the evaluation costs. The ERPN mainly examines the costs of internal and external errors that are directly related to the failure modes in question [8].
The aim of the paper is to create a new hybrid model of PFMEA, DEMATEL, and ERPN. This model reflects the requirements of producers in the post-communist countries of Europe, where the standard of living is lower compared to the developed countries of Europe, America, and Asia. This is accomplished by the extended risk number ERPN. This is extended by internal and external costs, which, given the standard of living in these countries, are a very important indicator. The DEMATEL model, in addition to its classical use as a multi-criteria analysis model (MCDM), will be used as a design indicator that will help predict the functionality of the models and methods used in the hybrid model. For the comparison parameter, we will select the number of defective products, probability of occurrence (O), and risk priority number (RPN). The hybrid model will be applied to the production process of transfer pressing in the production of a brake element for the automotive industry. An economic model will also be created to evaluate the contribution of individual models and fulfil the requirements of manufacturers.
The DEMATEL model has been used by many authors [7,21,32,33,34,35,36]. It is part of many scientific studies. DEMATEL methodology has been used in our research. We directly followed the research of Tsai et al. [21]. In contrast to that study, we applied these results in practice and proposed measures according to the resulting DEMATEL digraph. The results of the digraph, which shows the relations between failure modes, were used to outline which model is predicted to have the lowest number of defective products.
The ERPN model was created by Nguyen [8], and is a little-known extension of PFMEA. In our study, we validated the effectiveness of this model in practice by prioritizing the results to propose measures. Moreover, we used the data obtained in the ERPN model for the economic evaluation of all the proposed models.
The intended outcome of the study was the proposal of a hybrid model where the advantages of each of the PFMEA, DEMATEL, and ERPN models were exploited.
2. Materials and Methods
2.1. Solution Procedure of the Examined Task
- Selection of the research object;
- Creation of an evaluation team;
- Failure mode identification and development of PFMEA;
- Creation of the DEMATEL model;
- Creation of the ERPN model;
- Applying the models of the hybrid model PFMEA, DEMATEL, and ERPN to the production process;
- Prediction of the functionality of the models based on the DEMATEL model;
- Evaluation.
2.2. Object of Research
The monitored product was a component for the brake system of a car (Figure 1), produced by transfer pressing technology in a production organization focused on the production of components for the automotive industry. The material of the component is steel 5355 MC (EN10149). The production organization aims to produce a product of light construction for maximum weight savings. This saves raw materials, costs, and energy when using the products. The brake component is produced on the ARISA pressing line. We will focus on transfer production within the transfer pressing technology. Transfer production is a type of pressing process. In transfer pressing, a blank is cut at the beginning of the process, which is then moved to the next steps of the tool via the transfer system, where it is subsequently shaped. In transfer pressing, a semi-finished product is cut at the beginning of the process and then moved to the next steps of the tool via the transfer system, where it is subsequently shaped. The component is gradually created with seven strikes of the ram.
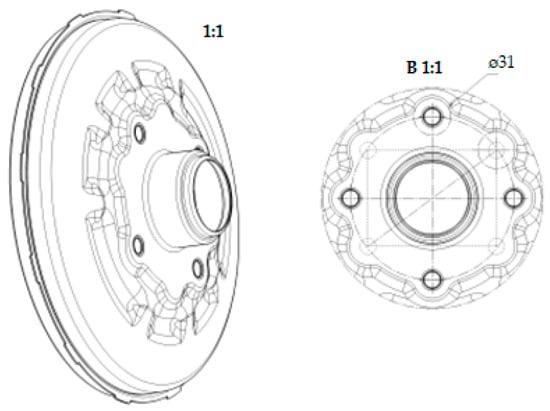
Figure 1.
The brake component.
2.3. Creation of an Evaluation Team
We created an evaluation team that participated in the presented analyses and research. The evaluation team consists of three authors of the research paper, three project managers, two quality managers, and one production manager. Although the proposed number (nine members) does not meet the requirements of the conventional FMEA for team size (four to six members), it does meet the requirements of the DEMATEL model. With the DEMATEL model, it is necessary to involve as many experts as possible in the evaluation. We selected experts from the domestic sources of the production organization and scientific and research workers at universities.
2.4. Identifying Failure Modes and Creating an Initial PFMEA
Initial PFMEA progression:
- Identification of failure modes in the selected process;
- Identification of the effects of failure modes;
- Classification of the severity (S) of the failure mode concerning the failure mode effect;
- Severity scale (S) (1–10), where S = 1 means the lowest severity, and S = 10 means the highest severity;
- Identification of the cause of the failure mode;
- Probability of occurrence (O) scale (1–10), with 1 indicating a very unlikely occurrence and 10 an almost certain occurrence;
- Description of the current process controls to prevent the failure mode method—controls that will either prevent the failure mode from occurring or detect the failure mode should it occur;
- Evaluation of the probability of detection (D) that the failure mode cause will be detected;
- Detection scale (1–10), with 1 being “almost certain” detection and 10 being “almost impossible”;
- Multiplying S, O, and D to determine the Risk Priority Number (RPN) for each potential failure mode;
- Determination of the average number of defective products on average per week of production in continuous operation. Observation period—3 weeks.
2.5. Creation of DEMATEL Model
We used the well-known DEMATEL methodology, primarily following Tsai et al. [21]. This methodology [21] was used to develop the model on which we built our research (Section 2.7).
Establishing a direct-relation matrix (Equation (1)):
Each team member will determine the intensity of the relations between the selected failure modes as an expert, and thus the basis of the initiation matrix for the DEMATEL model will be created. The coupling between failure modes (FM’s) will be evaluated on a scale of 0–6, where 0 means no relations and 6 is the maximum number of relations (Figure 2).
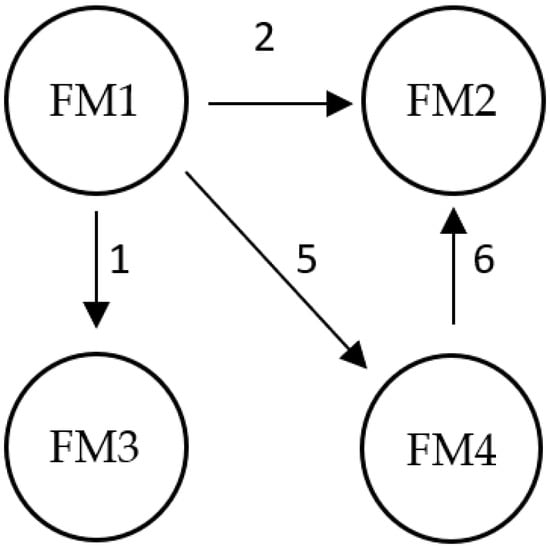
Figure 2.
Relations by DEMATEL.
Subsequently, a direct-relation matrix is created (Equation (1))
Determination of Cronbach’s alpha and CITC:
Cronbach’s alpha (Equation (2)) will be used to assess the reliability of the survey data, and CITC will be calculated. The test results will show how reliable the questionnaires used in the DEMATEL analyses are. The acceptable limit value of Cronbach’s alpha is 0.7 [33,39].
where k is the number of experts, Vi is the sum of item variances, and Vt response variance of total scores.
A corrected total item correlation (CITC) score is determined for each item and each expert. The CITC expresses how well each item contributes to the internal consistency of a particular construct, as measured by Cronbach’s alpha coefficient [40]. CITC was evaluated by Pearson’s product-moment correlation coefficient.
Determination of the normalized direct-relation matrix N:
Using column vectors and maximum values (Equation (3)) as the basis for matrix normalization (Equation (4)) [21].
Determination of the direct/indirect relation matrix (T) or the total-relation matrix (Equation (5)):
where I represents the identity matrix.
Determination of the values in each row and column:
This is followed by performing a mathematical summation of the values in each row and column of the total relation matrix (T). We denote Di (Equation (6)) as the sum of the i-th column and Ri (Equation (7)) as the sum of the j-th row. These values of Di and Ri consider both indirect and direct influences [21].
Creating the DEMATEL cause and effect diagram:
The horizontal axis (D + R) and vertical axis (D − R) are used to represent the cause and effect diagram, respectively. The diagram simplifies complex causal relations into an easy-to-understand visual structure. Decision-makers can determine factor types based on the characteristics of the factors and formulate appropriate solutions based on the extent of influence of each factor [21].
Attribute k is either a cause or effect attribute when (Dk − Rk) is a positive or negative value, respectively. The size of (Dk + Rk) represents the extent of the attribute’s cause or effect [21].
Based on the coordinates in (Dk + Rk) and (Dk − Rk), k can be categorized into four categories:
- Positive (Dk − Rk) and large (Dk + Rk) values: k is a cause factor and an actuating factor for solving the problem;
- Positive (Dk − Rk) and small (Dk + Rk) values: k is an independent factor and influences only a small number of other factors;
- Negative (Dk − Rk) and small (Dk + Rk) values: k is an independent factor and is influenced by only a small number of factors;
- Negative (Dk − Rk) and large (Dk + Rk) values: k is a core problem that requires resolution. However, it is an effect attribute; thus, it cannot be directly improved [21,41,42].
2.6. Determination of ERPN
It is an extended risk number that is created by including internal and external costs as a result of failure modes in the model. We used the methodology proposed by Nguyen [8]. This methodology [8] was used to develop the model on which we built our research (Section 2.7).
Internal Failure Cost (IFC) is the cost incurred as a result of product quality non-conformance, assuming that defective products are detected at the production stage. If no defective product is detected, then IFC = 0 [8].
External Failure Costs (EFC) are the costs that are incurred by a non-conformity detected by the customer. If they do not occur, EFC = 0. EFC is divided into two parts:
- Without-casualty costs (WoC): field servicing and handling complaints; recalls, returns, and replacements; warranty; other indirect costs, etc.;
- Casualty costs (CC): the cost of compensating customers for damage caused by a defective product. Then, IFC = WoC + CC.
Additionally, IFC and EFC can be converted to SI and SE as follows [8]:
- We follow up on the conventional PFMEA and the determined RPN.
- Internal costs are determined—IFC (for 1 defective product).
- External costs—EFC are determined, considering WoC costs and CC costs (per one defective product).
- The probability of occurrence of the mode—PO is determined. PO (Equation (8) is based on the probability of occurrence of O:
- 5.
- We determine the detection probability of the mode—PD. The PD (Equation (9)) is based on the detection parameter D.
- 6.
- The internal costs of the IFC will be taken into account when determining the severity level (SI) (Equation (10)).
- 7.
- The IFC’s internal expenditures will be taken into consideration when establishing a severity level (SI) (Equation (10)).
- 8.
- The external costs of the CC will be taken into account when establishing a severity level (SC) (Equation (12)).
- 9.
- We determine the poc—the probability of the failure mode. For WoC costs, we consider poc = 0. For CC costs, we consider poc = 1.
- 10.
- The ERPN calculation for the extended FMEA is calculated according to Equation (13):
- 11.
- The comparison of the RPN calculated for conventional PFMEA with the calculated ERPN.
2.7. Creation of a Hybrid Model
After the development of the initial state of the PFMEA, a hybrid PFMEA–DEMATEL–ERPN model is created.
We have proposed three models to solve the research problem:
- Conventional PFMEA;
- Combined PFMEA with the DEMATEL model;
- Combined PFMEA with the ERPN model.
For all models, the procedure will be as follows:
- Monitored criteria—number of defective products, probability of occurrence—O, risk priority number—RPN;
- Proposal of measures for the four most important failure modes;
- ○
- With conventional PFMEA for failure modes with the highest RPN;
- ○
- With the PFMEA and DEMATEL model for the most significant failure modes according to the basic DEMATEL model;
- ○
- In the hybrid model for failure modes with the highest ERPN;
- ○
- Measures will be designed to reduce the number of defective products; regarding reducing the occurrence of O.
- Prediction and estimation of models’ functionality based on defined relations in the DEMATEL model;
- ○
- Estimation of monitored criteria based on four proposed measures for each model;
- ○
- Based on the results of the digraph of the DEMATEL model, we have proposed a procedure where we show with a bold line the relations between the failure modes of the significant intensity of sizes 5 and 6, which are the values from experts for creating the initial matrix of the direct relation, and we show with a thin line the relations of average intensity (size 3 and 4). Relations of low intensity (size 1–2) will not be displayed. The location of the failure modes in the quadrants of the DEMATEL model digraph will also be crucial.
- The data collection process for each model will take three weeks;
- The average value of the occurrence of defective products for one week is considered reliable for obtaining results and defining random phenomena;
- A comparison of proposed models based on the modification of monitored criteria;
- The economic evaluation of the models is based on the determined costs of IFC and EFC for the elimination of the effect of each mode of failure according to Formulas (14) and (15).
3. Results and Discussion
3.1. Initial PFMEA
The evaluation team identified 54 failure modes that arise during a transfer manufacturing operation. These have been included in Table 2.

Table 2.
Initial PFMEA.
The average number of products produced per week in the observed period (at high OEE) was 41,200. We recorded an average of 2% of defective products (824 pieces) per week (stable value at the end of the monitored period). This was a high value that needed to be reduced.
3.2. Model DEMATEL
Table 3 shows the direct relation matrix, which is the same as the expert pairwise comparison matrix. Before that, we calculated Cronbach’s alpha and CITC based on the questionnaires from the experts.

Table 3.
Initial direct-relation matrix X.
The reliability of the questionnaire data was of a high level and reached 0.9971.
The survey results were very consistent. All the adjusted values were greater than 0.3. The values of the corrected item-total correlation for the nine experts were listed in Table 4.

Table 4.
Corrected item-total correlation value of validated respondents.
The normalized direct relation matrix was constructed based on Equation (3) and can be found in Table 5.

Table 5.
Use the column vectors and maximum values as the baseline for normalization.
The normalized direct-relation matrix N was determined based on Equation (4) and can be found in Table 6.

Table 6.
Normalized direct-relation matrix N.
The overall relation matrix T was determined from Equation (5) and is given in Table 7. It is an n × n matrix.

Table 7.
Total-relation matrix T.
We then created Table 8 according to Equations (6) and (7).

Table 8.
Summary of the prominence and relation of the 12 FM.
According to Figure 3, each factor can be assessed based on the following aspects:
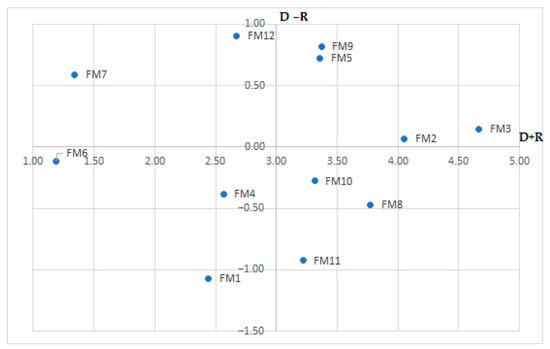
Figure 3.
Relational diagram of the 12 failure modes.
In terms of degree of importance, FM3 is ranked in first place, followed by FM2, FM8, FM9, FM5, FM10, FM11, FM12, FM4, FM1, FM7, and FM6.
In this study, FM2, FM3, FM5, FM7, FM9, FM12 are regarded as causal variables, and FM1, FM4, FM6, FM8, FM10, FM11 are regarded as an effect.
The division of failure modes according to their significance (Figure 3):
- High significance and high correlation: This quadrant include failure modes FM3, FM2, FM9 and FM5. These failure modes are the main causal factors influencing the other items. They are therefore triggers for problem-solving.
- Failure modes FM12 and FM7 were in the second quadrant. These are characterized by low significance and high relation. They are referred to as moderate causal. They moderately affect the other failure modes. They are thus relatively independent.
- In the third quadrant, failure modes FM4 and FM1 were found. These are characterized by low significance and low relation. They are moderately influenced by the other failure modes. Thus, they are relatively independent.
- In the fourth quadrant, failure modes FM8, FM10, and FM11 were located. These are characterized by low significance and low relation. They are the effects of other failure modes and significantly influenced by other failure modes. By being effect factors, they cannot be directly improved.
3.3. Model ERPN
Based on Section 2.6, costs have been assigned to each failure mode. These costs were incurred as a consequence of these failure modes and are shown in Table 9.

Table 9.
Determination of internal and external costs for each failure mode per one piece of a defective product.
Subsequently, based on the instructions in Section 2.6 and Formulas (8)–(13), we compiled Table 10.

Table 10.
Representation of PFMEA with the ERPN model.
3.4. Monitoring of Indicators at the Initial Status
Table 11 summarizes the results of the proposed models. We used these data as a basis for the innovative designs for the hybrid model.

Table 11.
Analysis of important parameters after creating conventional FMEA, DMEATEL model, and ERPN.
3.5. Hybrid Model PFMEA–DEMATEL–ERPN
3.5.1. Proposal of Measures
By proposing four measures, we want to improve the original state achieved by the conventional PFMEA.
An important parameter for meeting the objectives of the work is the probability of occurrence of failure modes O. The failure modes have 11 equal values (for FM2–12 is O = 2) and 1 abnormally high value (FM1 = 8). Therefore, the FM1 mode has been a matter of priority, as there was a human error in updating the data. Failure mode 1 was not considered in the final statistical evaluation in the other models. By solving the FM1 failure mode, the incidence of failure modes was reduced to 462, which represents 1.12%.
Measures for the model of the conventional PFMEA (according to the highest RPN):
- FM8—Increasing the amount of oil in the event of the formation of a vacuum bubble (the part remains stuck in the tool), the holes in the affected area responsible for the occurrence must be blinded, the release of tension elements if necessary;
- FM9—Tool setting (position of guiding elements);
- FM11—Tool maintenance;
- FM12—Production of a longer punch/underlaying of the existing punch; optimization of the internal diameter of the shear to a larger value.
Measures for the DEMATEL model (according to the first quadrant of the Figure 3):
- FM3—Resharpening the cutting knives in the trimming step, installing the waste brake during the process of cutting the central hole;
- FM2—Correct use of tools—retraining;
- FM9—Tool setting (position of guiding elements);
- FM5—The arresting area of the elements must be made with a wider diameter so that the clearance is as small as the process allows.
Measures for the ERPN model (according to the highest ERPN):
- FM5—The arresting area of the elements must be made with a wider diameter so that the clearance is as small as the process allows;
- FM2—Correct use of tools—retraining;
- FM12—Production of a longer punch/underlaying of the existing punch, optimization of the internal diameter of the shear to a larger value;
- FM11—Tool maintenance.
3.5.2. Prediction and Estimation of the Functionality of the Proposed Models
Based on the location of the failure modes in the individual quadrants of the DEMATEL model digraph (Figure 2), we estimated the success of the used models that make up the resulting hybrid model.
The location of the failure modes for the conventional PFMEA for which we proposed measures is shown in Figure 4. For each model, we divided the failure modes (for which we proposed measures) into cause and effect. At the same time, For each failure mode, we displayed the intensity of the relation to other failure modes. We have shown their quantity and intensity in Figure 4 (highlighted by blue arrows) and Table 12.
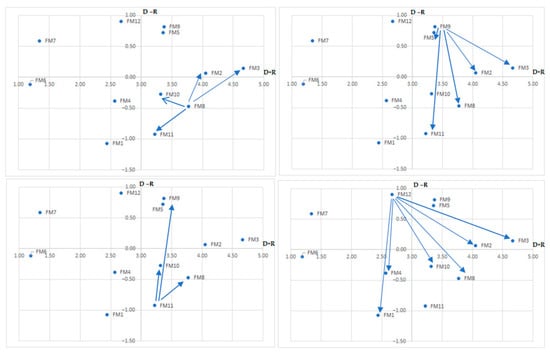
Figure 4.
Main failure modes of the conventional PFMEA and their relations on other failure model.

Table 12.
The number of bonds and their intensity for each model.
The location of the failure modes for the DEMATEL model for which we proposed measures is shown in Figure 5.
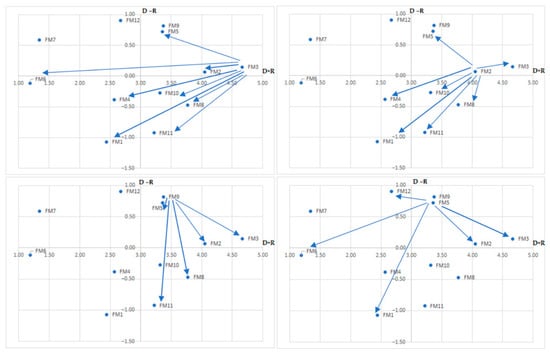
Figure 5.
Main failure modes in PFMEA combined with DEMATEL and their relations with the other failure modes.
The location of the failure modes for the model with ERPN for which we proposed measures is shown in Figure 6.

Figure 6.
Main failure modes in PFMEA combined with ERPN and their relations with the other failure modes.
Discussion of Table 12:
The DEMATEL model has all four failure modes (FM2, FM3, FM5, FM9) for which measures have been proposed, located in the first quadrant (Figure 4). All four failure modes are significant and causal, which means they also influence the emergence of other failure modes. If we, as an FMEA team, made the right decisions when creating the initial matrix of a given model, it should manifest itself as the model that manifests itself with the highest reduction in the monitored criteria. This is also indicated by the fact that these four failure modes influence the other 9 failure modes (with repetition) with a significant relation and influence 17 failure modes by the average intensity relation.
The ERPN model has two failure modes (FM2, FM5) in the first quadrant (Figure 5). The FM12 failure mode is in the second quadrant, so it is relatively independent, but it is very close to the border of the first quadrant. These three failure modes, FM2, FM5, and FM12, are causative and significant. Although FM11 failure mode is more influenced by other failure modes, its relations with other failure modes are significant. We estimate that the ERPN model will be successful and significantly reduce the monitored criteria. This is also indicated by the auxiliary criteria, as the given 4 failure modes influence the other 7 failure modes (with repetition) with a significant relation and influence 15 by the average intensity relation.
The conventional PFMEA model has only one failure mode (FM9) in the first quadrant, FM12 in the second quadrant (close to the first), and two failure modes (FM8, FM11) only in the third, although both with higher significance (Figure 6). We refer to only two failure modes as causative, namely FM9 and FM12. We assume that this model will also reduce the monitored criteria, though as compared to the DEMATEL and ERPN models with a lower success rate. This is also indicated by auxiliary criteria regarding the number of affected failure modes with average and lower intensity.
In our case, the success of the models is determined by the relations of average and low intensity, but also by the distribution of failure modes in the quadrants of the digraph (Figure 2) of the DEMATEL model.
3.5.3. Evaluation of Models
In Table 13, we can see the results obtained after application in the transfer molding process.

Table 13.
Analysis of the monitored criteria after application of all proposed models.
We converted the monitored criteria into a graphical representation for better visualization (Figure 7).
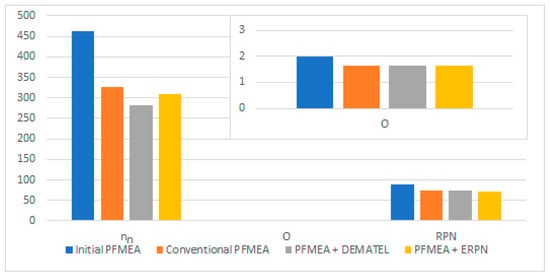
Figure 7.
Comparison of the different models and methods used based on the monitored criteria. Legend: nn—number of defective products; O—occurrence; RPN—risk priority number.
Based on Figure 7, we can conclude that our prediction of the estimation of the model’s functionality was correct. We recorded the lowest number of defective products with the DEMATEL model. The categorization of occurrence O was at the same level for all proposed models. Improvements occurred only in failure modes to which measures were specifically applied. We recorded the lowest average RPN value for the ERPN model. However, it should be emphasized that criteria O and RPN do not have such a telling value and are not as specific as the number of defective products.
The conventional PFMEA reduced the number of defective products the least.
It is important to emphasize that with the DEMATEL and ERPN models, we have a clearly defined prioritization for the possible further proposal of measures. PFMEA groups failure modes with the same RPN and O, which is one of the most common limitations of PFMEA.
3.5.4. Economic Evaluation of Models
Based on the costs of a specific failure mode for one component listed in Table 9, we compiled an economic evaluation of the number of defective products. This was reflected in Table 14.

Table 14.
The economic evaluation of models.
We evaluated the individual models economically. As can be seen (Table 14), the lowest cost of dealing with the consequences of failure modes was achieved by using DEMATEL. We observed higher costs when using the ERPN model. We found the highest costs when we used conventional PFMEA. It might seem that this is only due to the number of defective products, but this is not a correct interpretation. Each failure mode is uniquely costly to correct and this as a significant factor determines the final economic evaluation of the model.
3.6. Theoretical Analysis of the Proposed Models
In our research, we started with a real-world problem that often occurs when PFMEA is used in practice. PFMEA reaches its limits if we identify many failure modes with the same RPN. This was evident in one of the proposals for solving this problem. This was the classical continuation analysis of PFMEA (conventional PFMEA). For time, organizational reasons, and economic reasons, it is not possible to apply the measures and solve all the problems at once. It is therefore very important to establish a clear prioritization for the proposal of measures. We used the conventional PFMEA as a benchmark for comparison with other proposals, even though it was clear that the PFMEA would be ineffective and unable to reduce the monitored criteria. This was also confirmed.
Many authors have used the DEMATEL model to overcome these limitations [21,31,32,33,35,36,37,38,39,43,44]. This was also demonstrated in our research. Moreover, we confirmed these results by monitoring the proposed criteria, which we were able to reduce. Among the requirements of manufacturing organizations, the main aim is to reduce the number of defective products. The DEMATEL model results in a digraph that gives us information about the interaction between failure modes and categorizes the modes into influencing and influenced modes. We have used these results to estimate whether and how each of the proposed models can reduce the monitored criteria. In doing so, we also considered the strength of the interaction between the failure modes that were obtained from the experts’ evaluations and is presented in Table 3. The results showed that our estimation was correct. It should be emphasized that DEMATEL is highly dependent on the input values. This requires quality experts knowledgeable about the system being evaluated. If the input data are not exact, the DEMATEL results will be misleading and the estimation of the models functionality will be incorrect.
Based on the research by Nguyen et al. [8], we constructed the ERPN model. We confirmed the results of that research because we were able to determine the prioritization of failure modes. In our study, we again confirmed these results by validating them in practice. Subsequently, we proposed a model for the economic evaluation of the benefit of the models, where we used internal and external costs (they are created as an economic effect of the failure modes and are identified in the ERPN model). These data were the basis for the determination of the ERPN. At the same time, these data should be recorded by each production organization. We pointed out that determining the most successful model by the lowest number of defective products may not be correct since each failure mode produces different costs. This does not change the fact that in our research, the model with the lowest number of defective products also produced the lowest costs.
We hypothesize that based on the methodology set out in the paper, manufacturing organizations may be able to address the situation if PFMEA achieves its limits.
4. Conclusions
The aim of the paper was to create a new hybrid model PFMEA–DEMATEL–ERPN for practical requirements. One of the requirements was how to overcome the limitations of conventional PFMEA for the effective design of measures. The second request contained a proposal on whether it is possible to incorporate the costs arising as an effect of the failure mode into the PFMEA. DEMATEL was used as a tool to estimate the functionality of the proposed models. This required high-quality experts in the field of process knowledge. When used as an estimation tool, it requires high-quality experts in the area of the process under study. The extended risk priority number ERPN ensured the inclusion of costs as consequences of failure in the model, and the inputs to the model were used during the construction of the economic model to evaluate the models from an economic point of view as well. In addition, the ERPN model also ensured that the limitations of the conventional PFMEA were overcome. Both models reduced the monitored criteria proposed by the aim of the paper.
The conventional PFMEA reduced the monitored criteria the least; moreover, in practice, it brought a few critical situations when it was difficult to prioritize failure modes for the design of measures. Our research shows that for the 12 failure modes, we identified several failure modes with the same RPN and the same occurrence of O. We managed to solve this problem with both the DEMATEL model and the ERPN model.
Our research paper deals with real problems in practice (operations, technology, and product) and guides on how to effectively use DEMATEL in managing these problems. In our paper, we have proved both the positives of the DEMATEL model in combination with PFMEA, which many other authors have completed as well [21,31,32,33,35,36,37,38,39,45,46], and the ability to specific situations where PFMEA is unusable, where it is necessary to use the DEMATEL model.
We achieved the following benefits in our work:
- Use of an innovative combination of models within the hybrid model;
- Defining border situations where conventional PFMEA is of limited applicability;
- Defining border situations when it is important to use the DEMATEL and ERPN model for PFMEA;
- Using the prediction of model functionality estimation based on the DEMATEL model and confirming its success (extended innovative use of the well-known DEMATEL model);
- Reduction in monitored criteria (occurrence of defective products, probability of occurrence of failure modes, and resulting risk number) for designed models;
- Designing and evaluating the economic benefits of the models (extended innovative use of ERPN);
- Proving the economic benefits of the models.
The proposed models solved real problems in practice and provided instructions on how to effectively use them to solve problems in the production process. The proposed ERPN and DEMATEL models combined with conventional PFMEA have shown their validity in solving various requirements of manufacturers.
It is important to emphasize that the results are applicable if we have identified failure modes with the same RPN in the PFMEA analysis. This means that the PFMEA has reached a limit regarding the prioritization of the proposed measures.
Author Contributions
Conceptualization, M.B.; methodology, M.B., M.K. (Milan Kadnár) and C.K.L.; validation, M.B., M.K. (Milan Kadnár) and C.K.L.; formal analysis, M.B. and C.K.L.; investigation, M.B.; resources, M.B.; data curation, M.B., J.B. and M.K. (Maroš Korenko); writing—original draft preparation, M.B.; writing—review and editing, M.K. (Milan Kadnár) and M.B.; visualization, M.B.; supervision, M.B.; funding acquisition, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research work has been supported by Ministry of Education, Science, Research and Sport of the Slovak Republic by the grant VEGA: 1/0236/21 and by Drive4SIFood 313011V336, co-financed by the European Regional Development Fund.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author after obtaining permission of authorized person.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Markulik, S.; Šolc, M.; Petrík, J.; Balážiková, M.; Blaško, P.; Kliment, J.; Bezák, M. Application of Fta Analysis for Calculation of the Probability of the Failure of the Pressure Leaching Process. Appl. Sci. 2021, 11, 6731. [Google Scholar] [CrossRef]
- Liu, H.-C. FMEA Using Uncertainty Theories and MCDM Methods. In FMEA Using Uncertainty Theories and MCDM Methods; Springer: Berlin/Heidelberg, Germany, 2016; pp. 13–27. [Google Scholar] [CrossRef]
- Kamp, B.; Ochoa, A.; Diaz, J. Smart Servitization within the Context of Industrial User–Supplier Relationships: Contingencies According to a Machine Tool Manufacturer. Int. J. Interact. Des. Manuf. 2017, 11, 651–663. [Google Scholar] [CrossRef]
- Lo, H.W.; Shiue, W.; Liou, J.J.H.; Tzeng, G.H. A Hybrid MCDM-Based FMEA Model for Identification of Critical Failure Modes in Manufacturing. Soft Comput. 2020, 24, 15733–15745. [Google Scholar] [CrossRef]
- Carlson, C. Effective FMEAs: Achieving Safe, Reliable, and Economical Products and Processes Using Failure Mode and Effects Analysis; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Rimantho, D.; Noor, E.; Eriyatno; Effendi, H. Risk Assessment on Failure Factors of E-Waste Management Process Using FMEA Method. Int. J. Adv. Sci. Eng. Inf. Technol. 2020, 10, 2504–2510. [Google Scholar] [CrossRef]
- Bujna, M.; Matušeková, E. New Trends by FMEA; Richter-Altman, J., Ed.; RAM-Verlag: Lüdenscheid, Germany, 2018; ISBN 9783942303781. [Google Scholar]
- Nguyen, T.L.; Shu, M.H.; Hsu, B.M. Extended FMEA for Sustainable Manufacturing: An Empirical Study in the Non-Woven Fabrics Industry. Sustainability 2016, 8, 939. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Lin, Q.L.; Li, H. Risk Assessment in System FMEA Combining Fuzzy Weighted Average with Fuzzy Decision-Making Trial and Evaluation Laboratory. Int. J. Comput. Integr. Manuf. 2015, 28, 701–714. [Google Scholar] [CrossRef]
- Salmeron, J.L.; Gutierrez, E. Fuzzy Grey Cognitive Maps in Reliability Engineering. Appl. Soft Comput. J. 2012, 12, 3818–3824. [Google Scholar] [CrossRef]
- Netto, T.A.; Honorato, H.J.; Qassim, R.Y. Prioritization of Failure Risk in Subsea Flexible Pipes via Data Envelopment Analysis. Mar. Struct. 2013, 34, 105–116. [Google Scholar] [CrossRef]
- Keskin, G.A.; Özkan, C. An Alternative Evaluation of FMEA: Fuzzy ART Algorithm. Qual. Reliab. Eng. Int. 2009, 25, 647–661. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chin, K.S.; Poon, G.K.K.; Yang, J.B. Risk Evaluation in Failure Mode and Effects Analysis Using Fuzzy Weighted Geometric Mean. Expert Syst. Appl. 2009, 36, 1195–1207. [Google Scholar] [CrossRef]
- Kumar, R. Systematic Failure Mode Effect Analysis (FMEA) Using Fuzzy Linguistic Modelling. Int. J. Qual. Reliab. Manag. 2005, 22, 986–1004. [Google Scholar]
- Tay, K.M.; Lim, C.P. Fuzzy FMEA with a Guided Rules Reduction System for Prioritization of Failures. Int. J. Qual. Reliab. Manag. 2006, 23, 1047–1066. [Google Scholar] [CrossRef]
- Ahmed, U.; Carpitella, S.; Certa, A. An Integrated Methodological Approach for Optimising Complex Systems Subjected to Predictive Maintenance. Reliab. Eng. Syst. Saf. 2021, 216, 108022. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Wu, Z.; Zhu, B. A Rough TOPSIS Approach for Failure Mode and Effects Analysis in Uncertain Environments. Qual. Reliab. Eng. Int. 2014, 30, 473–486. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Shan, M.M.; Shao, L.N. Failure Mode and Effects Analysis Using Intuitionistic Fuzzy Hybrid TOPSIS Approach. Soft Comput. 2015, 19, 1085–1098. [Google Scholar] [CrossRef]
- Chang, C.L.; Liu, P.H.; Wei, C.C. Failure mode and effects analysis using grey theory. Integr. Manuf. Syst. 2001, 12, 211–216. [Google Scholar] [CrossRef]
- Liu, H.C.; Li, P.; You, J.X.; Chen, Y.Z. A Novel Approach for FMEA: Combination of Interval 2-Tuple Linguistic Variables and Gray Relational Analysis. Qual. Reliab. Eng. Int. 2015, 31, 761–772. [Google Scholar] [CrossRef]
- Tsai, S.B.; Zhou, J.; Gao, Y.; Wang, J.; Li, G.; Zheng, Y.; Ren, P.; Xu, W. Combining FMEA with DEMATEL Models to Solve Production Process Problems. PLoS ONE 2017, 12, e0183634. [Google Scholar] [CrossRef]
- Seyed-Hosseini, S.M.; Safaei, N.; Asgharpour, M.J. Reprioritization of Failures in a System Failure Mode and Effects Analysis by Decision Making Trial and Evaluation Laboratory Technique. Reliab. Eng. Syst. Saf. 2006, 91, 872–881. [Google Scholar] [CrossRef]
- Kutlu, A.C.; Ekmekçioǧlu, M. Fuzzy Failure Modes and Effects Analysis by Using Fuzzy TOPSIS-Based Fuzzy AHP. Expert Syst. Appl. 2012, 39, 61–67. [Google Scholar] [CrossRef]
- Tay, K.M.; Jong, C.H.; Lim, C.P. A Clustering-Based Failure Mode and Effect Analysis Model and Its Application to the Edible Bird Nest Industry. Neural Comput. Appl. 2015, 26, 551–560. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Fan, X.J.; Lin, Q.L. Failure Mode and Effects Analysis Using D Numbers and Grey Relational Projection Method. Expert Syst. Appl. 2014, 41, 4670–4679. [Google Scholar] [CrossRef]
- Aguirre, P.A.G.; Pérez-Domínguez, L.; Luviano-Cruz, D.; Noriega, J.J.S.; Gómez, E.M.; Callejas-Cuervo, M. PFDA-FMEA, an Integrated Method Improving FMEA Assessment in Product Design. Appl. Sci. 2021, 11, 1406. [Google Scholar] [CrossRef]
- Safari, H.; Faraji, Z.; Majidian, S. Identifying and Evaluating Enterprise Architecture Risks Using FMEA and Fuzzy VIKOR. J. Intell. Manuf. 2016, 27, 475–486. [Google Scholar] [CrossRef]
- Sharma, R.K.; Sharma, P. Integrated Framework to Optimize RAM and Cost Decisions in a Process Plant. J. Loss Prev. Process. Ind. 2012, 25, 883–904. [Google Scholar] [CrossRef]
- Alrifaey, M.; Hong, T.S.; Supeni, E.E.; As’arry, A.; Ang, C.K. Identification and Prioritization of Risk Factors in an Electrical Generator Based on the Hybrid FMEA Framework. Energies 2019, 12, 649. [Google Scholar] [CrossRef]
- Shieh, J.I.; Wu, H.H.; Huang, K.K. A DEMATEL Method in Identifying Key Success Factors of Hospital Service Quality. Knowl. Based Syst. 2010, 23, 277–282. [Google Scholar] [CrossRef]
- Liu, Z.; Bi, Y.; Liu, P. An Evidence Theory-Based Large Group FMEA Framework Incorporating Bounded Confidence and Its Application in Supercritical Water Gasification System. Appl. Soft Comput. 2022, 129, 109580. [Google Scholar] [CrossRef]
- Cheshmberah, M.; Naderizadeh, A.; Shafaghat, A.; Nokabadi, M.K. An Integrated Process Model for Root Cause Failure Analysis Based on Reality Charting, FMEA and Dematel. Int. J. Data Netw. Sci. 2020, 4, 225–236. [Google Scholar] [CrossRef]
- Díkmen, C.F.; Taş, Y. Applying DEMATEL Approach to Determine Factors Affecting Hospital Service Quality in a University Hospital: A Case Study. J. Adm. Sci. Cilt. 2018, 16, 11–28. [Google Scholar]
- Mzougui, I.; el Felsoufi, Z. Proposition of a Modified FMEA to Improve Reliability of Product. Procedia CIRP 2019, 84, 1003–1009. [Google Scholar] [CrossRef]
- Fei, H.; Zhu, Y.; Kang, Y.; Shi, S.; Xu, X. Identifying Root Causes of Important Service Failures across Medical Examination Processes with Integration of 4M1E, ITLV, GRA, DEMATEL and FMEA. Healthcare 2022, 10, 2283. [Google Scholar] [CrossRef] [PubMed]
- Hua, Z.; Jing, X.; Martínez, L. An ELICIT Information-Based ORESTE Method for Failure Mode and Effect Analysis Considering Risk Correlation with GRA-DEMATEL. Inf. Fusion 2023, 93, 396–411. [Google Scholar] [CrossRef]
- Jin, G. Selection of Virtual Team Members for Smart Port Development Projects through the Application of the Direct and Indirect Uncertain TOPSIS Method. Expert Syst. Appl. 2023, 217, 119555. [Google Scholar] [CrossRef]
- Song, W.; Zheng, J.; Niu, Z.; Wang, Q.; Tang, Y.; Zheng, P. Risk Evaluation for Industrial Smart Product-Service Systems: An Integrated Method Considering Failure Mode Correlations. Adv. Eng. Inform. 2022, 54, 101734. [Google Scholar] [CrossRef]
- Wang, W.C.; Lin, Y.H.; Lin, C.L.; Chung, C.H.; Lee, M.T. DEMATEL-Based Model to Improve the Performance in a Matrix Organization. Expert Syst. Appl. 2012, 39, 4978–4986. [Google Scholar] [CrossRef]
- Al-Shboul, M.A.R.; Barber, K.D.; Garza-Reyes, J.A.; Kumar, V.; Abdi, M.R. The Effect of Supply Chain Management Practices on Supply Chain and Manufacturing Firms’ Performance. J. Manuf. Technol. Manag. 2017, 28, 577–609. [Google Scholar] [CrossRef]
- Chen, H.M.; Wu, C.H.; Tsai, S.B.; Yu, J.; Wang, J.; Zheng, Y. Exploring Key Factors in Online Shopping with a Hybrid Model. Springerplus 2016, 5, 2046. [Google Scholar] [CrossRef]
- Deng, X.; Hu, Y.; Deng, Y.; Mahadevan, S. Environmental Impact Assessment Based on D Numbers. Expert Syst. Appl. 2014, 41, 635–643. [Google Scholar] [CrossRef]
- Rouhani, S.; Ashrafi, A.; Afshari, S. Fuzzy DEMATEL Model for Evaluation Criteria of Business Intelligence. In Proceedings of the ICEIS 2014 16th International Conference on Enterprise Information Systems, Lisbon, Portugal, 27–30 April 2014; SciTePress: Setubal, Portugal, 2014; Volume 1, pp. 456–463. [Google Scholar]
- Wang, X.; Zhang, Y.; Shen, G. An Improved FMECA for Feed System of CNC Machining Center Based on ICR and DEMATEL Method. Int. J. Adv. Manuf. Technol. 2016, 83, 43–54. [Google Scholar] [CrossRef]
- Tseng, M.L. A Causal and Effect Decision Making Model of Service Quality Expectation Using Grey-Fuzzy DEMATEL Approach. Expert Syst. Appl. 2009, 36, 7738–7748. [Google Scholar] [CrossRef]
- Wu, W.W. Choosing Knowledge Management Strategies by Using a Combined ANP and DEMATEL Approach. Expert Syst. Appl. 2008, 35, 828–835. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).