Abstract
In reinforcement learning (RL), a reward formed with a scalar value is seen as a sufficient means to guide an agent’s behavior. A reward drives an agent to seek out an optimal policy to solve a problem (or to achieve a goal) under uncertainty. In this paper, we aimed to probe the benefit of such a scalar reward in the shaping of coordination policy using artificial football scenarios. In a football setting, a team normally practices two types of strategies: one is a primary formation, that is, the default strategy of a team regardless of their opponents (e.g., 4-4-2, 4-3-3), and the other is an adaptive strategy, that is, a reactive tactic responding to the spontaneous changes of their opponents. We focused here on the primary formation as a team coordination policy that can be trained by a reward using multi-agent RL (MARL) algorithms. Once a team of multiple football agents has successfully learned a primary formation based on a reward-driven approach, we assumed that the team is able to exhibit the primary formation when facing various opponent teams they have never faced in due course to receive a reward. To precisely examine this behavior, we conducted a large number of simulations with twelve artificial football teams in an AI world cup environment. Here, we trained two MARL-based football teams with a team guided by a random walk formation. Afterwards, we performed the artificial football matches with the most competitive of the twelve teams that the MARL-based teams had never played against. Given the analyses of the performance of each football team with regard to their average score and competitiveness, the results showed that the proposed MARL teams outperformed the others with respect to competitiveness, although these teams were not the best with respect to the average score. This indicated that the coordination policy of the MARL-based football teams was moderately consistent against both known and unknown opponents due to the successful learning of a primary formation following the guidance of a scalar reward.
1. Introduction
The theory of reinforcement learning (RL) presents a mathematical foundation to formulate how agents learn from past experience. Owing to a breakthrough in deep learning in conjunction with a steep increase in computing power, there have been remarkable advances in designing artificial agents with super-human performance [1,2]. The goal of RL is to find an optimal policy that specifies a choice of action for each state of a given subject so as to maximize the expected future reward [3]. An RL agent, therefore, is able to learn how to act and/or interact optimally with complex environments.
A reward formed with a scalar value plays a crucial role in this learning process. Given the environment, a scalar reward drives an RL agent to seek out an optimal policy, that is, a sequence of actions to achieve a goal, which in turn achieves the maximum utility. In this context, Silver et al. [4] posit that the concept of reward maximization is enough to drive the high-level intelligence of all agents including learning, perception, social interaction, and generalization. This allows us to demonstrate the applicability of RL in a variety of problems. For instance, remarkable progress has been made toward designing RL algorithms in order to solve a variety of large-scale Markov decision problems [3,5,6]. In automatic control, RL agents can solve non-linear and stochastic optimal control problems, without an explicit representation of environments [7,8,9,10].
Based on this theoretical foundation, in this paper, we aimed to probe the role and the benefit of such a scalar reward from a practical point of view using artificial football scenarios. As is widely known, football is a sport in which multiple players cooperate with each other to compete against an opposing team. A set of game plans are required to win as a team, while individual players carry out their own roles coordinated by the plans. The game plans are usually composed of: (i) the team’s primary formation, referring to a default strategy based on the optimal team formation aligned with each member’s expertise (e.g., 4-4-2, 4-3-3, 3-5-2), and (ii) adaptive strategies that are a rather reactive tactic to respond to spontaneous changes in opponents [11].
We focused here more on establishing a primary formation as a team’s optimal coordination policy, trained by a reward, using multi-agent RL (MARL) algorithms. In effect, the primary formation is exhibited invariably as a representative strategy, regardless of the opponent being faced. It is frequently seen either at the beginning of the game or on many occasions during the game when the reconfiguration of the team is necessary. Within this context, our assumption was that, once an artificial football team successfully learns the primary formation based on a reward-driven approach, the team is able to exhibit this primary formation against various opponent teams they have never encountered in due course. In other words, the optimal coordination policy that the reward shapes will be habitually seen in games when competing with new opponents that the artificial football team has never faced. We presumed that a team of multiple football agents would show relatively high competitiveness in gaining a reward in football games against various types of opponents if the reward was effective in training the team’s primary formation.
To precisely examine this behavior, we designed an empirical study and conducted a large number of simulations with twelve artificial football teams in an AI world cup environment [12]. Here, we trained two MARL-based football teams against a baseline opponent, a team guided by a random walking formation. Afterwards, we performed the artificial football games between the two proposed MARL-based teams, a baseline random walk team, and the two most competitive teams shortlisted from the simulations that the MARL-based teams had never encountered. Considering the analyses of the performance, the results showed that the proposed MARL teams outperformed the others with respect to competitiveness, although these teams were not the best in terms of average score. These results potentially indicate that the coordination policy of the MARL-based football teams was moderately consistent against both previously encountered and new teams due to the successful learning of a primary formation following the guidance of a scalar reward. The contribution of this paper is that, by using a multi-agent football setting, we empirically evinced the potential of the invariable trait of multiple football agents’ behavior and a coordination policy, regardless of the team’s experience with the opponents, once the behavior and/or the coordination policy had been shaped by a scalar reward.
This paper is organized as follows. In Section 2, we briefly overview the computational theory of RL, illustrating the theoretical foundation of RL algorithms that enable a reward-based learning process. This is followed by a presentation of the experimental settings with descriptions of the football agents’ design in Section 3. Afterwards, we present the results of the simulations, along with discussions, in Section 4. We conclude the paper with contributions and future works in Section 5.
2. Reinforcement Learning: Background
The theory of RL is a normative framework accounting for the general principle of how agents perform reward-based, sequential decision making [1]. RL algorithms in computer science are usually based on Markov decision processes (MDPs) [13], which commonly model various sequential decision problems incorporating uncertainty in the environment. In this section, we start with an overview of sequential decision making and MDPs as a foundation of algorithmic RL models and then present algorithmic approaches addressing how a reward-based RL is formalized by those foundations.
2.1. Sequential Decision Making
Sequential choices, which occur in a range of real-world problems, are fundamental tasks that any intelligent agent encounters in extended actions/interactions with their environment [14]. Since the environment in which the agents reside is full of uncertainties, agents will iteratively try to make an optimal decision in order to achieve a goal following the ‘perceive-reason-act’ principle [15] in a sequential manner and subject to the changes in the environmental states.
Given a set of actions, an agent chooses the action resulting in the maximal utility, which in turn changes the states of the environment. As soon as the action is taken, the agents make an observation about the effect of that action, i.e., the updated state of the environment. This is followed by the selection of another action and another observation of the effect of that action, and so on [16], in order to increase the expected amount of utility depending on the changes in the environmental states. Thus, the goal of the agent is to estimate an expected amount of utility for each state that encodes information about the distant future’s rewards.
Sequential decision problems are commonly modeled as Markov decision processes (MDPs) [13]. The problem is solved either by planning given a model of the MDP (i.e., the model-based approach, e.g., dynamic programming methods [17]), or by learning through actions/interaction with an unknown MDP (i.e., the model-free approach, e.g., temporal difference [18]). During the process, the desirability or undesirability of actions that agents choose in each state and their effects are evaluated by a reward codified as a single scalar objective function. The objective of the agents is then the maximization of the (discounted) expected sum of the scalar reward at each step over time [19]. In Section 2.2, we present the formal model of the MDP and how the MDP contributes to solving RL problems with a reward.
2.2. Reinforcement Learning
The idea behind the MDP is the Markov assumption: “The future is independent of the past history, given the present” [3]. It is reasonable to deduce that as long as the current state captures all relevant information about past events, the past history may no longer be informative. An environment here is modeled as a set of states. The goal is to maximize its performance while choosing actions that can have an effect on these states [20].
The MDP shown in Figure 1 can be described formally with four components: states, actions, a transition function, and a reward function. A finite MDP is a tuple , where S is a finite set of states; A is a finite set of actions; is a transition function, which specifies for each state an action and a subsequent state and the probability of the next state being brought about; is a reward function specifying for each state, action, and subsequent state the sum of expected immediate and discounted rewards; and is a discount factor specifying the relative importance of immediate rewards.
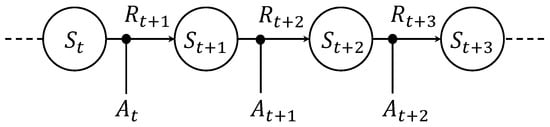
Figure 1.
Markov decision process from the reinforcement learning perspective: each node represents state S, denotes action A, and denotes reward R.
States S play a role in an outcome in addition to providing whatever information is necessary for choosing an action. Actions A can be used to control the state. The transition function T determines how the system will move to the next state. By performing an action in a state, the agent makes the transition from the current state to a new state based on a probability distribution over the set of possible transitions. Reward functions ℜ specify rewards for being in a state or performing some action in a state. They implicitly specify the goal of the agent [20] (Figure 2).
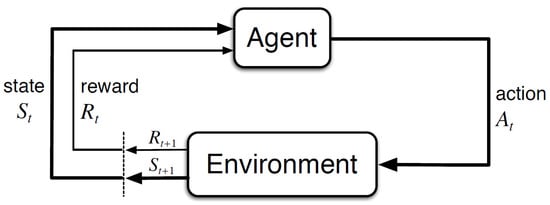
Figure 2.
Reinforcement learning agents: An RL agent is situated in an environment composed of a finite or infinite number of states. Given the state with a reward , the RL agent chooses an action that maximizes the cumulative rewards. Taking the action leads the RL agent to the new state with a new reward . After evaluating the effect of the previous action given the new state , the RL agent repeats such a cycle iteratively in order to achieve a goal in the environment. (Copyright © Sutton and Barto (1998). This figure was taken from [3].)
A solution to the MDP is characterized by the Bellman optimality equation [3]:
where the tuple refers to the current state s, an action a, and the state in the next time step , and refers to the state–action value. and R refer to the state–action–state transition probability and an immediate reward, respectively.
The Bellman optimality equation specifies that the value estimate for states and actions in each state (seen in Equation (2)) is given by the expectation over a state–space distribution of the future reward, which consists of an immediate reward amount plus the value estimate of the possible next state (often dubbed as the “TD target”). For example, an MF RL approximates this process under the assumption that the state transition is stationary, so the expectation over the state–space transitions can be empirically estimated by sampling actions for the environment.
Solving the MDP means computing an optimal policy (Equation (3)) by estimating the expected amount of reward for each state or action (Equation (1)), and then developing a policy that favors more valuable actions, leading to the maximization of the amount of future outcomes (Equation (2)). As a means to solve the equation, classical RL employed various iterative methods such as dynamic programming (DP) [21] and model-free algorithms such as Monte Carlo (MC) methods [22,23] or the temporal difference approach (TD) [18].
Since it is essential for RL agents to have exact representations of value functions and policies, the applicability of classical RL algorithms is limited to small-scale problems and problems that can be specified by discrete state spaces. However, the majority of real-world problems require the consideration of a large number of states and actions, and, moreover, they are often defined as continuous variables. Within this context, there are two main challenges in RL tasks: one is the requirement for a large-scale memory to store a huge number of states and/or actions, which may cause latency issues during the search and load operations while learning; the other is that they are computationally expensive. It would therefore be too slow to learn the value of each state, even for a single episode.
To tackle this issue, state-of-the-art RL models are now actively adopting the latest machine learning (ML) techniques to perform function approximation. A good example is the use of (deep) neural networks, which are non-linear, parameterized function approximation techniques that have been demonstrated to outperform the generic class of neural networks. ML has been used to approximate almost all RL components, including value functions (Equation (4)), policies (Equation (5)), and models (consisting of the state transition and its associated reward):
The parameter denotes the weights in deep neural networks, s specifies the state, and a specifies the action.
The combination of RL and deep learning has led to rapid advances in RL algorithm design, showing exceptional performance in many applications, such as games, robot control, and virtual environments. Moreover, ‘deep approximate RL’ has been developed in the disciplines of (i) value function approximation (e.g., DQN [1], DDQN [24]); (ii) policy gradient methods (e.g., DPG [25], DPG [26]); and (iii) asynchronous methods (e.g., A3C [27]).
3. Experimental Setting to Probe the Role of a Reward Using Football Scenarios
In the previous section, we presented the theoretical foundation of RL accounting for a reward-based learning process.In this section, we consider the practical aspect of scalar rewards that not only influence agents’ behavior but also have the potential to enforce agents to exhibit the target behavior invariably, regardless of context. To this end, we empirically inspected the agents’ behavior in a complex context, namely, a football scenario, as an exploratory example. In this Section, we specifically examine the reward’s influence and how well the influenced behavior is consistently performed against a variety of opponents’ strategies using a virtual football environment called AI World Cup with multi-agent techniques.
3.1. Environment: AI World Cup
The AI World Cup environment [12] is a virtual environment facilitating artificial football games where multiple artificial agents interact in a team to compete for the win. Figure 3A shows a screenshot of AI World Cup. As can be seen, the environment provides two teams, each of which has five football agents (four field players and one goalkeeper) on a virtual football field. The players are two-wheeled robots. The goal of this environment is to build a team of artificial football agents who are able to win against opponents by employing optimal strategies using AI techniques.
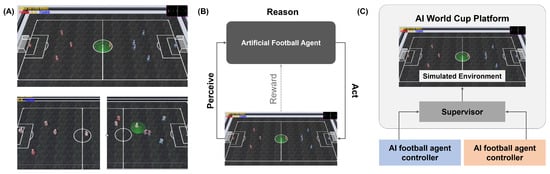
Figure 3.
Environment: (A) AI World Cup environment (top) and its working examples (bottom). (B) An abstract framework of artificial football agents. (C) The layout of the AI World Cup system.
Users can build a team of artificial football agents using various AI techniques such as dynamic planning [28], cognitive architecture [29], or learning agents [3]. For each frame, the environment broadcasts the game information, including all football agents’ coordinates and their directions and the ball’s coordinates and direction. With this information, users can design each agent’s behavior depending upon roles and strategies within the cycle of ‘perceive-reason-act’ (Figure 3B). The artificial football agent can move to the planned coordinates by controlling the wheel speed, which in turn sets their moving speed. The agent’s offensive and defensive behavior can be set by adjusting the kick and jump motions and their movement. The rules of the football game are basically similar to the rules of football in the real world, but there are no restrictions on physical tussles here. There are no energy limits for the artificial football agents.
The AI World Cup environment [12] was initially built using Webots Robot Simulator [30], which is a robot simulation software developed with a physics engine using Open Dynamics Engine [31]. The platform’s structure is shown in Figure 3C. In the platform, a supervisor process acts as a governor of the simulator. It collects all information, including all football agents, the ball, and the environmental states, and governs the rules of the football games in the simulator. In addition, it communicates with the artificial football agents developed by users via the AI World Cup’s application programming interfaces (AIWC APIs). Based on this, it distributes the game information to the user’s football agents and accepts the requests to control the agents. Employing this platform, we simply deployed the artificial football agents that we developed using the APIs on the basis of three AI techniques. In practice, we put the developed agents into a specific folder with a configuration file to integrate our agents into the platform as introduced in the programming guide of AI World Cup [32]. See [12] for more details.
3.2. Engineering Artificial Football Agents
To develop the multi-agent-based artificial football agents, we considered three types of agents—(i) random walk, (ii) dynamic planning [28], and (iii) RL agents [29]. After the design and training of each agent, we performed an iterative improvement of each agent by making them compete with each other. This competitive approach provided opportunities enabling (i) the development of an optimal human-designed curriculum for the design of dynamic planning agents and (ii) the evolution of the optimal policies of RL agents, taking into account the various opponents’ strategies. In the following, we briefly describe the various teams’ strategies with engineering details. We note that the implementation examples can be found at [33].
Random walk (RW) agent. This agent performs purely random actions with no restrictions. In other words, an RW agent does not have a strategy itself and thus does not take into account its surroundings. It plays the game only through randomly selected actions. In detail, the RW agents’ actions are determined by a random selection of their wheel speed, which is sampled on a uniform distribution.
There is no cooperation between team members at all. Although this type of artificial football agent has the lowest level of intelligence out of the three approaches, it is useful for training and evaluating agents with other approaches. It acts entirely in random policies, so that these agents are able to bring about purely unforeseen situations for the other agents. They therefore provide uncertainty about both the individual agent’s behavior and team strategies. In addition, randomly generated individuals and team strategies might present unpredictable complexity. Since this RW-type agent could present training scenarios full of complexity and unpredictability for other artificial football teams, we used it as an experimental baseline to measure other agents’ ability to cope with complexity/uncertainty, accordingly.
Dynamic planning agent. Dynamic planning is known as an agent design framework providing the agent programming language and its interpreter to implement intelligent agents [28,29,34]. It enables the engineering of various plans and strategies on the basis of the designer’s insights and expert knowledge. Dynamic plans are usually in the form of logical formulas that determine the most situationally appropriate plans subject to the belief that the agent is perceived in the environment. Figure 4 shows an example plan implementing Gegenpressing, the extremely defensive strategy proposed in Yi et al. [35].
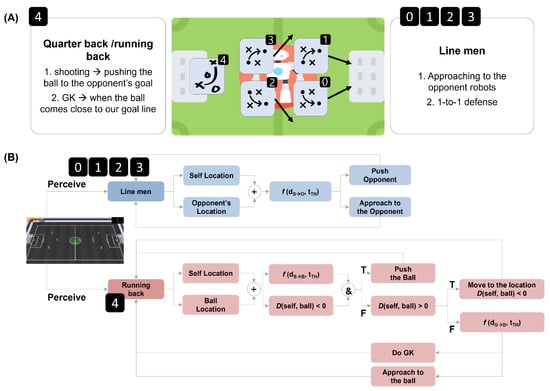
Figure 4.
Engineering dynamic planning agents. (A) An illustration of an AI football strategy, called Gegenpressing, proposed in Yi et al. [35]. (B) Dynamic plans for Gegenpressing.
The advantage of this framework is its efficiency in the design of intelligent agents. Since there is no adaptation and learning process at all, it is straightforward to implement the plans for both individual agent behavior and multiple teams in a short time. In addition, the designers can also easily modify and fine-tune strategies immediately based on the opponents’ behavior, changes in the environment, and unexpected uncertainty. However, it is very hard to respond to a rapidly changing environment, since these agents are developed on a set of reasoning rules and there is thus no adaptive capacity. In this paper, we used this approach to model the AI football agents’ behavior as observed in actual football matches. Based on this, we designed individual football agents’ roles, attributes, team coordination strategies, and plans in relation to the ball position and the location of other players.
Here, we developed nine sets of artificial football teams (Figure 5). In brief, standard role-based players refer to a team following a standard formation in which two attackers, two defenders, and a goalkeeper play their own roles in pre-defined areas. Gegenangriff (GGA) is a team following the most aggressive strategy, in which all football agents except the goalkeeper persistently focus on the attack regardless of the opponent’s strategy. Gegenpressing is a strategy in which three defenders press the opponents and two attackers focus on offensive behavior to score. Becoming sprinter is the same strategy as that of standard role-based players, but with a faster moving speed. Becoming defenders in the penalty area refers to a strategy whereby all agents become defenders and are located in the team’s area. There is no offensive movement in this strategy. Becoming man-to-man defenders is when agents become defenders and focus on the man-to-man defense. They only defend, and there is no offensive behavior. In becoming ball-hunters, there is neither defensive nor offensive behavior. All agents just track the ball’s location and chase the ball without a consideration of the opponents’ behavior. All becoming goalies #1 and all becoming goalies #2 involve the same strategy: all agents simply become goalkeepers; however, in the former, all agents stand in a row in front of the opponent’s goal, whereas in the the latter, they stand in front of their team’s goal. We used these dynamic planning agents as training partners for the RL agents.
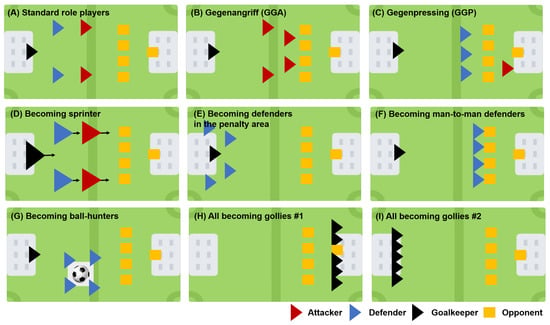
Figure 5.
Nine sets of artificial football teams implemented by the dynamic planning approach.
RL agent. This agent focuses on training agents to optimally perform a sequential decision in the environment to maximize a reward. The scalar-valued reward shapes the agent’s behavior by providing a signal that the agent can use to estimate the value of the actions. The agent learns from past experiences by associating the reward signal with actions—higher rewards come from better actions and lower rewards come from worse actions when estimating the expected cumulative reward. Over time, the agent finally learns the optimal policy to achieve a goal that can maximize the cumulative reward. The scalar reward has played an important role in building artificial agents with human-level performance in several domains [36,37,38]. Now, the impact of rewards drastically affects the domain of MARL algorithms in which multiple agents in a team cooperate and collaborate to achieve their common goals [39,40,41,42].
In the AI World Cup environment, we focused on engineering MARL-based football agents. In particular, we simulated the football agents’ behavior with regard to the team’s main strategy, the so-called formation of the team, which can be exhibited persistently regardless of the opponent once the agents are well-trained. Two approaches were employed to this end: independent Q-learning (IQL hereinafter; Figure 6) [43] and QMIX [42]. The former, IQL, is a representative MARL algorithm based upon the principle of ‘decentralized training and decentralized execution’. In IQL, there is no centralized, unified Q-value for the entire team; each agent has a separate Q-value for each state–action pair to learn from past experiences instead. Thus, each agent learns the optimal policy subject to its own partially observed experience, which is shaped by a scalar reward for individuals. It is not expected that communications take place between agents to cooperate and/or coordinate their behavior. Without considering others, the agent is only governed by its own reward signal, and thus the team’s performance is limited due to the partial overall observability (Figure 6A).
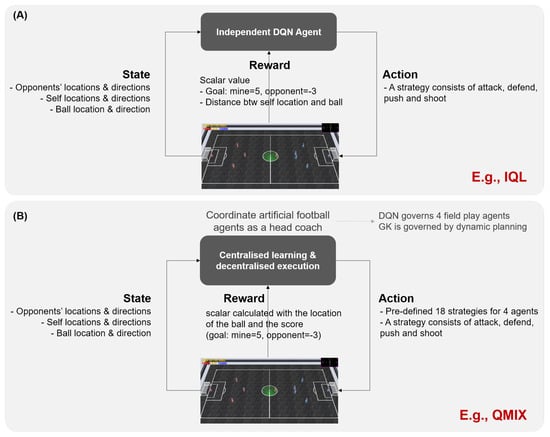
Figure 6.
Two multi-agent RL techniques to build artificial football agents. (A) A framework for a single DQN agent in IQL. (B) A framework for QMIX.
In contrast, the latter approach, QMIX, is based upon the principle of ’centralized training and decentralized execution’. In QMIX, there is a centralized, total Q-value for the entire team. The total Q-value is actually a mixture of all individual agents’ Q-values—specifically, a linear combination of them. Here, individual Q-values for each agent are not shaped by the individual’s reward signal. Instead, they are shaped by the team’s collective reward signal, which allows for opportunities to observe other agents’ observations, thus embodying cooperation with full observability. The output of the centralized Q-value consists of all agents’ actions. This implements the ‘decentralized execution’ in which each agent carries out its own action determined by the centralized Q-value. Since the actions are implicitly coordinated due to the centralized training, it was anticipated that the stability and performance could be better than those of IQL (Figure 6B).
Figure 7 shows the internal design of the QMIX-based football agents. A team using a QMIX approach consists of four field players and one goalkeeper. The goalkeeper here takes its genuine role, and the other four agents perform the actions of defence, offence, pushing, and shooting, as defined in standard role-based players. The states of each agent are (i) the coordinates and directions of all agents and (ii) the ball’s location and direction observed in the last four frames. The reward for the centralized QMIX is a scalar value, that is, +5 points are received when the team scores, and 3 points are deducted when the opponents score or the agents compute actions using the state information, including the ball location in the environment. QMIX produces 18 pre-defined, high-level action sets, each of which contains a set of primitive actions governing the four field players’ behavior. For example, a vector of (A, D, P, S) means that agent one is obliged to perform an attack, agent two to play defence, agent three to push, and agent four to shoot. For IQL, all settings are the same as those of QMIX, but there are four Q-networks, each of which is dedicated to each agent. The output of IQL’s Q-network is one of the primitive actions ‘attack’, ‘defense’, ‘push’, and ‘shoot’.
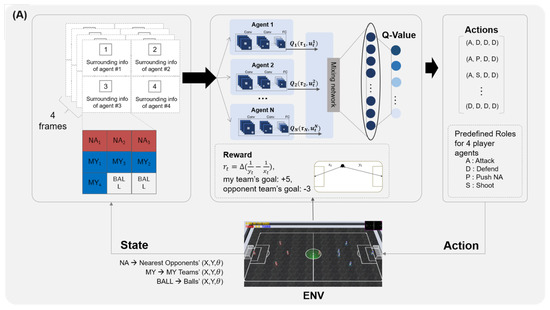
Figure 7.
An overview of the artificial football team using QMIX algorithm.
4. Results
In the previous section, we presented experimental settings to simulate multi-agent football scenarios to inspect the benefit of reward-based learning in the shaping of coordination policy. We first introduced the virtual football environment, AI World Cup, and described the details of the developed methods in conjunction with the artificial football teams implemented by these methods (e.g., dynamic planning, MARL algorithms). In this section, we fully illustrate the simulation procedures and present the results and discussions.
4.1. Simulation Settings
In addition to these agent engineering approaches, we conducted experiments based on artificial football games using twelve teams. The artificial football games took place in a league format: each team played against all other teams except itself. Among the teams, we shortlisted five: random walk (RW), Gegenangriff (GGA), Gegenpressing (GGP), IQL, and QMIX. RW was a training partner for IQL and QMIX, so we included it as a baseline, specifically as a lower bound. GGA and GGP, as described, represented the most extreme offensive and defensive strategies, respectively; thus, they showed the best performance in both the average score and winning rate. We used them as an upper bound.
Only RW was used to train the two MARL-based football teams, IQL and QMIX. If each agent acted in a pre-defined area and performed well in offense and defense according to its role (as shown in Figure 2), we expected the team to receive higher rewards. These two MARL-based football teams had never encountered the other teams before the simulations, meaning that the simulation result with regard to the score and winning rate against the GGA and GGP teams could be seen as a measure of the trained policies reflecting the role and responsibility of a scalar-valued reward signal. Figure 8 shows a screenshot of each team’s play during the games.
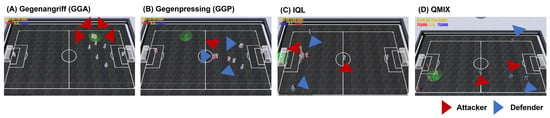
Figure 8.
Screenshots of the simulations. Blue and red triangles refer to the defenders and the attackers, respectively. (A) GGA, (B) GGP, (C) QMIX, (D) IQL.
We performed 200 simulation games with the shortlisted teams (=five teams × four opponents × ten games for each match). Afterwards, an average score, an average winning rate, and the reliability of each agent were analyzed. Here, the average score was the mean of the scores relative to the average difference between one team’s score and the other’s based on Equation (6):
where and refer to team A’s and team B’s scores, respectively, and N refers to the number of artificial football games.
For the winning rate, we simply counted the number of positive average scores of each team and calculated the ratio based on the total number of games:
where refers to the number of games with positive scores, and refers to the total number of games. One average positive score stands for one winning game. The more positive scores the team had, the higher the winning rate of the team.
Reliability is the ratio between the mean and the standard deviation; in this case, reliability was the value of the average score divided by the standard deviation:
where is an average score, and is a standard deviation of the scores. This measure indicated the extent to which the team scored consistently over all the games. The larger the reliability, the more consistent the performance of the team, regardless of their opponent.
All simulations were performed on a Microsoft Windows 10 operating system with 128 gigabytes of RAM and a GeForce RTX 2080 Ti GPU installed. All agents were developed in the Python programming language, version 3.74.
4.2. Experimental Results
The overall results from 200 simulations are shown in Figure 9. The results confirmed that GGA and GGP were qualified as the upper bound of all teams. With respect to the average score in Figure 9A, GGA showed the best performance. It outperformed all other teams’ strategies, except for GGP, the most defensive strategy. Unlike the other teams (usually consisting of two defenders and two attackers), GGA was composed of four attackers, as shown in Figure 5B. We therefore assumed that GGA was able to score more than the others (Figure 9A).
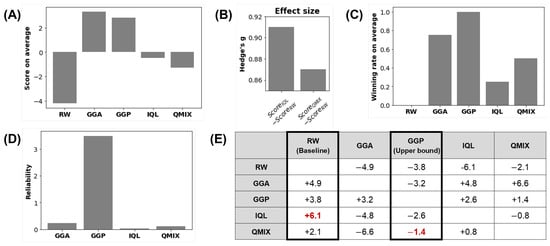
Figure 9.
Simulation results: (A) Average score. (B) Effect size between IQL and RW and between QMIX and RW (Hedge’s g). (C) Average winning rate. (D) Reliability. (E) Simulation results in terms of average scores. The first column refers to the team, and the first row refers to the opponent. A positive number refers to the score with which the team won the game. A negative number refers to the number of points by which the team failed to win the game.
Despite the fact that the GGP ranked second in the average score, GGP showed the highest winning rate among the shortlisted teams. It could thus be seen as the most competitive winning strategy of all the teams. Based on strong physical contact with their opponents, the GGP pursued quick and aggressive behavior to score. This resulted in a consistent performance for all opponents. Since football is a game wherein winning rates are more important than scores, it is rational to conclude that the best strategy was GGP (Figure 9C).
Using these results, we analyzed the performance of the two MARL-based football teams. As expected, they were superior to the baseline, RW, but inferior to the upper bound, GGA and GGP. RW never won against any other teams. First, the two MARL-based football teams outperformed the RW team with regard to the score and winning rate (Figure 9A,C,D). The average scores of the two MARL-based teams were approximately three times higher than that of RW.
To examine the impact of the reward signal, we measured the effect size between IQL and RW and between QMIX and RW using Hedge’s g: RW was a baseline implementation for an artificial football team without using a reward signal, whereas the two MARL-based teams formed the treatment group of artificial football teams using a reward signal (Figure 9B). We intended to measure the effect with or without a reward signal to indirectly present the impact of a reward in the design of artificial football teams. The Hedge’s g values were 0.91 for the RW and IQL pair and 0.87 for the RW and QMIX pair. This result highlighted the strong effect when using a reward signal to design artificial football agents’ behavior.
Compared to GGA and GGP, the upper bounds, the two MARL-based football teams showed a lower performance with respect to both the average score and the winning rate. However, the MARL-based teams interestingly exhibited the most competitiveness against GGP. Since no teams were able to defeat GGP, we compared the average scores of all the teams. With GGP, we assumed that the lower the score by which the team lost, the more competitive the team was. The two MARL-based teams showed the best performance (−1.4 and −2.6 for QMIX and IQL, respectively) out of all other teams in this regard. In particular, they even outperformed the GGA (−3.2) team that specialized in offense and presented the best average score (Figure 9E).
4.3. Discussion
Building artificial football agents based upon random walk, dynamic planning, and reinforcement learning techniques, we performed 200 simulations with five types of artificial football teams. The main purpose of this experiment was to empirically investigate the role and impact of a reward signal in the shaping of football agents’ behavior and associated coordination policies. In particular, we focused on shaping the primary formation of the football team, which could be consistently exhibited against various opponents.
The experimental results showed that the MARL-based football teams, whose behaviors and coordination policies were guided by a scalar-valued signal, achieved higher performance than a baseline team (e.g., RW). The results of the effect size indicated that the use of a reward signal in the design of multiple football agents’ behavior showed a stronger effect with regard to the average score than that of the baseline agent. Further analysis of the MARL-based teams’ competency against the upper-bound team, GGP, confirmed that reward-signal-guided teams performed remarkably better than the rest of the teams with respect to the average score. Taken together, the reward signal moderately and persistently guided the football agents’ behavior, in conjunction with a strong impact.
However, there were some shortcomings to this study. The proposed reward-guided artificial football teams failed to defeat GGA and GGP and showed lower average scores, winning rates, and reliabilities. Since these two football teams were developed in the form of learning agents, they were in effect supposed to be able to learn flexibly, so as to exhibit high adaptivity against teams in many cases. However, the reward signal was only given to the behavior established by (i) the extent to which each player complied with its own role and responsibility in relation to the ball’s location and opponents’ positions, as defined in the primary formation, and (ii) the number of goals they scored. Since the opportunity to score rarely happened in a game, we assumed that the former, a reward signal computed by the compliance of the primary formation, would be able to influence the shaping of the football agents’ behavior more. In addition, these two MARL-based teams had never encountered the GGA and GGP strategies; thus, there were definitely no reward signals to adapt to these competitive teams in the past. Since the reward signal they experienced was only dedicated to the primary formation, their performance against GGA and GGP was inferior.
The two MARL-based teams might have needed to adapt to defeat GGA and GGP, which would require a totally new learning process based on new strategies. During the new process, a newly designed reward signal would shape the football agents’ behavior in response to GGA and GGP. Meta-RL approaches employing a meta-level reward signal also seem to be promising [44,45,46,47]; additionally, a multi-task learning approach, so-called meta-learning, would be beneficial to improve the capacity of these MARL-based teams to adapt in a dynamically changing environment with few-shot or zero-shot learning methods, such as memory-based RL algorithms [38].
5. Conclusions
It is widely accepted that a reward is a central means to build generalized and adaptive intelligence in artificial agents [4]. In this regard, this paper proposed an empirical study to investigate the role and impact of a scalar-valued reward signal in the design and implementation of multi-agent behavior. After the introduction to the essence of RL, which comprehensively described how agents learn from past experiences based upon a scalar reward, we presented the principles and practices of engineering artificial football agents. Using these artificial agents, we conducted simulations with five types of artificial football teams, including two MARL-based football teams. The analyses of the average score, the effect size of the score, the winning rate, and the reliability indirectly indicated that the football teams guided by a reward signal demonstrated persistent behaviors and showed a strong effect size in performance.
In the future, we plan to study artificial football agents using more diverse and complex strategies. In terms of MARL, further research will be conducted to develop meta-RL agents in which a meta-level reward signal guides the multi-task learning so the agents can flexibly adapt to the changes in opponents and/or strategies. We anticipate that a high-level reward signal will ensure a richer coordination policy and agent behavior, being sufficient to enhance the scores, winning rate, and reliability against the upper-bound teams (i.e., GGA and GGP). To more precisely examine the role of a reward, strategies and formations will be further analyzed using the game histories and trajectories of each game.
Author Contributions
Conceptualization, J.H.L., S.H.K. and J.H.K.; methodology, J.H.L.; software, J.H.K.; validation, J.H.L., S.H.K., and J.H.K.; formal analysis, J.H.L.; writing—original draft preparation, S.H.K. and J.H.L.; writing—review and editing, J.H.L.; visualization, J.H.L.; supervision, J.H.L.; project administration, J.H.L.; funding acquisition, J.H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a 2020–2021 Research Grant from Sangmyung University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, UK, 1998; Volume 1. [Google Scholar]
- Silver, D.; Singh, S.; Precup, D.; Sutton, R.S. Reward is enough. Artif. Intell. 2021, 299, 103535. [Google Scholar] [CrossRef]
- Szepesvári, C. Algorithms for reinforcement learning. Synth. Lect. Artif. Intell. Mach. Learn. 2010, 4, 1–103. [Google Scholar]
- Sigaud, O.; Buffet, O. Markov Decision Processes in Artificial Intelligence; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bertsekas, D.P.; Tsitsiklis, J.N. Neuro-dynamic programming: An overview. In Proceedings of the 34th IEEE Conference on Decision and Control, New Orleans, LO, USA, 13–15 December 1995; Volume 1, pp. 560–564. [Google Scholar]
- Si, J. Handbook of Learning and Approximate Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 2. [Google Scholar]
- Busoniu, L.; Babuska, R.; De Schutter, B.; Ernst, D. Reinforcement Learning and Dynamic Programming Using Function Approximators; CRC Press: Amsterdam, The Netherlands, 2010; Volume 39. [Google Scholar]
- Soni, K.; Dogra, D.P.; Sekh, A.A.; Kar, S.; Choi, H.; Kim, I.J. Person re-identification in indoor videos by information fusion using Graph Convolutional Networks. Expert Syst. Appl. 2022, 210, 118363. [Google Scholar] [CrossRef]
- Tuyls, K.; Omidshafiei, S.; Muller, P.; Wang, Z.; Connor, J.; Hennes, D.; Graham, I.; Spearman, W.; Waskett, T.; Steel, D.; et al. Game Plan: What AI can do for Football, and What Football can do for AI. J. Artif. Intell. Res. 2021, 71, 41–88. [Google Scholar] [CrossRef]
- Hong, C.; Jeong, I.; Vecchietti, L.F.; Har, D.; Kim, J.H. AI World Cup: Robot-Soccer-Based Competitions. IEEE Trans. Games 2021, 13, 330–341. [Google Scholar] [CrossRef]
- Bellman, R. A Markovian Decision Process. J.Math. Mech. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Littman, M.L. Algorithms for Sequential Decision Making. Ph.D. Thesis, Brown University, Providence, RI, USA, 1996. [Google Scholar]
- Winston, P.H. Artificial Intelligence, 3rd ed.; Addison-Wesley: Boston, MA, USA, 1992. [Google Scholar]
- Krause, A.; Golovin, D.; Converse, S. Sequential decision making in computational sustainability via adaptive submodularity. AI Mag. 2014, 35, 8–18. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming and Lagrange multipliers. Proc. Natl. Acad. Sci. USA 1956, 42, 767–769. [Google Scholar] [CrossRef]
- Sutton, R.S. Learning to predict by the methods of temporal differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Roijers, D.M.; Vamplew, P.; Whiteson, S.; Dazeley, R. A survey of multi-objective sequential decision-making. J. Artif. Intell. Res. 2013, 48, 67–113. [Google Scholar] [CrossRef]
- van Otterlo, M.; Wiering, M. Reinforcement Learning and Markov Decision Processes. In Reinforcement Learning: State-of-the-Art; Wiering, M., van Otterlo, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 3–42. [Google Scholar]
- Watkins, C.J.C.H. Learning from Delayed Rewards. Ph.D. Thesis, University of Cambridge England, Cambridge, UK, 1989. [Google Scholar]
- Barto, A.G.; Duff, M. Monte Carlo matrix inversion and reinforcement learning. Adv. Neural Inf. Process. Syst. 1994, 6, 687. [Google Scholar]
- Singh, S.P.; Sutton, R.S. Reinforcement learning with replacing eligibility traces. Recent Adv. Reinf. Learn. 1996, 22, 123–158. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. In Proceedings of the AAAI, Phoenix, AZ, USA, 12–17 February 2016; pp. 2094–2100. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on Machine Learning (ICML-14), Beijing, China, 21–26 June 2014; pp. 387–395. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Brooks, R.A. Intelligence without representation. Artif. Intell. 1991, 47, 139–159. [Google Scholar] [CrossRef]
- Bordini, R.H.; Hübner, J.F.; Wooldridge, M. Programming Multi-Agent Systems in AgentSpeak Using Jason; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Michel, O. Cyberbotics ltd. webotsTM: Professional mobile robot simulation. Int. J. Adv. Robot. Syst. 2004, 1, 5. [Google Scholar] [CrossRef]
- Open Dynamic Engine. Available online: https://www.ode.org/ (accessed on 4 February 2023).
- AI Soccer 3D. Available online: https://github.com/aisoccer/aisoccer-3d/releases/ (accessed on 4 February 2023).
- Examples of AI Football Agents. Available online: https://github.com/idea-lab-smu/ai-football-pilot (accessed on 4 February 2023).
- Bryson, J.J. The behavior-oriented design of modular agent intelligence. Lect. Notes Comput. Sci. 2003, 2592, 61–76. [Google Scholar]
- Yi, S.; Lee, J.; Lee, C.; Kim, J.; An, S.; Lee, S.W. A Competitive Path to Build Artificial Football Agents for AI Worldcup. In Proceedings of the IEEE/IEIE International Conference on Consumer Electronics (ICCE) Asia, Jeju, Republic of Korea, 24–26 June 2018. [Google Scholar]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science 2018, 362, 1140–1144. [Google Scholar] [CrossRef]
- Schrittwieser, J.; Antonoglou, I.; Hubert, T.; Simonyan, K.; Sifre, L.; Schmitt, S.; Guez, A.; Lockhart, E.; Hassabis, D.; Graepel, T.; et al. Mastering atari, go, chess and shogi by planning with a learned model. Nature 2020, 588, 604–609. [Google Scholar] [CrossRef]
- Hessel, M.; Danihelka, I.; Viola, F.; Guez, A.; Schmitt, S.; Sifre, L.; Weber, T.; Silver, D.; Van Hasselt, H. Muesli: Combining improvements in policy optimization. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 4214–4226. [Google Scholar]
- Foerster, J.; Chen, R.Y.; Al-Shedivat, M.; Whiteson, S.; Abbeel, P.; Mordatch, I. Learning with opponent-learning awareness. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 122–130. [Google Scholar]
- Wang, T.; Gupta, T.; Mahajan, A.; Peng, B.; Whiteson, S.; Zhang, C. Rode: Learning roles to decompose multi-agent tasks. arXiv 2020, arXiv:2010.01523. [Google Scholar]
- Wang, J.; Ren, Z.; Liu, T.; Yu, Y.; Zhang, C. Qplex: Duplex dueling multi-agent q-learning. arXiv 2020, arXiv:2008.01062. [Google Scholar]
- Rashid, T.; Samvelyan, M.; De Witt, C.S.; Farquhar, G.; Foerster, J.; Whiteson, S. Monotonic value function factorisation for deep multi-agent reinforcement learning. J. Mach. Learn. Res. 2020, 21, 7234–7284. [Google Scholar]
- Tan, M. Multi-agent reinforcement learning: Independent vs. cooperative agents. In Proceedings of the Tenth International Conference on Machine Learning, Amherst, MA, USA, 27–29 July 1993; pp. 330–337. [Google Scholar]
- Wang, J.X.; Kurth-Nelson, Z.; Tirumala, D.; Soyer, H.; Leibo, J.Z.; Munos, R.; Blundell, C.; Kumaran, D.; Botvinick, M. Learning to reinforcement learn. arXiv 2016, arXiv:1611.05763. [Google Scholar]
- Wang, J.X.; Kurth-Nelson, Z.; Kumaran, D.; Tirumala, D.; Soyer, H.; Leibo, J.Z.; Hassabis, D.; Botvinick, M. Prefrontal cortex as a meta-reinforcement learning system. Nat. Neurosci. 2018, 21, 860. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Shimojo, S.; O’Doherty, J.P. Neural computations underlying arbitration between model-based and model-free learning. Neuron 2014, 81, 687–699. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Seymour, B.; Leibo, J.Z.; An, S.J.; Lee, S.W. Toward high-performance, memory-efficient, and fast reinforcement learning—Lessons from decision neuroscience. Sci. Robot. 2019, 4, eaav2975. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).