Experimental Analysis of the Influence of Gear Design and Catch Weight on the Fluid–Structure Interaction of a Flexible Codend Structure Used in Trawl Fisheries
Abstract
1. Introduction
2. Material and Methods
2.1. Choice and Design of the Codends
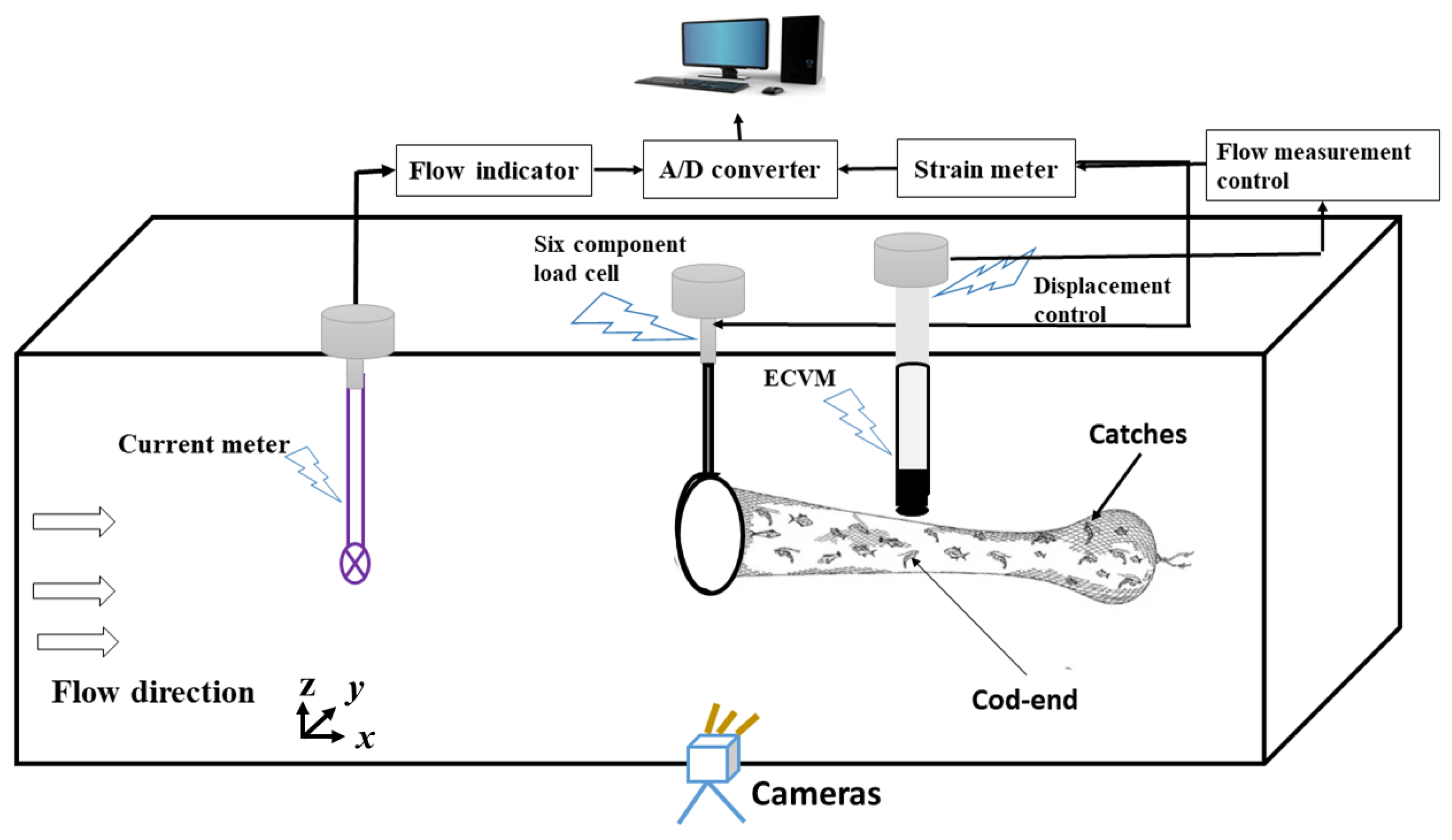
2.2. The Measurement of the Hydrodynamic Forces in the Flume Tank
- (1)
- The voltage signals of hydrodynamic forces are transmitted to the strain meter using the sensor during the flow passage thought the combining codend and circular frame system;
- (2)
- The strain meter amplifies and integrates sensor signals, producing analog signal information that can be displayed continuously online;
- (3)
- The analog signals are changed to digital signals by an A/D converter;
- (4)
- Hydrodynamic forces are represented using computer calibration coefficients. In the above manner, flow velocity signals are also obtained from the propeller tachometer sensor.
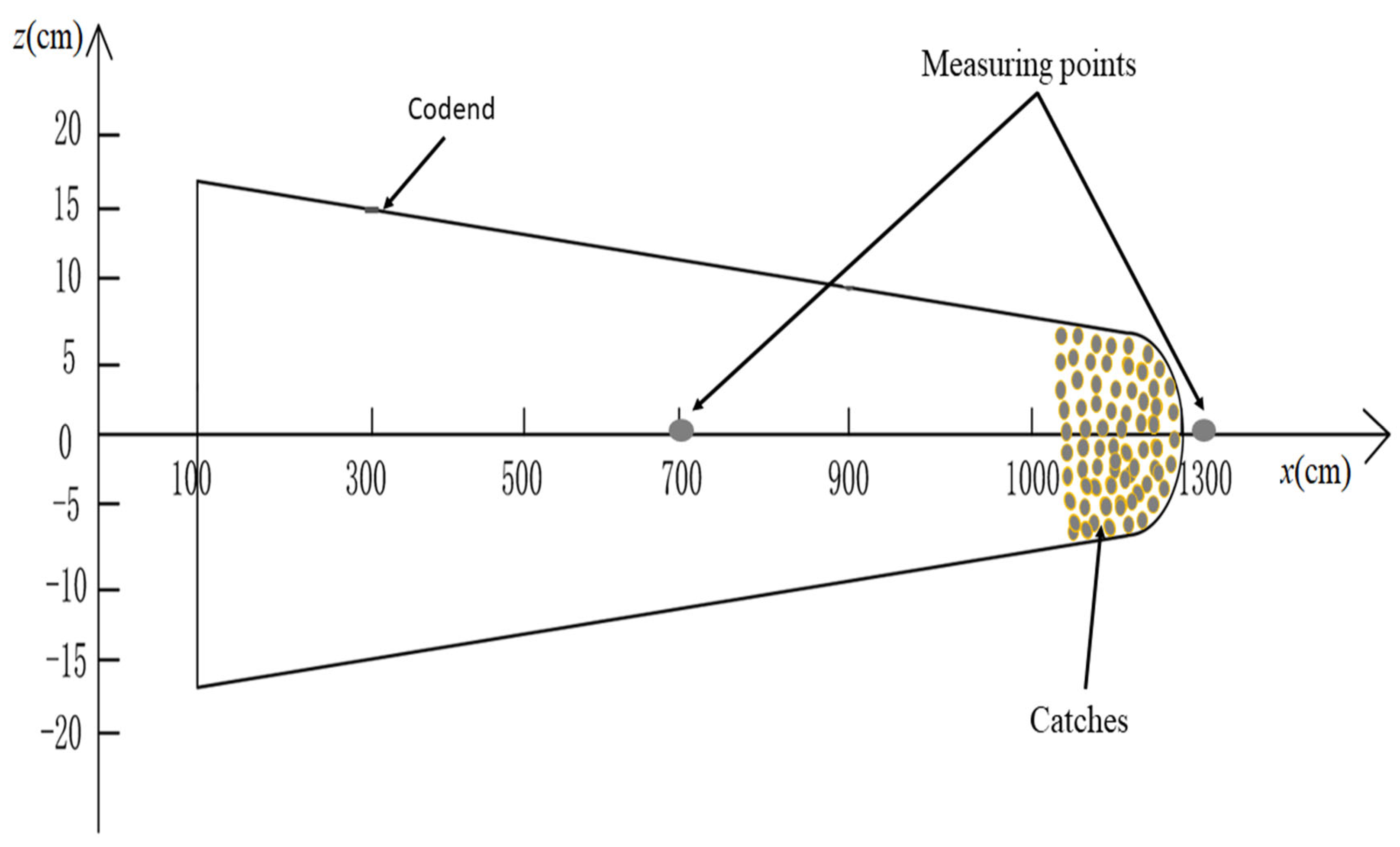
2.3. Measurement of the Codend Shape and Motions
2.4. Flow Measurements
2.5. Power Spectral Density Features from Fast Fourier Transform
2.6. Statistical Analysis
3. Results
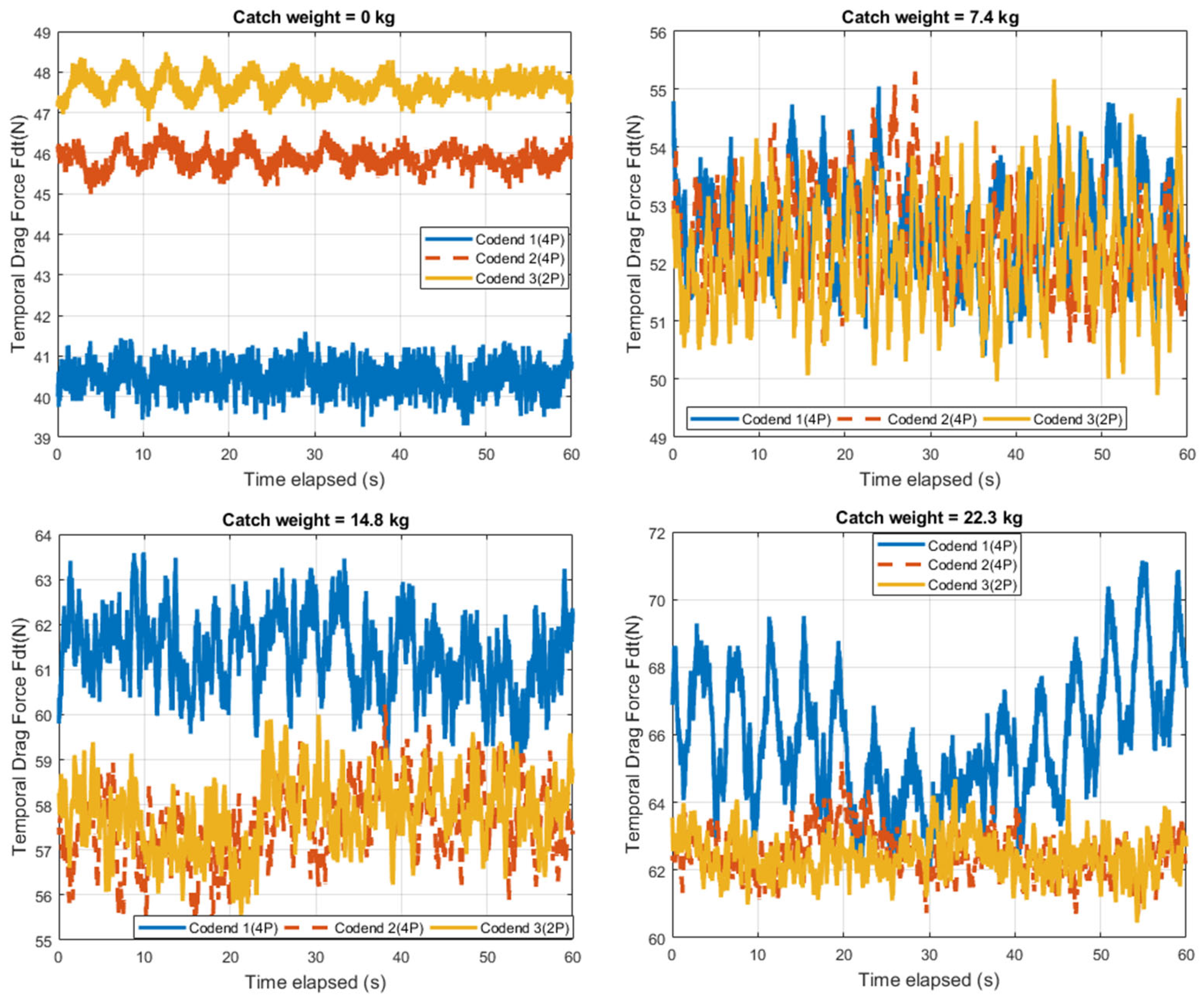
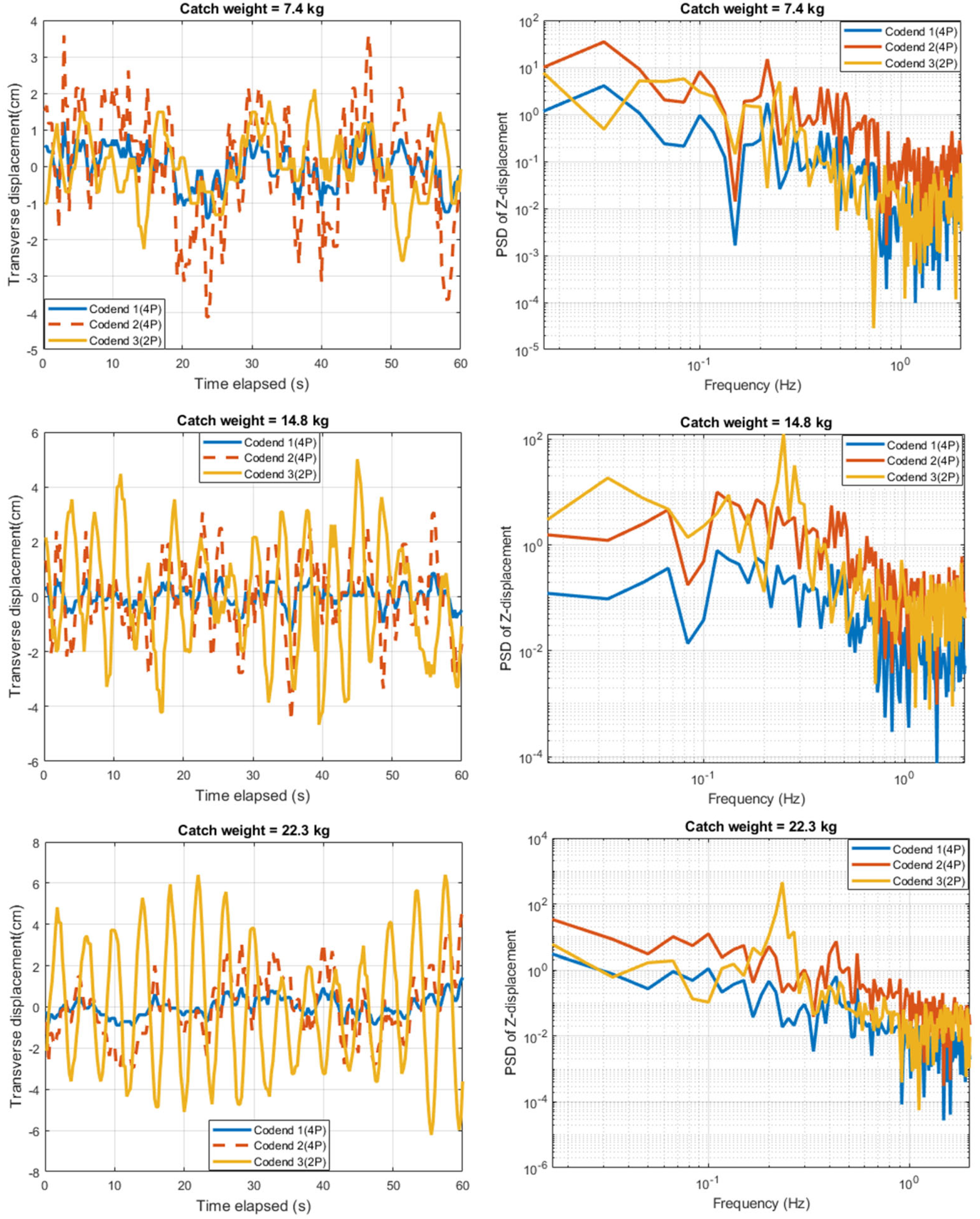
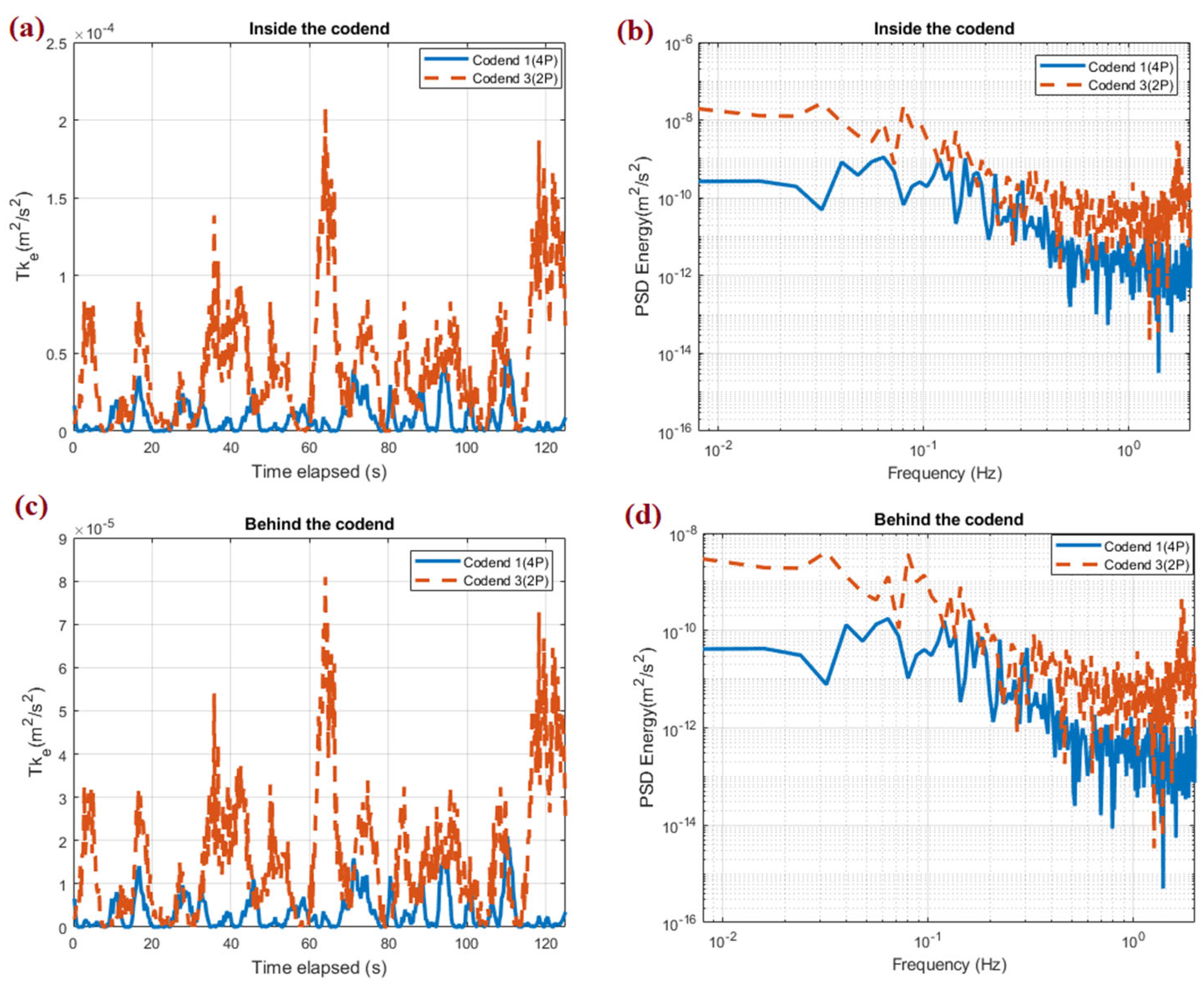
3.1. Spectral Analysis of Effect of Catch Weight and Gear Design on the Codend Drag
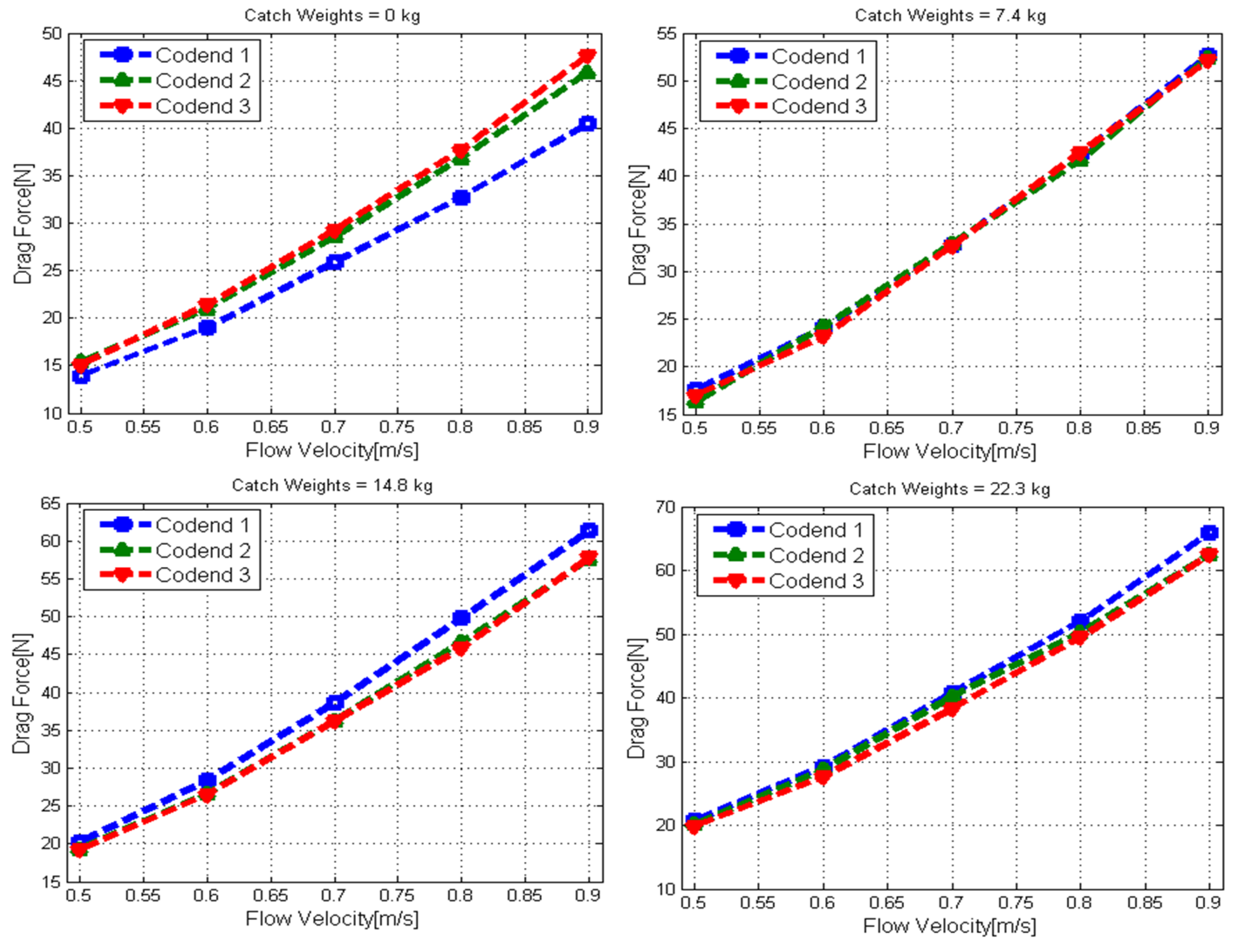
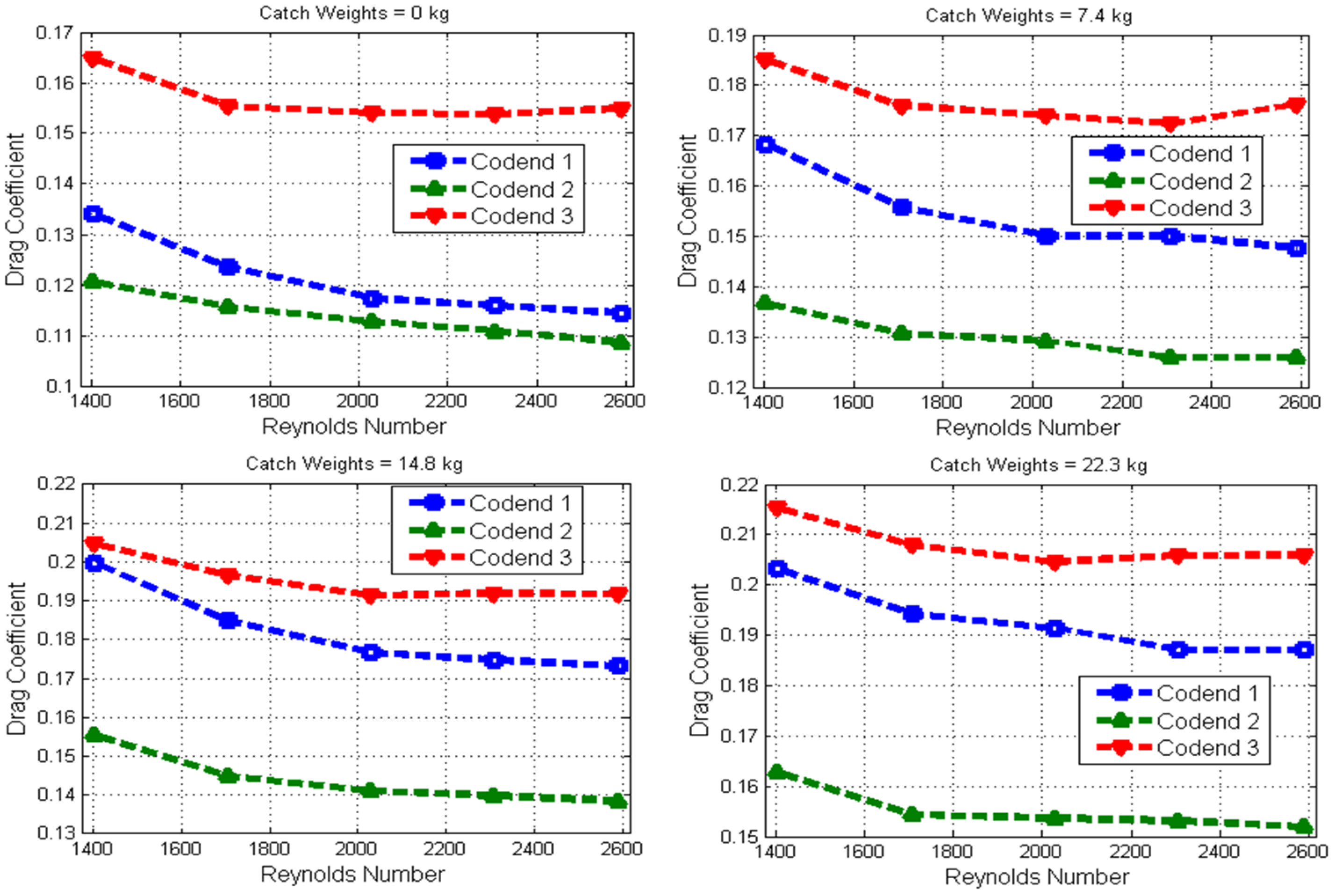
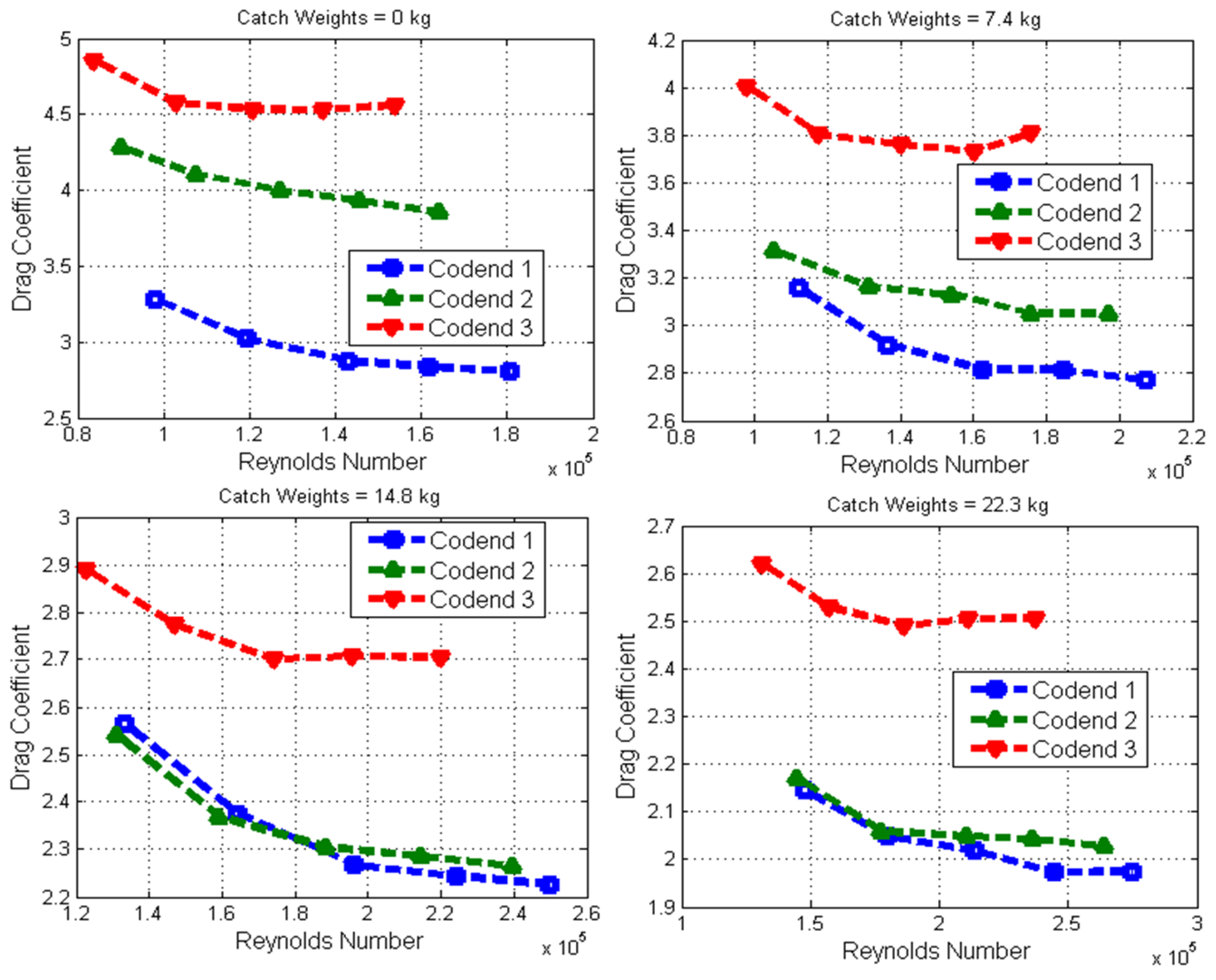
3.2. Analysis of the Mean Hydrodynamic Characteristics of Different Codends
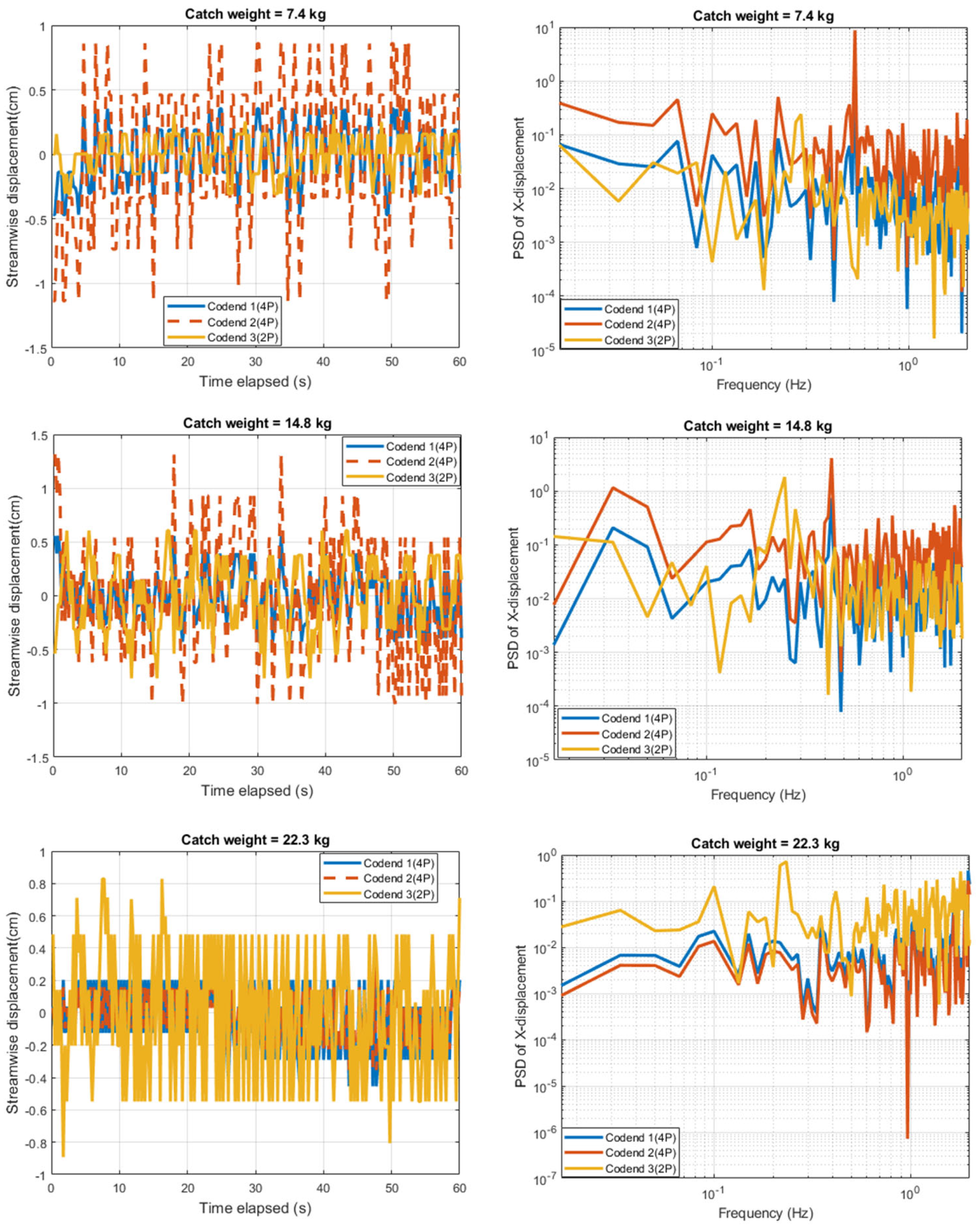
3.3. Analysis of the Fluttering Motions of the Different Codends
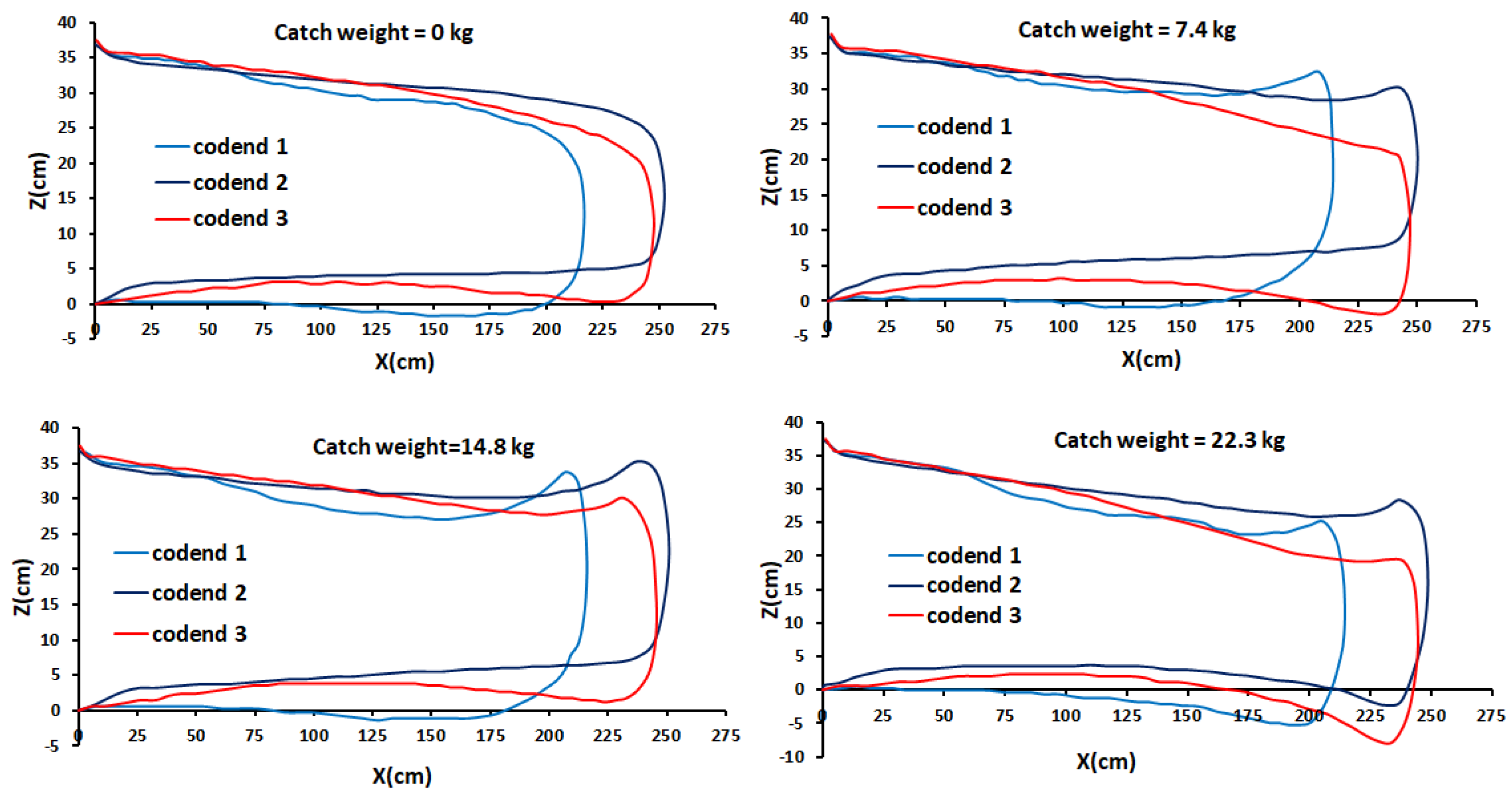
3.4. Analysis of the of Cross-Section of the Three Codends at Different Catch Weights
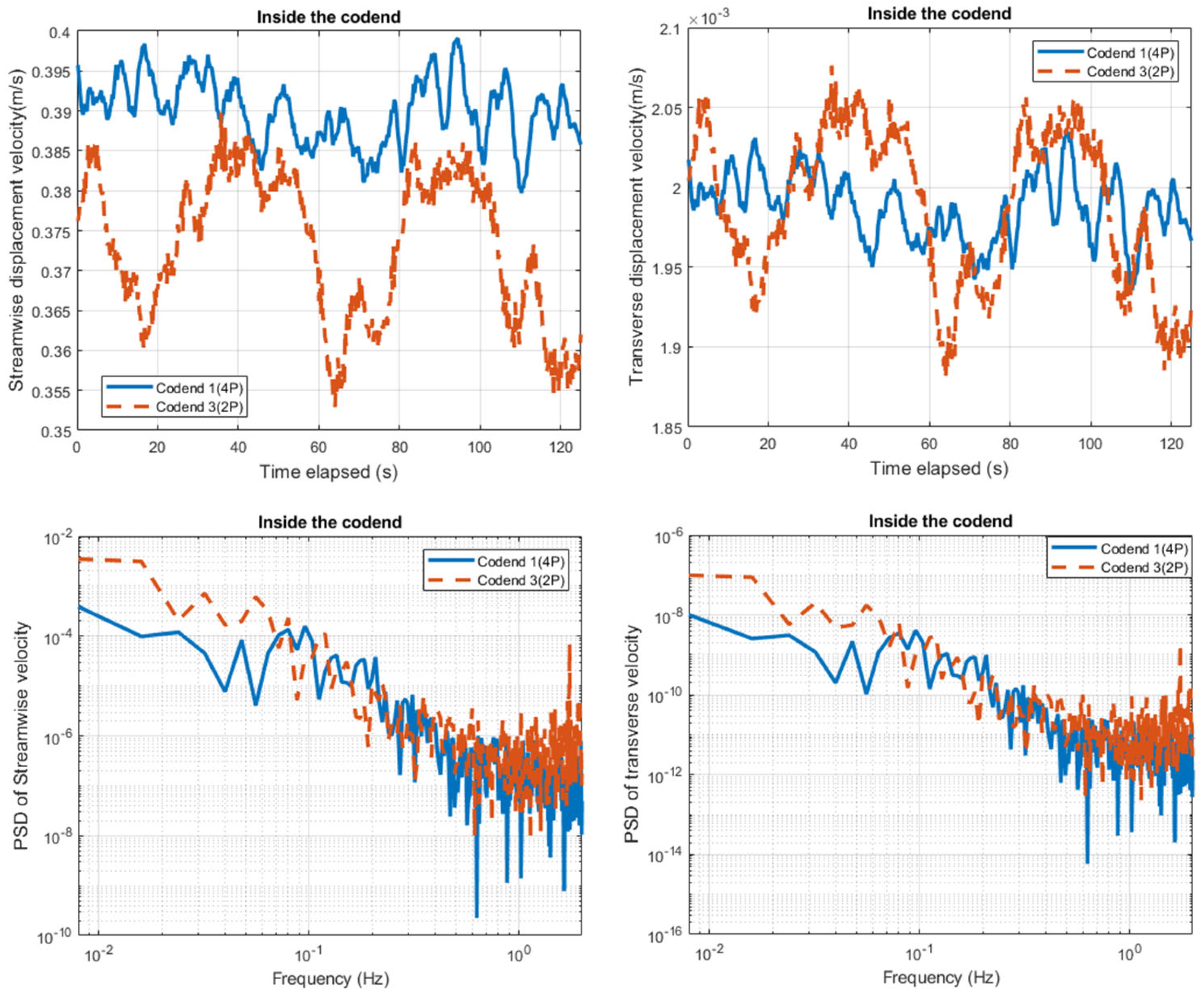
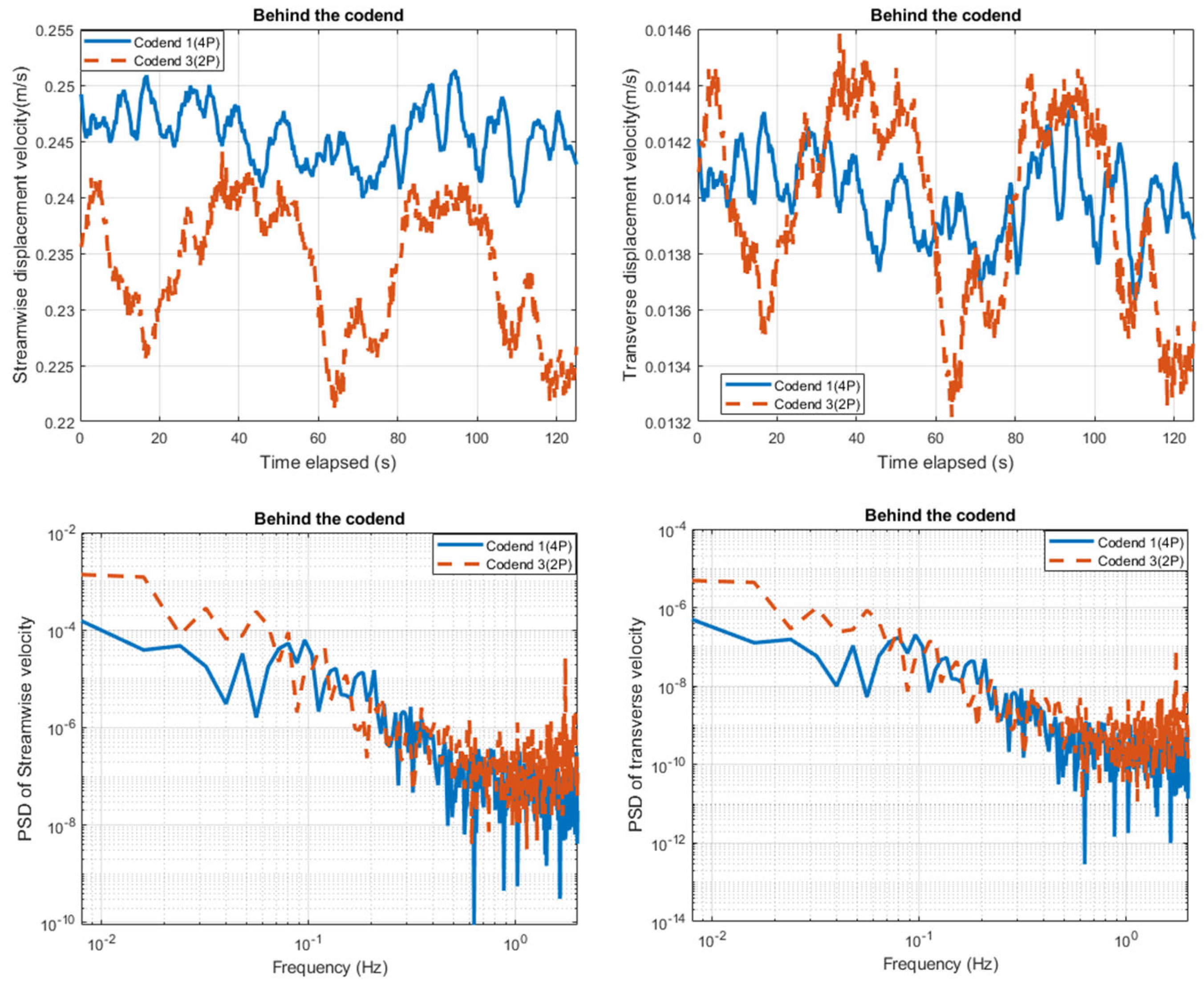
3.5. Analysis of the Effect of Gear Design on the Unsteady Turbulent Flow Organization Inside and behind the Codend
4. Discussion
5. Conclusions
- (1)
- The drag forces, codend motions, codend deformation, and Reynolds number increased as the catch weight, number of netting panels, and flow velocity increased, while the drag coefficient decreased as the catch weight and number of netting panels increased.
- (2)
- The circumference of the catch regions of the 2P codend was significantly smaller than that of the 4p codends. As a consequence, this codend had lower drag but it is less selective and can impact the catch quality than the 4p codends.
- (3)
- The analysis of temporal flow velocities presents an oscillation of quasi-periodic nature and clearly showed that inside and behind the 4P and 2P codends, the flow velocity field recovered between 0.48–0.79 and 0.45–0.75 , respectively. In addition, the analysis of TKE has underlined that the TKE is mainly produced inside the codend (about 60% greater) compared to those obtained behind the codend, and this turbulent kinetic energy is greater inside and behind the 2P codend compare to that obtained on 4P codend. Thus, the distribution of the turbulent fluctuation inside and behind the 2P codend was more important.
- (4)
- The spectra content obtained on the motions of the 2P codend exhibited a dominant low frequency component compared to those obtained on the motions of the 4p codends. Moreover, it was found that the vortex frequency of the 2P codend structure are greater than that of the 4P codend structure. Therefore, the gear design and catch weight greatly influenced the codend behavior.
- (5)
- These basic results from the measurements of flow field, drag forces, and fluttering motions could help with understanding the complex fluid-structure interactions that induce large deformation and oscillation of the codend which modifies the drag force instantaneously, the mouth opening, and herding response or escape behavior of fish due to the towing velocity. In this case, it can be concluded that 2p codend has very good performance in terms of drag force, but considering the improvement in fish behavior and selectivity we recommend the codend 2 (4p codend).
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sterling, D.; Balash, C. Engineering and catching performance of five netting materials in commercial prawn-trawl systems. Fish. Res. 2017, 193, 223–231. [Google Scholar] [CrossRef]
- Tang, H.; Hu, F.; Xu, L.; Dong, S.; Zhou, C.; Wang, X. Variations in hydrodynamic characteristics of net panels with various twine materials, knot types, and weave patterns at small attack angles. Sci. Rep. 2019, 9, 1923. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Nsangue, B.T.N.; Pandong, A.N.; He, P.; Liuxiong, X.; Hu, F. Flume Tank Evaluation on the Effect of Liners on the Physical Performance of the Antarctic Krill Trawl. Front. Mar. Sci. 2022, 8, 2144. [Google Scholar] [CrossRef]
- Jung, J.-M.; Matsushita, Y.; Kim, S. Study on Reducing Towing Drag by Varying the Shape and Arrangement of Floats and Gears. Appl. Sci. 2022, 12, 7606. [Google Scholar] [CrossRef]
- Priour, D. Modelling axisymmetric codends made of hexagonal mesh types. Ocean Eng. 2014, 92, 1–11. [Google Scholar] [CrossRef]
- Liu, W.; Tang, H.; You, X.; Dong, S.; Xu, L.; Hu, F. Effect of Cutting Ratio and Catch on Drag Characteristics and Fluttering Motions of Midwater Trawl Codend. J. Mar. Sci. Eng. 2021, 9, 256. [Google Scholar] [CrossRef]
- Thierry, N.N.B.; Tang, H.; Liuxiong, X.; You, X.; Hu, F.; Achile, N.P.; Kindong, R. Hydrodynamic performance of bottom trawls with different materials, mesh sizes, and twine thicknesses. Fish. Res. 2019, 221, 105403. [Google Scholar] [CrossRef]
- Thierry, N.N.B.; Tang, H.; Achile, N.P.; Xu, L.; Hu, F.; You, X. Comparative study on the full-scale prediction performance of four trawl nets used in the coastal bottom trawl fishery by flume tank experimental investigation. Appl. Ocean Res. 2019, 95, 102022. [Google Scholar] [CrossRef]
- Nsangue, B.T.N.; Tang, H.; Pandong, A.N.; Xu, L.; Adekunle, D.M.; Hu, F. Examining engineering performance of midwater trawl with different horizontal spread ratio, floatage, and weight parameters: A case study of model net for Antarctic krill fisheries. Int. J. Nav. Arch. Ocean Eng. 2022, 14, 100448. [Google Scholar] [CrossRef]
- O′Neill, F.; Knudsen, L.; Wileman, D.; McKay, S. Cod-end drag as a function of catch size and towing speed. Fish. Res. 2004, 72, 163–171. [Google Scholar] [CrossRef]
- Brinkhof, J.; Herrmann, B.; Sistiaga, M.; Larsen, R.B.; Jacques, N.; Gjøsund, S.H. Effect of gear design on catch damage on cod (Gadus morhua) in the Barents Sea demersal trawl fishery. Food Control. 2020, 120, 107562. [Google Scholar] [CrossRef]
- Nsangue, B.T.N.; Tang, H.; Xu, L.; Hu, F.; Dong, S.; Achille, N.P.; Zou, B. Comparison between physical model testing and numerical simulation using two-way fluid-structure interaction approach of new trawl design for coastal bottom trawl net. Ocean Eng. 2021, 233, 109112. [Google Scholar] [CrossRef]
- Thierry, N.N.B.; Tang, H.; Xu, L.-X.; Hu, F.; You, X.; David, M.A.; Achille, N.P. Identifying the turbulent flow developing inside and around the bottom trawl by Electromagnetic Current Velocity Meter approach in the flume tank. J. Hydrodyn. 2021, 33, 636–656. [Google Scholar] [CrossRef]
- Bouhoubeiny, E.; Germain, G.; Druault, P. Time-resolved PIV investigations of the flow field around rigid cod-end net structure. Fish Res. 2011, 108, 344–355. [Google Scholar]
- Druault, P.; Germain, G. Analysis of hydrodynamics of a moving trawl codend and its fluttering motions in flume tank. Eur. J. Mech. B/Fluids 2016, 60, 219–229. [Google Scholar] [CrossRef]
- Kim, Y.-H. Analysis of the turbulent flow and tilt in the cod-end of a bottom trawl during fishing operations. Ocean Eng. 2013, 64, 100–108. [Google Scholar] [CrossRef]
- Madsen, N.; Hansen, K.; Madsen, N.A.H. Behavior of different trawl codend concepts. Ocean Eng. 2015, 108, 571–577. [Google Scholar] [CrossRef]
- Priour, D.; La Prada, D. An experimental/numerical study of the catch weight influence on trawl behavior. Ocean Eng. 2015, 94, 94–102. [Google Scholar] [CrossRef]
- Larsen, R.B.; Herrmann, B.; Sistiaga, M.; Brinkhof, J.; Tatone, I.; Langård, L. New approach for modelling size selectivity in shrimp trawl fisheries. ICES J. Mar. Sci. 2017, 75, 351–360. [Google Scholar] [CrossRef]
- Thierry, B.N.N.; Tang, H.; Achile, N.P.; Xu, L.; Zhou, C.; Hu, F. Experimental and Numerical Investigations of the Hydrodynamic Characteristics, Twine Deformation, and Flow Field Around the Netting Structure Composed of Two Types of Twine Materials for Midwater Trawls. J. Ocean Univ. China 2021, 20, 1215–1235. [Google Scholar] [CrossRef]
- Wilson, G.J. Australian polymer banknote: A review, Optical Security and Counterfeit Deterrence Techniques II. Proc. SPIE 1998, 3314, 2–7. [Google Scholar] [CrossRef]
- O′Neill, F.; McKay, S.; Ward, J.; Strickland, A.; Kynoch, R.; Zuur, A. An investigation of the relationship between sea state induced vessel motion and cod-end selection. Fish. Res. 2002, 60, 107–130. [Google Scholar] [CrossRef]
- Kim, Y.-H. Analysis of turbulence and tilt by in-situ measurements inside the cod-end of a shrimp beam trawl. Ocean Eng. 2012, 53, 6–15. [Google Scholar] [CrossRef]
- Cheng, Z.; Winger, P.D.; Bayse, S.M.; Kelly, D. Hydrodynamic Performance of Full-Scale T0 and T90 Codends with and without a Codend Cover. J. Mar. Sci. Eng. 2022, 10, 440. [Google Scholar] [CrossRef]
- Nguyen, V.Y.; Bayse, S.M.; Cheng, Z.; Winger, P.D.; DeLouche, H.; Kebede, G.E.; Legge, G. Developing a full-scale shaking codend to reduce the capture of small fish. PLoS ONE 2023, 18, e0280751. [Google Scholar] [CrossRef]
- Hu, F.; Tadashi, T.; Seiichi, T.; Daisuke, S.; Hiroshi, I.; Yasuhisa, H. The Performance of the New Circulating Water Channel of Tokyo University of Marine Science and Technology. Jpn. Soc. Fish. Eng. 2004, 41, 153–163. (In Japanese) [Google Scholar]
- Thierry, N.N.B.; Tang, H.; Achille, N.P.; Xu, L.; Hu, F. Unsteady turbulent flow developing inside and around different parts of fluttering trawl net in flume tank. J. Fluids Struct. 2021, 108, 103451. [Google Scholar] [CrossRef]
- Gupta, H.R.; Mehra, R. Power spectrum estimation using Welch method for various window techniques. Int. J. Sci. Res. Eng. Technol. 2013, 2, 389–392. [Google Scholar]
- Jwo, D.-J.; Chang, W.-Y.; Wu, I.-H. Windowing Techniques, the Welch Method for Improvement of Power Spectrum Estimation. Comput. Mater. Contin. 2021, 67, 3983–4003. [Google Scholar] [CrossRef]
- Tummers, M.J.; Passchier, D.M. Spectral estimation using a variable window and the slotting technique with local normalization. Meas. Sci. Technol. 1996, 7, 1541–1546. [Google Scholar] [CrossRef]
- Johnsson, R.C.F.; Zijerveld, J.C.; Schouten, C.M.; van den Bleek, B. Leckner Characterization of fluidization regime by time-series analysis of pressure fluctuations. Int. J. Multiph. Flow 2000, 26, 663–715. [Google Scholar] [CrossRef]
- Tropea, C.; Nobach, H.; Ramond, A.; Reulet, P. Turbulent Velocity Spectra from Laser Doppler Data. In Proceedings of the 3rd ONERA-DLR Aerospace Symposium, Paris, France, 20–22 June 2001. [Google Scholar]
- Abbasi, M.; Sotudeh-Gharebagh, R.; Mostoufi, N.; Mahjoob, M.J. Non-intrusive monitoring of bubbles in a gas–solid fluidized bed using vibration signature analysis. Power Technol. 2009, 196, 278–285. [Google Scholar] [CrossRef]
- Zakaria, R.; Ruyet, D.L. Theoretical Analysis of the Power Spectral Density for FFT-FBMC Signals. IEEE Commun. Lett. 2016, 20, 1748–1751. [Google Scholar] [CrossRef]
- McCulloch, C.E. An introduction to generalized linear mixed models. Conf. Appl. Stat. Agric. 1996. [Google Scholar] [CrossRef]
- Jones, E.G.; Summerbell, K.; O′Neill, F. The influence of towing speed and fish density on the behaviour of haddock in a trawl cod-end. Fish. Res. 2008, 94, 166–174. [Google Scholar] [CrossRef]
- O′Neill, F.G.; O′Donoghue, T. The fluid dynamic loading on catch and the geometry of trawl cod–ends. Proc. R. Soc. A Math. Phys. Eng. Sci. 1997, 453, 1631–1648. [Google Scholar] [CrossRef]
- Priour, D. Numerical optimization of trawls design to improve their energy efficiency. Fish. Res. 2009, 98, 40–50. [Google Scholar] [CrossRef]
- Nepali, R.; Ping, H.; Han, Z.; Zhou, D.; Yang, H.; Tu, J.; Zhao, Y.; Bao, Y. Two-degree-of-freedom vortex-induced vibrations of two square cylinders in tandem arrangement at low Reynolds numbers. J. Fluids Struct. 2020, 97, 102991. [Google Scholar] [CrossRef]
- Druault, P.; Germain, G.; Facq, J.-V. PIV measurements combined with the motion tracking technique to analyze flow around a moving porous structure. J. Fluids Struct. 2015, 56, 190–204. [Google Scholar] [CrossRef]
- Pichot, G.; Germain, G.; Priour, D. On the experimental study of the flow around a fishing net. Eur. J. Mech. B/Fluids 2009, 28, 103–116. [Google Scholar] [CrossRef]
- Krag, L.A.; Herrmann, B.; Iversen, S.A.; Engås, A.; Nordrum, S.; Krafft, B.A. Size Selection of Antarctic Krill (Euphausia su-perba) in Trawls. PLoS ONE 2014, 9, e102168. [Google Scholar] [CrossRef] [PubMed]
- Juáres, M.A.; Casaux, R.; Corbalán, A.; Blanco, G.; Pereira, G.A.; Perchivale, P.J.; Coria, N.R.; Santos, M.M. Diet of Adélie penguins (Pygoscelis adeliae) at Stranger Point (25 de Mayo/King George Island, Antarctica) over a 13-year period (2003–2015). Polar Biol. 2018, 41, 303–311. [Google Scholar] [CrossRef]
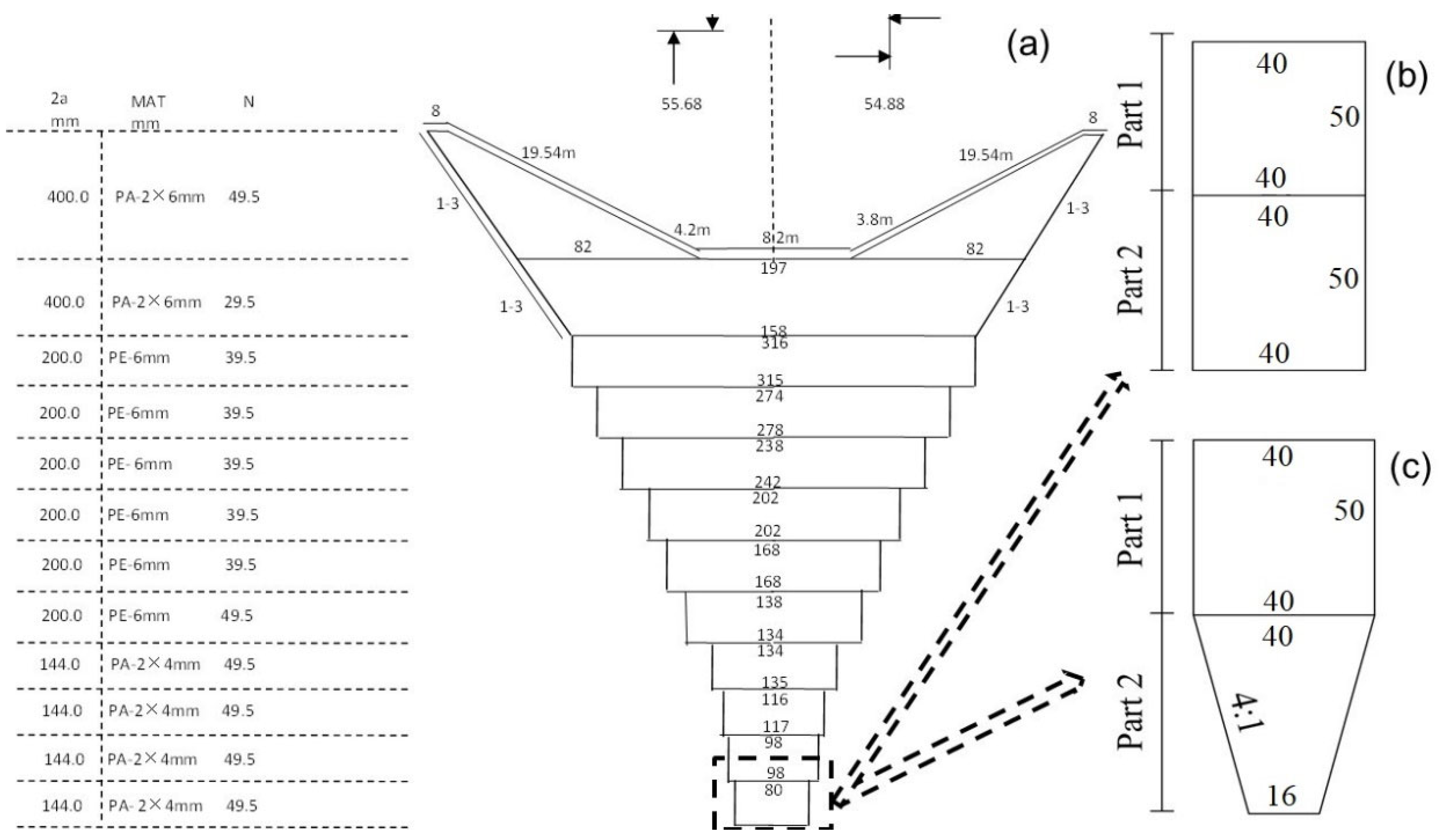


| Codend | Twine Materials | Mesh Size (mm) | Twine Diameter (mm) | Cutting Ratio | Cutting Sequence (Subscripts Represent Cycle Index) | |
|---|---|---|---|---|---|---|
| Part 1 | PA | 30 | 3 | No cutting ratio | [N]22 | |
| Part 2 | Codend 1 | PA | 30 | 3 | No cutting ratio | [N]25 |
| Codend 2 | PA | 30 | 3 | 4:1 | N [NBNBN]16 | |
| Codend 3 | PA | 30 | 3 | No cutting ratio | [N]25 | |
| Codend | Diameter (m) | ||||
|---|---|---|---|---|---|
| 0 kg | 7.4 kg | 14.8 kg | 22.3 kg | ||
| Codend 1 | 28,800 | 0.21 | 0.24 | 0.29 | 0.32 |
| Codend 2 | 24,480 | 0.19 | 0.23 | 0.28 | 0.31 |
| Codend 3 | 14,400 | 0.18 | 0.21 | 0.26 | 0.28 |
| Codends | Catch Weights | ||||
|---|---|---|---|---|---|
| Codend 1 | 0 kg | 26.41 10.59 | 2.96 0.196 | 0.12 0.0081 | 140,467.92 32,882.28 |
| 7.4 kg | 33.88 14.02 | 2.86 0.156 | 0.15 0.0083 | 160,607.39 37,654.54 | |
| 14.8 kg | 39.64 16.45 | 2.33 0.141 | 0.18 0.011 | 193,508.74 46,289.02 | |
| 22.3 kg | 41.70 17.94 | 2.03 0.071 | 0.2 0.0066 | 211,988.54 50,384.62 | |
| Codend 2 | 0 kg | 29.53 12.17 | 4.04 0.16 | 0.11 0.0047 | 126,906.05 29,338.69 |
| 7.4 kg | 33.47 14.20 | 3.14 0.11 | 0.13 0.0044 | 152,805.04 36,011.46 | |
| 14.8 kg | 37.24 15.31 | 2.35 0.12 | 0.14 0.0068 | 186,676.91 43,151.27 | |
| 22.3 kg | 40.34 16.84 | 2.07 0.57 | 0.15 0.0043 | 206,588.87 47,033.56 | |
| Codend 3 | 0 kg | 30.23 12.92 | 4.61 0.13 | 0.156 0.0047 | 119,711.53 27,563.24 |
| 7.4 kg | 33.23 14.20 | 3.81 0.11 | 0.176 0.0049 | 138,395.59 31,510.67 | |
| 14.8 kg | 37.11 15.32 | 2.75 0.81 | 0.195 0.0057 | 171,871.21 38,497.62 | |
| 22.3 kg | 39.53 16.97 | 2.52 0.53 | 0.207 0.0043 | 184,693.12 42,263.68 |
| Codend | Inside | Behind | ||
|---|---|---|---|---|
| u | v | u | v | |
| 4P codend | 0.395 0.032 | 0.014 ± 0. 0016 | 0.241 0.089 | 0.002 0.0047 |
| 2P codend | 0.372 0.029 | 0.0139 ± 0.0044 | 0.234 0.094 | 0.0019 ± 0.0043 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nyatchouba Nsangue, B.T.; Tang, H.; Zhang, J.; Liu, W.; Xu, L.; Hu, F. Experimental Analysis of the Influence of Gear Design and Catch Weight on the Fluid–Structure Interaction of a Flexible Codend Structure Used in Trawl Fisheries. Appl. Sci. 2023, 13, 2505. https://doi.org/10.3390/app13042505
Nyatchouba Nsangue BT, Tang H, Zhang J, Liu W, Xu L, Hu F. Experimental Analysis of the Influence of Gear Design and Catch Weight on the Fluid–Structure Interaction of a Flexible Codend Structure Used in Trawl Fisheries. Applied Sciences. 2023; 13(4):2505. https://doi.org/10.3390/app13042505
Chicago/Turabian StyleNyatchouba Nsangue, Bruno Thierry, Hao Tang, Jian Zhang, Wei Liu, Liuxiong Xu, and Fuxiang Hu. 2023. "Experimental Analysis of the Influence of Gear Design and Catch Weight on the Fluid–Structure Interaction of a Flexible Codend Structure Used in Trawl Fisheries" Applied Sciences 13, no. 4: 2505. https://doi.org/10.3390/app13042505
APA StyleNyatchouba Nsangue, B. T., Tang, H., Zhang, J., Liu, W., Xu, L., & Hu, F. (2023). Experimental Analysis of the Influence of Gear Design and Catch Weight on the Fluid–Structure Interaction of a Flexible Codend Structure Used in Trawl Fisheries. Applied Sciences, 13(4), 2505. https://doi.org/10.3390/app13042505







