Abstract
Scientific workflows consist of numerous tasks subject to constraints on data dependency. Effective workflow scheduling is perpetually necessary to efficiently utilize the provided resources to minimize workflow execution cost and time (makespan). Accordingly, cloud computing has emerged as a promising platform for scheduling scientific workflows. In this paper, level- and hierarchy-based scheduling approaches were proposed to address the problem of scheduling scientific workflow in the cloud. In the level-based approach, tasks are partitioned into a set of isolated groups in which available virtual machines (VMs) compete to execute the groups’ tasks. Accordingly, based on a utility function, a task will be assigned to the VM that will achieve the highest utility by executing this task. The hierarchy-based approach employs a look-ahead approach, in which the partitioning of the workflow tasks is performed by considering the entire structure of the workflow, whereby the objective is to reduce the data dependency between the obtained groups. Additionally, in the hierarchy-based approach, a fair-share strategy is employed to determine the share (number of VMs) that will be assigned to each group of tasks. Dividing the available VMs based on the computational requirements of the task groups provides the hierarchy-based approach the advantage of further utilizing the VMs usage. The results show that, on average, both approaches improve the execution time and cost by 27% compared to the benchmarked algorithms.
1. Introduction
Workflow has become a frequently used model for large-scale scientific computing and data-intensive applications operating on infrastructure-as-a-service (IaaS) platforms. A workflow involves hundreds or even thousands of tasks subject to data dependency constraints. Typically, workflow scheduling encounters decreasing cost or execution duration (makespan) issues. Cloud computing has developed as an encouraging computing paradigm that presents elastic, scalable, and highly available resources. In cloud computing, virtualization is an important factor that cost-effectively divides physical machines into virtual machines (VMs) [1]. Organizations and companies that use cloud computing can initiate operations without investing time and money into infrastructure. Accordingly, cloud service customers can be charged based on their consumption of the VMs. Such characteristics (e.g., cost-effectiveness and fee flexibility) underline the premise of cloud computing as a promising workflow execution platform [2].
Workflow task execution involves high communication and computation costs, specifically in scientific workflow domains (e.g., biology and astronomy, see Figure 1). The challenge in workflow scheduling [3] is to determine the workflow task execution order and the optimal mapping of tasks to VMs to achieve the scheduling objective. Typically, workflow scheduling involves minimizing the execution time or cost where these objectives conflict in practice. Given its combinatorial characteristic, this scheduling problem is by nature NP-Complete, which has inspired researchers to suggest near-optimal solutions [4]. Accordingly, to address the problem, several studies have investigated the use of nature-inspired optimization methods [5], such as particle swarm optimization (PSO) and simulated annealing (SA). Additionally, other studies [5,6,7,8] have investigated the use of heuristic approaches to schedule workflows. In Refs. [9,10,11,12,13], the authors have investigated building scheduling solutions by employing greed-based mechanisms that schedule the tasks to reduce their execution time. Others [6,8,14,15] have built their solution by considering the entire structure of the workflow, whereas the main distinguisher between these proposals is in the employed strategy that utilizes the extracted structure-related feature. The structure-related information is typically used to establish semi-balanced task groups (partitions) in terms of computational requirements. Unlike the previous studies [6,8,14,15], in this work, the structure-related information is used to establish a lookahead workflow partitioning strategy, which results in minimizing the dependency between the obtained groups of tasks. Additionally, the employed fair share division strategy aims to determine each group’s share of VMs based on the overall computational requirements for the group’s tasks.
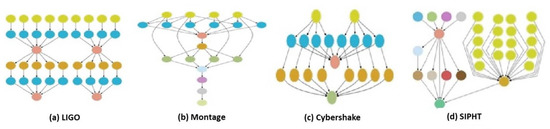
Figure 1.
Examples of scientific workflows [16].
Workflows have different structures, in which inside the same workflow, the number of tasks and data dependency constraints frequently change between the levels of the workflow. Workflow structures capture the dependency constraints that eventually impact the quality of the obtained schedule. To further clarify the relationship between the workflow structure and the expected schedule efficiency, consider the workflow depicted in Figure 2. In this example, the levels of the workflow are separated by dashed lines, and the entry-level tasks are 1, 2, 3, and 4. A task can start its execution once all the required data are received from its parents, among whom the last parent to finish its execution is termed the most influential parent (MIP). For example, task 6 cannot start its execution before tasks 2 and 3 finish their execution and transfer the required data to task 6. From the figure, we can see that before starting the execution of the workflow, the overall structure of the workflow should be analyzed. In this example, regardless of the number of VMs assigned to execute the entry-level tasks (first level), at most three VMs can be used to execute the second-level tasks. Additionally, it is evidence that the subtree rooted at task 14 is more computationally intensive compared to the subtree rooted at task 13. Accordingly, more VMs should be assigned to execute the task 14 subtree compared to the task 13 subtree. Overall, from a scheduling perspective, the structure information captures the important aspects that a solution must consider to obtain an efficient solution.
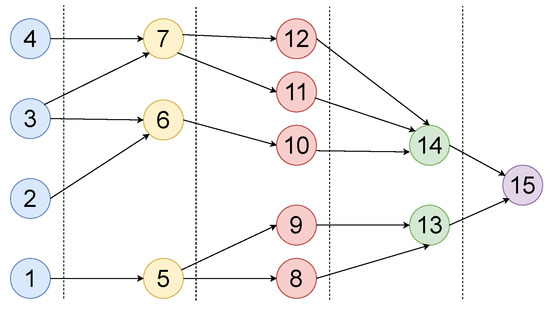
Figure 2.
Structure-aware example.
In this paper, by utilizing the structure-related information, we propose a structure-aware fair-share scheduling approach that aims to achieve a balanced solution by minimizing cost and execution time. This paper extends the authors’ previous work [17] by proposing a complementary structure-aware scheduling approach. The contributions of this paper can be summarized as follows:
- We refine the level-based approach (LBA) introduced in Ref. [17] by adding further analysis and discussion. The LBA treats the available VMs as isolated agents that will benefit from executing tasks. Accordingly, tasks are assigned to VMs based on a utility function value, in which such an assignment aims to maximize the overall obtained utility value;
- We propose the hierarchy-based approach (HBA) that uses a look-ahead mechanism in which the task scheduling considers the entire workflow structure. In HBA, tasks are divided into groups in a top-down manner that aims to reduce dependency across groups. Thus, tasks with data dependency constraints are expected to belong to the same group. Once the groups are identified, the VMs are divided between the groups using a fair-share mechanism. Such a mechanism uses the information available about the group tasks to determine the VMs share of each group. Similar to level-based scheduling, tasks are mapped to VMs, using a utility-based mechanism to optimize the available VMs usage;
- We have conducted several sets of experiments to evaluate the performance of the presented approach. Compared to the benchmark algorithms, the results demonstrated that the LBA and HBA algorithms improved the execution time and cost on average 25% and 30%, respectively. Additionally, the results have shown that the performance of the HBA is impacted by the number of available VMs. The performance of this approach is improved when the number of available VMs is sufficient to utilize the advantages of the fair-share division strategy.
The rest of this paper is organized as follows. In Section 2, we discuss the most related literature. The system model and the problem formulation are presented in Section 3. Section 4 presents and discusses the level- and hierarchy-based scheduling approaches. Section 5 presents the settings and results of the experiments. The paper is concluded in Section 6.
2. Related Work
Several studies have investigated the problem of scheduling scientific workflows on the cloud. Tang et al. [18] formulated the scheduling issue as a mixed integer linear program (MILP) in which several scheduling strategies were discussed to minimize the schedule length. Al-Khanak et al. [19] reported a statistical analysis of single-, hybrid-, and hyper-based heuristic approaches. The authors’ analysis demonstrated that hybrid- and hyper-based heuristics were expected to achieve better results compared to the single-based heuristic.
Topcuoglu et al. [10] suggested the HEFT algorithm to minimize the execution time. The HEFT algorithm first ranks tasks based on their workflow locality and computational requirements. Subsequently, each task is scheduled based on the VM that minimizes the overall makespan. Sandokji et al. [20] extended the HEFT algorithm by proposing an additional dynamic step to reallocate the scheduled tasks, based on new dynamic scheduling requirements. Both Calheiros et al. [12] and Yu et al. [13] attempted to decrease the execution time while adhering to budget constraints. Yu et al. [13] proposed a rescheduling approach to ensure fairness and load balancing in task distribution between VMs, which considers the workflow execution deadline. While the proposed method utilized VMs, dynamic resource leasing or releasing available in a hybrid cloud was not considered. Calheiros et al. [12] proposed a dynamic resource management system that aids the addressing of unforeseen demands by off-loading a portion of the workload to public cloud computing resources. Arabnejad et al. [21] proposed a scheduler designed for random environments, in which tasks could be received at any time.
Wu et al. [22] suggested a greed-based approach to reduce execution time while adhering to budget constraints, which used the budget-level concept to determine task execution order in a homogeneous cloud environment. Chen et al. [23] extended the proposed greed-based approach [22] by involving the heterogeneous cloud computing environment. Ali et al. [24] proposed a grouping-based algorithm to decrease the execution time, in which tasks are divided into categories or classes based on their characteristics (user type and task type, size, and latency). Subsequently, the scheduling process determines each task class and the execution order in each.
Charrada et al. [25] proposed a hybrid approach that mainly establishes the execution environment (private or public) according to the execution cost. In this method, provided the privacy-related constraints are not assumed, every task can be performed on the public cloud. Bossche et al. [26] also suggested a hybrid approach to decrease the execution cost. Both data transfer and computational costs are considered to determine the potential cost of public or private clouds and select the cost-efficient cloud while meeting task deadlines.
In Refs. [6,8], the authors focus on minimizing both execution time and cost. In Ref. [6], a partitioning-based algorithm that utilizes a slack parameter (B) was proposed to determine the priority of each objective with a value of either 0 or 1. The proposed algorithm prioritizes minimizing the execution time when B = 0 while prioritizing execution cost when B = 1. The proposed algorithm sequentially partitions workflow tasks beginning with entry-level tasks. The number of VMs assigned per partition is determined according to the B value, which ensures that each task is implemented at its earliest starting time (EST). In this line, the RDAS algorithm [8] apportions VMs using a fair allocation approach between workflow tasks to decrease the makespan and efficiently uses VMs to reduce the total execution cost.
Arabnejad et al. [27] proposed a deadline-aware workflow scheduling strategy that involves planning deadline-constrained scientific workflows on dynamically provisioned cloud resources while reducing the execution cost. The authors suggested two algorithms: Deadline Constrained Critical Path (DCCP) and Proportional Deadline Constrained (PDC). The two algorithms resolve workflow scheduling on a dynamically provisioned cloud resource to identify the suitable VMs according to the proportional deadline constraints of the tasks to achieve the minimum cost with a good response time. The problem studied in this work was similar to the bi-objective scheduling issue discussed in Refs. [5,7], in which a data-locality-aware scheduling algorithm was proposed. The proposed solution considered workload privacy, private cloud power use, and billing cycles of different public clouds. Costs were compared to identify the appropriate cloud environment to decrease the cloud bursting cost while pondering data privacy. Nonetheless, the private cloud component could not utilize the VMs to effectively implement tasks within their anticipated deadlines when the workload privacy percentage increased.
Several optimization techniques were proposed to address cloud scientific workflow scheduling. For example, a genetic-based scheduling algorithm was proposed [28] in which the authors improved the performance of the overall performance by reducing repetitions. Azzize et al. [29] also proposed a genetic-based approach to decrease the computational cost while accommodating deadline and budget constraints. A hybrid evolutionary algorithm (HEA) [4] was proposed for data assignment and task scheduling issues, which jointly processed such issues to enhance scientific workflow scheduling. Amandeep Verma et al. [30] suggested a multi-objective hybrid particle swarm optimization algorithm to resolve multi-objective workflow scheduling issues. The algorithm optimizes makespan and cost based on a non-dominance sorting procedure and presents the user with a set of Pareto optimal solutions from which the best solution can be selected. Efficient swarm-based Pareto techniques were investigated in Refs. [1,2].
Farid et al. [3] suggested a multi-objective scheduling algorithm with fuzzy resource utilization, which optimizes workflow scheduling by studying the data transmission order and the location of task execution (VM). The proposed method decreases execution cost and makespan while adhering to reliability constraints via particle swarm optimization. Zhu et al. [31] proposed an evolutionary multi-objective optimization-based algorithm for cloud workflow scheduling. The proposed method aims to reduce the workflow makespan and execution cost by producing schedules with different tradeoffs between makespan and execution cost to enable users to determine the schedule that satisfies their requirements.
In Ref. [32], the authors proposed a structure-aware scheduling approach that starts by determining the optimal number of required VMs to schedule the workflow tasks. Typically, due to cost limitations and VMs availability, hiring the optimal number of VMs is not expected to be guaranteed. Based on the available number of VMs (lower-bound), the proposed approach divides the workflow tasks into a set of groups using a level-based strategy. The number of tasks assigned to each group is bounded by the number of available VMs. Accordingly, a group might include tasks from several levels. Such a strategy is used to improve the efficiency of the obtained schedule. However, the efficiency of the proposed method is impacted by the number of used VMs and the complexity of the data dependency constraints.
Moreover, there are inherited relationships between the problem presented in this work and the problem of monitoring the service level in the business domain [33]. In such a domain, services are generally represented as a workflow, and an efficient schedule must be obtained to enforce the services level agreements. Accordingly, exploring the relationship between the two problems may lead to tuning the performance of the employed scheduling solution in a cloud computing context. Such an exploration can be performed by introducing a transformation process between the instances of the two problems.
Unlike the studies discussed in the literature, the proposed approach aims to reduce the dependency between the task’ groups by applying a look-ahead strategy. Such a strategy works in a top-down fashion in which tasks that have the same descendant are expected to be grouped together. Accordingly, based on the group’s computational demands, the available VMs are divided between the groups, using a fair share strategy to ensure the ease of workflow execution.
3. Model and Problem Formulation
This section presents the system model and the problem formulation used in this paper.
3.1. Scientific Workflows
A workflow can be represented as a Direct acyclic graph (DAG), , where V is a set of tasks, and E is a set of edges that represents the data dependency constraints between the tasks. Additionally, we are given a set of VMs to execute the workflows’ tasks . For each , the execution of this task must wait until receiving all of the required data from its parent tasks. The last parent task to transmit its data to is termed the most influential parent (MIP) for . A task starts its execution by using the initial data submitted with the workflow or the intermediate data that are received from the task’s parents. The time required to transmit data between any two tasks is referred to as the communication cost. In situations where the two tasks are executed on the same VM, the communication cost between these two tasks is considered zero.
3.2. Cost and Execution Time
In public clouds, the cost is mainly impacted by the billing cycle () for the rented VMs. Other factors, such as the allocated storage and the consumed bandwidth, also contribute toward this cost. However, this work focuses on the since it is the dominant factor in determining the overall cost. The for a (R is the available VMs) is not always expected to be fully utilized. For instance, if the allocated tasks for a are only using of the VM billing cycle, the reset of the billing cycle can be considered as an unutilized paid time period.
The actual finishing time () of a task on is defined as follows:
where represent the actual finishing time for the MIP for task and denote the execution time for task . d(, ) captures the execution delay. For instance, if the is at minute 15 and is busy executing other tasks until minute 17 m, executing on will be delayed by 2 m. The execution time for the entire workflow is denoted by the for the last task to be executed in the workflow.
3.3. Problem Statement
This work addresses the bi-objective problem of minimizing execution cost and time. Minimizing the execution cost implies reducing the total of the used . Such a reduction may increase the execution time. Accordingly, in this paper, to achieve the desired object, the proposed solutions aim to increase the utilization of the available VMs. By increasing the utilization of the VMs, the number of is expected to be reduced. Additionally, VMs utilization is expected to improve the execution time since VMs will be working in an efficient manner.
4. Algorithmic Solutions
The inter-task data dependency constraints influence the efficiency of the scheduling approach. The workflow structure imposes the data dependency; therefore, the scheduling strategy must consider the influence of the structure to decrease the effect of the data dependency constraints. To this end, the level- and hierarchy-based scheduling approaches are presented in this article. The level-based approach (LBA) minimizes the task execution time at each level to achieve its goal while the hierarchy-based approach (HBA) uses a look-ahead strategy that considers the entire workflow structure while constructing the execution schedule.
4.1. Level-Based Approach
In this approach, the tasks of each workflow level are considered an isolated group. Using this representation, the LBA applies a divide-and-conquer strategy to minimize the task execution time of each level. Accordingly, the approach begins at the first-level group by calculating the average execution of the task group under consideration and the expected finishing time for each task group. The execution and finishing times are subsequently used to determine the task execution schedule, in which tasks are assigned to VMs by calculating the task execution utility on each VM. The utility function is established to reduce the overall execution cost and time. Tasks are assigned to VMs that obtain the highest utility. The proposed LBA algorithm consists of level preparation and task assignment steps, which work recursively to establish the workflow execution schedule.
4.1.1. Level Preparation
The level preparation step (Algorithm 1) is used to calculate the scheduling-related parameters used in task assignments. The earliest starting time (EST) and the MIP for each task are determined once the tasks have been divided into groups. The task EST represents the best task run time. Subsequently, the total run time for the tasks of each group is determined and used to establish the execution upper bound for each VM. All values obtained in this step are used as input for the task assignment step.
| Algorithm 1: Level Preparation |
 |
4.1.2. Task Assignment
In task assignment, each is expected to profit from executing a task. Accordingly, each task is assigned to the VM that obtains the maximum profit (utility). The profit is formulated to contribute towards minimizing the execution cost and time. Task assignment begins by organizing the tasks according to their EST (Algorithm 2, line 2). Beginning with the task with the earliest EST, the VM that achieves the highest utility from executing the task is identified (lines 4–10). For , the execution utility of task is determined using the following equation:
where is the actual starting time (AST) of task on . The AST and EST are indirectly related to the obtained schedule efficiency. When the AST and EST values are equal, the ensuing schedule can be presumed to attain the best execution time results. Nevertheless, such a condition cannot be certain given the limited number of VMs available. Thus, a compromise is required to address both the execution time and the cost. Accordingly, the presented utility function aims to allocate a task to the VM, which reduces the gap between the EST and AST for the considered task. Nonetheless, a VM will not execute a task that will increase the VM run time to exceed the execution time upper bound, which is calculated by dividing the total running time of the group tasks by the total number of available VMs. Such constraints enable the establishment of an inter-VM load-balancing mechanism.
| Algorithm 2: Task Assignment |
 |
4.2. Hierarchy-Based Approach
The main idea of the hierarchy-based approach (HBA) is to consider the entire workflow structure. Accordingly, the approach uses a partitioning strategy to minimize the dependency between the obtained task groups. Once obtained, the available VMs are divided between the groups using a fair share mechanism. Similar to level-based scheduling, tasks are mapped to VMs using the utility-based mechanism discussed in Section 4.2.1 to optimize resource utilization. The HBA approach consists of (1) partitioning, (2) resource allocation, and (3) scheduling.
4.2.1. Partitioning
Through partitioning, the groups that do not depend on the tasks of other groups can begin their execution immediately. As between-group dependency cannot be eliminated, each obtained group in the partitioning step is assigned a dependency value. In this context, a group with dependency can be assigned to VMs once all groups with higher dependency values are mapped to the assigned VMs. Algorithm 3 illustrates the partitioning steps.
Beginning from entry-level tasks, a group is initialized to contain the first task (line 7). The group under consideration is expanded to include the descendant tasks of all tasks assigned to the group. Once a group cannot be expanded any further, the tasks assigned to that group are excluded from consideration in a subsequent step. Subsequently, the following group is initialized to contain the available entry-level tasks. The dependency value of each group () is assigned sequentially such that the first constructed group has the highest dependency (one). Once all groups have been constructed, group merging is triggered to examine the obtained groups. An obtained group that spans a single workflow level is merged with another. Merging is important as relatively small groups have small VMs shares, and merging is expected to improve scheduling efficiency. A group with dependency value n is merged with the latest previously constructed group (dependency value n-1). Partitioning results in a set of task groups in which each group is associated with a dependency value ().
| Algorithm 3: Partitioning |
 |
4.2.2. Resource Allocation
In resource allocation, the available VMs were distributed between task groups based on their computational requirements. Resource allocation (Algorithm 4) begins by calculating the weight of each group . The obtained weight represents the total run time of the group tasks compared to the total run time of the workflow tasks and is calculated as follows:
where is the total run time for group tasks and is the total run time for the workflow tasks. The obtained weights highlight the computational demand associated with each group. After the group weights are determined, the resource share of each group is calculated as follows:
where is the total number of available VMs. Based on the group weight, the obtained share values range , where is assigned as the group resource share when all workflow tasks are assigned to a single group. Accordingly, some group resource shares might be , and groups are expected to share VMs. To achieve resource sharing, the groups are sorted in ascending resource share order (Algorithm 4, line 1). Beginning with the first group, the resource share for the group under consideration is examined to establish the actual resource number assigned to this group. When a group has a resource share , the resource share is rounded to the nearest lowest integer (line 8). When a group has a resource share , all groups with resource shares are determined. Consequently, the cumulative resource share of all identified groups is calculated, such that these groups are considered a single group if the cumulative share . Otherwise, these groups are merged with the smallest group with a resource share . In situations in which a single group has a resource share of less than one, the group’s share will be rounded to one.
| Algorithm 4: Resource Allocation |
 |
4.2.3. Scheduling
In scheduling, tasks are allocated to VMs, and each task AST is determined. Algorithm 5 depicts the scheduling step. Scheduling begins with the group with the highest dependency value. Tasks are assigned to their group VMs iteratively such that the assignment begins from the entry-level tasks. Scheduling is performed to identify the VMs responsible for executing each task. The VM identification uses the same utility mechanism presented in the level-based approach. Nevertheless, the utility mechanism in this approach considers only the VMs assigned to the group during the assignment. In each iteration, the process begins by determining the for the task under consideration. When the and task under consideration are in the same group, the utility mechanism is executed to determine the VM responsible for executing the task. When two tasks are in different groups, the scheduling status is examined. Accordingly, if the is assigned to a VM, the utility mechanism is executed to schedule the task under consideration. Nonetheless, if the has not been assigned to a VM, the scheduling for the current group is paused until the has been assigned to a VM (line 12).
| Algorithm 5: Scheduling |
 |
4.3. Discussion and Limitation
To discuss the performance of the LBA and HBA, let us consider the example in Figure 3. In this discussion, we focus on the execution time (makespan), as the cost is also impacted by the number of available VMs. The running time for tasks , and 14 are assigned to be 250 s each, whereas the running time for the rest of the tasks is assigned to be 100 s each. Furthermore, we assume that the number of available VMs equals 4. In the LBA, the workflow is divided into five groups highlighted by the dashed lines, in which each group contains tasks from the same level (Figure 3b). Regarding the makespan, the number of available VMs equals the number of tasks in the widest established group, and thus the availability of the VMs will not influence this approach’s performance. The identity of the tasks assigned to each VM is shown in Table 1. Starting from the entry-level group, to maximize the overall utility, each task is assigned to a separate VM. Once group (i) tasks are assigned to MVs, the approach moves to assign the next group () tasks, in which the starting time for group () tasks depends on the latest finishing time for group (i) tasks. For example, in Figure 3b, group 2 starts their execution after 250 s, which is the execution time for task 1. In each level, the maximum execution time for a task is 250 s, and therefore, the total execution time for the workflow is . The introduced waiting time (idle time) before each group (level) task assignment is impacted by the number of available VMs. In situations where the number of available VMs is close to the number of tasks in the largest group, the introduced waiting time becomes noticeable as for each task, several tasks are expected to obtain the same utility. However, this is not expected to occur frequently as the number of available VMs is typically significantly smaller than the number of tasks to be scheduled.
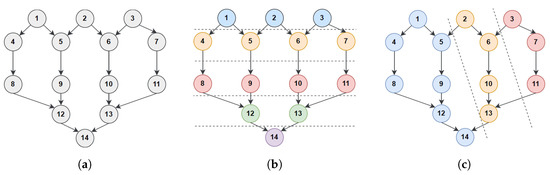
Figure 3.
Scheduling example. (a) Input DAG; (b) Level-based approach; (c) Hierarchy-based approach.

Table 1.
Tasks assignment.
The task groups obtained using the HBA are shown in Figure 3c. Once the groups are established, this approach calculates the weight and share of each group as shown in Table 2. In this example, as we can see from the table, two VMs will be allocated to group one and a single VM to the second group, where the third group will also be allocated a single VM. Accordingly, by using such a division strategy, the execution time for group one plays a dominant factor in determining the overall execution time. The execution of groups two and three is expected to occur without any noticeable dependency-related delay. Each group has a dependency value that represents the dependency of a group’s tasks on other groups’ data. Group one has the highest dependency value, whereas the second group has a higher dependency value compared to the third group. Such dependency is addressed by the employed sharing mechanism as groups expected to take longer to execute will be assigned more VMs (as shown in Table 2). In the presented example, based on the structure of the groups, each group is assigned enough VMs to ensure the execution of the tasks without any interruption. In this line, the total execution time for the workflow using the hierarchy-based scheduling is 1100 s, which is 150 s shorter than that obtained by the LBA.

Table 2.
Resource allocation (share calculation).
The efficiency of the HBA is influenced by the available number of VMs and the heterogeneity of the tasks’ execution times. To clarify this dependency, let us re-visit the example shown in Figure 3. In this example, if the number of available VMs is reduced to three, the LBA will obtain a better schedule, as the number of VMs is not enough to utilize the hierarchy-based scheduling strategy. In this line, a pre-processing step can be introduced to determine a lower bound on the number of required VMs by the hierarchical strategy. Such a lower bound can be calculated using the groups’ weights, and whether the available VMs is enough for an envy-free distribution of the VMs among the groups. The calculation of this lower bound is outside the scope of this paper since we aim to investigate the efficiency of the proposed approach without any imposed restriction on the number of available VMs. Additionally, in the presented example, if we assume that all tasks have the same execution time, both approaches will obtain the same execution time. Such an observation highlights the importance of considering the heterogeneity of the tasks’ execution times during the designing of the scheduling solution. In situations where the workflow has a balanced structure and tasks have relatively the same running time, the mechanism employed by the LBA is expected to perform efficiently. This efficiency is due to the fact that the computational and communication requirement of the workflow’s levels is relatively the same.
The proposed approaches do not consider the communication cost during the construction of the schedule. However, considering this cost is not expected to reduce the overall performance of the presented approaches. In the LBA, scheduling the workflow levels is performed in an isolated manner. The execution of a level’s tasks starts once all tasks in the previous level have finished their execution. Accordingly, the utility function employed by the LBA can be modified to incorporate the communication cost. Tasks with data dependency constraints can be executed on the same VM if such an execution will not result in increasing the total execution time. In the HBA, the mechanism works by reducing the data dependency between the constructed groups. Such a mechanism reduces the communication cost since tasks with data dependency constraints are more likely to be executed on the same VM. With respect to the probability of hardware failure, the HBA is expected to be highly impacted by this probability compared to the LBA. In the HBA, VMs are divided between the groups based on their calculated weight. Thus, in situations where some of the VMs become unavailable due to hardware failure, the expected share of VMs will not be satisfied for all the groups. Such a situation might degrade the performance of the HBA since groups that lost some of their assigned VMs might create a performance bottleneck. In the LBA, all available VMs will be used during the execution of any level tasks. Accordingly, the probability of hardware failure might reduce the number of available VMs to execute the tasks of any given level. However, the impact of such probability will be smaller compared to the HBA since, for each level, all of the VMs will be used.
5. Results
This section discusses in detail the settings and the results of the experiments used to evaluate the performance of the LBA and HBA. The input workflows for the presented experiments represent four real-world applications (LIGO, CyberShake, Montage, and SIPHT [16]). The size of each workflow is 1000 tasks, and each experiment shows the average for 10 different runs (10 workflows). Additionally, to execute the tasks, we have used two types of VMs, and . was designed to be two times faster than . The and charging rates were 10 and 20 cents per hour; respectively. In the presented experiments, we are interested in evaluating the performance of the proposed approaches in terms of cost and makespan. Cost and makespan are defined as follows:
- Makespan (m) is defined as the total execution time for the entire workflow tasks, and it is denoted by the for the last task to be executed (exit task ) ();
- Cost (c) is defined as the total charges for the used VMs, where an hourly rate is used as the billing cycle formulation (). The cost (c) is calculated as follows:
The performance of the proposed algorithms was validated against the RDAS [25], PBWS [18], and HEFT [3] algorithms. The HEFT algorithm uses a greedy mechanism that schedules tasks in a sequential fashion. Accordingly, for each task, the VM that results in reducing the AFT for this task will be selected. The RDAS algorithm partitions workflow tasks based on the structure of the workflow. Then, by employing a fair division strategy, the available VMs are fairly divided among the partitions with the objective of minimizing makespan and cost. In the PBWS algorithm, based on the pre-determined weight for each objective (makespan or cost), the algorithm works by determining the number of VMs and the execution schedule to achieve the desired objective. To ensure the fairness of the comparison, the PBWS was run first, and the number of used VMs by the PBWS was used as the input for the HBA, LBA, RDAS, and HEFT algorithms. Table 3 summarizes the results of the performed experiments.

Table 3.
Comparison of the experimental results.
LIGO: Figure 4 depicts the LIGO workflow results. The LIGO workflow structure is well-organized, which is expected to result in the use of similar VM numbers for each group execution. Both proposed algorithms significantly outperformed the benchmark algorithms regarding execution cost. Allocating tasks uniformly over the available VMs decreased the idle timeslot numbers and thus reduced the total cost of the schedules obtained by the HBA and LBA algorithms. Nevertheless, the proposed algorithms produced makespan values highly similar to those of the benchmarks. The LBA algorithm obtained slightly higher makespan values stemming from the bottleneck task in the LIGO structure, which limited the performance of this strategy for makespan. The HBA algorithm obtained acceptable makespan values that were relatively better than those of the PBWS and RDAS algorithms, which was due to the advantage of using the lookahead strategy.
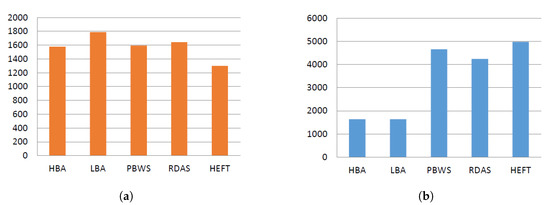
Figure 4.
LIGO workflow experiment results. (a) makespan ; (b) cost (¢).
CyberShake: Figure 5 depicts the CyberShake workflow results. The CyberShake workflow structure is extensive with numerous tasks at every level. The two proposed algorithms significantly outperformed the HEFT and RDAS algorithms regarding makespan and cost. The grouping and fair share strategies used in the LBA and HBA algorithms increased the utilization of the available VMs by identifying the necessary number of VMs needed to execute each group. The PBWS algorithm achieved a relatively close performance as compared to the HBA algorithm for cost, which was due to the grouping strategy used by both algorithms. The LBA algorithm achieved better makespan results as compared to the RDAS and HEFT algorithms, whereas the HBA approach outperformed all other algorithms. The HBA behavior was mainly due to the parallel executions of groups, which conferred a significant advantage on the HBA algorithm.
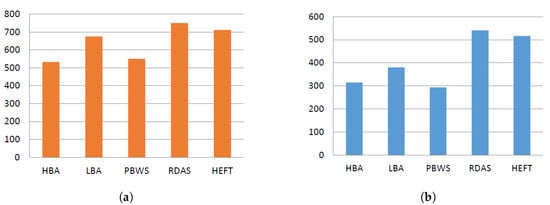
Figure 5.
CyberShake workflow experiment results. (a) makespan ; (b) cost (¢).
Montage: Most montage workflow levels have a small number of tasks, and most levels in the workflow have one task each, which increases the data dependency between levels. The proposed approaches demonstrated the best behavior for makespan compared to the benchmark algorithms (Figure 6), in which the utility-based mechanism used in the LBA algorithm reduced the time required to execute tasks by >50% compared to the benchmarks. The utility-based mechanism demonstrated the highest reduction when applied under the HBA. Such performance fully utilized the resource shares while applying the proposed scheduling approaches. Nonetheless, the proposed algorithms also attained the highest cost values, which was due to the structure of the Montage workflow. Therefore, having numerous VMs waiting to execute a single task (idle mode) increases the execution cost.
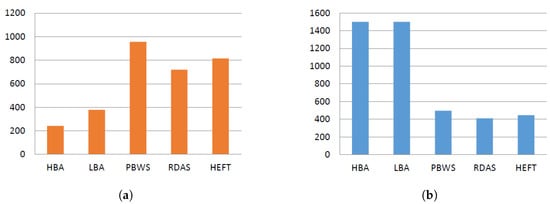
Figure 6.
Montage workflow experiment results. (a) makespan ; (b) cost (¢).
SIPHT: The SIPHT workflow structure is unorganized, where levels have different numbers of tasks with different computational requirements. The SIPHT workflow results are illustrated in Figure 7 where the two proposed algorithms significantly outperformed the benchmark algorithms in terms of both makespan and execution cost. This result was linked to the task-grouping strategies in workflow structure handling. The SIPHT workflow structure emphasized the advantages of the LBA and HBA algorithms that treat task groups as sequestered objects, which minimized the inter-dependency between those groups during execution. Furthermore, the fair share resource distribution mechanism used in the proposed algorithms increased the resource utilization efficiency. The hierarchy-based approach performed best for execution cost and makespan compared to the other algorithms due to the parallel executions of the groups.
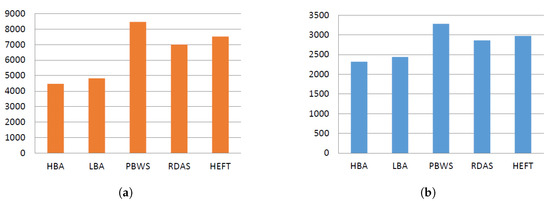
Figure 7.
SIPHT workflow experiment results. (a) makespan ; (b) cost (¢).
6. Conclusions and Future Work
The structure of the workflow impacts the scheduling efficiency. In this paper, two workflow scheduling approaches are presented to utilize the structure-related information. By employing a look ahead strategy, the HBA scheduling approach has shown its advantages compared to the LBA strategy. Such advantages are due to the fact that the HBA works to minimize the data dependency between the task groups. As illustrated in the results section, the efficiency of the HBA is influenced by the number of available VMs. Increasing the number of available VMs further increases the advantages of the VMs’ fair share division strategy. In situations where the number of available VMs is relatively small, the discussion has shown that the LBA is more likely to achieve better performance compared to the HBA. Overall, the results demonstrated that the proposed algorithms outperformed the benchmarked algorithms for makespan and execution cost in most scenarios.
The HBA can be extended further to address situations where hardware failure is expected to occur. The simplest mechanism to address such situations is to calculate the percentage of hardware failure for each group. Such a calculation can be based on the structure of each group and the expected execution time for the workflow tasks. Based on the calculated percentage, the weight of each group can be adjusted to capture the requirements of adding additional VMs to address the expected hardware failure.
Author Contributions
Formal analysis, A.A., F.Y., K.A. and N.M.M.N.; Methodology, A.A., K.A. and N.M.M.N.; Validation, A.A., F.Y. and K.A.; Supervision, F.Y., K.A. and N.M.M.N.; Writing—original draft, A.A.; Writing—review & editing, K.A. and N.M.M.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable since no new data are created during this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saeedi, S.; Khorsand, R.; Ghandi Bidgoli, S.; Ramezanpour, M. Improved many-objective particle swarm optimization algorithm for scientific workflow scheduling in cloud computing. Comput. Ind. Eng. 2020, 147, 106649. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Masdari, M.; Gharehchopogh, F.S.; Jafarian, A. A hybrid multi-objective metaheuristic optimization algorithm for scientific workflow scheduling. Clust. Comput. 2021, 24, 1479–1503. [Google Scholar] [CrossRef]
- Farid, M.; Latip, R.; Hussin, M.; Abdul Hamid, N.A.W. Scheduling Scientific Workflow Using Multi-Objective Algorithm With Fuzzy Resource Utilization in Multi-Cloud Environment. IEEE Access 2020, 8, 24309–24322. [Google Scholar] [CrossRef]
- Teylo, L.; de Paula, U.; Frota, Y.; de Oliveira, D.; Drummond, L. A hybrid evolutionary algorithm for task scheduling and data assignment of data-intensive scientific workflows on clouds. Future Gener. Comput. Syst. 2017, 76, 1–17. [Google Scholar] [CrossRef]
- Pasdar, A.; Lee, Y.C.; Almi’ani, K. Hybrid scheduling for scientific workflows on hybrid clouds. Comput. Netw. 2020, 181, 107438. [Google Scholar] [CrossRef]
- Almi’ani, K.; Lee, Y.C. Partitioning-Based Workflow Scheduling in Clouds. In Proceedings of the 2016 IEEE 30th International Conference on Advanced Information Networking and Applications (AINA), Crans-Montana, Switzerland, 23–25 March 2016; pp. 645–652. [Google Scholar] [CrossRef]
- Pasdar, A.; Lee, Y.C.; Almi’ani, K. Toward Cost Efficient Cloud Bursting. In Service-Oriented Computing, Proceedings of the 17th International Conference, ICSOC 2019, Toulouse, France, 28–31 October 2019; Yangui, S., Bouassida Rodriguez, I., Drira, K., Tari, Z., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 299–313. [Google Scholar]
- Almi’ani, K.; Lee, Y.C.; Mans, B. Resource demand aware scheduling for workflows in clouds. In Proceedings of the 2017 IEEE 16th International Symposium on Network Computing and Applications (NCA), Cambridge, MA, USA, 30 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Abrishami, S.; Naghibzadeh, M.; Epema, D.H. Deadline-constrained workflow scheduling algorithms for Infrastructure as a Service Clouds. Future Gener. Comput. Syst. 2013, 29, 158–169. [Google Scholar] [CrossRef]
- Topcuoglu, H.; Hariri, S.; Wu, M.Y. Performance-effective and low-complexity task scheduling for heterogeneous computing. IEEE Trans. Parallel Distrib. Syst. 2002, 13, 260–274. [Google Scholar] [CrossRef]
- Malawski, M.; Juve, G.; Deelman, E.; Nabrzyski, J. Algorithms for cost- and deadline-constrained provisioning for scientific workflow ensembles in IaaS clouds. Future Gener. Comput. Syst. 2015, 48, 1–18. [Google Scholar] [CrossRef]
- Calheiros, R.N.; Buyya, R. Cost-Effective Provisioning and Scheduling of Deadline-Constrained Applications in Hybrid Clouds. In Proceedings of the Web Information Systems Engineering—WISE 2012, Paphos, Cyprus, 28–30 November 2012; Wang, X.S., Cruz, I., Delis, A., Huang, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 171–184. [Google Scholar]
- Yu, J.; Buyya, R.; Tham, C.K. Cost-based scheduling of scientific workflow applications on utility grids. In Proceedings of the First International Conference on e-Science and Grid Computing (e-Science’05), Melbourne, VIC, Australia, 5–8 December 2005; pp. 8–147. [Google Scholar] [CrossRef]
- Almi’ani, K.; Lee, Y.C.; Mans, B. On efficient resource use for scientific workflows in clouds. Comput. Netw. 2018, 146, 232–242. [Google Scholar] [CrossRef]
- Toussi, G.K.; Naghibzadeh, M.; Abrishami, S.; Taheri, H.; Abrishami, H. EDQWS: An enhanced divide and conquer algorithm for workfow scheduling in cloud. J. Cloud Comput. Adv. Syst. Appl. 2022, 11, 1–18. [Google Scholar] [CrossRef]
- Bagga, S.K.P.; Hans, R.; Kaur, H. Quality of Service (QoS) Aware Workflow Scheduling (WFS) in Cloud Computing: A Systematic Review. Arab. J. Sci. Eng. 2019, 44, 2867–2897. [Google Scholar] [CrossRef]
- Albtoush, A.; Noor, N.M.M.; Yunus, F. Utility-based Scheduling Solution for Scientific Workflow on Cloud. In Proceedings of the 2021 International Symposium on Networks, Computers and Communications (ISNCC), Dubai, United Arab Emirates, 31 October–2 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Tang, Q.; Zhu, L.H.; Zhou, L.; Xiong, J.; Wei, J.B. Scheduling directed acyclic graphs with optimal duplication strategy on homogeneous multiprocessor systems. J. Parallel Distrib. Comput. 2020, 138, 115–127. [Google Scholar] [CrossRef]
- Al-Khanak, E.N.; Lee, S.P.; Khan, S.U.R.; Behboodian, N.; Khalaf, O.I.; Verbraeck, A.; van Lint, H. A Heuristics-Based Cost Model for Scientific Workflow Scheduling in Cloud. Comput. Mater. Contin. 2021, 67, 3265–3282. [Google Scholar] [CrossRef]
- Sandokji, S.; Eassa, F. Dynamic Variant Rank HEFT Task Scheduling Algorithm Toward Exascle Computing. Procedia Comput. Sci. 2019, 163, 482–493. [Google Scholar] [CrossRef]
- Arabnejad, V.; Bubendorfer, K.; Ng, B. Dynamic multi-workflow scheduling: A deadline and cost-aware approach for commercial clouds. Future Gener. Comput. Syst. 2019, 100, 98–108. [Google Scholar] [CrossRef]
- Wu, Z.; Ni, Z.; Gu, L.; Liu, X. A Revised Discrete Particle Swarm Optimization for Cloud Workflow Scheduling. In Proceedings of the 2010 International Conference on Computational Intelligence and Security, Nanning, China, 11–14 December 2010; pp. 184–188. [Google Scholar] [CrossRef]
- Chen, W.; Xie, G.; Li, R.; Bai, Y.; Fan, C.; Li, K. Efficient task scheduling for budget constrained parallel applications on heterogeneous cloud computing systems. Future Gener. Comput. Syst. 2017, 74, 1–11. [Google Scholar] [CrossRef]
- Gamal El Din Hassan Ali, H.; Saroit, I.A.; Kotb, A.M. Grouped tasks scheduling algorithm based on QoS in cloud computing network. Egypt. Inform. J. 2017, 18, 11–19. [Google Scholar] [CrossRef]
- Charrada, F.B.; Tata, S. An Efficient Algorithm for the Bursting of Service-Based Applications in Hybrid Clouds. IEEE Trans. Serv. Comput. 2016, 9, 357–367. [Google Scholar] [CrossRef]
- Van den Bossche, R.; Vanmechelen, K.; Broeckhove, J. Cost-Efficient Scheduling Heuristics for Deadline Constrained Workloads on Hybrid Clouds. In Proceedings of the 2011 IEEE Third International Conference on Cloud Computing Technology and Science, Athens, Greece, 29 November–1 December 2011; pp. 320–327. [Google Scholar] [CrossRef]
- Arabnejad, V.; Bubendorfer, K.; Ng, B. Scheduling deadline constrained scientific workflows on dynamically provisioned cloud resources. Future Gener. Comput. Syst. 2017, 75, 348–364. [Google Scholar] [CrossRef]
- Akbari, M.; Rashidi, H.; Alizadeh, S.H. An enhanced genetic algorithm with new operators for task scheduling in heterogeneous computing systems. Eng. Appl. Artif. Intell. 2017, 61, 35–46. [Google Scholar] [CrossRef]
- Aziza, H.; Krichen, S. A hybrid genetic algorithm for scientific workflow scheduling in cloud environment. Neural Comput. Appl. 2020, 32, 15263–15278. [Google Scholar] [CrossRef]
- Verma, A.; Kaushal, S. A hybrid multi-objective Particle Swarm Optimization for scientific workflow scheduling. Parallel Comput. 2017, 62, 1–19. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, G.; Li, M.; Liu, X. Evolutionary Multi-Objective Workflow Scheduling in Cloud. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 1344–1357. [Google Scholar] [CrossRef]
- Kanagaraj, K.; Swamynathan, S. Structure aware resource estimation for effective scheduling and execution of data intensive workflows in cloud. Future Gener. Comput. Syst. 2018, 79, 878–891. [Google Scholar] [CrossRef]
- Górski, T.; WOźniak, A.P. Optimization of Business Process Execution in Services Architecture: A Systematic Literature Review. IEEE Access 2021, 9, 111833–111852. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).