Featured Application
The method studied in this paper is applied to the control calculation of manipulator, especially the matrix chain multiplication in the calculation of forward and inverse kinematics solutions of manipulator.
Abstract
Intelligence development has put forward increasing requirements of real-time planning and dynamic feedback in controlling robotic arms. It has become essential in engineering applications to complete the kinematics calculation of complex manipulators in real time. This paper proposes a matrix cascading multiplication equivalent reduced-order parallel computing method for the multiplication of homogeneous matrices in the process of forward and inverse kinematics solutions, which reduces the order of the matrix according to the distribution of zero vectors in the homogeneous matrix calculations. The method removes the unnecessary multiplication in joint homogeneous matrixes containing zero vectors. It obtains the optimal calculation order of the cascade matrix multiplication through dynamic planning searches, improving the efficiency of effective dot product calculation by parallel computation. Calculation processes and specific examples are presented in this paper. Compared with the previous algorithms, the proposed algorithm reduces the calculation cycle by 90%, effectively improving the real-time calculation efficiency in the complex control process.
1. Introduction
Matrix multiplication dominates over 90% of the control calculations in robotic arms, especially the reconfigurable robotic arm. Therefore, the forward and inverse solution calculation process becomes key to the real-time autonomous planning of the robotic arm [1]. With the development of intelligent robots, sophisticated and complex operations place an increasing demand on real-time kinematics calculations [2], and traditional matrix calculations alone cannot achieve such high performance [3].
The degrees of freedom of the robotic arms are generally less than seven, which also leads to the application of some acceleration algorithms with high degrees of freedom [4]. At the same time, unlike image processing, classification, and other calculations that can reduce matrix multiplication by cutting and approximation [5], the control of robotic arms requires higher precision and more precise matrix multiplication calculations. In some fine operation application scenarios where the end moves at a close distance and with low speed, sometimes a double precision floating point base is inevitable to meet the application requirements. Thus, it is necessary to consider the impact on the accuracy of the calculation results in the algorithm design process [6], and directly applying the control training method based on neural networks in the high-precision control process is inappropriate [7]. In addition, for the calculation process of matrix multiplication with sparse features, parallel computing based on digital logic or dedicated processor chips can improve the calculation rate [8,9], and the cycle of accessing the cache can also be reduced after processing zero data [10].
Currently, there are three main methods for matrix computing acceleration. The first is to use high-performance processors such as GPUs to achieve real-time computing [11]. However, its heat rate is usually high and difficult to be applied in miniaturized or long-term work scenarios [12]. The second is to design digital logic to implement a special matrix computing architecture [13], which takes up substantial hardware resources, making it challenging to implement a flexible matrix computing mode [14]. Especially for specific calculation scenarios, such as the calculation of a homogeneous matrix in the process of computing the forward solution of a manipulator, it is hard to reduce the amount of calculation by using the sparse nature of the matrix itself [15]. Another immediate improvement of fast matrix multiplication [16], such as Strassen and Cannon’s fast matrix multiplication, is combined with multi-core parallel computing to improve the system efficiency. There is an upper limit in improving fast matrix multiplication, and the implementation of parallel multi-core computing mainly focuses on the block parallelism of matrix data, not considering the optimization of matrix chain multiply–add operations [17].
In reference [15], the forward and inverse kinematics solution module based on FPGA was designed to realize the millisecond-level control rate of the medical robot. The analytical solution was adopted without considering the factor of shape reconstruction. Based on searching for optimal matrix chain multiplication in dynamic programming and adding the interaction cost between multiple processors, the optimal calculation method closer to the real-world application is designed in the literature [16]. In the literature [18], a single matrix multiplication module completed the chain multiplication of forward and inverse solutions, and the calculation time reached 87.25 milliseconds. Reference [19] realized the parallel distribution of the dot product in the matrix chain process based on GPU design and parallel C++ calculation, which reduced the computation time by 97.27%. Previous design methods in the literature mainly focused on improving the efficiency of matrix cascade multiplication through fixed digital logic acceleration or process optimization of multi-core parallel processors. However, it also brought about problems such as increased power consumption and complex logic code, which is often unacceptable in some scenarios with low power consumption, light miniaturization, and high reliable computing requirements [20]. Therefore, optimizing the design based on the parallel multi-processing core and the calculation characteristics of the matrix multiplication of forward and inverse solutions of the robotic arm to meet the real-time processing performance is of great significance.
In practical engineering applications, real-time computing requirements for forward and inverse kinematics solutions reach milliseconds. For example, autonomous path planning based on force feedback and visual feedback requires a single planning time at the microsecond level in fine control. In previous studies, Xilinx’s XC5VLX330T was adopted to design a calculation module for path planning based on a 40-bit single-precision floating point, and the calculation time was less than 2.3 milliseconds [21]. This method was only an engineering design with no optimization in the algorithm itself.
Based on the results of [21], this paper presents a method for calculating high-speed matrix cascade multiplication for robotic arm control, which includes three parts: equivalent order reduction calculation, optimal order calculation, and parallel dot product calculation. The equivalent order reduction calculation is implemented to remove unnecessary multiplication and accumulation operations in the matrix with a large number of zero vectors by the statistical partition of the zero vector of the matrix. When the row vector in the multiplication matrix or the column vector in the multiplication matrix is 0, the multiplication and accumulation operation of the vector is considered unnecessary. The optimal order calculation is calculated according to the equivalent reduced-order matrix to obtain the optimal multiplication order. Through parallel dot product calculation, the efficiency of practical vector dot product calculation is improved, thereby improving the calculation speed of matrix cascade multiplication.
The arrangement of this paper is as follows. The calculation model of matrix cascade multiplication is given in Section 2. In Section 3, the equivalent reduced-order simplification method is presented for the application process of robotic arm control. Section 4 discusses the experimental verification, the result analysis, and the comparison with the previous designs. Section 5 summarizes the thesis.
2. Kinematic Calculation Matrix Chain Multiplication
Forward and inverse kinematics solutions of robotic arms mainly include the rotation and translation matrix multiplication of each joint angle position or the known end joint position and velocity to obtain inverse solutions. Reference [21] provides the calculation process of the homogeneous end pose transformation matrix. is defined as the homogeneous transformation matrix of joint , and then the terminal homogeneous pose transformation matrix is
where represents the number of joints, and . and represent the number of rows and columns of the kth matrix, , , and .
It can be seen from Formula (1) that the kinematic solution process of robotic arm control is a standard matrix multiplication calculation problem, so traditional dynamic programming can be used to search for the optimal multiplication order to reduce the amount of calculation [22]. The multiplication amount of any two adjacent matrices and is . For the multiplication chain of matrices, the optimal order is defined as , where , and then the recursive optimal order of traditional matrix multiplication is
The order of the homogeneous matrix is unified in the kinematic solution of the robotic arm. It is difficult to directly reduce the amount of calculation to search for optimal multiplication by matrix multiplication dynamic programming alone. Therefore, an equivalent order reduction mechanism should be established according to the sparsity of the homogeneous matrix in the settlement process of the robotic arm movement, and then the optimal multiplication order should be searched according to dynamic programming.
3. Equivalent Order Reduction Method
In matrix calculation, especially in the process of robotic arm control calculation, is often sparse. Considering that the dimension of the matrix in the calculation process of robotic arm control is generally less than eight, the matrix is only divided into four blocks, which are expressed as follows:
Then the calculation result of matrix and multiplication is
where
Considering the partitioned matrix (), when it is zero matrix or identity matrix, the calculation amount of matrix multiplication is zero, and let the proportion of partial columns and columns be , then the calculation amount of adjacent matrix multiplication of four partitioned blocks is
If the zero value of the multiplied matrix partially occupies rows () and the zero value of the multiplied matrix partially occupies columns (), the value of is as follows:
Substitute Formula (6) into Formula (5), and obtain
According to Formula (7), after the sparse matrix zero vector is counted, the column number of the multiplied matrix and the row number of the multiplied matrix can be equivalent to
Therefore, after sparse matrix statistics, the recursive optimal order of matrix multiplication is changed to be
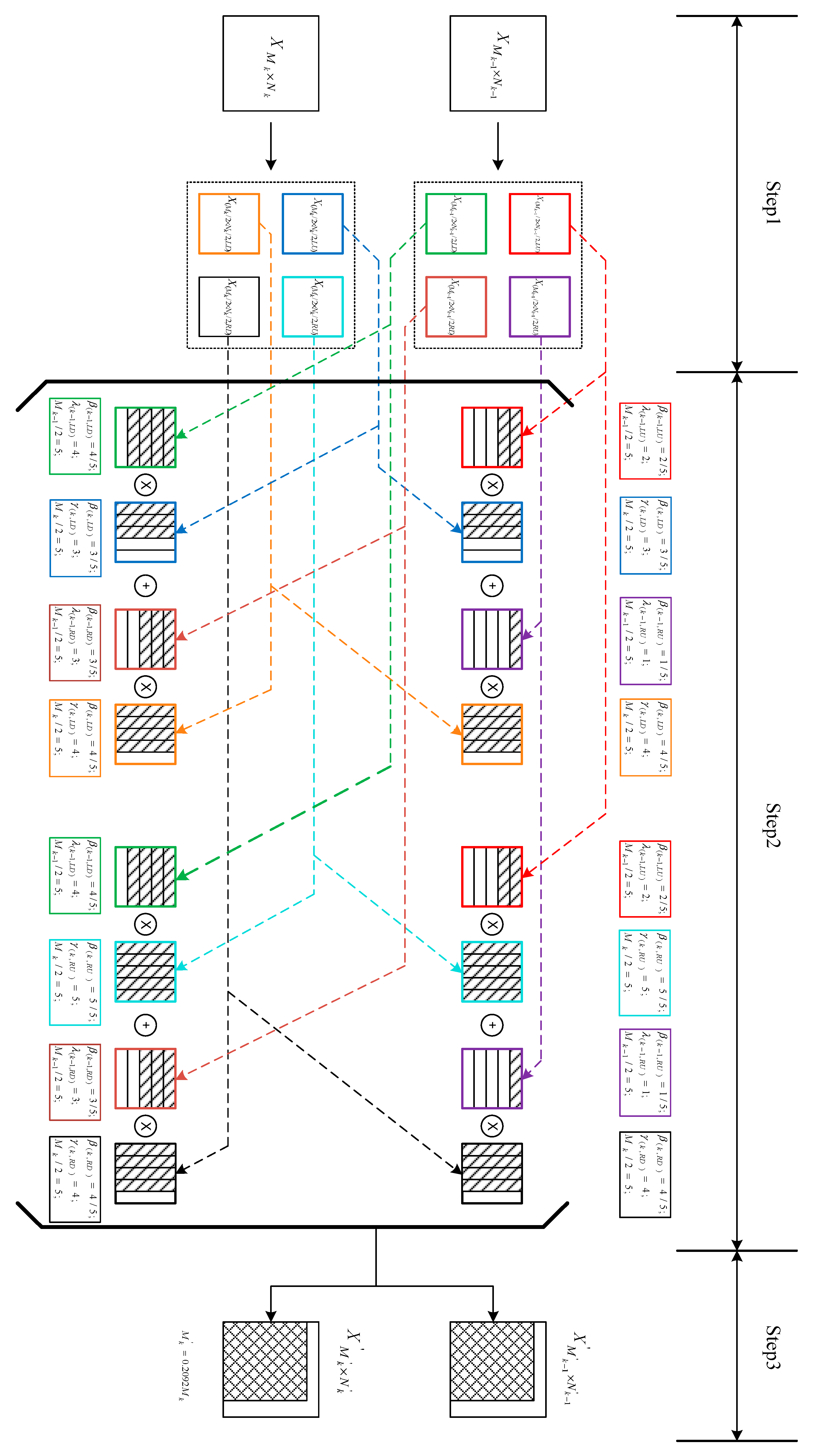
For the equivalent order reduction process, as shown in Figure 1, the equivalent order reduction calculation steps based on the sparse feature of block matrix are as follows:
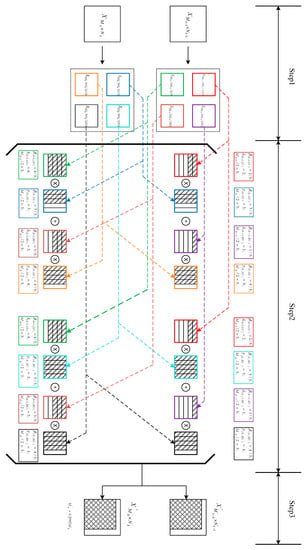
Figure 1.
Equivalent reduced-order calculation based on sparse features of block matrix.
Step 1: The matrix of row and column and the matrix of row and column are divided into four blocks according to Formula (3) to obtain , , , , , , , and .
Step 2: Calculate the block multiplication of the block matrix according to Formula (4), detect the number of the zero vector of each multiplied matrix to obtain , and detect the number of the zero-column vector of each multiplied matrix to obtain .
Step 3: According to Formula (8), the matrix order after the equivalent reduced order is obtained.
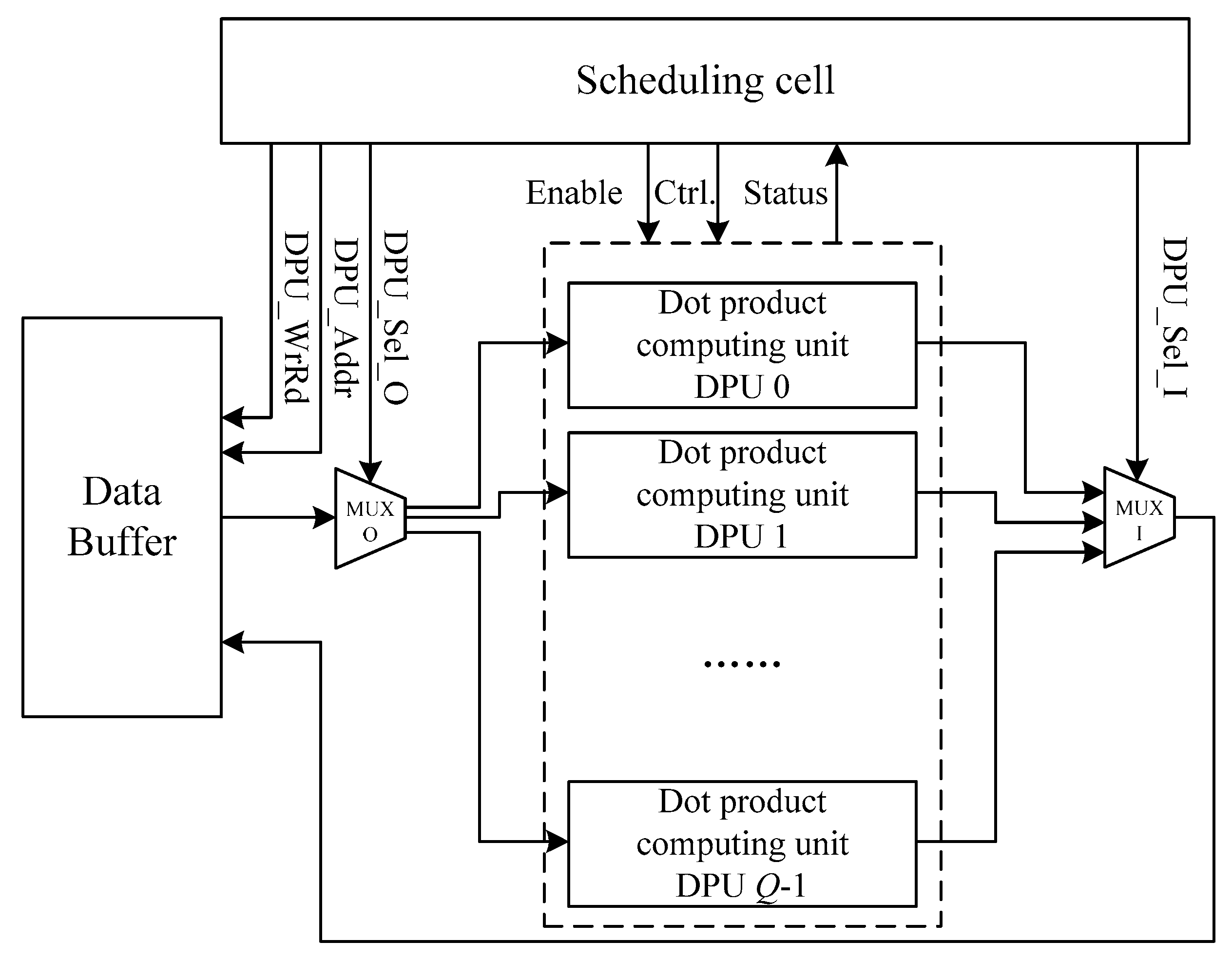
For the matrix chain multiplication calculation, as in Figure 2, the flow chart of high-speed matrix cascade multiplication calculation includes the following steps:
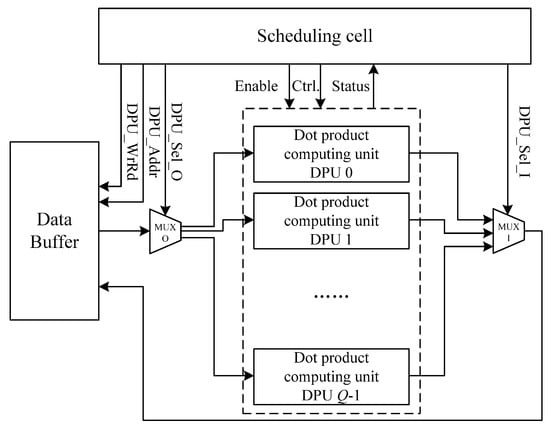
Figure 2.
Hardware design block diagram of high-speed matrix chain multiplication parallel dot product calculation.
Step 1: Wait for the chain calculation of matrix multiplication to start, create statistics of each matrix in the cascade according to Formula (8), and do the equivalent reduced-order calculation.
Step 2: Calculate the optimal calculation order of the cascade matrix according to Formula (9).
Step 3: Transform the matrix chain multiplication into parallel dot product calculation.
4. Parallel Dot Product Matrix Calculation
This section presents the calculation design of the parallel dot product matrix based on the algorithm in Section 3 and the performance comparison of verification results. High-speed matrix chain multiplication includes equivalent order reduction calculation, optimal order calculation, and parallel dot product calculation. In practical applications, equivalent order reduction calculation is implemented to remove unnecessary multiplicative accumulation operations in matrices with a large number of zero vectors. When the row vector or column vector in the multiplicative matrix is 0, the multiplicative accumulation operation of the vector is considered unnecessary, saving time and improving performance.
4.1. Parallel Dot Product Matrix Computing Architecture
The hardware design block diagram of parallel dot product matrix calculation controlled by the mechanical arm is shown in Figure 2, including the scheduling computing unit, data cache, dot product computing unit, and gating MUX_O and MUX_I. Among them, the scheduling computing unit controls the data cache through the cache read and write control signal DPU_WrRd and cache address access signal DPU_Addr. According to the read and write needs, the read data sent to the gate MUX_O are sent to the dot product computing unit group as the optional communication signal DPU_Sel_O. The output result of the dot product unit group passes through the MUX_I and is sent to the data cache by DPU_Sel_I as the optional communication signal. The scheduling cell can enable and control its parameters according to the output state of the clicking cell group.
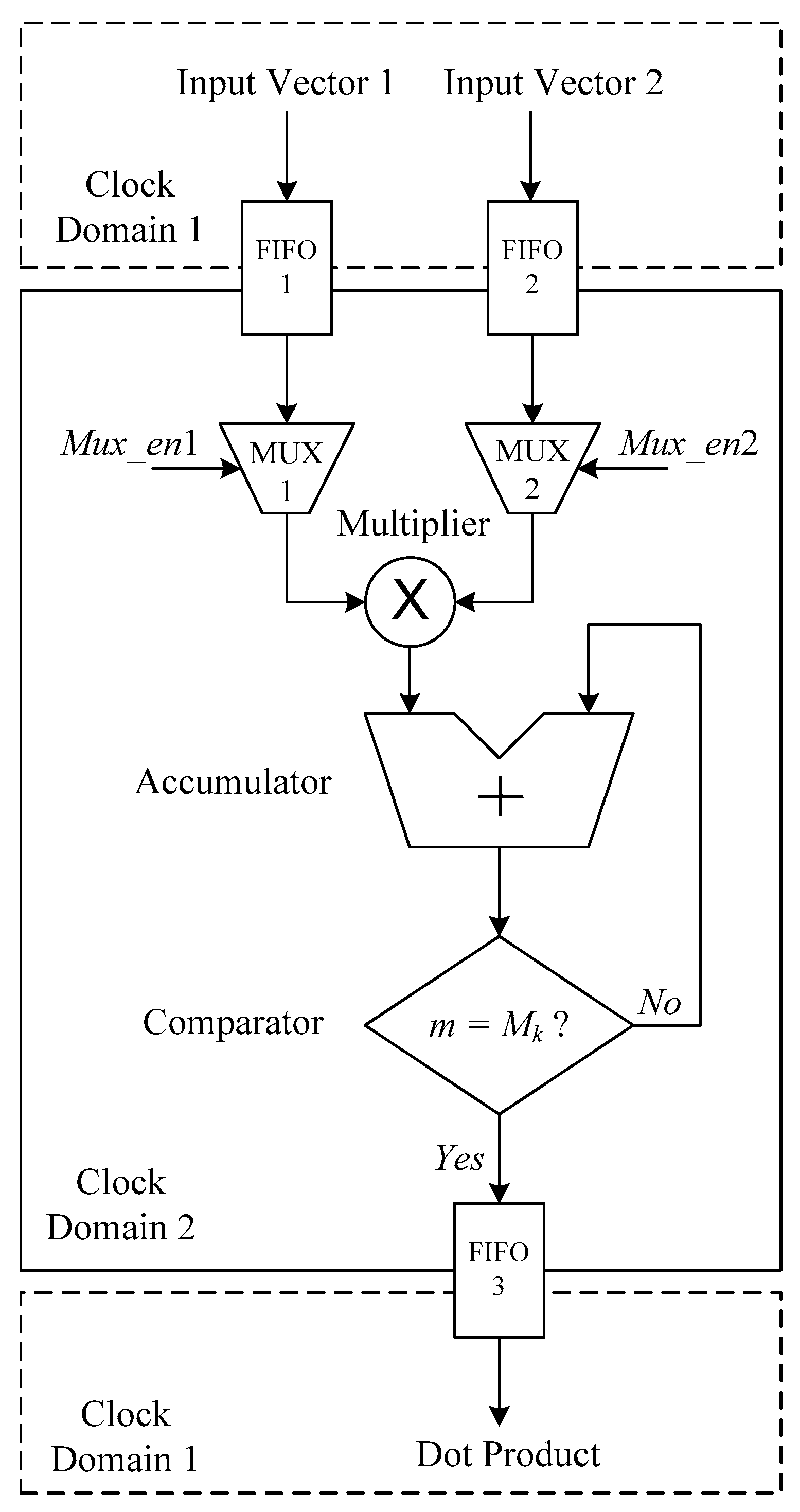
The hardware design block diagram of the dot product computing unit is depicted in Figure 3. It includes FIFO, gate MUX, a multiplier, an adder, and a comparator. Two computational vectors 1 and 2 are input as FIFO1 and FIFO2, respectively. The data of the two FIFOS control the output time according to the enable signals Mux_en1 and Mux_en2 of the gating devices MUX1 and MUX2, and the output results enter the multiplier at the same time. The multiplication result is input into the accumulator, and the number of accumulative times m and the number of rows of the multiplied matrix Mk are compared by the comparator. If the number of accumulative times reaches Mk, the result output is FIFO3, and the final dot product result is output by FIFO3. The external interface and the internal computing module are divided into two clock domains.
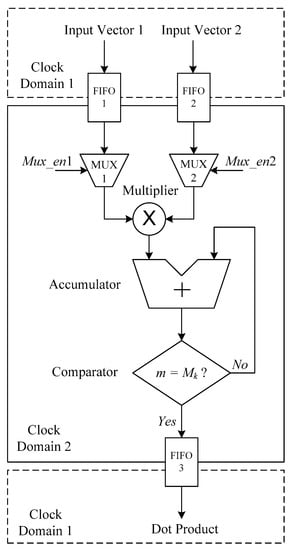
Figure 3.
Hardware design block diagram of the dot product computing unit.
4.2. Calculation Examples and Results
Based on the algorithm in Section 3 and the hardware architecture in Section 4.1, this section takes the forward kinematics solution of a six-DOF robotic arm as an example to analyze and compare the equivalent order reduction and parallel computing process and result performance.
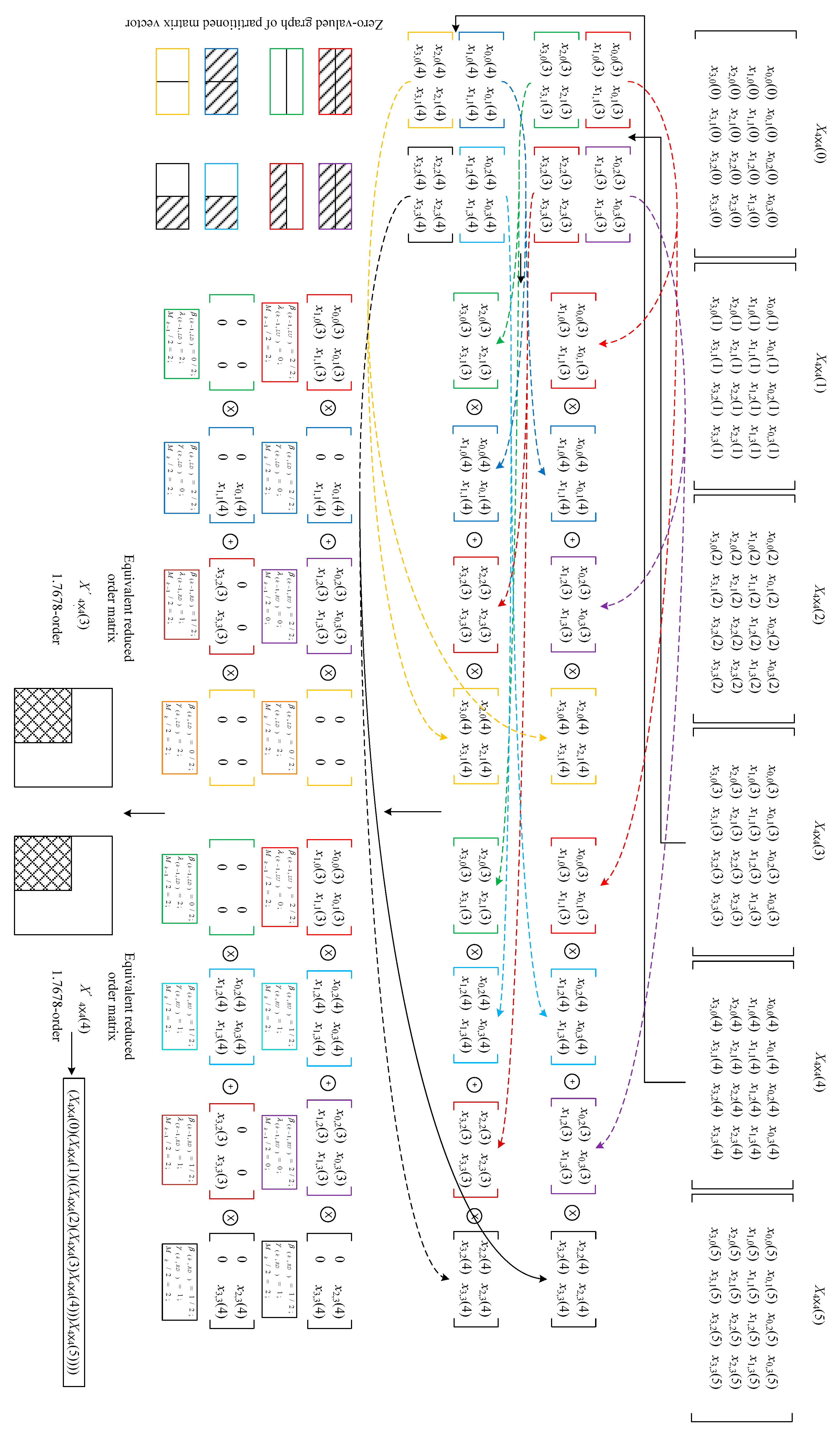
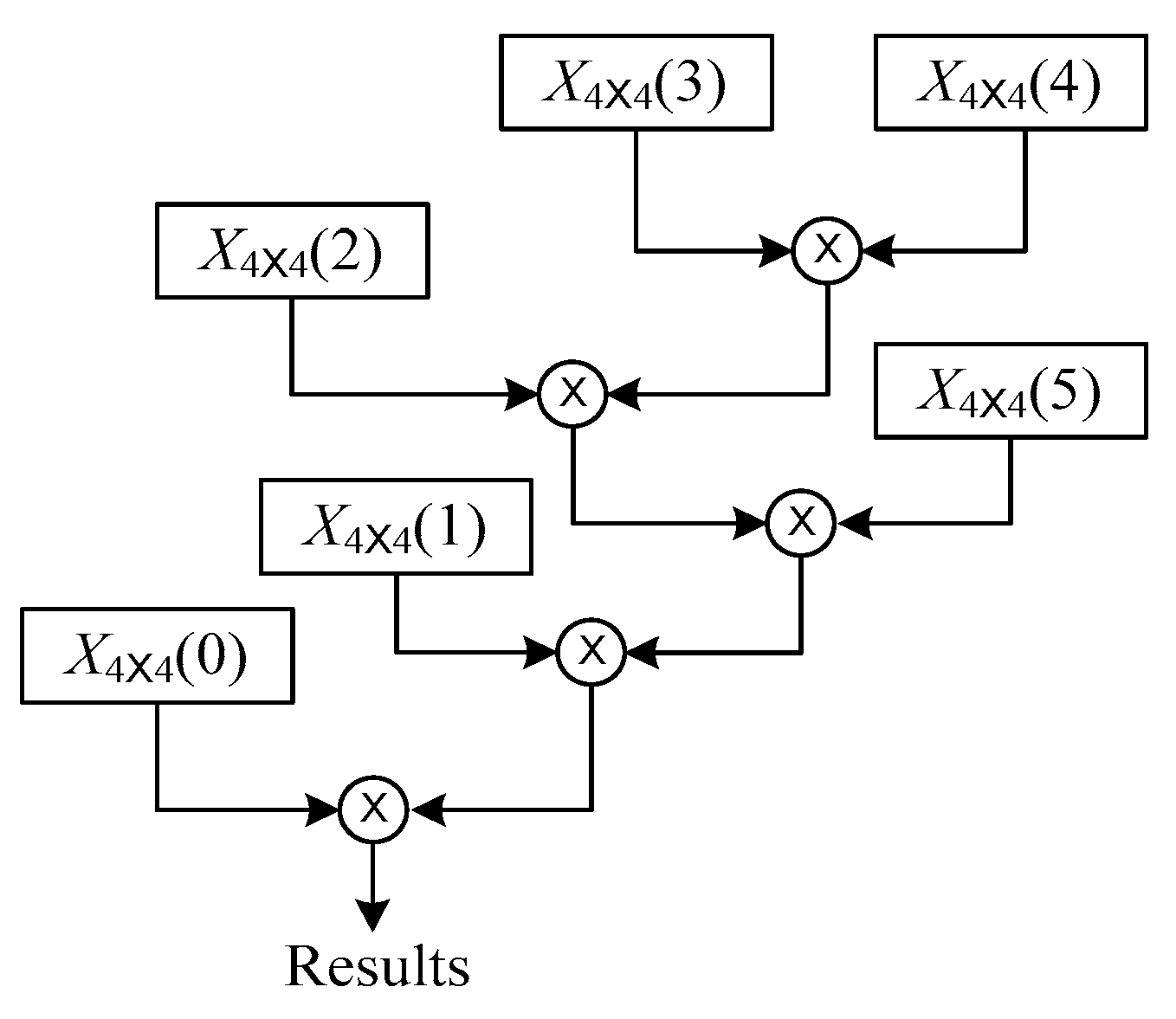
Figure 4 is an example of the calculation process of the forward solution cascade multiplication of a homogeneous matrix. In the calculation, six homogeneous 4 × 4 matrices X4×4(k) (k = 0, 1, …, 5) perform the multiplication operation, create statistics of X4×4 (3) and X4×4 (4), and perform equivalent order reduction. First, the 4 × 4 matrix is divided into four blocks according to Formula (3) to obtain the 2 × 2 matrix representation of the multiplication result. Then, each 2 × 2 order matrix is counted, and the zero-value graph of the block matrix vector and its parameters are obtained according to Formula (6). Finally, according to Formula (8), the matrix order after the equivalent reduced order is obtained. Finally, the equivalent order of X4×4 (3) and X4×4 (4) is 1.7678.
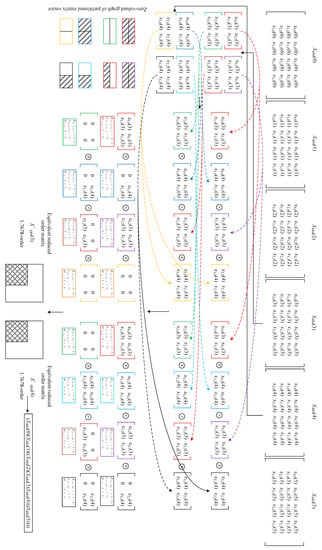
Figure 4.
Calculation process of chain multiplication of forward solution of the six-DOF homogeneous matrix.
Figure 5 is an example of the optimal order for the chain multiplication of the forward solutions of homogeneous matrices. According to Formula (9), the optimal order of the cascade multiplication in Figure 5 is obtained.
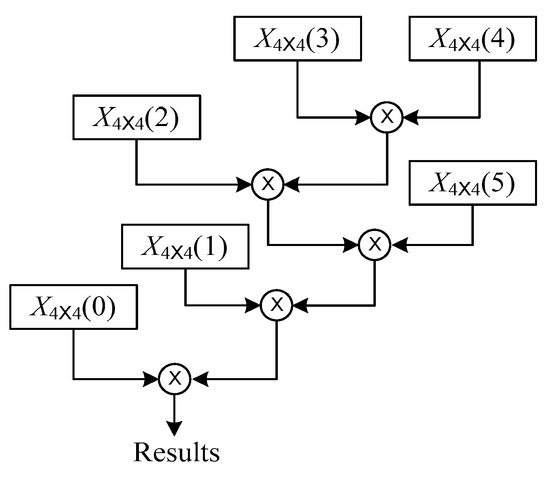
Figure 5.
Example of the optimal order of the forward solution cascade multiplication of the homogeneous matrix.
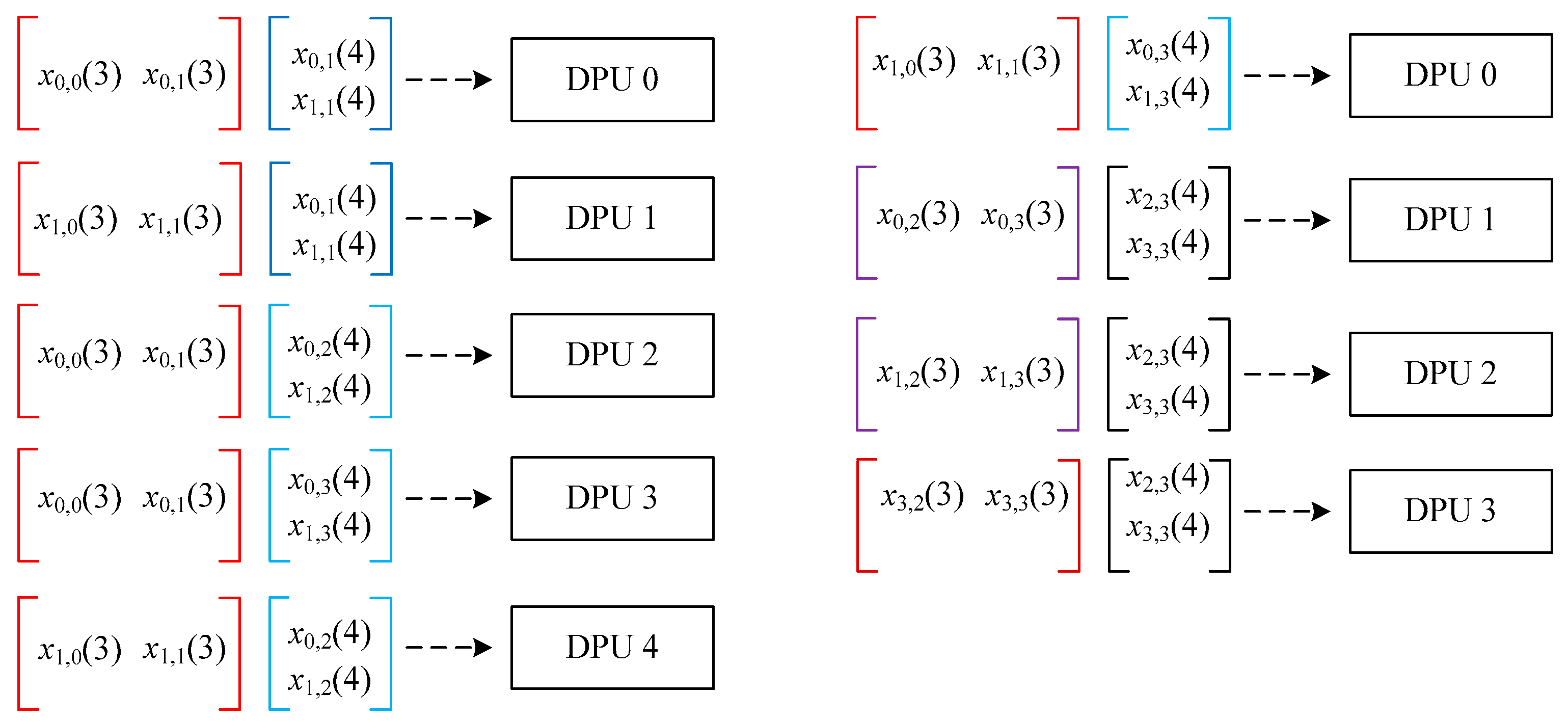
According to the calculation process in Figure 5, parallel tasks are assigned to the dot product computing unit DPU in Figure 2. Figure 6 depicts the example of the matrix multiplication dot product sample cell group task allocation, when the number of dot product parallel computing is 5. Figure 6 shows the distribution of each non-zero vector in each dot product computing unit during the multiplication of matrix X4×4 (3) and X4×4 (4). The first five vector dot products are allocated to five units, and the last four vector dot products are allocated to the first four vector dot products after the first calculation process is completed.
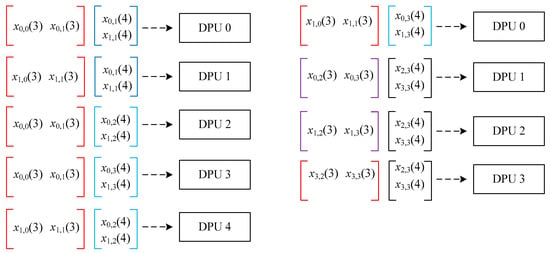
Figure 6.
Task allocation of the matrix multiplication dot product computing unit group.
4.3. Performance Comparison
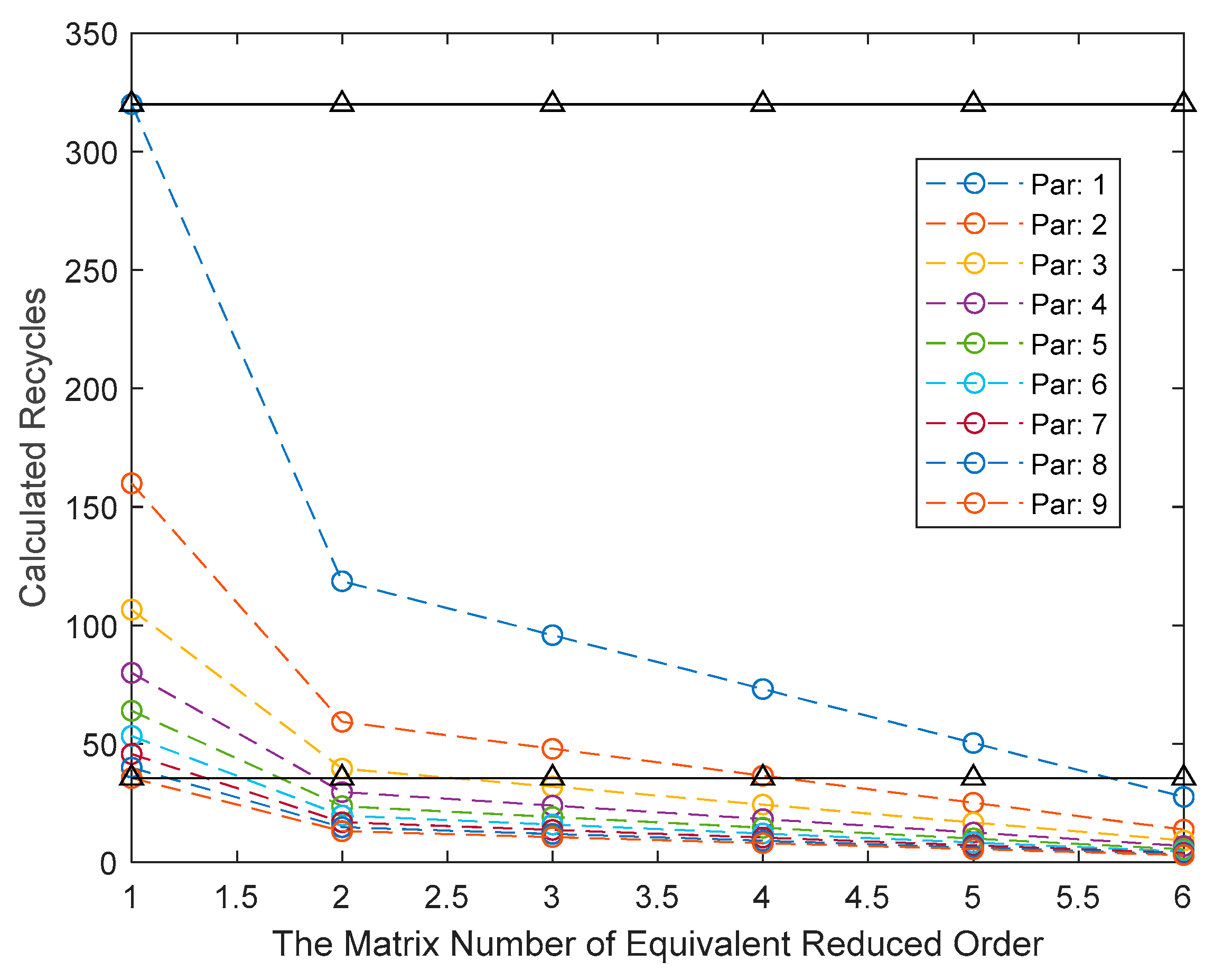
The calculation amount of traditional matrix multiplication is , and the matrix multiplication algorithm running on parallel devices is designed in reference [16], which makes the calculation amount inversely proportional to the number of parallel devices. In the design method of this paper, Section 4.2 only describes the equivalent order reduction for the third and fourth joints, but since the structure of the robotic arm’s homogeneous matrix is the same, and the distribution of zero values of the homogeneous matrix vectors of each joint is consistent, the calculation amount of the whole serial product is related to the number of equivalent order reduction matrices and the number of parallel dot product computing units, as shown in Figure 7.
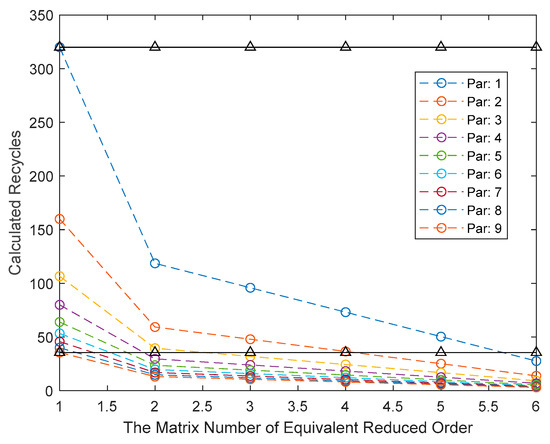
Figure 7.
Comparison of computational performance between the proposed method and previous parallel algorithms [16].
In Figure 7, the dotted line is the calculation cycle of the forward kinematics solution with different numbers of equivalent reduced-order matrices under different parallel dot product computing units. The two black lines on the top and bottom represent the computing cycle under the parallel computation of a single computing unit and nine computing units in reference [16]. It can be seen that the algorithm in this paper is more flexible under the same degree of parallelism, which can effectively improve the computing performance and reduce the computing time by 90%.
The design method in this paper is used in the experimental platform in [21], and the parallel dot product matrix calculation architecture in Section 4.1 is used to replace the traditional parallel matrix multiplication. The core calculation adopts Xilinx’s XC5VLX330T chip, which is used to complete the path planning motion of the entire seven-DOF robotic arm. Eight DPUs are used for parallel acceleration in the implementation, and the whole FPGA runs at 150 MHz. As shown in Table 1, the maximum operating frequency and logical Slice resource occupancy of the FPGA implementation based on the proposed design method are not much different from those in [21]. The DSP48E resource is increased by 20%, and the 18 Kb Block RAM resource is increased by 15%. In the conventional terminal line planning calculation mode, the calculation time of a single path planning is not more than 0.37 ms, which is 84% lower than that in [21].

Table 1.
Resource usage and performance comparison.
5. Conclusions
This paper proposed a parallel and fast calculation of matrix cascade multiplication for robotic arm kinematics solution control. By counting the zero vector in the homogeneous matrix, a high-order matrix is regarded as a low-order matrix, and the optimal chain multiplication structure is searched by dynamic programming. The hardware framework of parallel dot product calculation and the logic block diagram of the dot product calculation are designed to realize the parallel operation of matrix multiplication. This paper presents the continuous multiplication of the homogeneous matrix of each joint in the forward kinematics calculation process of the six-DOF robotic arm. The design method proposed is used to optimize the algorithm and parallelize the hardware design, which reduces the calculation time by 90% compared with the traditional matrix calculation and effectively improves the real-time performance of the robotic arm control process calculation.
Author Contributions
Conceptualization, J.Y.; methodology, D.H.; software, X.S.; validation, J.Y. and W.L.; formal analysis, D.H. and X.W.; investigation, X.S.; resources, X.S.; data curation, W.L.; writing—original draft preparation, J.Y.; writing—review and editing, D.H.; visualization, X.S.; supervision, D.H.; project administration, J.Y.; funding acquisition, D.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study aims to improve and optimize the computational process of the robotic arm and does not involve human or animal studies. Therefore, ethical review and approval was waived for this study.
Informed Consent Statement
This study is not applicable. This study did not involve human studies.
Data Availability Statement
This research is mainly aimed at the optimization of principle algorithm. Experimental data and results are mainly obtained by repeated experimental statistics. Experimental data can be obtained according to the formula in the paper, and comparison data can be obtained according to references.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, P.; Long, J.; Yang, W.; Leng, J. Inverse Kinematics Solution of Underwater Manipulator Based on Jacobi Matrix. In Proceedings of the OCEANS 2021: San Diego—Porto, San Diego, CA, USA, 20–23 September 2021; pp. 1–4. [Google Scholar]
- Li, T.; Calandra, R.; Pathak, D.; Tian, Y.; Meier, F.; Rai, A. Planning in Learned Latent Action Spaces for Generalizable Legged Locomotion. IEEE Robot. Autom. Lett. 2021, 6, 2682–2689. [Google Scholar] [CrossRef]
- Wiedmeyer, W.; Altoé, P.; Auberle, J.; Ledermann, C.; Kröger, T. A Real-Time-Capable Closed-Form Multi-Objective Redundancy Resolution Scheme for Seven-DoF Serial Manipulators. IEEE Robot. Autom. Lett. 2021, 6, 431–438. [Google Scholar] [CrossRef]
- Hu, C.; Lin, S.; Wang, Z.; Zhu, Y. Task Space Contouring Error Estimation and Precision Iterative Control of Robotic Manipulators. IEEE Robot. Autom. Lett. 2022, 7, 7826–7833. [Google Scholar] [CrossRef]
- Plancher, B.; Brumar, C.D.; Brumar, I.; Pentecost, L.; Rama, S.; Brooks, D. Application of Approximate Matrix Multiplication to Neural Networks and Distributed SLAM. In Proceedings of the 2019 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 24–26 September 2019; pp. 1–7. [Google Scholar]
- Wang, Y.; Tang, Z.; Li, D.; Zeng, L.; Zhang, X.; Wang, N. Research and Software Implementation of Accuracy Analysis of Space Manipulator. Manned Spacefl. 2021, 27, 59–65. [Google Scholar]
- Bhardwaj, G.; Sukavanam, N.; Panwar, R.; Balasubramanian, R. An Unsupervised Neural Network Approach for Inverse Kinematics Solution of Manipulator following Kalman Filter based Trajectory. In Proceedings of the 2019 IEEE Conference on Information and Communication Technology, Allahabad, India, 6–8 December 2019; pp. 1–6. [Google Scholar]
- Liu, Q.; Liu, C. Calculation Optimization for Convolutional Neural Networks and FPGA-based Accelerator Design Using the Parameters Sparsity. J. Electron. Inf. Technol. 2018, 40, 1368–1374. [Google Scholar] [CrossRef]
- Li, Y.; Xue, W.; Chen, D.; Wang, X.; Xu, P.; Zhang, W.; Yang, G. Performance Optimization for Sparse Matrix-Vector Multiplication on Sunway Architecture. Chin. J. Comput. 2020, 43, 1010–1024. [Google Scholar]
- Pligouroudis, M.; Nuno, R.A.G.; Kazmierski, T. Modified Compressed Sparse Row Format for Accelerated FPGA-Based Sparse Matrix Multiplication. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar]
- Tang, Y.; Zhao, D.; Huang, Z.; Dai, Z. High Performance Row-based Hashing GPU SpGEMM. J. Beijing Univ. Posts Telecommun. 2019, 42, 106–113. [Google Scholar] [CrossRef]
- Finean, M.N.; Merkt, W.; Havoutis, I. Simultaneous Scene Reconstruction and Whole-Body Motion Planning for Safe Operation in Dynamic Environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3710–3717. [Google Scholar]
- Zhang, Z.; Wang, J.; Zhang, L.; Xiao, J. FPGA based Floating Point Separable Convolutional Neural Network Acceleration Method. Chin. High Technol. Lett. 2022, 32, 441–453. [Google Scholar]
- Ran, D.; Wu, D.; Qian, L. Design of Matrix Multiplication Accelerator for Deep Learning Inference. Comput. Eng. 2019, 45, 40–45. [Google Scholar]
- Zhang, R.; Zhang, J.; Dai, Y.; Shang, H.; Li, Y. Forward and Inverse Kinematics of the Robot Based on FPGA. Acta Sci. Nat. Univ. Nankaiensis (Nat. Sci. Ed.) 2018, 51, 18–23. [Google Scholar]
- Weiss, E.; Schwartz, O. Computation of Matrix Chain Products on Parallel Machines. In Proceedings of the IEEE International Parallel and Distributed Processing Symposium (IPDPS), Rio de Janeiro, Brazil, 20–24 May 2019; pp. 491–500. [Google Scholar]
- Song, Y.; Zheng, Q.; Wang, Z.; Zhang, D. A large dimensional matrix chain matrix multiplier for extremely low IO bandwidth requirements. Appl. Electron. Tech. 2019, 45, 32–38. [Google Scholar]
- Han, L.-L.; Ye, P.; Sun, H.; Ji, X. A Jacobian Matrix Inversion Method for Redundant Robotic Manipulator Base on QR Decomposition. Comput. Eng. Softw. 2013, 11, 64–66. [Google Scholar]
- Shyamala, K.; Kiran, K.R.; Rajeshwari, D. Design and implementation of GPU-based matrix chain multiplication using C++AMP. In Proceedings of the International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 22–24 February 2017; pp. 1–6. [Google Scholar]
- Ma, R.; Chen, Q.; Zhang, H.; Mei, Z.; Wang, R.; Wei, W. Low Power Visual Odometry Technology Based on Monocular Depth Estimation. J. Syst. Simul. 2021, 33, 3001–3011. [Google Scholar] [CrossRef]
- Yu, J.-Y.; Huang, D.; Liang, C.-C.; Wang, B.; Zhang, X.-D.; Lu, L. On-board Real-time Path Planning Design for Large-scale 7-DOF Space Manipulator. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; pp. 1501–1506. [Google Scholar]
- Fan, X.; Saldivia, A.; Soto, P.; Li, J. Coded Matrix Chain Multiplication. In Proceedings of the IEEE/ACM 29th International Symposium on Quality of Service (IWQOS), Tokyo, Japan, 25–28 June 2021; pp. 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).