Abstract
Landslide caused by rainfall are easily produced when excavating conduct in sandstone-covered mudstone strata. The expansion project of the Heishan Village to Jixi section of Dan-A Highway is used as an example to study the formation and damage mechanism of rainfall-induced landslide in sandstone-covered mudstone cutting slope. Finite element numerical is used to analyze the stability of the slope by using Geo-Studio and ANSYS software for the three different rainfall-influencing factors of rainfall intensity, duration and rainfall form. The study indicates that rainfall time and intensity will decrease the stability of the cutting slope, and that the effect of rainfall on the slope is lagging behind. When rainfall intensity is 80 mm, rainfall duration is 1 d, and stagnation is 5 h, the slope instability is in the critical state. The front slope toe is the first unstable part in the process of slope instability. Rock and artificial construction are important reasons for this phenomenon.
1. Introduction
In Northeast China, sandstone-mudstone interbedding is a typical stratigraphic distribution. Both sandstone and mudstone are sedimentary rocks. Among them, sandstone has great weathering resistance and good permeability, and surface water can easily permeate it. Mudstone, on the other hand, has low strength, weak permeability and is quickly absorbed and softened by water [1]. It is a slippery stratum in engineering construction. In recent years, the trend of summer rainfall in Northeast China increased [2]. Due to the rain erosion and temperature change, the exposed mudstone interlayer will disintegrate and soften quickly. This weakens the layer and reduces its strength, which causes a significant drop in the slope safety factor and even destabilization [3,4]. Therefore, the sandstone–mudstone interlayer’s slope stability problem has increasingly caught the attention of academics working in the area.
The geotechnical structure and influencing factors are the two main areas of attention for studies on the stability of sandstone and mudstone slopes at the moment. According to Tingguo Peng’s [5] analysis of the stability of mudstone and muddy siltstone landslides, impermeable siltstone is a necessary element for landslide formation, and surface water infiltration and rainfall both contribute to landslide deformation. However, there is no in-depth analysis of the rainfall factor. By examining the structural characteristics of mudstone rock, Zhenghui Tang [6] made the observation that the rate of rainfall infiltration into the rock affects the rate of expansive argillization, but neglected the intensity of the rainfall infiltration and duration of rainfall infiltration. Based on the instability of siltstone slopes, Q. Li et al. [7] hypothesized that slope deformation can be divided into a slow creep period caused by excavation and an accelerated sliding period caused by rainfall. Considering the three factors of rainfall intensity, duration and slope gradient, Zhongming He et al. [8] found that gradient had a bigger impact on slope safety coefficient than rainfall factor. Instead, Xianqi Luo [9] simulated infiltration characteristics and deformation damage characteristics of landslide under different rainfall conditions by artificial rainfall testbed. However, none of them took into account the impact of stratigraphic lithology on slope stability. Using indoor simulated rainfall experiments, Zhishui Liang et al. [10] investigated the effects of slope angle, rainfall intensity, and vegetation coverage on sandstone slopes, and concluded that rainfall intensity has the greatest impact on slopes. Researchers both domestically and internationally agree that, according to analysis of the above research, rainfall causes sandstone and mudstone slopes to become unstable. However, there are few studies on landslides caused by rainfall infiltration in sandstone-covered mudstone formations. Determining the crucial range of landslides in intricate rock under different rainfall conditions is thus necessary.
In order to further deepen the understanding of mudstone softening caused by rainfall infiltration, this paper takes the typical landslide along the Heishan Village to Jixi section of Dan-A Highway Expansion Project as an example. Based on extensive field work and laboratory tests, the landslide mechanism and instability state under different rainfall conditions are studied by numerical analysis. Additionally, the influence of different rainfall intensity and duration on the stability of sandstone-covered mudstone slopes is analyzed. Therefore, this case is used to explore the causes of landslides in such slopes so as to better prevent landslide disasters and provide reference for highway construction in the world’s sandstone–mudstone distribution areas.
2. Regions and Methods
2.1. Study Area
Dan-A highway expansion project from Heishan village to Jixi is where this paper’s research object is situated. The geographical location of the study area is 44°58′8″ N and 130°42′8″ E, with a height of 438.5 m, as indicated in Figure 1. The study area is located near the permafrost degradation zone, which has a great influence on the stability of mudstone [11,12]. This stretch of the highway is excavated by cutting with a maximum slope excavation depth of 18.8 m, according to the survey. As soon as the construction was finished at the end of October 2019, the mudstone of the first of grade slope in the cutting was softened and disintegrated by water, due to exposure. This also led to the collapse of sandstone on the secondary slope. Subsequently, numerous collapses and significant landslides started to happen. The maximum landslide angle of the slope is 29.81°, and length is 33.21 m. Figure 2 features images of the location.
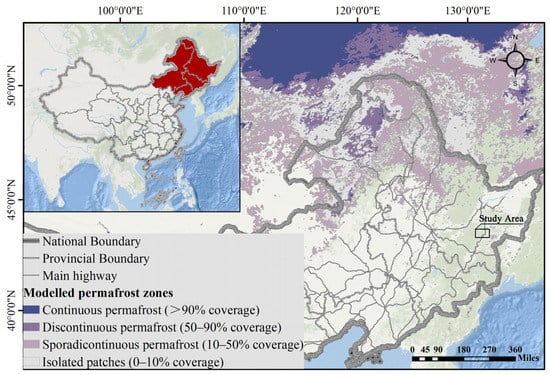
Figure 1.
Distribution of permafrost in Northeast China and the project location of the study area.

Figure 2.
Landslide of the study area.
2.1.1. Meteorology and Hydrology
The research region is a part of the middle temperate continental monsoon climate zone and is situated in the mid-latitude zone. All four seasons see considerable climate change: the spring is drought and windy, the summer is hot and brief with concentrated rain, the fall is chilly and cooling, and the winter is chilly and long. The annual sunshine number is 2565 h, the annual average temperature is 4.2 °C, the extreme maximum temperature is 38 °C, the extreme minimum temperature is −37 °C. The annual average rainfall is 540 mm, and the rainfall period is concentrated in June to August, accounting for more than 60% of annual rainfall. The average frost-free period is 144 d. The ground temperature is lower than 0 °C for 5 months of the year, the permafrost layer is 1.5~2.0 m, the standard freezing depth is 2.0 m, and the maximum freezing depth can reach 2.2 m [13,14,15]. Strong sunlight and precipitation make it simple for the slope to be in the cycle of water-saturation and drying crack. Strong sunlight causes mudstone to weather quickly and lose shear strengths completely. In addition, precipitation causes mudstone to relax and soften, and changes the structure of the rock, all of which cause the slope to become unstable.
2.1.2. Stratigraphic Lithology
The stratum lithologic serves as the foundation for studying landslides. The location where the slope is located is a low hill area with a complicated distribution of geologic rock layers, substantial relief, a natural slope of 10~35°, and relative height difference within 100 m. Based on the procedures of geological exploration and sampling [16], geological survey maps were mapped and the soil were drilled on the site of the study area. The composition of the rocks was determined through indoor tests. The slope is covered with Quaternary residual slope (Qdel), which is mainly clay mixed with clastic rock and gravel; the underlying bedrock is weathered sandstone, mudstone, weathered conglomerate, and strongly weathered conglomerate of Lower Cretaceous Muling Formation (K1m). Rainwater can pass through the upper sandstone layer and be blocked by the lower mudstone layer, creating a water-rich layer in the mudstone layer. The mudstone softens and disintegrates in water, and creeps towards the road, which is insufficient to support the force of the sandstone above. The sandstone is then broken up into blocks, causing a continual collapse and landslide.
2.2. Model Building
2.2.1. Mathematical Model
In the analysis of porous flow of the slope under rainfall conditions, the flow of rainwater in unsaturated soil and in saturated soil below the groundwater level is a two-dimensional saturated–unsaturated problem. The Darcy’s Law is still used to describe the law of saturated and unsaturated seepage. The two-dimensional saturated and unsaturated seepage control equation has the following form [17]:
where and are the hydraulic conductivity of the soil in and directions, is the height of the head, is sink/source term, is the specific weight of the water, and is the slope of the soil moisture characteristic curve.
The finite element equations are solved in combination with the following boundary conditions.
Head boundary:
Fluid boundary:
The initial conditions for the non-constant seepage:
2.2.2. Geometric Model and Physical Parameters
According to the geological survey report, the main slide surface was selected as the calculation profile, and a two-dimensional geometric model of 46 m in length and 19 m in height was established (Figure 3). It can be separated into three sections, including the sliding surface (mudstone softened soil), sliding mass (weathered sandstone, silty clay), and sliding bed (mudstone). The landslide model uses PLANE82 element from ANSYS Library, with 6379 nodes and 6218 finite elements.
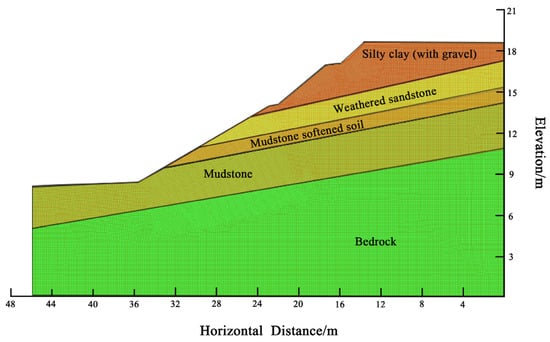
Figure 3.
Finite element mesh schematic diagram of the main slide’s cross-section.
In order to study the failure mechanism of the cutting slope clearly, it is very necessary to conduct indoor tests on the soil properties of undisturbed soil samples in the study area. The laboratory tests include the natural moisture content test, the Atterberg limits test, proportion test, grain composition measurement, direct shear test, and variable head permeability test, etc. As a result, the parameters of the sliding zone soil model that were fitted based on engineering geological survey data and laboratory test results are shown in Table 1.

Table 1.
Table of calculation parameters.
2.2.3. Boundary Conditions and Initial Conditions of the Model
According to the landslide mechanism of mudstone softening caused by rainfall, the phreatic line is selected on the interface between mudstone and sliding bed in a natural state. According to detailed geological survey, the groundwater level at the landslide is below the sliding bed, and the study area is a cutting slope, so the problem of landslide is not related to the groundwater level. Therefore, the model conditions do not consider the groundwater level. In addition, the following boundary conditions are also established.
Infiltration boundary: The upper boundary is the fluid boundary of rainfall infiltration. The pore water pressure is supposed to be numerically equal to the matrix suction and the slope surface pressure is assumed to be atmospheric pressure. The water flow rate is set to zero, and the model’s left and right boundaries are impermeable.
Stress boundary: The bottom of the model is fixed both horizontally and vertically, whereas the left and right boundaries are fixed horizontally and free vertically.
In order to analyze the influence of rainfall intensity, rainfall duration. and stagnation time on the stability of soil slope, the calculation and analysis scheme is established and shown in Table 2.

Table 2.
Rainfall design table under different working conditions.
3. Results
It is necessary to couple the fluid field and solid stress field during rainfall infiltration analysis. Based on the investigation on the interaction mechanism of the fluid field and solid stress field, Geo-Studio and ANSYS software are combined to conduct a numerical simulation of landslide. Geo-Studio is used to analyze the cutting slope stability and obtain the most unfavorable rainfall condition when the slope is damaged. The seepage field of the slope is simulated by using the seepage analysis module (SEEP/W) in Geo-Studio. Then, the pore water pressure results were imported into the slope stability analysis module (SLOPE/W) to calculate the stability coefficients of the slope under various working conditions. In addition, considering the deformation behavior of the solid under the influence of the seepage field, and the influence of the solid deformation on the seepage field, the specific weight of soil, cohesion, and the internal friction angle of landslide soil under different content is assigned in ANSYS. On the basis of strength reduction method, ANSYS software is used to calculate and analyze the critical state and the development process of slope instability under rainfall infiltration.
3.1. Slope Stability Analysis under Natural Working Conditions
The geological survey has determined that the groundwater level is within the sliding bed and does not pass through the sliding zone soil; thus, only the unsaturated state is taken into consideration for the slope stability of the cutting slope in its natural state. The Morgenstern–Price method is used to analyze the overall stability of the slope, and the Bishop method is used to automatically search the local stability of the most dangerous slip surface. The stability factors obtained by these two methods are 1.350 and 1.289, respectively, which are stable. The front slope toe of the landslide is the first unstable location in the natural state. This section of the highway is an expansion project; serious excavation was required to meet the road-smoothness requirements. As a result, the location of the foot of the slope were influenced by the construction excavation, creating a local void at the foot, and increasing the slope angle of the slide surface here. This increases the local sliding force and reduces the safety stability coefficient.
3.2. Slope Stability Analysis under Different Rainfall Conditions
This paper examines the impact on the stability of sandstone-covered mudstone cutting slopes, considering rainfall infiltration from three perspectives: rainfall duration, rainfall intensity, and rainfall lag time.
- (1)
- Analysis of pore water pressure variation for different working conditions
Compare the pore water pressure maps of working conditions I and II when the rainfall intensity is the same, but the rainfall duration varied (see Figure 4). The pore water pressure contours and phreatic line is basically parallel in the two conditions, and the distribution has a certain regularity. When the rate of precipitation is 80 mm/d, the rising of the saturation line is proportional to the rainfall duration. The pore water pressure change after half a day of rainfall duration in Case I is more than after one day in Case II, and the seepage change is more noticeable. When the rainfall has just occured, the soil moisture is low and the permeability is strong. As the rainfall continues, the soil moisture increases continuously, there is a transition from unsaturated to saturated soil in the sliding zone, and the suction of the soil to water decreases, which in turn leads to the permeability of Case II being smaller than that of Case I. This is consistent with the change rule that the unsaturated hydraulic conductivity decreases with the increase in water. Additionally, by comparing the phreatic line’s positions, it can be seen that the phreatic line in Condition II is higher than that in Condition I, which is clearly affected by the total rainfall. In the layer for mudstone and weathered sand, rainfall infiltration makes the sliding zone soil transition from unsaturated to saturated. With the continuous rainfall, the unsaturated part of the sliding zone soil decreases and the negative pore water pressure decreases gradually. A new saturated zone is formed between sandstone and mudstone.
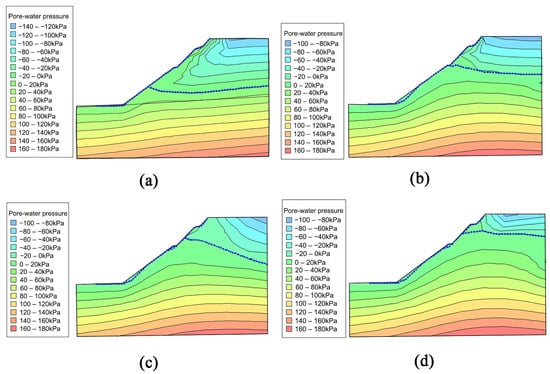
Figure 4.
Pore water pressure distribution for each working condition, where the blue dashed line is the phreatic line. (a) Working condition I; (b) Working condition II; (c) Working condition III; (d) Working condition IV.
The pore water pressure maps of working conditions II and III, when the total amount of precipitation is the same, but the intensity of the precipitation varies, was compared. The pore water pressure of rainfall intensity 80 mm/d varies more quickly than that of rainfall intensity 40 mm/d when the rainfall amounts are equal, but the total change value of pore water pressure is the reverse. In the early stage of rainfall, rainwater quickly fills all the voids and cracks and infiltrates the lower layer because the natural moisture content of the surface soil is low. However, because of the high intensity of the rainfall, when the intensity exceeds the saturated hydraulic conductivity of the soil itself, rainwater will form runoff along the slope surface, and will not infiltrate into the soil. This process corresponds to the working Condition II. In Working condition III, the rainfall intensity is low but the duration is long. The rain will infiltrate into the soil as time passes, increasing the saturation zone and the gravity of the slip zone soil, and lifting the phreatic line obviously, which reduces the stability of the landslide in this condition.
Compare the pore water pressure maps of Conditions II and IV, where the stagnation time is varied, but the rainfall time and intensity are the same. After one day of rain stoppage, the pore water pressure on the surface of the cutting slope decreases significantly. The rise of the saturation line in the working condition IV is mainly due to the stagnation for one day, which is correlated with the hydraulic conductivity of the top soil layer in the slip zone and the creep of mudstone.
A comparison of pore water pressure diagrams under natural and other working conditions was made (see Figure 5). The height of the saturation line, moisture content, and gravity of soil have great changes under the test conditions. These phenomena indicate that the downslide strength of sliding soil increases, and the anti-sliding force and slope stability decrease. It also accurately reflects the fact that rainfall is a notable consideration in the formation of the landslide.
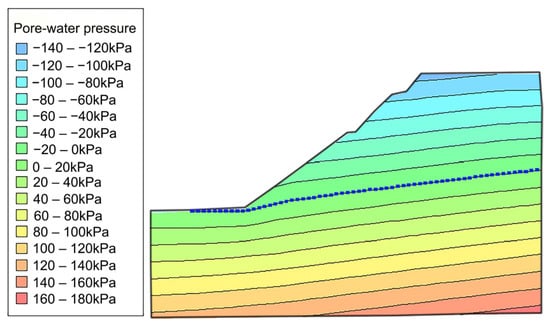
Figure 5.
Pore water pressure distribution in a natural state, where the blue dashed line is the phreatic line.
- (2)
- Slope stability analysis for each working condition
The stability coefficient of cutting slope under different working conditions is obtained by different calculation methods, and the average value of these slope stability coefficients is used as the final reference index. Figure 6 displays the statistics of the slope stability coefficients.
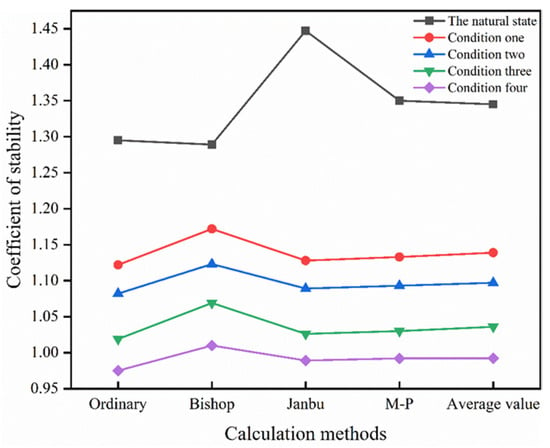
Figure 6.
Statistics of stability coefficients for different working conditions in the study area.
As shown in Figure 6, increasing rainfall intensity causes the stability coefficient of slopes in the study area to trend downward for the same rainfall duration. In the working condition IV, the stability coefficient is less than 1.05, at which point the slope was damaged. In order to determine the critical state of failure in the study area, it is necessary to analyze the deformation and damage of different time nodes under the condition of working condition IV.
3.3. Analysis of Landslide Deformation and Damage in the Study Area
Numerous researchers domestically and internationally have investigated the combination of the strength reduction method and numerical analysis to calculate the stability coefficient of the slope, in order to overcome the drawback that the numerical analysis method cannot give the stability coefficient of slope intuitively, such as the limit equilibrium method [18,19,20,21,22]. The principle behind the strength reduction method is to continually reduce the rock slope’s shear strength parameter, and repeat the iterative calculation until the slope reaches the critical failure state. The reduction coefficient at this time represents the stability coefficient of the slope. That is the following:
The slope stability coefficient calculated by the working condition II is 1.097, while that calculated by the working condition IV is 0.992. Rainwater infiltration by rainfall stagnation is the primary cause of slope instability. In order to analyze the critical state when the slope is unstable, the calculation and analysis scheme as shown in Table 3 is established.

Table 3.
Rainfall design table under different working conditions of rainfall stagnation.
The plastic strain diagrams and X-axis displacement diagrams of the four cases are analyzed (see Figure 7 and Figure 8).
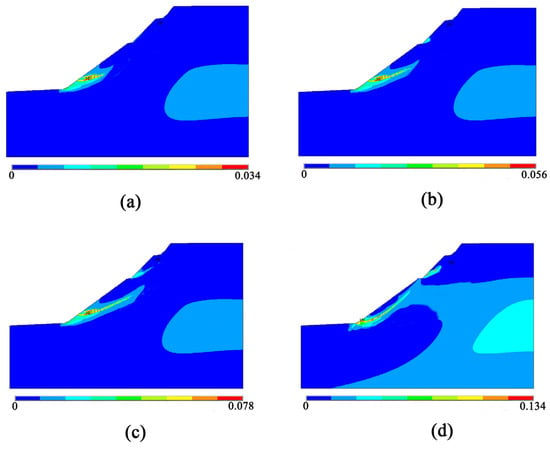
Figure 7.
Plastic strain diagrams. (a) Working condition V; (b) Working condition VI; (c) Working condition VII; (d) Working condition VIII.
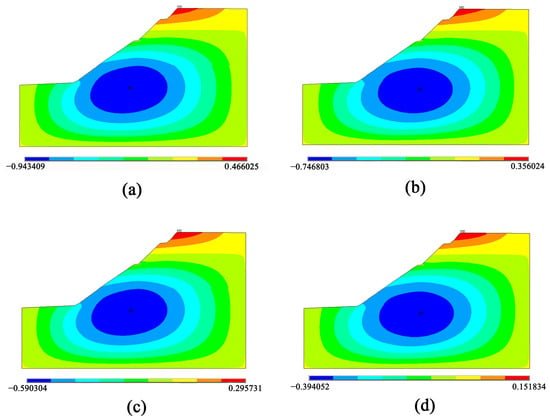
Figure 8.
X-direction displacement diagrams at the top of the slope, where the unit is m. (a) Working condition V; (b) Working condition VI; (c) Working condition VII; (d) Working condition VIII.
As indicated in Figure 7, the foot of the slope experiences the maximal strain, and the maximum strain at the critical state of slope instability is 0.078. The primary cause of the strain at the foot is that rainfall causes the mudstone to soften and the strength to deteriorate. So, the stresses accumulate here. Secondly, the location of the foot of the slope was influenced by the construction excavation, creating a local void at the foot and increasing the slope angle of the slide surface here. This increases the local sliding force and reduces the safety stability coefficient. Similarly, it can be seen from Figure 7 that the critical state of slope failure is that the rainfall intensity of 80 mm lasts for 1 day and stagnates for 5 h. At this time, the plastic strain runs through the entire landslide zone, causing the cutting slope to fail.
Figure 8 displays the maximum displacement of the X-axis of the slope top. Compared with the four plots, it can be seen that the maximum displacement decreases from 466.025 mm to 151.834 mm with the increase in rainfall, indicating that the slope is prone to local instability.
4. Conclusions
In northeast China, the sandstone-covered mudstone layer is a slide-prone stratum, and rainfall infiltration is the primary factor inducing cutting slope landslide.
In this paper, the causes of landslide as well as the characteristics and process of mudstone softening are recorded and analyzed in the expansion project of Heishan village to Jixi section of Dan-A highway. The landslide mechanism and instability state of the study area under different working conditions are studied by finite element numerical analysis, and the following conclusions are drawn.
- (1)
- Rainfall duration, rainfall intensity, and rainfall lag condition will decrease the stability of the cutting slope in study area. When the precipitation is the same, the duration of rainfall is positively correlated with the change of pore water pressure and the rise of phreatic line. However, rainfall intensity is negatively correlated with pore water pressure and phreatic line change. When the rainfall intensity is the same, the change of pore water pressure will increase with the extension of rainfall time, and the maximum change rate of pore water pressure is in the initial rainfall stage. In addition, the influence of rainfall on the slope has a lag effect, which may be related to the hydraulic conductivity of sliding zone soil and mudstone creep.
- (2)
- It is concluded that the critical state of slope instability in the study area is when the rainfall intensity is 80 mm, the rainfall intensity is 1d, and the stagnation is 5 h. It is primarily caused by rainfall intensity being greater than the infiltration rate and hysteresis effect.
- (3)
- In the slope stress analysis, the first instability is the front slope toe of the landslide. The maximum strain at the critical state of slope instability is 0.078. The first reason is that rainfall makes mudstone soften and strength attenuate, so the stress gathers here. Second, improper excavation makes the toe of the cutting slope locally free, resulting in a decrease in the stability coefficient. In the X-direction displacement analysis at the top of the slope, the maximum displacement decreases with the increase in rainfall, indicating that the slope is prone to local instability. In addition, with the increase in rainfall infiltration time, the plastic strain penetrates from the mudstone softening layer to the whole slip surface, which verifies that the mudstone is extremely easy to soften and disintegrate in water.
- (4)
- The analysis of the influence of different rainfall factors on slope stability and the critical condition of slope instability in this study can provide an effective basis for landslide early warning work in sandstone–mudstone interbedding areas. Take the rainfall value under the critical condition of slope instability, as the rainfall threshold can effectively prevent the occurrence of such landslide disasters.
Author Contributions
Conceptualization, Y.G.; formal analysis, Y.G. and W.S.; methodology, Y.D. and M.L.; writing—original draft, Y.D. and M.L.; writing—review and editing, Y.G., Y.D., W.S., M.L. and C.Z.; supervision, Y.G.; funding acquisition, Y.G. and W.S. All authors have read and agreed to the published version of the manuscript.
Funding
We thank the National Natural Science Foundation of China (Grant No. 41641024) and Carbon Neutrality Fund of Northeast Forestry University (CNF-NEFU) and the Science and Technology Project of Heilongjiang Communications Investment Group (Grant No. JT-100000-ZC-FW-2021-0182) for providing financial support and the Field scientific observation and research station of the Ministry of Education-Geological environment system of permafrost area in Northeast China (MEORS-PGSNEC).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Acknowledgments
We would like to thank all staff members who contributed to this study who are not named here.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rinaldi, M.; Casagli, N. Stability of Streambanks Formed in Partially Saturated Soils and Effects of Negative Pore Water Pressures: The Sieve River (Italy). Geomorphology 1999, 26, 253–277. [Google Scholar] [CrossRef]
- Kong, F.; Wang, Y.; Fang, J.; Lv, L. Pre-estimation on variations of rainfalls with different intensities and their contributions to total rainfall under emission scenarios in China from 2006 to 2100. Water Resour. Hydropower Eng. 2017, 48, 14–21+40. [Google Scholar] [CrossRef]
- Pan, D.; Yan, M. The Summary of Research on the Softening and Disintegration Mechanism of Mudstone. Yunnan Water Power 2016, 32, 28–30+33. [Google Scholar] [CrossRef]
- Zhu, S.; Cao, X.; Liu, Y. Model Experimental Research on Disintegration Behaviors of Argillaceous Rock. Mod. Transp. Technol. 2022, 19, 1–6. [Google Scholar] [CrossRef]
- Peng, T. Characteristics of a certain landslip in inter-bedded area of mudstone and argillaceous siltstone in Nanning and its control measures. Miner. Resour. Geol. 2013, 27, 421–423. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, Z.; Nong, C. The Distortion Principle and Protection Method of Longlin-Baise Highway Tertiary Side slope. West. China Commun. Sci. Technol. 2009, 9, 11–14+19. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.M.; Zhang, K.B.; Yu, H.; Tao, Z.Y. Field Investigation and Numerical Study of a Siltstone Slope Instability Induced by Excavation and Rainfall. Landslides 2020, 17, 1485–1499. [Google Scholar] [CrossRef]
- He, Z.; Yu, T.; Cai, Z.; Qin, Y. Finite Element Analysis for Soil Slope Stability Considering Rainfall Infiltration Influence. Min. Metall. Eng. 2012, 32, 9–11+16. [Google Scholar] [CrossRef]
- Luo, X.; Liu, D.; Wu, J.; Cheng, S.; Shen, H.; Xu, K.; Huang, X. Model Test Study on Landslide under Rainfall and Reservoir Water Fluctuation. Chin. J. Rock Mech. Eng. 2005, 24, 2476–2483. Available online: http://rockmech.whrsm.ac.cn/CN/abstract/abstract21665.shtml (accessed on 19 January 2023).
- Liang, Z.; Liu, H.; Zhao, Y.; Wang, Q.; Wu, Z.; Deng, L.; Gao, H. Effects of Rainfall Intensity, Slope Angle, and Vegetation Coverage on the Erosion Characteristics of Pisha Sandstone Slopes under Simulated Rainfall Conditions. Environ. Sci. Pollut. Res. 2020, 27, 17458–17467. [Google Scholar] [CrossRef]
- Shan, W.; Ma, M.; Guo, Y.; Zhang, C. Numerical Analysis of the Influence of Foundation Replacement Materials on the Hydrothermal Variation and Deformation Process of Highway Subgrades in Permafrost Regions. Water 2022, 14, 2642. [Google Scholar] [CrossRef]
- Obu, J.; Westermann, S.; Bartsch, A.; Berdnikov, N.; Christiansen, H.H.; Dashtseren, A.; Delaloye, R.; Elberling, B.; Et-zelmüller, B.; Kholodov, A.; et al. Northern Hemisphere Permafrost Map Based on TTOP Modelling for 2000–2016 at 1 km2 Scale. Earth-Sci. Rev. 2019, 193, 299–316. [Google Scholar] [CrossRef]
- China Meteorological Data Service Centre. Available online: http://data.cma.cn/ (accessed on 19 January 2023).
- Lu, Y.; Song, G.; Sun, L.; Yang, C.; Zhang, J.; Chen, Y.; Chen, M.; Gao, L.; Liu, Y. The Analysis of Distribution Characteristics of Main Meteorological Factors in the Northeast China. Chin. Agric. Sci. Bull. 2012, 28, 290–294. [Google Scholar] [CrossRef]
- Wei, Z.; Jin, H.; Zhang, J.; Yu, S.; Han, X.; Ji, Y.; He, R.; Chang, X. Prediction of permafrost changes in Northeastern China under a changing climate. Sci. China Earth Sci. 2010, 41, 74–84. [Google Scholar] [CrossRef]
- Technical Secification for Engineering Geological Prospecting and Sampling of Constructions. Available online: https://www.mohurd.gov.cn/ (accessed on 19 January 2023).
- Bodman, G.B.; Colman, E.A. Moisture and Energy Conditions during Downward Entry of Water Into Soils. Soil Sci. Soc. Am. J. 1944, 8, 116–122. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lane, P.A. Slope Stability Analysis by Finite Elements. Géotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, D.F.; Li, C.G. Slope Stability Analysis Based on Elasto-Plastic Finite Element Method. Int. J. Numer. Methods Eng. 2005, 64, 1871–1888. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Lansivaara, T.; Wei, W.B. Two-Dimensional Slope Stability Analysis by Limit Equilibrium and Strength Reduction Methods. Comput. Geotech. 2007, 34, 137–150. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R.W. Associated and Non-Associated Visco-Plasticity and Plasticity in Soil Mechanics. Géotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Yuan, W.; Hu, Y.; Li, X.; Bai, B.; Wang, W.; Chen, X.; Ji, X. An Approach to Determining Critical Slip Surface Based on Displacement Field Analysis. Rock Soil Mech. 2016, 37, 1791–1798. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).