Kernel Density Derivative Estimation of Euler Solutions
Abstract
1. Introduction
2. Materials and Methods
2.1. Tensor Euler Deconvolution
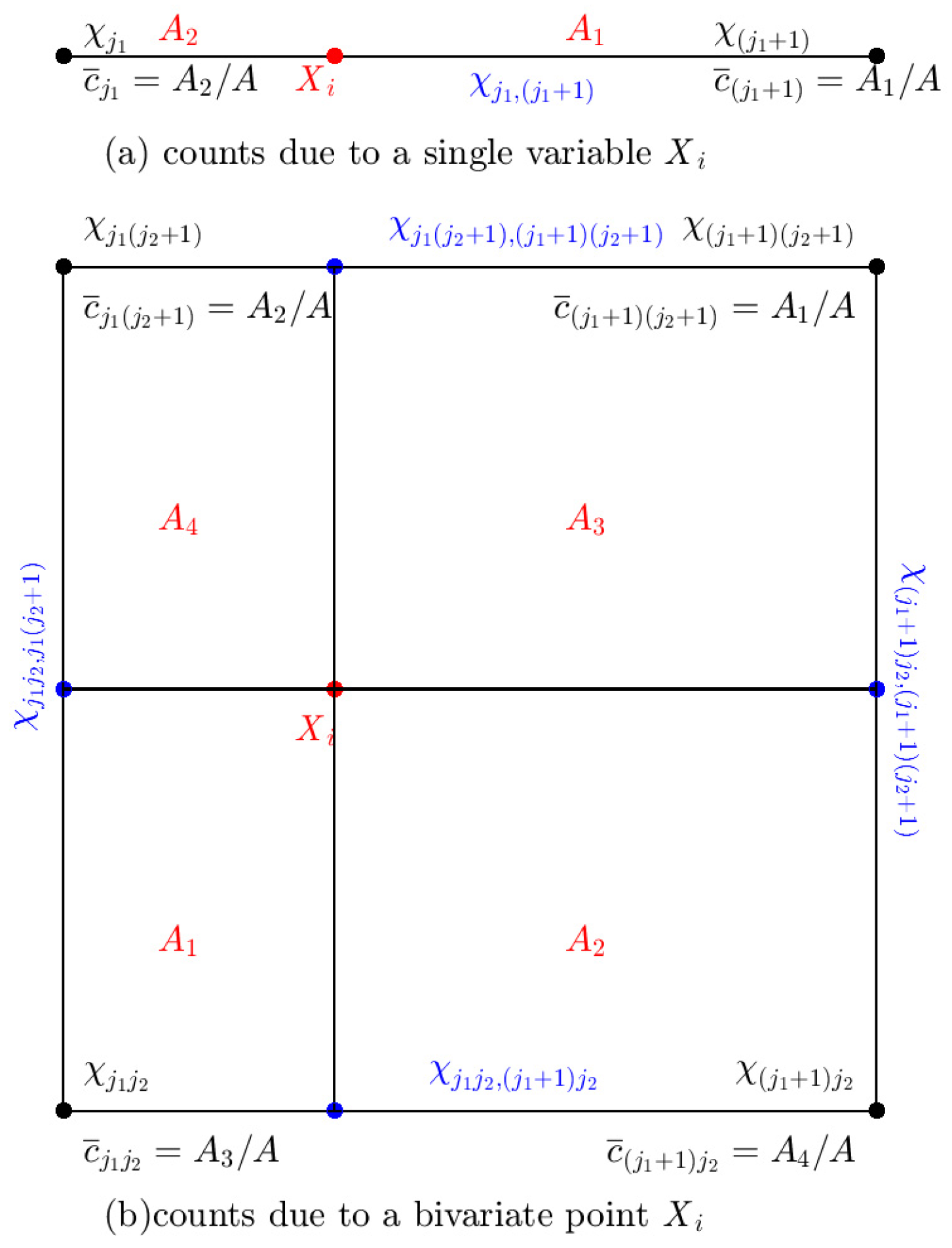
2.2. Multivariate KDDE of the Euler Solution Datasets
2.2.1. Computational Algorithm for Multivariate KDDE
| Algorithm 1. Multivariate kernel density derivative estimation (KDDE). |
2.2.2. Computational Performance of Multivariate KDDE
3. Results
3.1. Model Studies
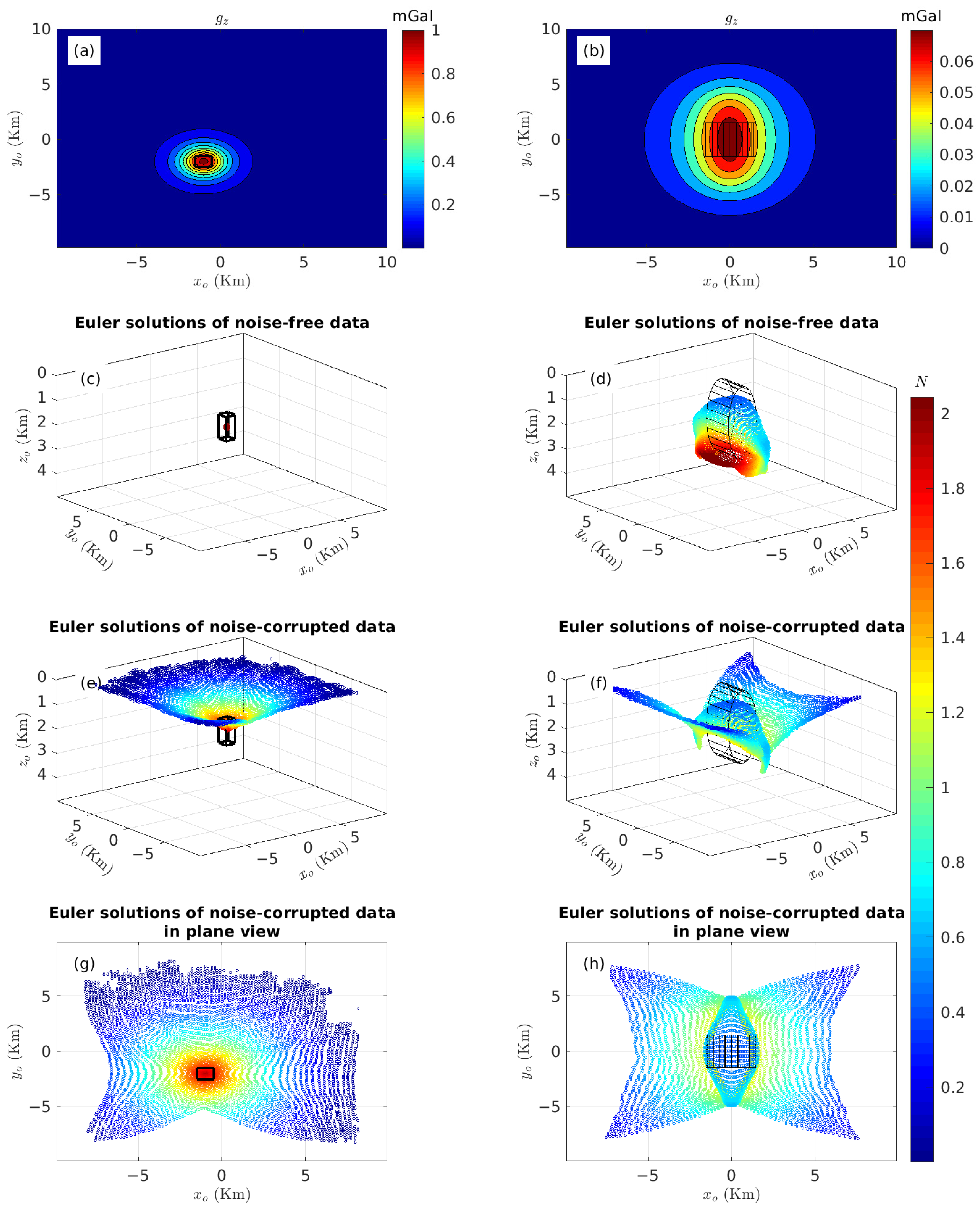
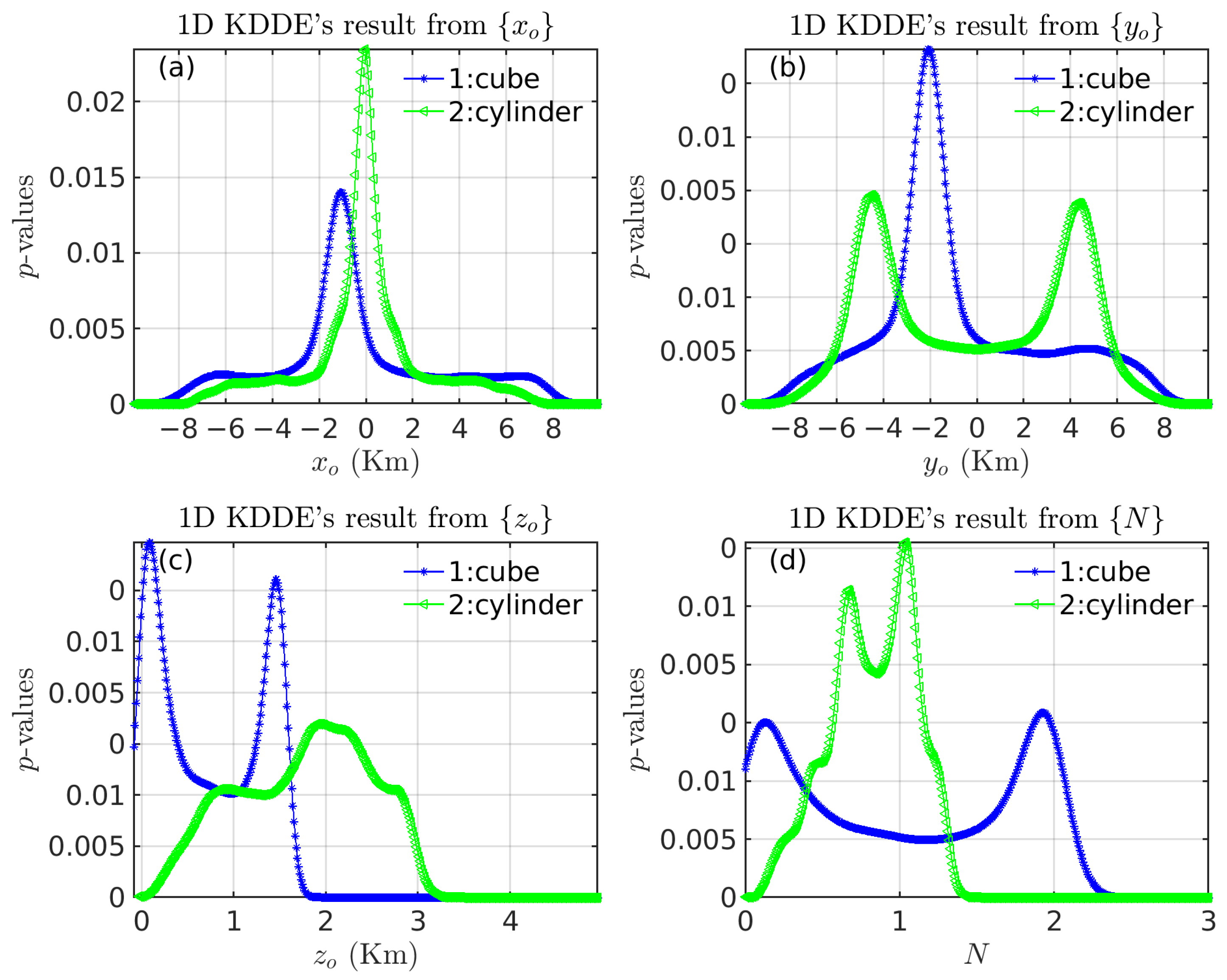
3.1.1. Verification of the Validity of the Multivariate KDDE Algorithm
3.1.2. Sensitivity of 3-D KDDE to Separations
3.1.3. Sensitivity of 3-D KDDE to Gaussian Noises
3.1.4. Sensitivity of 3-D KDDE to Grid Size
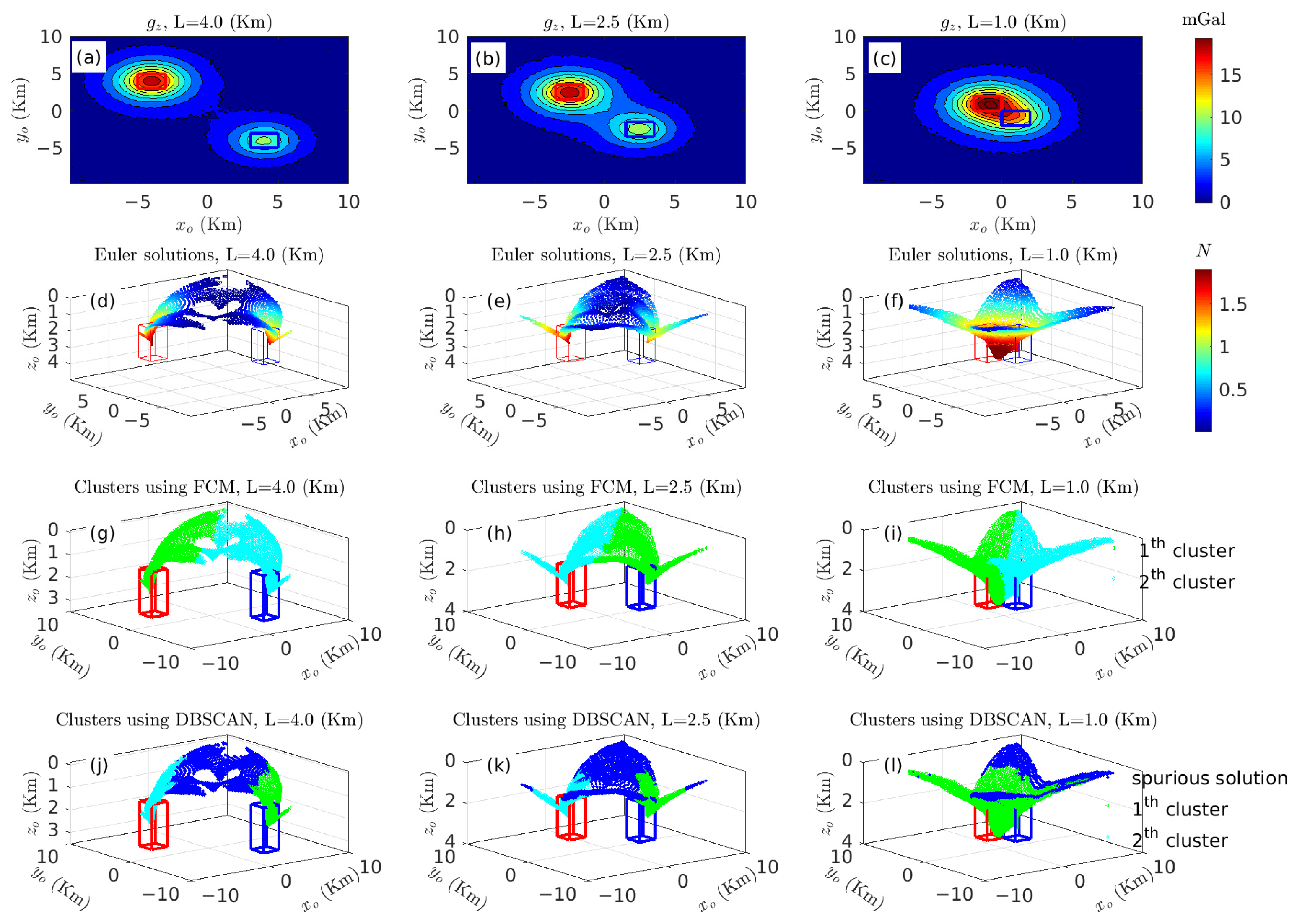
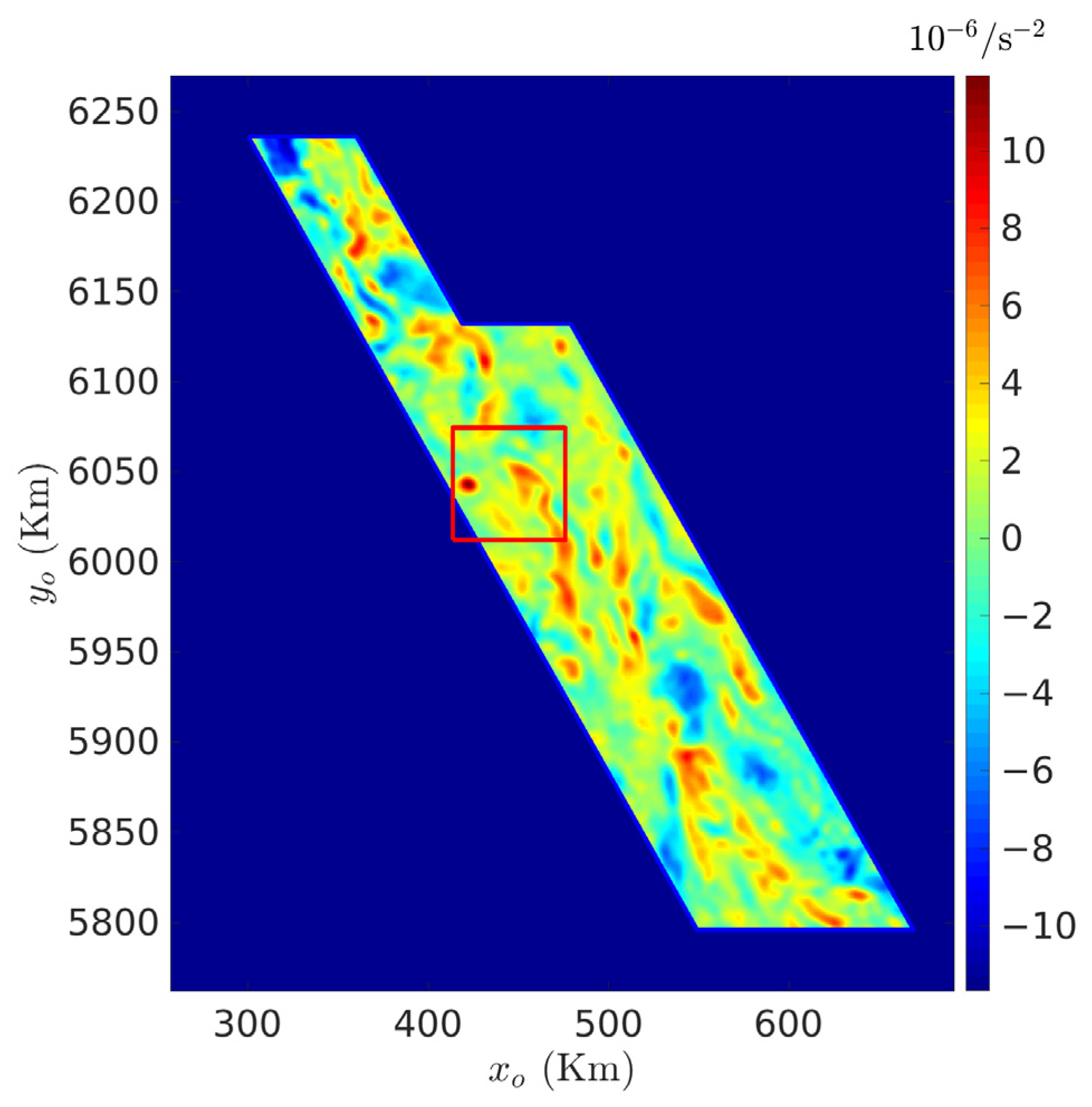
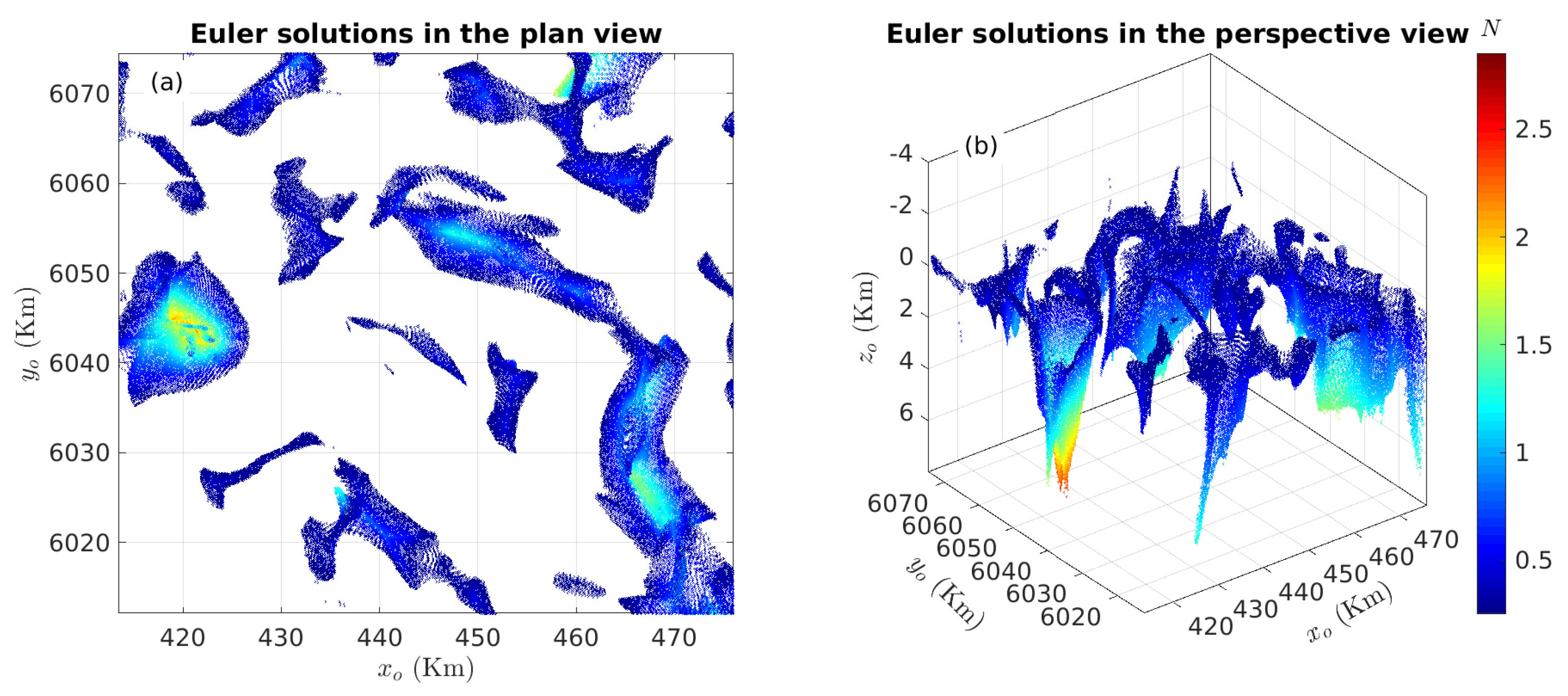
3.2. Case Study in British Columbia, Canada
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ugalde, H.; Morris, W. Deriving geological contact geometry from potential field data. Explor. Geophys. 2010, 41, 40–50. [Google Scholar] [CrossRef]
- Zheng, S.; Meng, X.; Wang, J. An edge-assisted smooth method for potential field data. J. Geophys. Eng. 2021, 18, 113–123. [Google Scholar] [CrossRef]
- Bertete-Aguirre, H.; Cherkaev, E.; Oristaglio, M. Non-smooth gravity problem with total variation penalization functional. Geophys. J. Int. 2002, 149, 499–507. [Google Scholar] [CrossRef]
- Namaki, L.; Gholami, A.; Hafizi, M.A. Edge-preserved 2-D inversion of magnetic data: An application to the Makran arc-trench complex. Geophys. J. Int. 2011, 184, 1058–1068. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Ellis, R.; Mukherjee, S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics 2004, 69, 925–937. [Google Scholar] [CrossRef]
- DiFrancesco, D.; Grierson, A.; Kaputa, D.; Meyer, T. Gravity gradiometer systems—Advances and challenges. Geophys. Prospect. 2009, 57, 615–623. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, C.; Lu, G.; CAO, S. Euler deconvolution of analytic signals of gravity gradient tensor. J. Cent. South Univ. (Sci. Technol.) (Chin.) 2015, 46, 217–222. [Google Scholar]
- Pan, Q.; Liu, D.; Feng, S.; Feng, M.; Fang, H. Euler deconvolution of the analytic signals of the gravity gradient tensor for the horizontal pipeline of finite length by horizontal cylinder calculation. J. Geophys. Eng. 2017, 14, 316–330. [Google Scholar] [CrossRef]
- Thompson, D. EULDPH: A new technique for making computer-assisted depth estimates from magnetic data. Geophysics 1982, 47, 31–37. [Google Scholar] [CrossRef]
- Reid, A.; Allsop, J.; Granser, H.; Millett, A.; Somerton, I. Magnetic interpretation in three dimensions using Euler deconvolution. Geophysics 1990, 55, 80–91. [Google Scholar] [CrossRef]
- Hearst, R.; Morris, W. Interpretation of the Sudbury structure through Euler deconvolution. In SEG Technical Program Expanded Abstracts 1993; Society of Exploration Geophysicists: Washington, DC, USA, 1993; pp. 421–424. [Google Scholar]
- Silva, J.B.C.; Barbosa, V.C.F. 3D Euler deconvolution: Theoretical basis for automatically selecting good solutions. Geophysics 2003, 68, 1962–1968. [Google Scholar] [CrossRef]
- Keating, P.; Pilkington, M. Euler deconvolution of the analytic signal and its application to magnetic interpretation. Geophys. Prospect. 2004, 52, 165–182. [Google Scholar] [CrossRef]
- Gerovska, D.; Araúzo-Bravo, M.J. Automatic interpretation of magnetic data based on Euler deconvolution with unprescribed structural index. Comput. Geosci. 2003, 29, 949–960. [Google Scholar] [CrossRef]
- Nabighian, M.; Hansen, R. Unification of Euler and Werner deconvolution in three dimensions via the generalized Hilbert transform. Geophysics 2001, 66, 1805–1810. [Google Scholar] [CrossRef]
- Stavrev, P.; Reid, A. Euler deconvolution of gravity anomalies from thick contact/fault structures with extended negative structural index. Geophysics 2010, 75, I51–I58. [Google Scholar] [CrossRef]
- Beiki, M. TSVD analysis of Euler deconvolution to improve estimating magnetic source parameters: An example from the Åsele area, Sweden. J. Appl. Geophys. 2013, 90, 82–91. [Google Scholar] [CrossRef]
- Wang, J.; Meng, X.; Li, F. New improvements for lineaments study of gravity data with improved Euler inversion and phase congruency of the field data. J. Appl. Geophys. 2017, 136, 326–334. [Google Scholar] [CrossRef]
- Dewangan, P.; Ramprasad, T.; Ramana, M.V.; Desa, M.; Shailaja, B. Automatic interpretation of magnetic data using Euler deconvolution with nonlinear background. Pure Appl. Geophys. 2007, 164, 2359–2372. [Google Scholar] [CrossRef]
- Ekinci, Y.L.; Balkaya, Ç.; Şeren, A.; Kaya, M.A.; Lightfoot, C.S. Geomagnetic and geoelectrical prospection for buried archaeological remains on the Upper City of Amorium, a Byzantine city in midwestern Turkey. J. Geophys. Eng. 2014, 11, 015012. [Google Scholar] [CrossRef]
- Rabeh, T.; Khalil, A. Characterization of fault structures in southern Sinai Peninsula and Gulf of Suez region using geophysical data. Environ. Earth Sci. 2015, 73, 1925–1937. [Google Scholar] [CrossRef]
- Ravat, D. Analysis of the Euler Method and Its Applicability in Environmental Magnetic Investigations. J. Environ. Eng. Geophys. 1996, 1, 229–238. [Google Scholar] [CrossRef]
- Hsu, S.K. Imaging magnetic sources using Euler’s equation. Geophys. Prospect. 2002, 50, 15–25. [Google Scholar] [CrossRef]
- Melo, F.F.; Barbosa, V.C.F. What to expect from Euler deconvolution estimates for isolated sources. In Proceedings of the 15th International Congress of the Brazilian Geophysical Society & EXPOGEF, Rio de Janeiro, Brazil, 31 July–3 August 2017; pp. 1092–1097. [Google Scholar]
- Mikhailov, V.; Pajot, G.; Diament, M.; Price, A. Tensor deconvolution: A method to locate equivalent sources from full tensor gravity data. Geophysics 2007, 72, I61–I69. [Google Scholar] [CrossRef]
- Cooper, G. Iterative Euler deconvolution. Explor. Geophys. 2021, 52, 468–474. [Google Scholar] [CrossRef]
- Beiki, M. Analytic signals of gravity gradient tensor and their application to estimate source location. Geophysics 2010, 75, I59–I74. [Google Scholar] [CrossRef]
- Wang, M.; Guo, Z.; Luo, Y.; Luo, F.; Guo, H.; Qu, J. The application of Tilt-Euler deconvolution method to potential field data processing and interpretation. Geophys. Geochem. Explor. (Chin.) 2012, 36, 126–132. [Google Scholar]
- Florio, G.M.R. On the application of Euler deconvolution to the analytic signal. Geophysics 2006, 71, L87–L93. [Google Scholar] [CrossRef]
- Reid, A.B.; Thurston, J.B. The structural index in gravity and magnetic interpretation: Errors, uses, and abuses. Geophysics 2014, 79, J61–J66. [Google Scholar] [CrossRef]
- Zhou, W.; Nan, Z.; Li, J. Self-constrained Euler deconvolution using potential field data of different altitudes. Pure Appl. Geophys. 2016, 173, 2073–2085. [Google Scholar] [CrossRef]
- Farrelly, B. What is Wrong with Euler Deconvolution? In Proceedings of the 59th EAGE Conference & Exhibition. Geneva, Switzerland, 26–30 May 1997; p. cp-131-00225. [Google Scholar] [CrossRef]
- Zhang, C.; Mushayandebvu, M.; Reid, A.; Fairhead, J.; Odegard, M. Euler deconvolution of gravity tensor gradient data. Geophysics 2000, 65, 512–520. [Google Scholar] [CrossRef]
- FitzGerald, D.; Reid, A.; McInerney, P. New discrimination techniques for Euler deconvolution. Comput. Geosci. 2004, 30, 461–469. [Google Scholar] [CrossRef]
- Reid, A.B.; Ebbing, J.; Webb, S.J. Avoidable Euler errors—The use and abuse of Euler deconvolution applied to potential fields. Geophys. Prospect. 2014, 62, 1162–1168. [Google Scholar] [CrossRef]
- Silva, J.; Barbosa, V.; Medeiros, W. Scattering, symmetry, and bias analysis of source-position estimates in Euler deconvolution and its practical implications. Geophysics 2001, 66, 1149–1156. [Google Scholar] [CrossRef]
- Li, X. On the use of different methods for estimating magnetic depth. Lead. Edge 2003, 22, 1090–1099. [Google Scholar] [CrossRef]
- Barbosa, V.C.; Silva, J.B.; Medeiros, W.E. Stability analysis and improvement of structural index estimation in Euler deconvolution. Geophysics 1999, 64, 48–60. [Google Scholar] [CrossRef]
- Fedi, M. DEXP: A fast method to determine the depth and the structural index of potential fields sources. Geophysics 2007, 72, I1. [Google Scholar] [CrossRef]
- Melo, F.F.; Barbosa, V.C. Correct structural index in Euler deconvolution via base-level estimates. Geophysics 2018, 83, J87–J98. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, H.; Sekelani, S.; Wu, Z. An improved Tilt-Euler deconvolution and its application on a Fe-polymetallic deposit. Ore Geol. Rev. 2019, 114, 103114. [Google Scholar] [CrossRef]
- Salem, A.; Ravat, D. A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data. Geophysics 2003, 68, 1952–1961. [Google Scholar] [CrossRef]
- Salem, A.; Ravat, D.; Smith, R.; Ushijima, K. Interpretation of magnetic data using an enhanced local wavenumber (ELW) method. Geophysics 2005, 70, L7–L12. [Google Scholar] [CrossRef]
- Salem, A.; Williams, S.; Fairhead, D.; Smith, R.; Ravat, D. Interpretation of magnetic data using tilt-angle derivatives. Geophysics 2008, 73, L1–L10. [Google Scholar] [CrossRef]
- Ma, G. Combination of horizontal gradient ratio and Euler (HGR-EUL) methods for the interpretation of potential field data. Geophysics 2013, 78, J53–J60. [Google Scholar] [CrossRef]
- Cooper, G.R.; Whitehead, R.C. Determining the distance to magnetic sources. Geophys. J. Soc. Explor. Geophys. 2016, 81, J25–J34. [Google Scholar] [CrossRef]
- Cooper, G.R.J. Determining the depth and location of potential field sources without specifying the structural index. Arab. J. Geosci. 2017, 10, 438. [Google Scholar] [CrossRef]
- Yao, C.; Guan, Z.; Wu, Q.; Ahang, Y.; Liu, H. An analysis of Euler deconvolution and its improvement. Geophys. Geochem. Explor. (Chin.) 2004, 28, 150–155. [Google Scholar]
- Sanchez-Rojas, J.; Palma, M. Crustal density structure in northwestern South America derived from analysis and 3-D modeling of gravity and seismicity data. Tectonophysics 2014, 634, 97–115. [Google Scholar] [CrossRef]
- Mikhailov, V.; Galdeano, A.; Diament, M.; Gvishiani, A.; Agayan, S.; Bogoutdinov, S.; Graeva, E.; Sailhac, P. Application of artificial intelligence for Euler solutions clustering. Geophysics 2003, 68, 168–180. [Google Scholar] [CrossRef]
- Gvishiani, A.D.; Mikhailov, V.O.; Agayan, S.M.; Bogoutdinov, S.R.; Graeva, E.M.; Diament, M.; Galdeano, A. Artificial intelligence algorithms for magnetic anomaly clustering. Izv. Phys. Solid Earth 2002, 38, 545–559. [Google Scholar] [CrossRef]
- Husson, E.; Guillen, A.; Séranne, M.; Courrioux, G.; Couëffé, R. 3D Geological modelling and gravity inversion of a structurally complex carbonate area: Application for karstified massif localization. Basin Res. 2018, 30, 766–782. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kim, D.-H.; Chung, C.-W. Multi-dimensional selectivity estimation using compressed histogram information. SIGMOD Rec. 1999, 28, 205–214. [Google Scholar] [CrossRef]
- Dal Moro, G.; Pipan, M.; Gabrielli, P. Rayleigh wave dispersion curve inversion via genetic algorithms and marginal posterior probability density estimation. J. Appl. Geophys. 2007, 61, 39–55. [Google Scholar] [CrossRef]
- Trainor-Guitton, W.; Hoversten, G.M. Stochastic inversion for electromagnetic geophysics: Practical challenges and improving convergence efficiency. Geophysics 2011, 76, F373–F386. [Google Scholar] [CrossRef]
- Boschetti, F.; Hornby, P.; Horowitz, F.G. Wavelet based inversion of gravity data. Explor. Geophys. 2001, 32, 48–55. [Google Scholar] [CrossRef]
- Fregoso, E.; Palafox, A.; Moreles, M.A. Initializing cross-gradients joint inversion of gravity and magnetic data with a Bayesian surrogate gravity model. Pure Appl. Geophys. 2020, 177, 1029–1041. [Google Scholar] [CrossRef]
- Bosch, M.; Meza, R.; Jiménez, R.; Hönig, A. Joint gravity and magnetic inversion in 3D using Monte Carlo methods. Geophysics 2006, 71, G153–G156. [Google Scholar] [CrossRef]
- Ekinci, Y.L.; Balkaya, Ç.; GÖKtÜRkler, G. Parameter estimations from gravity and magnetic anomalies due to deep-seated faults: Differential evolution versus particle swarm optimization. Turk. J. Earth Sci. 2019, 28, 860–881. [Google Scholar] [CrossRef]
- Bosch, M.; McGaughey, J. Joint inversion of gravity and magnetic data under lithologic constraints. Lead. Edge 2001, 20, 877–881. [Google Scholar] [CrossRef]
- Sheather, S.J. Density estimation. Stat. Sci. 2004, 19, 588–597. [Google Scholar] [CrossRef]
- Duong, T.; Cowling, A.; Koch, I.; Wand, M.P. Feature significance for multivariate kernel density estimation. Comput. Stat. Data Anal. 2008, 52, 4225–4242. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.O.R.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar] [CrossRef]
- Daszykowski, M.; Walczak, B.; Massart, D.L. Looking for natural patterns in data. Chemom. Intell. Lab. Syst. 2001, 56, 83–92. [Google Scholar] [CrossRef]
- Ugalde, H.; Morris, W. Cluster analysis of Euler deconvolution solutions: New filtering techniques and geologic strike determination. Geophysics 2010, 75, L61–L70. [Google Scholar] [CrossRef]
- Michel, H.; Nguyen, F.; Kremer, T.; Elen, A.; Hermans, T. 1D geological imaging of the subsurface from geophysical data with Bayesian Evidential Learning. Comput. Geosci. 2020, 138, 104456. [Google Scholar] [CrossRef]
- Eckert-Gallup, A.; Martin, N. Kernel density estimation (KDE) with adaptive bandwidth selection for environmental contours of extreme sea states. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Allsop, J.M.; Evans, C.J.; McDonald, A.J.W. Visualizing and interpreting 3-D Euler solutions using enhanced computer graphics. Surv. Geophys. 1991, 12, 553–564. [Google Scholar] [CrossRef]
- Reid, A.B. Euler deconvolution: Past, present and future—A review. In Proceedings of the 65th SEG Meeting, Houston, TX, USA, 8–13 October 1995; pp. 272–273. [Google Scholar] [CrossRef]
- Gramacki, A. Nonparametric Kernel Density Estimation and Its Computational Aspects: Studies in Big Data; Springer: Cham, Switzerland, 2018; Volume 37, pp. 58–59. [Google Scholar]
- Grana, D.; Della Rossa, E. Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion. Geophysics 2010, 75, O21–O37. [Google Scholar] [CrossRef]
- Buland, A.; Kolbjørnsen, O.; Hauge, R.; Skjæveland, Ø.; Duffaut, K. Bayesian lithology and fluid prediction from seismic prestack data. Geophysics 2008, 73, C13–C21. [Google Scholar] [CrossRef]
- Zhou, W.-Y.; Ma, G.-Q.; Hou, Z.-L.; Qin, P.-B.; Meng, Z.-H. The study on the joint Euler deconvolution method of full tensor gravity data. Chin. J. Geophys. (Chin.) 2017, 60, 4855–4865. [Google Scholar] [CrossRef]
- Florio, G.; Fedi, M. Multiridge euler deconvolution. Geophys. Prospect. 2014, 62, 333–351. [Google Scholar] [CrossRef]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 161–167. [Google Scholar]
- Chacón, J.E.; Duong, T. Multivariate Kernel Smoothing and Its Applications; CRC Press: Boca Raton, FL, USA, 2018; pp. 185–190. [Google Scholar]
- Gramacki, A.; Gramacki, J. FFT-Based Fast Computation of Multivariate Kernel Density Estimators With Unconstrained Bandwidth Matrices. J. Comput. Graph. Stat. 2017, 26, 459–462. [Google Scholar] [CrossRef]
- Guidoum, A.C. Kernel Estimator and Bandwidth Selection for Density and Its Derivatives. The Kedd Package, Version 1.03, October 2015. Available online: https://rdrr.io/cran/kedd/f/inst/doc/kedd.pdf (accessed on 28 January 2023).
- Van Kerm, P. Adaptive kernel density estimation. Stata J. 2003, 3, 148–156. [Google Scholar] [CrossRef]
- Wand, M.P. Fast computation of multivariate kernel estimators. J. Comput. Graph. Stat. 1994, 3, 433–445. [Google Scholar] [CrossRef]
- González-Manteiga, W.; Sánchez-Sellero, C.; Wand, M.P. Accuracy of binned kernel functional approximations. Comput. Stat. Data Anal. 1996, 22, 1–16. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: New York, NY, USA, 1986; pp. 61–65. [Google Scholar]
- Rao, S. Interpolation Models. In The Finite Element Method in Engineering, 6th ed.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 81–127. [Google Scholar] [CrossRef]
- Cook, S.A.; Aanderaa, S.O. On the minimum computation time of functions. Trans. Am. Math. Soc. 1969, 142, 291–314. [Google Scholar] [CrossRef]
- Agarwal, R.; Cooley, J.W. New algorithms for digital convolution. IEEE Trans. Acoust. Speech Signal Process. 1977, 25, 392–410. [Google Scholar] [CrossRef]
- Winograd, S. Arithmetic Complexity of Computations; SIAM: Philadelphia, PA, USA, 1980; Volume 33. [Google Scholar] [CrossRef]
- Teukolsky, S.A.; Flannery, B.P.; Press, W.H.; Vetterling, W.T. Numerical Recipes in C: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar] [CrossRef]
- Arndt, J. Matters Computational: Ideas, Algorithms, Source Code; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mikhailov, V.O.; Diament, M. Some aspects of interpretation of tensor gradiometry data. Izv. Phys. Solid Earth 2006, 42, 971–978. [Google Scholar] [CrossRef]
- Pašteka, R.; Kušnirák, D.; Götze, H.J. Stabilization of the Euler deconvolution algorithm by means of a two steps regularization approach. In Proceedings of the EGM 2010 International Workshop, Capri, Italy, 11–14 April 2010; p. cp-165-00058. [Google Scholar] [CrossRef]
- Phillips, N.; Thi, N.H.N.; Thomson, V.; Mira, G.A.G.I. 3D inversion modelling, integration, and visualization of airborne gravity, magnetic, and electromagnetic data: The Quest Project. Geosci. BC Rep. 2009, 2009–2015. [Google Scholar] [CrossRef]
- Reichheld, S.A. Documentation and Assessment of Exploration Activities Generated by Geoscience BCData Publications, QUEST Project, Central British Columbia (NTS 093A, B, G, H, J, K, N, O, 094C, D); Geoscience BC: Vancouver, BC, Canada, 2013; pp. 125–130. [Google Scholar]
- Montaj, G.O. The Core Software Platform for Working with Large Volume Gravity and Magnetic Spatial Data; Geosoft Inc.: Toronto, ON, Canada, 2008. [Google Scholar]
- Li, Y.; Oldenburg, D. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- LaBrecque, D.J.; Owen, E.; Dailey, W.; Ramirez, A.L. Noise and occam’s inversion of resistivity tomography data. In SEG Technical Program Expanded Abstracts 1992; Society of Exploration Geophysicists: New Orleans, LA, USA, 1992; pp. 397–400. [Google Scholar] [CrossRef]
- Siripunvaraporn, W.; Sarakorn, W. An efficient data space conjugate gradient Occam’s method for three-dimensional magnetotelluric inversion. Geophys. J. Int. 2011, 186, 567–579. [Google Scholar] [CrossRef]
- Hou, Z.-L.; Wang, E.-D.; Zhou, W.-N.; Wu, G.-C. Euler deconvolution of gravity gradiometry data and the application in Vinton Dome. Oil Geophys. Prospect. (Chin.) 2019, 54, 472–479+242. [Google Scholar] [CrossRef]




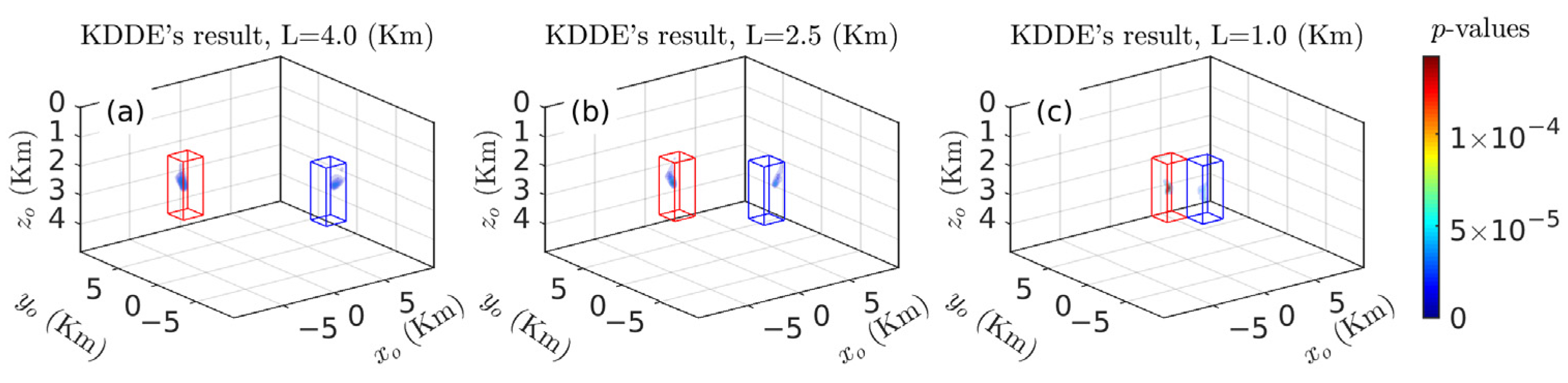

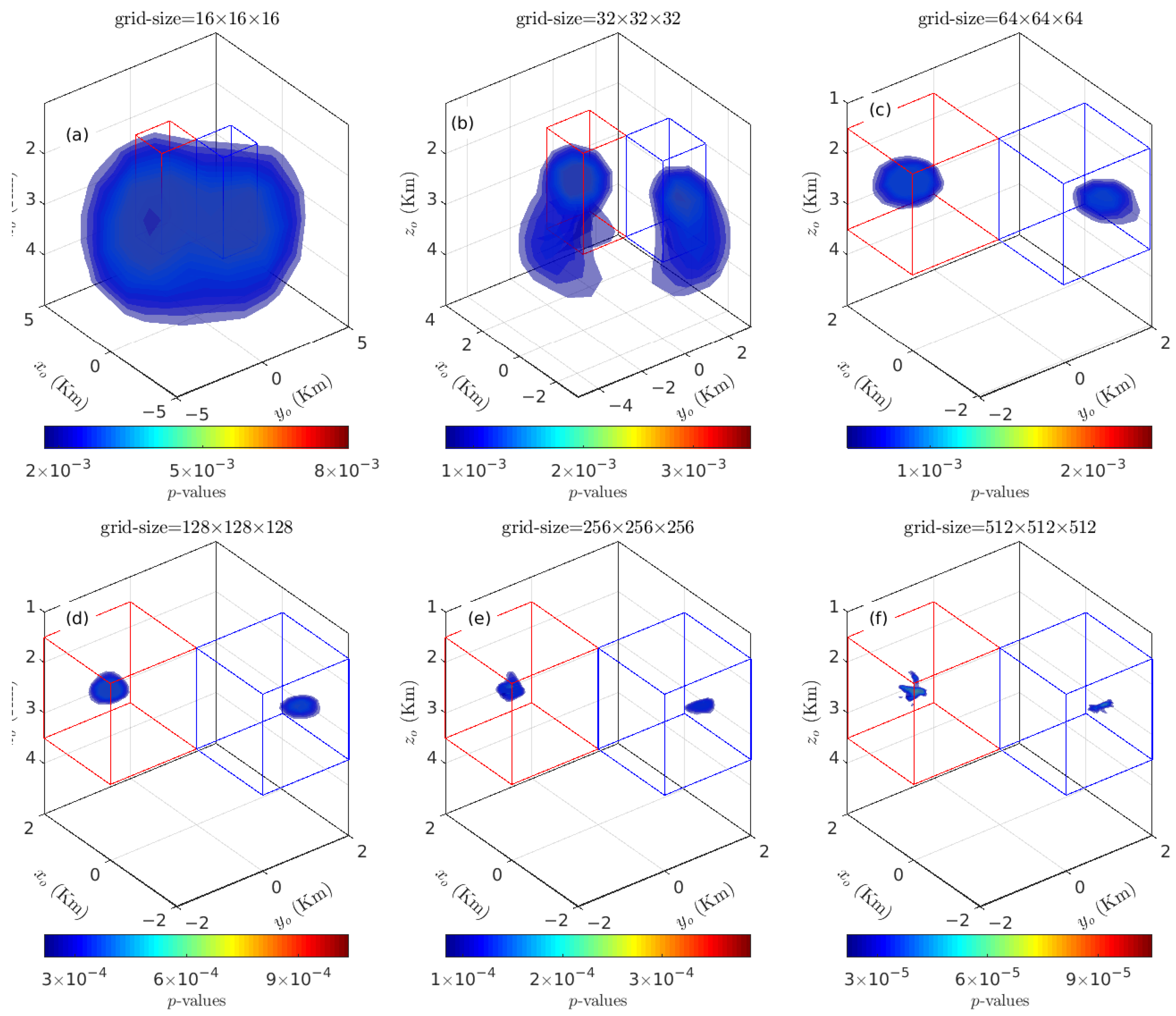




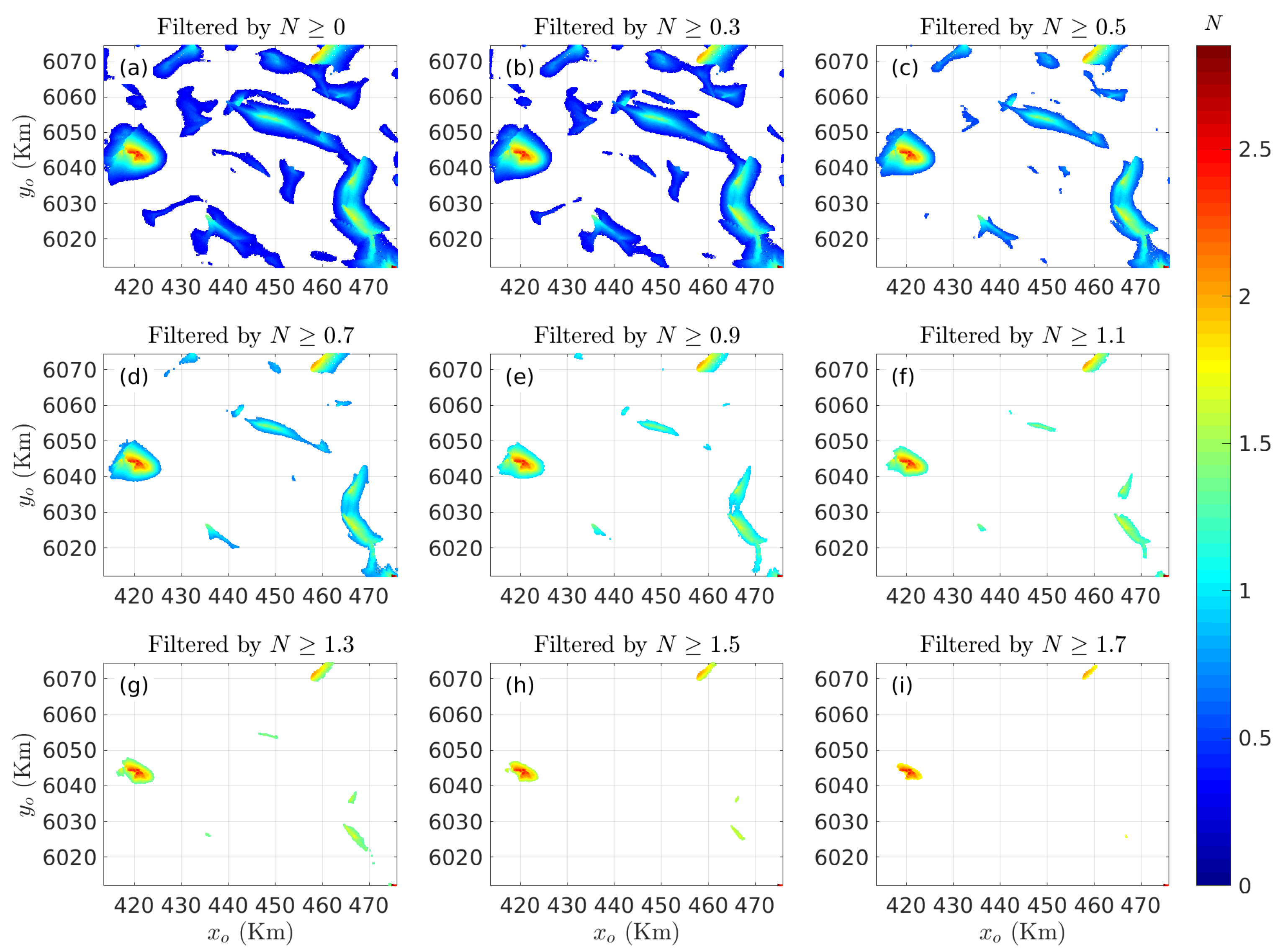

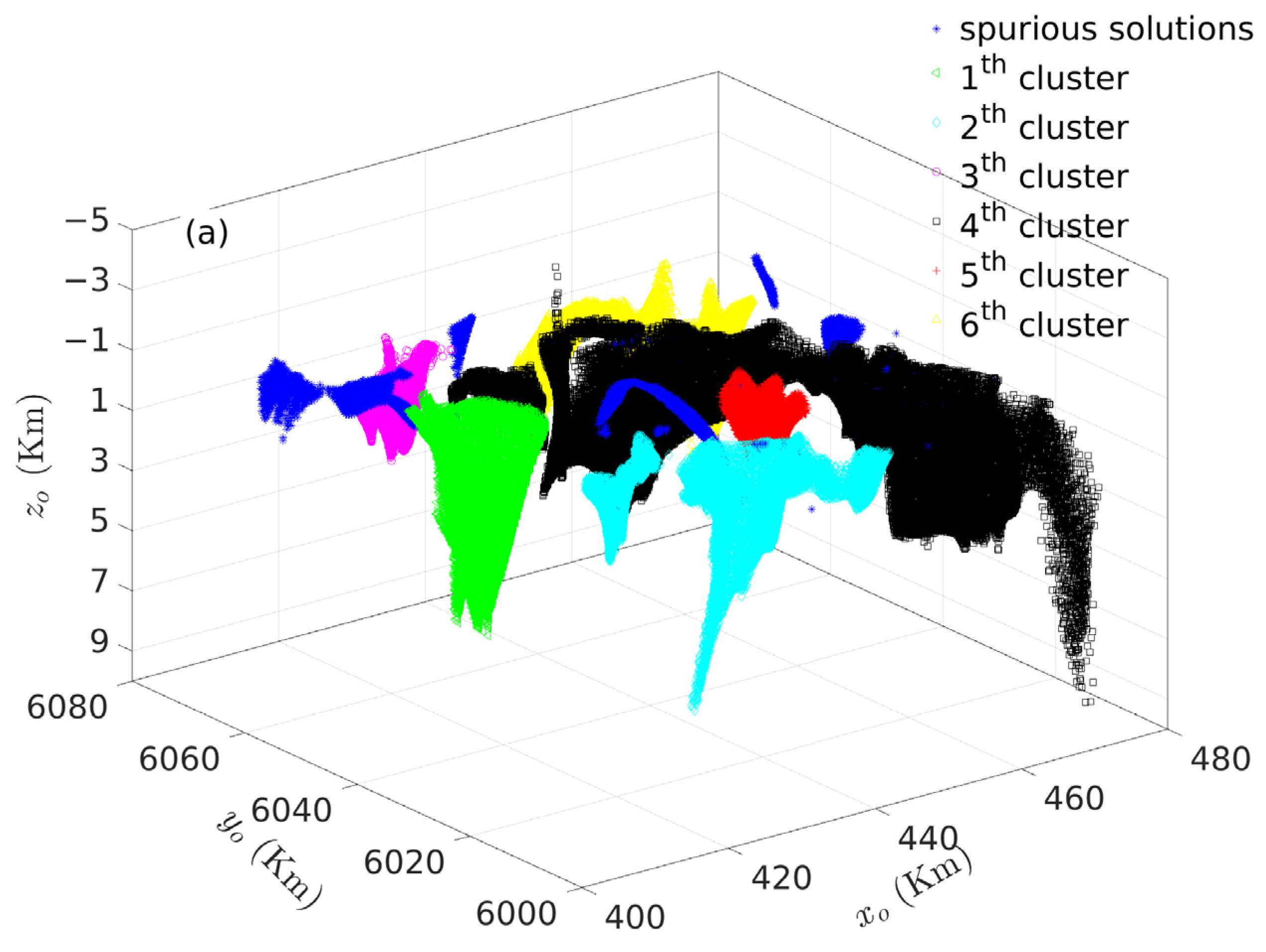



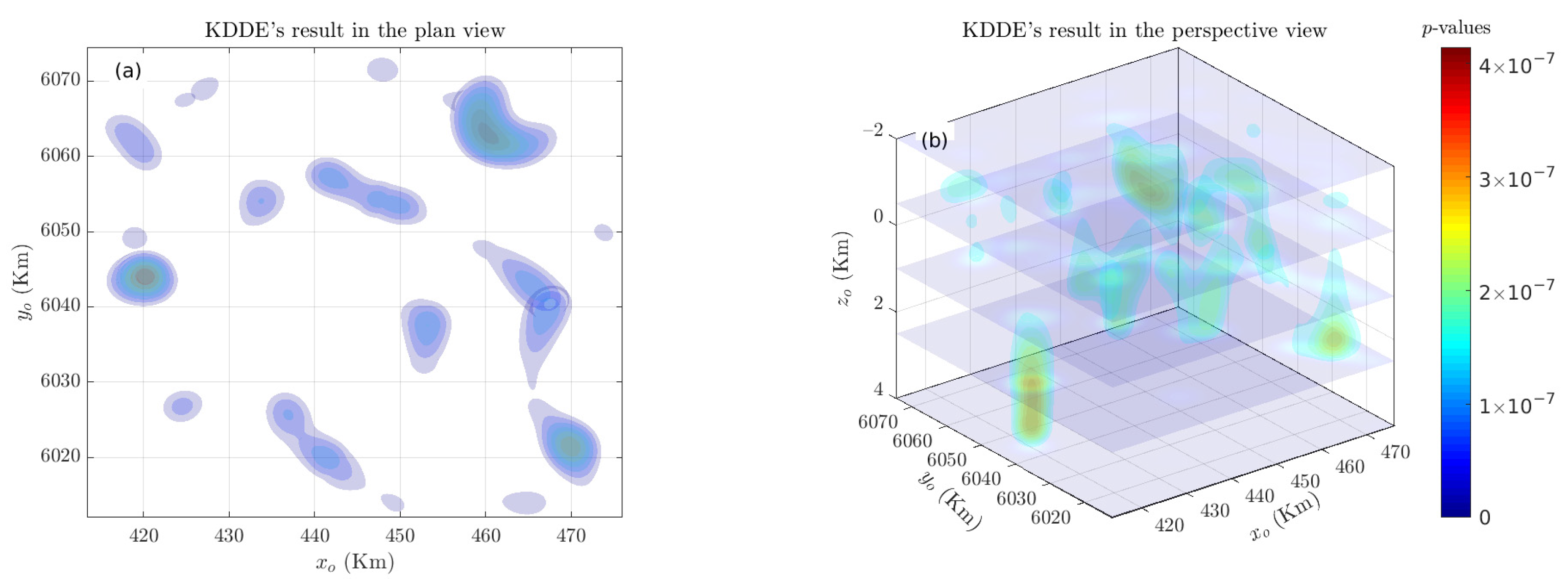
| Model | Centroid | Radii | Lengths | Theoretical N |
|---|---|---|---|---|
| Cube | (−1000, −2000, 1500) | / | 1000 × 1000 × 1000 | 2 |
| Cylinder | (0, 0, 2500) | 1000 | 4000 | 1~2 |
| Separations | Centroid of Left Cube | Centroid of Right Cube |
|---|---|---|
| 4000 | (−4000, 4000, 2500) | (4000, −4000, 2500) |
| 2500 | (−2500, 2500, 2500) | (2500, −2500, 2500) |
| 1000 | (−1000, 1000, 2500) | (1000, −1000, 2500) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, S.; Deng, Y.; Yang, B.; Lu, G.; Hu, X.; Mao, Y.; Hu, S.; Zhu, Z. Kernel Density Derivative Estimation of Euler Solutions. Appl. Sci. 2023, 13, 1784. https://doi.org/10.3390/app13031784
Cao S, Deng Y, Yang B, Lu G, Hu X, Mao Y, Hu S, Zhu Z. Kernel Density Derivative Estimation of Euler Solutions. Applied Sciences. 2023; 13(3):1784. https://doi.org/10.3390/app13031784
Chicago/Turabian StyleCao, Shujin, Yihuai Deng, Bo Yang, Guangyin Lu, Xiangyun Hu, Yajing Mao, Shuanggui Hu, and Ziqiang Zhu. 2023. "Kernel Density Derivative Estimation of Euler Solutions" Applied Sciences 13, no. 3: 1784. https://doi.org/10.3390/app13031784
APA StyleCao, S., Deng, Y., Yang, B., Lu, G., Hu, X., Mao, Y., Hu, S., & Zhu, Z. (2023). Kernel Density Derivative Estimation of Euler Solutions. Applied Sciences, 13(3), 1784. https://doi.org/10.3390/app13031784






