1. Introduction
Owing to its high aesthetic value, laminated glass enjoys an ever growing interest in modern architecture. It typically consists of several layers of glass and polymeric viscous interlayers [
1]. This constitution retains the functional properties of an ordinary glass, but its properties after cracking are improved [
2] as interlayers hold individual fragments of fractured glass together, thus partially preventing a catastrophic failure. Although experimental work plays a key role in promoting new structures to practical applications, an effective structure can hardly be designed without numerical simulations addressing the response of a given structure to a variety of conditions not generally accessible experimentally.
Developing a robust and accurate computational model for glass laminates is a complex task. While layered configuration may prevent collapse and improves post breakage behavior, its simulation proves complicated as glass is essentially damaged by brittle failure with a very small process zone and negligible ductility. Although a number of numerical techniques applied to float or laminated glass have been proposed, this scientific topic is still widely open to further investigation. See, for example, [
3] for an extensive overview of numerical methods applied to float glass, where the standard finite element method with the Rankine failure criterion is compared to the extended finite element method, discrete element method, and their combinations. Similarly, some critical aspects and several modeling techniques applied to laminated glass structures are presented in [
4,
5]. The application of peridynamic models [
6] is also worth mentioning.
At present, a very promising approach to the modeling of brittle fracture is the application of the phase-field model [
7,
8]. The principal advantage of this family of models is its ability to predict crack initialization as well as crack branching [
9] with no additional ad hoc criteria. This is attributed to variational consistency as the crack development arises directly from the energy minimization of the regularized functional for a brittle material.
The present paper examines the ability of the phase field model to simulate gradual fracture of a laminated glass subjected to several consecutive low velocity impacts. This issue has already been investigated in [
10] with the help of commercial LS-DYNA software where the results of an extensive experimental program were also presented. Attention is therefore afforded to theoretical and computational aspects of the phase field model in light of plates [
11], while experimental measurements used to support our numerical implementation are outlined only briefly just for the sake of completeness. Proceeding in the footsteps of [
10], the five (5LG) and seven (7LG) layer laminates consisting of three and four plies of a float glass bonded to a PVB (polyvinyl butyral) interlayers are examined, respectively. In particular, the ability of the phase field model to estimate the response of a laminated glass observed experimentally is tested by comparing the measured and simulated distributions of contact force and gradually evolving crack patterns.
The remainder of the paper is structured as follows. We begin with a short review of the experimental part of the project in
Section 2. Essential details of the spatially reduced Mindlin Reissner model with phase field damage are introduced in
Section 3. Remarks on time integration and implementation of the Hertz contact and interlayer viscoelasticity are also presented. Numerical implementation including the modeling strategy is discussed first in
Section 4 in the framework of a single glass ply (SG) followed by the simulation of the two selected laminates in
Section 5. A thorough discussion arising from a comparative study with experimental measurements is also provided. The principal outcomes are finally summarized in
Section 6.
2. Experiments
The concept of sacrificial-glass-ply design [
12] was adopted in [
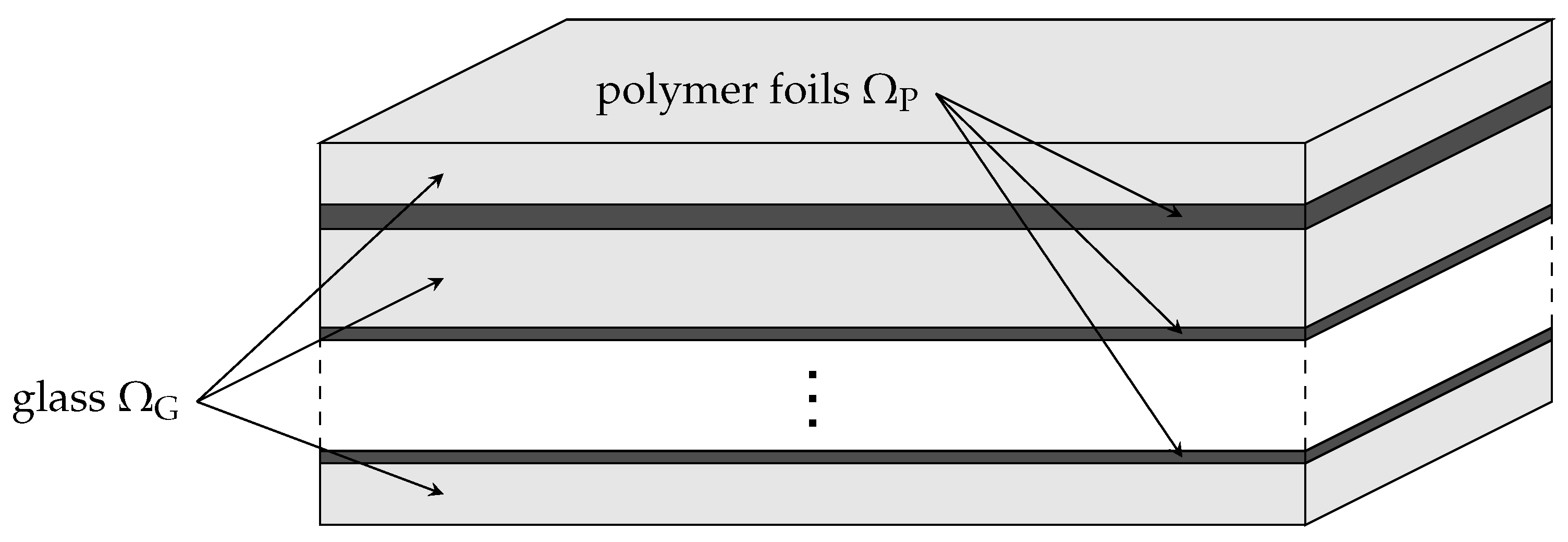
10] to propose two specific geometries. In such a case, the outer glass layers are made thinner as they mainly serve to protect the inner glass layers, which in turn play the key role in accommodating the applied load. Additionally, the outer glass layers are expected to crack to dissipate, together with the polymer interlayers, the impactor energy thus enhancing the bearing capacity of the laminated structure. Herein, the 5LG laminate is composed of three glass layers and two PVB interlayers, whereas the 7LG laminate consists of four glass layers bonded to three PVB interlayers. An illustrative example of such a laminate is displayed in
Figure 1. Geometrical details of both composites are stored in
Table 1.
The tested samples were suspended in a vertical position on a pair of steel ropes along vertical edges to approximate free boundary conditions [
13], thus eliminating the effect of mechanical supports. The low velocity impact was induced horizontally via an 800 mm long pendulum device (impactor) having a cylindrical shape with a hemispherical nose with the diameter of 50 mm. The required impact energy, defined as the kinetic energy of the impactor
with the impact velocity
, was achieved by dropping the 48.2 kg impactor from a given height
. To examine the influence of subsequent impacts of growing intensity on a laminate fracture response, the impact height was gradually increased by 5 cm as seen in
Table 2.
For illustration, we present the results of three particular samples of the two laminates. The response of individual samples after individual impacts is summarized in
Table 2. Considering the impacted glass on the left-hand side, the empty circle |∘| indicates the onset of damage in a given ply, whereas the filled circle |•| identifies a glass layer which has already been broken during previous impacts. Empty spaces | | represent unbroken glass layers.
Although limited to three samples only, the results confirm the advantage of a sacrificial-glass-ply design which expects the outer glass layers to fracture, so the inner glass layers are still capable of sustaining further loads. This is particularly evident for samples where the impacted glass layer fractured at the initial stage of loading (5LG-1, 7LG-1, 7LG-3). Unfortunately, the results also suggest a certain degree of variability in fracture response of laminates potentially attributed to a random distribution of initial surface flaws of unprotected (outer) glass layers. This was also confirmed by our study on a single glass ply in [
14] devoted merely to the application of various damage models implemented in the LS-DYNA software. These findings make the predictive capability of any numerical model rather difficult especially in the framework of deterministic modeling. To perform stochastic simulations goes, however, beyond the present scope owing mainly to insufficient experimental data to identify, for example, a statistical distribution of impact energies. Instead, we concentrate on tuning the computational model to represent one particular experiment. If successful, this will serve as a stepping stone for more complex stochastic analysis.
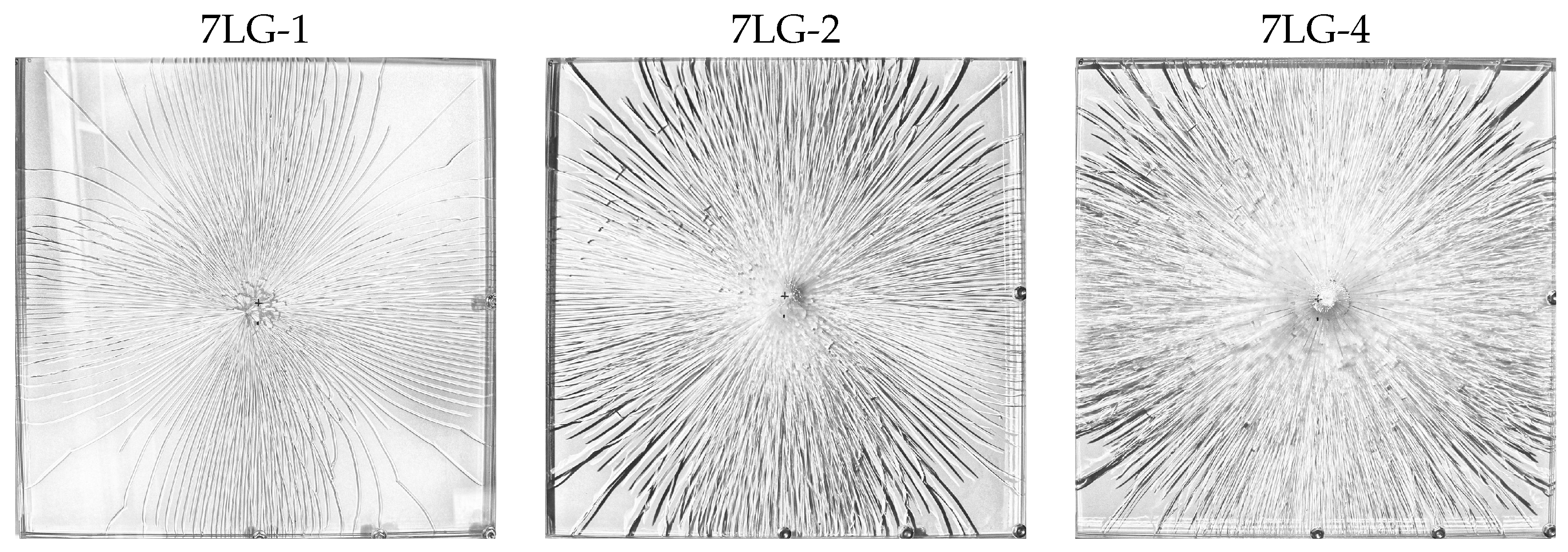
The final crack patterns are presented in
Figure 2 and
Figure 3 showing a typical distribution of radial cracks of different lengths seldomly connected by short parts of secondary cracks. In addition, notice that, apart from diagonal cracks, the cracks bend to arrive at the sample edges in a perpendicular direction. This is discussed when comparing the fracture patterns with numerical predictions.
3. Phase-Field Model
The application of phase field model to damage has afforded considerable attention; see [
8,
15,
16] (to cite a few), so only the basic relations are reviewed in this section focusing on the formulation in the context of layered plate theory, time integration, aspects of implementation of the Hertz contact, and the issue of viscoelasticity.
The model is based on variational framework of a brittle fracture [
17], where the bulk energy competes with the dissipated energy via energy minimization. To this end, the Hamilton’s principle of stationary action is employed and the displacement field
and crack topology
are obtained by minimizing the action integral
where
is the time from a given range. Minimizing this functional may prove unfeasible as it is performed over all admissible crack topologies
. To remedy this, the phase-field model brings regularization and introduces a scalar damage field
d, which represents a relative measure of damage as a transition from the intact material
to a fully damaged material
indicating a crack. Therefore, the action integral is dependent on two continuous fields
u and
d instead of a discontinuous topological set
, i.e.,
which is more suitable for finite element implementation. The kernel of this integral is called the Lagrangian
and, for a linear dynamic system, it reads
where
,
,
,
are the kinetic energy, the elastic energy, the dissipated energy, and the external work, respectively. We assume that the first and the last terms are not affected by the phase field model. Thus, assuming an elastic domain
with the density
loaded by external tractions
over
provides
The remaining two terms, i.e., the elastic potential
, representing the stored energy of an undamaged material, and dissipated energy
then allow for the transition from a purely elastic response to the phase-field damage model. The present formulation complies with the physical requirement permitting the compressive stress to be transmitted across the crack even for a fully damaged material with
. Hence, the elastic energy is decomposed into an active (tensile) part
, which is degraded by the damage field, and a passive (compressive) part
, which remains independent of the damage field, to obtain
where the strain energy densities
are defined later in
Section 3.4.
The last term in the Lagrangian (
3) is the regularized dissipated energy
given by
where
and
l are the material parameters, and function
controls the type of regularization. Moreover, the constant
is fully determined by function
as
; see [
15] for detailed description of individual terms. A specific format of function
is elaborated later in
Section 3.4 providing details of the assumed decomposition.
3.1. Time Discretization
Standard finite difference method is used to integrate Equation (
2) in time which gives the discrete form of the action integral for time instances
in the form
The adopted discrete form of the Lagrangian
leads to the explicit central difference scheme for fields
,
, where
represents the time step assumed constant in the present study. This is particularly advantageous as minimization of Equation (
7) can be performed for the displacement field
u and the damage parameter
d separately.
We begin with a weak form of Equation (
3) to write
where
These equations are identical to purely elastic response except for the elastic energy being divided into an active and a passive part. Note that this decomposition is performed on the displacement field at time instant , while the unknown displacement field at time is determined explicitly. The only difficulty of this scheme is thus the decomposition of strain energy density .
Minimizing the discrete format of action integral (
7) (
) with respect to the phase-field damage parameter
d yields
In order to arrive at a physically correct crack evolution and no crack healing, the pointwise irreversibility condition must be additionally imposed
Regardless of the choice of function
, the irreversibility condition (
13) makes the weak form (
12) a nonlinear problem that needs to be solved as a variational inequality.
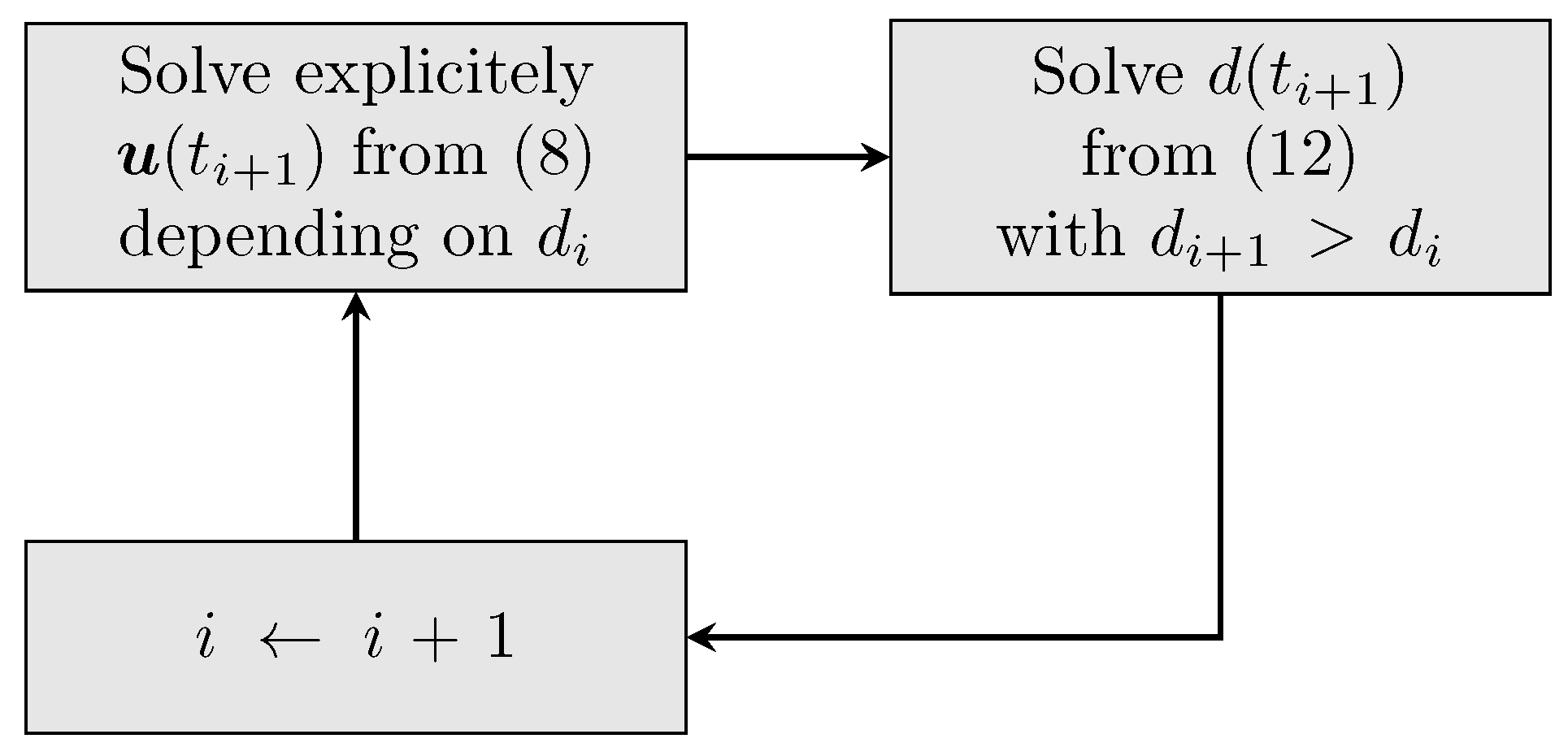
For the sake of clarity, the presented explicit dynamic procedure [
18] is schematically represented in
Figure 4. Finally, note that the spatial distribution of fields
u and
d is found in a standard way using the finite element method.
3.2. Mindlin Plate Model
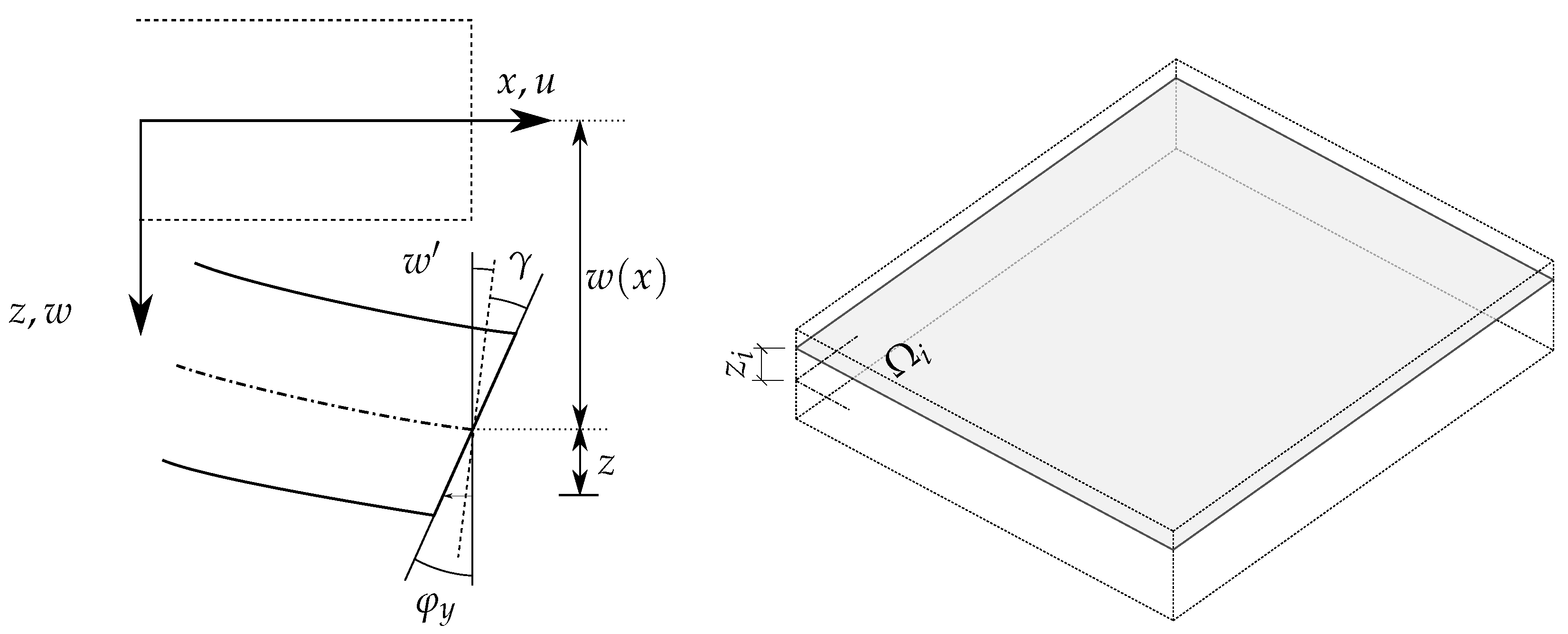
A full 3D model is computationally demanding which suggests that application of a more effective spatially reduced plate model. We start from a single layer model which will be subsequently extended to laminated plates. The Mindlin–Reissner theory, which assumes that the cross-section remains planar after deformation but not necessarily perpendicular to the midsurface of the plate, is adopted. Commonly, the model is obtained by assuming a linear distribution of displacements and rotations and subsequent through-thickness integration. Owing to damage, this integration must be carried out numerically. The elastic energy then receives the form
where the overall thickness
h is numerically divided into individual layers
i of thickness
with in-plane stress
and strain
vectors, see
Figure 5. The midsurface
with the
coordinate system is the new spatially reduced domain of interest. Point out that the parameter
is an auxiliary material constant which indicates that the amount of shear subjected to damage, i.e., whether the shear stress is still transmitted across the crack. Notice that only the part of out-of-plane shear contribution that enters the active part of strain energy density
is degraded by function
.
The constitutive equations for in-plane stress
and strain
fields and out-of-plane shear stresses
and strains
are provided by
where
represents the plane stress stiffness tensor expressed in terms of Lame’s coefficients
and
and
is the identity tensor.
The strains
and
follow from standard strain–displacement relations and are written in terms of in-plane displacements
, out of plate deflection
w, and rotations of the cross section
as
where the matrix
is given by
Equation (
12) is also subjected to spatial reduction via through-thickness integration to obtain
where the integrated active part of the strain energy density
drives the damage evolution. In this regard, it appears useful to replace the strain energy density
by a constant
representing the strain energy density calculated on the basis of the maximum tensile stress. This rewrites Equation (
21) as
3.3. Layered Mindlin Plate Model
Consider a plate consisting of
N layers indexed by
, recall
Figure 1. The indices
are therefore reserved for the glass layers. Several options are available to enforce displacement continuity at common interfaces. In some applications, the use of Lagrangian multipliers proves advantageous as these are directly linked to the interface shear stresses. However, grounding the formulation of the present model on explicit dynamics calls for the reduction of the number of degrees of freedom as much as possible. Therefore, the continuity of in-plane displacement
u is enforced directly by substitution considering the following two kinematic constraints:
The first equation enforces the out-of-plane incompressibility of the layers and the latter one represents the in-plane displacement continuity at the interfaces. The formulation for glass layers, identified by odd indices
, remains intact, whereas kinematic variables of damage-free interlayers with even indices
are substituted by expressions determined by restrictions (
24) and (
25) as
As an illustrative example, consider a 5-layer laminate (three solid glasses and two interlayers) which, after substitution, is fully described by seven unknowns: .
It should also be mentioned that the layered plate model requires solving Equation (
23) for each glass layer. This allows for different crack patterns to develop in individual layers.
3.4. Model Selection and Decomposition
The phase field model is determined by the decomposition of strain energy density into active and passive parts and by the selection of function .
The most physically sound response is simulated using spectral decomposition of functional (
5) proposed in [
19]. However, this decomposition contains singularities in the finite element application and resulted in instabilities in our simulations. On the hand, stable solutions were experienced when considering the decomposition based on a volumetric-deviatoric split as suggested in [
20]. The active and passive contributions to the strain energy density
are then given by
where
is a deviatoric part of the strain tensor
, and
K is the bulk modulus.
As for the dissipation function, the model is valid for an arbitrary choice of
. The present formulation follows Pham [
21] and considers a simple relation
with the degradation function defined as
Unlike common representation of a dissipation function
suggested by Bourdin et al. [
17], which considers damage evolution already at the onset of loading, the adopted linear version allows for postponing the damage initiation beyond this point, and so not affecting the initial transfer of energy from the impactor into the plate.
For the present choice of
, the fracture energy
can be written in terms of the tensile strength
, Young’s modulus
E, and the length scale parameter
l as [
22]
While strictly valid for one-dimensional (1D) setting, Equation (
33) is generally adopted also for simulations in higher dimensions. Owing to the presence of length scale parameter
l, typically equal to two times the characteristic length of the smallest element in the finite element mesh [
19]; this relation is also mesh dependent.
For a typical edge length of a triangular element of 2 mm employed for the analysis of laminates discussed in
Section 2, the fracture energy stored in
Table 3 may considerably exceed a typical value of
Jm
used for glass. While the value of
MPa corresponds to the characteristic quasi-static strength in tensile bending defined by the European Standard EN 16612 [
23], the larger values, e.g.,
MPa, used particularly in the analysis of a single glass ply, represents the initial value of tensile strength we adopted to postpone the onset of damage in numerical simulations and consequently to arrive at the glass response comparable with experimental observations. Point out that even larger values of the initial tensile strength were considered in [
10]. Since at the onset of damage this value almost immediately drops down to the actual strength of 45 MPa, the associated fracture energy enters the analysis only at a very beginning stage of fracture process; see
Section 4 ahead for further details. Nevertheless, realistic values of
would still call for much smaller elements to avoid snap-back at a material level. On the contrary, this would lead to computationally unfeasible simulations. Thus, only the large values around 300 Jm
to simulate the crack propagation were tested in all present calculations.
3.5. Hertz Contact
The transfer of kinetic energy from the impactor to the glass plate is implemented through a simple Hertz relation. The contact force is then given by
where
is the displacement of the impactor,
is the out of plane displacement of the impacted node with the coordinate
. The positive part operator
ensures that the contact force is transmitted during the impactor penetration only. The proportionality constant
k (contact stiffness) is written as
where
R is the radius of the impactor and
and
are the Young modulus and Poisson ratio of the glass plate and impactor, respectively. Although the force is nonlinear, it can be introduced into the variational framework using pseudopotential
The impactor represents an additional degree of freedom so its contribution
must be supplemented to the overall kinetic energy.
3.6. Viscoelasticity of Interface Layer
The response of a polymer interlayer is significantly time-dependent. However, even in a low velocity impact, the response time is in the range of milliseconds, so that the rate dependency can be neglected and an empirical rule can be used to evaluate its current shear stiffness. In particular, adopting the
rule [
24], the instantaneous shear modulus of the interlayer
is provided by
where
is the current time and
is the actual temperature. Function
can be approximated by the Generalized Maxwell chain model [
25] as
where
N stands for the number of Maxwell units. The corresponding shear stiffnesses
associated with the selected relaxation times
are obtained by fitting Equation (
39) to experimental measurements [
26,
27]. The temperature shift factor
follows from the well known Williams–Landel–Ferry equation
In the present study, we adopt the results derived for the PVB interlayer in [
26]. These are summarized in
Table 4 complemented with
kPa. The constants
and
were found for the reference temperature
T0 = 20 °C.
4. Damage of Single Glass Ply
The explicit dynamic model is first validated for a single glass ply focusing on both the state before and after the crack initiation. A nondestructive step allows us to check the ability of the computational model and the Hertz contact to predict the dynamic response of glass, whereas the damage step identified the capability of the phase field model. To this end, both the evolution of contact force and displacements at points recorded experimentally were monitored to gain information on how the energy is transferred from the impactor into the glass laminate. While the experiment is described in detail in [
14], the presented experimental results have not been published yet.
With reference to tested samples, a glass plate with dimensions 0.5 m × 0.5 m, recall also
Table 1, is examined. Because of symmetry, only a quarter of the model with appropriate symmetry boundary conditions is considered. The material parameters of both the glass and impactor needed in numerical simulations are summarized in
Table 5. As already mentioned in
Section 2, the radius
R of the impactor head entering Equation (
35) is set to 50 mm.
An example of the finite element mesh made of triangular elements is presented in
Figure 6. To support the use of these elements in numerical analysis of laminates, the application of bilinear quadrilateral plate elements with reduced integration of out-of-plane shear is also tested and compared with a full three-dimensional (3D) calculations exploiting higher order tetrahedral elements. Details of the adopted finite element meshes are listed in
Table 6.
The impact of element type and the corresponding mesh on the ply response is tested first considering a simple example of a plate weakened by an initial crack. The plate is impacted with the energy of 148 J (impact height of 30 cm). The initial crack is introduced by enforcing the damage
for coordinates
to spread over the width of two elements (
Figure 7 left) for a given value of the shear parameter
; recall Equations (
14) and (
15). In accordance with
Section 3.4, we set
, where
is the edge length of the smallest element in the mesh.
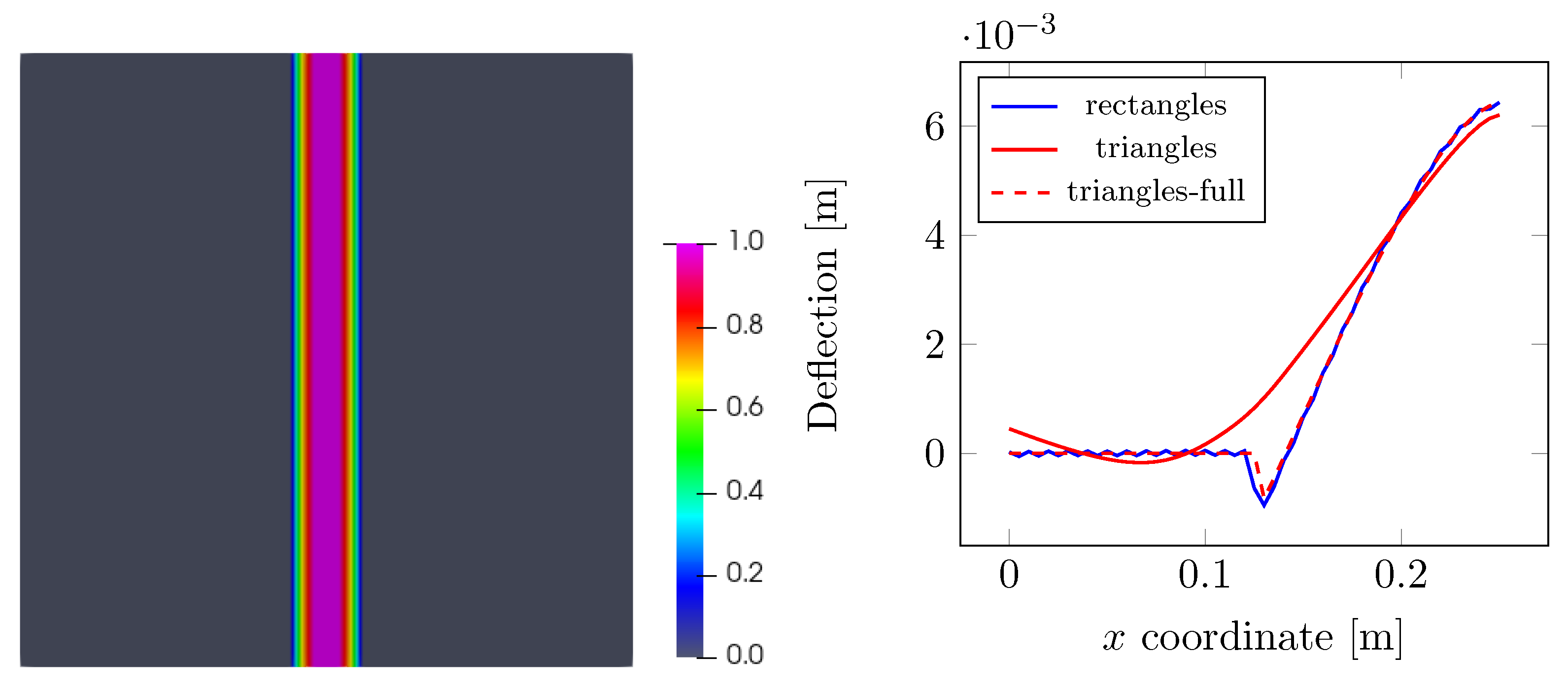
The variation of deflection across the crack at the selected time
s is plotted in
Figure 7 on the right side. The solid lines represent the case of no damage in shear with
; thus, only the bending part in Equation (
15) is affected by damage and the shear strains contribute entirely to
. While the mesh with quadrilateral elements provides reasonable response, we see that, for a triangular mesh, the wave passes across the crack. This can be attributed to spurious shear strain transfer. However, when degrading the the whole out-of-plane shear contribution by setting
(the shear contribution now taken entirely by
is fully degraded by function
) in the analysis with a triangular mesh, we arrive at the expected response as shown by the dashed line.
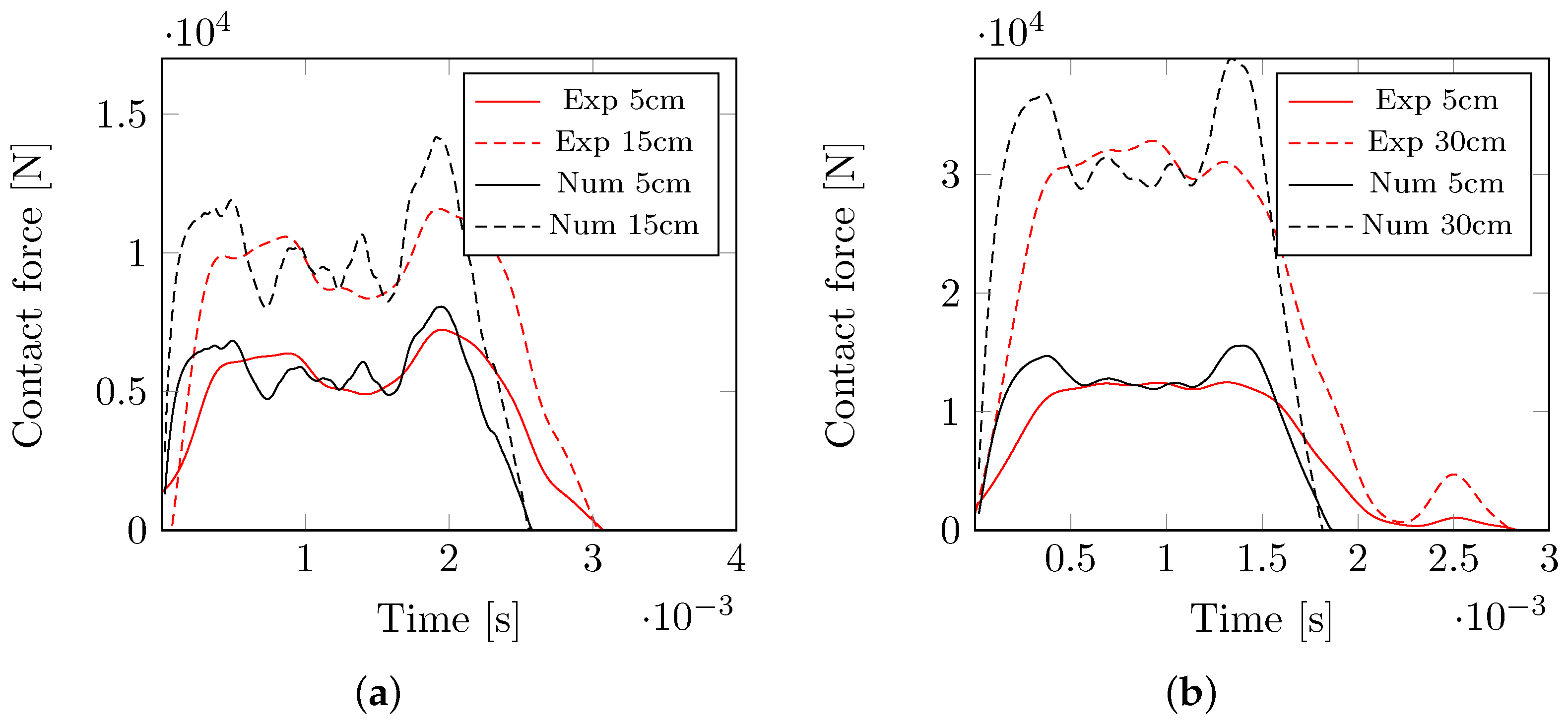
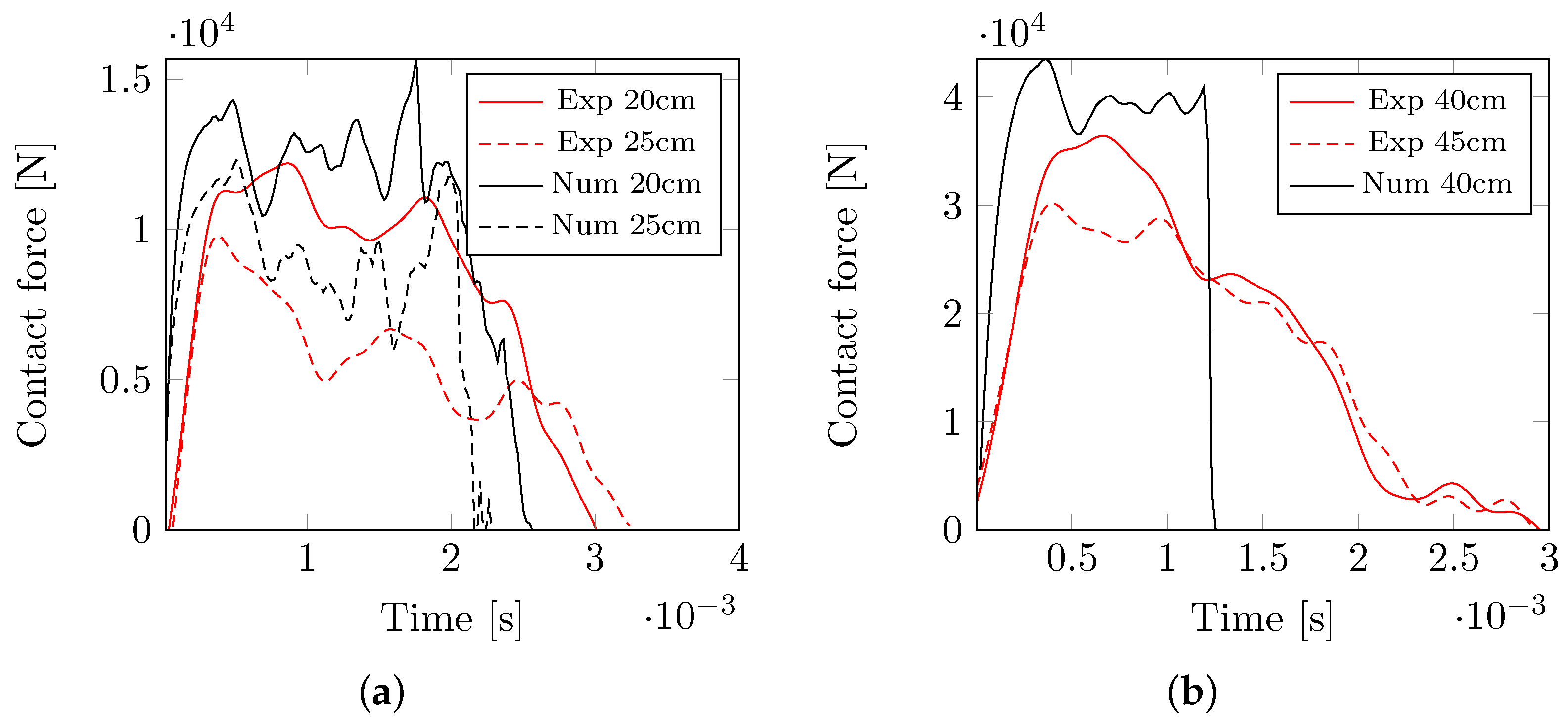
The next example addresses a non-destructive test allowing us to compare the experimentally measured contact force with numerical predictions up to the impact height of 30 cm. The results for various types of meshes, recall
Table 6, are presented in
Figure 8a for
cm. As seen, all meshes provide a comparable response matching well the experimental measurements. However, it has been observed that four node quadrilateral elements, albeit using one point integration in shear, experience a zero energy mode manifested by local vibration from element to element. For that reason and given the results in
Figure 7, the triangular mesh in
Figure 6 with shear degradation option was used in all subsequent analyses. Its applicability is further promoted by the comparative study displayed in
Figure 8b, where a reasonable agreement with experimental results is suggested even for a relatively high impact energy.
The last experiment is concerned with adjusting the onset of damage. This is because the stress calculated in the contact zone between an impactor and glass exceeds the glass strength
earlier than the glass breaks in experiments [
13,
28]. This is quite important also with the phase-field analysis. For illustration, we consider a destructive test where the tested sample broke already at the impact height
cm. The results appear in
Figure 9,
Figure 10 and
Figure 11.
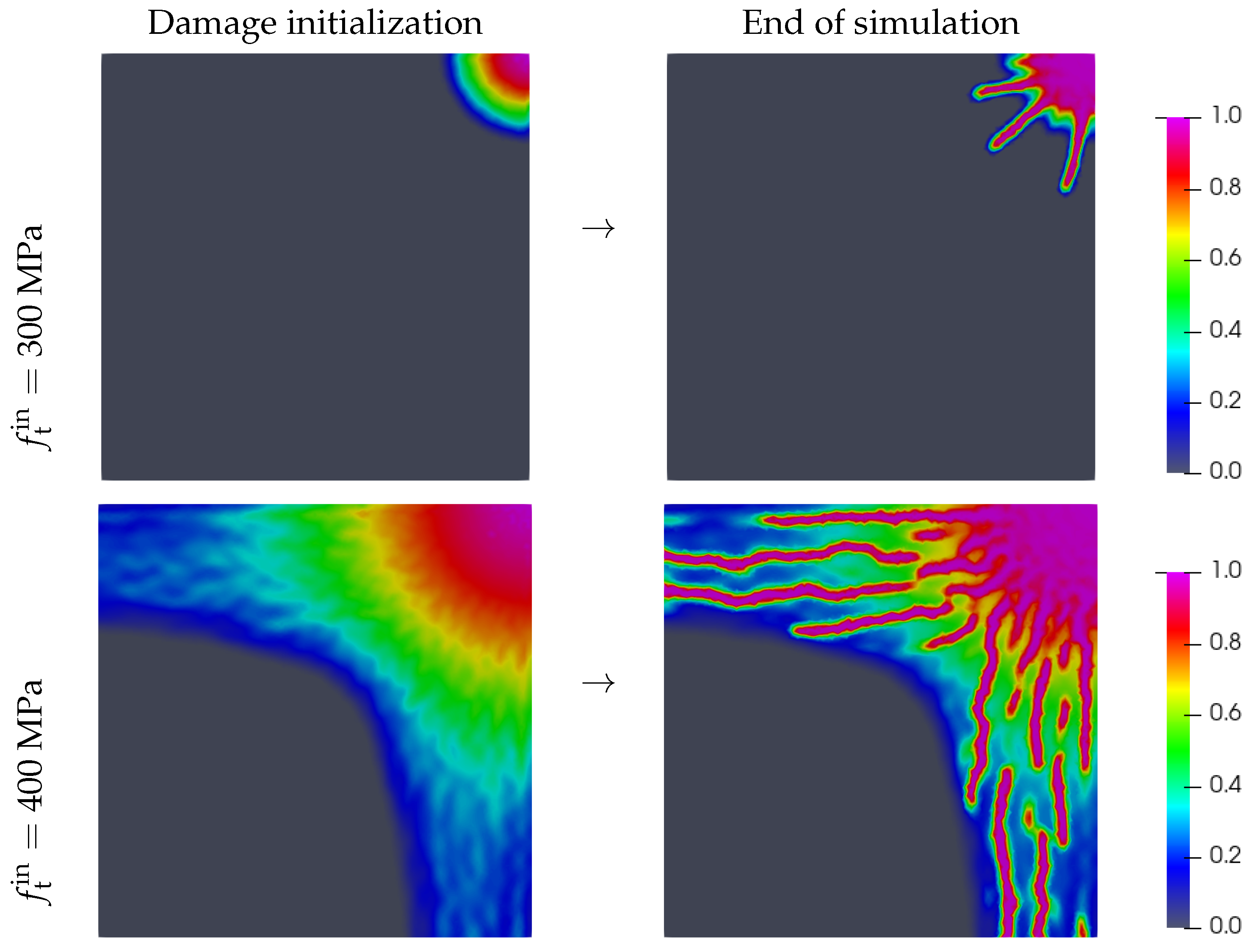
Figure 9a indicates that assuming the actual static tensile strength
MPa promotes the damage initiation too early in comparison to the experimental results, while delaying the onset of damage via artificially increasing the tensile strength to
MPa shows a considerable improvement in the prediction of the contact force.
Figure 10 further suggests that controlling the crack initiation by
MPa does not generate sufficient energy to drive a rapid crack evolution and crack branching as observed experimentally [
10,
14].
A remedy is provided by restoring the initial high tensile strength to its physically correct value at the onset of damage [
10], i.e.,
MPa. The former value ensures accommodation of sufficient energy, whereas the latter value allows its rapid dissipation leading to more realistic crack pattern. While seemingly simple, this step still deserves attention, particularly in the framework of the presented phase field model.
Remind that the evolution of damage is driven by fracture energy. However, the relationship between the tensile strength
and fracture energy
provided by Equation (
33) is valid for 1D analysis only. When used with a general 3D analysis, such calculated fracture energy may lead to damage initiation for stresses, which do not exceed the prescribed tensile strength. Thus, in the present study, the point of switching the analysis from initial state controlled by the initial value of fracture energy to the one associated with the actual tensile strength of
MPa, recall
Table 3, is determined by reaching the value of the damage parameter
in the most stressed element. This can be mathematically represented as
From that point on, the subsequent fracturing process in an arbitrary element continues with the value of associated with MPa and the mesh dependent length scale parameter l set to mm in all simulations involving the triangular mesh.
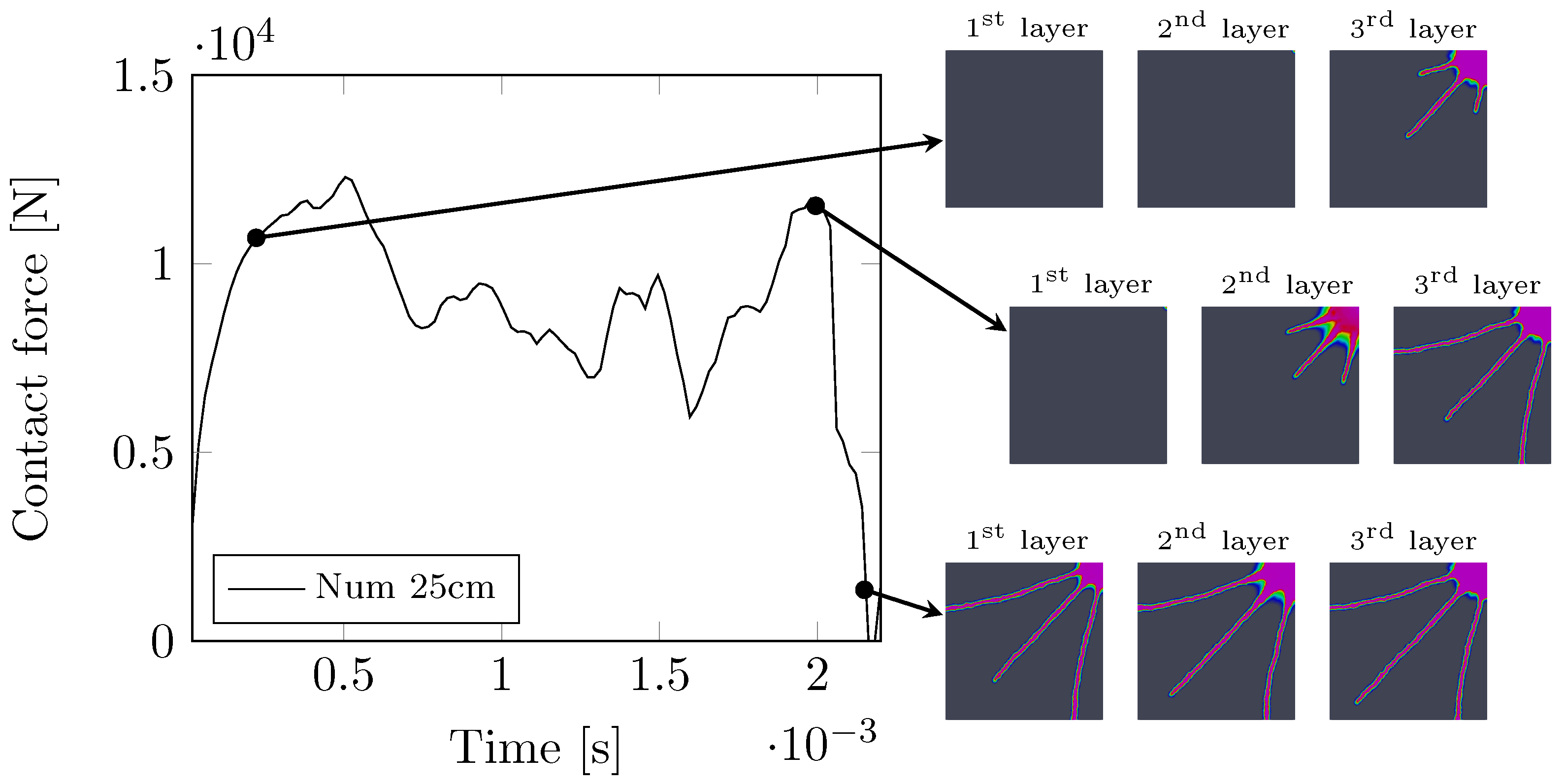
This approach resulted in the damage pattern seen in
Figure 11 with the corresponding evolution of the contact force depicted in
Figure 9b. Note that the shear reduction parameter
was set to a threshold value of
to avoid through thickness penetration of the impactor. The accumulation of energy by using increased initial tensile strength
allows for formation of more random crack patterns. With a sufficiently large difference between the actual
and initial
tensile strengths, the model promotes cracks in multiple directions. On the other hand, we see a notable mismatch in the descending part of the measured and predicted contact force,
Figure 9b. This can be attributed to the fact that the impactor gradually penetrates into the already broken fragments. Similar results, derived with the help of LS-DYNA software, have been observed in [
14] both in terms of crack pattern and contact force evolution.
5. Damage of Laminated Glass Plate
The results presented in the previous section now open the door to the simulation of laminates exploiting the theoretical framework outlined in
Section 3.3.
Similar to the experimental program discussed in
Section 2, we address both types of laminates with their geometrical details provided in
Table 1. The material properties of the impactor and glass layers are taken from
Table 5. For the polymer interlayer, we set the density
kg/m
. The Poisson ratio
0.49 is considered to approach a volumetrically incompressible material while avoiding a significant shear locking. Given the room temperature during experiments in the range of 24.9 °C to 26 °C, we set
in Equation (
40) to 25 °C. As suggested in
Section 3.6, the viscoelastic properties of the interlayer are included only empirically via Equation (
38). No other material parameters of the PVB interlayer are needed as damage is expected to occur in the glass layers only.
To validate implementation of the layered plate theory, we begin again with nondestructive tests. For the sake of brevity, attention is limited to 5LG-3 and 7LG-2 samples as these show a similar evolution of gradual damage due to repeating impacts of variable intensity; see
Table 2. The response of both types of laminates is examined through the distribution of contact force for two impact heights causing no damage. The results plotted in
Figure 12 indicate a satisfactory agreement between numerical predictions and experimental measurements, thus excluding any systematic error potentially linked to numerical implementation. The observed differences are merely associated with the 8th-pole Butterworth low-pass filter (2× CFC 1000 filter) we used to filter out the frequencies associated with vibrations of the impactor from the measured accelerations [
10]. Apart from eliminating the initial data before the largest amplitudes (approximately 0.3–0.4 ms of a signal) and the final part (after 20 ms) with small oscillations affected significantly by the experimental noise, the filter was applied to the entire time domain associated with experimental measurements. The eliminated data could have affected the initial slope of the experimentally observed contact force so its direct comparison with numerical predictions might be misleading.
Moving to damage brings to mind the key role of the initial tensile strength we suggested in the previous section. Its value influences the amount of energy available in the glass to drive the fracture process. This is illustrated in
Figure 13 assuming two different values of the initial tensile strength
. Similarly to the result presented in
Figure 11, the strength was reduced to
MPa according to Equation (
41). The damage patterns at the onset of cracking and at the time when the damage fully localized into isolated cracks are shown for the back glass layer (the furthermost from the impacted one) of a 5LG-laminate loaded by the impact energy of 236 J (impact height of 50 cm). It is evident that the value of the initial tensile strength qualitatively changes the result of the simulation. One may therefore consider this value as another material parameter albeit depending on a given computational model. For
MPa, the damage initiated at
ms, whereas, for
MPa, it was delayed to
ms. While the time to stabilize the crack growth was in both cases about the same, the larger amount of energy dissipated in the latter case resulted in a significantly denser crack pattern. It follows that choosing the value of
sensitively the model is able to control the branching and development of multiple cracks with no additional ad hoc criteria.
As the solution depends on the length scale parameter
l, which in turn is estimated from the underlying finite element mesh, it appears useful to briefly address this issue. Proceeding with the previously studied 5LG laminate, we keep the initial tensile strength
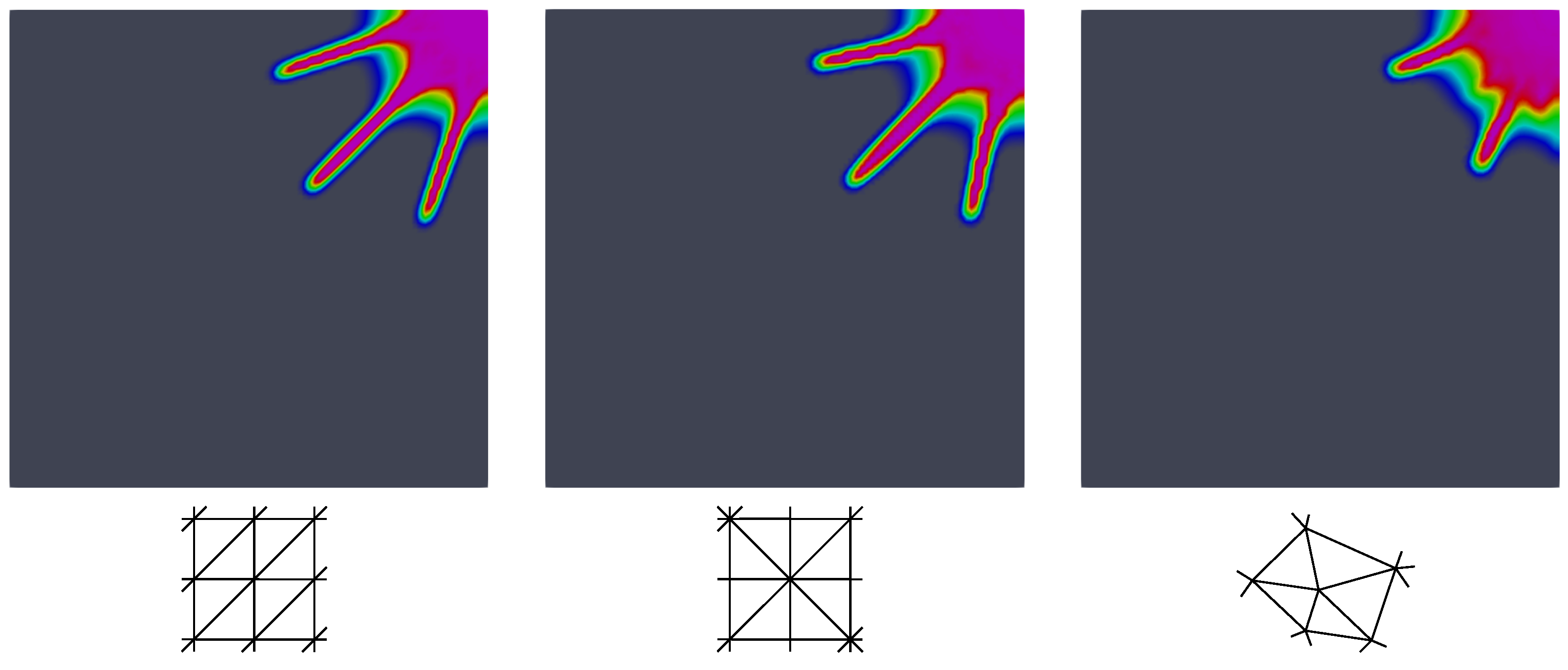
MPa and assume the impact energy of 236 J (impact height of 50 cm). The first example compares structured and unstructured meshes sketched in
Figure 14 (bottom figures). Considering a comparable mesh density, the length of the process zone is set to
mm for all tested meshes. The damage patterns for the time instant
ms are compared in
Figure 14 (top figures) for two examples of structured meshes and one example of the unstructured mesh; recall
Figure 6. The evolution of damage along preferential direction associated with the structured meshes is evident.
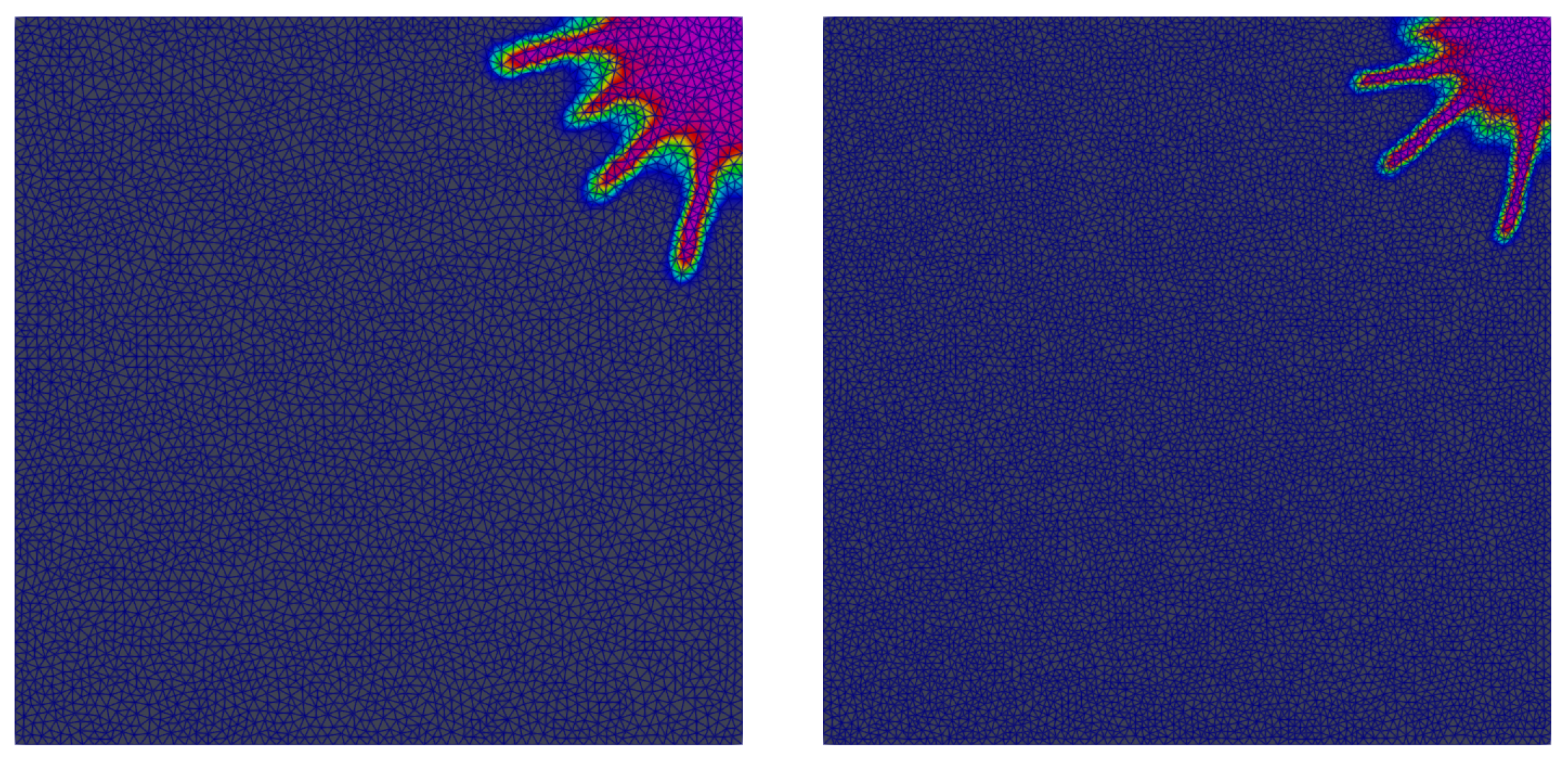
The second example addresses the effect of mesh refinement considering two mesh densities, a coarser mesh with 9425 elements and the process zone
mm (left) and a finer mesh with 19,119 elements and the process zone
mm (right) being essentially the one in
Figure 6. It has been found that the mesh density influences the onset of damage, i.e., the transition point
. The damage initiation is delayed with increasing the element size with the time at the onset of damage
ms and
ms for the coarser and finer mesh, respectively. The damage patterns plotted in
Figure 15 correspond to time
ms. While the onset of damage and partially also the crack pattern differ, the crack growth velocity appears similar for both meshes. A potential reason for decreasing the initiation time
with increasing the mesh refinement can be attributed to the reduction of the fracture process zone leading to a brittle failure when approaching this parameter to zero. This issue is under current investigation.
The above findings are finally exploited in the simulation of gradual damage caused by several consecutive impacts for the selected laminates. The finer element mesh in
Figure 15, recall also
Figure 6, was used providing a satisfactory agreement between the measured and predicted contact force. Point out that, with repeating impacts, the new calculation always started from the damage state associated with the previous loading step. We begin with the 5LG-3 sample. To correctly predict the onset of damage for a given impact height
cm, the initial tensile strength
MPa was used. The distribution of the contact forces is presented in
Figure 16a.
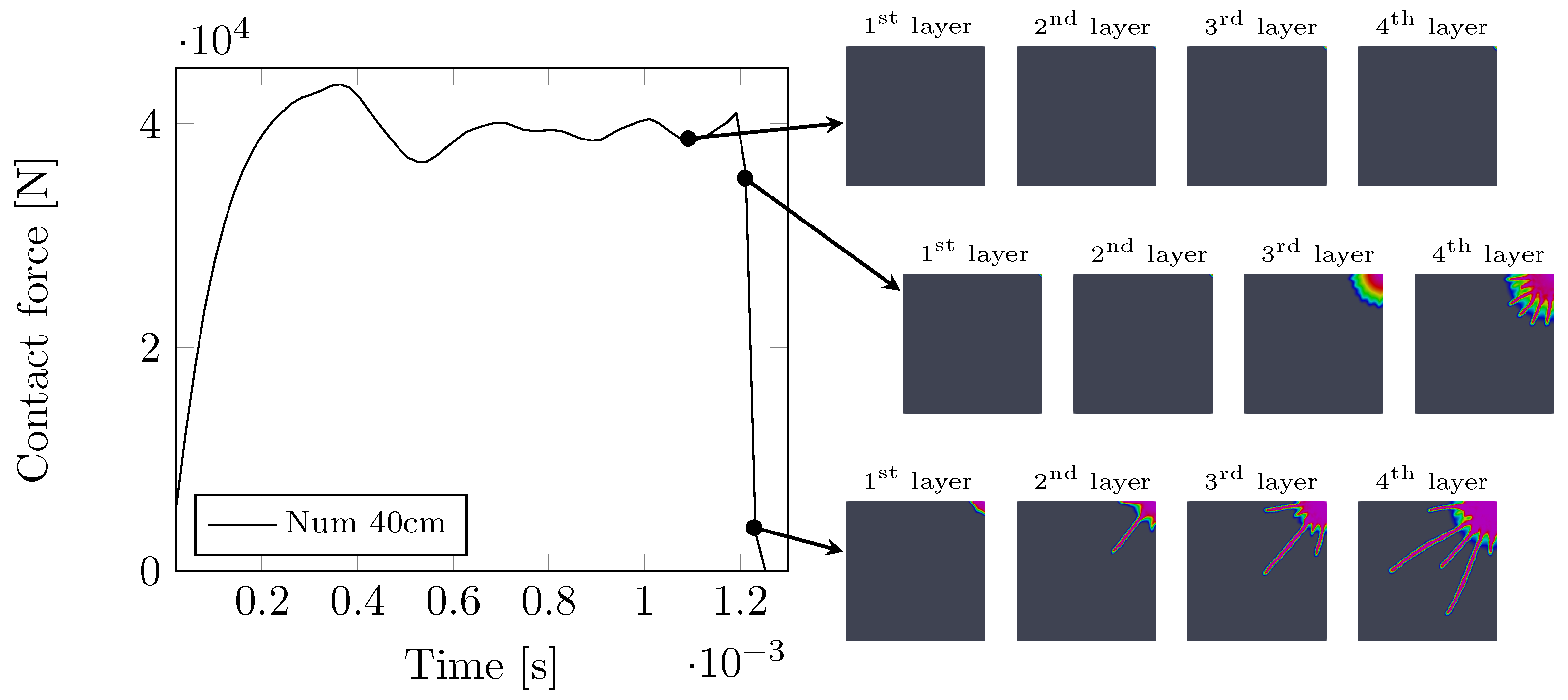
In agreement with experiment, the back layer fractured first. To force the damage to progress to another layer required increasing the impact height to 25 cm. Similarly to experiments, the layers cracked gradually from the back layer towards the impacted one. Unlike experiments, however, both remaining layers cracked at this simulation step. The evolution of damage in individual layers is displayed in
Figure 17 for the selected time instances. It is worth mentioning that the same value of
was prescribed to all layers, whereas, in [
10], each layer was assigned a different value of
to follow the experimentally observed cracking sequence as close as possible. Since this was not the principal objective of this study, primarily focusing on the potential of phase field to model fracture in laminated glass, we did not investigate this issue any further.
Similar conclusions can be drawn from the simulations of the 7LG laminate as only the onset of damage was meant to be captured in agreement with the experiment performed on 7LG-2 sample. To this end, the value of
was considered. As the same value was again assigned to all layers, it is not surprising, pointing out a relatively large impact energy that all layers fractured within this single simulation step. This is also why only one numerically generated contact force is presented in
Figure 16b. The corresponding evolution of cracks at selected simulation times is available in
Figure 18.
To arrive at better agreement with experiment, both in terms of the contact force variation and fracture sequence, would require more gentle tuning of the initial tensile strength on the one hand and assigning a different value of this parameter to individual layers on the other hand. The latter option would cause the contact force to decay more gradually [
10]. However, as already mentioned, this goes beyond the present scope.