Abstract
In the present work attention is focused on the friction-yielding damper CAR1 (first prototype of Control-Absorb-Retain damper), which belongs to passive energy dissipation systems. This damper consists of very simple materials; it does not need to be accomplished in heavy industry so enables its use in both developing and undeveloped countries. This paper presents and compares two alternative solutions with the use of the CAR1 to seismic retrofit an existing two-story reinforced-concrete (RC) structure with a moment-resisting frame located in Greece and constructed in 1979 and no longer meets the requirements of current anti-seismic regulations. A nonlinear static pushover analysis is performed to assess the performance of the framed building under different levels of shaking (“Life Safety” and “Collapse”). The pushover analysis is carried out in both the x and y directions. The use of damper CAR1 in seismic retrofitting not only provides a base shear load of up to 149.2% and 135.6% for the first and second redesign solutions but also protects steel diagonal braces from buckling. The appropriate characteristics of the dampers CAR1 has been selected from a wide variety of choices and the strengthening level can be easily adjusted or modified during the years based to the appropriate selection or modification of the number, the dimensions, and the elastoplastic properties of the blades.
1. Introduction
During an earthquake, the seismic energy introduced into a building leads to the creation of plastic deformations, hinges, and cracks [1]. Passive energy dissipation dampers have widely been used in recent years to reduce the dynamic response of civil engineering structures subjected to seismic loads. One of their advantages is easy replacement and repair, and they are effective because they minimize structural damage by absorbing structural vibrational energy and dissipating energy through their hysteresis behavior. More generally, they can be categorized into dampers that depend on displacement, dampers that depend on speed, and dampers with a combination of the two. The types of dampers that dissipate energy in construction include metallic dampers, friction dampers, viscous or viscoelastic dampers, self-centering dampers, and tuned mass dampers [2,3,4,5,6]. Other researchers focused their study in seismic-resistant steel framing system capable of providing stiffness and ductility to new or existing structures [7,8], or the use of buckling-restrained braces [9,10].
The pall damper is one type of friction damper presented in the literature, and it works based on the mechanism of solid friction for dissipating vibration energy [11]. As the joints slip, the cantilevered walls provide the elastic restraint required to create the centering action that ensures negligible residual displacement after an earthquake. Pall friction dampers have been used in both existing and new buildings in the USA and in Canada. According to Pall and Pall [12], by 1996, several types of Pall friction dampers had been incorporated into six existing buildings and seven new ones, with more important applications in the Concordia University Library in Montreal and the Montreal Casino in Canada. The Concordia University Library in Montreal was designed so that the required stiffness was provided by 143 Pall-type dampers. The conventional solution was not used for the walls because, even though it would provide the required stiffness, it would limit the number of parking spaces in the basement of the building and would lead to greater foundational needs. Finally, the solution involving Pall dampers reduced the total construction costs by 1.5%, which corresponded to USD 65,000,000 [13]. The Montreal Casino, an eight-story metal building constructed in 1966 by the French government for the Expo 67 exhibition in Montreal, Canada, needed to be retrofitted, as the building no longer met the requirements of current anti-seismic regulations. The solution that was chosen after nonlinear dynamic analyses was to strengthen the structure with 32 Pall-type friction dampers, as they were less expensive and time-consuming than other conventional reinforcement solutions [14,15].
The most popular friction-yielding damper is the ADAS (Added Damping and Stiffness) damper studied by Whittaker [16,17]. The layout consists of flat steel plates in a row, in which their bottoms are connected to the top of the diagonal braces and their upper parts are connected at the ceiling level. These dampers have been applied to the seismic reinforcements of the Wells Fargo Bank in San Francisco [18] but have also been applied to many other buildings in the USA, Mexico, and Japan. One of such buildings reinforced with ADAS-type metal dampers is the Izazaga building in Mexico. The building suffered moderate damage in 1985 during an earthquake, and further damage occurred during another earthquake in 1986. It was finally reinforced with 250 ADAS dampers, which were incorporated into metal diagonal bars on the perimeter of the building [19].
Titirla et al. [20,21] proposed an innovative energy dissipation system known as CAR1, consisting of very simple materials and which does not need to be accomplished in heavy industry so enables its use in both developing and undeveloped countries. The damper takes its name due its triple ability: (i) to Control the axial forces, (ii) to Absorbed seismic energy and (iii) to Retain the plastic displacements up to a desired level, while the number 1 of the acronym refers to the fact that the analyzed system corresponds to prototype # 1 of the damper fabricated at the Laboratory of Structural Analysis & Dynamics of Structures at Aristotle University of Thessaloniki.
In this paper, it is presented and compared two alternative solutions using dampers CAR1 in steel diagonal braces to seismic retrofit an existing two-story RC structure with a moment-resisting frame located in Greece. The investigated building was constructed in Zagliveri in 1979 (Section 2) and no longer meets the requirements of current anti-seismic regulations. A nonlinear static pushover analysis following the ATC-40 [22] procedures is performed to assess the performance of the framed building under two different levels of shaking (“Life Safety” and “Collapse”). The pushover analysis is carried out in both the x and y directions. In this study, the effectiveness of the friction-yielding damper CAR1 has been successfully investigated for an existing low-rise (2-story) RC building that no longer meets the requirements of current anti-seismic regulations. The use of the damper CAR1 in the steel diagonal braces for the selected displacement level (drift = 2%) minimizes the plastic hinges of the columns as well as protects the steel diagonal braces from buckling. This study highlights the easily process to select the appropriate characteristics of the dampers from a wide variety of choices [20,21,23].
2. Description
2.1. Benchmark Building
The investigated building, BM0, is illustrated in Figure 1, was constructed in Zagliveri, Thessaloniki in 1979 and no longer meets the requirements of current anti-seismic regulations. It is part of a group of four tobacco warehouses. Therefore, for many years, it has been used as a tobacco warehouse, and recently, the re-use of this building was proposed but with a new unknown function. The dimensions of its sides are 28.40 m × 39.60 m. In the x-x direction, it consists of four frames. The external ones have an opening of 7.20 m, and the rest are 7.00 m. In the y-y direction, BM0 consists of seven frames. Similarly, the external ones have an opening of 5.80 m, and the rest are 5.60 m. The height of the first floor is 5.00 m and the second floor is 4.20 m. The concrete that was used is class B225 (≈C16/20, with characteristic cylinder compressive strength and elastic modulus , the steel of the longitudinal steel bars is STIII (≈S400, with min. yielding strength , min. ultimate strength min. fracture strain and the steel of the transverse steel bars is STI (≈S220, with , and .
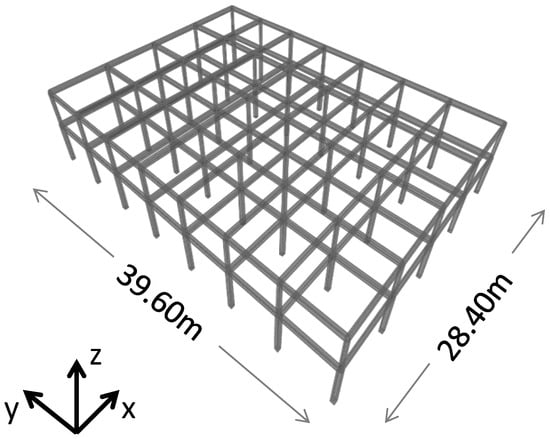
Figure 1.
Description of the investigated building constructed in Zagliveri in 1979.
The dimensions of the columns of the ground floor are 0.40 × 0.40 m, and those of the first floor are 0.30 × 0.30 m. The beams of the ground floor are 0.25 × 0.70 m, and those of the first floor are 0.25 × 0.60 m. The thickness of the floor slab is equal to 0.15 m. All this information is provided in Table 1.

Table 1.
Geometry of the structural elements.
Beams and columns of the building have been modeled as frame elements with rectangular cross sections (see Table 1), and it was assumed a rigid floor diaphragm for the model, as the buildings are regular in both plan and elevation (EN 1998–1:2004, pages 42–43, section 4.2.3.3) [24]. The building is subjected to gravity and lateral loads. Under this study, it is assumed that the additional permanent load of the floors (excluding the self-weight) is equal to and that the live load is equal to , as the new function of the building is unknown. The area of Zagliveri belongs to the second Hazard Zone of Greece (ZII). Therefore, for the model’s design, it is used a ground acceleration equal to and a soil category of B.
2.2. CAR1 Damper
Here, a brief description of the CAR1 damper is provided, as it has been described in detail in previous research [20,21]. It consists of very simple materials, which does not need to be accomplished in heavy industry so enables its use in both developing and undeveloped countries. Its main element is a group of superimposed blades, of which only a certain number of them are used, and the blades’ dimensions as well as their elastoplastic properties define the constitutive law of the diagonal braces under axial loads. Device CAR1 has three functions: (i) controlling the axial forces of the diagonal steel braces using an appropriate selection of the number and dimensions of the superimposed blades and their elastoplastic properties; (ii) absorbing seismic energy; and (iii) retaining plastic displacements up to a desired level due to the existence of a restraint bolt [21]. Figure 2a shows the device, and Figure 2b shows the non-linear behavior of the diagonal steel brace with CAR1 under tension (positive P) and compression (negative N) stress.
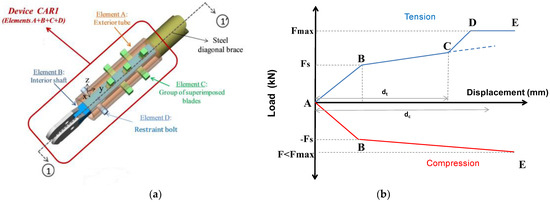
Figure 2.
(a) Damper CAR1; (b) Non-linear behavior of the diagonal steel brace with CAR1 [18].
3. Methodology
3.1. Developing the 3D FEM BM0
The building is modeled as a three-dimensional frame with a fixed base at the foundation level, and beams and columns as frame elements with the centerlines jointed at nodes. The section stiffness is used according to FEMA-356 [25] to model the initial stiffness of the structural sections, and it is assumed a rigid floor diaphragm to model each story [24]. It is used the yield moment and yield curvature to define the plastic hinges for all sections. The moment–curvature curves of beams and columns depended on i) the compressive strength of concrete, ii) the yield strength of reinforced steel, and iii) the approximate initial effective stiffness values according to ATC-40 [22] ( for beams and for columns). Therefore, beam and column elements are modeled as nonlinear frame elements by assigning concentrated flexural (M3) and axial load-flexural (P-M3) plastic hinges, respectively, to both ends. Hinge properties are defined through the definition of the moment–curvature relation determined in accordance with FEMA-356 [25].
3.2. Pushover Analysis of BM0 in x-x and y-y Direction
The first step is to establish the performance parameters, such as the drift of particular floor levels and restrictions on the rotation of the plastic hinges of specific plastic hinge points.
Figure 3 presents the pushover curve with the performance levels. These points are specified according to FEMA to determine the hinge rotation behavior of RC members [25]. The points between B and C represent acceptance criteria for the hinge, which are IO (“Immediate Occupancy”), LS (“Life Safety”), and CP (“Collapse Prevention”). A floor displacement drift of 1.6% corresponds to a seismic performance level of “Life Safety” ), and a drift of 2.1% corresponds to a seismic performance level of “Collapse” (). We assumed a relative floor displacement equal to 2% for our construction. Therefore, the relative displacement for the ground floor is equal to , and for the first floor, it is equal to , which gives a total displacement at the top of the building of 18.4 cm.
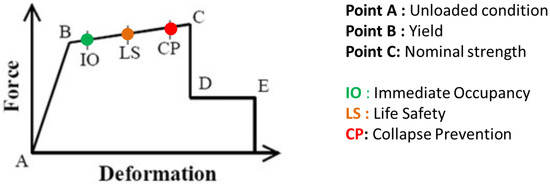
Figure 3.
Typical pushover curve with performance levels.
The pushover analysis is performed separately for the two directions to study its performance in both directions. Push-X is the side pushover analysis for x-x direction while Push-Y is for the y-y direction. Pushover analysis is achieved using a displacement control strategy. Pushover curves are presented in Section 4.
3.3. Does BM0 Meet the Criteria of New Regulations?
The eigenperiod of the structure is . We obtained a soil coefficient for type-B soil equal to . The period of the lower limit of the constant spectral acceleration branch is , the period of the upper limit of the constant spectral acceleration branch is , and the value defining the beginning of the constant displacement response range of the spectrum is .
According to the provisions of EC8 regarding the value of the behavior factor q, this value can be calculated for each direction from the equation (§5.2.2.2(1) of EC8 [24]) where is the basic value of the behaviour factor, dependent on the type of the structural system and on its regularity in elevation, and is the factor reflecting the prevailing failure mode in structural systems. We assumed that , (EC8 §5.2.2.2(5) [24]), , and finally coefficient q took the value of: . The elastic response spectrum for is defined by Equation (1), as follows:
From the analysis of the vertical loads of BM0, it is noticed that the seismic base shear load is ΣF = 20236 kN. In order to meet the requirements of current anti-seismic regulations, the appropriate/needed seismic base shear is calculated by the equation , equal to ΣFneeded = 4007.20 kN in each direction. Therefore, the building must be able to receive a base shear load greater than 4007.20 kN to achieve the criteria of Eurocode 8 [24].
3.4. Redesign Solution RD1
Based on the work of Papadopoulos [26], the behavior of a structure with a random topology of steel diagonal braces is better in terms of floor displacement, inter-story displacement, and the distribution of bending moments and shear loads. Therefore, the placement of the steel diagonal braces in this study (both for RD1 and RD2) is random. However, we placed importance on ensuring that the dampers and the steel diagonal braces are located in a configuration that does not introduce eccentricity into the structure [27]. For redesign solution RD1, steel diagonal braces with X shape have been selected for only one frame in each direction and on each side of the building’s center of mass for the two stories (see Figure 4). As expected, on the ground floor, greater reinforcement is required compared with the first floor. Cross-sections of the diagonal steel bars were selected based on the available cross-sections on the market in order to obtain the required force, so the steel circular hollow diagonal braces of larger diameters were placed in these locations (CHS 219.1 × 4.5 on the ground floor and CHS 168.3 × 4 on the first floor).
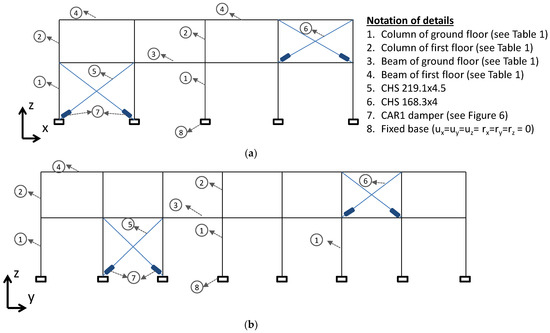
Figure 4.
Redesign of building BM1 (a) x-x direction; (b) y-y direction.
Pushover analyses have been conducted of redesign solution RD1 by taking into account (i) the existence of the steel diagonal braces and (ii) the existence of CAR1 in the steel diagonal braces. In every strengthening frame, two CAR1 dampers were positioned, with one of them working under compression and the other one working under tension (Figure 5). CAR1 dampers were modeled with two parallel N-link elements: Plastic, which simulates the behavior of the group of superimposed blades, and Hook, which simulates the existence of the restraining bolt (Figure 6). The behavior of the plastic element modeled by the stiffness and the yield strength witch results from a slight reduction in the maximum load that the compressive steel braces can carry out (see Table 2 and Table 3). For the Hook element, the most important parameters is the opening of the gap (see Section 4). The properties of each CAR1 damper have been selected based on previous experimental and numerical results [21] in such a way that the dampers are able to protect the steel diagonal braces from premature buckling (see Section 4) by controlling the maximum axial load of the diagonal steel braces using an appropriate selection of the number and dimensions of the superimposed blades and their elastoplastic properties.
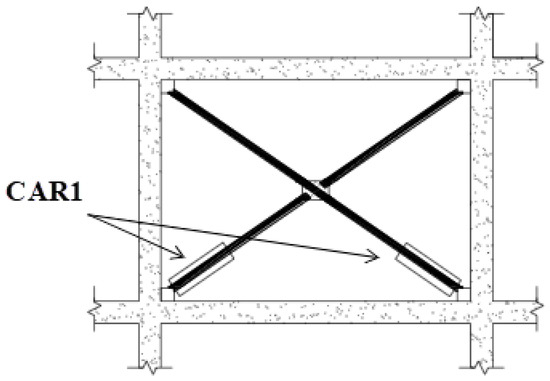
Figure 5.
Installation of two CAR1 dampers in X-shaped steel diagonal braces.
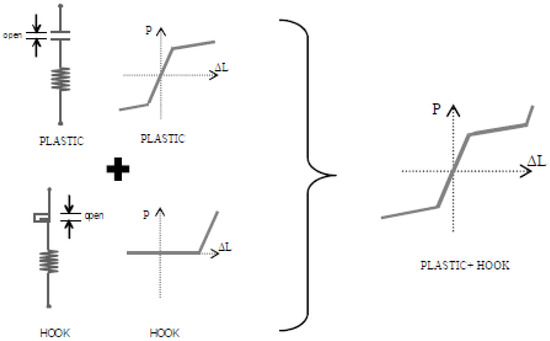
Figure 6.
Model configuration of CAR1 damper.

Table 2.
Description of the selected characteristics of the CAR1 dampers for RD1.

Table 3.
Description of the selected characteristics of the CAR1 dampers for RD2.
3.5. Redesign Solution RD2
For redesign solution RD2, it is selected X-shaped steel diagonal braces in two frames in each direction and on each side of the building’s center of mass for each of the two stories (see Figure 7). As expected, on the ground floor, greater reinforcement is required compared with the first floor. cross-sections of the diagonal steel bars were selected based on the available cross-sections on the market in order to obtain the required force, so the steel circular hollow diagonal braces of larger diameters were placed in these locations (CHS 168.3 × 4.5 on the ground floor and CHS 133 × 4 on the first floor).
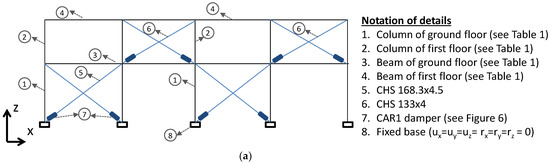
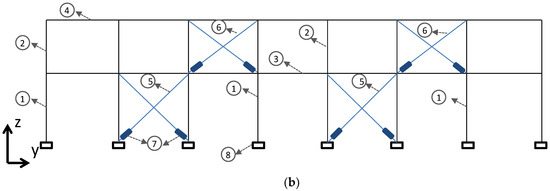
Figure 7.
Redesign of building BM2 (a) x-x direction; (b) y-y direction.
Pushover analyses have been conducted of redesign solution RD2 by taking into account (i) the existence of the steel diagonal braces and (ii) the existence of CAR1 in the steel diagonal braces. In every strengthening frame, two CAR1 dampers were positioned, with one of them working under compression and the other one working under tension (Figure 5).
4. Results
Figure 8 shows the pushover curves of the benchmark building BM0 in the x-x direction and in the y-y direction. It is observed that, for a drift level of 2% (displacement at the top of the building equal to 18.4 cm), the base shear load is equal to 2350 kN and 2500 kN in the x-x and y-y directions, respectively. The building no longer meets the requirements of current anti-seismic regulations, as it was calculated the appropriate/needed seismic base shear as ΣFneeded = 4007.20 kN in each direction.
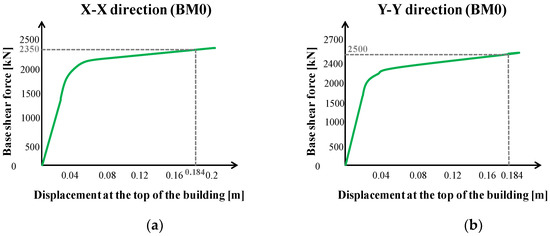
Figure 8.
Pushover curves of BM0: (a) x-x direction; (b) y-y direction.
In the x-x direction, it is noticed that the hinges of the columns remain in the Life Safety (LS) performance level, so the building has not suffered substantial damage due to the horizontal displacement of 18.4 cm at the top of the building (Figure 9a). In the y-y direction, the columns of the ground floor have not suffered substantial damage (IO), but the columns of the first floor are in the yellow zone (C), which means that several failures have occurred (Figure 9b). In the y-y direction, the building remains in the LS zone with a displacement of 16.7 cm at the top of the building.
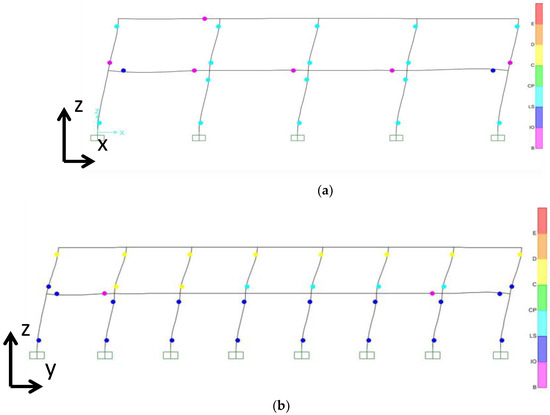
Figure 9.
Plastic hinges of BM0 for a displacement level of 18.4 cm at the top of the building: (a) x-x direction; (b) y-y direction.
Figure 10 shows the plastic hinges of the RD1 building without the installation of CAR1 dampers for the displacement level of 18.4 cm at the top of the building, and it shows the axial load–displacement curves for the steel diagonal braces of the ground and first floor. It is noticed that the steel diagonal braces were buckling under compression, their most common problem [28,29,30], equal to 990 kN for the brace of the ground floor with a displacement of 3.7 cm at the top of the building (drift = 0.4%) and 610 kN for the brace of the first floor with a displacement of 3.1 cm at the top of the building (drift = 0.38%).
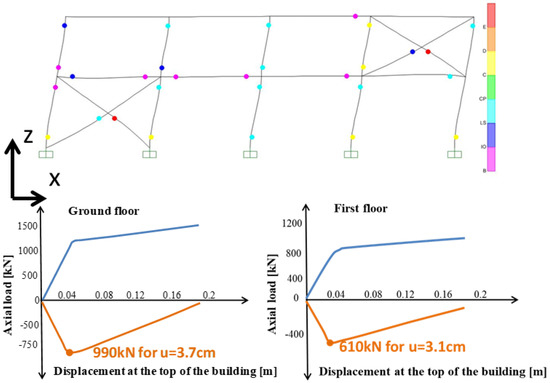
Figure 10.
Plastic hinges of RD1 without the installation of CAR1 dampers for a displacement level of 18.4 cm, and axial load–displacement curves for the steel diagonal braces.
The aim of the CAR1 is to protect the braces from buckling and also to dissipate energy [23,31]. In order to select the appropriate characteristics of the CAR1 dampers, we used the tables and diagrams proposed by Titirla et al., who offer a wide variety of choices [21,23].
The selected characteristics are presented in Table 2 for RD1. For the ground floor, it is selected a damper with an external diameter of 22 cm based on the diameter of the steel diagonal braces, and for the first floor, a damper with a diameter of 17.5 cm. For the ground floor, in the x-x direction, eight groups of superimposed steel blades with four blades with thicknesses of 12.5 mm constitute CAR1, and in the y-y direction, it is used only seven groups of blades with the same characteristics. For the first floor, eight groups of steel superimposed blades with four blades with thicknesses of 17.5 mm constitute the CAR1 damper in both directions. An appropriate configuration/geometry in the area of the stoppage bolt (oval hole) eliminates any additional compression forces on the diagonal elements and allows only tensional forces to be developed (dc > dt). Therefore, the restraining bolt needs to be activated before the horizontal displacement of 3.7 cm and 3.1 cm (at the top of the building), which is equal to 4.4 cm of displacement parallel to the axes of the damper for the ground floor and 3.7 cm for the first floor in the x-x direction.
The selected characteristics of the CAR1 dampers are presented in Table 3 for RD2. In this study, to highlight the variety of dampers, we chose different characteristics for each direction for the RD2 building, but to reduce the cost, having the same characteristics is usually preferred. For the ground floor, it is selected a damper with diameter of 17.5 cm based on the diameter of the steel diagonal braces, and for the first floor, it is selected a damper with a diameter of 14 cm. For the ground floor, in the x-x direction, eight groups of superimposed steel blades with four blades with thicknesses of 7.5 mm constitute the CAR1 damper in both directions. For the first floor, in the x-x direction, it is selected a damper with five groups of superimposed steel blades with fives blades with thicknesses of 6 mm, and in the y-y direction, it is selected a CAR1 damper with five groups of superimposed steel blades with three steel blades with thicknesses of 8 mm and two brass blades with thicknesses of 3 mm. The restraining bolt needs be activated before the horizontal displacement of 3.3 cm and 2.3 cm (at the top of the building), which is equal to 3.8 cm of displacement parallel to the axes of the damper for the ground floor and 2.7 cm for the first floor in both directions.
Figure 11 compares the pushover curves of all buildings (BM0, RD1 with CAR1 and RD2 with CAR1) in the x-x direction and in the y-y direction. It is noticed that the RD1 building is able to take a 149.2% (6080 kN) and 135.6% (5960 kN) higher base shear load in the x-x and y-y directions, respectively, and the RD2 building is able to take a 212.3% (7620 kN) and 198.8% (7560 kN) larger base shear load in the x-x and y-y directions, respectively, for the same level of displacement (drift = 2%).
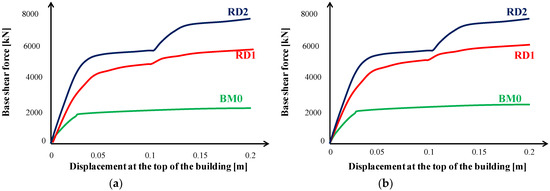
Figure 11.
Pushover curves of all buildings: (a) x-x direction; (b) y-y direction.
Figure 12 presents the plastic hinges of RD1 and RD2 for a horizontal displacement at the top of the building of 18.4 cm in both directions. The hinges of the columns remain in the Life Safety (LS) performance level in both buildings and in both directions, so the buildings have not suffered substantial damage as a result of this horizontal displacement (Figure 12a–d). In addition, with the installation of the CAR1 dampers the buckling of the steel diagonal braces was prevented (Figure 13).
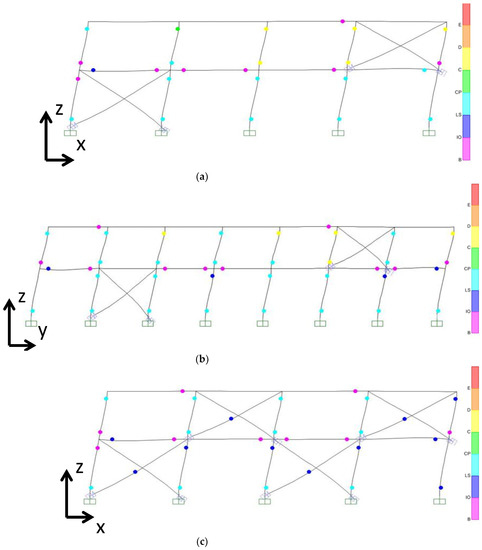
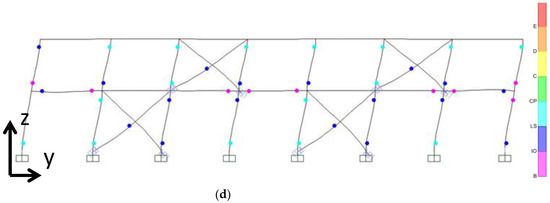
Figure 12.
Plastic hinges of redesign buildings for a displacement level of 18.4 cm (at the top) (a) RD1 in x-x direction; (b) RD1 in y-y direction, (c) RD2 in x-x direction; (d) RD2 in y-y direction.
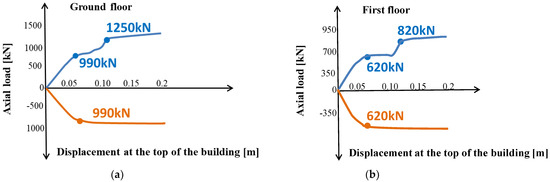
Figure 13.
Axial load–displacement curves for the steel diagonal braces of RD1 in x-x direction: (a) ground floor and (b) first floor.
Figure 13a shows the axial load–displacement curves for the steel diagonal braces of RD1 in the x-x direction of the ground floor, and Figure 13b shows those of the first floor. The activation of the restraining bolt increases the axial load of the tensional di-agonal brace, so the compressed diagonal brace is protected against buckling.
A preliminary estimation of the overall inadequacy of existing RC buildings and a proper choice of effective retrofitting strategies are fundamental phases for seismic protection of RC buildings [32]. In this study, the effectiveness of the friction-yielding damper CAR1 has been successfully investigated for an existing low-rise (2-story) RC building that no longer meets the requirements of current anti-seismic regulations. For medium-rise and high-rise buildings (existing that no longer meet the requirements of current anti-seismic regulations), the use of the dampers CAR1 needs to further investigate additionally with other techniques like FRP that would restore or improve the column original design strength for possible axial, shear, or flexure and in some cases allow the structure to carry more load than it was designed for.
5. Conclusions
The friction-yielding damper CAR1 has been used to improve the seismic behavior of an existing two-story RC structure located in Greece, constructed in 1979 and no longer meets the requirements of current anti-seismic regulations. In this paper, two alternative solutions with the use of CAR1 positioned in the steel diagonal braces are presented and compared. A nonlinear static pushover analysis in both directions is performed following the ATC 40 procedures [19] to assess the performance of the framed building under different levels of shaking (“Life Safety” and “Collapse”). For the first redesign of the building RD1, we selected steel diagonal braces with an X shape in only one frame in each direction and on each side of the building for the two stories, and for the second redesign RD2, we selected steel diagonal braces with an X shape in two frames in each direction and on each side for both stories. The properties of each damper CAR1 have been selected based on previous experimental and numerical results [21,31] to protect the steel diagonal braces from buckling.
Based on the findings of this paper new conclusions are drawn.
i. The effectiveness of the friction-yielding damper CAR1 has been successfully investigated for an existing low-rise (2-story) RC building that no longer meets the requirements of current anti-seismic regulations. Τhe seismic base shear load of the BM0 building is ΣF = 20236 kN, but the appropriate/needed seismic base shear as ΣFneeded = 4007.20 kN is calculated in each direction to achieve the criteria of EC8 [23]. It is noticed that RD1 can take 149.2% (6080 kN) and 135.6% (5960 kN) larger base shear loads in the x-x and y-y directions, respectively, and RD2 can take 212.3% (7620 kN) and 198.8% (7560 kN) larger base shear loads in the x and y directions, respectively, for the same level of displacement (drift = 2%) compared with the appropriate/needed seismic base shear.
ii. The damper CAR1 can be used in existing buildings that no longer meet the requirements of current anti-seismic codes, minimizing the plastic hinges of the columns, and protecting the steel diagonal braces from buckling. This study highlights the easily process to select the appropriate characteristics of the dampers from a wide variety of choices [20,21,31]. Also, the strengthening level can be easily adjusted or modified during the years based to the appropriate selection or modification of the number, the dimensions, and the elastoplastic properties of the blades.
iii. The plastic hinges of the columns of BM0 remain in the Life Safety (LS) performance level, so the building has not suffered substantial damage as a result of the horizontal displacement of 18.4 cm at the top of the building. In the y-y direction, the columns of the ground floor have not suffered substantial damage (IO), but the columns of the first floor are in the yellow zone (collapse C), which means that severe failures have occurred. The hinges of the columns remain in the Life Safety (LS) performance level in both redesign buildings (RD1 and RD2) and in both directions so the buildings have not suffered significant damage as a result of the horizontal displacement of 18.4 cm at the top of the building due to the use of the dampers CAR1. In addition, with the installation of the dampers CAR1, the buckling of the steel diagonal braces has been prevented.
For medium-rise and high-rise buildings (existing that no longer meet the requirements of current anti-seismic regulations), the use of the dampers CAR1 needs to further investigate additionally with other techniques like FRP that would improve the column original design strength for possible axial, shear, or flexure and in some cases allow the structure to carry more load than it was designed for.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
To ex-assistant Panikos Papadopoulos from Aristotle University of Thessaloniki, Greece.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Housner, G.W.; Bergaman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Marsi, S.F.; Skelton, R.E.; Soong, T.T.; Spenver, B.F.; Yao, J.T.P. Structural Control: Past, Present and future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Soong, T.T.; Spencer, B.F., Jr. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy dissipation systems for seismic applications: Current practice andrecent developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Forcellini, D.; Kalfas, K.N. Inter-story seismic isolation for high-rise buildings. Eng. Struct. 2023, 275, 115–175. [Google Scholar] [CrossRef]
- Amendola, A.; Smith, C.J.; Goodall, R.; Auricchio, F.; Feo, L.; Benzoni, G.; Fraternali, F. Experimental response of additively manufactured metallic pentamode materials confined between stiffening plates. Compos. Struct. 2016, 142, 254–262. [Google Scholar] [CrossRef]
- Benzoni, G.; Casarotti, C. Effects of Vertical Load, strain rate and cycling on the response of lead-rubber seismic isolators. J. Earthq. Eng. 2009, 13, 293–312. [Google Scholar] [CrossRef]
- Maheri, M.R.; Hadjipour, A. Experimental investigation and design of steel brace connection to RC Frame. Eng. Struct. 2003, 25, 1707–1714. [Google Scholar] [CrossRef]
- Giannuzzi, D.; Ballarini, R.; Huckelbridge, A.; Pollino, M.; Valente, M. Braced Ductile Shear Panel: New Seismic-Resistant Framing System. J. Struct. Eng. ASCE 2014, 140, 04013050. [Google Scholar] [CrossRef]
- Di Sarno, L.; Elnashai, A.S.E. Bracing systems for seismic retrofitting of steel frames. J. Constr. Steel Res. 2009, 65, 452–465. [Google Scholar] [CrossRef]
- Di Sarno, L.; Manfredi, G. Experimental tests on full-scale RC unretrofitted frame and retrofitted with buckling-restrained braces. Earthq. Eng. Struct. Dyn. 2012, 41, 315–333. [Google Scholar] [CrossRef]
- Pall, A.S.; Marsh, C.; Fazio, P. Friction joints for seismic control of large panel structures. J. Prestress. Concr. Inst. 1980, 25, 38–61. [Google Scholar] [CrossRef]
- Pall, A.S.; Pall, R. Friction-Dampers for Seismic Control of Buildings: A Canadian Experience. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Pall, A.S.; Verganelakis, V.; March, C. Friction-Dampers for seismic control of Concordia University Library Building. In Proceedings of the 5th Canadian Conference on Earthquake Engineering, Ottawa, ON, Canada, 6–8 July 1987; pp. 191–200. [Google Scholar]
- Pasquin, C.; Pall, A.; Pall, R. High-Tech Seismic Rehabilitation of Casino de Montreal; Structures Congress: Atlanta, Georgia, 1994; Volume 2, pp. 1292–1297. [Google Scholar]
- Pall, A.S.; Pall, R. Friction-Dampers Used for Seismic Control of New and Existing Building in Canada. In Proceedings of the ATC-17–1 Seminar on Isolation, Energy Dissipation and Active Control, San Francisco, CA, USA, 11–12 March 1993; Volume 2, pp. 675–686. [Google Scholar]
- Whittaker, A.S.; Bertero, V.V.; Alonso, J.L.; Thompson, C.L. Earthquake Simulator Testing of Steel Plate Added Damping and Stiffness Elements; Report No. UCB/EERC 89/02; University of California: Berkley, CA, USA, 1989. [Google Scholar]
- Whittaker, A.S.; Bertero, V.V.; Thompson, C.L.; Alonso, J.L. Seismic testing of steelplate energy dissipating devices. Earthq. Spectra 1991, 7, 563–604. [Google Scholar] [CrossRef]
- Perry, C.; Fiero, E.; Sedarat, H.; Scholl, R. Seismic retrofit in san francisco using energy dissipation devices. Earthq. Spectra 1993, 9. [Google Scholar] [CrossRef]
- Μartinez-Romero, E. Experiences on the Use of Supplemental Energy Dissipators on Building Structures. Earthq. Spectra 1993, 9, 581–624. [Google Scholar] [CrossRef]
- Titirla, M.; Katakalos, K.; Zuccaro, G.; Frabbrocino, F. On the mechanical response of an innovative energy dissipation device. Ing. Sismica-Int. J. Earthq. Eng. 2017, 2, 126–138. [Google Scholar]
- Titirla, M.; Papadopoulos, P.; Doudoumis, I. Finite Element modelling of an innovative passive energy dissipation device for seismic hazard mitigation. Eng. Struct. 2018, 68, 218–228. [Google Scholar] [CrossRef]
- Applied Technology Council, Seismic Evaluation and Retrofit of Concrete Buildings; Report No. SSC 9601: ATC-40; Seismic Safety Commission, State of California: Redwood City, CA, USA, 1996; Volume 1.
- Titirla, M. Experimental and Numerical Investigation of a Novel Seismic Energy Absorption Steel Device for the Protection of Structures. Ph.D. Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2016. [Google Scholar] [CrossRef]
- CEN. Eurocode 8: Design of Structures for Earthquake Resistance. In Part 1: General Rules, Seismic Actions and Rules for Buildings; EN 1998–1; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Federal Emergency Management Agency. Pre Standard and Commentary for the Seismic Rehabilitation of Buildings FEMA-356; Federal Emergency Management Agency: Washington, DC, USA, 2000.
- Papadopoulos, P.; Athanatopoulou, A. Building reinforced with steel diagonals braces. In Proceedings of the 13th Hellenic Concrete Congress, Rethymnon, Greece, 13–16 June 1999; Volume III, pp. 314–323. (In Greek). [Google Scholar]
- Mrad, C.; Titirla, M.D.; Larbi, W. Comparison of Strengthening Solutions with Optimized Passive Energy Dissipation Systems in Symmetric Buildings. Appl. Sci. 2021, 11, 10103. [Google Scholar] [CrossRef]
- Nip, K.H.; Gardner, L.; Elghazouli, A.Y. Cyclic testing and numerical modelling of carbon steel and stainless steel tubular bracing members. Eng. Struct. 2010, 32, 424–441. [Google Scholar] [CrossRef]
- Salawdeh, S.; Goggins, J. Numerical simulation for steel brace members incorporating a fatigue model. Eng. Struct. 2013, 46, 32–349. [Google Scholar] [CrossRef]
- Lotfollahi, M.; Alinia, M.M.; Taciroglu, E. Validated finite element techniques for quasi-static cyclic response analyses of braced frames at sub-member scales. Eng. Struct. 2016, 106, 222–242. [Google Scholar] [CrossRef]
- Titirla, M. Finite Element Simulation of the Device CAR1 on Braced Frames. In Proceedings of the ICCM2016, Berkeley, CA, USA, 1–4 August 2016. [Google Scholar]
- Valente, M.; Milani, G. Alternative retrofitting strategies to prevent the failure of an under-designed reinforced concrete frame. Eng. Fail. Anal. 2018, 89, 271–285. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).