The Experiments and Stability Analysis of Hypersonic Boundary Layer Transition on a Flat Plate
Abstract
:1. Introduction
2. Experiment Facility and Model
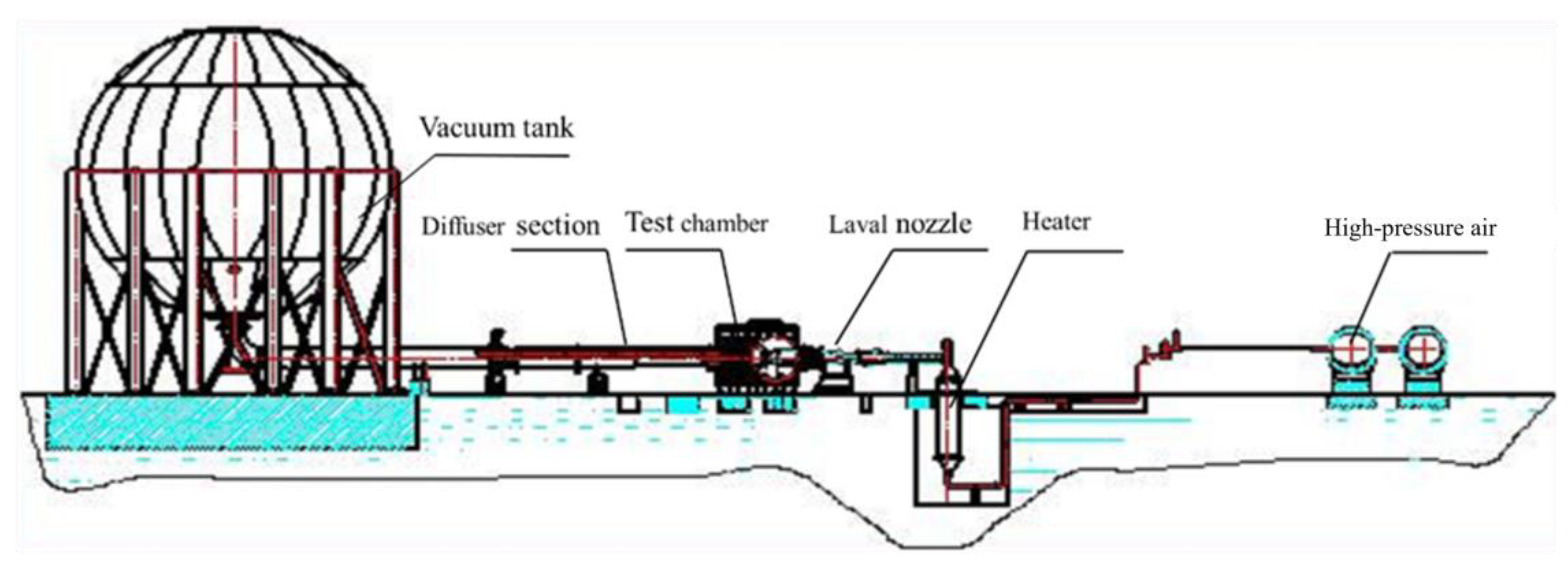
2.1. Wind Tunnel
2.2. Experiment Model
2.3. Heat Flux Calculating
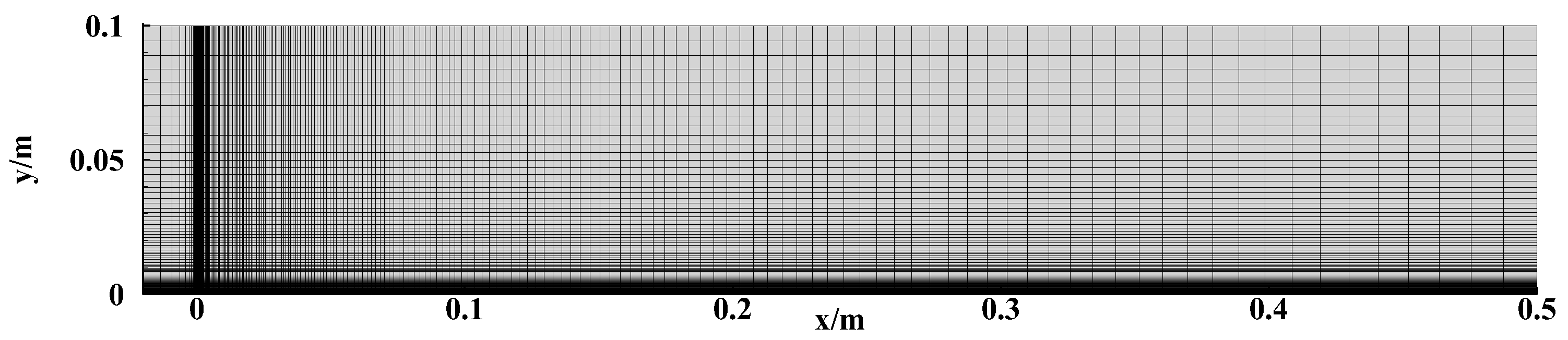
2.4. Numerical Setup
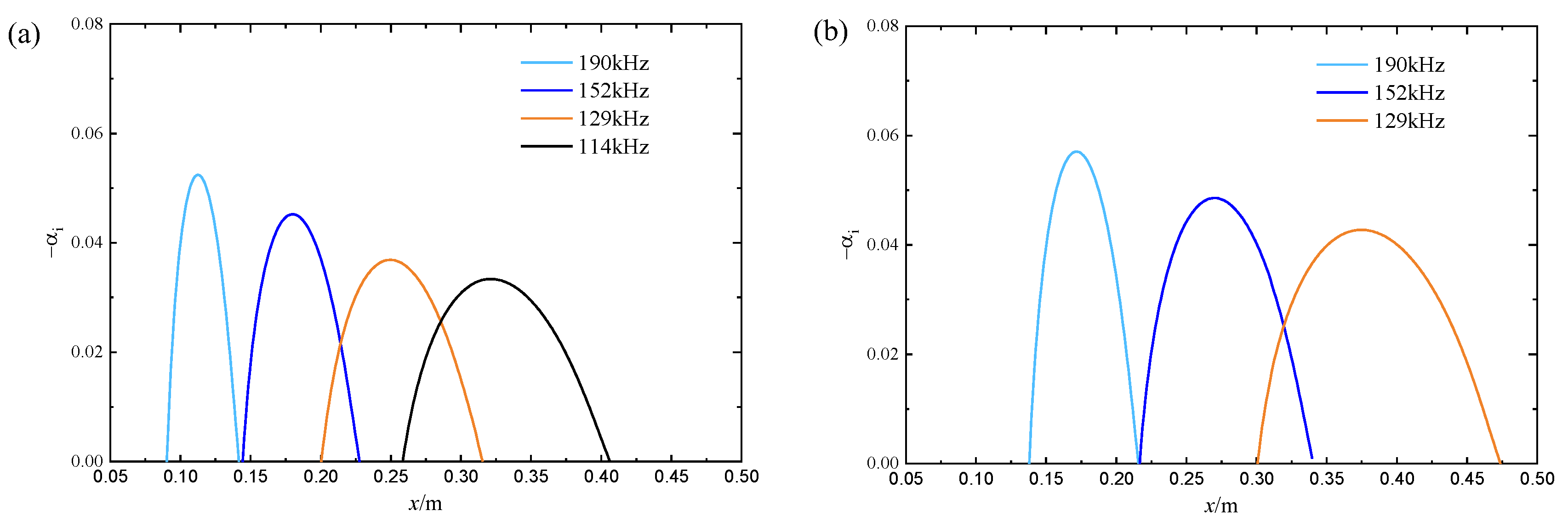
2.5. Linear Stability Theory
2.6. Steady Base Flow
3. Experimental Results and Stability Analyses
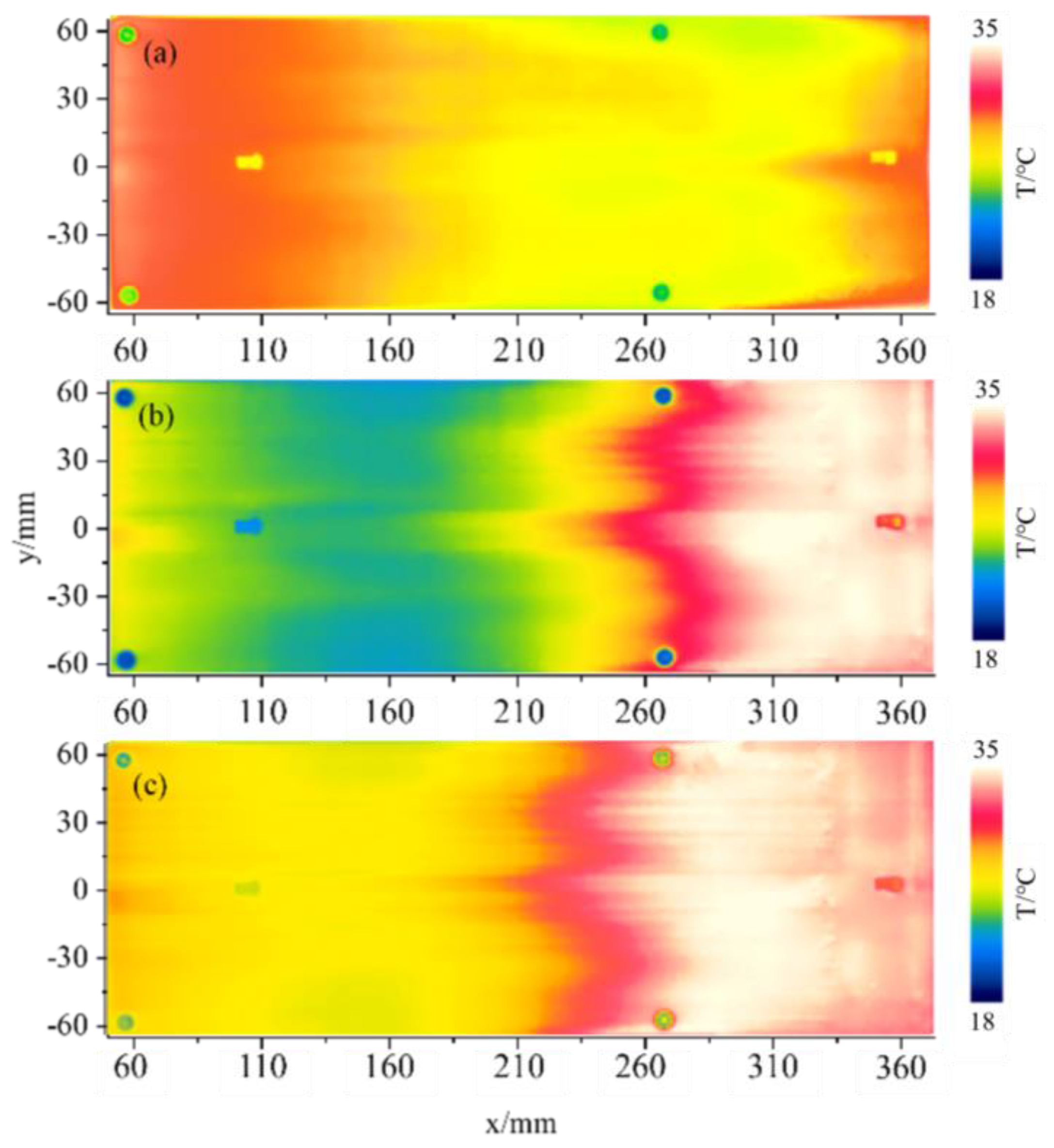
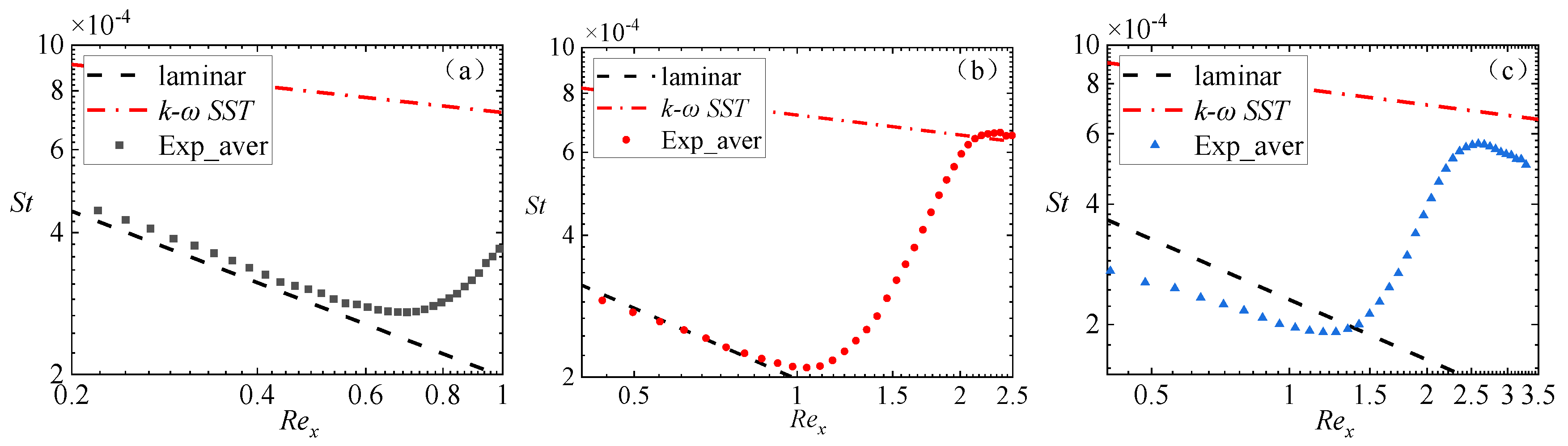
3.1. IR Results
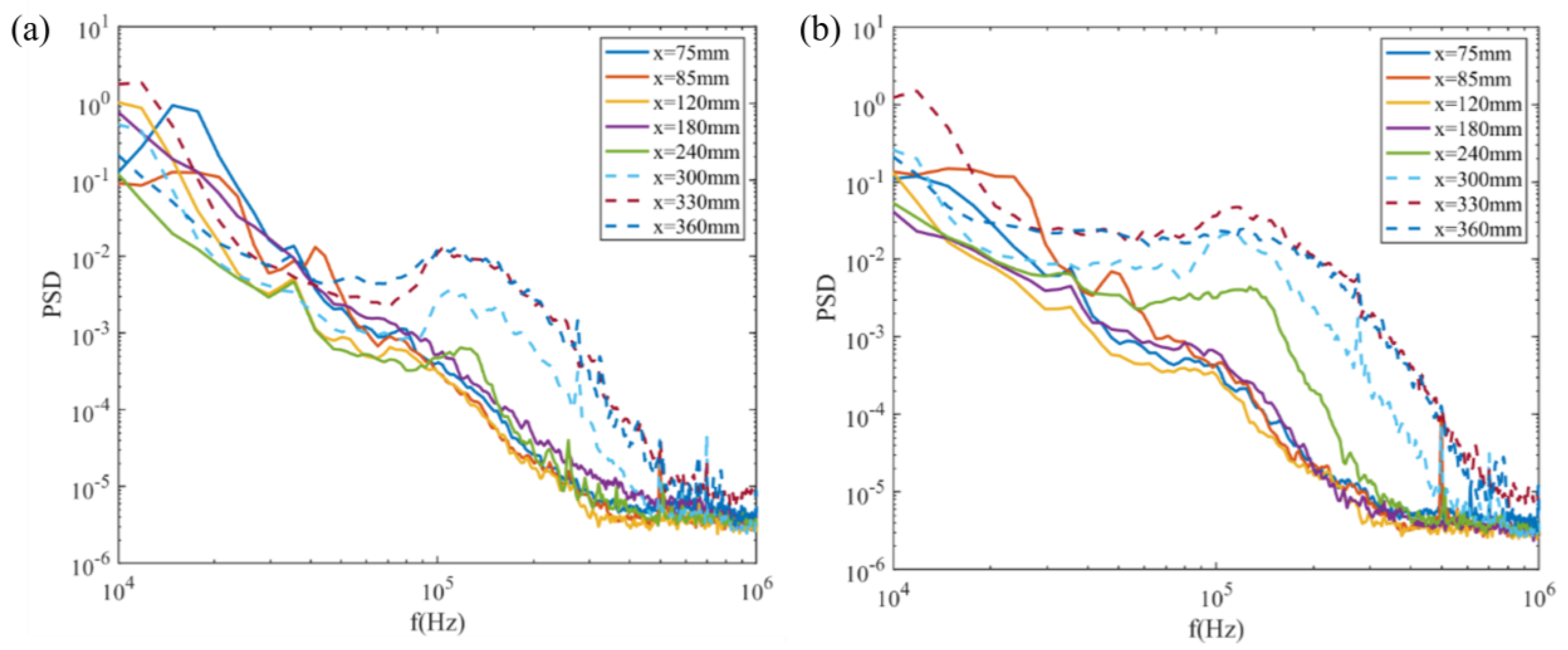
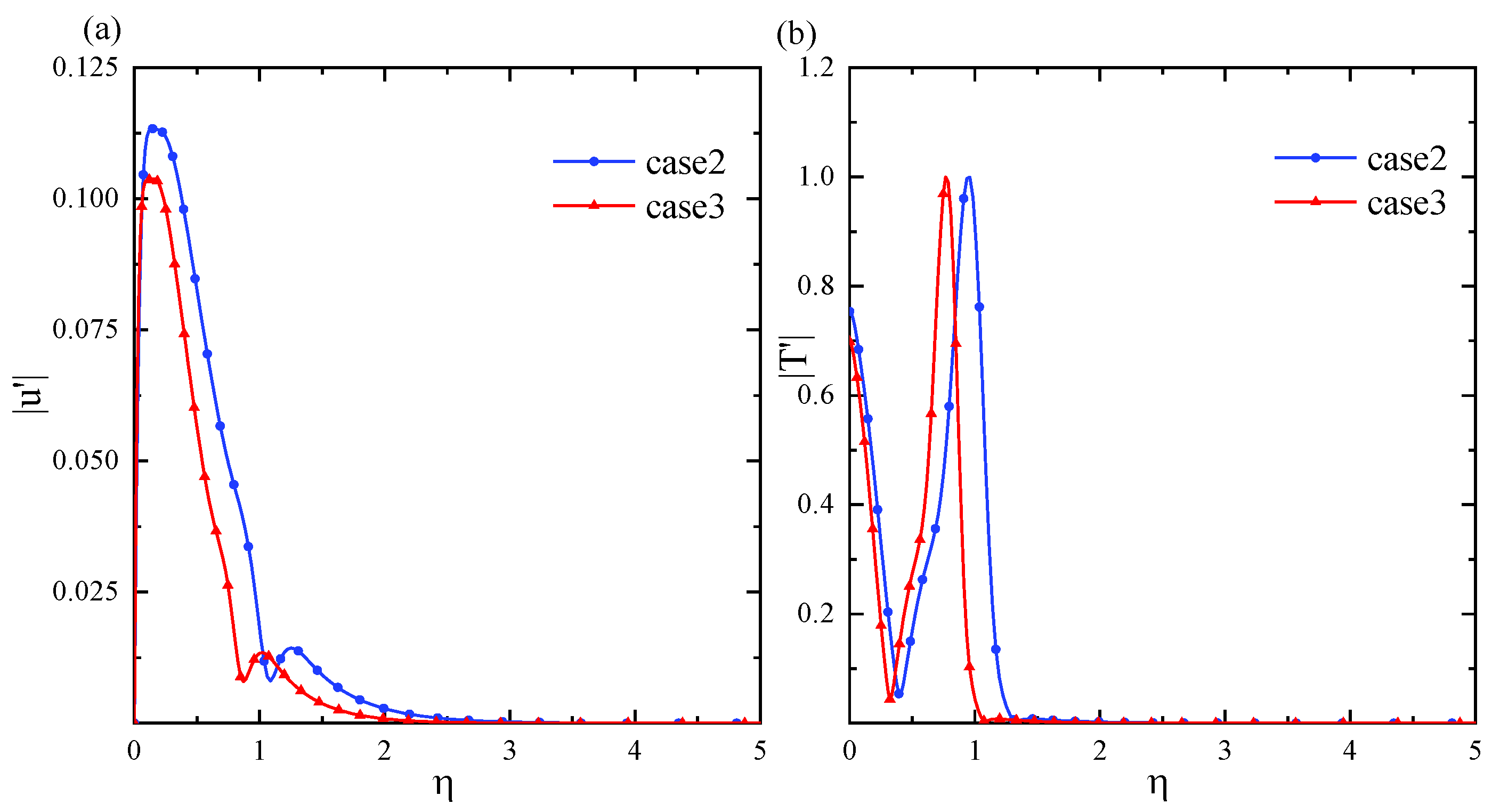
3.2. Instability Characteristics along Streamwise Direction
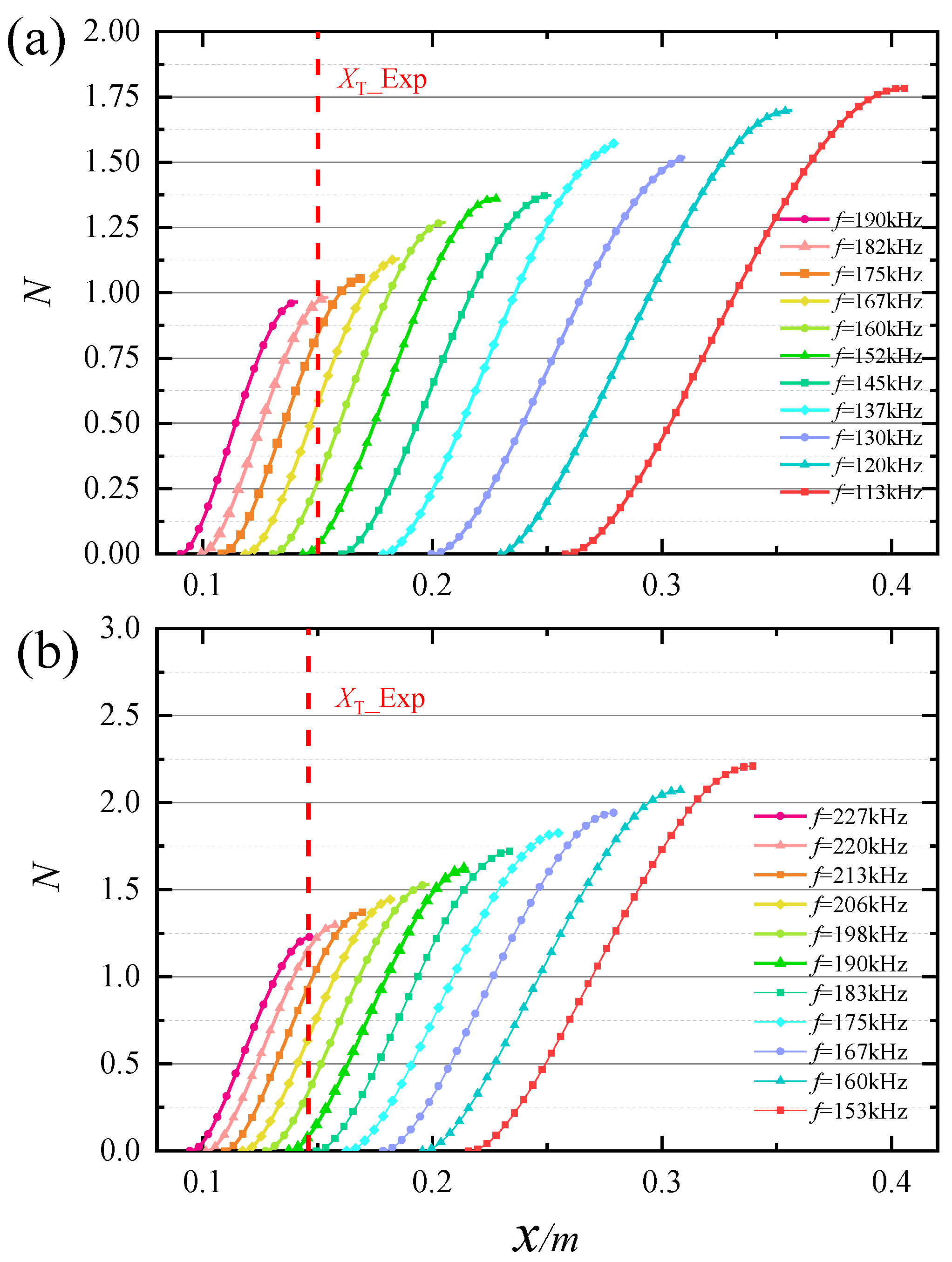
3.3. eN Method
4. Discussion
- (1)
- The transition model based on compressibility correction can better predict the transition position of the hypersonic boundary layer, and the simulation results are in good agreement with the experimental results. Moreover, the freestream unit Reynolds number has a great effect of the transition Reynolds number of the flat-plate boundary layer. As the unit Reynolds number increases, the transition position moves forward, and the transition Reynolds number also increases;
- (2)
- The LST results show that the first mode and the second mode are both present in the hypersonic boundary layer at the Mach number 5. Combined with the PCB results of the experiments, the second-mode frequency range predicted by the LST matches the frequencies measured in the experiments, with a second-mode frequency range from 100 to 250 kHz;
- (3)
- The N-factor of wind tunnel transition location predicted by LST is about 0.98 and 1.25 for Reunit = 6.38 × 106 and 8.20 × 106, respectively. With the increase in the unit Reynolds number, although the transition position moves forward, the N- factor of the transition position increases due to the increase in the magnification of the disturbance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| f | Frequency |
| Ma | Mach number |
| Pr | Prantl number |
| p | Pressure |
| Re | Reynolds number |
| u | Velocity |
| T | Temperature |
| ρ | Density |
| x, y, z | Cartesian coordinates |
| q | Heat flux |
| St | Stanton number |
| LST | Liner stability theory |
| α | Streamwise wave number |
| −αi | Spatial amplification rate |
| γ | Ratio of specific heat |
| ω | Angular frequency |
| β | Spanwise wave number |
| Cp | Specific heat capacity |
| T0 | Stationary temperature |
| T∞ | Freestream temperature |
| U∞ | Freestream velocity |
| ρ∞ | Freestream density |
| k | Heat conductivity |
| PEEK | Poly-ether-ether-ketone |
References
- Marineau, E.C.; Grossir, G.; Wagner, A.; Leinemann, M.; Radespiel, R.; Tanno, H.; Chynoweth, B.C.; Schneider, S.P.; Wagnild, R.M.; Casper, K.M. Analysis of second-mode amplitudes on sharp cones in hypersonic wind tunnels. J. Spacecr. Rocket. 2019, 56, 307–318. [Google Scholar] [CrossRef]
- Jianqiang, C.; Guohua, T.; Yifeng, Z.; Guoliang, X.U.; Xianxu, Y.; Cheng, C. Hypersonic boundary layer transition: What we know where shall we go. Acta Aerodyn. A Sin. 2017, 35, 311–337. [Google Scholar]
- Quintanilha, H.; Paredes, P.; Hanifi, A.; Theofilis, V. Transient growth analysis of hypersonic flow over an elliptic cone. J. Fluid Mech. 2022, 935, A40. [Google Scholar] [CrossRef]
- Mack, L.M. Boundary-Layer Linear Stability Theory; California Inst of Tech Pasadena Jet Propulsion Lab: Pasadena, CA, USA, 1984. [Google Scholar]
- Mack, L.M. Linear stability theory and the problem of supersonic boundary-layer transition. AIAA J. 1975, 13, 278–289. [Google Scholar] [CrossRef]
- Laurence, S.J.; Wagner, A.; Hannemann, K. Experimental study of second-mode instability growth and breakdown in a hy-personic boundary layer using high-speed schlieren visualization. J. Fluid Mech. 2016, 797, 471–503. [Google Scholar] [CrossRef]
- Estorf, M.; Radespiel, R.; Schneider, S.; Johnson, H.; Hein, S. Surface-pressure measurements of second-mode instability in quiet hypersonic flow. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 1153. [Google Scholar]
- Wendt, V.; Simen, M.; Hanifi, A. An experimental and theoretical investigation of instabilities in hypersonic flat plate boundary layer flow. Phys. Fluids 1995, 7, 877–887. [Google Scholar] [CrossRef]
- Zhao, J.S.; Liu, S.; Zhao, L.; Zhang, Z. Numerical study of total temperature effect on hypersonic boundary layer transition. Phys. Fluids 2019, 31, 114105. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, Z. Nonlinear wave interactions in a transitional hypersonic boundary layer. Phys. Fluids 2022, 34, 114106. [Google Scholar] [CrossRef]
- Cheng, J.; Huang, R.; Liu, W.; Wu, J. Influence of Single Roughness Element on Hypersonic Boundary-Layer Transition of Cone. AIAA J. 2023, 61, 3210–3218. [Google Scholar] [CrossRef]
- Thele, M.; Selcan, C.; Sander, T.; Rödiger, T.; Mundt, C. Bluntness-Dependent Hypersonic Boundary-Layer Modes’ Excitation. J. Spacecr. Rocket. 2022, 59, 1613–1622. [Google Scholar] [CrossRef]
- Borg, M.P.; Kimmel, R.L. Ground test of transition for HIFiRE-5b at flight-relevant attitudes. J. Spacecr. Rocket. 2018, 55, 1329–1340. [Google Scholar] [CrossRef]
- Yao, S.; Duan, Y.; Yang, P.; Wang, L.; Zhao, X.; Min, C. Experimental study of hypersonic boundary layer transition on a flat plate delta wing. Exp. Therm. Fluid Sci. 2020, 112, 109990. [Google Scholar] [CrossRef]
- Xu, X.; Yi, S.; Han, J.; Quan, P.; Zheng, W. Effects of steps on the hypersonic boundary layer transition over a cone at 10° angle-of-attack. Phys. Fluids 2022, 34, 034114. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, C.; Chen, X.; Yuan, H.; Wu, J.; Chen, S.; Lee, C.; Gad-El-Hak, M. Transition in hypersonic boundary layers: Role of dilatational waves. AIAA J. 2016, 54, 3039–3049. [Google Scholar] [CrossRef]
- Liu, S.; Wang, M.; Dong, H.; Xia, T.; Chen, L.; Zhao, A. Infrared thermography of hypersonic boundary layer transition induced by isolated roughness elements. Mod. Phys. Lett. B 2021, 35, 2150500. [Google Scholar] [CrossRef]
- Nakagawa, K.; Tsukahara, T.; Ishida, T. DNS Study on Turbulent Transition Induced by an Interaction between Freestream Turbulence and Cylindrical Roughness in Swept Flat-Plate Boundary Layer. Aerospace 2023, 10, 128. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, Z.; Lu, Y.; Wang, Y.; Yan, C. Direct numerical simulation of complete transition to turbulence via first-and second-mode oblique breakdown at a high-speed boundary layer. Phys. Fluids 2022, 34, 074101. [Google Scholar] [CrossRef]
- Saric, W.; Reshotko, E.; Arnal, D. Hypersonic Laminar-Turbulent Transition; AR-3l9; AGARD: Seine, France, 1998. [Google Scholar]
- Mason, W.H. Fundamental Issues in Subsonic/Transonic Expansion Corner Aerodynamics; AIAA Paper; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1993; p. 0649. [Google Scholar]
- Chen, F.J.; Malik, M.R.; Beckwith, I.E. Boundary-layer transition on a cone and flat plate at mach 3.5. AIAA J. 1989, 27, 687–693. [Google Scholar] [CrossRef]
- Juliano, T.J.; Paquin, L.; Borg, M.P. Measurement of HIFiRE-5 boundary-layer transition in a Mach-6 quiet tunnel with infrared thermograph. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 0595. [Google Scholar]
- Tao, S.; Su, C.; Huang, Z. Improvement of the e N method for predicting hypersonic boundary-layer transition in case of modal exchange. Acta Mech. Sin. 2023, 39, 122416. [Google Scholar] [CrossRef]
- Zhu, W.; Shi, M.; Zhu, Y.; Lee, C. Experimental study of hypersonic boundary layer transition on a permeable wall of a flared cone. Phys. Fluids 2020, 32, 011701. [Google Scholar] [CrossRef]
- Chen, X.L.; Fu, S. Linear stability analysis of hypersonic boundary layer on a flat-plate with thermal-chemical non-equilibrium effects. Acta Aerodyn. Sin. 2020, 38, 316–325. [Google Scholar]
- Klothakis, A.; Quintanilha Jr, H.; Sawant, S.S.; Protopapadakis, E.; Theofilis, V.; Levin, D.A. Linear stability analysis of hypersonic boundary layers computed by a kinetic approach: A semi-infinite flat plate at 4.5 ≤ M∞ ≤ 9. Theor. Comput. Fluid Dyn. 2022, 36, 117–139. [Google Scholar] [CrossRef]
- Boyd, C.F.; Howell, A. Numerical Investigation of One-Dimensional Heat-Flux Calculations; Technical Report NSWCDD/TR-94/114; Dahlgren Division Naval Surface Warfare Center: Silver Spring, MD, USA, 1994. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Chedevergne, F. A double-averaged Navier-Stokes k–ω turbulence model for wall flows over rough surfaces with heat transfer. J. Turbul. 2021, 22, 713–734. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw-Hill Series in Mechanical Engineering; McGraw-Hill Higher Education: New York, NY, USA, 2006. [Google Scholar]
- Willems, S.; Gülhan, A.; Steelant, J. Experiments on the effect of laminar–turbulent transition on the SWBLI in H2K at Mach 6. Exp. Fluids 2015, 56, 49. [Google Scholar] [CrossRef]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A correlation-based transition model using local variables—Part I: Model formulation. J. Turbomach. 2006, 128, 413–422. [Google Scholar] [CrossRef]
- Guo, X.; Tang, D.; Shen, Q. Boundary layer stability with multiple modes in hypersonic flows. Mod. Phys. Lett. B 2009, 23, 321–324. [Google Scholar] [CrossRef]

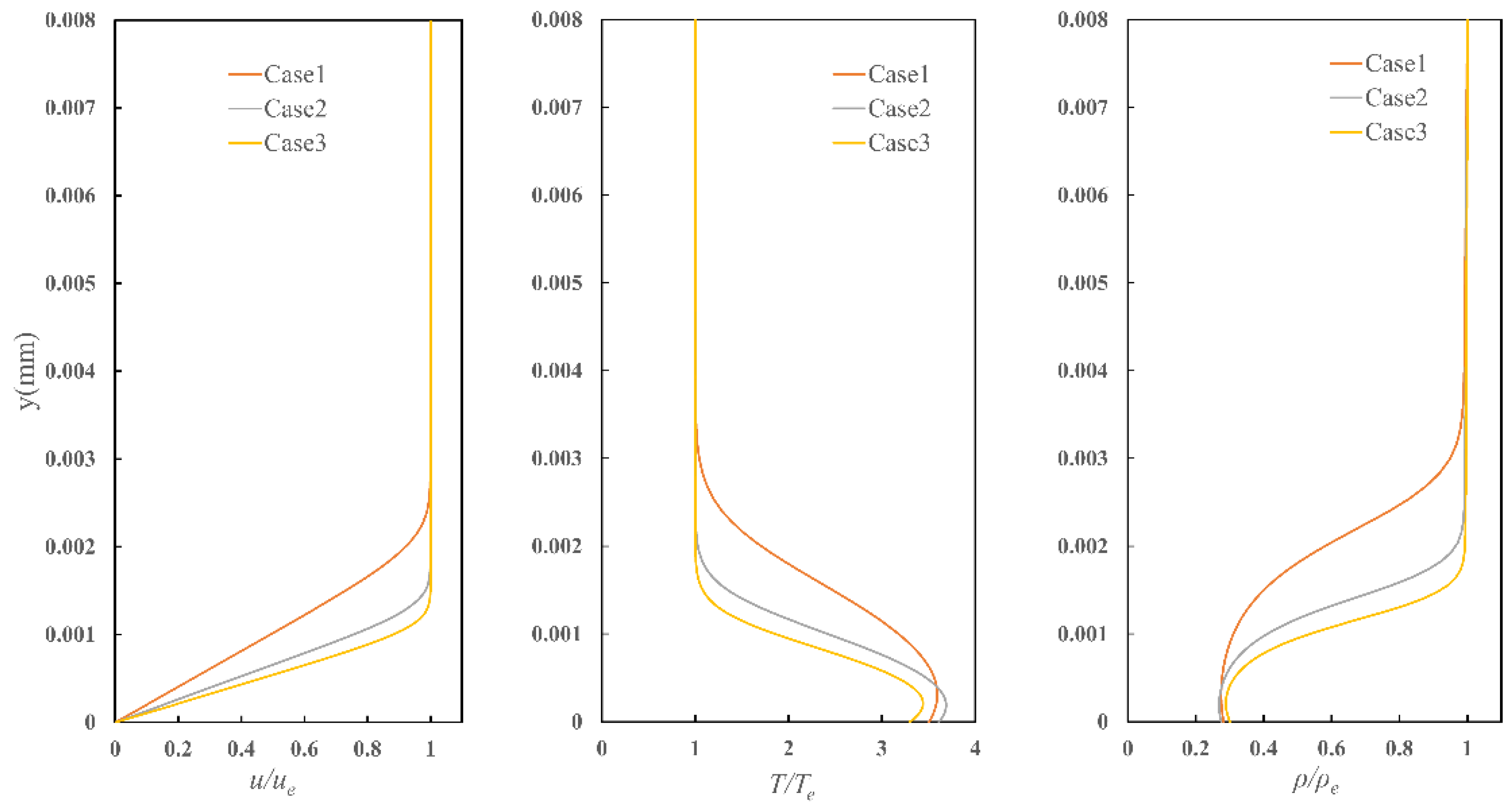


| Flow Condition | P0/kPa | T0/K | Re/m/106 | |
|---|---|---|---|---|
| Ma = 5 | Case1 | 200.1 | 501 | 2.52 |
| Case2 | 490.5 | 491 | 6.38 | |
| Case3 | 729.9 | 539 | 8.20 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Jiang, Y.; Liu, S.; Dong, H. The Experiments and Stability Analysis of Hypersonic Boundary Layer Transition on a Flat Plate. Appl. Sci. 2023, 13, 13302. https://doi.org/10.3390/app132413302
Yin Y, Jiang Y, Liu S, Dong H. The Experiments and Stability Analysis of Hypersonic Boundary Layer Transition on a Flat Plate. Applied Sciences. 2023; 13(24):13302. https://doi.org/10.3390/app132413302
Chicago/Turabian StyleYin, Yanxin, Yinglei Jiang, Shicheng Liu, and Hao Dong. 2023. "The Experiments and Stability Analysis of Hypersonic Boundary Layer Transition on a Flat Plate" Applied Sciences 13, no. 24: 13302. https://doi.org/10.3390/app132413302
APA StyleYin, Y., Jiang, Y., Liu, S., & Dong, H. (2023). The Experiments and Stability Analysis of Hypersonic Boundary Layer Transition on a Flat Plate. Applied Sciences, 13(24), 13302. https://doi.org/10.3390/app132413302







