Performance Evaluation Model of Landport and Seaport Collaboration Using the Support Vector Machine

Abstract

This study delves into the pivotal role of shipper satisfaction in cultivating efficacious cooperation between dry ports and seaports. The research endeavors herein present a comprehensive indicator system tailored to evaluate the efficacy of the cooperation of the sea ports and dry ports. This system encompasses 14 key indicators, thoughtfully categorized into four dimensions, offering a holistic perspective on the multifaceted factors that underscore the synergy between dry ports and seaports. The establishment of a performance evaluation model for this collaborative nexus draws upon the support vector machine (SVM) technique, a choice substantiated by its suitability for the available dataset and its relevance within the research context. Leveraging the indicator data as a training dataset, the SVM approach culminates in the construction of a cooperative matrix, ultimately facilitating the discernment of performance rankings within dry port and seaport collaboration. This research methodology not only yields valuable insights into the evaluation of this distinct collaboration but also presents a versatile framework with potential application for addressing various challenges encountered within the cooperative milieu of dry ports and seaports.

1. Introduction

Dry port refers to a “port without water”, which actually refers to a logistics center with many logistics services built in the inland far from the seaport [1], as the result of seaports extending their services to the inland. In 2013, China introduced the “One Belt, One Road” initiative, aimed at accelerating transportation integration between Asia and Europe. In this endeavor, it is crucial and worthwhile to consider the effective interconnection of multimodal transport. According to statistics, Europe boasts more than 300 dry ports, while the United States hosts nearly 400 cargo transfer centers and dry ports. Additionally, Asia houses over 300 dry ports [2].

Dry ports serve as storage facilities for empty containers, mitigating terminal congestion and addressing land shortage concerns [3] (Le et al., 2023). Simultaneously functioning as an extension of seaports, the operational efficiency of dry ports to a certain extent determines the operational efficiency of the container supply chain. The alignment between seaports and dry ports necessitates contemplation of numerous factors. For instance, the site area, supporting facilities, and operational procedures of a dry port should be in harmony with the scale, cargo throughput, and staffing of the seaport. The alignment between seaports and dry ports necessitates contemplation of numerous factors. Furthermore, the seaports and dry ports should synergize efforts for a mutually advantageous outcome. Dry ports should leverage facility sharing, attract high-quality cargo sources through cost-effective services, optimize the aggregation of goods, expedite the integration process of the seaports and dry ports, and assume certain functions of the seaport, thereby establishing a cooperative mechanism that yields mutual benefits. Simultaneously, effective cooperation between the “two ports” necessitates a mature and comprehensive regulatory framework [4]. Only within a fixed and standardized model can the seaports and dry ports ensure sustained and efficient collaboration between the involved parties, ultimately arriving at a consensus for mutual development. The dynamic nature of interactive cooperation between the “two ports” necessitates ongoing evolution. Consequently, the establishment of a performance model for cooperation between the two ports warrants thorough examination and study.

At present, the research on dry ports mainly focuses on the site selection of dry ports, the network design of dry ports, and the cooperation with seaports. The research on the location of dry ports is very mature at present. Ambrosino et al. have proposed a hub location model to determine the best location of a medium-sized dry port considering the flow direction of containers in multimodal transport [5].

The establishment of dry ports is influenced by a diverse array of stakeholders, encompassing dry ports themselves, the corresponding cities/regions, seaports, shippers, shipping companies, railway operators, and road operators. Employing a methodology rooted in multi-participant and multi-criteria analysis, Khaslavskaya has considered the objectives and perspectives of these various stakeholders in order to assess different scenarios. The research findings underscore the paramount importance of the fundamental services provided by the examined dry port in the initiation of operations.Castrellon delves into two strategies routed through dry ports, scrutinizing both their environmental and economic implications. Various cooperation scenarios among shipping lines, each entailing different levels of container substitution, are taken into account.

Wang and Wei proposed a new method to evaluate the priority of site selection of dry ports, and systematically analyzed the factors affecting the facilities of dry ports to establish an evaluation model considering the feedback and the relationship between these factors [6]. Nguyen and Notteboom proposed a site selection framework of dry ports based on multiple standard analyses, and the whole framework was divided into four steps including the preliminary study of candidate sites, stakeholder classification, method application, and case study [7]. Alumur et al., proposed a site selection problem of hub ports by considering service time limitations and transport congestion. They considered cargo transportation time, loading and unloading time, and delay time on the hub network, and established a dispatching model with consideration of single and multiple hubs [8]. Awad et al. proposed exploring the variable factors affecting the sustainable development of site selection of dry ports as well as how to evaluate such sustainable development. Further, they established a model by employing the multiple decision analysis method and Bayesian network to find out the key variables [9]. Ka regarded the site selection optimization of dry ports as a multi-objective decision-making process, and combined the two optimization models of Fuzzy-AHP and ELECTRE [10]. Castrellon et al., developed a mathematical model that minimizes the sum of transport and fixed costs associated with opening and closing dry ports. They conducted sensitivity analysis on model parameters [11]. Wang et al. put forward a three-stage model on the basis of the existing one, which is respectively used to weigh decision criteria, determine potential locations and evaluate these alternatives [12]. The research on the network design of dry ports mainly focuses on the network traffic optimization model. Song et al. propose a multi-period shipping network including the location of dry ports on the basis of considering the problem of empty containers, cargo routes and cargo volume [13]. Kamran proposes a two-stage dry port network design model, which integrates strategic and operational decision considering the stochastic nature of demand [14]. Daniela and Ann, considering the wharf space resources, used the mathematical programming model of the two-stage weighted dynamic graph to transport container flows by using multimodal transport through establishing dry ports [15]. Teodor et al. believed that there was some room for the optimization of dry ports in the multimodal transport system, and proposed a mixed integer programming model to solve the route optimization and scheduling problems of vehicle transportation in the combined transport system of dry ports [16]. Dukkanci and Kara considered the location of hub ports in the network and the distribution of these hubs by demand nodes, proposed a multi-modal transport hub network based on a hierarchical structure, and solved the problem by using the heuristic algorithm based on the sub-gradient method [17]. In addition, there are also some studies on the cooperation between dry ports and seaports. Notteboom and Winkelmans pointed out that cooperation between ports can improve the market share of cooperative ports [18]. Nguyen used game theory to study the cooperation effect and cooperation relationship of Pakistani ports against the background of competition [19].

At present, the research on dry ports mainly focuses on the site selection of dry ports, the network design of dry ports, and the cooperation with seaports. The research of dry ports is very mature at present. The performance evaluation of the cooperation between ports will help both parties find out the problems in time and strengthen their own construction. At present, the performance evaluation methods of ports mainly include the neural network, analytic hierarchy process, grey theory, clustering, and other analysis methods. However, these methods can only unilaterally reflect the recent level of cooperation between seaports and dry ports. There are many factors that affect the cooperation between dry ports and seaports, and these factors have different degrees of influence.

The cooperation between dry ports and seaports directly affects the collaboration benefits of both parties and their future development trends. When conducting a cooperative assessment, we should not only consider the immediate interests of both parties but also take into account the satisfaction of cargo owners, all of which should align with the common interests of both. In order to measure the cooperative performance between dry ports and seaports, we use the balanced scorecard, which can effectively transform the strategic objectives of the seaport and dry port cooperation into performance indicators and actions at all levels, from four aspects, to achieve the balance between financial and non-financial measurement methods: the balance between long-term goals and short-term goals, the external and internal balance, the result and process balance, and the balance between management performance and operating performance. The cooperation between dry ports and seaports is a nonlinear classification problem which is difficult to study. Based on the actual situation of sea port and dry port cooperation and the basic principles and main characteristics of the support vector machine (SVM), this paper will use SVM in machine learning to evaluate the performance of cooperation between seaports and dry ports.

The remainder of this paper is organized as follows. Section 2 describes collaboration between seaports and dry ports, the related method. Section 3 formulates the performance evaluation model for the cooperation between dry ports and seaports. The case studies are presented in Section 4, with the conclusions drawn in Section 5.

2. Support Vector Machine (SVM)

2.1. Support Vector Machine

The support vector machine (SVM) is a machine learning method which is a part of statistical learning theory. The SVM originally evolved from optimal segmentation surfaces in linearly separable cases. Through coefficient normalization, the linearly separable sample set $\left(x_i,y_i\right),i=1,2,\dots ,n,x\in R^d,y_i\in \left\{+1,-1\right\}$ satisfies the following constraint conditions:

(1)

Global optimal solution

The SVM method transforms the quadratic programming problem under the original constraints into the dual quadratic optimization problem, and the solution it seeks must be the global optimal solution, thus avoiding the local optimal solution that may occur in the learning methods such as a neural network.

(2)

Dimension independence

The problem studied in this paper belongs to nonlinear classification problems. When SVM is solving nonlinear classification problems, the kernel function is skillfully applied in the dual form of optimization problems, which overcomes the algorithm complexity.

(3)

Avoidance of ill-posed problems

The SVM method is specifically proposed for learning problems in the case of a small number of samples. Coincidentally, the number of analysis samples used in this study is small, and the SVM method is suitable for the problem in this study.

(4)

Good self-adaptation

The only freedom of the SVM method is the choice of kernel function, thus avoiding the dependence of methods like neural networks on techniques.

(5)

Diverse derivation methods

In the SVM method, learning algorithms such as poly approximation and the RBF method can be implemented as long as different kernel functions are selected.

2.2. Nonlinear Support Vector Machine

In most cases, the samples are not separable, so it is necessary to construct an optimal classification surface in this high-dimensional space. When an appropriate mapping function is chosen, the formerly linearly inseparable situation can be transformed into a linearly separable one. For nonlinear problems, SVM can reduce the difficulty of high-dimensional space operation by defining kernel function, thus avoiding dimension disaster.

According to the functional theory, as long as the Mercer condition is satisfied for $K(x_i,x_j)$, $K(x_i,x_j)$ would satisfy the inner product of a certain spatial transformation. When $0<{\zeta }_i<1$, the sample point $x_i$ can still be correctly classified; when ${\zeta }_i\ge 1$, the sample point $x_i$ would be misclassified. At this point, the problem of optimal classification surface can be transformed into a quadratic programming problem as follows:

$$\min \psi (w,\zeta )=\frac{1}{2}{w}^{T}w+C{\displaystyle \sum _{i=1}^n{\zeta }_i}$$

(1)

$$y_i(w^T{x}_i+b)\ge 1+{\zeta }_i,i=1,2,\dots ,n.$$

(2)

When the two categories of samples are linearly inseparable, a relaxation variable ${\zeta }_i$$({\zeta }_i\ge 0,i=1,2,\dots ,n)$ can be introduced to make the hyperplane $w^{T}x+b=0$

The constant C in Equation (11) represents the penalty value for sample classification error, which can realize the compromise between the generalization ability of machine learning and the classification error. Thus, the problem of optimal classification surface is further transformed into solving the dual problem, namely, finding the maximum value of the following function:

$$W(\alpha )={\displaystyle \sum _{i=1}^n{\alpha }_i}-\frac{1}{2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{i=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i^{},x_j)}}$$

(3)

Here, the constraint conditions are:

$${\displaystyle \sum _{i=1}^n{y}_i{\alpha }_i}=0,0\le {\alpha }_i\le C,i=1,2,\dots ,n$$

(4)

where $K(·)$ is the kernel function. At this point, the coefficient vector of the optimal classification surface is:

$$W={\displaystyle \sum _{i=1}^n{\alpha }_i{y}_i\varphi (x_i)}$$

(5)

By solving Equation (6), the coefficient ${\alpha }_i$ can be obtained. Thus, the classification function can be expressed as:

$$f(x)=\mathrm{sgn}\left[(w^{T}x)+b\right]=\mathrm{sgn}\left({\displaystyle \sum _{i=1}^n{\alpha }_i^{}{y}_{i}K(x,x_i^{})+b^{*}}\right)$$

(6)

3. Collaboration between Seaports and Dry Ports

3.1. Cooperative Performance

The cooperative performance of the cooperation between seaports and dry ports involves multiple aspects, including the scale, functionality, objectives, and more; for both the seaport and the dry port, we can elaborate on the following aspects:

(1)

The cooperation between seaports and dry ports should be coordinated internally. For example, the site area, supporting facilities, and formalities of the dry port should match the size, cargo throughput, and staffing of the seaport.

(2)

In cooperation, seaports and dry ports need to work together for win-win results. Dry ports should give play to the advantages of facility sharing, attract goods sources with high-quality and low-cost services, maximize the aggregation effect of goods, accelerate the integration process of “two ports”, complete some of the functions of seaports from dry ports, and form a cooperative mechanism of mutual benefit.

(3)

The cooperation between seaport and dry port needs a mature and perfect normative system. The cooperation between seaports and dry ports can only ensure lasting and efficient cooperation between the two sides under a fixed and standardized mode and reaching a consensus of common development.

(4)

The system platform of the cooperation between seaports and dry ports needs to be open and transparent, and the closed and independent system is not conducive to the real-time transmission of information. In fact, the process of interaction and cooperation between the seaports and dry ports is that the internal systems are unified and adapt to each other, and ultimately maintain a dynamic balance. Only in this way can we ensure smooth and convenient communication between the two sides.

(5)

The interaction and cooperation between seaports and dry ports are constantly changing and developing. There may be a time difference between the seaports and dry ports in the process of information transmission, resulting in delayed information transmission. In the case of information inconsistency, both parties need to communicate and improve in time to avoid information inconsistency. The two sides faced the problems together, reached a coordinated pace in a dynamic manner, and finally formed the common progress and development of the cooperation between seaports and dry ports.

3.2. Indicator Selection

(1)

Customer satisfaction degree

From the perspective of the supply chain, the performance indicators of customer satisfaction degree for the cooperation between dry ports and seaports include customer satisfaction degree, market share, customs clearance time, and generalized transportation cost.

(2)

Financial indicators

Enterprises are sensitive to financial data, and the relevant financial data cannot be obtained directly. In view of this, the indicators indirectly related to enterprise finance are selected. Since the financial status of dry port enterprises is directly proportional to their annual throughput and trade volume, the growth amount of import and export is taken as an indicator to indirectly reflect the financial performance of both parties.

(3)

Cooperative relationship of both parties

For the cooperation between seaports and dry ports, the cooperation performance indicators include customs declaration and inspection business, information sharing degree, connected railways, and the cooperation degree of both parties. Since it is difficult to characterize the degree of cooperation between the two parties, it is necessary to quantify the signed cooperation agreement with a score in the range of 0~10.

(4)

Non-market tools

In addition to external cooperation evaluation indicators, the internal factors of dry ports should also be considered. (1) Regional transport scale is the most fundamental reason for the emergence of dry ports, and the cargo capacity of dry ports determines that they can absorb more goods. (2) The number of relevant promotion policies for developing dry ports is one of the indicators for measuring the competitiveness of dry ports. (3) The port facility level of dry ports depends on the amount of fixed asset investment (which is a monetary activity), and it is an important indicator reflecting the scale of fixed asset investment.

According to the cooperation performance evaluation indicators for dry ports and seaports, the specific cooperation performance evaluation system is shown in

Table 1. Cooperation performance evaluation system.

First Level	Second Level	Third Level
		Suzhou	Ningbo	Zhengzhou	Xi’an
Customer satisfaction degree	Added value of tertiary industry (CNY billion) C1	73.26	103.53	50.07	39.56
	Growth rate of tertiary industry (%) C2	10.1	17.7	14.1	11.7
	Market share (%) C3	38	45	60	40
	Generalized transportation cost (CNY/TEU) C4	1184.7	1472.3	4431.1	4510.8
	Customs clearance time (h) C5	2	0.8	1	4.5
Financial indicator	Growth amount of import and export (USD billion) C6	39.17	59.65	8.57	6.67
	Growth rate of import and export (%) C7	14.3	13.3	10.9	36.4
Cooperative relationship of both parties	Customs clearance business C8	7	7	7	8
	Information share degree C9	8	8	7	7
	Number of connected railways C10	3	1	4	2
	Cooperation degree of both parties C11	9	9	8	6
Non-market tools	Regional transport scale (million tons) C12	262.57	301.70	251.30	238.88
	Relevant promotion policies (article) C13	2	4	3	3
	Fixed asset investment (CNY billion) C14	562.96	585.44	707.57	519.14

.

4. Establishment of the Performance Evaluation Model for the Cooperation between Dry Ports and Seaports

4.1. Original Data Processing

The indicators in the performance evaluation system of the “two-port” cooperation constructed in this study belong to different types. In order to eliminate the interference caused by the order of magnitude, it is necessary to normalize the indicators. The common indicator types include the maximum-type indicator, that is, the larger the indicator value, the better; the minimum-type indicator, that is, the smaller the indicator value, the better; and the interval-type indicator, that is, the indicator value is best within a limited range. The following three mathematical models can be used to normalize the 14 indicators.

• For the maximum-type indicator,

$$X_{ij}^{\prime }=\frac{X_{ij}-\min X_j}{\max X_j-\min X_j}$$

(7)

2.

For the minimum-type indicator,

$$X_{ij}^{\prime }=\frac{\max X_j-X_{ij}}{\max X_j-\min X_j}$$

(8)

3.

For the interval-type indicator,

$$X_{ij}^{\prime }=\{\begin{array}{l}1-\frac{a-X_{ij}}{\max (a-\min X_j,\max X_j-b)},X_{ij}<a\\ 1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ,a\le X_{ij}\le b\\ 1-\frac{X_{ij}-b}{\max (a-\min X_j,\max X_j-b)},X_{ij}>b\end{array}$$

(9)

where $X_{ij}$ is the $j$-th indicator of the $i$-th dry port to be evaluated; $X_{ij}^{\prime }$ is the normalized value; $\min X_j$ is the minimum value of the $j$-th column of indicators; $\max X_j$ is the maximum value of the $j$-th column of indicators; and $(a,b)$ is the ideal interval of $X$.

4.2. Selection of Kernel Function and Kernel Parameters

The selection of kernel function and related parameters is an important process in designing the SVM evaluation model. On the premise of the research on the “two-port” cooperation performance, the kernel function and related parameters need to be determined. In this study, RBF is used as the inner product function in cooperative performance rating. For the RBF kernel function $K(x,y)=\exp (-||x-y||/2{\sigma }^2)$, the kernel width $\sigma$ has the following properties:

Theorem 1. 

In the RBF kernel function $K\left(x,y\right)$, when $\sigma$ tends to 0, all sample points are support vectors.

Theorem 2. 

When $\sigma$ tends to $\infty$, the discriminant function of the SVM of the RBF kernel function is a constant; namely, all samples are classified into the same one category.

It can be inferred from the above two theorems that, for a given training sample set, as long as $\sigma$ > 0 is sufficiently small, the SVM of the RBF kernel function can correctly classify the samples; the larger the value of $\sigma$, the poorer the classification ability of the SVM.

The penalty coefficient C can find a compromise between the model’s complexity and the training sample errors of the kernel function, which endows the model with good generalization ability.

The insensitivity coefficient $\epsilon$ can ignore the error within a certain range of the true value and simultaneously ensure the existence of the global minimum solution.

4.3. Model Training and Classification Implementation

Assume that m is the number of dry ports to be evaluated, n is the number of indicators in the evaluation indicator system, and $X_{ij}$ corresponds to the score of the $j$-th indicator of the $i$-th dry port. The cooperation indicator of the $i$-th dry port can be expressed as a dimension vector: $X_i=(X_{i1},X_{i2},\dots ,X_{in}),i=1,2,\dots ,m$.

In this study, the performance evaluation problem of the cooperation between dry ports and seaports needs to be transformed into a classification problem based on the SVM method. At first, the advantages and disadvantages of the two dry ports to be evaluated should be clarified. The comparison results can be divided into three categories: $i$ is superior to $j$, $i$ is comparable to $j$, and $i$ is inferior to $j$. Assume there is a vector set $\left\{Y_{ij}\right\}$, $Y_{ij}=(X_{i1},X_{j1}{X}_{i2},X_{j2},\dots ,X_{in},X_{jn}),i,j=1,2,\dots ,m$, and $i\ne j$. In $\left\{Y_{ij}\right\}$, each vector $Y_{ij}$ can be composed of vectors $X_i$ and $X_j$, and $Y_{ij}$ can be classified into three categories according to the advantages and disadvantages of the two dry ports to be evaluated:

$$Y_{ij}=\{\begin{array}{l}1,f(X_i)>f(X_j)\\ 0,f(X_i)=f(X_j)\\ -1,f(X_i)<f(X_j)\end{array}.$$

(10)

In Equation (10), $f(X_i)$ represents the advantages and disadvantages of the i-th dry port to be evaluated; the larger the value of $f(X_i)$, the better. Through this method, SVM can be used to classify $\left\{Y_{ij}\right\}$, and then the advantages and disadvantages of dry ports $i$ and $j$ can be determined according to the classification labels.

When evaluating the performance of the cooperation between dry ports and seaports, the vectors corresponding to the two dry ports are spliced into a 2n dimensional vector, which is treated as the new evaluation object. The vector of the cooperation performance indicator of the $i$-th dry port is $(X_{i1},X_{i2},\dots ,X_{in})$, and that of the $j$-th dry port is $(X_{j1},X_{j2},\dots ,X_{jn})$. Thus, the two vectors can be spliced into $Y_{ij}=(X_{i1},X_{j1}{X}_{i2},X_{j2},\dots ,X_{in},X_{jn}),i,j=1,2,\dots ,m$, and $i\ne j$. After the two vectors are spliced, we make the following stipulations: if the $i$-th dry port is superior to the $j$-th, then the corresponding classification label is +1; if the two dry ports are comparable, then the classification label is 0; if the $i$-th dry port is inferior to the $j$-th, then the corresponding classification label is −1.

4.4. Determination of Cumulative Sum Score

In the above, the SVM method was introduced into the performance evaluation of the cooperation between dry ports and seaports through the judgement of the splicing vector, be seen as Figure 1. In order to obtain the total ranking of the dry ports to be evaluated, it is necessary to transform the classification results into absolute values. Here, an evaluation matrix is established to compare each dry port with the other dry ports to be evaluated. Assume $g_i(X_j)$ is the score of the $i$-th dry port to be evaluated, relative to the $j$-th dry port. In this study, we make the following stipulations: if the $i$-th dry port to be evaluated is superior to the $j$-th, the $i$-th dry port scores 2; if the $i$-th dry port to be evaluated is comparable to the $j$-th, the $i$-th dry port scores 1; if the $i$-th dry port to be evaluated is inferior to the $j$-th, the $i$-th dry port scores 0. These stipulations can be summarized as follows:

$$g_i\left(X_j\right)=\{\begin{array}{l}2,Y_{ij}=1\hfill \\ 1,Y_{ij}=0\dots i,j=1,2,\dots ,m\hfill \\ 0,Y_{ij}=-1\hfill \end{array}$$

(11)

The total score $f^{\prime }(X_i)$ of the $i$-th dry port to be evaluated can be obtained by adding up the scores of all dry ports. The calculation formula is as follows:

$$f^{\prime }(X_i)={\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^m{g}_i(X_j)}\hspace{1em}\hspace{1em}i=1,2,\dots ,m$$

(12)

Finally, the dry port with the best performance can be figured out through the above steps.

5. Case Analysis

5.1. Brief Introduction to Shanghai Port

Shanghai Port is close to rivers and seas, with numerous economic hinterlands. As an international shipping center, goods from and to all over China will pass through here for import and export activities. The main economic hinterlands of Shanghai Port include many big cities in Jiangsu, Zhejiang, and south China, as well as some cities in central and western China. Shanghai Port has convenient land and water transportation and developed collection and distribution systems, which can rapidly radiate outwards with the help of a developed transportation network.

5.2. Performance Evaluation for the Cooperation between Dry Ports and Shanghai Port

The increasingly fierce port competition and limited development space of the ports themselves promote more and more ports to expand their economic hinterlands towards the inland. The same is true for Shanghai Port. Shanghai Port has established cooperative relations with many inland dry ports and hopes to continue to cooperate with potential dry ports. In this study, on the basis of selecting Suzhou, Ningbo, Zhengzhou, and Xi’an [20], we further selected Xiaoshan, Jinhua, Shaoxing, and Lishui in the economic hinterland of Shanghai Port as the cooperation objectives of Shanghai Port. Thus, the cooperation performance of Suzhou (1), Ningbo (2), Xiaoshan (3), Jinhua (4), Shaoxing (5), Lishui (6), Zhengzhou (7), and Xi’an (8) with Shanghai Port are evaluated separately.

In Section 4, the cooperation performance evaluation system was established. Based on that evaluation system, this section evaluates the cooperation between the eight dry ports and Shanghai Port. The cooperation indicators are scored quantitatively and qualitatively; namely, some indicators are scored through actual data search and some are scored by experts.

(1)

Data pre-processing

According to Equations (8)–(10), the scores in

Table 2. Evaluation scores of the eight dry ports.

	City	1	2	3	4	5	6	7	8
Indicator
C1		732.6	1035.3	951.3	876.5	2181.5	427,032	500.7	395.6
C2		10.1	17.7	12.1	11.8	6.9	8	14.1	11.7
C3		38	45	14	16	25	41	60	40
C4		1184.7	1472.3	1534.7	1374.1	1479.3	1638.1	4431.1	4510.8
C5		2	0.8	2.5	1.5	1	1.5	1	4.5
C6		391.7	596.5	22.6	419.8	−19.5	39,465.1	85.7	66.7
C7		14.3	13.3	16	13.5	−1.8	14.2	10.9	36.4
C8		7	7	5	6	5	5	7	8
C9		8	8	6	7	7	7	7	7
C10		3	1	1	2	2	2	4	2
C11		9	9	7	8	7	8	8	6
C12		26,257	30,170	48.8	903.7	12,447.4	479	25,130	23,888
C13		2	4	2	3	2	3	3	3
C14		5629.6	5854.4	800.3	2084	2882.5	641,238	7075.7	5191.4

are normalized (a = 0.1 and b = 0.7), and the normalization results are shown in

Table 3. Normalization results of the performance evaluation scores for the cooperation between the eight dry ports and Shanghai Port.

	City	1	2	3	4	5	6	7	8
Indicator
C1		0.28	0.34	0.62	0.42	0.18	0.67	0.2	0.16
C2		0.31	0.56	0.72	0.49	0.21	0.01	0.52	0.41
C3		0.14	0.15	0.85	0.7	0.36	0.01	0.23	0.16
C4		0.45	0.48	1	0.66	0.12	0.2	0.18	0.19
C5		0.79	0	0.97	0	0.1	0.47	0	0.1
C6		0.15	0.2	0.14	0.2	0	0.62	0.33	0.27
C7		0.47	0.41	0.98	0.58	0.14	0	0.39	0.14
C8		0.19	0.21	0.26	0.22	0.2	0.46	0.24	0.25
C9		0.23	0.24	0.33	0.64	0.21	0.86	0.24	0.21
C10		0.38	0.63	0	0.24	0.72	0.8	0.12	0.39
C11		0.27	0.27	0.39	0.31	0.21	0.37	0.79	0.17
C12		1	0.87	0.61	0.43	1	0.74	0.67	0.84
C13		0	0.11	0.65	0.72	0.17	0.34	0.8	0.42
C14		0.21	0.19	0.52	1	0.23	1	0.28	0.22
Classification label		1	1	1	1	−1	−1	−1	−1

.

(2)

Parameter selection

It is not difficult for SVM to handle nonlinear sample problems, which can be simplified by appropriate functions. Similarly, the algorithm has a significant influence on the kernel function. When the kernel function is stable, the influence of kernel parameters on the model should also be considered. In this study, considering the actual characteristics of dimensionality and sample number, we adopt the radial basis function (RBF).

During the debugging of RBF, the penalty coefficient C, kernel width σ, and insensitivity coefficient ε are the important influencing factors. It is found that if different parameters are selected, the results would have different degrees of fluctuation. Hence, it is necessary to constantly debug RBF in order to achieve an ideal state.

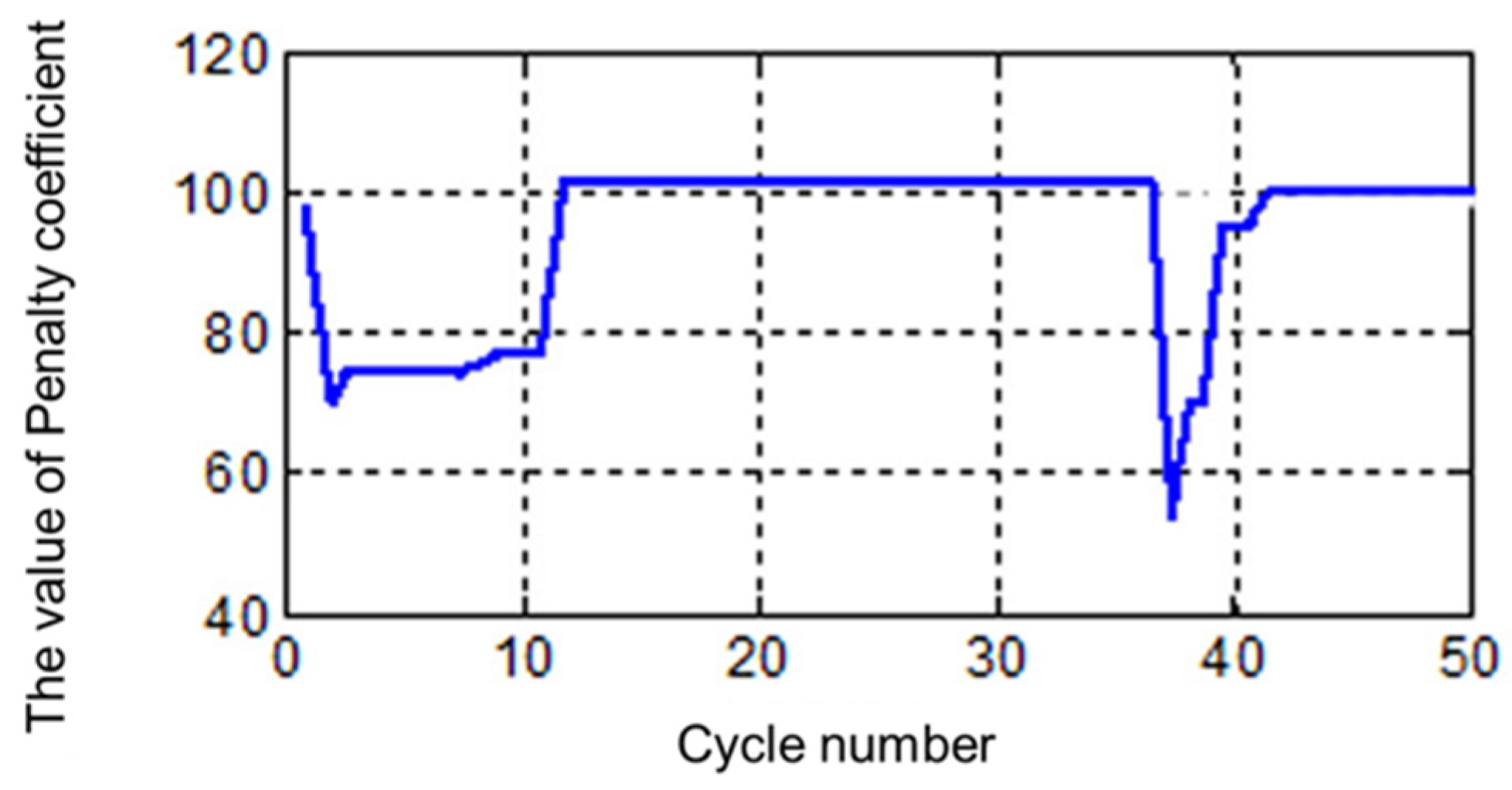
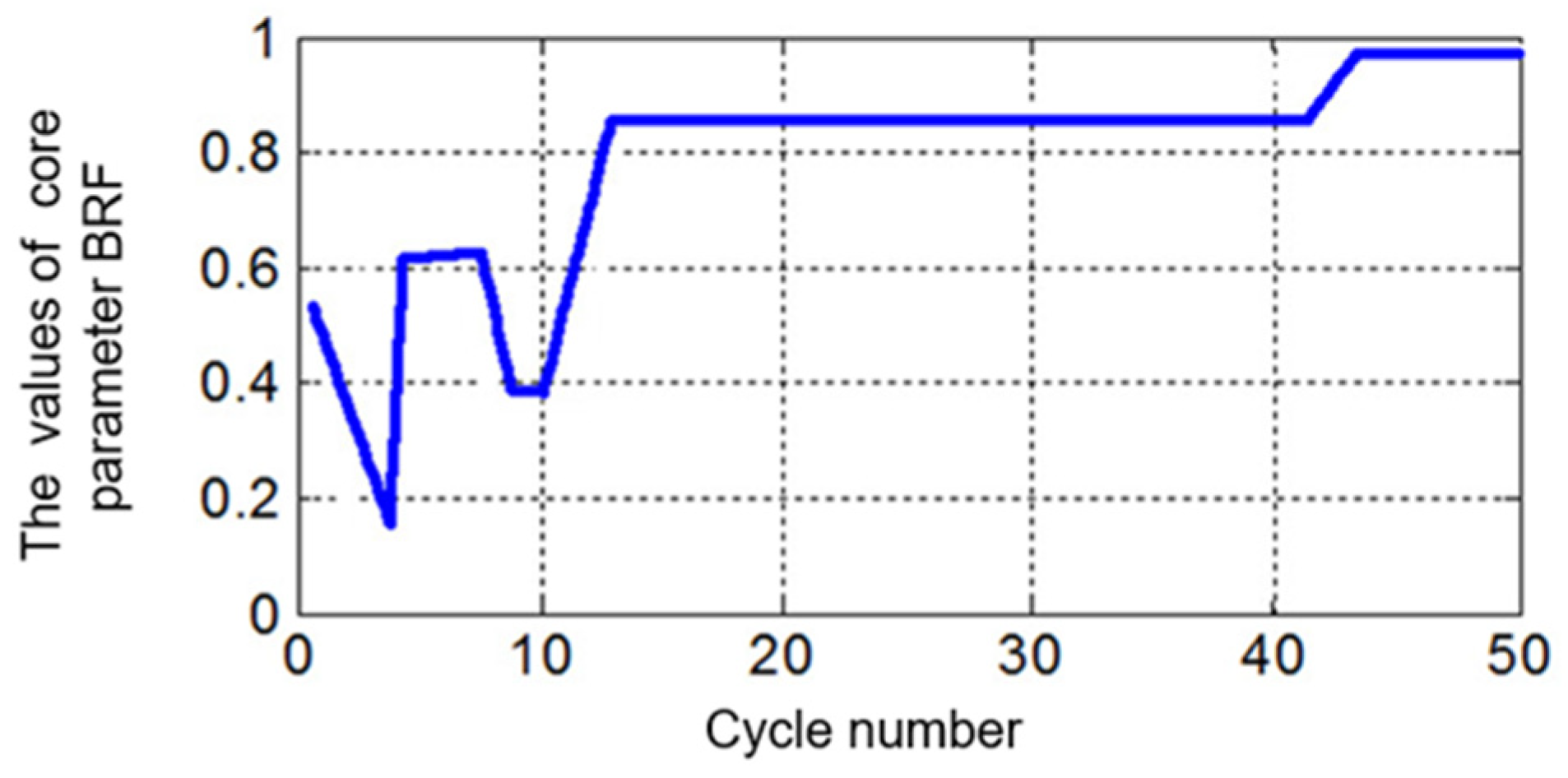
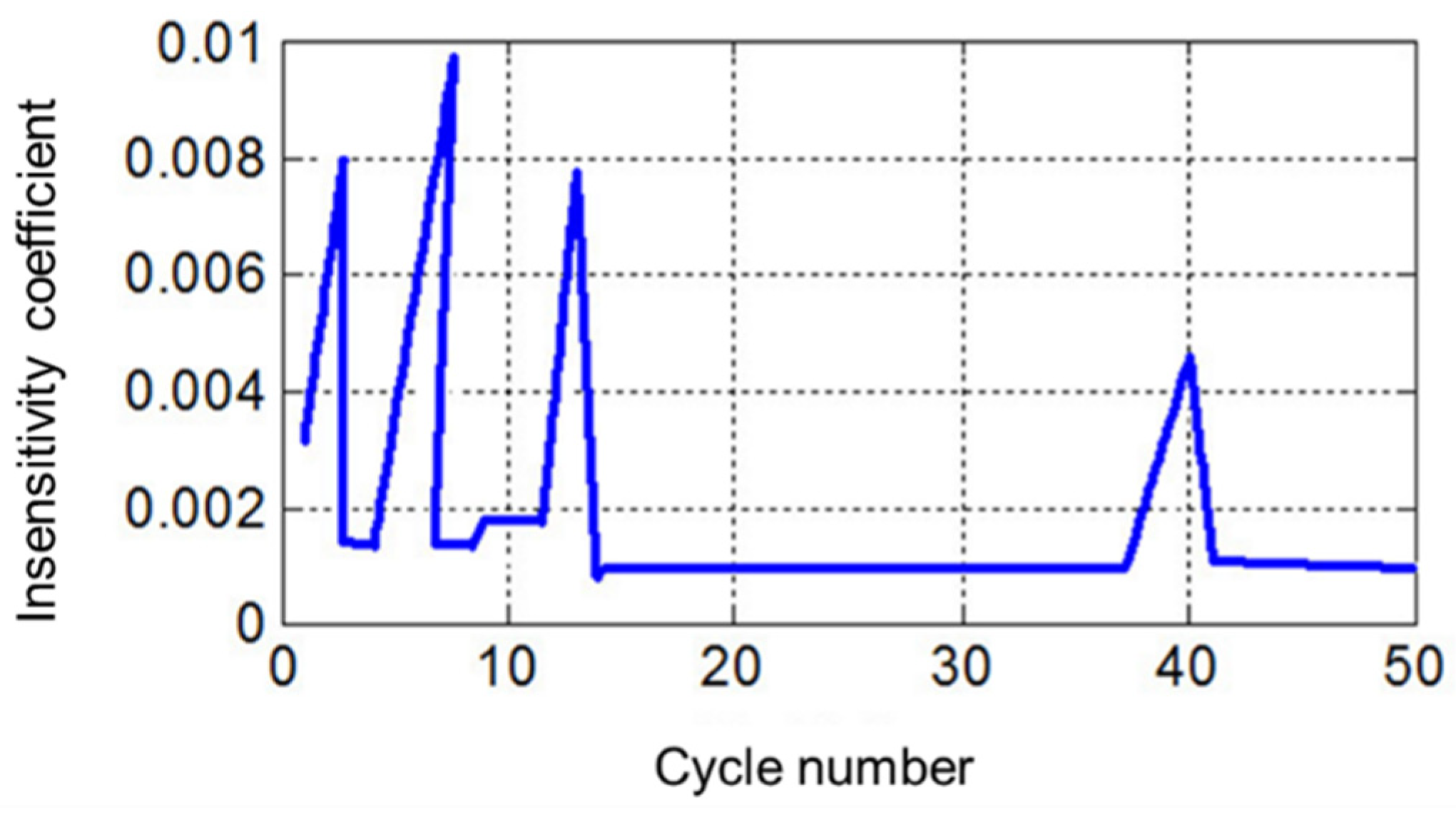
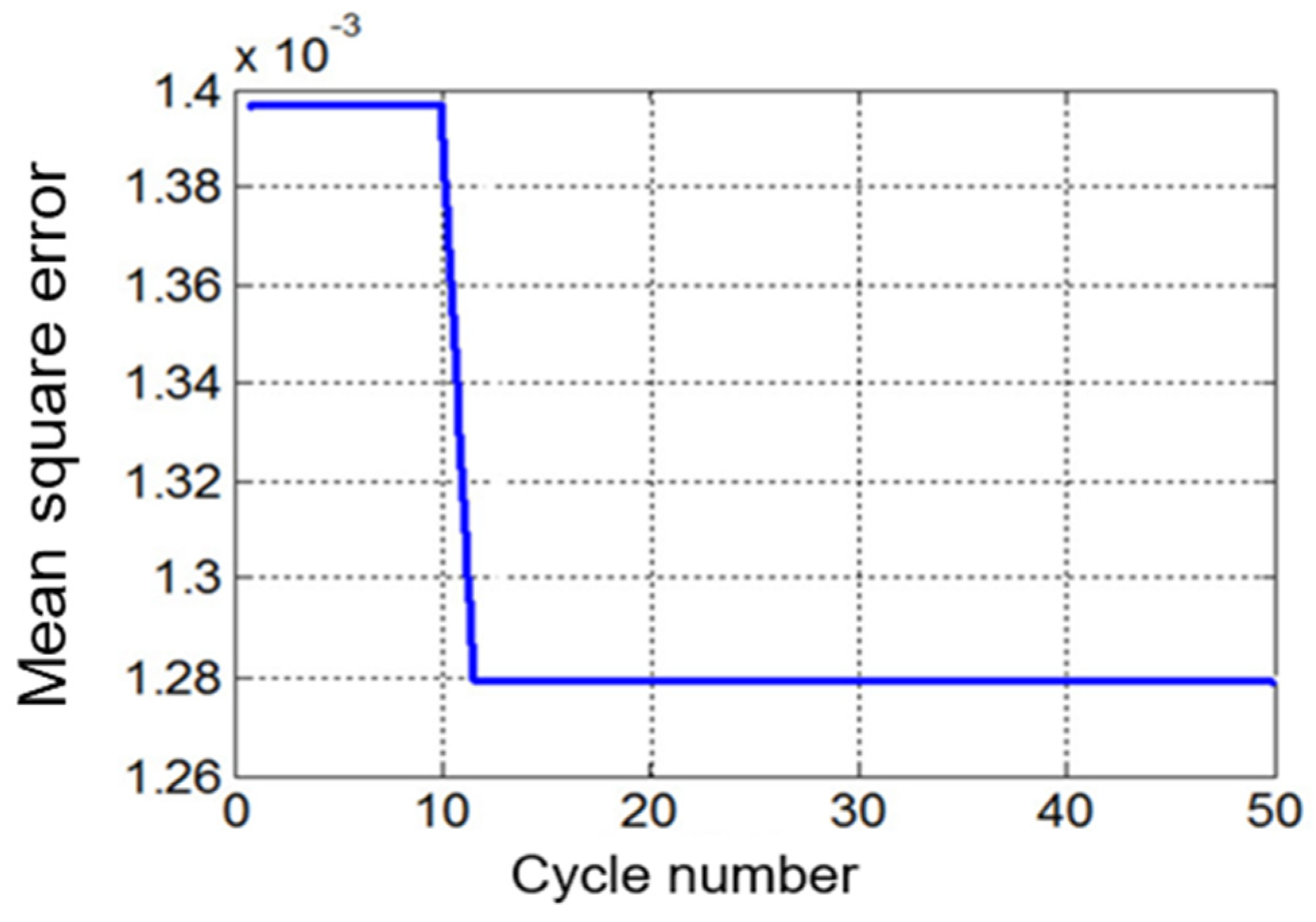
We input the training samples and labels, and set the initialization range for the three parameters as C = [0, 100], σ = [0.01, 10], and ε = [0.009, 3]. During the training process, the parameters are adjusted in time. When the training error tends to 0, the training process is terminated. After the adjustment and training process of parameters, Figure 2, Figure 3, Figure 4 and Figure 5 can finally be obtained.

When the parameters and mean squared error all tend to be stable, the optimal state is reached. At this point, the coefficient values are as follows: the penalty coefficient C = 96, the kernel width σ = 0.95, the insensitivity coefficient ε = 0.0012, and the minimum mean squared error MSE = 0.00128.

5.3. Trained Classification and Score Accumulation

According to Equation (11) in the above classification implementation model, the advantage and disadvantage comparison matrix after splicing is established, that is, the eight dry ports are compared in pairs, respectively, to obtain the advantages and disadvantages order of the dry ports. After comparing the advantages and disadvantages of any two dry ports, the score for the accumulated values of the cooperation performance between the dry ports to be evaluated and Shanghai Port can be obtained through the score of the accumulative formulas of Equations (10) and (11). Finally, the dry port with the best cooperation performance can be obtained.

5.4. Result Analysis

From

Table 4. Advantages and disadvantages of dry ports and the corresponding score accumulated value score.

City	1	2	3	4	5	6	7	8	Accumulated Value Score
1	-	−1	1	1	1	1	−1	1	10
2	1	-	1	1	1	1	−1	1	12
3	−1	−1	-	0	1	1	−1	0	4
4	−1	−1	0	-	1	1	−1	−1	5
5	−1	−1	−1	−1	-	1	0	−1	3
6	−1	−1	−1	−1	0	-	−1	−1	1
7	1	1	1	1	1	1	-	1	14
8	−1	−1	0	1	1	1	−1	-	7

, it can be concluded that the priority order from high to low of dry ports in terms of the cooperation performance with Shanghai Port is Zhengzhou (7) > Ningbo (2) > Suzhou (1) > Xi’an (8) > Jinhua (4) > Xiaoshan (3) > Shaoxing (5) > Lishui (6).

(1)

Zhengzhou

Zhengzhou is the hub of China; the multimodal transport of railway transportation, sea transportation, and road transportation within its radius range of 1500 km covers three-quarters of China’s provinces, and extends to the Asia–Pacific region. Relying on the cooperation agreements between the Zhengzhou Economic Development Zone, Zhengzhou Materials Group and Lianyungang Port Group, Zhengzhou has further attracted Lianyungang Port, Tianjin Port, Shanghai Port, and Qingdao Port to establish themselves there. Zhengzhou set up dry port customs as well as inspection and quarantine departments to provide convenient customs clearance services, which attracted freight forwarders, shipping agents, and shipping companies to set up branches in the dry port, thus improving the transit capacity of international goods. Therefore, Zhengzhou has the highest score in the performance evaluation for the cooperation between dry ports and Shanghai Port. Consequently, Shanghai Port is preferred for cooperation with Zhengzhou.

(2)

Ningbo

Ningbo has strategically established a port economic circle, leveraging its inherent port strengths. The establishment of dry ports will amplify Ningbo’s port advantages within the framework of the Silk Road Economic Belt, consequently catalyzing the progress of inland cities along this economic corridor. Capitalizing on its own inland port, Suzhou possesses three distinct advantages: a customs inspection linkage function, a secure logistics mode, and a favorable logistics cost structure. Furthermore, Suzhou’s proximity to Shanghai Port bolsters the competitiveness of the Suzhou dry port.

(3)

Xi’an

Xi’an International Port Zone relies on the connecting facilities for Xi’an Comprehensive Free Trade Zone, Xi’an Railway Container Central Station, Xi’an Highway Wharf, and airports, and is building China’s largest international land port and important modern international logistics center and business hub on the Eurasia Land Bridge. Through the strategic cooperation of Xi’an with China’s eastern coastal ports and western Khorgos port, as well as with Central Asian countries, a new pattern of regional integration of logistics has gradually formed.

(4)

Jinhua, Xiaoshan, Shaoxing, and Lishui

Jinhua, Xiaoshan, Shaoxing, and Lishui are all located in Zhejiang Province. They are close to each other, so there is direct competition among them. Their sources of goods can be diverted to a certain extent by each other, and their separate competitiveness is weak at present. Despite this, their geographical positions and traffic conditions are superior, and these cities have broad development prospects.

5.5. Corresponding Countermeasures

• Signing the cooperation agreement

The customs of the city where the dry port is located and the Entry Inspection and Quarantine Bureau of the seaport city have signed more reciprocal cooperation agreements to develop dry ports and extend the seaport services to dry ports. For goods imported from seaports and transported to dry ports, they can be declared, inspected and released at dry ports; for the goods transported from the dry port to the seaport, the inspection declaration and other exit work can be carried out at the dry port, and no re-inspection is required after the goods are transported to the seaport.

2.

Cargo priority at the dry port

The flow direction of goods can be implemented by giving priority to release and loading and unloading, and delimiting special areas to improve the efficiency and smoothness of goods.

(1)

Warehouse: an appropriate warehouse area shall be set aside as a dedicated warehouse for the dry port.

(2)

Parking lot: this is convenient for the management of vehicles, and a certain number of special vehicles are established in the existing parking lot.

3.

Establish a dry-port information platform.

The efficient operation of the dry port is inseparable from the close cooperation with customs declaration and other aspects to ensure the timely and accurate information flow of incoming and outgoing goods. The waterless port information platform will integrate the logistics information and customs management platform, and become the center of information communication between various parties.

4.

Most favorable sea-port treatment

The most-favored-nation treatment for sea ports includes streamlining customs procedures, offering special trade financing terms, entering into trade cooperation agreements, and other measures designed to attract a greater volume of trade activities to the port. This serves to bolster the port’s competitiveness, stimulate economic development, and foster trade cooperation.

(1)

The most favorable agreement can be signed between the dry port and the seaport to provide convenient, efficient and low-cost services for the goods of both parties and form the mutual adsorption effect.

(2)

The goods shall be graded, and those with high risk coefficient shall be inspected with emphasis; those with a medium risk coefficient shall be spot-checked according to a certain proportion; a direct release policy shall be adopted for those with a low risk coefficient.

6. Conclusions

This paper is based on sea port and dry port cooperation as a guide, combined with the balanced scorecard method to establish internal and external factors of the cooperation performance evaluation index system. According to the relevant data collected from the evaluation indicators, the cooperation between Shanghai Port and dry ports such as Suzhou, Ningbo and Zhengzhou is calculated. The support vector machine method is used to explore the cooperation, and the evaluation results are sorted to further ensure the rationality and objectivity of the cooperation. However, due to the large number, only some of the dry ports were considered as subjects in this study. Therefore, it is necessary to expand the selection scope of dry ports. Additionally, the evaluation index system used in this paper is somewhat rudimentary. Further correlation analysis is needed to identify more refined indicators. This is a deficiency in this paper regarding the issue of cooperation. In the next stage of the research, we will contemplate how to refine and select cooperation indicators to make the results for dry ports more accurate and objective.