Anomaly Detection in Machining Centers Based on Graph Diffusion-Hierarchical Neighbor Aggregation Networks
Abstract
:1. Introduction
- In this study, a machining center anomaly detection model is proposed to detect the operation execution process of machining centers by using the anomaly detection method of graph diffusion and graph neighbor hierarchical aggregation (GraphDHNA). Possessing a high-precision capability for identifying processing anomalies, it can determine whether the machining quality is abnormal based on the state parameters. It provides a reliable anomaly detection tool for predictive and energy-oriented maintenance strategies, which can be widely applied in specific maintenance plans.
- In this study, a data augmented module based on the diffusion principle is introduced in the graph neighbor aggregation network model to cope with the data quality problem.
- In this study, the strategy of hierarchical aggregation is adopted in the process of neighbor aggregation; skip connections are added after each layer and attention connections are carried out in the last layer of the graph neighbor aggregation network, which fully considers the importance of the information of each step of neighbor aggregation, so that the features learned by the model are closer to the essence.
- The model proposed in this study attains a higher level of accuracy (96%) and F1 score (94) when compared to both the classical GNN method and the presently popular GNN method. This performance improvement is observed across four datasets collected from real-world production environments.
2. Background and Related Work
2.1. Maintenance Strategy
- Regular maintenance (time-based maintenance): Regular maintenance is a basic maintenance strategy that involves conducting scheduled maintenance according to a predetermined maintenance plan. This approach is convenient to implement and is particularly suitable for components whose risk of failure increases with extended usage over time.
- Predictive maintenance: Through real-time monitoring and data analysis, predictive maintenance anticipates the potential time of failure for equipment or systems, allowing for proactive maintenance measures to be taken before issues arise. The objective of this strategy is to minimize unplanned downtime, enhance equipment reliability and performance, and reduce maintenance costs.
- Energy-oriented maintenance: Emphasizing the enhancement of equipment performance, reliability, and efficiency through the management and optimization of energy usage. This strategy incorporates energy efficiency into the scope of maintenance considerations. When certain devices and systems exhibit abnormal operating conditions, energy efficiency indicators can undergo significant changes. By monitoring energy efficiency, rational energy management measures can be implemented, leading to prolonged equipment lifespan, reduced energy wastage, and an overall improvement in equipment operational performance.
2.2. Methods of Detection
- 1.
- Traditional surface inspection: The conventional surface inspection involves the detection and identification of surface damage, substrate damage, internal defects, geometric dimensions, etc., through means such as visual inspection, dimension measurement, and nondestructive testing. These methods heavily rely on the proficiency of the personnel and the quality of their operations.
- 2.
- With the advancement of the informatization level in production workshops, the vast amount of production data has given rise to efficient diagnostic methods based on data analysis [15]. Early methods of data analysis involved examining the statistical features of historical data to identify early symptoms of faults. Adequate preparations were made to reduce the waste of manpower and spare part resources. However, early data analysis only explored the statistical characteristics of production data and failed to reveal the underlying features of fault occurrence, limiting the improvement of diagnostic accuracy. In the realm of machine learning, deep learning techniques involve the utilization of extensive datasets to train multilayered stacked neural network models for the acquisition of data features and are the most popular and effective data-driven class of anomaly detection methods today. Common deep learning anomaly detection models can be different according to their core neural network type; the more popular methods are as follows: convolutional neural network-based methods [5], recurrent neural network-based methods [6], Graph Neural Network-based methods, and so on [16]. They each possess their respective merits and limitations (as shown in Table 1), and enhanced diagnostic performance can be attained by selecting the suitable neural network architecture tailored to the particular context of the task data.
- Graph diffusion augment: We designed the graph diffusion data augment module for multisensor variable graph data with the aim of obtaining better training samples. Because the edges and features of the graph are usually noisy, and graph diffusion smooths the neighborhoods on the graph, which can recover the regions where useful information exists in the noisy graph, it can, thus, be regarded as a denoising process [30], so that the new graph obtained by this processing will not lose the key information but, instead, the noisy information has been preliminarily filtered, and the newly added sample of the graphs has a higher information density in the original sample, so the graph diffusion augment module creates favorable conditions for model training.
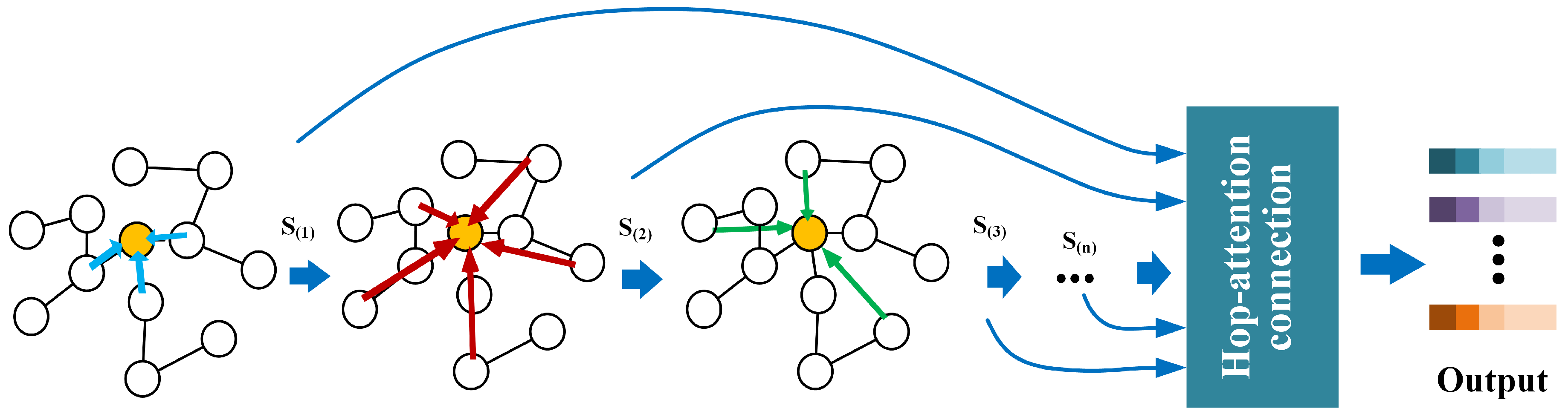
- Neighborhood hierarchical aggregation: The fundamental concept underlying Graph Neural Networks is to depict the target node as a consolidation of information gleaned from its neighboring nodes. This approach iteratively collects information from higher-order neighboring nodes, continually refining the representation of the target node throughout the process. In order to fully utilize higher-order relationships, it is often necessary to stack multiple graph convolutional layers together. However, previous research has identified that with an increase in the number of layers and model depth, a loss of gradient or excessive smoothing occurs, resulting in a marked decline in performance [31,32]. In order to break through the limit of the number of layers, RestNet [33] designed a residual connection in the field of image processing; this strategy has achieved good results. Inspired by the idea of residual connection, we considered adopting a sparse aggregation method in the neighbor node information aggregation link. In this context, the process involves discreetly aggregating neighbor information at each order while simultaneously elevating the output of each layer, facilitating a direct transition to the output layer within the Graph Neural Network.
- Hop-attention: Incorporating an attention mechanism enables a comprehensive evaluation of interrelationships among multiple variables, and the consideration of contextual information plays a big role in natural language processing [34]. The neighbor aggregation link in each layer output, after the skip connection, directly to the final layer of the graph neighbor aggregation network, where these are inputs for the attention connection; because each input represents the node representation of a certain hop neighbor, it is called the hop-attention layer; the mechanism comprehensively considers the weight of each layer on the final result in order to highlight the most important part of the information of the neighbors of each order. The immunity of the model to noise is improved.
3. Preparation
3.1. Definition of Sensors Network Graph
3.2. Connection between Nodes
4. Methodology
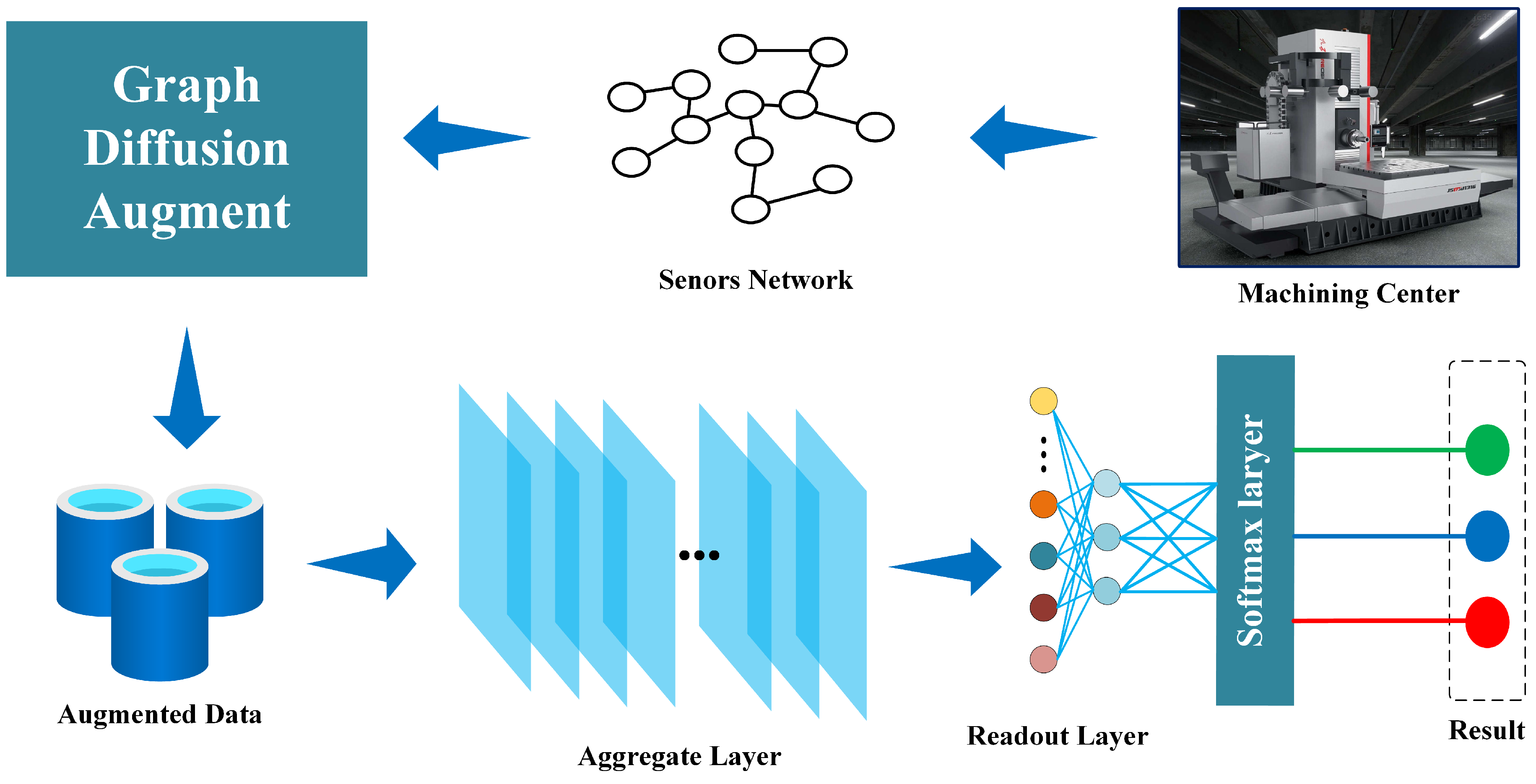
4.1. General Model Framework
4.2. Diffusion Augmentation Module
4.3. Neighborhood Information Aggregate
4.3.1. Aggregate Layer
4.3.2. Hop-Attention
4.3.3. Readout Layer
5. Experiments
5.1. Data Description
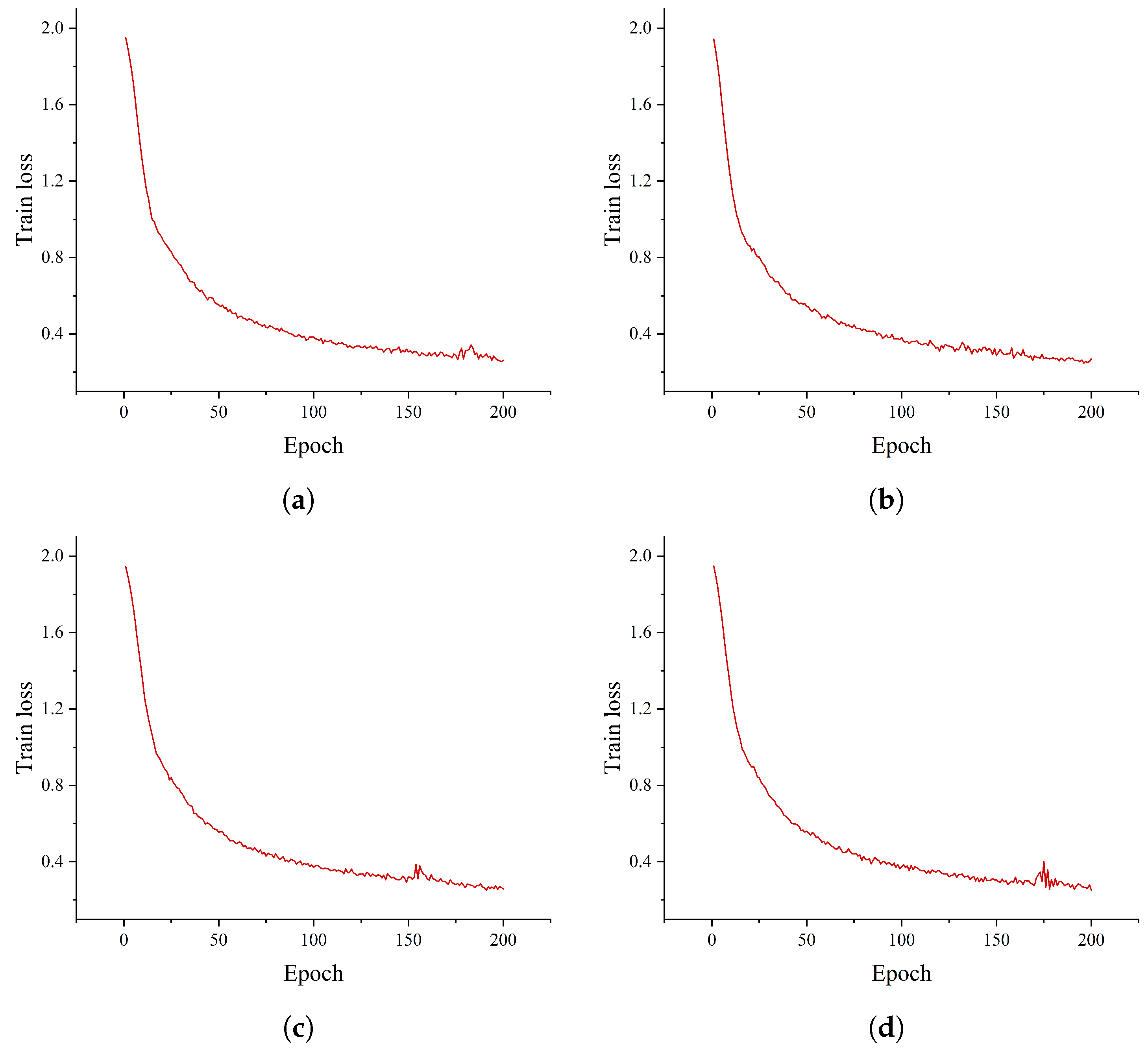
5.2. Experimental Setups
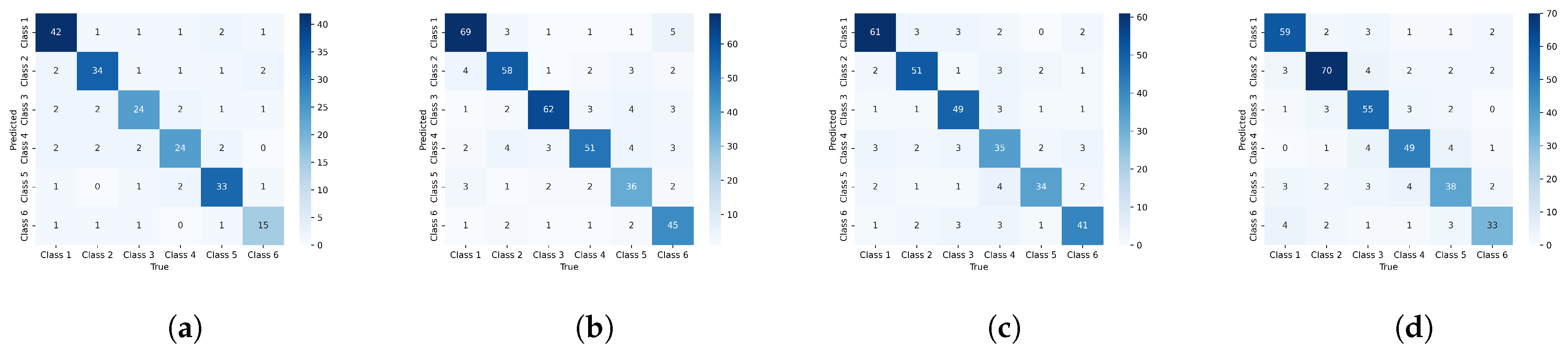
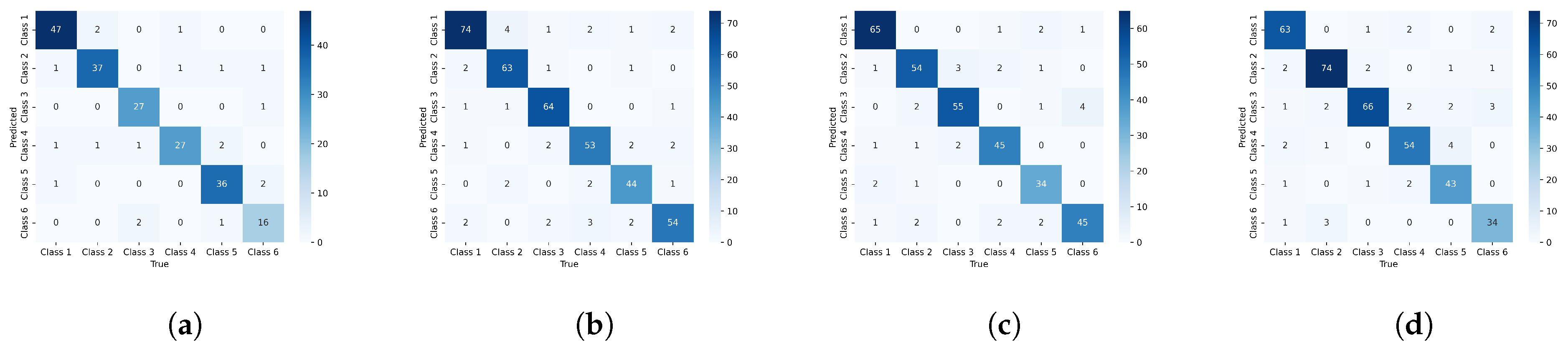
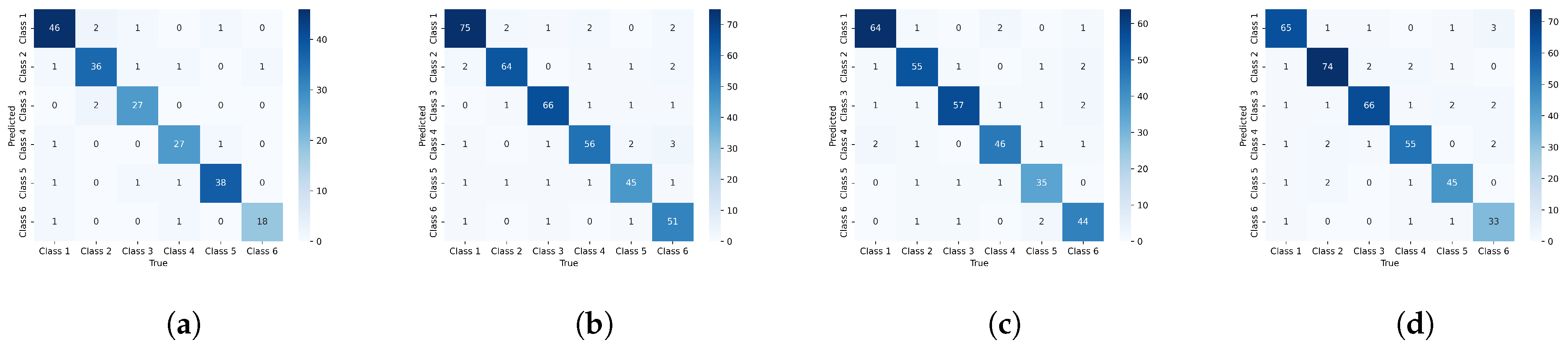
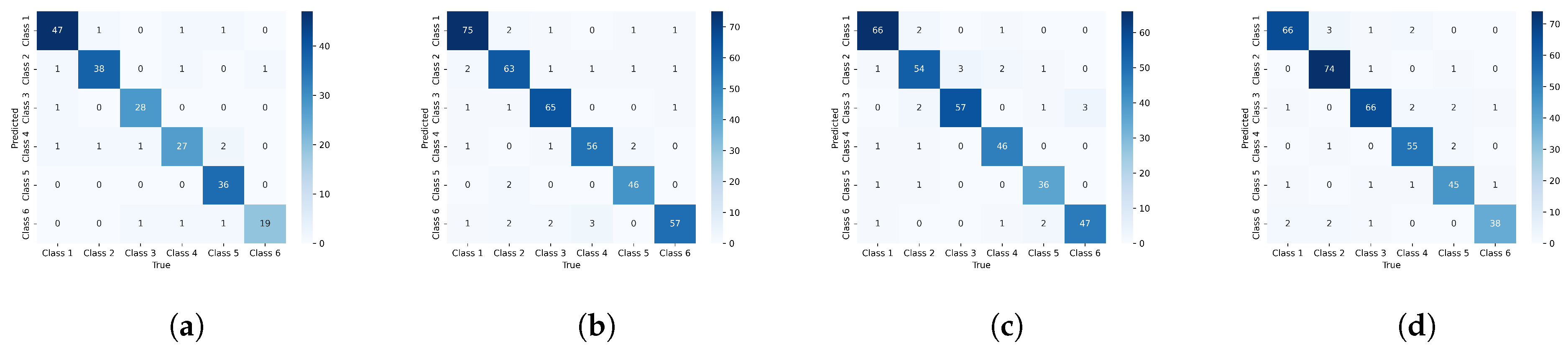
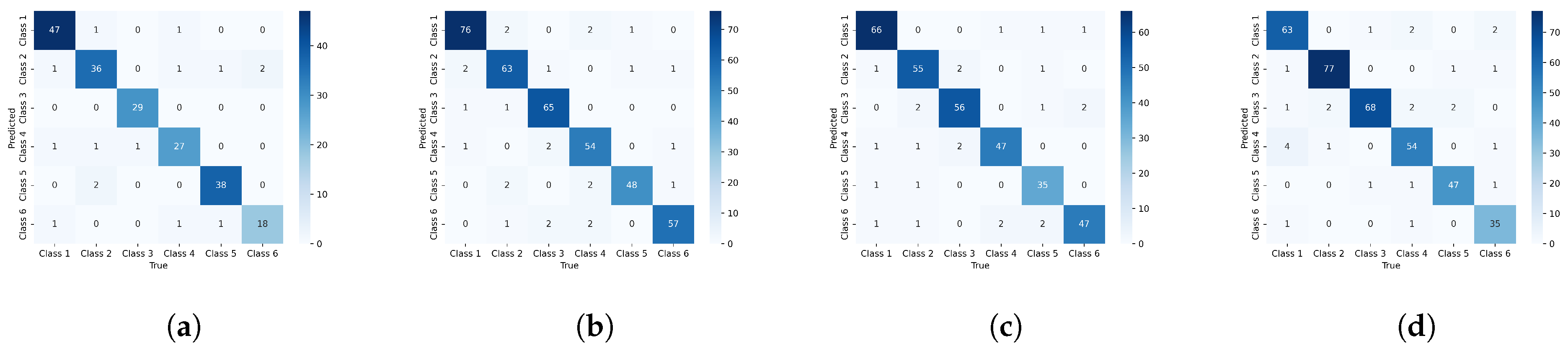
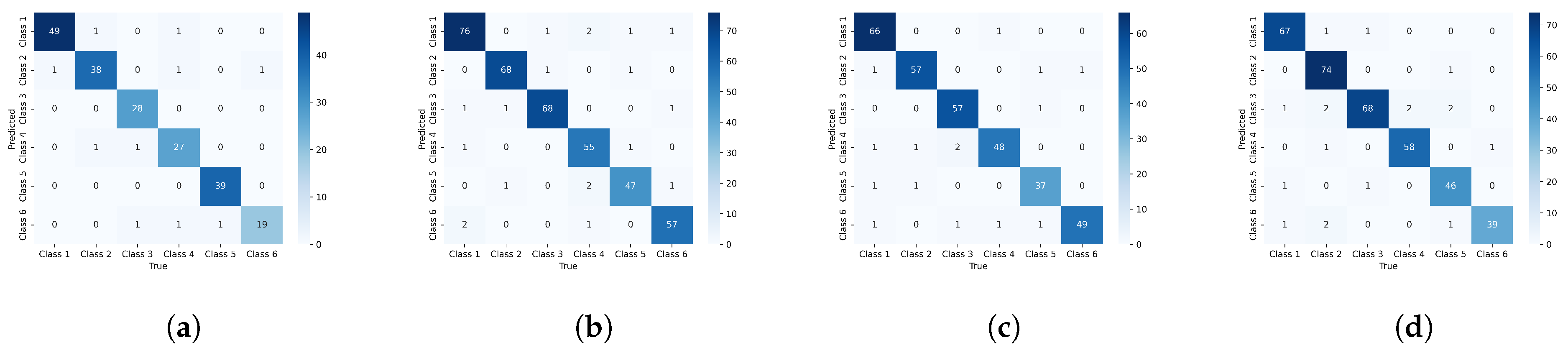
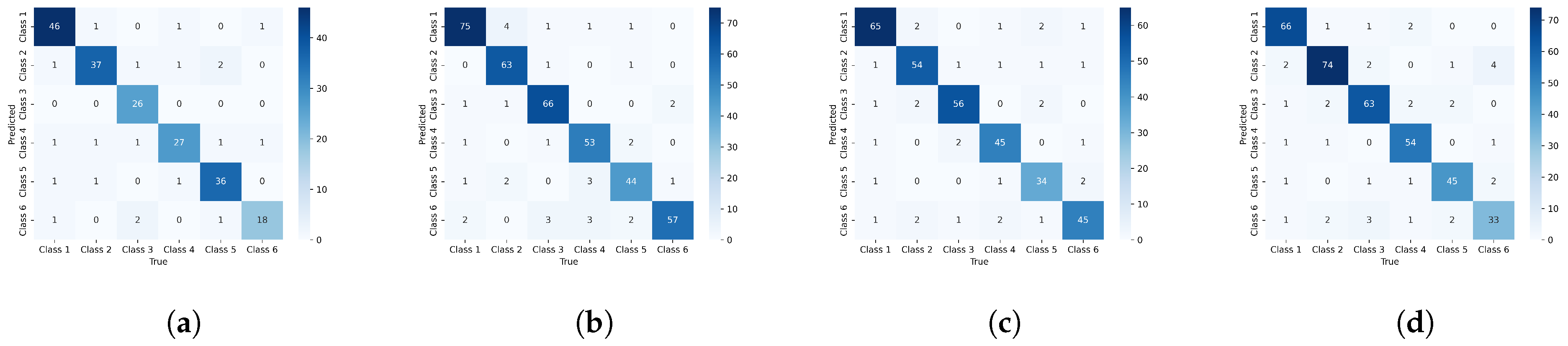
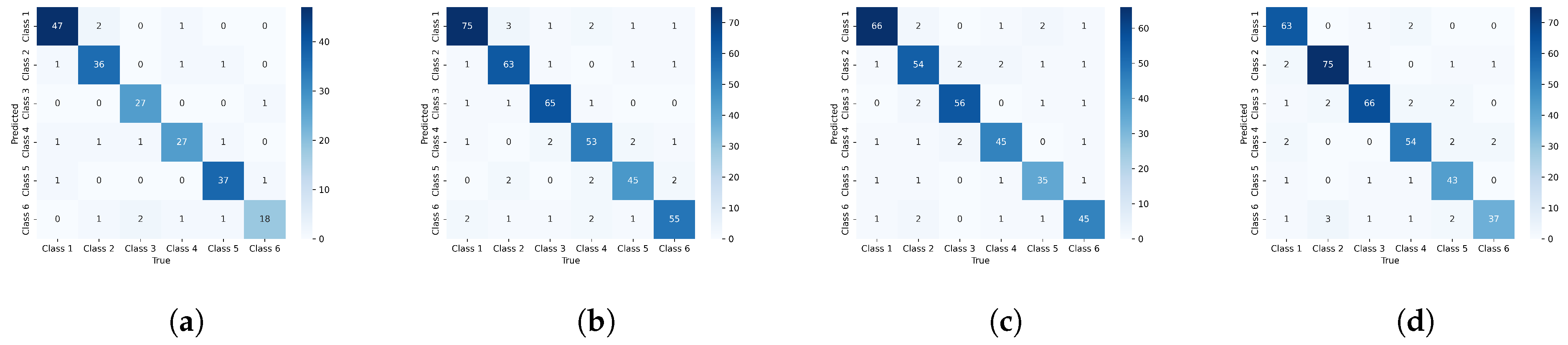
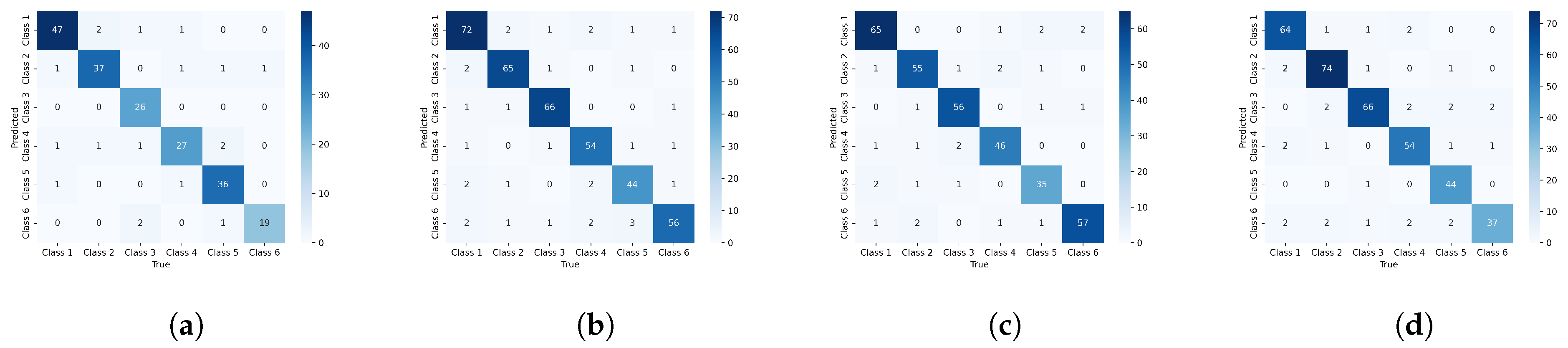
5.3. Experimental Results
5.4. Ablation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A



References
- Zhou, B.; Yi, Q. An energy-oriented maintenance policy under energy and quality constraints for a multielement-dependent degradation batch production system. J. Manuf. Syst. 2021, 59, 631–645. [Google Scholar] [CrossRef]
- Orošnjak, M.; Brkljač, N.; Šević, D.; Čavić, M.; Oros, D.; Penčić, M. From predictive to energy-based maintenance paradigm: Achieving cleaner production through functional-productiveness. J. Clean. Prod. 2023, 408, 137177. [Google Scholar] [CrossRef]
- Orošnjak, M.; Jocanović, M.; Čavić, M.; Karanović, V.; Penčić, M. Industrial maintenance 4(.0) horizon Europe: Consequences of the iron curtain and energy-based maintenance. J. Clean. Prod. 2021, 314, 128034. [Google Scholar] [CrossRef]
- Xia, T.; Xi, L.; Du, S.; Xiao, L.; Pan, E. Energy-oriented maintenance decision-making for sustainable manufacturing based on energy saving window. J. Manuf. Sci. Eng. 2018, 140, 051001. [Google Scholar] [CrossRef]
- Eren, L.; Ince, T.; Kiranyaz, S. A generic intelligent bearing fault diagnosis system using compact adaptive 1D CNN classifier. J. Signal Process. Syst. 2019, 91, 179–189. [Google Scholar] [CrossRef]
- Zhu, J.; Jiang, Q.; Shen, Y.; Qian, C.; Xu, F.; Zhu, Q. Application of recurrent neural network to mechanical fault diagnosis: A review. J. Mech. Sci. Technol. 2022, 36, 527–542. [Google Scholar] [CrossRef]
- Hamilton, W.L. Graph Representation Learning; Morgan & Claypool Publishers: San Rafael, CA, USA, 2020. [Google Scholar]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: Going beyond euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Zhang, M.; Chen, Y. Link prediction based on graph neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-gcn: A temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
- Lee, J.B.; Rossi, R.; Kong, X. Graph classification using structural attention. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1666–1674. [Google Scholar]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, J.; Alippi, C.; Ding, S.X.; Shardt, Y.; Peng, T.; Yang, C. Graph neural network-based fault diagnosis: A review. arXiv 2021, arXiv:2111.08185. [Google Scholar]
- Yu, J.; Zhang, Y. Challenges and opportunities of deep learning-based process fault detection and diagnosis: A review. Neural Comput. Appl. 2023, 35, 211–252. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-valued convolutional neural network and its application in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Ajad, A.; Saini, T.; Niranjan, K.M. CV-CXR: A Method for Classification and Visualisation of Covid-19 virus using CNN and Heatmap. In Proceedings of the 2023 5th International Conference on Recent Advances in Information Technology (RAIT), Dhanbad, India, 3–5 March 2023; pp. 1–6. [Google Scholar]
- Toharudin, T.; Pontoh, R.S.; Caraka, R.E.; Zahroh, S.; Lee, Y.; Chen, R.C. Employing long short-term memory and Facebook prophet model in air temperature forecasting. Commun. Stat. Simul. Comput. 2023, 52, 279–290. [Google Scholar] [CrossRef]
- Farah, S.; Humaira, N.; Aneela, Z.; Steffen, E. Short-term multi-hour ahead country-wide wind power prediction for Germany using gated recurrent unit deep learning. Renew. Sustain. Energy Rev. 2022, 167, 112700. [Google Scholar] [CrossRef]
- Busch, J.; Kocheturov, A.; Tresp, V.; Seidl, T. NF-GNN: Network flow graph neural networks for malware detection and classification. In Proceedings of the 33rd International Conference on Scientific and Statistical Database Management, Tampa, FL, USA, 6–7 July 2021; pp. 121–132. [Google Scholar]
- Bilgic, M.; Mihalkova, L.; Getoor, L. Active learning for networked data. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 79–86. [Google Scholar]
- Moore, C.; Yan, X.; Zhu, Y.; Rouquier, J.B.; Lane, T. Active learning for node classification in assortative and disassortative networks. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 841–849. [Google Scholar]
- Cai, H.; Zheng, V.W.; Chang, K.C.C. Active learning for graph embedding. arXiv 2017, arXiv:1705.05085. [Google Scholar]
- Gao, L.; Yang, H.; Zhou, C.; Wu, J.; Pan, S.; Hu, Y. Active discriminative network representation learning. In Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018. [Google Scholar]
- Liu, J.; Wang, Y.; Hooi, B.; Yang, R.; Xiao, X. LSCALE: Latent Space Clustering-Based Active Learning for Node Classification. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Grenoble, France, 19–23 September 2022; pp. 55–70. [Google Scholar]
- Regol, F.; Pal, S.; Zhang, Y.; Coates, M. Active learning on attributed graphs via graph cognizant logistic regression and preemptive query generation. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual Event, 13–18 July 2020; pp. 8041–8050. [Google Scholar]
- Wu, Y.; Xu, Y.; Singh, A.; Yang, Y.; Dubrawski, A. Active learning for graph neural networks via node feature propagation. arXiv 2019, arXiv:1910.07567. [Google Scholar]
- Gilhuber, S.; Busch, J.; Rotthues, D.; Frey, C.M.; Seidl, T. DiffusAL: Coupling Active Learning with Graph Diffusion for Label-Efficient Node Classification. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Turin, Italy, 18 September 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 75–91. [Google Scholar]
- Zhao, L.; Akoglu, L. Pairnorm: Tackling oversmoothing in gnns. arXiv 2019, arXiv:1909.12223. [Google Scholar]
- Sun, J.; Cheng, Z.; Zuberi, S.; Pérez, F.; Volkovs, M. Hgcf: Hyperbolic graph convolution networks for collaborative filtering. In Proceedings of the Web Conference 2021, Ljubljana Slovenia, 19–23 April 2021; pp. 593–601. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Aggarwal, A.; Mittal, M.; Battineni, G. Generative adversarial network: An overview of theory and applications. Int. J. Inf. Manag. Data Insights 2021, 1, 100004. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Z.; Song, Y.; Hong, S.; Xu, R.; Zhao, Y.; Zhang, W.; Cui, B.; Yang, M.H. Diffusion models: A comprehensive survey of methods and applications. ACM Comput. Surv. 2022, 56, 105. [Google Scholar] [CrossRef]
- Li, P.; Chien, I.; Milenkovic, O. Optimizing generalized pagerank methods for seed-expansion community detection. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Kloumann, I.M.; Ugander, J.; Kleinberg, J. Block models and personalized PageRank. Proc. Natl. Acad. Sci. USA 2017, 114, 33–38. [Google Scholar] [CrossRef]
- Berberidis, D.; Giannakis, G.B. Node embedding with adaptive similarities for scalable learning over graphs. IEEE Trans. Knowl. Data Eng. 2019, 33, 637–650. [Google Scholar] [CrossRef]
- Faerman, E.; Borutta, F.; Busch, J.; Schubert, M. Semi-supervised learning on graphs based on local label distributions. arXiv 2018, arXiv:1802.05563. [Google Scholar]
- Borutta, F.; Busch, J.; Faerman, E.; Klink, A.; Schubert, M. Structural graph representations based on multiscale local network topologies. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence, Thessaloniki, Greece, 14–17 October 2019; pp. 91–98. [Google Scholar]
- Gasteiger, J.; Bojchevski, A.; Günnemann, S. Predict then propagate: Graph neural networks meet personalized pagerank. arXiv 2018, arXiv:1810.05997. [Google Scholar]
- Faerman, E.; Borutta, F.; Busch, J.; Schubert, M. Ada-LLD: Adaptive Node Similarity Using Multi-Scale Local Label Distributions. In Proceedings of the 2020 IEEE/WIC/ACM International Joint Conference on Web Intelligence and Intelligent Agent Technology (WI-IAT), Melbourne, Australia, 14–17 December 2020; pp. 25–32. [Google Scholar]
- Busch, J.; Pi, J.; Seidl, T. PushNet: Efficient and adaptive neural message passing. arXiv 2020, arXiv:2003.02228. [Google Scholar]
- Gasteiger, J.; Weißenberger, S.; Günnemann, S. Diffusion improves graph learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Zeng, H.; Zhou, H.; Srivastava, A.; Kannan, R.; Prasanna, V. Graphsaint: Graph sampling based inductive learning method. arXiv 2019, arXiv:1907.04931. [Google Scholar]
| Networks | Advantage | Disadvantage | Applications |
|---|---|---|---|
| MLP | Simple and intuitive; easy to understand and implement. | Sensitive to the structure and relationships of input data; limitations in processing sequence and graph structured data. | Used for basic classification and regression tasks with relatively simple structured data [17]. |
| CNN | With translation invariance, it is suitable for processing data such as images, parameter sharing, and local connection help to reduce model parameters. | Sensitive to the size of the input data. Not suitable for modeling serial data. | Computer vision tasks such as image classification and target detection [18,19]. |
| RNN | Capable of capturing timing information in sequence data and suitable for processing variable length input sequences. | Difficult to capture long-range dependencies and prone to gradient vanishing or exploding during the training process. | Natural language processing, time series prediction, and other tasks that require consideration of temporal relationships [20,21]. |
| GNN | Ideal for working with graph-structured data; capable of capturing relationships between nodes. | Computational efficiency issues. | Social network analysis, molecular mapping prediction, numerous correlated signal inputs, and other tasks that require consideration of graph structure relationships [22,23,24,25,26,27,28,29]. |
| Datasets | Graphs | Nodes | Edges | Features |
|---|---|---|---|---|
| S06_gear | 102 | 5148 | 16,329 | 1325 |
| S06_cylinder | 192 | 9331 | 25,746 | 1395 |
| S06_shaft | 168 | 8435 | 43,924 | 1665 |
| S06_piston | 183 | 9726 | 51,123 | 1495 |
| Metrics | Methods | S06_gear | S06_cylinder | S06_shaft | S06_piston |
|---|---|---|---|---|---|
| Acc | MLP | 82.23 ± 0.52 | 82.99 ± 0.38 | 83.52 ± 0.42 | 84.09 ± 0.33 |
| GCN | 90.29 ± 0.72 | 90.09 ± 0.29 | 90.52 ± 0.28 | 91.11 ± 0.11 | |
| GAT | 90.79 ± 0.12 | 91.50 ± 0.45 | 91.93 ± 0.19 | 92.35 ± 0.07 | |
| GraphSAGE | 91.28 ± 0.20 | 91.58 ± 0.34 | 92.01 ± 0.43 | 92.63 ± 0.23 | |
| GraphSAINT | 91.35 ± 0.13 | 92.15 ± 0.18 | 91.98 ± 0.67 | 92.57 ± 0.64 | |
| GDC | 92.86 ± 0.12 | 92.60 ± 0.46 | 93.03 ± 0.51 | 93.63 ± 0.38 | |
| DiffusAL | 92.95 ± 0.32 | 92.64 ± 0.33 | 93.07 ± 0.19 | 93.69 ± 0.26 | |
| GraphDHNA | 94.99 ± 0.25 | 94.83 ± 0.31 | 94.32 ± 0.18 | 96.13 ± 0.24 | |
| F1 | MLP | 80.29 ± 0.63 | 80.09 ± 0.41 | 81.52 ± 0.25 | 82.11 ± 0.24 |
| GCN | 86.67 ± 0.72 | 87.82 ± 0.67 | 86.36 ± 0.74 | 87.32 ± 0.53 | |
| GAT | 87.76 ± 0.46 | 87.91 ± 0.54 | 86.45 ± 0.33 | 88.41 ± 0.51 | |
| GraphSAGE | 88.89 ± 0.60 | 89.04 ± 0.48 | 87.58 ± 0.46 | 89.54 ± 0.46 | |
| GraphSAINT | 87.07 ± 0.39 | 89.22 ± 0.53 | 88.76 ± 0.64 | 89.72 ± 0.44 | |
| GDC | 89.54 ± 0.29 | 90.69 ± 0.19 | 89.23 ± 0.51 | 90.19 ± 0.49 | |
| DiffusAL | 90.35 ± 0.48 | 91.23 ± 0.35 | 90.04 ± 0.61 | 91.39 ± 0.42 | |
| GraphDHNA | 92.69 ± 0.36 | 92.13 ± 0.24 | 92.41 ± 0.16 | 94.38 ± 0.21 |
| Metrics | GDA | HA | HAT | S06_gear | S06_cylinder | S06_shaft | S06_piston |
|---|---|---|---|---|---|---|---|
| Acc | × | ✓ | × | 90.65 ± 0.05 | 89.76 ± 0.05 | 92.13 ± 0.06 | 93.17 ± 0.11 |
| ✓ | ✓ | × | 91.34 ± 0.05 | 92.58 ± 0.04 | 90.89 ± 0.04 | 94.21 ± 0.05 | |
| × | ✓ | ✓ | 91.34 ± 0.05 | 92.58 ± 0.04 | 90.89 ± 0.04 | 94.21 ± 0.05 | |
| ✓ | × | ✓ | 91.52 ± 0.05 | 92.02 ± 0.04 | 91.29 ± 0.05 | 92.51 ± 0.06 | |
| ✓ | ✓ | ✓ | 94.99 ± 0.25 | 94.83 ± 0.31 | 94.32 ± 0.18 | 96.13 ± 0.24 | |
| F1 | × | ✓ | × | 89.97 ± 0.11 | 90.58 ± 0.07 | 91.71 ± 0.13 | 91.88 ± 0.05 |
| ✓ | ✓ | × | 90.16 ± 0.05 | 89.63 ± 0.05 | 90.55 ± 0.06 | 92.38 ± 0.05 | |
| × | ✓ | ✓ | 91.39 ± 0.11 | 90.87 ± 0.09 | 91.02 ± 0.13 | 92.13 ± 0.08 | |
| ✓ | × | ✓ | 91.34 ± 0.05 | 92.58 ± 0.04 | 90.89 ± 0.04 | 94.21 ± 0.05 | |
| ✓ | ✓ | ✓ | 92.69 ± 0.36 | 92.13 ± 0.24 | 92.41 ± 0.16 | 94.38 ± 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Yang, Y. Anomaly Detection in Machining Centers Based on Graph Diffusion-Hierarchical Neighbor Aggregation Networks. Appl. Sci. 2023, 13, 12914. https://doi.org/10.3390/app132312914
Huang J, Yang Y. Anomaly Detection in Machining Centers Based on Graph Diffusion-Hierarchical Neighbor Aggregation Networks. Applied Sciences. 2023; 13(23):12914. https://doi.org/10.3390/app132312914
Chicago/Turabian StyleHuang, Jiewen, and Ying Yang. 2023. "Anomaly Detection in Machining Centers Based on Graph Diffusion-Hierarchical Neighbor Aggregation Networks" Applied Sciences 13, no. 23: 12914. https://doi.org/10.3390/app132312914
APA StyleHuang, J., & Yang, Y. (2023). Anomaly Detection in Machining Centers Based on Graph Diffusion-Hierarchical Neighbor Aggregation Networks. Applied Sciences, 13(23), 12914. https://doi.org/10.3390/app132312914





