Abstract
Conical emission is a typical nonlinear phenomenon that occurs during the filamentation of femtosecond laser pulses in transparent media. In this work, the conical emission induced by two kinds of typical vortex beams (i.e., Laguerre–Gaussian (LG) and Bessel–Gaussian (BG) beams) in water is experimentally studied. By recording the light spots of different spectra components from the supercontinuum induced by the vortex beams, the characteristics of the conical emission induced by femtosecond vortex beams are studied. It is found that the spots of the supercontinuum induced by the two kinds of vortex beams differ greatly from each other. The spots of the supercontinuum induced by the BG beams are a set of concentric rings like a rainbow with a white center, while the white light spots in the case of the LG beams are circular white disks, which are different from the commonly observed white light spots. By measuring the maximum divergence angle, it is observed that the divergence angle increases with a decrease in the wavelength, while it is merely affected by the topological charge, which is explained by the formation mechanism of conical emission in terms of self-phase modulation. Based on the observed results, we discuss the transfer of optical angular momentum during the supercontinuum induced by the filamentation of femtosecond vortex beams. This work may help to better understand the transfer of optical angular momentum in non-optical parametric processes as well as the interaction of high-intensity pulses with matter.
1. Introduction
Apart from spin angular momentum, photons can also carry another form of angular momentum: orbital angular momentum (OAM) [1]. It is related to the helical phase front and doughnut transversal profile of light. The helical phase front is expressed in exp(−ilϕ), where l is the topological charge (TC) and equals the orbital angular quantum number, and ϕ is the azimuth angle. Accordingly, a light beam carrying OAM is often called the vortex beam (i.e., the TC is larger than 0). Each photon in the vortex beams carries an OAM of lℏ. The doughnut transversal profile of the spatial distribution in intensity comes from the phase singularity at the center of the beam. The specific nature and characteristics of the vortex beam make it widely applied in many important and promising aspects, such as the optical manipulation of particles [2,3,4], information transmission and cryptography [5,6], super-resolution microscopy [7,8], and micro-processing of materials [9,10]. These applications rely on the interaction between the vortex laser beams and matter. It has been observed that the OAM carried by the vortex beams can be transferred to matter [11,12,13]. When the vortex laser beam is intense enough to induce some nonlinear parametric optical processes, such as frequency doubling, optical parametric down-conversion and four-wave mixing, spectral components with new frequency are generated, and the OAM transfer from the fundamental laser to the newly generated spectral components has been demonstrated in these nonlinear optical processes [14,15]. Since these newly generated components possess OAM, different phenomena can be observed, which in turn provides an approach to studying the nonlinear optical processes.
However, when the vortex beam is too intense, it will result in photoionization of the media, generating numerous plasmas, which makes the system complicated. As a result, fluorescence, terahertz wave, supercontinuum and other electromagnetic radiation are emitted during the interaction between high-intensity laser and matter, generating many new spectral components. Among the interactions between intense laser and matter, femtosecond laser filamentation is a typical one. Femtosecond filament is formed when the Kerr self-focusing effect and plasma-defocusing effect reach a dynamic balance [16,17]. Femtosecond filamentation has been observed in various transparent nonlinear media, including gas (e.g., air), liquid (e.g., water) and solidity (e.g., sapphire, glass). Compared with the gaseous media, it is much easier to generate filament in the condensed media due to their higher nonlinear refractivity. Theoretical and experimental research on the property, control and application of femtosecond filamentation have been conducted in the past few decades. Recently, the introduction of OAM has made the filamentation of femtosecond vortex beams a hot research topic [18,19,20,21,22,23,24,25,26,27,28], for the OAM can provide more freedom to study strong-field physics. Besides, the OAM can cause changes in the electron transition probability and selection rule within the atoms and molecules, affecting the excitation and photoionization of atoms and molecules [29,30,31].
In our recent work, we have studied the supercontinuum and fluorescence induced by the filamentation of femtosecond vortex beams in water and air [26,27,28]. By studying the influence of TC on the supercontinuum and fluorescence emission, we discussed the formation mechanisms of supercontinuum and fluorescence emission. The white light generated during the femtosecond filamentation in gases or condensed media generally consists of a white central part surrounded by a rainbow-like conical emission. The radial order of the spectral components is inverse of diffraction, with bluer frequencies appearing on the outside rings. Conical emission is a signature of femtosecond filamentation. As far as we know, few works focus on the conical emission induced by femtosecond vortex beams. In this paper, by using two typical kinds of vortex beams (i.e., Laguerre–Gaussian (LG) and Bessel–Gaussian (BG) beams), we study characteristics of the conical emission induced by the filamentation of the femtosecond vortex beams in water, explore the role that the OAM plays in the conical emission and discuss the transfer of optical angular momentum in the non-optical parametric processes according to the observed experimental results.
2. Experimental Setup
To explore the characteristics of the colored conical emission induced by the filamentation of femtosecond vortex beams in water, we design an experimental setup schematically shown in Figure 1. The experiment is carried out using an amplified Ti: sapphire laser (coherent Libra). The duration, central wavelength, energy and repetition rate of the emitted pulses are 50 fs, 800 nm, 3.0 mJ and 1 kHz, respectively. An energy attenuator, which consists of a half-wave plate, H and a Glan prism, G, adjusts the pulse energy to a desired value. Since the pulse energy emitted from the laser is too high for the femtosecond filamentation in water, it is attenuated to 188 μJ and fixed at this value throughout this paper. The laser beam spot size is adjusted by an iris, which is set as 10 mm in the experiment, and therefore, the light beam can perfectly enter the liquid crystal screen of a spatial light modulator SLM (Hamamatsu, LCOS-SLM, X13138-02, Shizuoka, Japan). The femtosecond laser pulses emitted from the laser system are linearly polarized, and their polarization direction is horizontal, which is identical to the alignment direction of liquid crystal molecules in the SLM. Vortex beams with different TCs can be generated by loading the corresponding phase diagrams (e.g., figures 2(a’)–2(c’) in Ref. [26]; figures 2(a)–2(c) in Ref. [28]) to the liquid crystal screen of the SLM. Since the SLM only modulates the phase of the laser beam and does not change the polarization state of the laser beam, the laser beams reflected by the SLM (i.e., the generated vortex beams) are still linearly polarized. In other words, the spin angular momentum of the generated vortex beam is zero. In the experiment, to study the characteristics of the colored conical emission induced by the femtosecond LG and BG beams, the vortex beams are focused by two kinds of optical lenses (which are placed at the dashed green frame): one is a plano-convex focusing lens (fused silica) with a focal length of f = 75 mm (generation LG beams), and the other one is an axicon lens with a top angle of 170 degrees (generation BG beams). The vortex beams are focused into a quartz cuvette C (50 mm × 10 mm × 40 mm) filled with water and form filaments, generating the supercontinuum. To avoid contribution from the cuvette walls, the beams are focused close to the center of the cuvette.
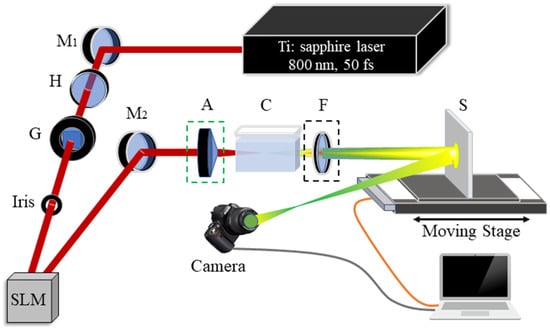
Figure 1.
Schematic diagram of the experimental setup to study the colored conical emission induced by the filamentation of femtosecond vortex beams in water. M1, M2: plane mirrors, H: half-wave plate, G: Glan prism, SLM: spatial light modulator, A: axicon lens (the dashed green rectangle indicates it can be replaced by a plano-convex focusing lens); C: quartz cuvette; F: band-pass filter; S: white screen.
The femtosecond filament has a certain length along the propagation direction of femtosecond laser pulses, and the filament length is affected by many factors, such as the parameters of the laser beam, the type and nature of the transparent medium and the focusing condition. It is not easy to determine the specific location of the filament in the water. More importantly, each part of the filament emits the supercontinuum. These factors make it difficult to determine the tip of the conical emission. As a result, we designed an indirect method to measure the divergence angle of supercontinuum induced by femtosecond vortex beams. The schematic diagram of the method is shown in Figure 2. A white screen S is placed on a moving stage, and its surface is perpendicular to the propagation direction of the femtosecond laser beam. By moving the white screen along the propagation direction, the light spots are captured at two selected positions, at which the distances between the back wall of the cuvette and the white screen are 8.1 cm and 23.1 cm, respectively. The spacing between the two positions is D = 15 cm. Once the radius of the light spot at the two positions is measured, we can obtain the maximum divergence angle of the supercontinuum θd:
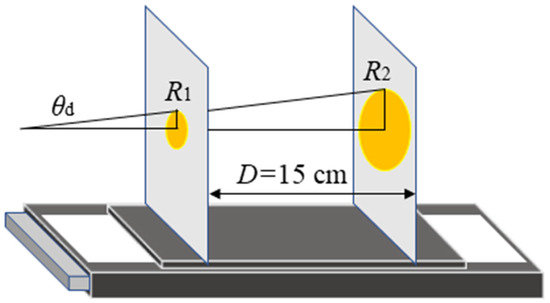
Figure 2.
Schematic diagram of the method to measure the divergence angle of supercontinuum induced by femtosecond vortex beams. θd is the divergence angle. By moving the white screen, the light spot is recorded at two selected positions along the propagation direction of the femtosecond beam. R1 and R2 are the radii of the light spots captured at the two positions.
Since the supercontinuum contains different spectral components which are mixed together, we cannot obtain the spot radius of the spectral component with a specific wavelength. By using a set of bandpass filters BFs (450 nm, 500 nm, 550 nm, 600 nm, 650 nm and 700 nm), different spectral components are picked out. Light spots with clear boundaries appear on the white screen, which are then recorded by a digital camera (Nikon, D300S). Since the camera is placed at the side of the light path, the light spots recorded by the camera are elliptical, which is the affine transformation of the actual light spots that appear on the white screen. Consequently, it is necessary to obtain profiles of the original circular light spots by the affine transformation of the captured light spots [32].
3. Results and Discussion
Figure 3 shows the patterns of the supercontinuum induced by the femtosecond BG and LG beams in water. These patterns are the results of the affine transformation of the light spots captured by the camera. Water is chosen as the medium in this paper because it can generate stable, ultrabroad, high-intensity supercontinuum at a low cost, standing out among the condensed state media to generate supercontinuum. The critical power for self-focusing (the linear and nonlinear refractive index of water are n0 = 1.33 and n2 = 4.1 × 10−16 cm2/W) in water for 800 nm pulse is Pcr = 1.761 MW [33], which is much lower than the filamentation threshold due to the strong dispersion effect [34]. In our previous work, the dependence of the filamentation threshold on the TC in the case of the LG beam was studied by interferometry [26]. It is found that the filamentation threshold of the femtosecond vortex pulse increases linearly with the TC value, and for the LG beam with l = 10, its filamentation threshold is 140 MW [26]. For the input femtosecond pulse, its energy is attenuated to 188 μJ, and the corresponding pulse power is 3.76 GW, which is much higher than the filamentation threshold of the femtosecond vortex beams in water. In this case, multiple filaments are generated.

Figure 3.
Patterns of the supercontinuum induced by the filamentation of the femtosecond (a–c) BG and (d–f) LG beams in water. The TC values of the vortex beams are (a,d) l = 0, (b,e) l = 1, and (c,f) l = 2.
The white light produced by the BG beams is distributed in a set of concentric rings like a rainbow with a white center, as shown in Figure 3a–c. In contrast, the spots of the white light induced by the LG beams are completely different, which are circular white disks, as shown in Figure 3d–f. Obviously, they are different from the white light spots that have been reported in many previous literature, which generally consist of a white central part surrounded by a set of rainbow-like rings. It can also be seen from Figure 3 that by increasing the TC value of the vortex beams, the characteristics of the white light patterns are almost the same as the zero-order ‘vortex’ beams (l = 0) for both the LG and BG beams. To make out the origin of the difference between the spots of white light induced by the two kinds of vortex beams, especially the abnormal white light spots in the case of the LG beams, in the following part, using a set of bandpass filters (450 nm, 500 nm, 550 nm, 600 nm, 650 nm and 700 nm), we study the light spots for different monochromatic components.
We take the white light induced by the filament generated by the zero-order BG and LG beams as examples and display the light spot patterns for different spectral components of the white light, as shown in Figure 4 and Figure 5. It can be seen from the figures that the radius of the light spot decreases with the increase in the wavelength both in the case of LG and BG beams, which is the feature of conical emission. However, there exists a significant difference between the profiles of light spots of the monochromatic components from the white light induced by the two kinds of vortex beams. In the case of BG beams, the white light spots are composed of a central bright spot and several concentric rings, as shown in Figure 4b,d,f,h,j,l). It results in a rainbow of concentric rings of white light when all spectral components are mixed together. The central part of the rings contains all the spectral components, making it a white dot, as shown in Figure 3a–c, which is similar to the commonly observed white light spots. In the case of LG beams, the spot of each monochromatic component from the white light induced by the filamentation of the femtosecond LG beam is a circular disk, as shown in Figure 5. The different spectral components are mixed together, making the white light spots circular white disks (see Figure 3d–f), which are different from the commonly observed white light spots.
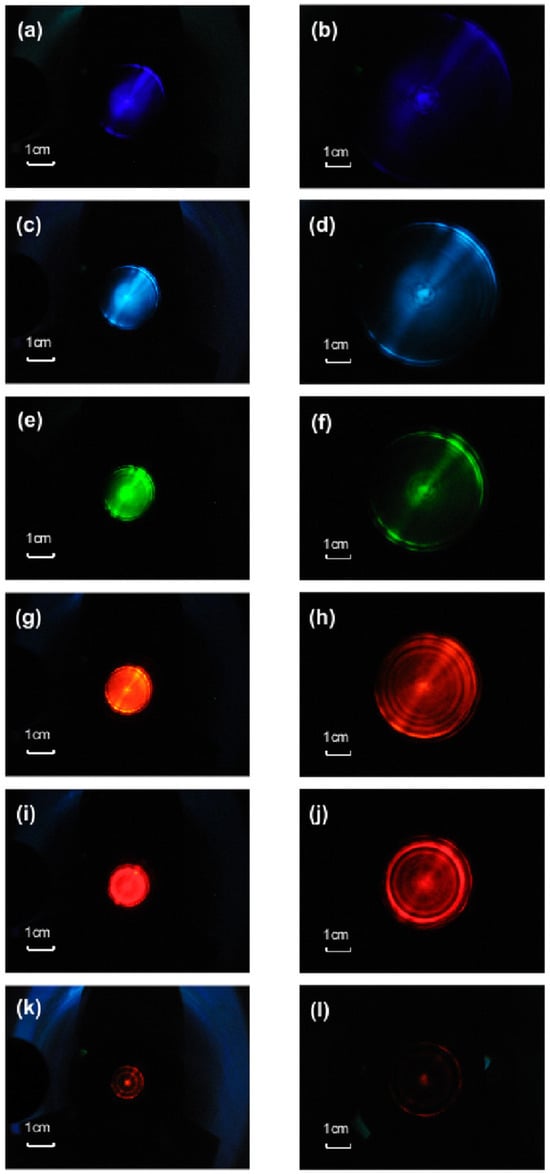
Figure 4.
Spots of the (a,b) 450 nm, (c,d) 500 nm, (e,f) 550 nm, (g,h) 600 nm, (i,j) 650 nm and (k,l) 700 nm spectral components after the filamentation of the BG beam with l = 0. (a,c,e,g,i,k) and (b,d,f,h,j,l) are measured when the distance between the back wall of the cuvette and the white screen is 8.1 cm and 23.1 cm, respectively.

Figure 5.
Spots of (a,b) 450 nm, (c,d) 500 nm, (e,f) 550 nm, (g,h) 600 nm, (i,j) 650 nm and (k,l) 700 nm spectral components after the filamentation of the LG beam with l = 0. (a,c,e,g,i,k) and (b,d,f,h,j,l) are measured when the distance between the back wall of the cuvette and the white screen is 8.1 cm and 23.1 cm, respectively.
Before conducting further analysis and discussion, we shall review the physical mechanism that accounts for the conical emission. Since the self-phase modulation (SPM) is taken as the predominant mechanism for the supercontinuum generation [16,17] and the conical emission is a characteristic phenomenon of supercontinuum generation, we prefer the SPM scheme to qualitatively interpret the conical emission in the following part (in effect, it has been carried out by numerous work).
The variation of the frequency induced by the SPM can be described by [16,17,26,27]:
where is the variation of the phase of the laser pulse, , z, n2, and are the central frequency of the laser pulse, the propagation distance in media, second order nonlinear refractive index of the transparent medium, plasma density and the critical plasma density (, , e and me are permittivity of vacuum, electron charge and electron mass), respectively. For the 800 nm pulses, the value of is about 2 × 1021 cm−3, though it is a little lower than the number density of water molecule . Limited by the ionization rate during femtosecond filamentation (about 1‰), the electron number density is still much lower than the critical electron number density . Besides, due to the high number density of water molecules, the distance between water molecules is about 1/10 of that between air molecules. As a result, the plasma will recombine shortly after they are generated.
During the femtosecond laser filamentation, the temporal evolution of plasma and laser intensity also brings variation to the wave vector, and the general wave vector is given by:
where and are the initial longitudinal and radial wave vectors of the incident femtosecond pulses, and are the variation in the longitudinal and radial wave vectors, and are the unit vectors of the longitudinal and radial components. Both and are related to the plasma generation and temporal evolution of laser intensity [16,17]. Since the conical emission arises from the variation in radial wave vector, here, we mainly consider the variation in radial wave vector, which is given by [16]:
The front of the pulse, where plasma can be neglected, induces a redshift associated with a positive kr(t), i.e., converging toward the filament axis, while the contribution of the plasma in the trail of the pulse leads to a blue shift associated with a negative radial phase derivative. Hence, the conical emission is interpreted as a divergence of the anti-Stokes components of the supercontinuum induced by the plasma. No conical emission was found at Stokes shifted wavelengths. In this paper, we focus on the spectral components at the blue side of the central wavelength (i.e., visible band), always takes the positive values. From Equations (2) and (4), it can be obviously seen that is positively related to . As shown in Figure 4a, for a newly generated spectral component, the more its frequency deviates from the central frequency of the laser pulse , the larger its divergence angle with respect to the filament axis is, which can well explain the feature of the conical emission.
The difference between the conical emission induced by the femtosecond LG and BG beams can be attributed to the use of a plano-convex focusing lens and axicon lens. In the experiment, after the femtosecond laser beams pass the plano-convex focusing lens and axicon lens, due to the different geometries of these lenses, the spatial distribution of the wave vectors differs much in the two cases, as shown in Figure 6b,c. Obviously, the different spatial distribution of the wave vectors results in the different spatial distribution of laser intensity. The spatial distribution of laser intensity affects the excitation and photoionization of the media and, thus, the accompanied light emission like fluorescence and supercontinuum.
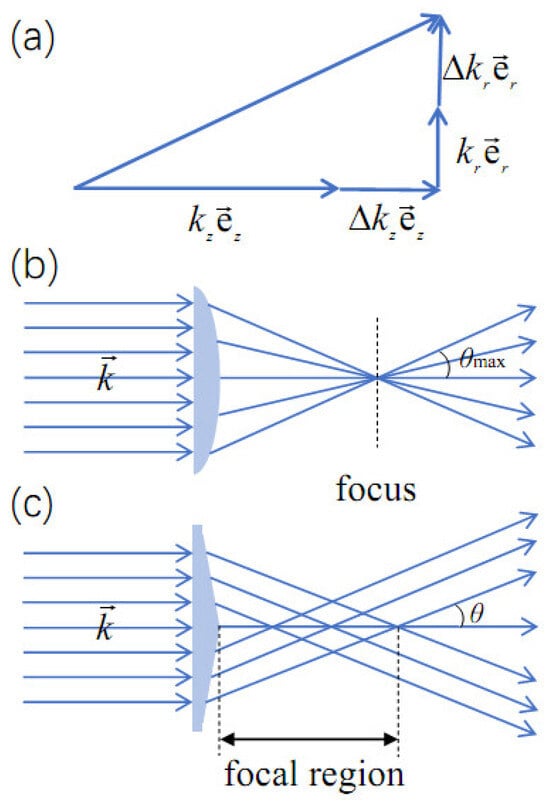
Figure 6.
(a) Illustration of the general wave vector. Spatial distribution of the wave vector of the laser beam after it passes the (b) plano-convex focusing lens and (c) axicon lens.
In our work, the focal lengths of the plano-convex focusing lens are much shorter than the focal length of the focusing lens adopted in many previous experiments about femtosecond filamentation. It leads to the tightly focusing condition, which makes the incident laser beam diverge greatly after the focus, and thus, the wave vectors point in different directions, as shown in Figure 6b. The divergence angle brought by the plano-convex focusing lens takes continuous values between 0° and 3.8°. According to the focal length of the selected focusing lens, the focusing regime can be divided into linear and nonlinear ones [35], which greatly affects the femtosecond laser filamentation process and the accompanied nonlinear phenomena like fluorescence and supercontinuum radiation [34,36].
For the tightly focusing case, linear focusing plays a dominant role in the femtosecond filamentation. Once the filament is formed, the wave vectors of the newly generated spectral components also point in different directions, and thus, the captured white light spots are circular white disks, which are completely different from the commonly observed white light spots. If we use a focusing lens with a much longer focal length, the directions of the wave vectors are almost uniform, pointing at the propagation direction. In this case, the femtosecond filamentation mainly results from self-focusing, and the normal white light spots can be observed. In contrast, after the laser beam passes the axicon lens, the direction of the wave vectors is the same (the divergence angle brought by the axicon lens is 5°), and thus the captured patterns are rings. Jukna et al. numerically simulated the propagation of a femtosecond BG beam in glass and found that the BG beam can generate a ring-shaped filamentary ionized channel, forming multiple helical filaments [37]. They also found that the ring-shaped filamentary ionized channel is merely affected by the TC value. As a consequence, the white light generated by the multiple helical filaments exhibits the rainbow-like conical emission. To conclude, the conical emission induced by the two kinds of vortex beams differs from each other, showing different profiles: the conical emission induced by the BG beams shows a conical surface with a hollow interior for all the monochromatic components, while that induced by the LG beams show a cone with a solid interior for all the monochromatic components. The different spatial intensity distributions for the two kinds of vortex beams can account for the difference.
In a tightly focusing condition, there exists spin-to-orbital angular momentum conversion [38]. Though the spin angular momentum carried by the vortex beams prepared by the SLM is zero, the axicon and plano-convex focusing lens cause strong focusing. In this case, the polarization state of the vortex beam may be changed due to the spin-to-orbital angular momentum coupling. As is known, the polarization state of a laser affects the ionization efficiency of the media: the linearly polarized pulse is more efficient in ionization than the circularly polarized one when they have the same power [39].
To study the role that the optical angular momentum plays in the conical emission induced by femtosecond vortex beams in water, we try to obtain the variation of the divergence angle of the supercontinuum with the wavelength and the TC. Through the radii of the light spots measured at the two selected positions, we can obtain the maximum divergence angle of the supercontinuum by using Equation (1), as shown in Figure 7 and Figure 8. Here, we use the divergence angle rather than the conical angle because the use of the lens contributes partly to the divergence angle. As has been stated in the previous part, the divergence angle θ brought by the plano-convex focusing lens and axicon lens are 0°–3.8° and 5°, respectively. Therefore, the real conical angle is . It can be seen from Figure 7a and Figure 8a that the divergence angle decreases with increasing wavelength, which agrees with the quantitative analysis performed with the SPM. Interestingly, for all the TC values adopted in our work, the change of the divergence angles of the supercontinuum induced by the femtosecond vortex beams with the wavelength is coincident. We also draw the curves showing the variation of the divergence angle with the TC value, as shown in Figure 7b and Figure 8b. It can be seen from the figures that within the error, the divergence angle does not change with the TC value for all the selected wavelengths. The above results suggest that the OAM does not affect the supercontinuum generation and conical emission induced by the filamentation of femtosecond vortex beams. Though the OAM affects the filamentation threshold [23,24,26], and the OAM can be transferred from the input pulse to the atoms/molecules in surrounding media during the interaction between laser and matter [11,12,13], in condensed state matters, the TC value does not affect the spectral broadening, provided the filament is formed [26,27].
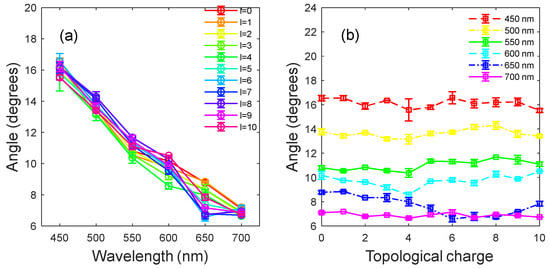
Figure 7.
(a) Variation of the maximum divergence angle of the supercontinuum induced by the BG beams with the wavelength. (b) Variation of the maximum divergence angle of different spectral components of the supercontinuum induced by the BG beams with the TC value.
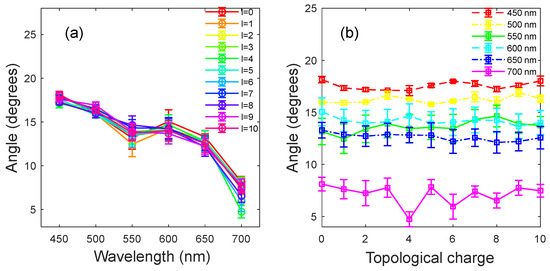
Figure 8.
(a) Variation of the maximum divergence angle of the supercontinuum induced by the LG beams with the wavelength. (b) Variation of the maximum divergence angle of different spectral components of the supercontinuum induced by the LG beams with the TC value.
According to the interpretation of the SPM, see Equations (2) and (4), the helical phase carried by the light waves does not evolve in time and radial direction in space. As a result, the OAM does not bring any additional information to the supercontinuum and conical emission. More importantly, in the interaction between the intense femtosecond laser pulses and condensed state matters, the OAM has nearly no effect on the generated phenomena, which can be attributed to several factors. Firstly, the number density of atoms/molecules in the condensed medium is high, and numerous plasmas are generated during the interaction. Consequently, the OAM carried by newly generated components in the supercontinuum is transferred to the electrons, atoms and molecules in the medium, leading to the depletion of the OAM [11,12,13]. Secondly, the angular momentum conservation is preserved in the optical parametric process like the optical parametric down-conversion [14], four-wave mixing [15], stimulated Raman scattering [40], high-harmonic generation [41], etc., leading to the fact that the newly generated spectral components carry the OAM, whereas, the photoionization, SPM and other nonlinear effects that occur during the femtosecond filamentation are non-optical parametric processes, in which the angular momentum conservation is broken. Consequently, during the filamentation of femtosecond vortex beams in condensed state matters like water, the newly generated spectral components do not carry the OAM; however, the supercontinuum induced by the femtosecond vortex beams in air possesses the OAM, which was confirmed by the interferometry [26]. Apart from the SPM, the four-wave mixing scheme may partly account for the supercontinuum generation in air, for the OAM can be transferred to the newly generated spectral components in the optical parametric processes. It seems that the density of the medium affects the mechanism of supercontinuum generation as well as the transfer of angular momentum during femtosecond filamentation. This interesting fact stimulates us to continue to study the interaction between the intense vortex beam and matter and thoroughly explore the transfer of angular momentum and the coupling of spin-orbital angular momentum during the interaction between high-intensity laser and matter.
4. Conclusions
In this paper, we experimentally study the conical emission of the white light induced by the filamentation of the BG and LG beams. It is found that the spots of the white light induced by the femtosecond BG beams show a rainbow structure with a white center, while those of the white light induced by the femtosecond LG beams are circular white disks. The discrepancy between them is mainly caused by the different geometries of the lenses used in the experiment (which lead to different spatial intensity distributions for the two kinds of vortex beams), and it is the high numerical aperture of the plano-convex focusing lens leads to the abnormal white light spots observed in the case of LG beam. By studying the divergence angles of the two types of vortex beams, it is found that the divergence angles of the white light induced by the femtosecond BG and LG beams both decrease with the increase in wavelength, while the TC value has no obvious effect on the divergence angles. According to the interpretation of the conical emission in terms of the self-phase modulation, the helical phase carried by the femtosecond vortex beams does not evolve in time and radial direction in space, and thus, the OAM does not affect the supercontinuum generation and conical emission induced by the filamentation of femtosecond vortex beams in condensed state matters.
Author Contributions
Conceptualization and methodology, Y.L.; formal analysis, H.Z., L.Z. and S.L.; writing—original draft, Y.L., H.Z. and S.L.; writing—review and editing, Y.L., Y.H., L.Z., M.J., H.Z., S.L. and W.H.; funding acquisition, Y.H., M.J. and W.H.; supervision, H.Z., S.L. and W.H.; project administration, Y.H., M.J. and W.H. All authors have read and agreed to the published version of the manuscript.
Funding
The research was partially supported by the Key Research Project of Zhejiang Lab (Nos. K2022PG1BB01 and 121005-PI2101) and the National Natural Science Foundation of China (Grant Nos. 11704145 and 11974138).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810. [Google Scholar] [CrossRef] [PubMed]
- Paterson, L.; MacDonald, M.P.; Arlt, J.; Sibbett, W.; Bryant, P.E.; Dholakia, K. Controlled rotation of optically trapped microscopic particles. Science 2001, 292, 912. [Google Scholar] [CrossRef] [PubMed]
- Andrade, U.M.S.; Garcia, A.M.; Rocha, M.S. Bessel beam optical tweezers for manipulating superparamagnetic beads. Appl. Opt. 2021, 60, 3422–3429. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Wei, Y.; Zhao, T.; Liu, S.; Su, R.; Yao, B.; Yu, Y.; Liu, J.; Wang, X. Bright solid-state sources for single photons with orbital angular momentum. Nat. Nanotechnol. 2021, 16, 302–307. [Google Scholar] [CrossRef]
- Chen, R.; Agarwal, K.; Sheppard, C.J.R.; Chen, X. Imaging using cylindrical vector beams in a high-numerical-aperture microscopy system. Opt. Lett. 2013, 38, 3111. [Google Scholar] [CrossRef]
- Torner, L.; Torres, J.P.; Carrasco, S. Digital spiral imaging. Opt. Express 2005, 13, 873–881. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Moreno, E.; Rudenko, A.; Faure, N.; Sedao, X.; Mauclair, C.; Colombier, J.P.; Stoian, R. Super-efficient drilling of metals with ultrafast non diffractive laser beams. Sci. Rep. 2022, 12, 2074. [Google Scholar] [CrossRef]
- Omatsu, T.; Miyamoto, K.; Toyoda, K.; Morita, R.; Arita, Y.; Dholakia, K. A new twist for materials science: The formation of chiral structures using the angular momentum of light. Adv. Opt. Mater. 2019, 7, 1801672. [Google Scholar] [CrossRef]
- He, H.; Friese, M.E.J.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity. Phys. Rev. Lett. 1995, 75, 826. [Google Scholar] [CrossRef]
- Alexandrescu, A.; Cojoc, D.; Fabrizio, E.D. Mechanism of angular momentum exchange between molecules and Laguerre-Gaussian beams. Phys. Rev. Lett. 2006, 96, 243001. [Google Scholar] [CrossRef] [PubMed]
- Picón, A.; Benseny, A.; Mompart, J.; De Vázquez Aldana, R.J.; Plaja, L.; Calvo, G.F.; Roso, L. Transferring orbital and spin angular momenta of light to atoms. N. J. Phys. 2010, 12, 083053. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313. [Google Scholar] [CrossRef]
- Walker, G.; Arnold, A.S.; Franke-Arnold, S. Trans-spectral orbital angular momentum transfer via four-wave mixing in Rb vapor. Phys. Rev. Lett. 2012, 108, 243601. [Google Scholar] [CrossRef] [PubMed]
- Couairon, A.; Mysyrowicz, A. Femtosecond filamentation in transparent media. Phys. Rep. 2006, 441, 47. [Google Scholar] [CrossRef]
- Chin, S.L. Femtosecond Laser Filamentation; Springer: New York, NY, USA, 2010. [Google Scholar]
- Vuong, L.T.; Grow, T.D.; Ishaaya, A.; Gaeta, A.L.; Gert, W.; Eliel, E.R.; Fibich, G. Collapse of optical vortices. Phys. Rev. Lett. 2006, 96, 133901. [Google Scholar] [CrossRef]
- Vincotte, A.; Berge, L. Femtosecond optical vortices in air. Phys. Rev. Lett. 2005, 95, 193901. [Google Scholar] [CrossRef]
- Chen, Y.; Man, X.; Liu, B.; Lin, Z. Nitrogen fluorescence emission pumped by femtosecond optical vortex beams. Front. Phys. 2023, 11, 192. [Google Scholar] [CrossRef]
- Polynkin, P.; Ament, C.; Moloney, J.V. Self-focusing of ultraintense femtosecond optical vortices in air. Phys. Rev. Lett. 2013, 111, 023901. [Google Scholar] [CrossRef] [PubMed]
- Ju, L.B.; Huang, T.W.; Xiao, K.D.; Wu, G.Z.; Yang, S.L.; Li, R.; Yang, Y.C.; Long, T.Y.; Zhang, H.; Wu, S.Z. Controlling multiple filaments by relativistic optical vortex beams in plasmas. Phys. Rev. E 2016, 94, 033202. [Google Scholar] [CrossRef]
- Fibich, G.; Gavish, N. Theory of singular vortex solutions of the nonlinear Schrödinger equation. Phys. D 2008, 237, 2696. [Google Scholar] [CrossRef]
- Fibich, G.; Gavish, N. Critical power of collapsing vortices. Phys. Rev. A 2008, 77, 045803. [Google Scholar] [CrossRef]
- Xu, L.; Li, D.; Chang, J.; Xi, T.; Hao, Z. Helical filaments array generated by femtosecond vortex beams with lens array in air. Results Phys. 2021, 26, 104334. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Lin, S.; Chang, M.; Yu, M.; Wang, Y.; Chen, A.; Jiang, Y.; Li, S.; Jin, M. Testing the coherence of supercontinuum generated by optical vortex beam in water. J. Phys. B 2021, 54, 165401. [Google Scholar] [CrossRef]
- Wu, J.; Huo, L.; Ni, Y.; Wu, Z.; Chen, T.; Gao, S.; Li, S. Supercontinuum induced by filamentation of Bessel-Gaussian and Laguerre-Gaussian beams in water. Appl. Sci. 2022, 12, 06005. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Zhang, Y.; Liang, C.; Yu, M.; Liu, Y.; Jin, M. Nitrogen fluorescence emission induced by femtosecond vortex beams in air. Phys. Scr. 2023, 98, 055508. [Google Scholar] [CrossRef]
- Rodrigues, J.D.; Marcassa, L.G.; Mendonça, J.T. Excitation of high orbital angular momentum Rydberg states with Laguerre–Gauss beams. J. Phys. B 2016, 49, 074007. [Google Scholar] [CrossRef]
- Böning, B.; Paufler, W.; Fritzsche, S. Above-threshold ionization by few-cycle Bessel pulses carrying orbital angular momentum. Phys. Rev. A 2018, 98, 023407. [Google Scholar] [CrossRef]
- Kaneyasu, T.; Iwayama, H.; Shigemasa, E.; Hikosaka, Y.; Konomi, T.; Katoh, M.; Fujimoto, M. Limitations in photoionization of helium by an extreme ultraviolet optical vortex. Phys. Rev. A 2017, 95, 023413. [Google Scholar] [CrossRef]
- Zhang, Y.; Sui, L.; Chen, A.; Zhang, D.; Wang, Q.; Xu, W.; Li, S.; Jin, M. Spectral resolved study of filamentation effect on the nonlinear absorption in carbon disulfide. Opt. Express 2019, 27, 20980. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008; p. 212. [Google Scholar]
- Li, S.; Wang, X.; Zhang, Y.; Yu, M.; Wang, Y.; Liu, F.; Jin, M. Femtosecond filamentation in water studied by the interference of supercontinuum. Phys. Scr. 2023, 98, 015501. [Google Scholar] [CrossRef]
- Lim, K.; Durand, M.; Baudelet, M.; Richardson, M. Transition from linear- to nonlinear-focusing regime in filamentation. Sci. Rep. 2014, 4, 7217. [Google Scholar] [CrossRef] [PubMed]
- Théberge, F.; Liu, W.; Simard, P.T.; Becker, A.; Chin, S.L. Plasma density inside a femtosecond laser filament in air: Strong dependence on external focusing. Phys. Rev. E 2006, 74, 036406. [Google Scholar] [CrossRef]
- Jukna, V.; Milian, C.; Xie, C.; Itina, T.; Dudley, J.; Courvoisier, F.; Couairon, A. Filamentation with nonlinear Bessel vortices. Opt. Express 2014, 22, 25410. [Google Scholar] [CrossRef]
- Zhao, Y.; Edgar, J.S.; Jeffries, G.D.M.; McGloin, D.; Chiu, D.T. Spin-to-orbital angular momentum conversion in a strongly focused optical beam. Phys. Rev. Lett. 2007, 99, 073901. [Google Scholar] [CrossRef]
- Kolesik, M.; Moloney, J.V.; Wright, E.M. Polarization dynamics of femtosecond pulses propagating in air. Phys. Rev. E 2001, 64, 046607. [Google Scholar] [CrossRef] [PubMed]
- Vieira, J.; Trines, R.M.G.M.; Alves, E.P.; Fonseca, R.A.; Mendonça, J.T.; Bingham, R.; Norreys, P.; Silva, L.O. Amplification and generation of ultra-intense twisted laser pulses via stimulated Raman scattering. Nat. Commun. 2016, 7, 10371. [Google Scholar] [CrossRef] [PubMed]
- Rego, L.; Dorney, K.M.; Brooks, N.J.; Nguyen, Q.L.; Liao, C.T.; Román, J.S.; Couch, D.E.; Liu, A.; Pisanty, E.; Lewenstein, M.; et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science 2019, 364, eaaw9486. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).