Free Vibration Analysis of Arches with Interval-Uncertain Parameters
Abstract
:1. Introduction
2. Model of the Arch and Procedure of Deterministic Free-Vibration Equations
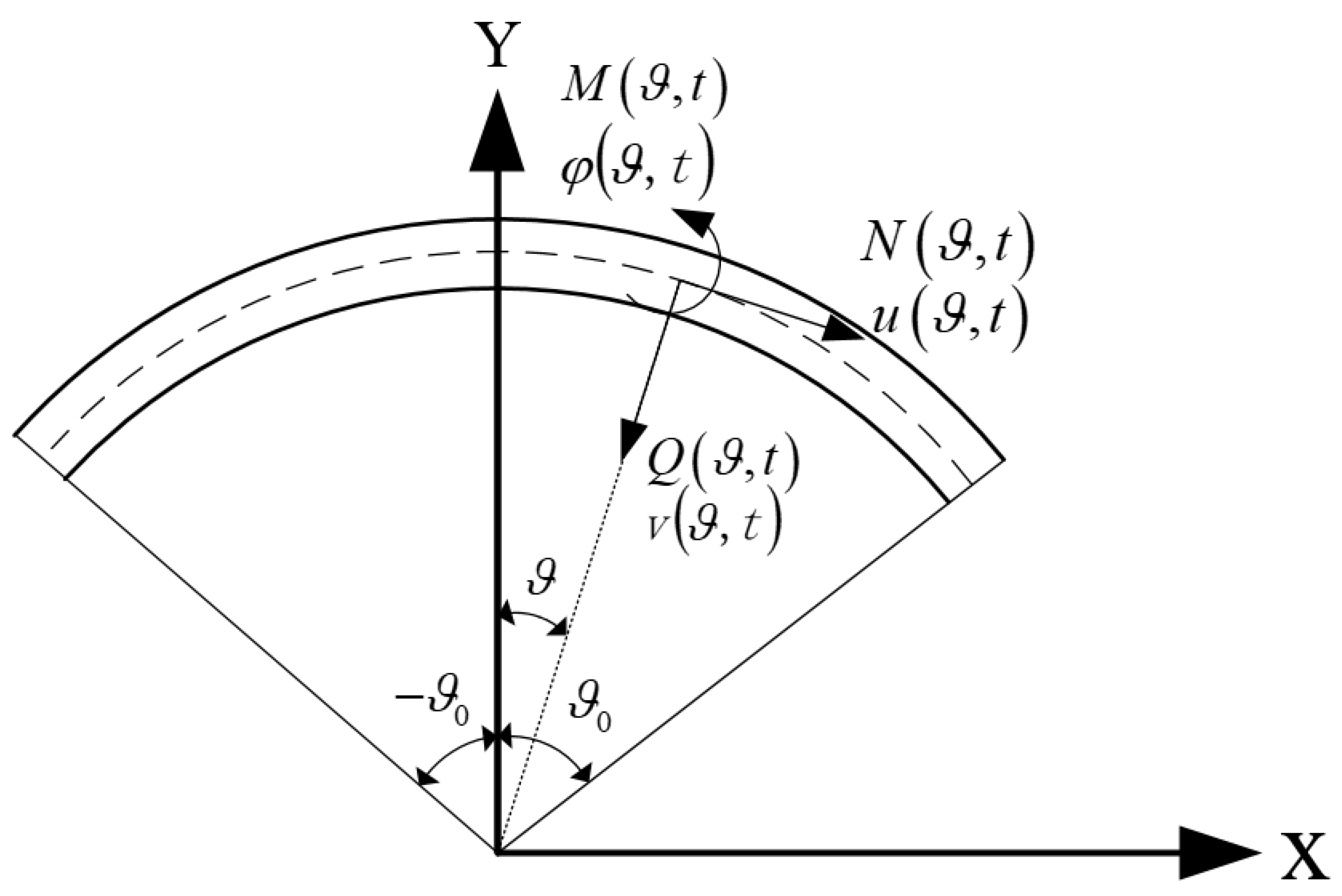
2.1. Establishment of Free-Vibration Equations
2.2. Establishment of Free-Vibration Equations
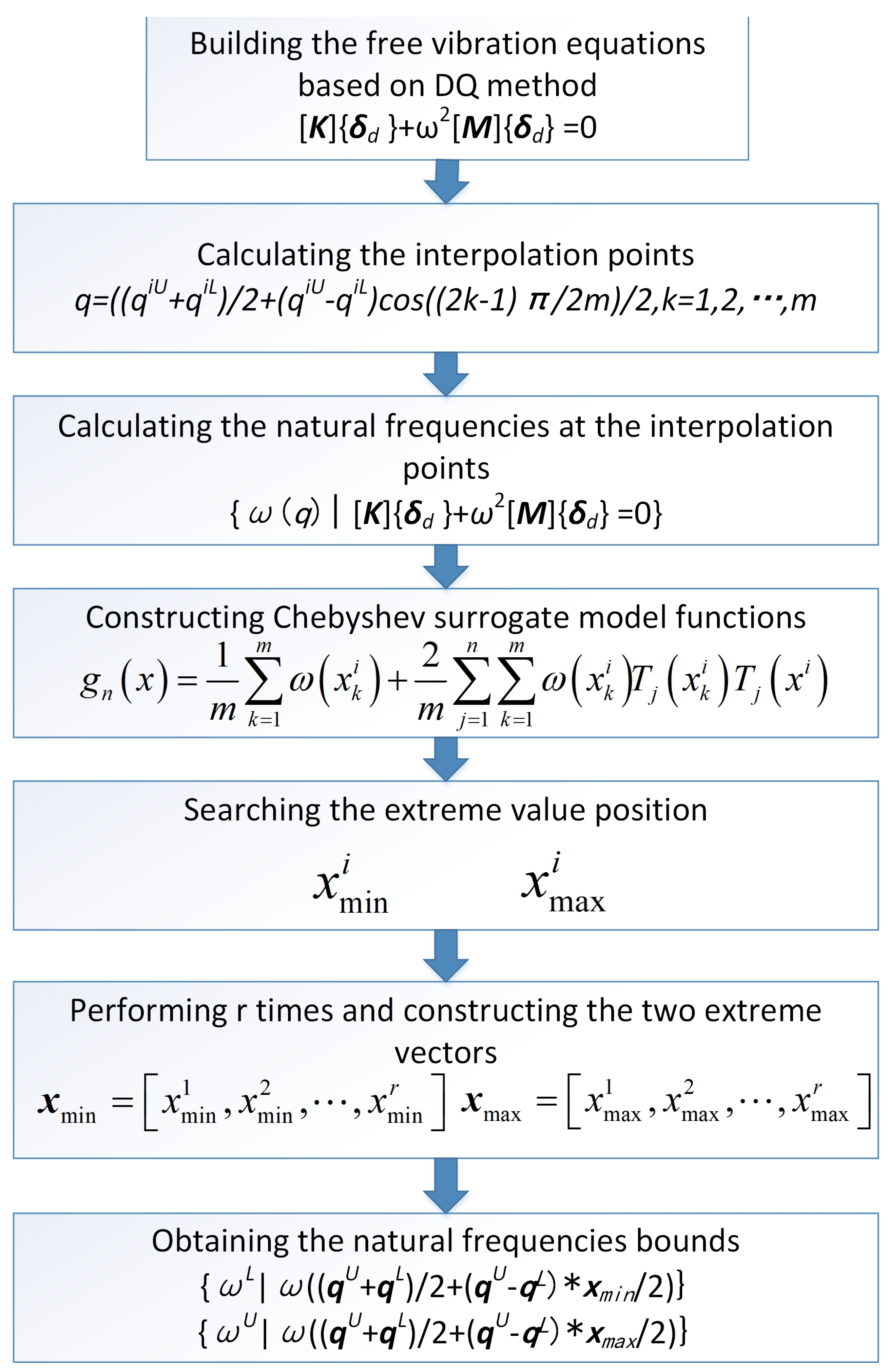
3. General Polynomial Surrogate Model for Interval Natural Frequency Analysis
4. Numerical Simulation and Discussion
4.1. The Natural Frequencies Based on the Traditional Deterministic Method
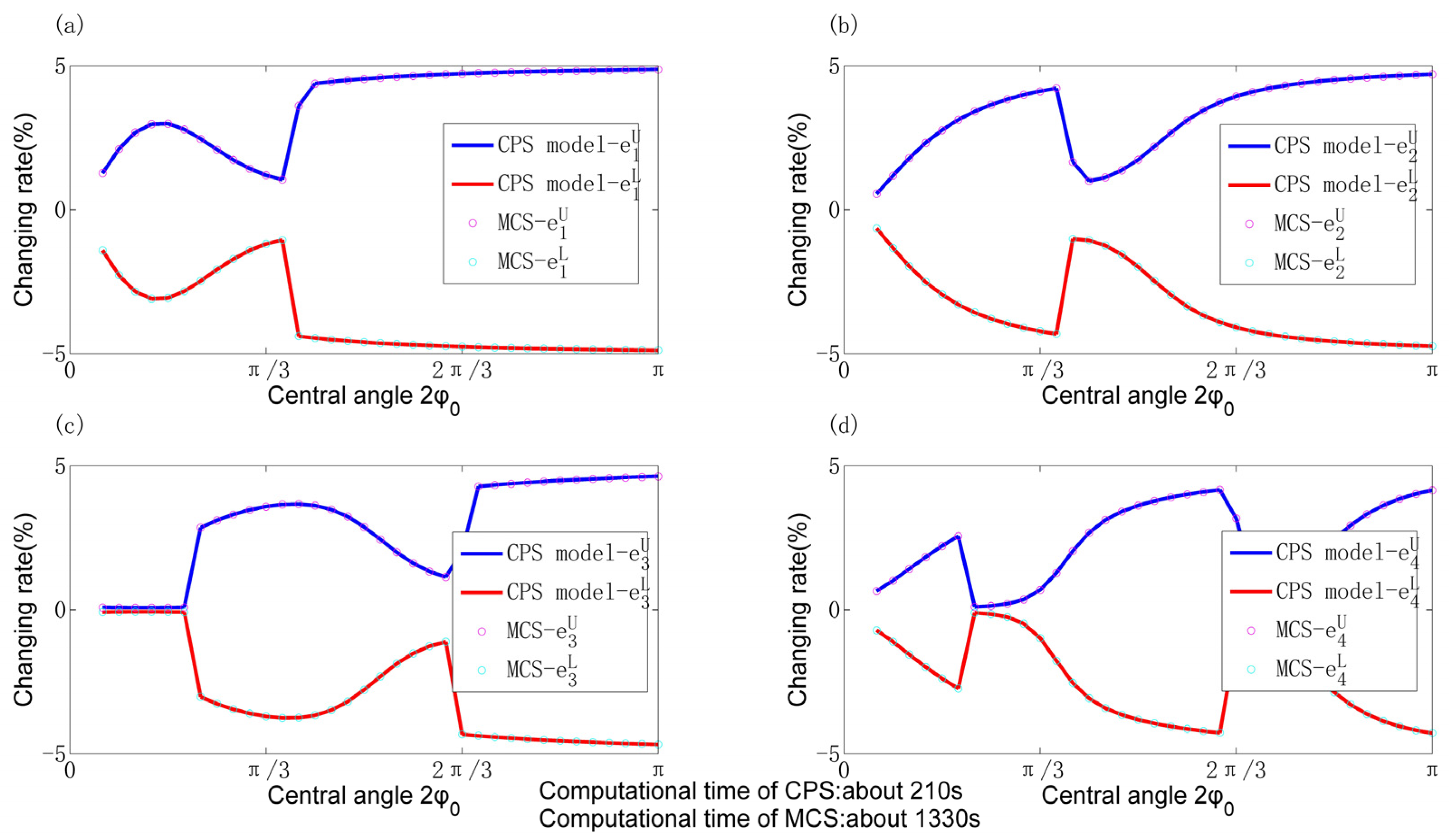
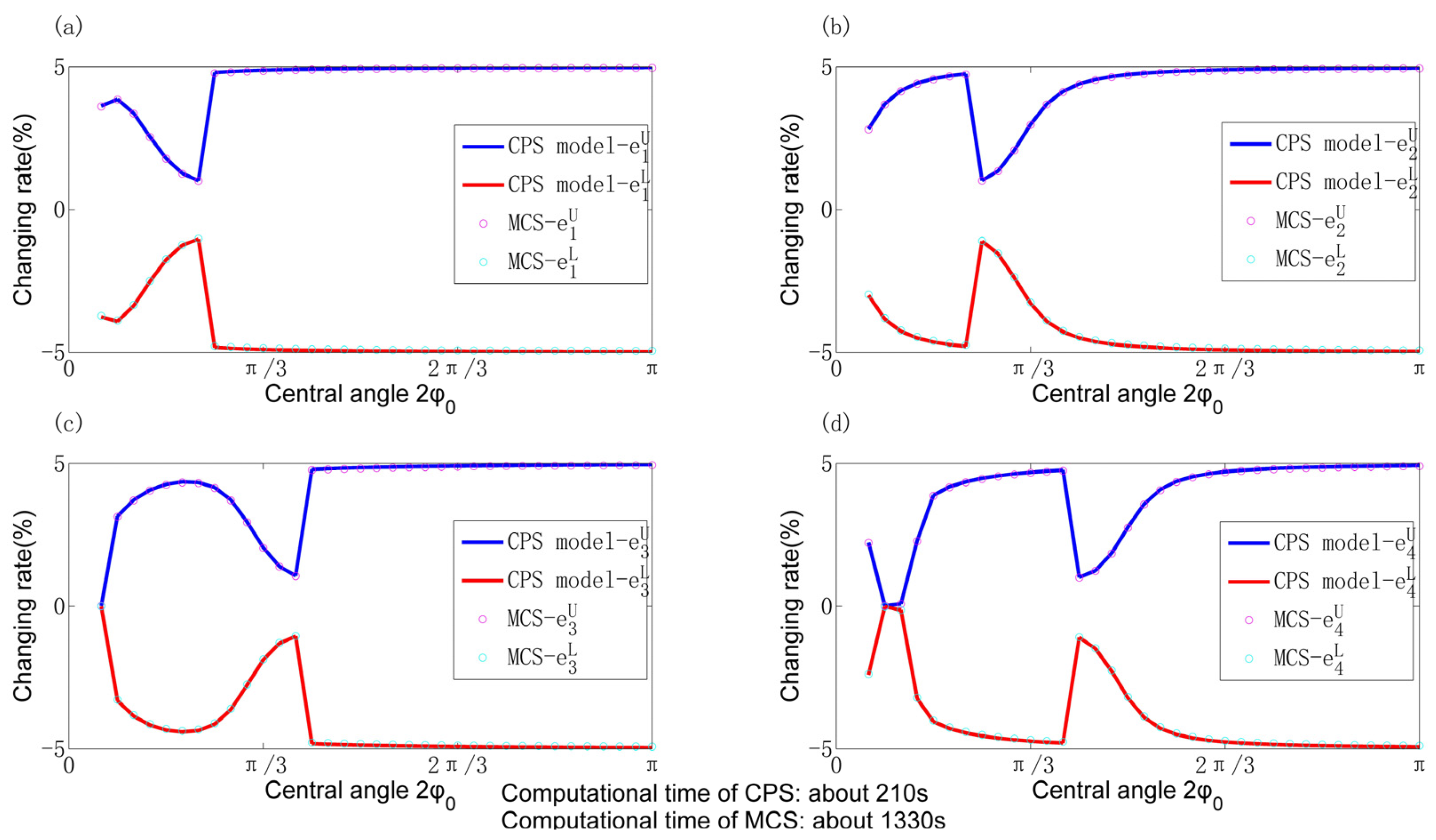
4.2. Comparisons of CPS Model with MCS in Calculating Natural Frequencies
4.3. Uncertain Natural Frequency Investigations Considering Different Uncertain Parameters
4.3.1. Single Uncertain Parameter
4.3.2. Multiple Uncertain Parameters
5. Conclusions
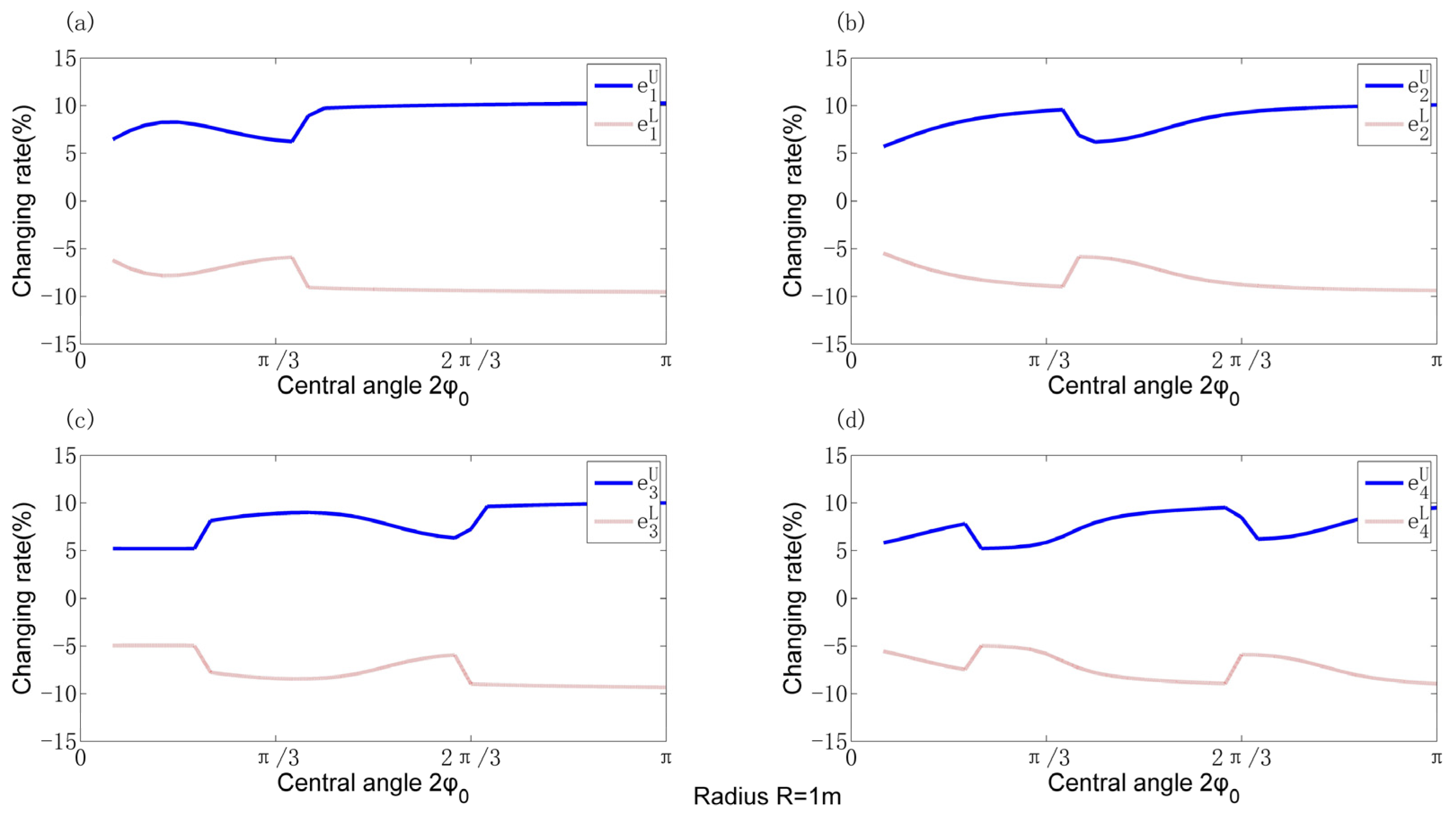
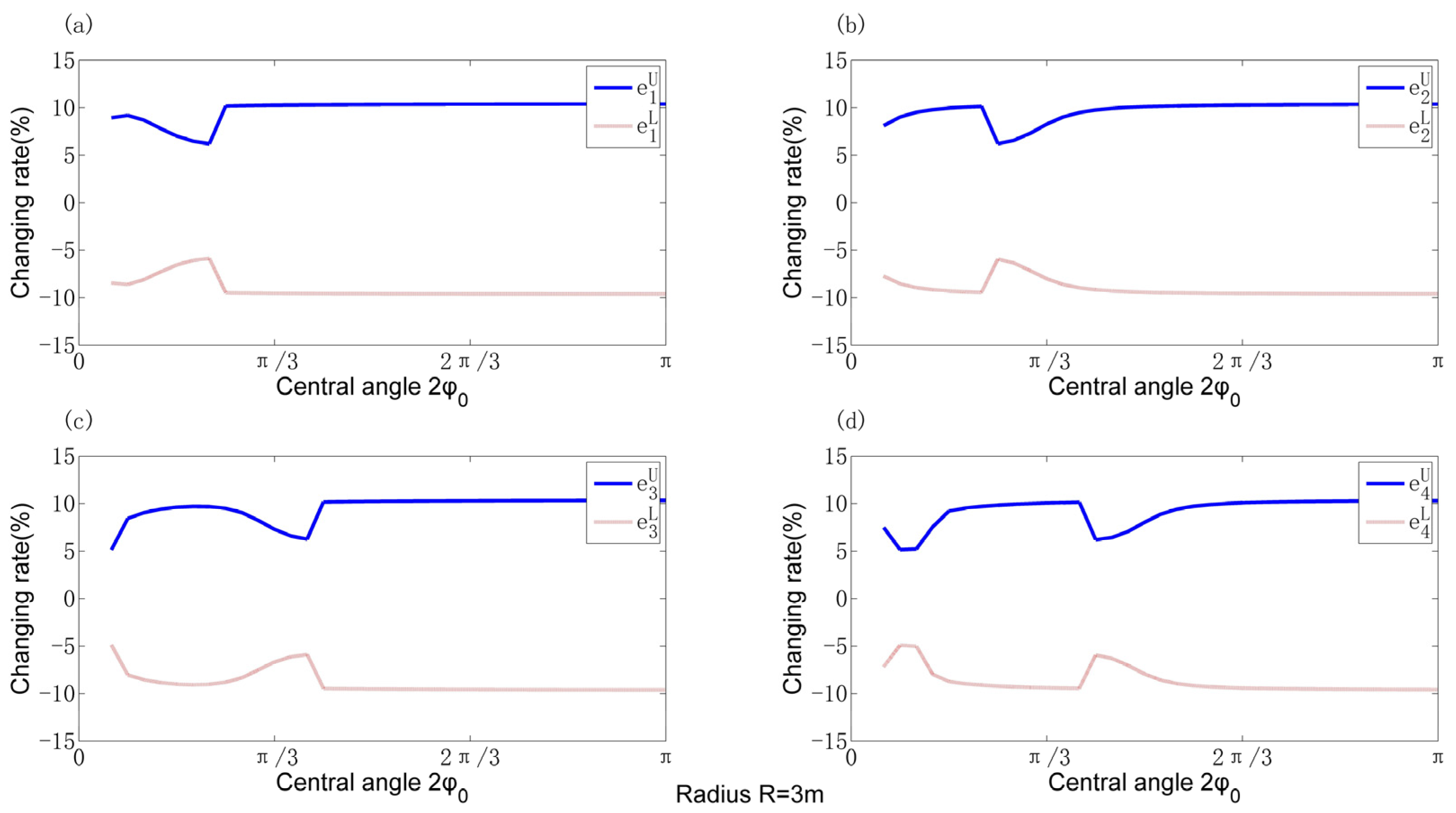
- Some geometrical parameters, such as the cross-sectional height, were found to be sensitive, which will cause large fluctuations in the dynamic properties.
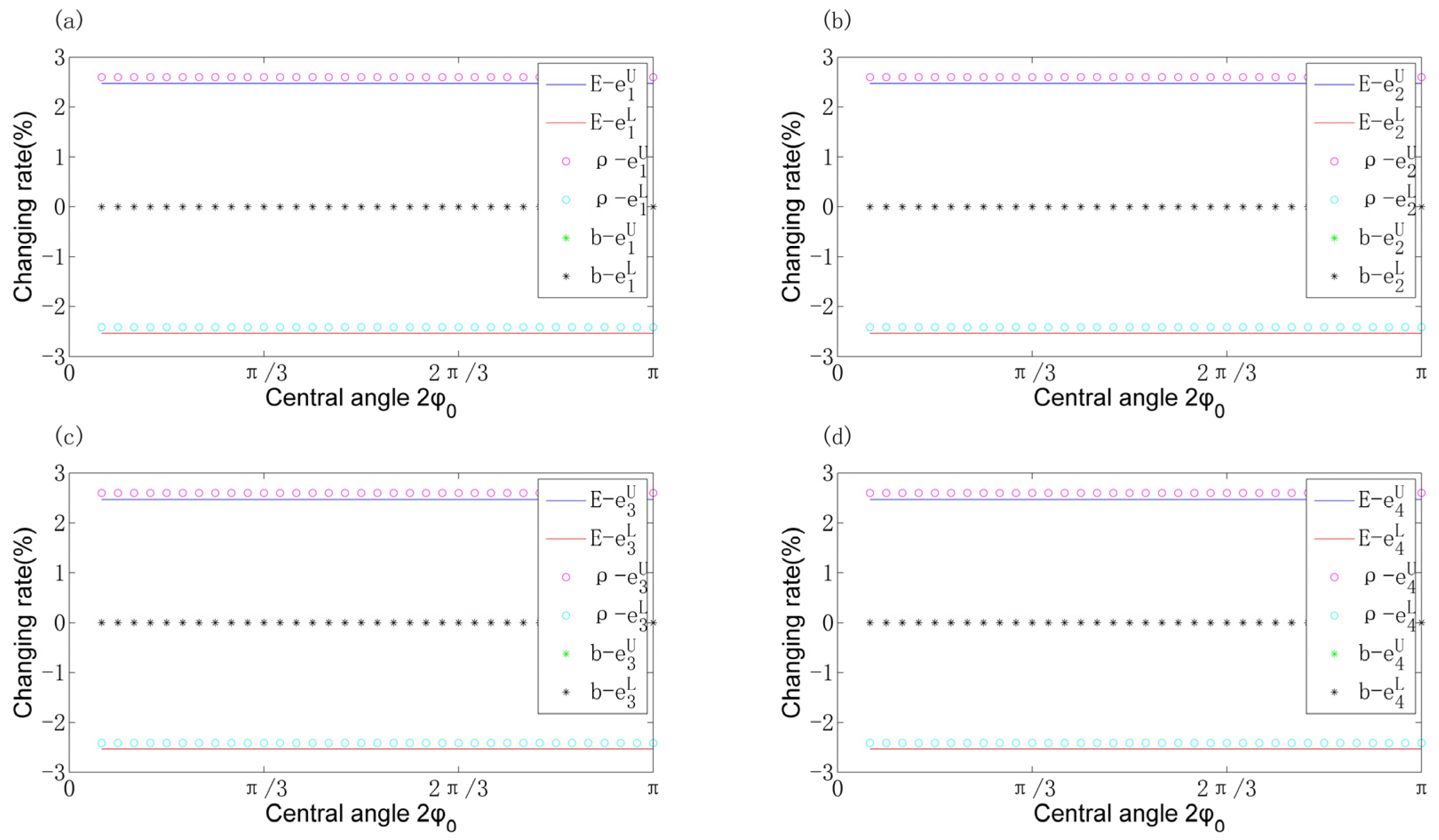
- The influence of most uncertain physical parameters on the natural frequencies exhibits a linear relationship which remains unaffected by variations in radius and central angle. However, different parameters yield distinct rates of change in frequency.
- In the case of multi-dimensional uncertainty, the changing rate of frequencies surpasses that of any individual parameter, as it represents a linear superposition of the combined influence exerted by each parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deraemaeker, A.; Worden, K. A comparison of linear approaches to filter out environmental effect in structural health monitoring. Mech. Syst. Signal Process. 2018, 105, 1–15. [Google Scholar] [CrossRef]
- Haichen, S.; Keith, W.; Elizabeth, J.C. A regime-switching cointegration approach for removing environmental and operational variations in structural health monitoring. Mech. Syst. Signal Process. 2018, 103, 381–397. [Google Scholar]
- Marco, C.; Giulia, C.; Luca, Z.F. System identification via Fast Relaxed Vector Fitting for the Structural Health Monitoring of masonry bridges. Structures 2021, 30, 277–293. [Google Scholar]
- Maes, K.; Van Meerbeeck, L.; Reynders, E.P.B.; Lombaert, G. Validation of vibration-based structural health monitoring on retrofitted railway bridge KW51. Mech. Syst. Signal Process. 2022, 165, 108380. [Google Scholar] [CrossRef]
- Doan, D.; Zenkour, A.; Thom, D. Finite element modeling of free vibration of cracked nanoplates with flexoelectric effects. Eur. Phys. J. Plus 2022, 137, 447. [Google Scholar] [CrossRef]
- Van Do, T.; Hong Doan, D.; Chi Tho, N.; Dinh Duc, N. Thermal buckling analysis of cracked functionally graded plates. Int. J. Struct. Stab. Dyn. 2022, 22, 2250089. [Google Scholar] [CrossRef]
- Ghemari, Z.; Belkhiri, S. Mechanical resonator sensor characteristics development for precise vibratory analysis. Sens. Imaging 2021, 22, 40. [Google Scholar] [CrossRef]
- Ghemari, Z.; Saad, S.; Khettab, K. Improvement of the vibratory diagnostic method by evolution of the piezoelectric sensor performances. Int. J. Precis. Eng. Manuf. 2019, 20, 1361–1369. [Google Scholar] [CrossRef]
- Ghemari, Z. Progression of the vibratory analysis technique by improving the piezoelectric sensor measurement accuracy. Microw. Opt. Technol. Lett. 2018, 60, 2972–2977. [Google Scholar] [CrossRef]
- Ekrem, T.; Oznur, O. Exact solution of free in-plane vibration of a stepped circular arch. J. Sound Vib. 2006, 295, 725–738. [Google Scholar]
- Erasmo, V.; Michele, D.; Francesco, T. Analytical and numerical results for vibration analysis of multi-stepped and multi-damaged circular arches. J. Sound Vib. 2007, 299, 143–163. [Google Scholar]
- Francesco, T.; Erasmo, V. Vibration analysis of spherical structural elements using the GDQ method. Comput. Math. Appl. 2007, 53, 1538–1560. [Google Scholar]
- Erasmo, V.; Francesco, T.; Nicholas, F. Generalized differential quadrature finite element method for cracked composite structures of arbitrary shape. Compos. Struct. 2013, 106, 815–834. [Google Scholar]
- Viola, E.; Rossetti, L.; Fantuzzi, N.; Tornabene, F. Generalized stress-strain recovery formulation applied to functionally graded spherical shells and panels under static loading. Compos. Struct. 2016, 156, 145–164. [Google Scholar] [CrossRef]
- Caliò, I.; Greco, A. Free vibrations of spatial Timoshenko arches. J. Sound Vib. 2014, 333, 4543–4561. [Google Scholar] [CrossRef]
- Moradi, S.; Tavaf, V. Crack detection in circular cylindrical shells using differential quadrature method. Int. J. Press. Vessel. Pip. 2013, 111–112, 209–216. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y. Free vibration analysis of multiple-stepped beams by the differential quadrature element method. Appl. Math. Comput. 2013, 219, 5802–5810. [Google Scholar] [CrossRef]
- Liu, B.; Ferreira, A.J.M.; Xing, Y.F.; Neves, A.M.A. Analysis of functionally graded sandwich and laminated shells using a layerwise theory and a differential quadrature finite element method. Compos. Struct. 2016, 136, 546–553. [Google Scholar] [CrossRef]
- Erasmo, V.; Francesco, T. Vibration analysis of damaged circular arches with varying cross-section. Struct. Durab. Health Monit. 2005, 1, 155–169. [Google Scholar]
- Li, F.; Lu, Z.; Feng, K. Improved chance index and its solutions for quantifying the structural safety degree under twofold random uncertainty. Reliab. Eng. Syst. Saf. 2021, 212, 107635. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, Z.; Jiang, X.; Wei, N.; Zhou, C. Time-dependent structural system reliability analysis model and its efficiency solution. Reliab. Eng. Syst. Saf. 2021, 216, 108029. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Z.; Shi, Y. Aircraft icing safety analysis method in presence of fuzzy inputs and fuzzy state. Aerosp. Sci. Technol. 2018, 82–83, 172–184. [Google Scholar] [CrossRef]
- Li, Z.; Zhong, Z.; Cao, X.; Hou, B.; Li, L. Robustness analysis of shield tunnels in non-uniformly settled strata based on fuzzy set theory. Comput. Geotech. 2023, 162, 105670. [Google Scholar] [CrossRef]
- Bai, Y.C.; Han, X.; Jiang, C.; Bi, R.G. A response-surface-based structural reliability analysis method by using non-probability convex model. Appl. Math. Model. 2014, 38, 3834–3847. [Google Scholar] [CrossRef]
- Xia, Y.; Qiu, Z.; Friswell, M.I. The time response of structures with bounded parameters and interval initial conditions. J. Sound Vib. 2010, 329, 353–365. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, Z. An interval perturbation method for exterior acoustic field prediction with uncertain-but-bounded parameters. J. Fluids Struct. 2014, 49, 441–449. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Chen, L.; Luo, Z. A Chebyshev interval method for nonlinear dynamic systems under uncertainty. Appl. Math. Model. 2013, 37, 4578–4591. [Google Scholar] [CrossRef]
- Wu, J.; Luo, Z.; Zhang, Y.; Zhang, N. An interval uncertain optimization method for vehicle suspensions using Chebyshev metamodels. Appl. Math. Model. 2014, 38, 3706–3723. [Google Scholar] [CrossRef]
- Fu, C.; Lu, K.; Xu, Y.D.; Yang, Y.; Gu, F.S.; Chen, Y. Dynamic analysis of geared transmission system for wind turbines with mixed aleatory and epistemic uncertainties. Appl. Math. Mech. 2022, 43, 275–294. [Google Scholar] [CrossRef]
- Wu, J.; Luo, Z.; Zhang, N.; Zhang, Y. A new interval uncertain optimization method for structures using Chebyshev surrogate models. Comput. Struct. 2015, 146, 185–196. [Google Scholar] [CrossRef]
- Wu, J.; Luo, Z.; Zhang, N.; Zhang, Y. A new uncertain analysis method and its application in vehicle dynamics. Mech. Syst. Signal Process. 2015, 50, 659–675. [Google Scholar] [CrossRef]
- Wu, J.; Luo, Z.; Zhang, Y.; Zhang, N.; Chen, L. Interval uncertain method for multibody mechanical systems using Chebyshev inclusion functions. Int. J. Numer. Methods Eng. 2013, 95, 608–630. [Google Scholar] [CrossRef]
- Feng, J.; Wu, D.; Gao, W.; Li, G. Hybrid uncertain natural frequency analysis for structures with random and interval fields. Comput. Methods Appl. Mech. Eng. 2018, 328, 365–389. [Google Scholar] [CrossRef]
- Wu, D.; Liu, A.; Huang, Y.; Huang, Y.; Pi, Y.; Gao, W. Time dependent uncertain free vibration analysis of composite CFST structure with spatially dependent creep effects. Appl. Math. Model. 2019, 75, 589–606. [Google Scholar] [CrossRef]
- Fu, C.; Ren, X.; Yang, Y.; Lu, K.; Wang, Y. Nonlinear response analysis of a rotor system with a transverse breathing crack under interval uncertainties. Int. J. Non-Linear Mech. 2018, 105, 77–87. [Google Scholar] [CrossRef]
- Fu, C.; Ren, X.; Yang, Y.; Lu, K.; Qin, W. Steady-state response analysis of cracked rotors with uncertain-but-bounded parameters using a polynomial surrogate method. Commun. Nonlinear Sci. Numer. Simul. 2019, 68, 240–256. [Google Scholar] [CrossRef]
- Xiang, W.; Yan, S.; Wu, J.; Niu, W. Dynamic response and sensitivity analysis for mechanical systems with clearance joints and parameter uncertainties using Chebyshev polynomial method. Mech. Syst. Signal Process. 2020, 138, 106596. [Google Scholar] [CrossRef]
- Yanhong, M.A.; Yongfeng, W.A.N.G.; Cun, W.A.N.G.; Jie, H.O.N.G. Interval analysis of rotor dynamic response based on Chebyshev polynomials. Chin. J. Aeronaut. 2020, 33, 2342–2356. [Google Scholar]
- Fu, C.; Sinou, J.J.; Zhu, W.; Lu, K.; Yang, Y. A state-of-the-art review on uncertainty analysis of rotor systems. Mech. Syst. Signal Process. 2023, 183, 109619. [Google Scholar] [CrossRef]
- Donatella, O.; Woula, T. Uniform weighted approximation on the square by polynomial interpolation at Chebyshev nodes. Appl. Math. Comput. 2020, 385, 125457. [Google Scholar]
- Wei, T.; Li, F.; Meng, G.; Li, H. A univariate Chebyshev polynomials method for structural systems with interval uncertainty. Probabilistic Eng. Mech. 2021, 66, 103172. [Google Scholar] [CrossRef]
- Yan, D.; Zheng, Y.; Liu, W.; Chen, T.; Chen, Q. Interval uncertainty analysis of vibration response of hydroelectric generating unit based on Chebyshev polynomial. Chaos Solut. Fractals 2022, 155, 111712. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Z.; Cheng, Y.; Wang, L. An efficient method for estimating failure probability bound functions of composite structure under the random-interval mixed uncertainties. Compos. Struct. 2022, 298, 116011. [Google Scholar] [CrossRef]

| Description | Value |
|---|---|
| Cross-sectional width b | 0.06 m |
| Cross-sectional height h | 0.08 m |
| Density of mass ρ | 7860 kg/m3 |
| Young’s modulus E | 2.1 × 1011 pa |
| Poisson’s coefficient ν | 0.3 |
| Shear factor κ0 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Z.; Ren, X.; Yang, Y.; Fu, C.; Zhao, J. Free Vibration Analysis of Arches with Interval-Uncertain Parameters. Appl. Sci. 2023, 13, 12391. https://doi.org/10.3390/app132212391
Nie Z, Ren X, Yang Y, Fu C, Zhao J. Free Vibration Analysis of Arches with Interval-Uncertain Parameters. Applied Sciences. 2023; 13(22):12391. https://doi.org/10.3390/app132212391
Chicago/Turabian StyleNie, Zhihua, Xingmin Ren, Yongfeng Yang, Chao Fu, and Jiepeng Zhao. 2023. "Free Vibration Analysis of Arches with Interval-Uncertain Parameters" Applied Sciences 13, no. 22: 12391. https://doi.org/10.3390/app132212391
APA StyleNie, Z., Ren, X., Yang, Y., Fu, C., & Zhao, J. (2023). Free Vibration Analysis of Arches with Interval-Uncertain Parameters. Applied Sciences, 13(22), 12391. https://doi.org/10.3390/app132212391







