Iterative Equalization and Decoding over an Additive White Gaussian Noise Channel with ISI Using Low-Density Parity-Check Codes
Abstract
:1. Introduction
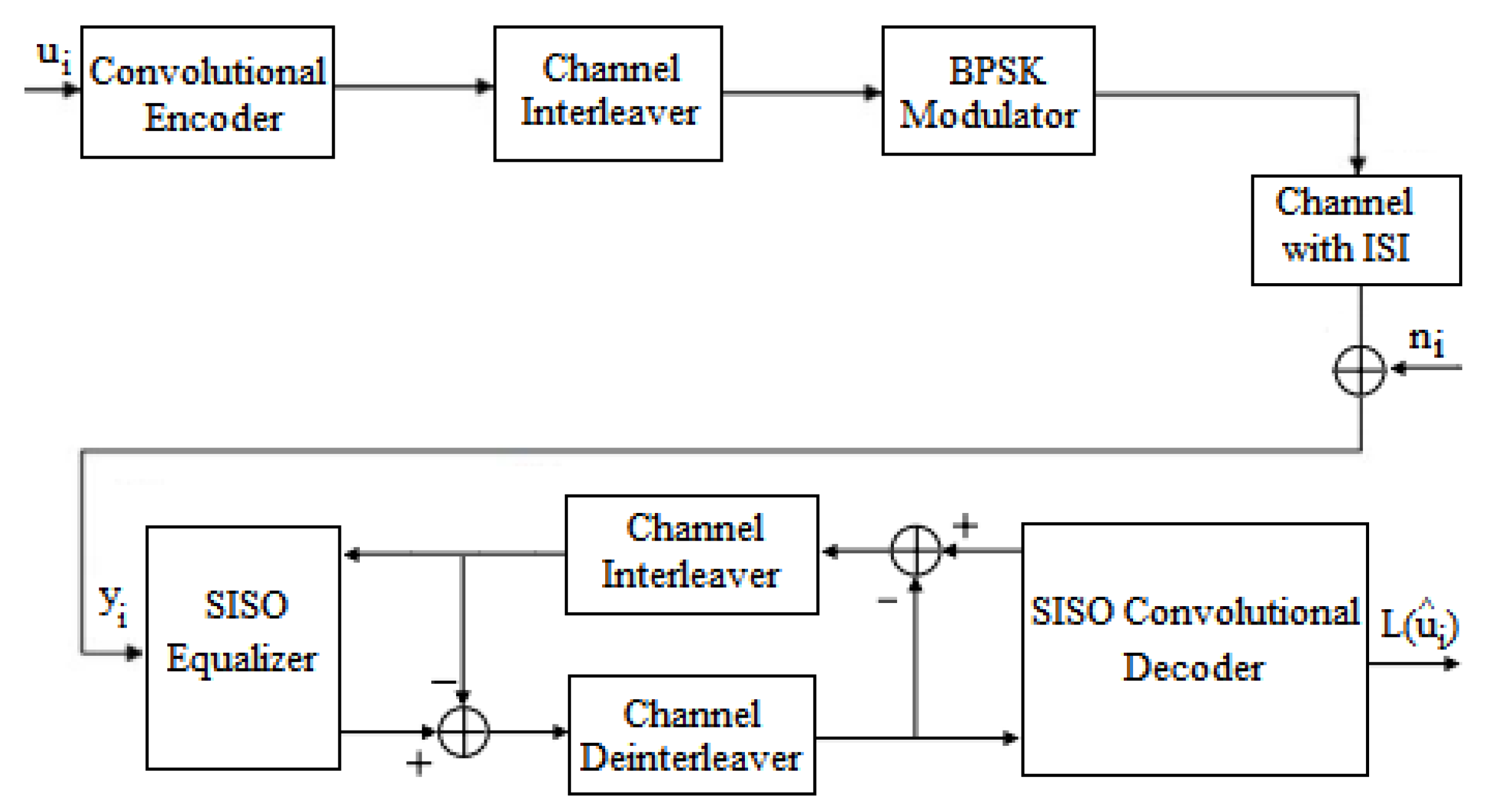
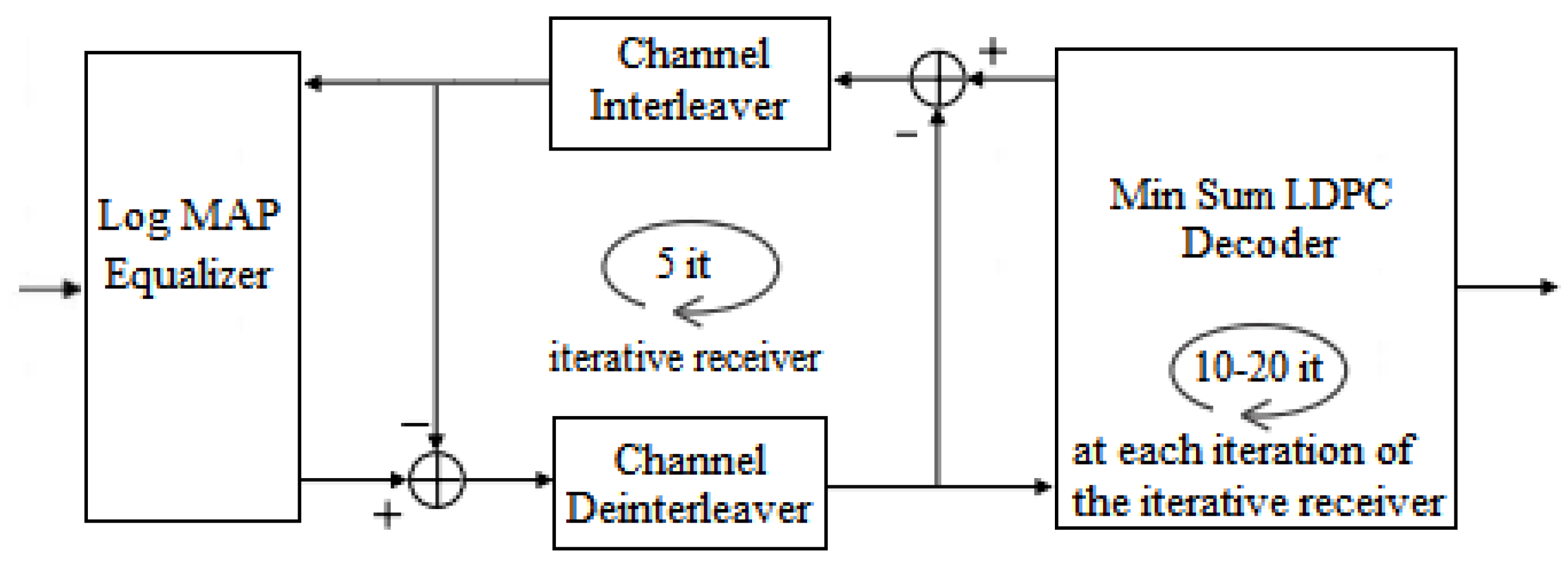
- We proposed a system, respecting the classic turbo equalization scheme, to fix the errors introduced by ISI over an AWGN channel. However, for transmission, we utilized LDPC coding. At reception, we used a system consisting of a Log-MAP equalizer and min-sum LDPC decoding, which differs from the existing systems;
- Then, the functional analysis of the proposed system was realized, depending on the number of iterations within the iterative process of equalization and decoding or the number of iterations within the LDPC decoder. The proposed system demonstrated the effectiveness of the equalizer in terms of BER vs. SNR;
- Then, taking three impulse responses’ h functions as mentioned in Section 4.3 and Section 5, the performances in terms of BER vs. SNR of the proposed system were compared. These performances differed depending on the h function that was used;
2. Related Work
3. Turbo Equalization Concept
3.1. The Basic Architecture of the Iterative Receiver Using the Turbo Principle
4. Methods for Achieving the Iterative Process of Equalization and Decoding Concerning the Proposed System
4.1. Log-MAP Equalizer
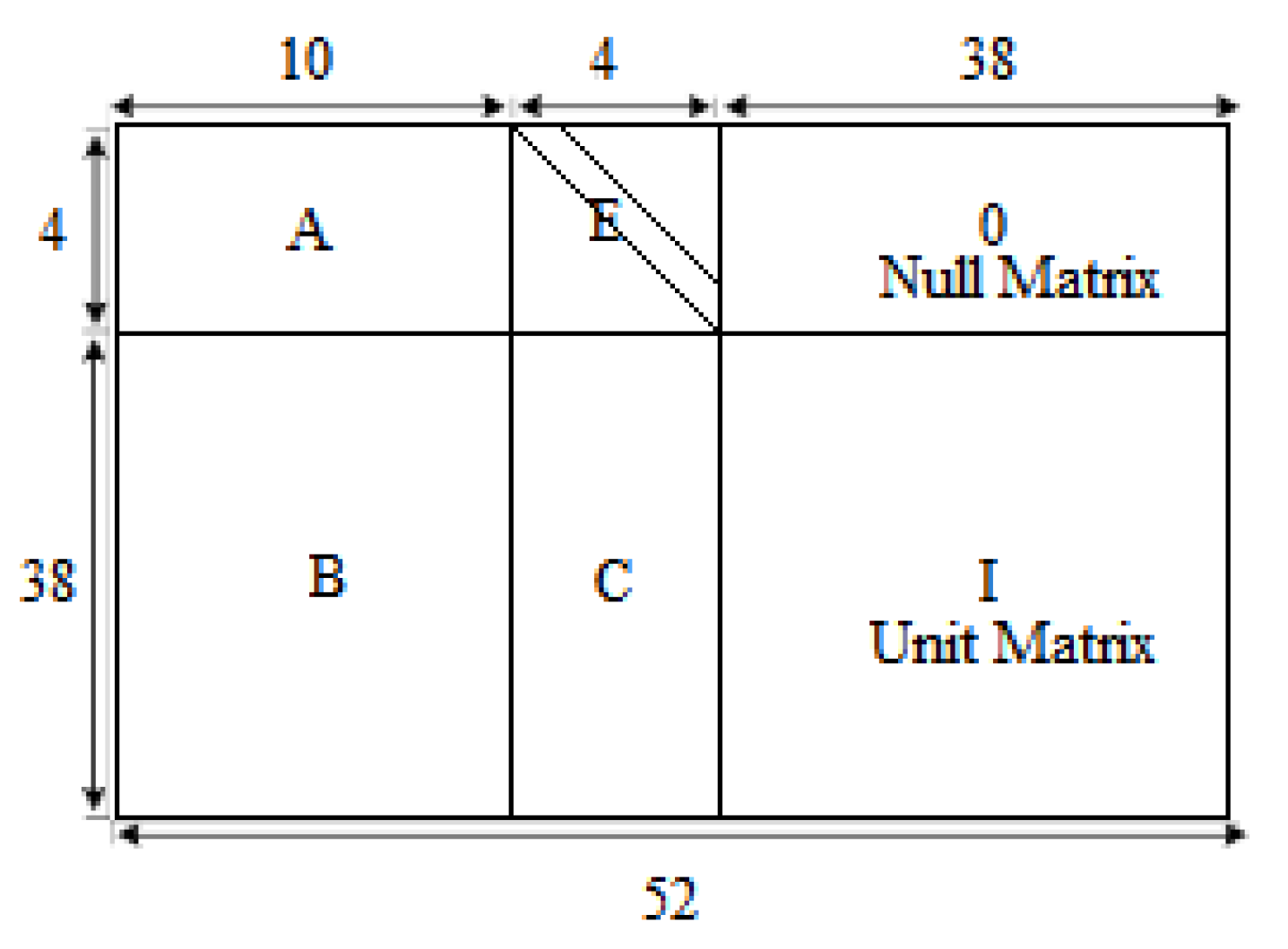
4.2. LDPC Codes
4.3. The Proposed System Model
5. Simulation Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Berrou, C. Codes and Turbo Codes, 1st ed.; Springer: Paris, France, 2010; pp. 359–412. [Google Scholar]
- Wang, L.; Qiao, P.; Liang, J.; Chen, T.; Wang, X.; Yang, G. Accurate Channel Estimation and Adaptive Underwater Acoustic Communications Based on Gaussian Likelihood and Constellation Aggregation. Sensors 2022, 22, 2142. [Google Scholar] [CrossRef] [PubMed]
- Yeap, B.L.; Hanzo, L. Reduced complexity I/Q turbo detection for space-time trellis-coded systems. IEEE Trans. Veh. Technol. 2004, 53, 1278–1286. [Google Scholar] [CrossRef]
- Douillard, C.; Picart, A.; Jézéquel, M.; Didier, P.; Berrou, C.; Glavieux, A. Iterative correction of intersymbol interference: Turbo-equalization. Eur. Trans. Commun. 1995, 6, 507–511. [Google Scholar] [CrossRef]
- Hanzo, L.; Liew, T.H.; Yeap, B.L.; Tee, R.Y.S.; Ng, S.X. Turbo Coding, Turbo Equalisation and Space-Time Coding: EXIT-Chart-Aided Near-Capacity Designs for Wireless Channels, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2011; pp. 253–384. [Google Scholar]
- Sahin, S.; Cipriano, A.M.; Poulliat, C.; Boucheret, M.-L. Iterative Decision Feedback Equalization Using Online Prediction. IEEE Access 2020, 8, 23638–23649. [Google Scholar] [CrossRef]
- Pan, Z.; Xie, C.; Wang, H.; Wei, Y.; Guo, D. Blind Turbo Equalization of Short CPM Bursts for UAV-Aided Internet of Things. Sensors 2022, 22, 6508. [Google Scholar] [CrossRef]
- Huang, X.; Cho, J.; Hashemizadeh, K.; Chen, R.-R. Extrinsic Neural Network Equalizer for Channels with High Inter-Symbol-Interference. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Xiamen, China, 28–30 July 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Yuan, Z.D.; Liu, F.; Guo, Q.H.; Wang, Z. Message passing based detection for orthogonal time frequency space modulation. ZTE Commun. 2021, 19, 34–44. [Google Scholar]
- Bahl, L.R.; Cocke, J.; Jelinek, F.; Raviv, J. Optimal decoding of linear codes for minimizing symbol error rate. IEEE Trans. Inf. Theory 1974, 20, 284–287. [Google Scholar] [CrossRef]
- Barry, J. Equalization. In Academic Press Library in Mobile and Wireless Communications Transmission Techniques for Digital Communications, 1st ed.; Wilson, K., Biglieri, E., Wilson, S.G., Eds.; Academic Press: Cambridge, MA, USA, 2016; pp. 283–331. [Google Scholar]
- Liu, H.; Zhang, L. Faster than Nyquist Signaling with Spatial Coupling; Tryckeriet i E-huset, Lund: Lund, Sweden, 2022. [Google Scholar]
- Cuc, A.-M.; Morgoș, F.L.; Grava, C. Performance Analysis of Turbo Codes, LDPC Codes, and Polar Codes over an AWGN Channel in the Presence of Inter Symbol Interference. Sensors 2023, 23, 1942. [Google Scholar] [CrossRef]
- Cuc, A.-M.; Morgoș, F.L.; Grava, C. Performances Analysis of Turbo Codes, LDPC Codes and Polar Codes using AWGN channel with and without Inter Symbol Interference. In Proceedings of the 2022 International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 10–11 November 2022; IEEE: New York, NY, USA, 2022; pp. 1–4. [Google Scholar]
- Shao, S.; Hailes, P.; Wang, T.Y.; Wu, J.Y.; Maunder, R.G.; Al-Hashimi, B.M.; Hanzo, L. Survey of Turbo, LDPC, and Polar Decoder ASIC Implementations. IEEE Commun. Surv. Tutor. 2019, 21, 2309–2333. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, T.; Han, C. Soft Decision Decoding with Cyclic Information Set and the Decoder Architecture for Cyclic Codes. Electronics 2023, 12, 2693. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiao, Y.; Yang, P.; Dong, B.; Hanzo, L. Joint Iterative Channel Estimation and Frequency-Domain Turbo Equalization for Single-Carrier Spatial Modulation. IEEE Trans. Commun. 2019, 67, 6327–6342. [Google Scholar] [CrossRef]
- Glavieux, A.; Laot, C.; Labat, J. Turbo-équalization over a frequency selective channel. In Proceedings of the International Symposium on Turbo Codes and Related Topics, Brest, France, 3–5 September 1997; Volume 962102, pp. 96–101. [Google Scholar]
- Tüchler, M.; Singer, A.C.; Koetter, R. Minimum mean squared error equalization using a priori information. IEEE Trans. Signal Process. 2002, 50, 673–683. [Google Scholar] [CrossRef]
- Laot, C.; Bidan, R.L.; Leroux, D. Low-Complexity MMSE Turbo Equalization: A Possible Solution for EDGE. IEEE Trans. Wirel. Commun. 2005, 4, 965–974. [Google Scholar] [CrossRef]
- Tüchler, M.; Singer, A.C. Turbo equalization: An overview. IEEE Trans. Inf. Theory 2011, 57, 920–952. [Google Scholar] [CrossRef]
- Dong, P.; Xiang, X.; Liang, Y.; Wang, P. A Block-Based Concatenated LDPC-RS Code for UAV-to-Ground SC-FDE Communication Systems. Electronics 2023, 12, 3143. [Google Scholar] [CrossRef]
- Li, H.; Yu, Q. Doubly-Iterative Sparsified MMSE Turbo Equalization for OTFS Modulation. IEEE Trans. Commun. 2023, 71, 1336–1351. [Google Scholar] [CrossRef]
- Yu, L.; Zhao, J.; Xu, W.; Liu, H. Design of Sparse FIR Decision Feedback Equalizers in MIMO Systems Using Hybrid l1/l2 Norm Minimization and the OMP Algorithm. Sensors 2018, 18, 1860. [Google Scholar] [CrossRef]
- Şahin, S.; Cipriano, A.M.; Poulliat, C.; Boucheret, M.-L. Iterative Equalization With Decision Feedback Based on Expectation Propagation. IEEE Trans. Commun. 2018, 66, 4473–4487. [Google Scholar]
- Plascencia, E.; Guan, H.; Chassagne, L.; Căilean, A.-M.; Barrois, O.; Shagdar, O. Addressing Multi-User Interference in Vehicular Visible Light Communications: A Brief Survey and an Evaluation of Optical CDMA MAC Utilization in a Multi-Lane Scenario. Sensors 2023, 23, 3831. [Google Scholar] [CrossRef]
- Altalbe, A.; Tahir, M. Performance of Iterative Coded CDMA Receivers with APP Feedback: A Use of a Weighted Delay Filter. Appl. Sci. 2023, 13, 9175. [Google Scholar] [CrossRef]
- Khittiwitchayakul, S.; Phakphisut, W.; Supnithi, P. Integer programming-based non-uniform window decoding schedules for spatially coupled low-density parity-check codes. IET Commun. 2022, 16, 2019–2035. [Google Scholar] [CrossRef]
- Fang, Y.; Han, G.; Cai, G.; Lau, F.C.M.; Chen, P.; Guan, Y.L. Design Guidelines of Low-Density Parity-Check Codes for Magnetic Recording Systems. IEEE Commun. Surv. Tutor. 2018, 20, 1574–1606. [Google Scholar] [CrossRef]
- Matar, M.O.; Jana, M.; Mitra, J.; Lampe, L.; Lis, M. A Turbo Maximum-a-Posteriori Equalizer for Faster-than-Nyquist Applications. In Proceedings of the 2020 IEEE 28th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Fayetteville, AR, USA, 3–6 May 2020; pp. 167–171. [Google Scholar]
- Mishra, K. Study & Simulation of MMSE IC-LE Turbo Equalization Scheme Using Block (BCH) Turbo Codes. 2006. Available online: https://www.semanticscholar.org/paper/STUDY-%26-SIMULATION-OF-MMSE-IC-LE-TURBO-EQUALIZATION-Mishra/6754173f1a471f536088fe03f1fc2d5b3184198b (accessed on 16 January 2023).
- Bauch, G.; Khorram, H.; Hagenauer, J. Iterative equalization and decoding in mobile communications systems. TG FACHBERICHT 1997, 145, 307–312. [Google Scholar]
- Naranjo, M.Á.P.; Gil Jiménez, V.P. CCSDS 131.2-B-1 Serial Concatenated Convolutional Turbo Decoder Architecture for Efficient FPGA Implementation. IEEE Access 2023, 11, 7698–7713. [Google Scholar] [CrossRef]
- Ye, Z. Traitement Statistique de L’information et du Signal Pour L’internet des Objets Sous-Marins; Institut Polytechnique: Paris, France, 2021. [Google Scholar]
- Cao, A.; Zhang, L.; Qiao, J.; He, Y. An LLR-Based Segmented Flipped SCL Decoding Algorithm for Polar Codes. In Proceedings of the 2019 IEEE/CIC International Conference on Communications in China (ICCC), Changchun, China, 11–13 August 2019; pp. 724–729. [Google Scholar]
- Dörner, S.; Clausius, J.; Cammerer, S.; Brink, S.T. Learning Joint Detection, Equalization and Decoding for Short-Packet Communications. IEEE Trans. Commun. 2023, 71, 837–850. [Google Scholar] [CrossRef]
- Charles-Darby, K.; Carrasco-Alvarez, R.; Parra-Michel, R. Complexity Reduction of MLSE and MAP Equalizers Using Modified Prolate Basis Expansion. Electronics 2019, 8, 1333. [Google Scholar] [CrossRef]
- Li, X.; Wu, J.; Heng, W.; Huang, Y. Iterative Receiver Design for Probabilistic Constellation Shaping in ISI Channel. IEEE Access 2020, 8, 210478–210489. [Google Scholar] [CrossRef]
- Le, V.H.S. Conception des Turbocodes à Très Haut-Débit; L’école Nationale Superieure Mines-Telecom Atlantique: Pays de la Loire, France, 2021. [Google Scholar]
- Islam, N.S. LDPC Codes Incorporating Source, Noise, and Channel Memory; Jacobs University: Bremen, Germany, 2022. [Google Scholar]
- Nguyen, T.T.B.; Nguyen Tan, T.; Lee, H. Efficient QC-LDPC Encoder for 5G New Radio. Electronics 2019, 8, 668. [Google Scholar] [CrossRef]
- Multiplexing and Channel Coding. Document TS 38.212 V17.3.0, 3GPP. 2022. Available online: https://www.etsi.org/deliver/etsi_ts/138200_138299/138212/17.03.00_60/ts_138212v170300p.pdf (accessed on 16 January 2023).
- Petrović, V.L.; El Mezeni, D.M.; Radošević, A. Flexible 5G New Radio LDPC Encoder Optimized for High Hardware Usage Efficiency. Electronics 2021, 10, 1106. [Google Scholar] [CrossRef]
- Yun, I.; Lee, H.; Kim, J.T. An Alternative Approach Obtaining a Normalization Factor in Normalized Min-Sum Algorithm for Low-Density Parity-Check Code. Wirel. Commun. Mob. Comput. 2018, 2018, 1398191:1–1398191:7. [Google Scholar] [CrossRef]
- Shrinidhi, J.; Sri Krishna, P.; Yamuna, B.; Pargunarajan, K. Modified Min Sum Decoding Algorithm for Low Density Parity Check Codes. Procedia Comput. Sci. 2020, 171, 2128–2316. [Google Scholar] [CrossRef]
- Chen, R.; Chen, L. Dual Threshold Self-Corrected Minimum Sum Algorithm for 5G LDPC Decoders. Information 2020, 11, 355. [Google Scholar] [CrossRef]
- Morgoș, F.L. Contribuţii Privind Îmbunătăţirea Tehnicilor de Egalizare ale Canalelor Radio; Politehnica: Timisoara, Romania, 2014. [Google Scholar]
- Hanzo, L.; Liew, T.H.; Yeap, B.L.; Tee, R.Y.S.; Ng, S.X. Turbo Equalisation. In Turbo Coding, Turbo Equalisation and Space–Time Coding for Transmission over Fading Channels, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2002; pp. 553–697. [Google Scholar]
- Gunnam, K.K.; Choi, G.S. Low Density Parity Check Decoder for Regular LDPC Codes. U.S. Patent US 8,656,250 B2, 18 February 2014. Available online: https://hdl.handle.net/1969.1/177060 (accessed on 13 June 2023).
- Kumar, D.D.; Selvakumari, R.S. Performance analysis of Min-Sum based LDPC decoder architecture for 5G new radio standards. Mater. Today Proc. 2022, 62, 4965–4972. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, M.; Chen, J.; Wang, J. High Performance Channel Decoders on CELL Broadband Engine for WiMAX System. Majlesi J. Electr. Eng. 2011, 5, 21–31. [Google Scholar] [CrossRef]
- Jiang, Y.; Kim, H.; Asnani, H.; Kannan, S.; Oh, S.; Viswanath, P. Turbo Autoencoder: Deep learning based channel codes for point-to-point communication channels. Neural Inf. Process. Syst. 2019, 248, 2758–2768. [Google Scholar]
- D3.3—Report on Link-Level Simulation Performance Final Results. Available online: https://ec.europa.eu/research/participants/documents/downloadPublic?documentIds=080166e5d3175eca&appId=PPGMS (accessed on 15 May 2023).


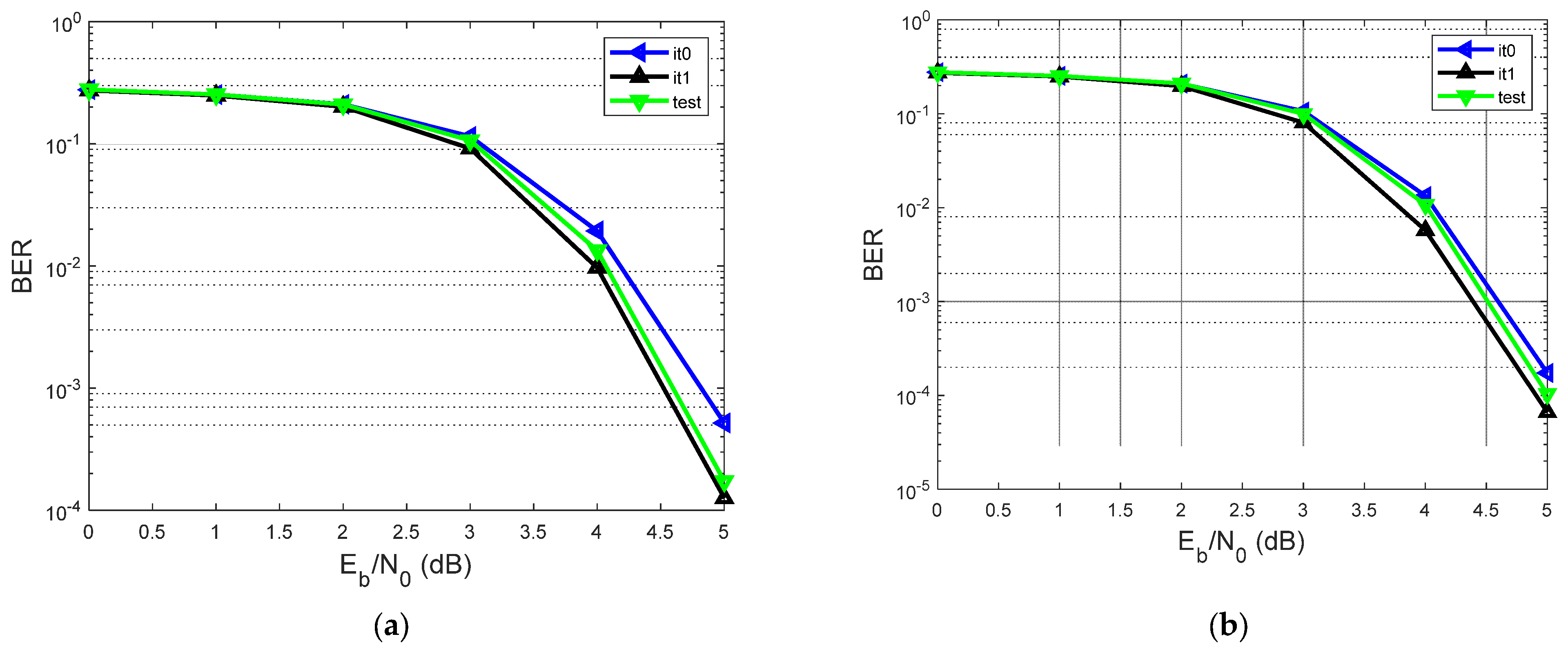
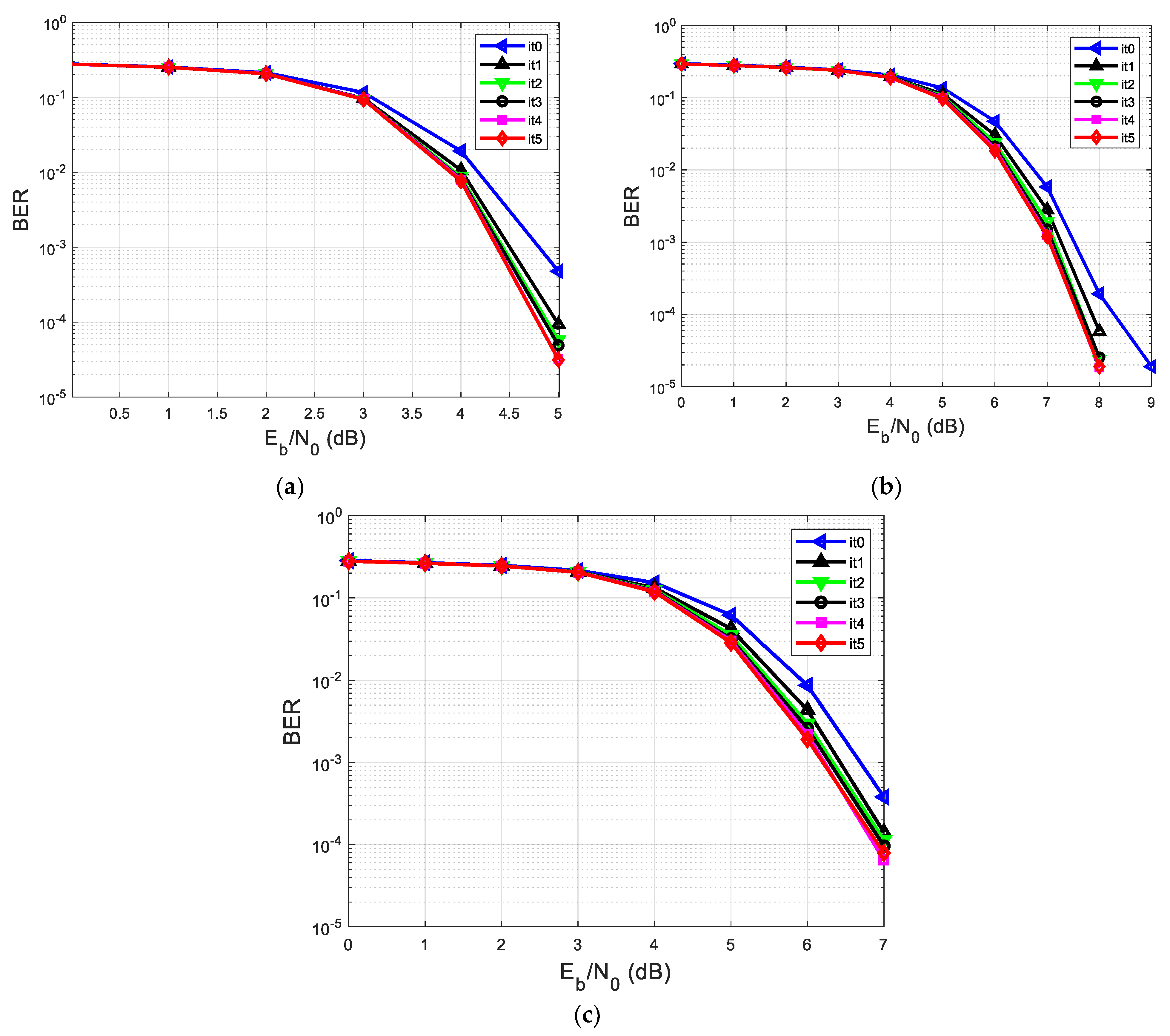
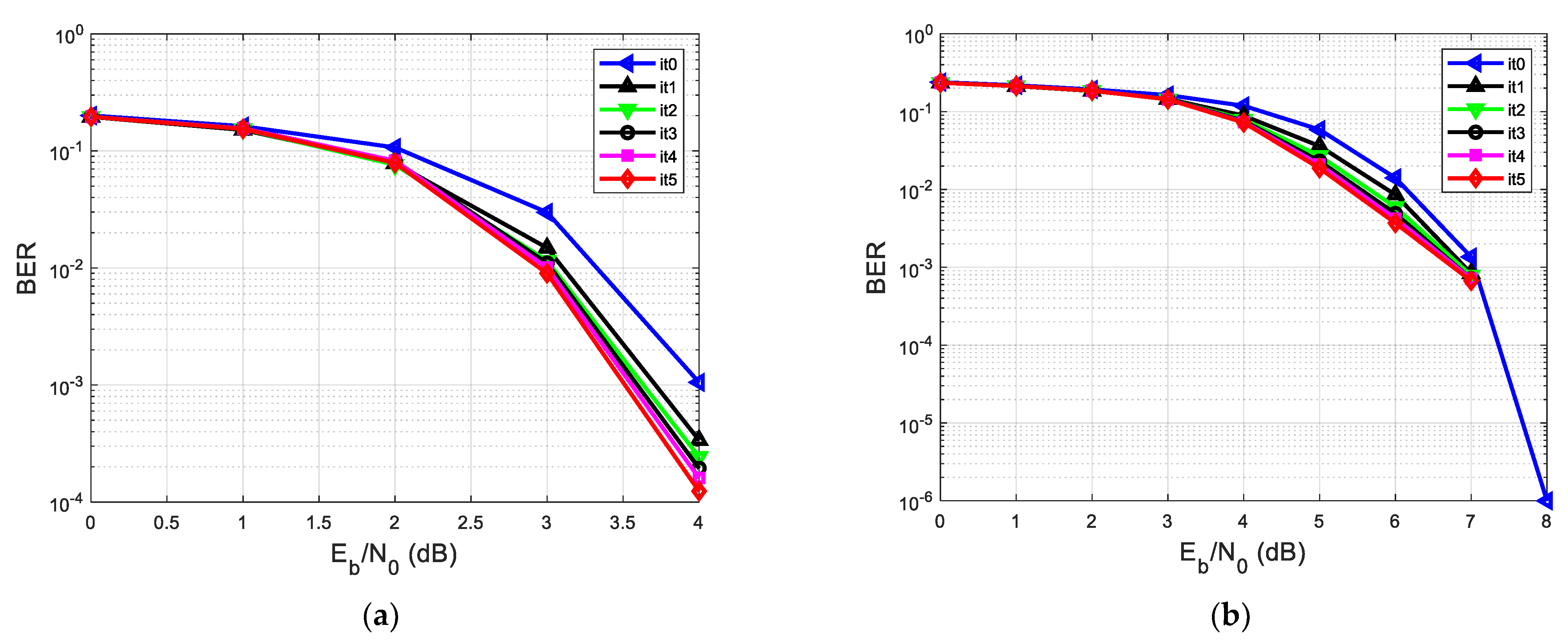
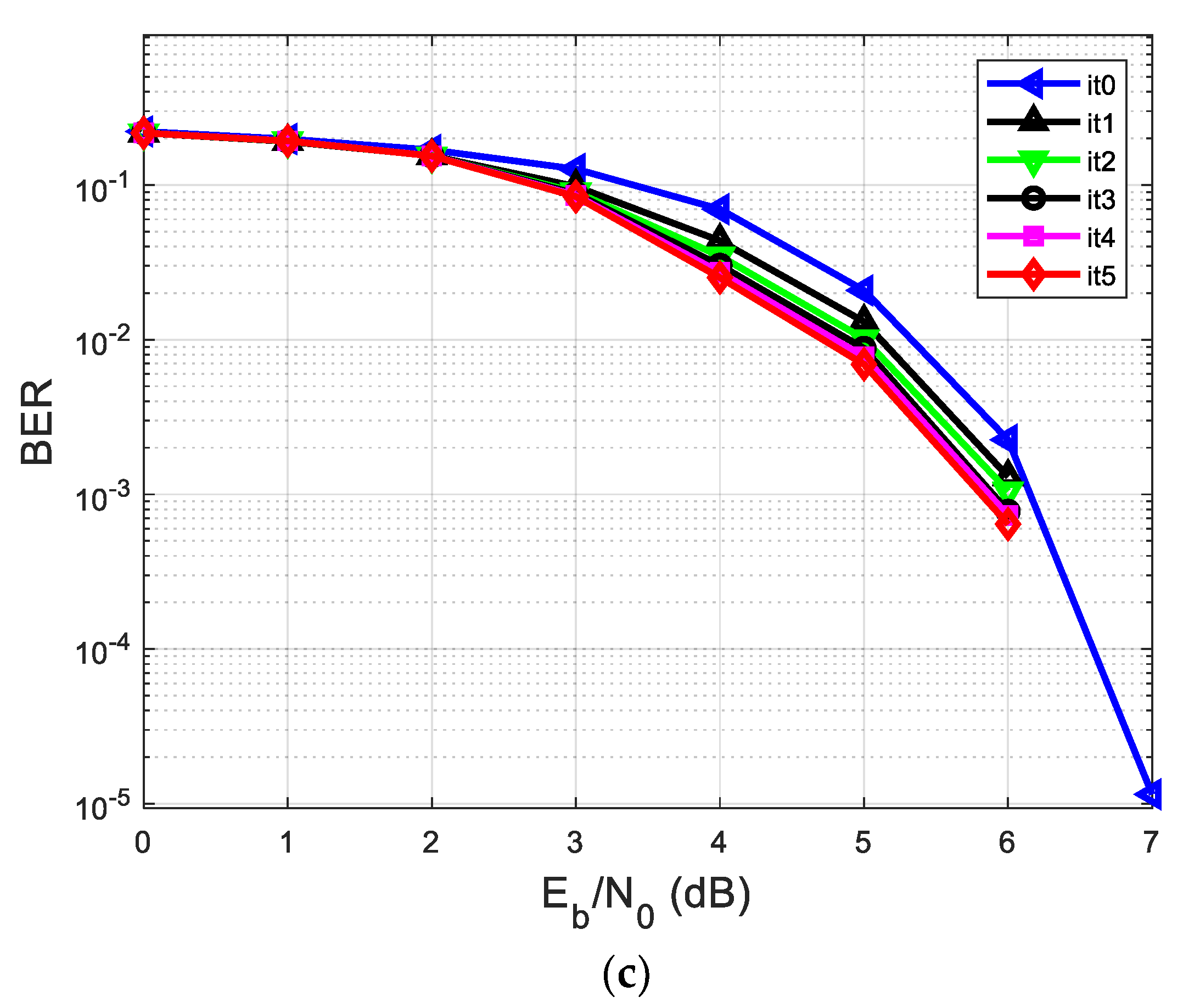
| A. Analyzing the Contribution of the Log-MAP Equalizer of the Proposed System in Terms of BER vs. SNR, Considering h1 = [0.18 0.85 0.32] | |||||
| Graphic/Scenario | Iterative Receiver | Min-Sum LDPC Decoder | |||
| Figure 6a/1st Scenario | 2 iterations (it0 and it1) | 10 iterations at each iteration it0 and it1 | |||
| Figure 6a/2nd Scenario | 1 iteration (test) | 20 iterations | |||
| Figure 6b/1st Scenario | 2 iterations (it0 and it1) | 20 iterations at each iteration it0 and it1 | |||
| Figure 6b/2nd Scenario | 1 iteration (test) | 40 iterations | |||
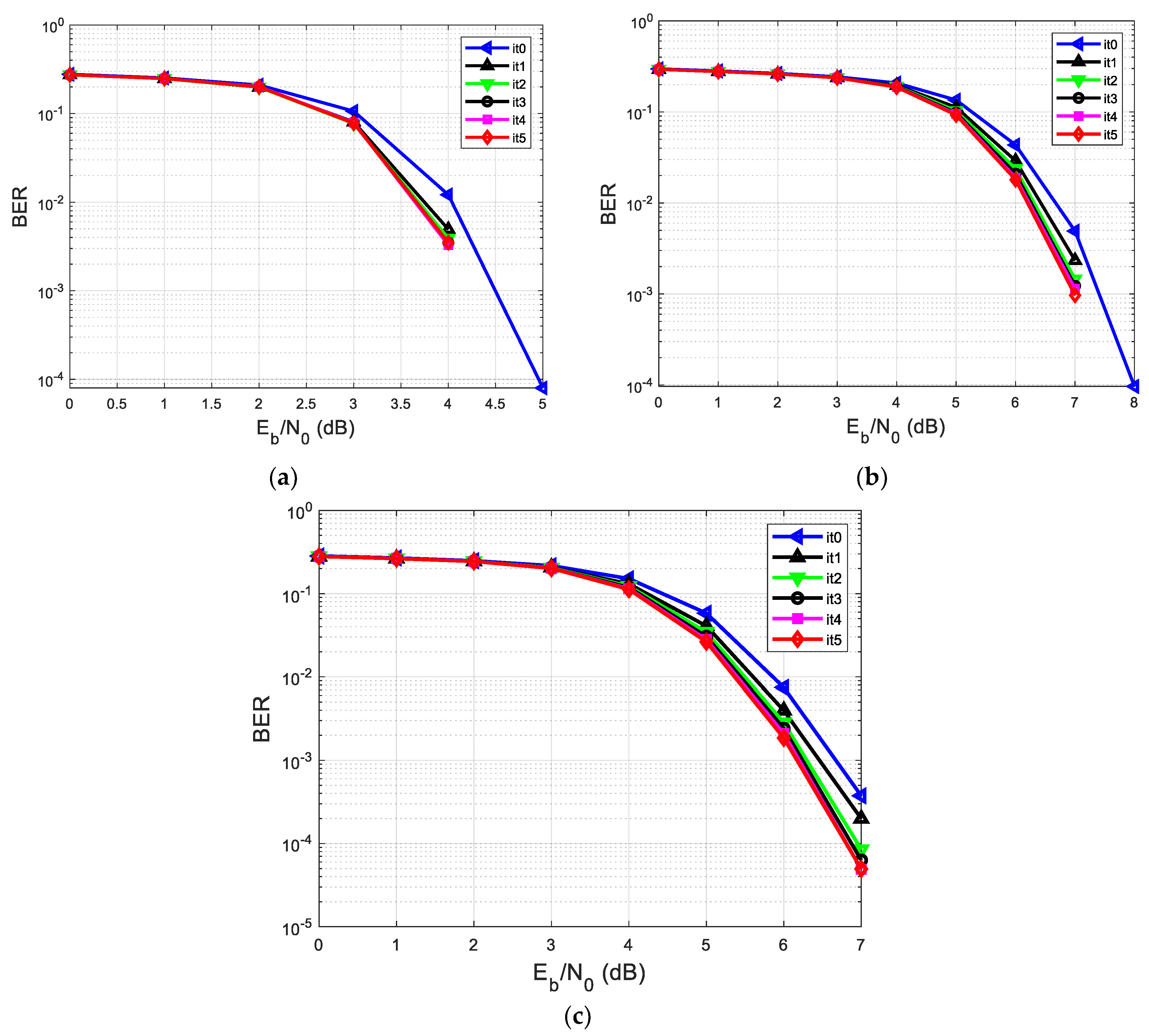
| B. Analyzing the performances in terms of BER vs. SNR of the proposed system, considering different h’s | |||||
| Graphic | Iterative Receiver | Min-Sum LDPC Decoder | h | ||
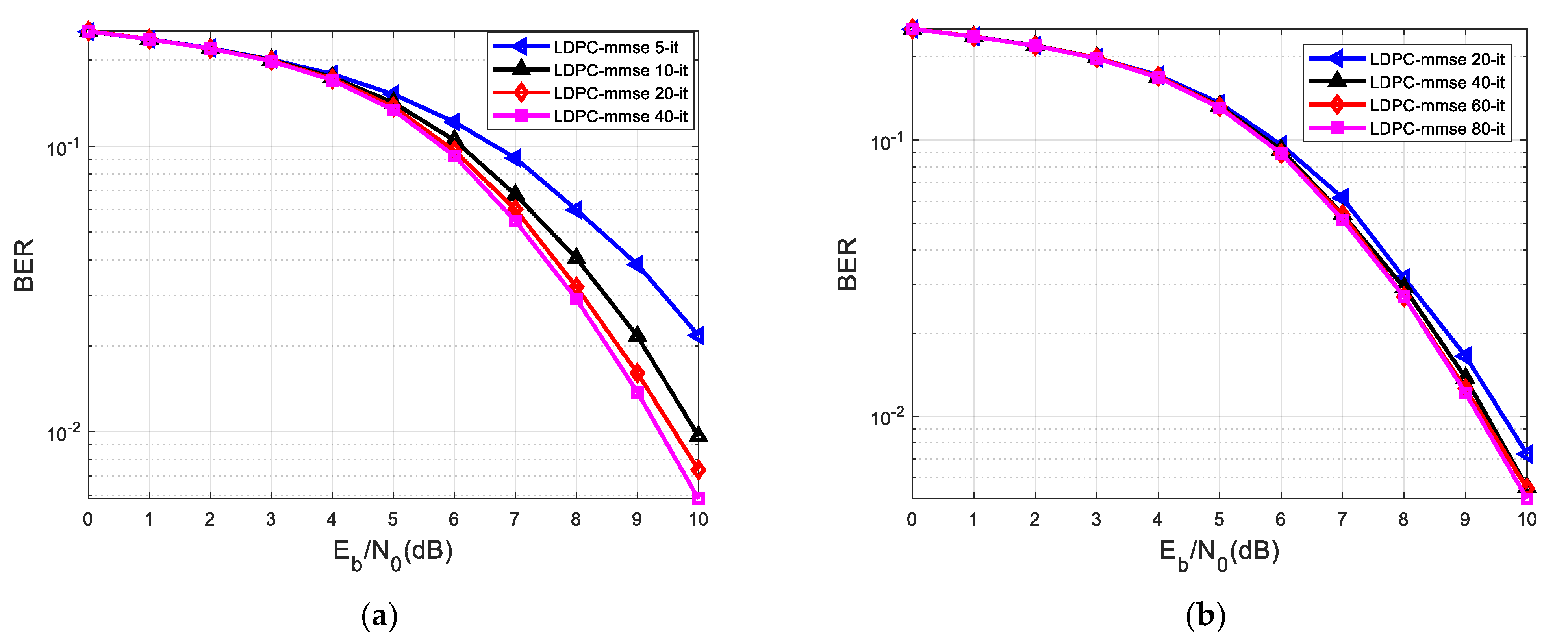
| Figure 7a | 5 iterations | 10 iterations | h1 = [0.18 0.85 0.32] | ||
| Figure 7b | 5 iterations | 10 iterations | h2 = [0.302 0.725 0.456] | ||
| Figure 7c | 5 iterations | 10 iterations | h3 = [0.407 0.815 0.407] | ||
| Figure 8a | 5 iterations | 20 iterations | h1 = [0.18 0.85 0.32] | ||
| Figure 8b | 5 iterations | 20 iterations | h2 = [0.302 0.725 0.456] | ||
| Figure 8c | 5 iterations | 20 iterations | h3 = [0.407 0.815 0.407] | ||
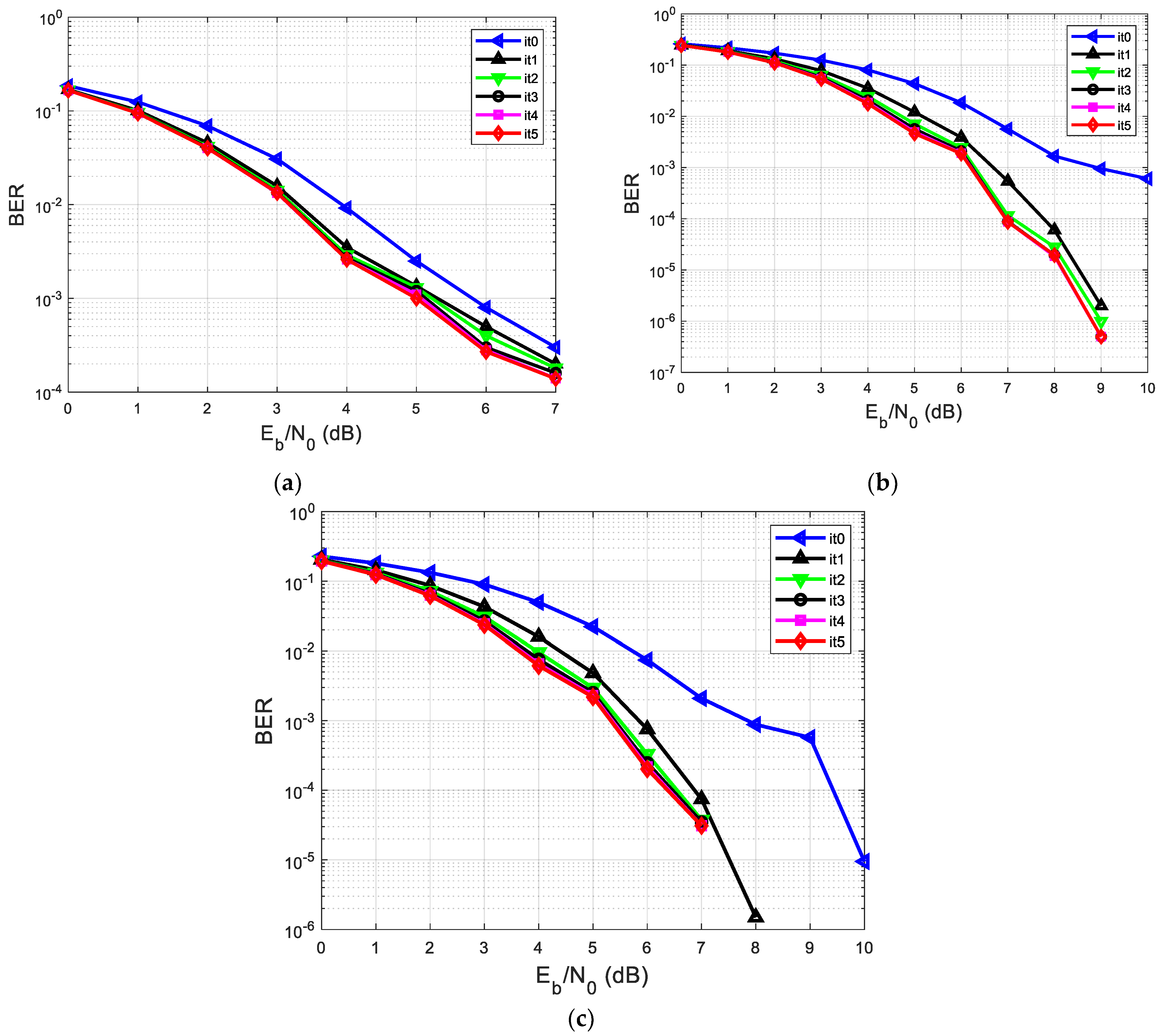
| C. The proposed system was analyzed by comparing its performance in terms of BER vs. SNR with two other equalization and decoding systems. | |||||
| C1. The BER vs. SNR performance of the first system using classic turbo equalization, considering different h’s | |||||
| Graphic | Turbo equalization process | h | |||
| Figure 9a | 5 iterations | h1 = [0.18 0.85 0.32] | |||
| Figure 9b | 5 iterations | h2 = [0.302 0.725 0.456] | |||
| Figure 9c | 5 iterations | h3 = [0.407 0.815 0.407] | |||
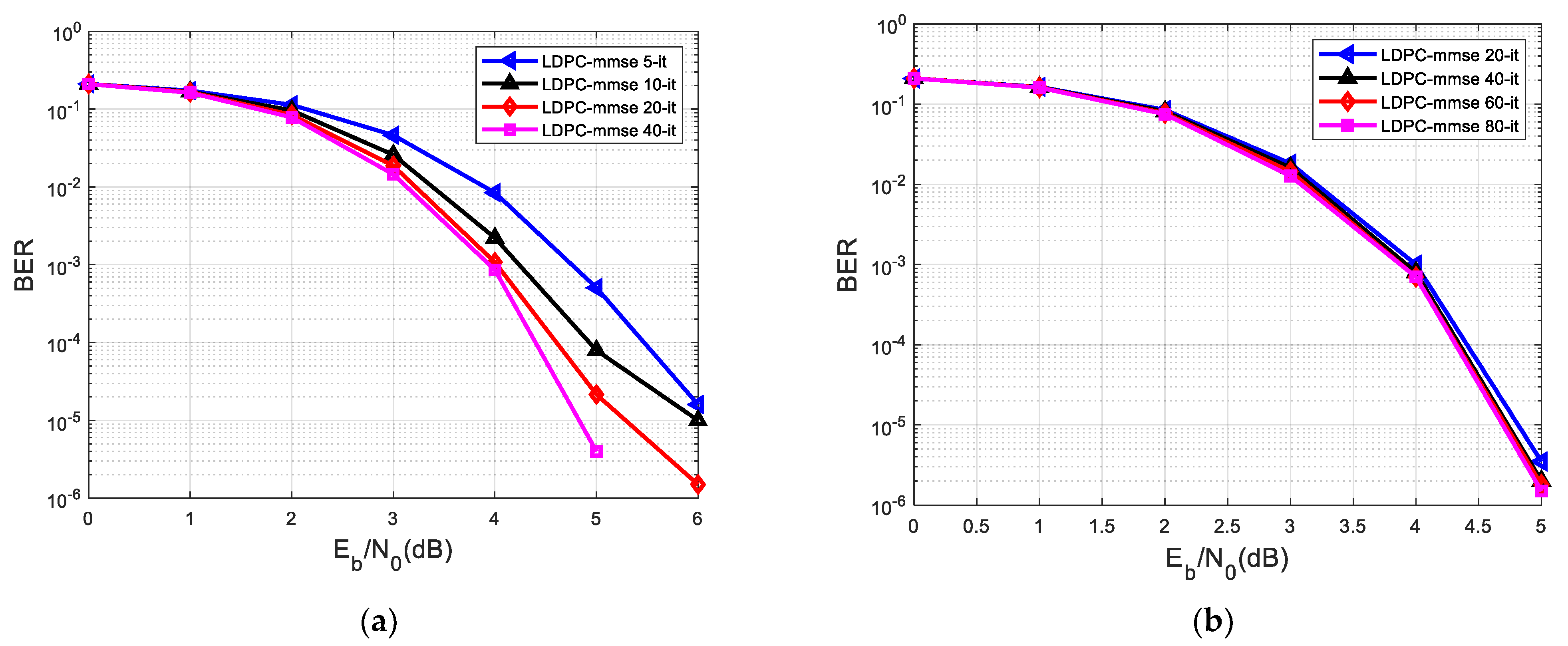
| C2. The BER vs. SNR performance of the second system in which the equalization was performed separately before the decoding process using MMSE equalizer and LDPC decoder, considering different h’s | |||||
| Graphic | LDPC decoder | h | |||
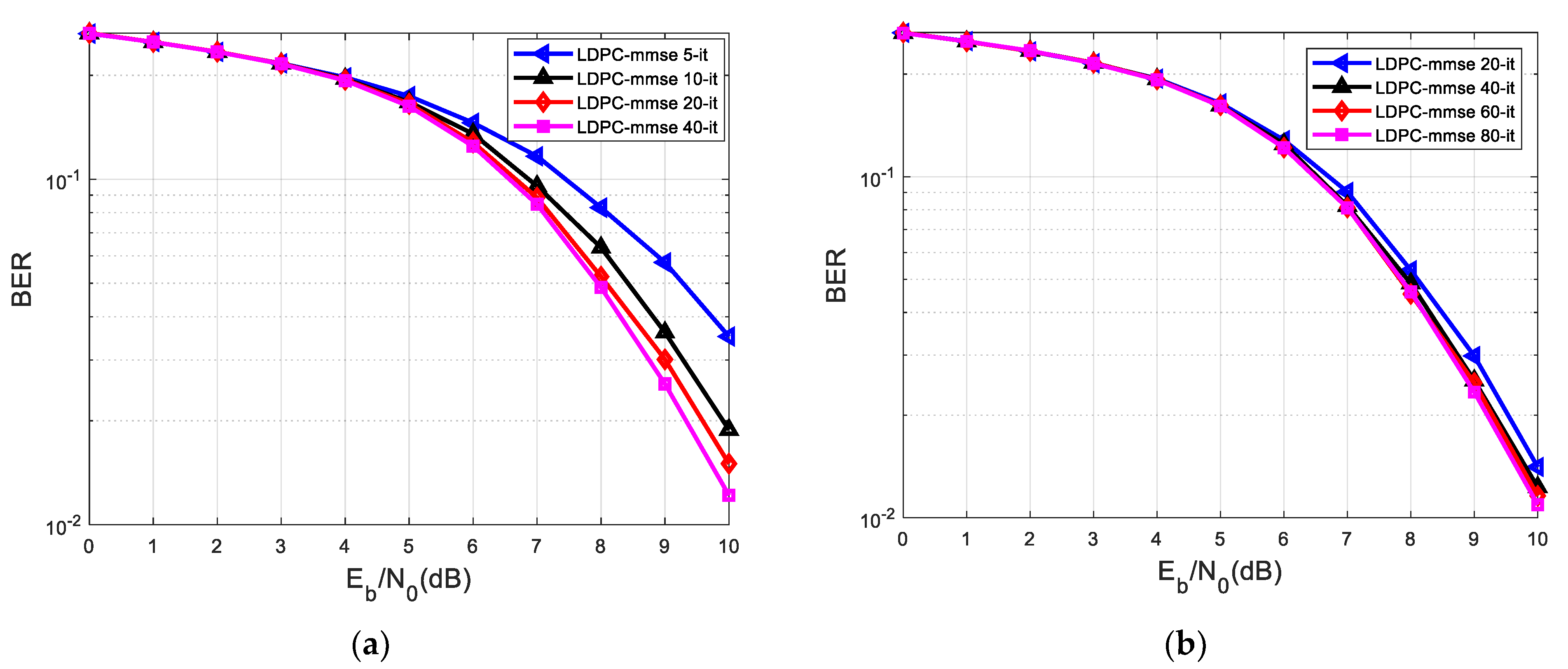
| Figure 10a | 40 iterations | h1 = [0.18 0.85 0.32] | |||
| Figure 10b | 80 iterations | h1 = [0.18 0.85 0.32] | |||
| Figure 11a | 40 iterations | h2 = [0.302 0.725 0.456] | |||
| Figure 11b | 80 iterations | h2 = [0.302 0.725 0.456] | |||
| Figure 12a | 40 iterations | h3 = [0.407 0.815 0.407] | |||
| Figure 12b | 80 iterations | h3 = [0.407 0.815 0.407] | |||
| D. Analyzing the performances in terms of BER vs. SNR of the proposed system, considering different h’s, when it was not punctured the first 2Zc bits (deviating from the standard) | |||||
| Graphic | Iterative Receiver | Min-Sum LDPC Decoder | h | ||
| Figure 13a | 5 iterations | 20 iterations | h1 = [0.18 0.85 0.32] | ||
| Figure 13b | 5 iterations | 20 iterations | h2 = [0.302 0.725 0.456] | ||
| Figure 13c | 5 iterations | 20 iterations | h3 = [0.407 0.815 0.407] | ||
| 5 it in the Iterative Process of Equalization and Decoding, 10 it in the LDPC Decoder | ||
| Graphic | h | BER (Range) |
| Figure 7a | h1 = [0.18 0.85 0.32] | 10−4–10−5 |
| Figure 7b | h2 = [0.302 0.725 0.456] | 10−1 |
| Figure 7c | h3 = [0.407 0.815 0.407] | 10−1–10−2 |
| 5 it in the iterative process of equalization and decoding, 20 it in the LDPC decoder | ||
| Graphic | h | BER (range) |
| Figure 8a | h1 = [0.18 0.85 0.32] | 0 |
| Figure 8b | h2 = [0.302 0.725 0.456] | 10−1–10−2 |
| Figure 8c | h3 = [0.407 0.815 0.407] | 10−1–10−2 |
| Turbo Equalization with 5 it. | ||
| Graphic | h | BER (Range) |
| Figure 9a | h1 = [0.18 0.85 0.32] | 10−3 |
| Figure 9b | h2 = [0.302 0.725 0.456] | 10−2–10−3 |
| Figure 9c | h3 = [0.407 0.815 0.407] | 10−2–10−3 |
| Separate MMSE equalization and LDPC decoding with 40 it. | ||
| Graphic | h | BER (range) |
| Figure 10a | h1 = [0.18 0.85 0.32] | 10−5–10−6 |
| Figure 11a | h2 = [0.302 0.725 0.456] | 100–10−1 |
| Figure 12a | h3 = [0.407 0.815 0.407] | 100–10−1 |
| Separate MMSE equalization and LDPC decoding with 80 it. | ||
| Graphic | h | BER (range) |
| Figure 10b | h1 = [0.18 0.85 0.32] | 10−5–10−6 |
| Figure 11b | h2 = [0.302 0.725 0.456] | 100–10−1 |
| Figure 12b | h3 = [0.407 0.815 0.407] | 100–10−1 |
| 5 it in the Iterative Process of Equalization and Decoding, 20 it in the LDPC Decoder | ||
| Graphic | h | BER (Range) |
| Figure 8a | h1 = [0.18 0.85 0.32] | 0 |
| Figure 8b | h2 = [0.302 0.725 0.456] | 10−1–10−2 |
| Figure 8c | h3 = [0.407 0.815 0.407] | 10−1–10−2 |
| Turbo equalization with 5 it. | ||
| Graphic | h | BER (range) |
| Figure 9a | h1 = [0.18 0.85 0.32] | 10−3 |
| Figure 9b | h2 = [0.302 0.725 0.456] | 10−2–10−3 |
| Figure 9c | h3 = [0.407 0.815 0.407] | 10−2–10−3 |
| Separate MMSE equalization and LDPC decoding with 40 it. | ||
| Graphic | h | BER (range) |
| Figure 10a | h1 = [0.18 0.85 0.32] | 10−5–10−6 |
| Figure 11a | h2 = [0.302 0.725 0.456] | 100–10−1 |
| Figure 12a | h3 = [0.407 0.815 0.407] | 100–10−1 |
| Separate MMSE equalization and LDPC decoding with 80 it. | ||
| Graphic | h | BER (range) |
| Figure 10b | h1 = [0.18 0.85 0.32] | 10−5–10−6 |
| Figure 11b | h2 = [0.302 0.725 0.456] | 100–10−1 |
| Figure 12b | h3 = [0.407 0.815 0.407] | 100–10−1 |
| Puncturing the First 2Zc Bits | ||
| Graphic | h | BER (Range) |
| Figure 8a | h1 = [0.18 0.85 0.32] | 0 |
| Figure 8b | h2 = [0.302 0.725 0.456] | 10−1–10−2 or (1/2 × 10−1) |
| Figure 8c | h3 = [0.407 0.815 0.407] | 10−1–10−2 |
| Not puncturing the first 2Zc bits | ||
| Graphic | h | BER (range) |
| Figure 13a | h1 = [0.18 0.85 0.32] | 0 |
| Figure 13b | h2 = [0.302 0.725 0.456] | 10−1–10−2 or (1/9 × 10−1) |
| Figure 13c | h3 = [0.407 0.815 0.407] | 10−2–10−3 |
| BER vs. SNR in an ISI Channel, at the SNR of 5 dB, Comparing the Proposed System to Others Published in the Literature | ||
| 1st Comparison | h | BER (Range) |
| The proposed system-5 it in the iterative process of equalization and decoding, 10 it in the LDPC decoder. | h1 = [0.18 0.85 0.32] | 10−4–10−5(1/8 × 10−4) |
| The proposed system-5 it in the iterative process of equalization and decoding, 20 it in the LDPC decoder. | h1 = [0.18 0.85 0.32] | 0 |
| The MAP turbo equalizer implemented in [1] performs 10 iterations. | h = [0.227 0.460 0.688 0.460 0.227] | 10−4 |
| 2nd comparison | h | BER (range) |
| The proposed system-5 it in the iterative process of equalization and decoding, 20 it in the LDPC decoder. | h1 = [0.18 0.85 0.32] | 0 |
| The MAP turbo equalizer implemented in [8] performs 6 iterations. | h = [0.227 0.460 0.688 0.460 0.227] | 10−3–10−4 |
| 3rd comparison | h | BER (range) |
| The proposed system-5 it in the iterative process of equalization and decoding, 20 it in the LDPC decoder. | h1 = [0.18 0.85 0.32] | 0 |
| The implemented system in [28] designed with cooperative decoding between a BCJR detector and the spatially coupled low-density parity-check decoder performs 5 iterations. | h = [1 1] | 10−4–10−5 (1/7 × 10−4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuc, A.-M.; Morgoș, F.L.; Grava, A.-M.; Grava, C. Iterative Equalization and Decoding over an Additive White Gaussian Noise Channel with ISI Using Low-Density Parity-Check Codes. Appl. Sci. 2023, 13, 12294. https://doi.org/10.3390/app132212294
Cuc A-M, Morgoș FL, Grava A-M, Grava C. Iterative Equalization and Decoding over an Additive White Gaussian Noise Channel with ISI Using Low-Density Parity-Check Codes. Applied Sciences. 2023; 13(22):12294. https://doi.org/10.3390/app132212294
Chicago/Turabian StyleCuc, Adriana-Maria, Florin Lucian Morgoș, Adriana-Marcela Grava, and Cristian Grava. 2023. "Iterative Equalization and Decoding over an Additive White Gaussian Noise Channel with ISI Using Low-Density Parity-Check Codes" Applied Sciences 13, no. 22: 12294. https://doi.org/10.3390/app132212294
APA StyleCuc, A.-M., Morgoș, F. L., Grava, A.-M., & Grava, C. (2023). Iterative Equalization and Decoding over an Additive White Gaussian Noise Channel with ISI Using Low-Density Parity-Check Codes. Applied Sciences, 13(22), 12294. https://doi.org/10.3390/app132212294








