The Ultimate Strength of Fully Transparent Pressure-Resistant Spherical Cabins
Abstract
1. Introduction
2. Material Properties
2.1. Specimens and Test Procedure
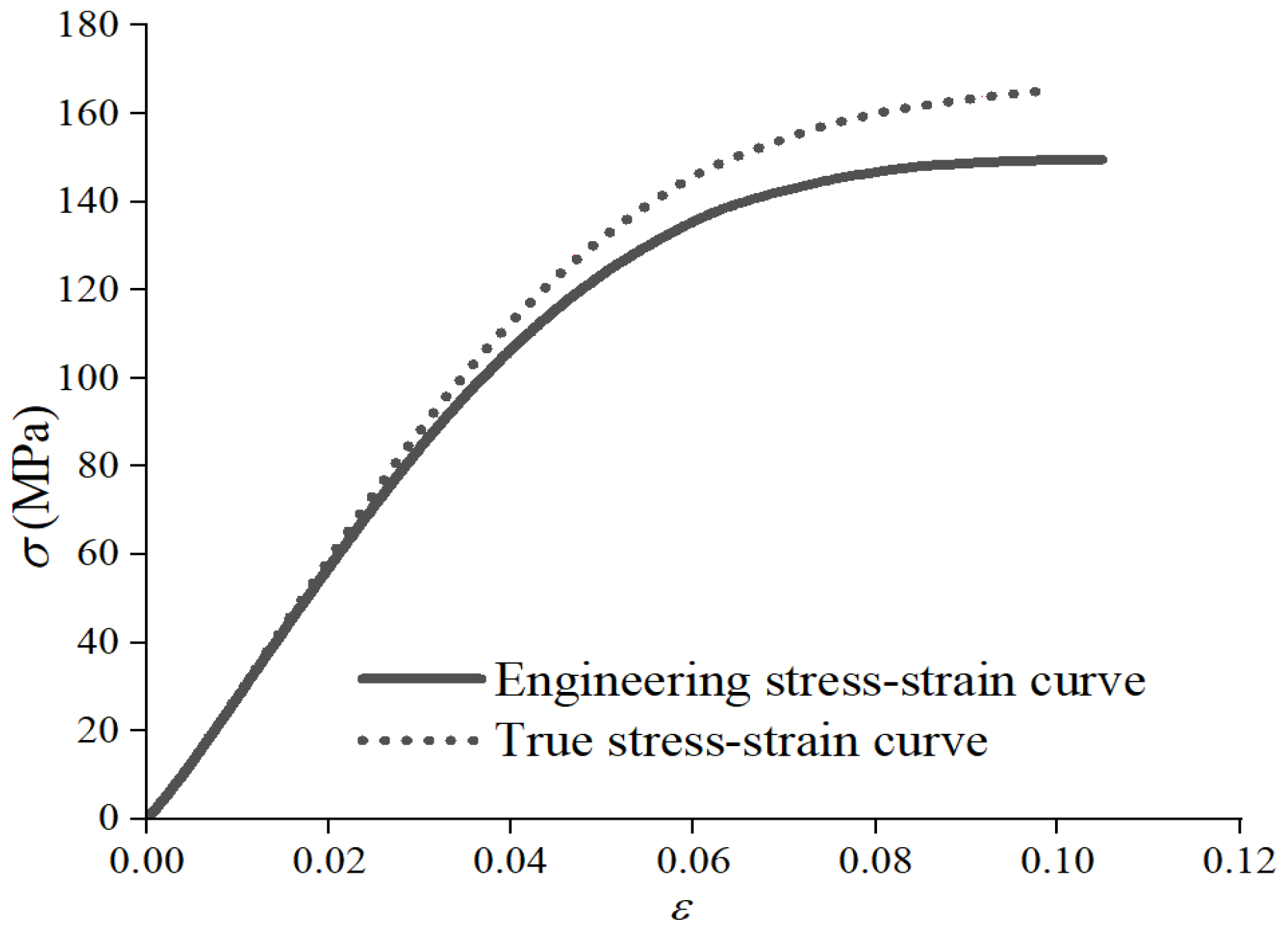
2.2. Material Test Results
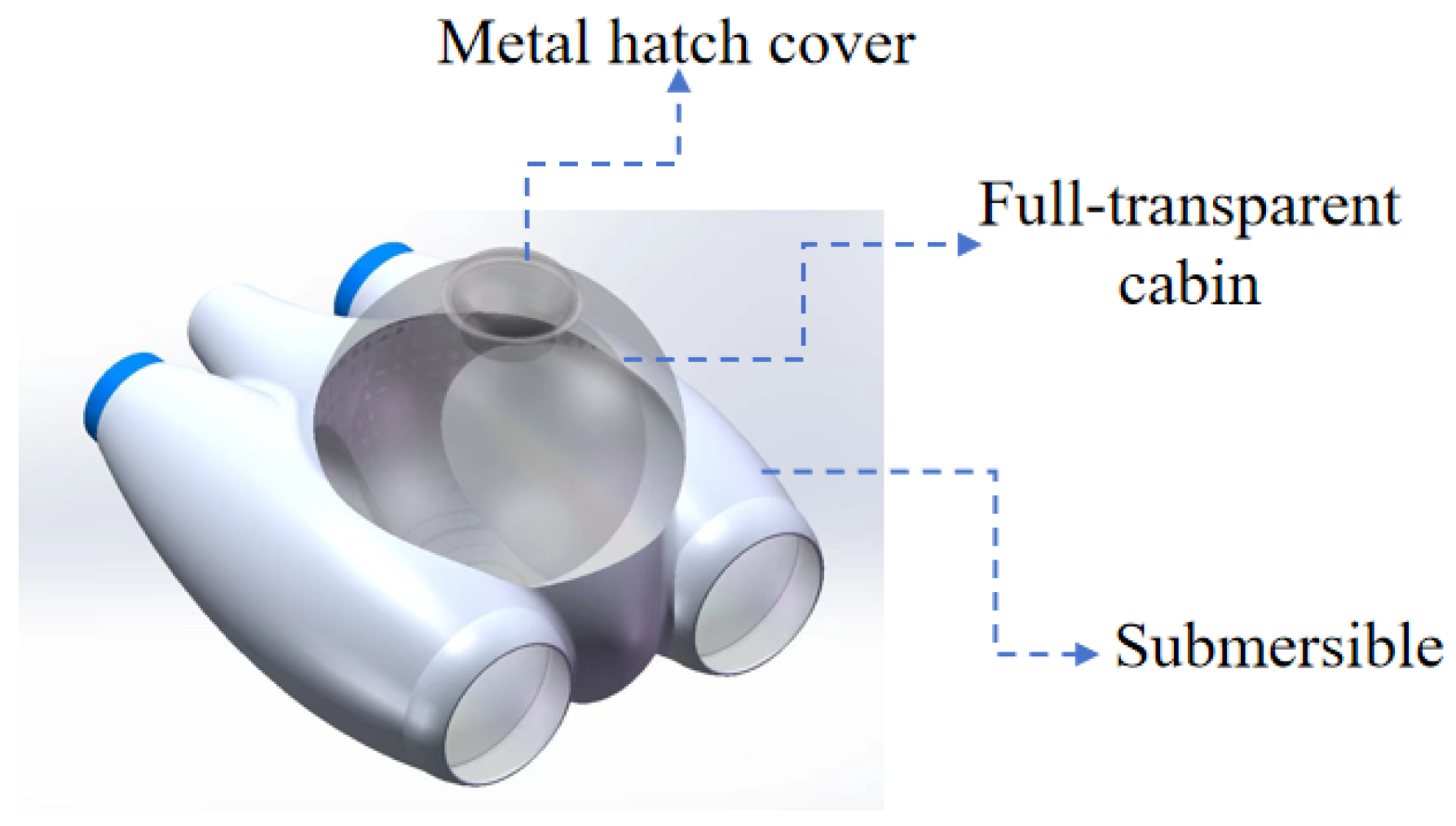
3. Ultimate Strength of PMMA Spherical Cabin
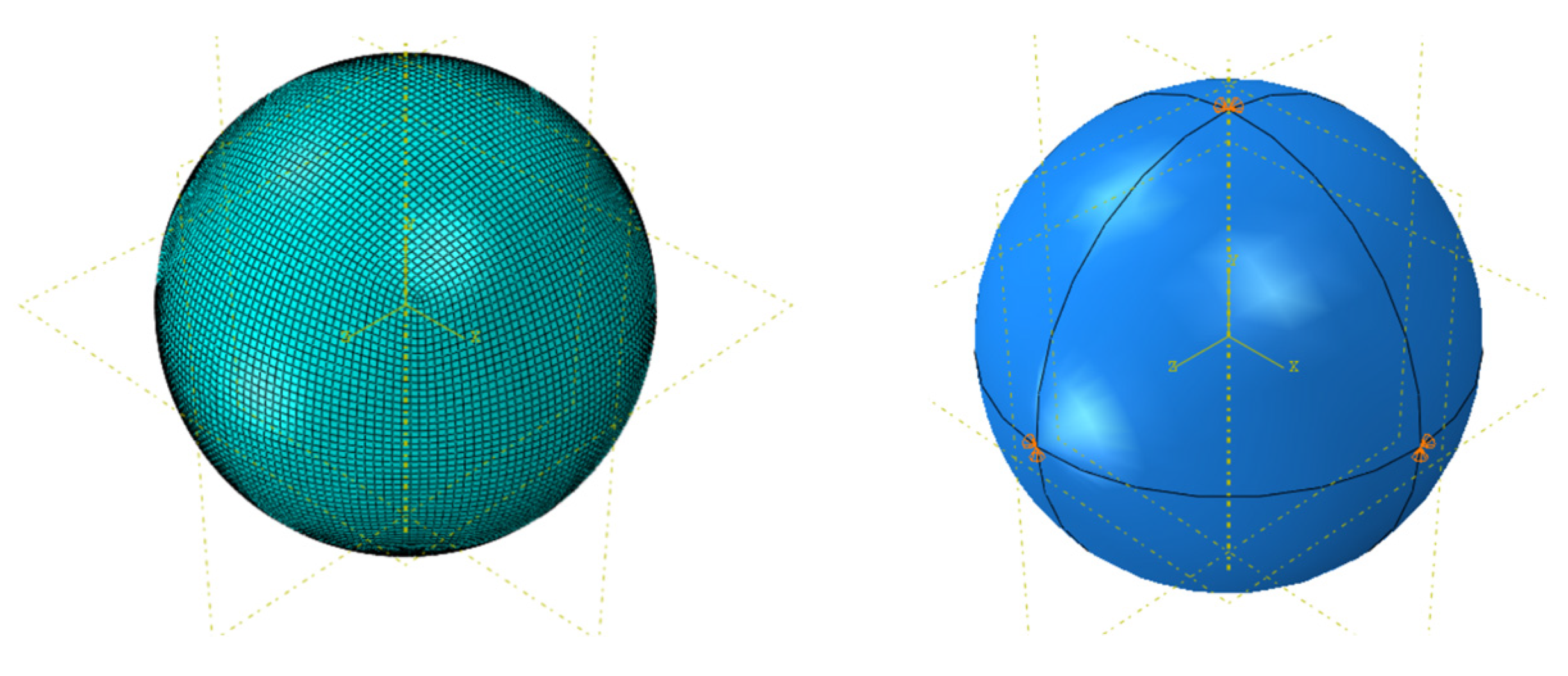
3.1. Intact Spherical Cabin
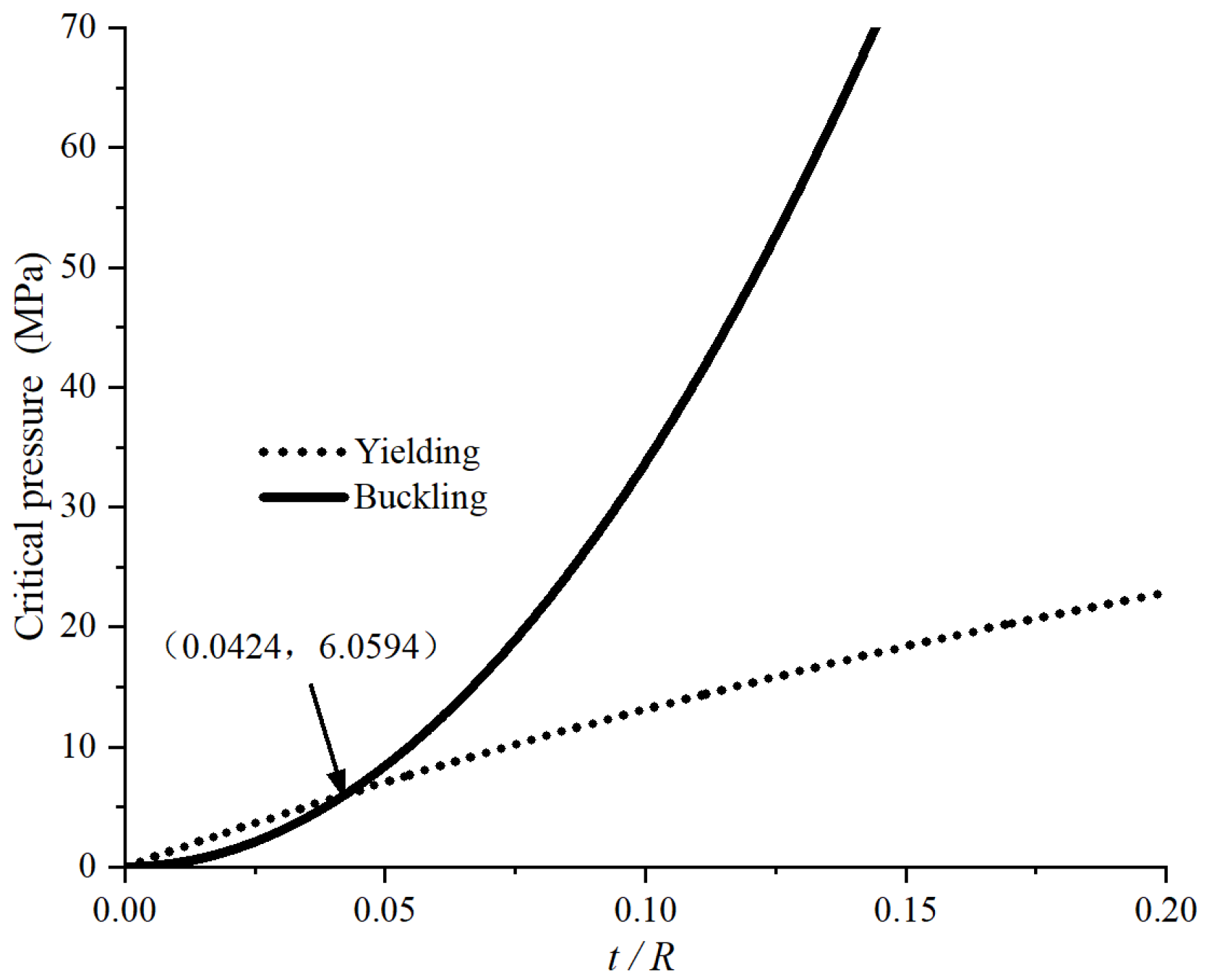
3.1.1. Failure Theory for Intact Spherical Cabin
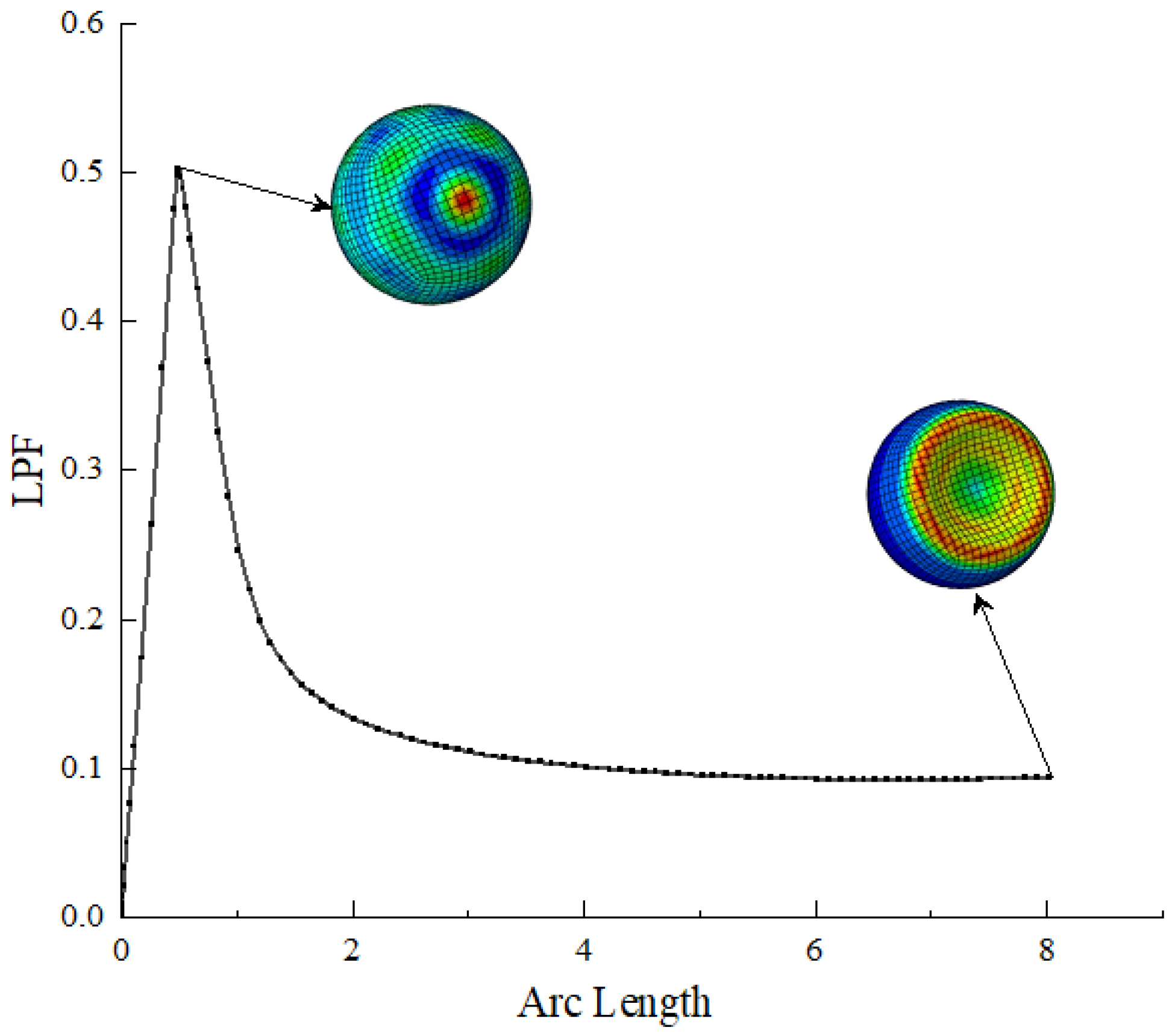
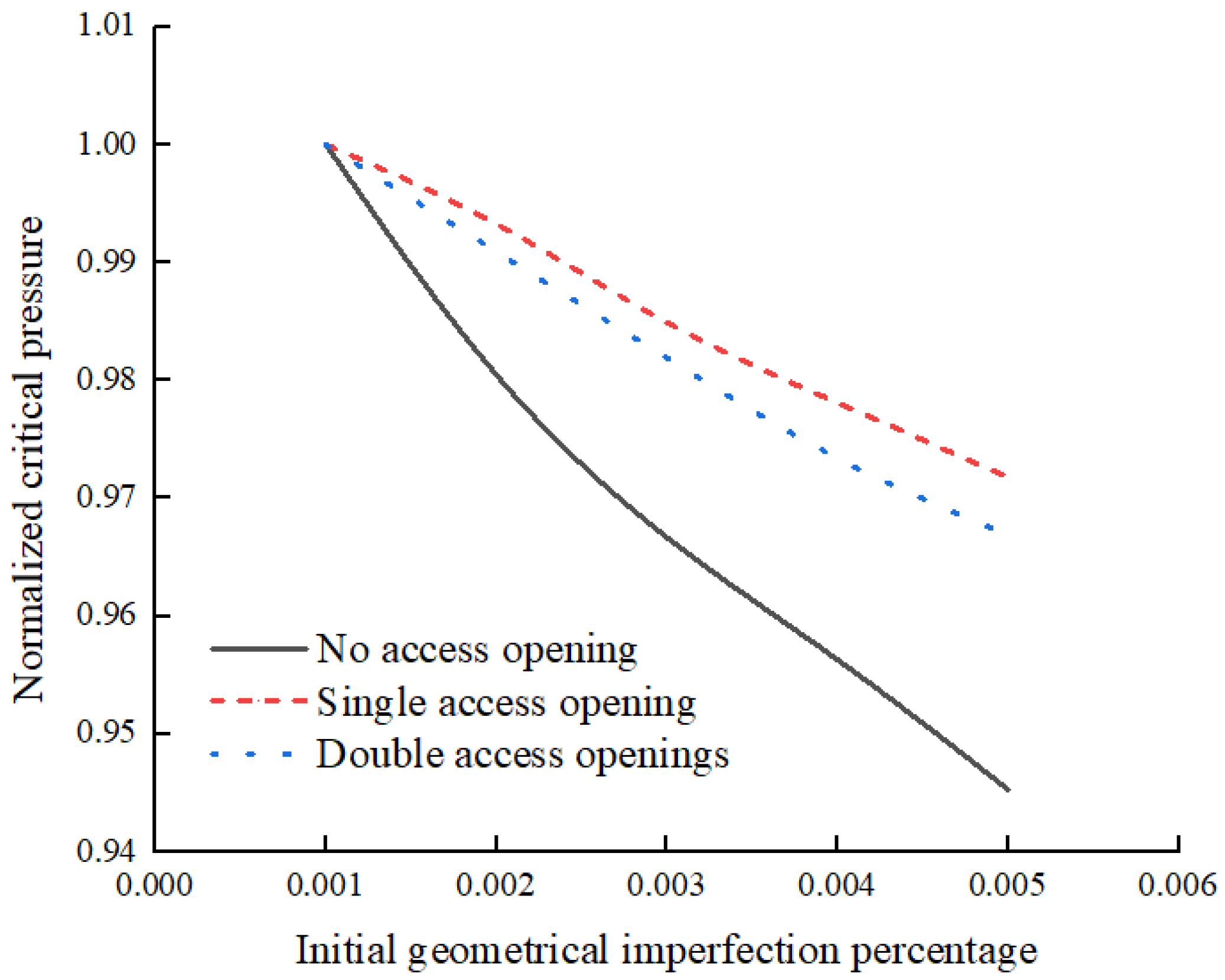
3.1.2. Effect of Initial Geometrical Imperfection
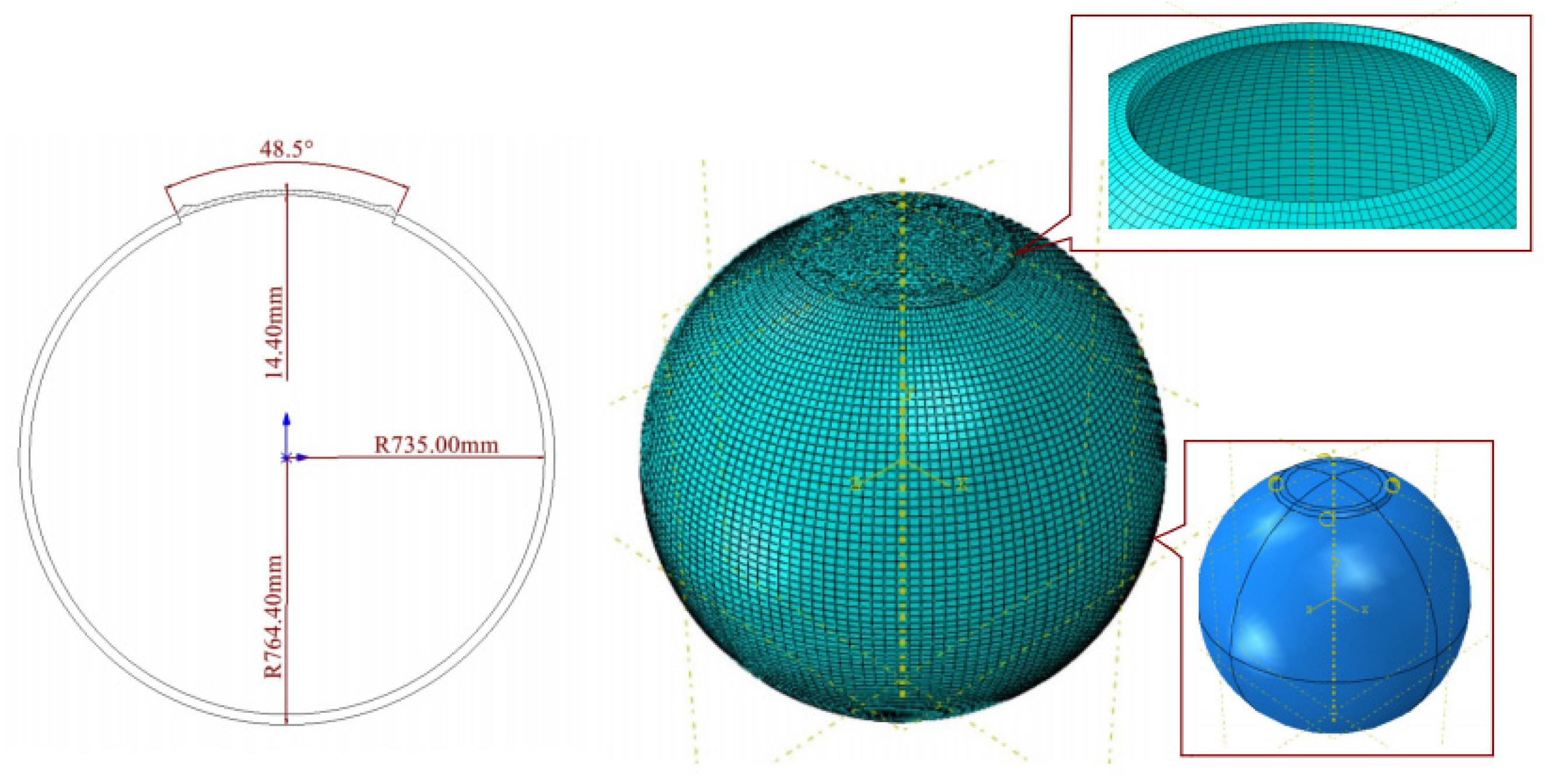
3.2. Spherical Cabin with a Single Access Opening
3.2.1. Numerical Analysis of the Spherical Cabin with a Single Access Opening
3.2.2. Effect of Initial Geometrical Imperfection
3.2.3. Effect of Hatch Stiffness
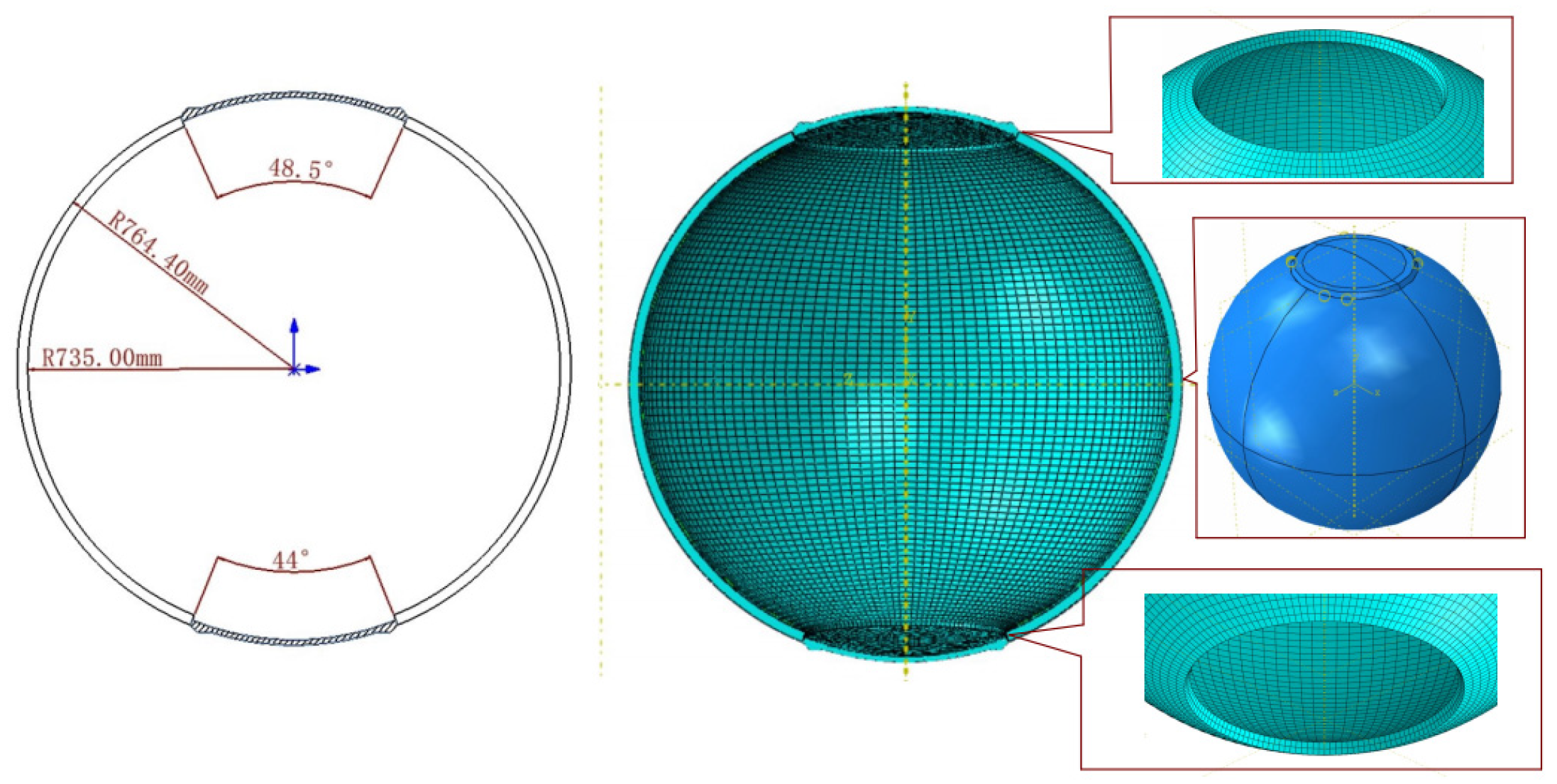
3.3. Spherical Cabin with Double Access Openings
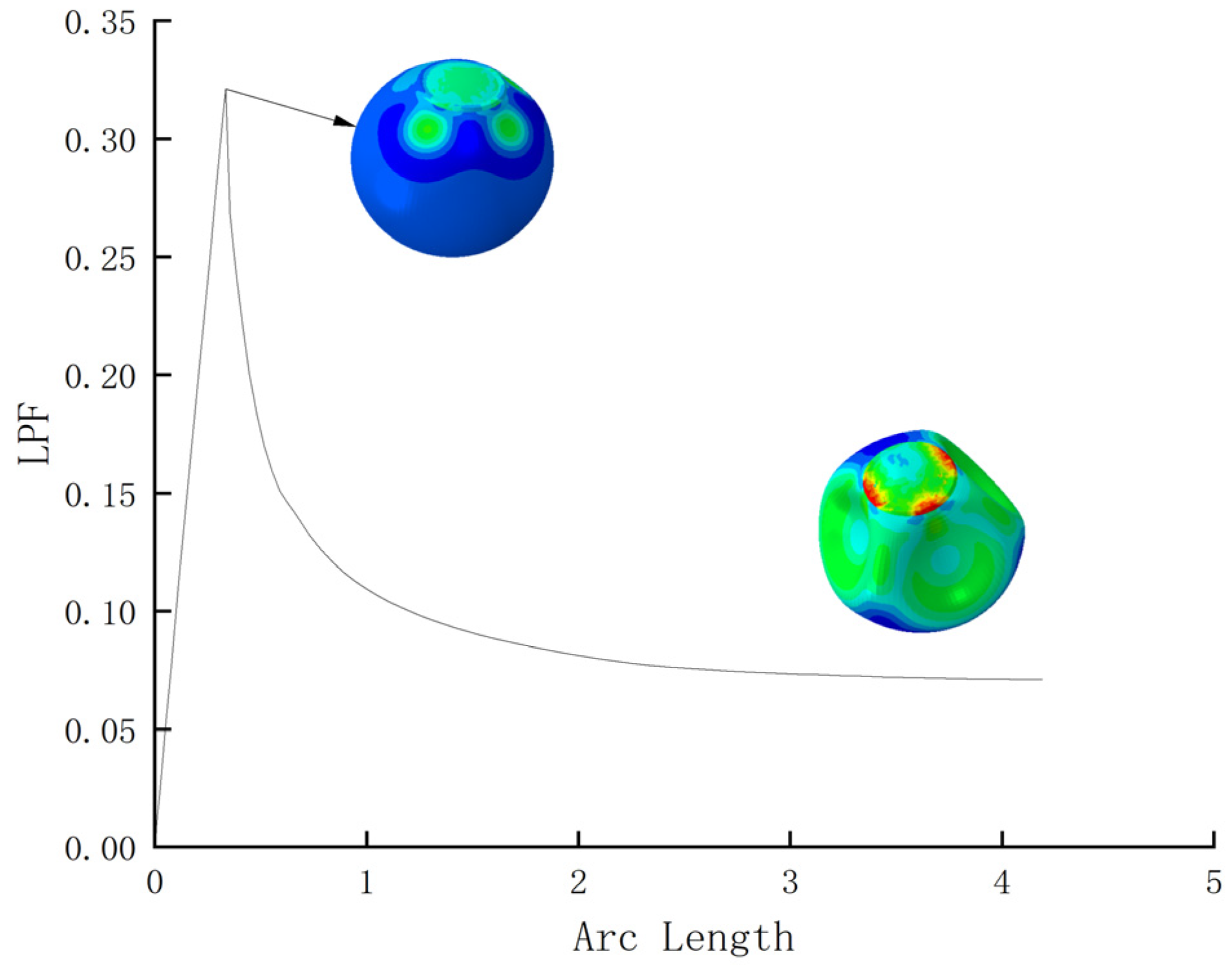
3.3.1. Effect of Initial Geometrical Imperfection
3.3.2. Effect of Hatch Stiffness
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, S.; Li, Y.S.; Wang, W.B. Development and prospects of non-metallic submersible pressure hull. Chin. J. Ship Res. 2020, 15, 9–18. [Google Scholar]
- Guo, D.Y.; Huang, X.P.; Wang, F. The Creep Properties and Numerical Simulation for PMMA Window. J. Shanghai Jiaotong Univ. 2019, 53, 513–520. [Google Scholar]
- Lu, B.; Liu, T.; Cui, W.C. Ultimate strength of pressure spherical hull in deep-sea manned submersibles. J. Ship Mwchanics 2004, 8, 51–58. [Google Scholar]
- Li, W.Y.; Wang, S.; Liu, T.; Shen, Y.S.; Ye, C. Current Status and Progress on Pressure Hull Structure of Manned Deep Submersible. Ship Build. China 2016, 57, 210–221. [Google Scholar]
- Das, P.S. Redesign of NEMO-type spherical acrylic submersible for manned operation to 3000 ft (914 m) ocean depth. J. Press. Vessel Technol.-Trans. ASME 2002, 124, 97–107. [Google Scholar] [CrossRef]
- Wang, F.; Wang, W.W.; Zhang, Y.K.; Du, Q.H.; Zhang, J.; Cui, W.C. Effect of Temperature and Nonlinearity of PMMA Material in the Design of Observation Windows for a Full Ocean Depth Manned Submersible. Mar. Technol. Soc. J. 2019, 53, 27–36. [Google Scholar] [CrossRef]
- Liu, S.; Ye, C.; Tang, G.W.; Cheng, F.; Jiang, L. Design and Development of the First Acrylic-hulled Submersible in China. Ship Build. China 2019, 60, 113–120. [Google Scholar]
- Wu, Y.; Li, Y.J.; Luo, R.L.; Zhang, Z.G.; Wang, F.; Zhao, B.X.; Yang, C.; Zhang, J.F.; Gaidai, O. Failure analysis on fully-transparent deep-sea pressure hulls used at 2,500 m depth. Front. Mater. 2023, 9, 1099610. [Google Scholar] [CrossRef]
- Zoelly, R. Über ein Knickungsproblem an der Kugelschale; Zürcher & Furrer: Zürich, Switzerland, 1915. [Google Scholar]
- Zhu, Y.M.; Liang, W.W.; Zhao, X.L.; Wang, X.R.; Xia, J. Strength and stability of spherical pressure hulls with different viewport structures. Int. J. Press. Vessel. Pip. 2019, 176, 13. [Google Scholar] [CrossRef]
- Rajput, N.S.; Pranesh, S.B.; Sathianarayanan, D.; Ramadass, G.A. Acrylic spherical pressure hull for Manned Submersible. Mater. Today: Proc. 2021, 46, 9412–9418. [Google Scholar]
- Jiao, P.; Chen, Z.; Ma, H.; Ge, P.; Gu, Y.; Miao, H. Buckling behaviors of thin-walled cylindrical shells under localized axial compression loads, Part 1: Experimental study. Thin-Walled Struct. 2021, 166, 108118. [Google Scholar]
- Kármán, T.V.; Tsien, H.S. The buckling of thin cylindrical shells under axial compression. J. Aeronaut. Sci. 2003, 40, 898–907. [Google Scholar]
- Donnell, L.H.; Wan, C. Effect of imperfections on buckling of thin cylinders and columns under axial compression. J. Appl. Mech. 1950, 17, 73–83. [Google Scholar] [CrossRef]
- Koiter, W.T. On the Stability of Elastic Equilibrium. Ph.D. Thesis, Technical University at Delft, Amsterdam, The Netherlands, 1945. [Google Scholar]
- Stein, M. The Influence of Prebuckling Deformations and Stresses on the Buckling of Perfect Cylinders; NASA: Washington, DC, USA, 1964. [Google Scholar]
- Pan, B.B.; Cui, W.C. An overview of buckling and ultimate strength of spherical pressure hull under external pressure. Mar. Struct. 2010, 23, 227–240. [Google Scholar]
- Pan, B.B.; Cui, W.C.; Shen, Y.S.; Liu, T. Further study on the ultimate strength analysis of spherical pressure hulls. Mar. Struct. 2010, 23, 444–461. [Google Scholar] [CrossRef]
- GB 150; Design of Pressure Vessels. Standardization Administration of China: Beijing, China, 2011.
- Cho, S.R.; Muttaqie, T.; Do, Q.T.; Kim, S.; Kim, S.M.; Han, D.H. Experimental investigations on the failure modes of ring-stiffened cylinders under external hydrostatic pressure. Int. J. Nav. Archit. Ocean. Eng. 2018, 10, 711–729. [Google Scholar]
- Cho, S.R.; Muttaqie, T.; Do, Q.T.; Park, S.H.; Kim, S.M.; So, H.; Sohn, J.M. Experimental study on ultimate strength of steel-welded ring-stiffened conical shell under external hydrostatic pressure. Mar. Struct. 2019, 67, 26. [Google Scholar]
- Shariati, M.; Rokhi, M.M. Numerical and experimental investigations on buckling of steel cylindrical shells with elliptical cutout subject to axial compression. Thin-Walled Struct. 2008, 46, 1251–1261. [Google Scholar]
- Zhu, Y.; Dong, J.H.; Gao, B.J. Buckling Analysis of Thin Walled Cylinder with Combination of Large and Small Stiffening Rings under External Pressure. Procedia Eng. 2015, 130, 364–373. [Google Scholar] [CrossRef][Green Version]
- ASTM D695-15; Standard Test Method for Compressive Properties of Rigid Plastics. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM D2990; Standard Test Methods for Tensile, Compressive, and Flexural Creep and Creep-Rupture of Plastics. ASTM International: West Conshohocken, PA, USA, 2011.
- Zhang, M.; Zhang, J.; Tang, W.X.; Wang, W.B.; Gao, J. Experimental and theoretical investigation on buckling of spherical shells. J. Jiangsu Univ. Sci. Technol. 2018, 32, 627–632. [Google Scholar]
- Liu, D.; Zhu, H.T.; Liu, F.; Cao, J.Q.; Ding, Z.J.; Zhang, Y. Buckling failure analysis of PMMA spherical pressure hull. Ocean Eng. 2022, 245, 8. [Google Scholar] [CrossRef]
- Xu, B.Y.; Liu, X.S. Applied Elasticity; Tsinghua University Press: Beijing, China, 1995. (In Chinese) [Google Scholar]
- Zhu, Y.M.; Ma, Q.L.; Dai, Y.; Zhang, J. Mechanical properties and fatigue analysis of spherical pressure shell with openings. Ship Sci. Technol. 2017, 39, 7–11. [Google Scholar]
- CCS. Rules for Classification of Diving Systems and Submersibles; China Communications Press: Beijing, China, 2018. [Google Scholar]
- Sosa, E.M.; Godoy, L.A.; Croll, J.G.A. Computation of lower-bound elastic buckling loads using general-purpose finite element codes. Comput. Struct. 2006, 84, 1934–1945. [Google Scholar] [CrossRef]
- Taheri-Behrooz, F.; Omidi, M.; Shokrieh, M.M. Experimental and numerical investigation of buckling behavior of composite cylinders with cutout. Thin-Walled Struct. 2017, 116, 136–144. [Google Scholar] [CrossRef]
- Shen, J.; Yang, J.; Ma, H.B. Static stability anaysis of K8 single-layer ellipsoid reticulated shell. Spat. Struct. 2009, 15, 69–72. [Google Scholar]





| Material Property | Value |
|---|---|
| Elastic Modulus/MPa | 2575 |
| Yield Strength/MPa | 126 |
| Poisson’s ratio | 0.35 |
| t/R | 0.04 | ||||
|---|---|---|---|---|---|
| Initial geometrical imperfection | 0.1% | 0.2% | 0.3% | 0.4% | 0.5% |
| Theoretical value of the buckling pressure (MPa) | 5.33 | 5.33 | 5.33 | 5.33 | 5.33 |
| Numerical results of buckling pressure (MPa) | 5.31 | 5.21 | 5.13 | 5.08 | 5.02 |
| Failure mode |  |  |  |  |  |
| t/R | 0.04 | ||||
|---|---|---|---|---|---|
| Initial geometrical imperfection | 0.1% | 0.2% | 0.3% | 0.4% | 0.5% |
| Numerical results of buckling pressure (MPa) | 3.2 | 3.18 | 3.15 | 3.13 | 3.11 |
| Failure Mode |  |  |  |  |  |
| t/R | 0.04 | ||
|---|---|---|---|
| Cover thickness (mm) | 9.6 | 14.4 | 19.2 |
| Numerical results of buckling pressure (MPa) | 3.05 | 3.11 | 2.69 |
| Failure Mode |  |  |  |
| t/R | 0.04 | ||||
|---|---|---|---|---|---|
| Initial geometrical imperfection | 0.1% | 0.2% | 0.3% | 0.4% | 0.5% |
| Numerical results of buckling pressure (MPa) | 3.32 | 3.29 | 3.26 | 3.23 | 3.21 |
| Failure Mode |  |  |  |  |  |
| t/R | 0.04 | ||
|---|---|---|---|
| Cover thickness (mm) | 9.6 | 14.4 | 19.2 |
| Numerical results of buckling pressure (MPa) | 3.06 | 3.21 | 3.08 |
| Failure Mode |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Li, Y.; He, Z.; Zhao, B.; Zhang, J.; Wu, Y. The Ultimate Strength of Fully Transparent Pressure-Resistant Spherical Cabins. Appl. Sci. 2023, 13, 12229. https://doi.org/10.3390/app132212229
Wang F, Li Y, He Z, Zhao B, Zhang J, Wu Y. The Ultimate Strength of Fully Transparent Pressure-Resistant Spherical Cabins. Applied Sciences. 2023; 13(22):12229. https://doi.org/10.3390/app132212229
Chicago/Turabian StyleWang, Fang, Youjie Li, Zhihao He, Bingxiong Zhao, Jinfei Zhang, and Yu Wu. 2023. "The Ultimate Strength of Fully Transparent Pressure-Resistant Spherical Cabins" Applied Sciences 13, no. 22: 12229. https://doi.org/10.3390/app132212229
APA StyleWang, F., Li, Y., He, Z., Zhao, B., Zhang, J., & Wu, Y. (2023). The Ultimate Strength of Fully Transparent Pressure-Resistant Spherical Cabins. Applied Sciences, 13(22), 12229. https://doi.org/10.3390/app132212229








