Abstract
Discrete element models are being increasingly applied to model rock failure processes. Bonded-particle models, based on circular or spherical particle systems, have been successfully used for two decades. More recently, bonded-block models, using polygonal or polyhedral elements, have proven to be a powerful alternative. This paper describes the basis of the application of these models in the numerical simulation of failure in rock materials. The critical governing parameters are identified, and their influence is discussed. The model calibration procedure based on the analysis of laboratory tests is discussed. An application example of an underground excavation problem is presented using a simple bonded-block model employing rigid blocks and a bilinear softening contact model. The results show the capability of this approach to reproduce observed failure modes involving block fractures.
1. Introduction
The safety assessment of underground structures in rock relies on the capability to analyze the response of the rock mass to the processes of excavation and support installation, as well as the effect of subsequent actions throughout its lifetime. Numerical modeling tools have steadily progressed in the representation of the non-elastic phenomena that govern the deformation and failure of rock masses. While equivalent-continuum models remain an important tool in many practical engineering situations, discontinuum models that explicitly incorporate the rock mass joints, possibly including the development of new fractures, are an attractive tool for the simulation of failure processes.
The numerical techniques classified as Discrete Element Methods (DEMs) comprise a wide range of formulations and computer codes, where the underlying concept is the representation of geomaterials as systems of particles, grains or blocks. Cundall [1] proposed numerical models of rigid polygonal or circular particles in which the mechanical response was governed by the constitutive relations of the contacts between discrete bodies. DEM models became an important tool in rock mechanics, allowing the study of complex block systems defined by rock mass discontinuities, joints, bedding planes and faults. The inclusion of block deformability through the use of internal finite element meshes became common in many problems. It allowed the non-elastic behavior or the intact rock material to be considered. An alternative approach involved the application of the discontinuum concept at a finer scale in order to analyze the internal behavior of the rock blocks [2]. The study of rock fracture by means of “Bonded-particle models”, composed of assemblies of circular or spherical particles, became a key investigation topic, allowing the simulation of complex responses of rock by means of relatively simple constitutive relations at the contact level [3]. The inclusion of rock mass discontinuities produced the “Synthetic rock mass” concept [4]. Advances in computational power have enabled the use of more complex shapes for the component particles, namely, polygonal or polyhedral, leading to the “Bonded-block model” (BBM) framework [5,6]. The progressive development of these models, aiming at more closely simulating physical fracture processes, has led to the generation of larger and more elaborate block assemblies, as well as more complex contact relations. Reviews of the multiple numerical formulations, considering both particle and block models and discussing their advantages and drawbacks, are available [7,8,9,10].
The present paper addresses the application of bonded-block models to underground works in rock; discusses the essential assumptions, the model generation and analysis procedures, and the results that can be obtained; and provides guidelines for their application. The proposed approach is based on a fairly simple numerical model using rigid blocks and a standard DEM contact formulation. The contact fracture model employs a bilinear post-peak softening curve that can be calibrated by given fracture energies. It is shown that this type of model is capable of reproducing the modes of fracture observed around underground openings, namely, spalling patterns.
The context of the problem is introduced in the next section by means of a literature review of the key developments in the discrete element modeling of rock fracture. Section 3 discusses the fundamental issues involved in the use of bonded-block models. The generation of block shapes using Voronoi or Delauney algorithms is addressed, and the outcomes of the two alternatives are compared. The procedure for the calibration of the micro-properties for a given randomly generated assembly using the experimental data is described. The role of contact constitutive models including fracture mechanics concepts is discussed. Section 4 presents a simple application to an underground opening, showing the ability of bonded-block models to represent the failure modes observed in the field. Some concluding remarks are finally provided.
2. Discrete Element Modeling of Rock Fracture
The essential concept of discontinuum modeling was stated by Cundall [2] as follows: “Assemblies of discrete particles (bonded together to represent rock, and unbonded to represent soil) capture the complicated behavior of actual material with simple assumptions and few parameters at the micro level. Complex overall behavior arises as an emergent property of the assembly”. In contrast, continuum modeling employs complex constitutive relations at the element level to reproduce physical nonlinear behavior.
2.1. Bonded-Particle Models
In the early Cundall paper [1], both polygonal and circular particles were already proposed. Rock mechanics codes typically resorted to polygonal or polyhedral blocks to simulate jointed rock, while soil mechanics made more use of circular particles. Circular-particle models have a high computational advantage since the procedures for contact detection and the calculation of contact forces are much faster than in the case of more complex shapes. Therefore, much larger systems can be addressed. By applying breakable bonds to the circular particles, Potyondy and Cundall [3] were able to study the fracture of intact rock. These models were able to reproduce the main features observed in laboratory tests. However, it was soon found that more complex particle shapes were necessary to fully account for the frictional effects, particularly for higher confinement stresses. The use of macro-particles or particle clumps allowed a more realistic representation of the various traits of the physical evidence [11,12,13] by using a higher bond density to improve the model performance. Various alternative formulations have been proposed for circular-particle models intended to more closely simulate the response of polygonal-block systems, namely, “grain-based models” [14], multiple-contact models [15], or the “flat-jointed material” concept [16]. The use of more elaborate contact relations was also proposed, namely, by introducing a tensile softening model to analyze the fracture initiation and propagation in tensile and compression lab tests [15,17]. Inserting the rock mass compartmentation and planar features, such as joints and faults, into the particle assemblies led to the “Synthetic rock mass” concept, accounting for the nonlinear behavior both at the block interfaces and in their interior [4].
2.2. Bonded-Block Models
Discrete element block models have been mainly employed in rock engineering to study failure modes defined by rock discontinuities. Researchers have taken advantage of the versatility of the method, creating randomly generated joint systems or detailed block assemblies, in order to examine stress distributions in rock masses [18], dam foundation problems [19,20] or local effects on slope stability [21,22]. Subsequently, it was recognized that the development of new fractures could be addressed by defining potential crack paths, initially bonded, which could then fail under the applied loading. This type of simulation of cracking and fracture was used, for example, to study underground waste storage projects [23,24] and to investigate fundamental issues of crack propagation [25]. The suitability of randomly generated Voronoi polygons/polyhedra to represent the internal structure of rock materials has been recognized in various studies [26]. These geometries resemble the observed patterns in some way, so the block assembly may be used to reproduce the grain shapes and size distributions of the various mineral components [5,27,28,29,30]. These block models are substantially more demanding in computational terms than circular-particle models, mainly due to the effort to detect and analyze the contact between interacting complex shapes. Therefore, 2D models of laboratory specimens were the first applications, but 3D models and field problems are presently feasible. The designation of “bonded-block models” (BBMs) for these block assemblies, with the intention to study the fracture of geomaterials, was adopted more recently [6,31]. The blocks are defined by a random network of potential cracks, forming triangles/tetrahedra or Voronoi polygons/polyhedra, which are initially bonded but allow the fracture process to progressively develop [9].
Three-dimensional Voronoi patterns were used to analyze uniaxial compression tests on anisotropic rocks [32], as well as triaxial tests on rock salt, relating the damage evolution characterized by the breakage of bonds with experimentally measured acoustic emissions [33]. Different geometries of the joint network have been investigated, for example, a triangular-block geometry in 2D models, allowing it to break into three parts [34]. Another way to generate a triangular-block geometry it to split the Voronoi polygons into triangles formed by connecting each vertex to a central point [35]. Therefore, the initial grains are able to break along these potential internal cracks. A 3D model of tetrahedral blocks can also be obtained by means of a Delauney algorithm, which was employed, for example, in the analysis of the fragmentation evolution in veined rock around underground openings [6].
Other numerical formulations, namely, those based on FDEM or FEM/DEM approaches [36,37], have been used in rock fracture studies. The underlying concepts are similar. The main differences with respect to DEM codes are typically related to the implementation of contact mechanics, their numerical treatment and the constitutive assumptions. For example, FDEM models were used in the analysis of crack development around underground excavations in rock [37]. A different BBM formulation in which fictitious stress is estimated inside the rigid blocks, which are allowed to split along an arbitrary plane, was applied in a study of the fracture of transversely isotropic rocks [38]. Alternative numerical implementations of fracture mechanics formulations have been proposed for analyzing failure processes in underground works [39] or slopes [40]. A reference should also be made to research on more complex block shapes, namely, involving smoothed boundaries [41].
The application of bonded-block models in rock mechanics has swiftly extended to more complex physical problems and diverse site conditions, including time-dependent damage evolution in sandstone [42]; hydro-mechanical problems [43]; dynamic fracture in the simulation of wave propagation experiments in a modified split Hopkinson pressure bar [44]; and thermo-mechanical problems [45,46,47]. Practical engineering applications have become more widespread in the design of rock bolt support in underground mines [48]; in the study of the stability of deep mining pillars [49]; in the investigation of design issues in underground works [50]; and coal-mining problems [51,52]. An issue of major importance in research using bonded-block models remains the calibration of input parameters using lab or field experiments in order to provide contributions for the progressive validation of these models [46,53].
The scope of bonded-block models has extended outside rock mechanics to include the fracture of other geomaterials and structures, for example, in the detailed analysis of lab tests on masonry specimens, prisms and wallettes [54,55,56]. Concrete fracture has also been approached with bonded-block models [57] and related numerical techniques employing polygonal or polyhedral elements [58].
Bonded-particle and bonded-block models are both effective tools to address rock fracture. The early circular-particle models were known to underestimate frictional effects [3]. Further developments, e.g., using particle clumps [11,13] or special contact formulations [14,15,16,17], allowed a more realistic simulation of the grain structure. Block models represent, in a natural way, polygonal grains using standard DEM contact formulations, which also allow the extension of the analysis into the large-displacement regime without the need to resort to special-purpose techniques. From a computational point of view, block models tend to be more demanding, given the additional complexity of the contact detection and update tasks. Thus, particle models may allow more refined analyses with reasonable run times. In summary, both types of modeling remain active fields of research and application in rock engineering, as discussed in various review articles [7,9,10,58].
3. Generation and Application of Bonded-Block Models
3.1. Modeling Assumptions and Block Patterns
A bonded-block model is composed of an assembly of discrete blocks, defined by two types of discontinuities: (i) the real rock mass discontinuities, namely, joints, faults and other features; (ii) a random network of potential discontinuities inside each intact rock block corresponding to conceivable crack paths. Figure 1 shows the conceptual representation of three rectangular blocks divided into Voronoi-shaped polygonal blocks, hereafter named “inner-blocks” (or sub-blocks). The joints between the rectangular blocks stand for real rock mass discontinuities. The interfaces between the inner blocks are initially bonded and are assigned the strength of the rock matrix. They can progressively fail in tension or shear, allowing the progressive fracture and fragmentation of the block.
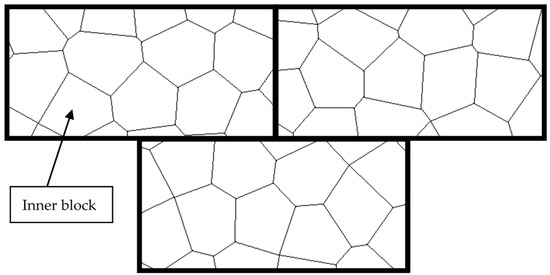
Figure 1.
Bonded-block model. Three rock blocks discretized with a pattern of bonded polygonal inner blocks.
Voronoi patterns resemble the grain structures of many types of rock, and thus, various authors have made inner blocks that correspond to different minerals. In this case, it is possible to refine the model by subdividing each Voronoi polygon into triangles built around a central point, thus allowing different properties for radial and peripheral joints to distinguish between inter-grain and intra-grain cracks [35]. Alternative shapes of inner blocks have been investigated. It is also possible to create an inner-block structure by means of a Delaunay algorithm, a triangular mesh built by connecting the centers of adjacent Voronoi polygons. In most instances, the inner-block pattern is simply understood as a means to create a network of potential cracks with random orientations. Cracking patterns in Voronoi-shaped models often resemble those observed in tensile failure. In 3D, tetrahedral inner blocks can also be built with a Delaunay triangulation algorithm [6]. These triangular or tetrahedral patterns produce a crack network with more continuity than the Voronoi shapes, since several planes meet at the nodes, generally allowing mechanisms of failure involving more extensive shearing and sliding.
The interaction between inner blocks typically follows the standard DEM representation based on point contacts. For matching edges, two point contacts are located at the endpoints. In the case of Figure 1, along the horizontal and vertical joints, a number of vertex–edge contacts are created to analyze the mechanical interaction between the blocks. The inner blocks may be numerically represented by either rigid or deformable blocks. In the former case, the total deformation takes place along the joints, which are assigned appropriate stiffness parameters. The option for deformable blocks may be implemented by creating an internal mesh of elements (sometimes designated as zones). The simplest solution relies on uniform-strain finite elements, either triangles or tetrahedra, which can be easily fit into arbitrary block shapes. Fine internal meshes require extra nodes to be placed along the edges, which will also contribute to improving the stress distribution along the joints between the blocks, as they provide more contact points. The mechanics of block contacts are described in the following section.
The bonded-block concept is intended to represent the fracture of the rock matrix by means of tensile cracking and shearing along the interfaces between the inner blocks. Failure under compressive loads is also accounted for by the progressive fracturing of the inner-block interface network. In the analysis of a real rock mass, the pre-existing discontinuities also have to be included. Major features can be inserted at known locations, and joint sets can be defined by a few representative discontinuities. Discrete fracture networks may also be used based on statistical parameters obtained in field studies. Once all of these real discontinuities are inserted into the numerical model, the inner-block patterns are generated inside the resulting blocks, thus allowing them to fracture in a natural way, for example, at regions of stress concentration, such as rock bridges.
3.2. Mechanical Micro- and Macro-Properties
As in bonded-particle models, a distinction is made between “micro-properties” and “macro-properties” [3]. Macro-properties are the properties of the global rock mass, defined by its deformation and strength parameters. Micro-properties are the material parameters required by the numerical model to control the mechanical behavior of inner blocks and their interfaces, the potential crack network. The size chosen for the inner blocks influences the global mechanical response of the system, as the joint density changes. Therefore, for a given block size, the micro-properties have to be calibrated to produce a global response consistent with the intended macro-properties, which are provided by laboratory experiments on rock specimens or field tests on the rock mass. The choice of the inner-block size depends on the computational resources available and the desired refinement of the analysis, considering, for example, the size of the underground excavation and the expected extent of failure zones. Once the block size is selected, calibration is performed using numerical specimens generated with similar block dimensions.
The deformability of the numerical model depends on the elastic moduli of the inner blocks and the stiffness of the joints or interfaces between them. The global deformation of the random-shaped block system should match the experimental data. There are different ways to split the deformation between the block material and the fictitious discontinuities. The simplest option is to assume the inner blocks to be rigid so that the entire block deformation is produced by the inner joints. At the other end, it is possible to adopt the desired Young’s modulus of the block for the inner blocks. In this case, the joints will have to be given a very high stiffness so that they do not influence the deformation. In explicit time-stepping solution algorithms, unreasonably high stiffness parameters penalize computational efficiency. Intermediate solutions are possible, for example, by assigning 90–95% of the deformability to the blocks, which gives approximately the same results without excessive run times [56]. In most bonded-block models, the inner blocks are assumed to be either rigid or elastic. It is certainly possible to assign non-elastic behavior to them, for example, by means of elasto-plastic or damage constitutive relations. However, this choice increases the complexity of the analysis and the calibration procedure. The dominant approach is to enrich the numerical representation response by refining the potential crack patterns, keeping the block or particle behavior as simple as possible.
The calibration of micro-properties typically starts with the definition of the deformability parameters in the elastic range. The target Young’s modulus can be that of the rock specimen, for example, in the simulation of lab tests, or the rock mass deformation modulus for field applications. The numerical joints in DEM models are zero-thickness interfaces, with the constitutive relations defined in terms of joint stresses in the normal or shear direction and the differences in the corresponding displacements across the joint. In the elastic range, the ratios of stress to relative displacement define the joint normal and shear stiffness. For the case of rigid inner blocks, a first approximation of the normal stiffness of the fictitious joints is given by kn = E/d, where E is the target Young’s modulus, and d is the average size of the inner blocks. Similarly, the shear stiffness may be estimated from the target shear modulus G as ks = G/d. These expressions are only a first estimate. A numerical test on a sample of the block arrangement with the assumed block size provides a better approximation. Typically, a few random systems are tested, and the average value is adopted. The Poisson’s ratio of the sample is rather dependent on the ratio of the joint shear and normal stiffness parameters, so the numerical tests may provide a refinement of the estimate of the shear stiffness.
For systems with deformable inner blocks, only a fraction of the deformation is assigned to the joints; therefore, the stiffnesses values will be proportionally higher. Comparisons of rigid-block models with deformable-block models in which the block material was assigned 50% and 95% of the total deformation have been presented [56]. The deformable-block model generally leads to a more realistic deformation pattern, but at a computational cost. If a fine discretization is sought to have a detailed fracture network, then rigid inner blocks would be the first choice.
The micro-properties of the strength parameters can be obtained by performing numerical tests involving uniaxial tension, uniaxial compression and biaxial compression setups. Many authors employ simple brittle failure models for the inner-block contacts, typically defined by the uniaxial tensile strength and the Mohr–Coulomb parameters, cohesion and friction angle. These micro-parameters can be varied until the desired macro-properties are achieved in a sample with the intended block geometry and size. The use of contact models considering post-peak softening is discussed in the following section.
3.3. Constitutive Model with Post-Peak Softening for Inner-Block Bonds
The mechanics of the contacts along the fictitious joints can be approached with various constitutive models. The simplest assumption is to assume brittle failure, governed by the peak values of tensile strength, cohesion and the friction angle. These micro-properties can be calibrated to obtain the intended global strength. More elaborate models add a post-peak-softening regime in tension and shear, which allow the consideration of fracture energies [37,38,55,56]. Research on fracture modeling has shown the importance of size effects due to the numerical element size. In practice, the contact discretization in bonded-block models cannot be made fine enough to eliminate these effects, but the inclusion of fracture energies in the bond breakage criteria may reduce them. Experimental data are available in the literature to characterize the fracture mechanics parameters for different types of rocks [59,60,61].
In the present BBM, the contact model proposed by Lemos and Sarhosis [56] is applied. In this formulation, the post-peak regime can be represented by a piecewise linear curve defined by a set of points. These authors compared linear, bilinear and trilinear softening curves, concluding that the intermediate case provides a sufficiently accurate approximation in practical applications. Therefore, in the examples presented, a simple bilinear softening curve is adopted in tension and shear, as shown in Figure 2. In the normal direction, the vertical axis represents the joint normal stress ratio, defined as the ratio of the tensile stress to the peak tensile strength. The horizontal axis is the joint normal displacement ratio, defined as the joint normal displacement over the normal displacement at peak stress. The first post-peak point corresponds to a fraction (βn1) of the peak tensile stress, and the second point corresponds to the residual stress, here assumed to be null. The corresponding displacements are defined by the parameters αn1 and αn2, multipliers of the peak elastic normal displacement. In compression, elastic behavior is assumed, using the same joint normal stiffness. In the shear direction, a similar type of post-peak curve is adopted, with the vertical axis denoting the ratio of the shear stress to the peak cohesive strength. The post-peak softening of the cohesive strength is defined by the parameters βs1, αs1 and αs2, as shown in Figure 2b. The friction angle is assumed to remain unchanged; thus, after the cohesive strength reaches the null value, the contact reverts to Coulomb friction. The areas under the curves measure the fracture energies involved in the failure processes in tension and shear.
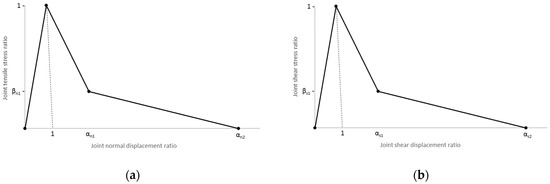
Figure 2.
Normalized contact post-peak softening curves. (a) Joint tensile stress ratio vs. joint normal displacement ratio; (b) joint shear stress ratio vs. joint shear displacement ratio.
The tensile strength parameters can be calibrated by performing a numerical uniaxial tensile test. Typically, in tension, the micro- and macro-properties are not very different; thus, the experimental strength value is often taken for the fictitious joints. The numerical uniaxial compression test is the critical one to calibrate the bond strength in shear. In Section 4.1, these numerical tests are analyzed for the examples presented.
It should be noted that BBM models typically represent compressive failure by simulating the progressive cracking and slip of the bonds along the random joint network. In compression, the contact constitutive model behaves elastically. Some authors have developed contact constitutive models that include failure in compression, for example, using cap-type formulations [62]. These models typically require the assumption of small displacements, as the overlap of the blocks in contact may create numerical difficulties.
3.4. Solution Methods
The bonded-block model presented herein was implemented in the discrete element code UDEC (Itasca [63]) by means of a user-defined contact constitutive law described in the previous section. This 2D block code is based on Cundall’s general approach [2], in which the solutions of both quasi-static and dynamic problems are executed by the same time-stepping algorithm. While in dynamic analyses, realistic block masses and damping are used, for quasi-static solutions, masses are scaled and artificial damping is employed to provide efficient convergence to the static equilibrium or to a collapse mechanism. Large-displacement analysis can be undertaken, taking into account block rearrangements and the updating of contact locations during the progressive deformation and failure process. This type of algorithm offers a robust solution for ultimate strength calculations, although long run times may be required for large 3D problems. The disadvantage of the algorithm is tied to the requirements for numerical stability, which depends on the mechanical properties. As a consequence, to improve computational efficiency, it is advisable to avoid very high stiffness parameters; otherwise, convergence to the solution may require many calculation steps. Very stiff blocks are preferably represented as rigid, while joint stiffness should not exceed physically reasonable bounds. This is the reason why the stiffness of the bonds between inner blocks should not be taken as nearly infinite, as it is feasible in implicit solution codes, but they should be assigned at least a small fraction of the block deformability. The simulation of uniaxial tensile or compression tests is usually performed by prescribing displacement histories at the loading plate, keeping the applied movement rates slow enough to allow the response to progress as smoothly as possible.
4. Analysis of Underground Structures
4.1. Example Problem
The case of a tunnel in a rock mass was selected to exemplify the application of bonded-block models at the scale of field problems. Because the aim is discuss the essential features and difficulties of using these models, a number of simplifying assumptions were made regarding unrelated issues. In particular, rock mass jointing was not explicitly represented, and thus, the only discontinuities in the numerical model are fictitious joints that are potentially involved in the fracture process. Therefore, it is possible to simplify the geometry by considering a vertical symmetry plane, as shown in Figure 3. The tunnel diameter is 8 m, and the domain around the opening, with an area of 8 × 16 m, is represented by the bonded-block assembly of rigid blocks in a Voronoi pattern with an average dimension of 0.3 m, also shown in detail in the figure. An alternative triangular-block pattern was also considered, as described in the following sections. The outer domain, with the overall dimensions 20 × 40 m, is assumed to remain elastic and is represented by deformable blocks with an internal triangular finite element mesh with the target elastic properties. These outer blocks are connected to each other and to the bonded blocks by numerical joints, which are prescribed to remain elastic. The nonlinear behavior is thus confined to the rectangular domain of randomly generated inner blocks surrounding the tunnel. Boundary conditions enforce the symmetry plane on the left-hand side, preventing horizontal displacements, while the lower boundary is fixed in the vertical direction. At the top boundary, vertical stress is applied, representing the overburden load. On the right-hand side, horizontal stress is applied, with a value equal to a given fraction of the vertical stress at the tunnel axis depth and a gradient in the vertical direction to account for the self-weight of the material. The main focus of the analysis is to simulate the effects of high compressive hoop stresses at the tunnel sidewalls in order to examine the development of spalling failure modes.
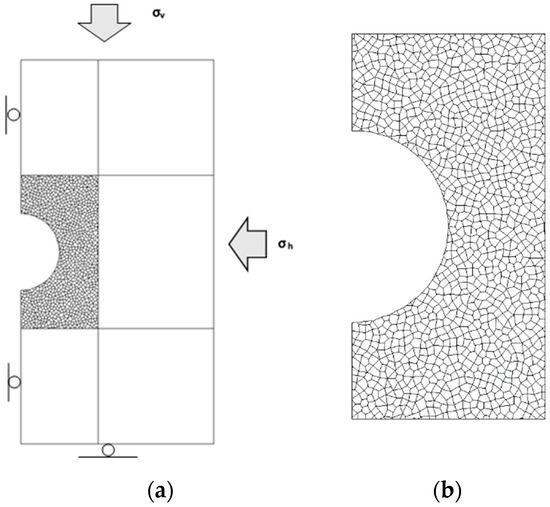
Figure 3.
(a) Domain for tunnel analysis; (b) randomly generated blocks around tunnel.
4.2. Selection of Micro-Parameters
The inner-block size in the tunnel model was chosen to be 0.3 m, providing a fine discretization around the opening. The target Young’s modulus was 20 GPa, and the target uniaxial compressive strength was set to 20 MPa. In order to calibrate the micro-properties, a numerical simulation of a uniaxial compression test was performed using a Voronoi pattern of the same size. In this example, the sample size was set to 8 × 16 m, as shown in Figure 4a. After a preliminary trial, the joint normal and shear stiffnesses were set to 96.6 GPa/m and 40.3 GPa/m, respectively, to provide a deformation modulus of 20.0 GPa, measured in the initial linear part of the obtained stress–strain curve. After a few trials, the following micro-property strength parameters were selected: tensile strength, 3 MPa; cohesion, 9.5 MPa; and friction, 250. The parameters defining the post-peak tensile curve (Figure 2) were βn1 = 0.5, αn1 = 1.7, and αn2 = 4.0. In shear, the corresponding parameters were βs1 = 0.5, αs1 = 1.3, and αs2 = 2.1. With these micro-properties, the peak stress attained in the uniaxial compression simulation was 20.7 MPa, considered sufficiently close to the target for this study. The failure mode, with the dominant vertical fracture pattern, is also shown in Figure 4b.

Figure 4.
Numerical uniaxial compression test. (a) Voronoi block pattern; (b) failure mode.
A second model was analyzed by employing a triangular-block pattern (Figure 5a), generated with UDEC’s Trigon option [63], instead of the Voronoi polygons. This generation procedure divides each polygon into triangles by inserting a central point. Therefore, it leads to a slightly more refined discretization with more joints meeting at each intersection, requiring different micro-properties to give the desired target macro-properties. In this case, the joint normal and shear stiffnesses were increased to 162 GPa/m and 68 GPa/m, respectively, resulting in a target deformation modulus of 20 GPa. The strength micro-parameters and the shape of the post-peak curve were similar to those of the Voronoi model given above. In this case, the peak stress in the uniaxial compression simulation reached a value of 20.3 MPa, close to the result of the other block pattern. Often, these triangular-block patterns lead to lower strength, requiring an increase of the micro-properties. In the present case, the difference was relatively small, so the micro-strength was maintained. The failure mode obtained with the triangular pattern is presented in Figure 5b.

Figure 5.
Numerical uniaxial compression test. (a) Triangular-block pattern; (b) failure mode.
4.3. Underground Opening Model
The circular tunnel model shown in Figure 3 was analyzed considering the two types of bonded-block patterns described in the previous section, the Voronoi polygon and triangular-block shapes, with the properties obtained in the calibration process. The elastic blocks surrounding the bonded-block model were assigned a global Young’s modulus of 20 GPa. A vertical overburden stress of 15 MPa was considered, with the horizontal stress component equal to half this value. Therefore, the largest compressive hoop stresses are expected to develop at the tunnel springline. Under these stresses, tunnel excavation without including any support leads to the failure of the blocks in the stressed sidewall regions. The failure mechanisms obtained by the two models involve block movements in the same region, but they are clearly influenced by the type of discontinuity network. The polygonal-block system (Figure 6a) is more likely to develop vertical fractures, followed by the failure of the columns into the opening. The triangular system (Figure 6b) allows more continuity of sliding, inducing the formation of a wedge that progressively detaches. The choice of the block pattern is an open issue that still requires further research. It is necessary to extend the comparative assessment of the performance of the various types of random networks intended to represent block fracture to practical situations of interest. It is also important to analyze how this internal block fracture system interacts with rock mass discontinuities, namely, when they are generated as discrete fracture networks.
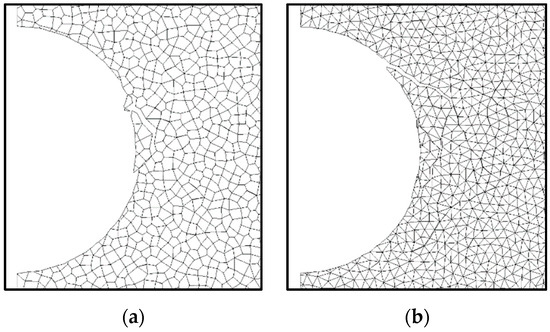
Figure 6.
Failure modes of circular tunnel. (a) Voronoi block model; (b) triangular-block model.
An alternative tunnel shape with vertical side walls was also analyzed. The failure modes obtained with the two types of bonded-block patterns are compared in Figure 7. The development of vertical fractures parallel to the walls is dominant, with the triangular pattern again showing more sliding on inclined joints.
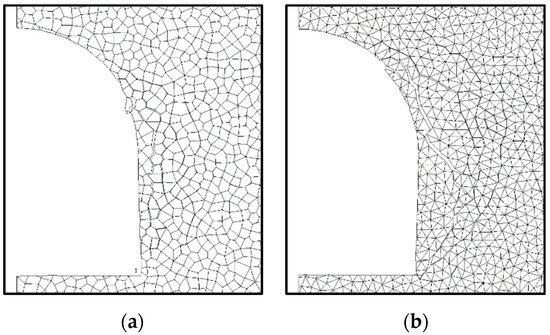
Figure 7.
Failure modes for the case of vertical side walls. (a) Voronoi block model; (b) triangular-block model.
5. Concluding Remarks
Discrete element models, a class that presently encompasses a wide variety of numerical formulations, have been primarily employed in rock mechanics to study collapse mechanisms induced by rock mass discontinuities. In such cases, rigid or elastic blocks are a common assumption and provide an effective performance. The bonded-block concept, by addressing the possibility of block fracture, enhances the range of applications of these models, namely, for underground excavation problems involving higher stress levels. Another important application lies in the analysis of block systems generated by discrete fracture network algorithms, in which bonded-block models may be used to take into account the possible breakage of rock bridges.
The present investigation shows that a bonded-block model based on simple mechanical assumptions is able to reproduce fairly complex modes of failure found in underground works in rock. This type of model can be built with a discrete element code based on a standard contact formulation and the use of rigid blocks. Fracture energies can be controlled by incorporating a bilinear softening curve into the contact models.
In the example presented, polygonal and triangular-block systems were used, both displaying suitable performance. Voronoi polygons provide a natural representation of a rock grain structure. Triangular networks facilitate mechanisms governed by dominant shearing patterns. Further research is required to assess their comparative advantages, in 2D and 3D, for typical underground excavation problems. The selection of the required block size, considering the excavation dimensions and the expected extent of failure regions, also requires more comprehensive studies of validation against field data. Another critical research topic is the development of robust procedures for the calibration of micro-properties in a systematic manner.
In order to focus on the key bonded-block concepts, the example analyzed was simplified by omitting pre-existing rock mass discontinuities. In practical problems, when rock mass jointing is included, the inner-block mesh is an important tool to allow the breakage of blocks, thus preventing non-realistic safety assessments. In these cases, the type of interior pattern may be less critical, while the calibration of the micro-properties that govern rock matrix fracture remains a central issue.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the author.
Conflicts of Interest
The author declares no conflict of interest.
References
- Cundall, P.A. A computer model for simulating progressive large scale movements in blocky rock systems. In Proceedings of the Symposium Rock Fracture (ISRM), Nancy, France, 4–6 October 1971; Volume 1. Paper II-8. [Google Scholar]
- Cundall, P.A. A discontinuous future for numerical modelling in geomechanics? Proc. Inst. Civ. Eng.-Geotech. Eng. 2001, 149, 41–47. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Mas Ivars, D.; Pierce, M.E.; Darcel, C.; Reyes-Montes, J.; Potyondy, D.O.; Young, R.P.; Cundall, P.A. The synthetic rock mass approach for jointed rock mass modelling. Int. J. Rock Mech. Min. Sci. 2011, 48, 219–244. [Google Scholar] [CrossRef]
- Lan, H.; Martin, C.D.; Hu, B. Effect of heterogeneity of brittle rock on micromechanical extensile behavior during compression loading. J. Geophys. Res. 2010, 115, B01202. [Google Scholar] [CrossRef]
- Garza-Cruz, T.V.; Pierce, M. A 3DEC Model for Heavily Veined Massive Rock Masses. In Proceedings of the 48th US Rock Mechanics/Geomechanics Symposium, Minneapolis, MN, USA, 1–4 June 2014; American Rock Mechanics Association: Alexandria, VA, USA, 2014; pp. 14–7660. [Google Scholar]
- Lisjak, A.; Grasselli, G. A review of discrete modeling techniques for fracturing processes in discontinuous rock masses. J. Rock Mech. Geotech. Eng. 2014, 6, 301–314. [Google Scholar] [CrossRef]
- Lemos, J.V. Rock failure analysis with discrete elements. In Numerical Methods in Geotechnical Engineering IX; Cardoso, A., Borges, J., Costa, P., Gomes, A., Marques, J., Vieira, C., Eds.; Taylor & Francis: London, UK, 2018; Volume 1, pp. 13–22. [Google Scholar]
- Yoon, J.S.; Hazzard, J. Coupled Fracture Modelling with Distinct Element Methods. In Modelling Rock Fracturing Processes Theories, Methods and Applications; Shen, B., Stephansson, O., Rinne, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 227–254. [Google Scholar]
- Li, Y.; Zhao, G.; Jiao, Y.; Yan, G.; Wang, X.; Shen, L.; Yang, L.; Liang, Z.; Li, W.; Zhou, X.; et al. A benchmark study of different numerical methods for predicting rock failure. Int. J. Rock Mech. Min. Sci. 2023, 166, 105381. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Yoon, J.S.; Jeon, S.; Zang, A.; Stephansson, O. Bonded particle model simulation of laboratory rock tests for granite using particle clumping and contact unbonding. In Continuum and Distinct Element Numerical Modeling in Geomechanics—2011; Sainsbury, D., Hart, R., Detournay, C., Nelson, M., Eds.; Itasca: Minneapolis, MN, USA, 2011; Paper 08-05. [Google Scholar]
- Scholtès, L.; Donzé, F.-V. A DEM model for soft and hard rocks: Role of grain interlocking on strength. J. Mech. Phys. Solids 2013, 61, 352–369. [Google Scholar] [CrossRef]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosyst. Eng. 2014, 17, 342–369. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, H. DEM analysis of failure mechanisms in the intact Brazilian test. Int. J. Rock Mech. Min. Sci. 2018, 102, 109–119. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Candeias, M.; Gouveia, F. A Rigid Particle Model for Rock Fracture Following the Voronoi Tessellation of the Grain Structure: Formulation and Validation. Rock Mech. Rock Eng. 2015, 48, 535–557. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Ivars, D.M. Simulating spalling with a flat-jointed material. In Applied Numerical Modeling in Geomechanics—2020; Billaux, D., Hazzard, J., Nelson, M., Schöpfer, M., Eds.; Itasca: Minneapolis, MN, USA, 2020; Paper 03-01. [Google Scholar]
- Brady, B.H.G.; Lemos, J.V.; Cundall, P.A. Stress measurement schemes for jointed and fractured rock. In Proceedings of the International Symposium in Rock Stress and Rock Stress Measurements, Stockholm, Sweden, 1–3 September 1986; Centec Publisher: Lulea, Sweden; pp. 167–176. [Google Scholar]
- Barla, G.; Bonini, M.; Cammarata, G. Stress and seepage analyses for a gravity dam on a jointed granitic rock mass. In Numerical Modeling of Discrete Materials in Geotechnical Engineering; Konietzky, H., Ed.; Balkema: Rotterdam, The Netherlands, 2004; pp. 263–268. [Google Scholar]
- Lemos, J.V. Representation of rock discontinuities in safety analysis of large dams. In Rock Engineering and Rock Mechanics: Structures in and on Rock Masses; Alejano, R., Perucho, Á., Olalla, C., Jiménez, R., Eds.; Taylor & Francis Group: London, UK, 2014; pp. 29–38. [Google Scholar]
- Alejano, L.R.; Ferrero, A.M.; Ramirez-Oyanguren, P.; Fernandez, M.I.A. Comparison of limit-equilibrium, numerical and physical models of wall slope stability. Int. J. Rock Mech. Min. Sci. 2011, 48, 16–26. [Google Scholar] [CrossRef]
- Brideau, M.-A.; Stead, D. Controls on Block Toppling Using a Three-Dimensional Distinct Element Approach. Rock Mech. Rock Eng. 2010, 43, 241–260. [Google Scholar] [CrossRef]
- Christianson, M.; Board, M.; Rigby, D. UDEC simulation of triaxial testing of lithophysal tuff. In Proceedings of the 41st US Symposium on Rock Mechanics, Golden, CO, USA, 17–21 June 2006; American Rock Mechanics Association: Alexandria, VA, USA, 2006. [Google Scholar]
- Damjanac, B.; Board, M.; Lin, M.; Kicker, D.; Leem, J. Mechanical degradation of emplacement drifts at Yucca Mountain—A modeling case study. Part II: Lithophysal rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 368–399. [Google Scholar] [CrossRef]
- Damjanac, B.; Fairhurst, C. Evidence for a Long-Term Strength Threshold in Crystalline Rock. Rock Mech. Rock Eng. 2010, 43, 513–531. [Google Scholar] [CrossRef]
- Herbst, M.; Konietzky, H.; Walter, K. 3D microstructural modeling. In Continuum and Distinct Element Numerical Modeling in Geo-Engineering; Hart, R., Detournay, C., Cundall, P., Eds.; Itasca: Minneapolis, MN, USA, 2008; pp. 435–441. [Google Scholar]
- Kazerani, T.; Zhao, J. Micromechanical parameters in bonded particle method for modeling of brittle material failure. Int. J. Num. Analyt. Meth. Geomech. 2010, 34, 1877–1895. [Google Scholar] [CrossRef]
- Chen, W.; Konietzky, H.; Tan, X.; Frühwirt, T. Pre-failure damage analysis for brittle rocks under triaxial compression. Comput. Geotech. 2016, 74, 45–55. [Google Scholar] [CrossRef]
- Xu, T.; Fu, T.; Heap, M.; Meredith, P.; Mitchell, T.; Baud, P. Mesoscopic Damage and Fracturing of Heterogeneous Brittle Rocks Based on Three-dimensional Polycrystalline Discrete Element Method. Rock Mech. Rock Eng. 2020, 53, 5389–5409. [Google Scholar] [CrossRef]
- Wang, F.; Konietzky, H.; Herbst, M.; Chen, W. Mechanical responses of grain-based models considering different crystallographic spatial distributions to simulate heterogeneous rocks under loading. Int. J. Rock Mech. Min. Sci. 2022, 151, 105036. [Google Scholar] [CrossRef]
- Lorig, L.; Potyondy, D.; Varun, J. Quantifying excavation-induced rock mass damage in large open pits. In Slope Stability 2020; Dight, P.M., Ed.; Australian Centre for Geomechanics: Perth, Australia, 2020. [Google Scholar]
- Ghazvinian, E.; Diederichs, M.S.; Quey, R. 3D random Voronoi grain-based models for simulation of brittle rock damage and fabric-guided micro-fracturing. J. Rock Mech. Geotech. Eng. 2014, 6, 506–521. [Google Scholar] [CrossRef]
- Müller, C.; Frühwirt, T.; Haase, D.; Schlegel, R.; Konietzky, H. Modeling deformation and damage of rock salt using the discrete element method. Int. J. Rock Mech. Min. Sci. 2018, 103, 230–241. [Google Scholar] [CrossRef]
- Kazerani, T.; Yang, Z.Y.; Zhao, J. A Discrete Element Model for Predicting Shear Strength and Degradation of Rock Joint by Using Compressive and Tensile Test Data. Rock Mech. Rock Eng. 2012, 45, 695–709. [Google Scholar] [CrossRef]
- Gao, F.Q.; Stead, D. The application of a modified Voronoi logic to brittle fracture modelling at the laboratory and field scale. Int. J. Rock Mech. Min. Sci. 2014, 68, 1–14. [Google Scholar] [CrossRef]
- Munjiza, A. The Combined Finite-Discrete Element Method; John Wiley & Sons Ltd.: Chichester, UK, 2004. [Google Scholar]
- Lisjak, A.; Grasselli, G.; Vietor, T. Continuum-discontinuum analysis of failure mechanisms around un-supported circular excavations in anisotropic clay shales. Int. J. Rock Mech. Min. Sci. 2014, 65, 96–115. [Google Scholar] [CrossRef]
- Rasmussen, L.L.; Min, K.-B. Developments to the Bonded Block Modeling technique for Discrete Element, simulation of transversely isotropic rock. Int. J. Rock Mech. Min. Sci. 2023, 170, 105518. [Google Scholar] [CrossRef]
- Shen, B.; Barton, N. Rock fracturing mechanisms around underground openings. Geomech. Eng. 2018, 16, 35–47. [Google Scholar]
- Eberhardt, E.; Stead, D.; Coggan, J.S. Numerical analysis of initiation and progressive failure in natural rock slopes—The 1991 Randa rockslide. Int. J. Rock Mech. Min. Sci. 2004, 41, 69–87. [Google Scholar] [CrossRef]
- Shao, L.; Mao, J.; Zhao, L.; Li, T. A three-dimensional deformable spheropolyhedral-based discrete element method for simulation of the whole fracture process. Eng. Fract. Mech. 2022, 263, 108290. [Google Scholar] [CrossRef]
- Chen, W.; Konietzky, H.; Abbas, S.M. Numerical simulation of time-independent and -dependent fracturing in sandstone. Eng. Geol. 2015, 193, 118–131. [Google Scholar] [CrossRef]
- Lisjak, A.; Kaifosh, P.; He, L.; Tatone, B.S.A.; Mahabadi, O.K.; Grasselli, G. A 2D, fully-coupled, hydro-mechanical, FDEM formulation for modelling fracturing processes in discontinuous, porous rock masses. Comput. Geotech. 2017, 81, 1–18. [Google Scholar] [CrossRef]
- Du, J.; Huang, X.; Yang, G.; Xue, L.; Wu, B.; Zang, M.; Zhang, X. UDEC Modelling on Dynamic Response of Rock Masses with Joint Stiffness Weakening Attributed to Particle Crushing of Granular Fillings. Rock Mech. Rock Eng. 2023, 56, 1823–1841. [Google Scholar] [CrossRef]
- Wang, F.; Konietzky, H.; Pang, R.; Zou, Y.; Pang, B.; Ismael, M. Grain-Based Discrete Element Modeling of Thermo-Mechanical Response of Granite under Temperature. Rock Mech. Rock Eng. 2023, 56, 5009–5027. [Google Scholar] [CrossRef]
- Radakovic-Guzina, Z.; Damjanac, B.; Lam, T.; Kasani, H.A. DEM-Based Methodology for Simulation of Long-Term Geomechanical Performance of a Placement Room in a Deep Geological Repository. Rock Mech. Rock Eng. 2022, 56, 2737–2761. [Google Scholar] [CrossRef]
- Lisjak, A.; Mahabadi, O.; Ha, J.; Mas Ivars, D. Analysis of thermo-mechanical damage around tunnel and deposition boreholes of an underground nuclear waste disposal facility at the Forsmark site (Sweden) by 3D coupled FDEM simulations. Int. J. Rock Mech. Min. Sci. 2023, 171, 105586. [Google Scholar] [CrossRef]
- Garza-Cruz, T.; Bouzeran, L.; Pierce, M.; Jalbout, A.; Ruest, M. Evaluation of ground support design at Eleonore Mine via Bonded Block Modelling. In Ground Support 2019: Proceedings of the Ninth International Symposium on Ground Support in Mining and Underground Construction; Hadjigeorgiou, J., Hudyma, M., Eds.; Australian Centre for Geomechanics: Perth, Australia, 2019; pp. 341–356. [Google Scholar]
- Lavoie, T.; Eberhardt, E.; Pierce, M.E. Numerical modelling of rock mass bulking and geometric dilation using a bonded block modelling approach to assist in support design for deep mining pillars. Int. J. Rock Mech. Min. Sci. 2022, 156, 105145. [Google Scholar] [CrossRef]
- Keneti, A.; Pouragha, M.; Sainsbury, B.-A. Review of design parameters for discontinuous numerical modelling of excavations in the Hawkesbury Sandstone. Eng. Geol. 2021, 288, 106158. [Google Scholar] [CrossRef]
- Sinha, S.; Walton, G. Modeling the behavior of a coal pillar rib using Bonded Block Models with emphasis on ground-support interaction. Int. J. Rock Mech. Min. Sci. 2021, 148, 104965. [Google Scholar] [CrossRef]
- Sunkpal, M.; Sherizadeh, T.; Guner, D. Quantifying coal rib stability and support requirements using bonded block modeling and reliability analysis based on the random set theory. Int. J. Rock Mech. Min. Sci. 2023, 163, 105332. [Google Scholar] [CrossRef]
- West, I.; Walton, G. Quantitative Evaluation of the Effects of Input Parameter Heterogeneity on Model Behavior for Bonded Block Models of Laboratory Rock Specimens. Rock Mech. Rock Eng. 2023, 56, 7129–7146. [Google Scholar] [CrossRef]
- Sarhosis, V.; Lemos, J.V. A detailed micro-modelling approach for the structural analysis of masonry assemblages. Comput. Struct. 2018, 206, 66–81. [Google Scholar] [CrossRef]
- Pulatsu, B.; Erdogmus, E.; Lourenço, P.B.; Quey, R. Simulation of uniaxial tensile behavior of quasi-brittle materials using softening contact models in DEM. Int. J. Fract. 2019, 217, 105–125. [Google Scholar] [CrossRef]
- Lemos, J.V.; Sarhosis, V. Discrete element bonded-block models for detailed analysis of masonry. Infrastructures 2022, 7, 31. [Google Scholar] [CrossRef]
- Prakash, P.R.; Pulatsu, B.; Lourenço, P.B.; Azenha, M.; Pereira, J.M. A meso-scale discrete element method framework to simulate thermo-mechanical failure of concrete subjected to elevated temperatures. Eng. Fract. Mech. 2020, 239, 107269. [Google Scholar] [CrossRef]
- Bolander, J.E.; Elias, J.; Cusatis, G.; Nagai, K. Discrete mechanical models of concrete fracture. Eng. Fract. Mech. 2021, 257, 108030. [Google Scholar] [CrossRef]
- Atkinson, B.K.; Meredith, P.G. Experimental fracture mechanics data for rocks and minerals. In Fracture Mechanics of Rock; Atkinson, B.K., Ed.; Academic Press: London, UK, 1987; pp. 477–525. [Google Scholar]
- Pijaudier-Cabot, G.; Hajimohammadi, A.; Nouailletas, O.; La Borderie, C.; Padin, A.; Mathieu, J.P. Determination of the fracture energy of rocks from size effect tests: Application to shales and carbonate rocks. Eng. Fract. Mech. 2022, 271, 108630. [Google Scholar] [CrossRef]
- Pérez-Rey, I.; Muñoz-Ibáñez, A.; González-Fernández, M.A.; Muñiz-Menéndez, M.; Penabad, M.H.; Estévez-Ventosa, X.; Delgado, J.; Alejano, L.R. Size effects on the tensile strength and fracture toughness of granitic rock in different tests. J. Rock Mech. Geotech. Eng. 2023, 15, 2179–2192. [Google Scholar] [CrossRef]
- Pulatsu, B. Coupled elasto-softening contact models in DEM to predict the in-plane response of masonry walls. Comput. Part. Mech. 2023, 10, 1759–1770. [Google Scholar] [CrossRef]
- Itasca. UDEC—Universal Distinct Element Code: Theory and Background; Version 6.0; Itasca Consulting Group: Minneapolis, MN, USA, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).