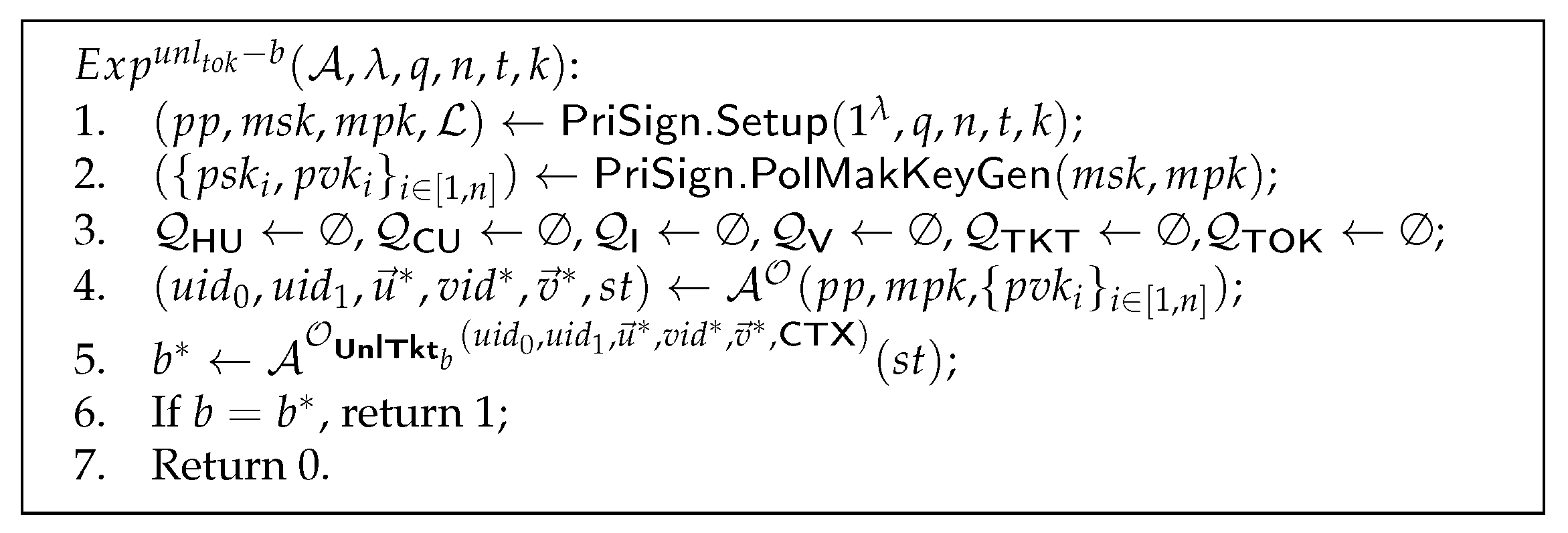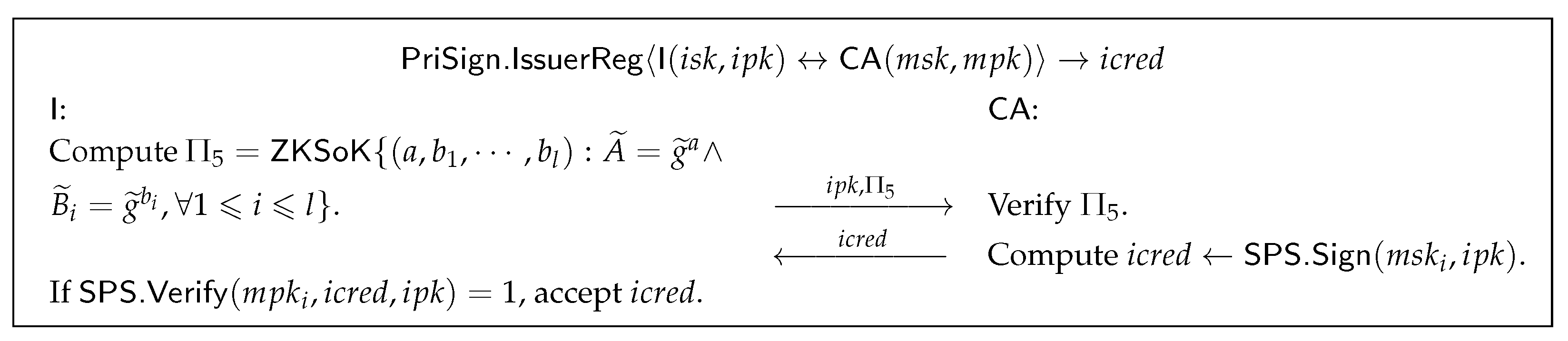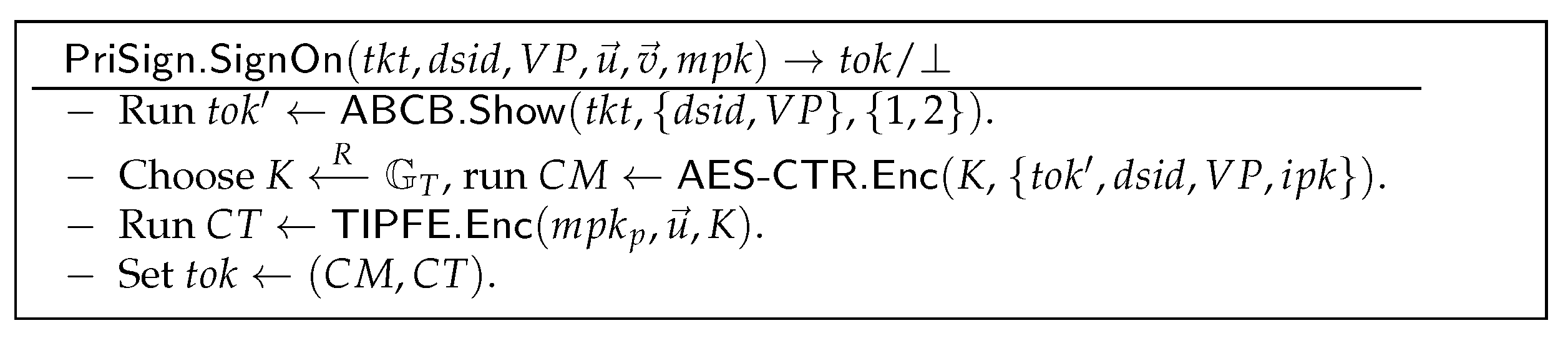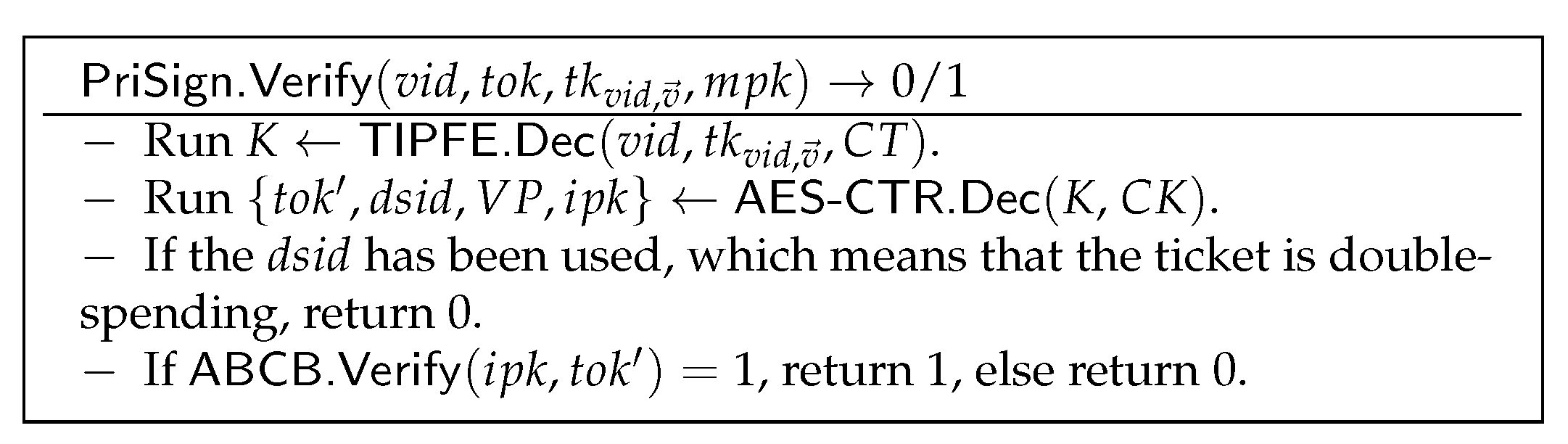Abstract
Anonymous single sign-on systems allow users to use a single credential to access multiple services protected by verifiers without revealing their personal information, which is especially important due to privacy regulations such as GDPR. In this paper, we introduce a new strong privacy-preserving single sign-on scheme, dubbed PriSign, based on our proposed attribute-based credential with traceability (ABCT), attribute-based credential with blindness (ABCB), and threshold inner-product functional encryption (TIPFE). Compared with the existing state-of-the-art solutions, PriSign presents three improvements: (1) users can obtain different types of tickets according to the attribute disclosure policies enforced by the ticket issuer to support fine-grained access control; (2) users can hide access tokens and designate a verifier for tokens according to a verifier’s policy jointly issued by multiple policymakers, meaning that non-designated verifiers cannot obtain any information about the tokens; (3) we innovatively use a threshold approach to issue policy keys online in order for verifiers to achieve proxy re-verification services in an unstable cloud environment. We implement PriSign and compare the performance with other ASSO systems in the personal laptop, and the results prove its practicability.
1. Introduction
Single sign-on systems (e.g., OpenID [1], Kerberos [2] etc.) allow users to access multiple services using one credential without requiring users to apply for different credentials for each service, which is very convenient for users in the cloud environment. Anonymous single sign-on (ASSO) systems provide authentication services while protecting the privacy of users from being known by malicious service providers, which complies with privacy regulations such as the General Data Protection Regulations (GDPR) [3] that seek to minimize personal information collection.
In many application contexts of ASSO, such as the electronic ticket system, it is necessary to support fine-grained access control based on user credentials. Consider the example of a transportation ticket system, where a user can prove to the ticket issuer that they have a credential that meets certain attribute disclosure policies (e.g., age, location, disability, etc.) without revealing anything else. For example, students, disabled persons, or soldiers can selectively disclose their identity attributes to purchase discounted tickets without revealing sensitive information such as specific schools, illnesses, or service units. Supporting attribute disclosure policies can greatly improve the application scope of ASSO systems. Unfortunately, this function is not available in existing ASSO schemes [4,5,6,7,8,9].
An ASSO system’s main security requirement is to protect users’ privacy. Most of the existing schemes only consider the unlinkability of user identities [4,5,6,7], and do not protect the privacy of the user’s service requests, i.e., any service providers can obtain and verify the user access tokens. Han et al. [8] proposed an ASSO scheme for designated verifiers; their scheme guarantees that user access tokens can only be verified by a designated service provider, while user access tokens can be obtained by any non-designated verifiers. This may disclose other information of tokens, such as the validity period, serial number, etc., thus destroying the privacy of user service requests.
Although the ASSO system for designated verifiers [8] protects user service requests from being validated by malicious service providers, it reduces the reliability of the verification service in cloud environments. Due to the complexity of the cloud environment, it is not guaranteed that the verifier of each service provider can perform the verification service online in real-time while ensuring that non-designated verifiers cannot verify the access tokens of the designated verifier. This causes the entire service to become unavailable when the designated verifier encounters a single point of failure. Han et al. [9] proposed a new ASSO system with proxy re-verification to address this problem. Unfortunately, their scheme re-verifies access tokens by introducing a trusted central verifier to generate keys for proxy verifiers. If the central verifier is attacked, the verification service is unavailable. Therefore, this scheme does not improve the reliability of verification services.
1.1. Contributions
To address the above requirements, we propose a strong privacy-preserving single sign-on scheme called PriSign, which uses our proposed attribute-based credential with traceability (ABCT), attribute-based credential with blindness (ABCB), and threshold inner-product functional encryption (TIPFE) schemes along with Groth’s structure-preserving signatures (SPS) scheme. The main contributions of our scheme are:
Fine-grained access control: PriSign allows users to anonymously disclose a subset of user attributes to the ticket issuer, thereby obtaining different types of tickets for fine-grained access control.
Designated verifiers and token-hiding: For the first time, we achieve perfect privacy protection for user service requests (i.e., access tokens); that is, users’ access tokens can only be verified by a verifier with the designated policy, and are hidden from any non-designated verifiers.
Threshold key issuance for verifiers and proxy re-verification: We innovatively deploy n policymakers in the PriSign scheme using threshold cryptography technology. As long as t policymakers are online, they can issue the verification key for proxy verifiers in order to achieve a stable proxy re-verification service in the unstable cloud environment.
Similar to existing schemes, PriSign supports the unlinkability of user identities and double-spending detection. In addition, PriSign supports the traceability of users to achieve strong security control. We prove that PriSign satisfies the formal security definitions by reducing them to either well-known complexity assumptions or the security of proven cryptography primitives. The performance of PriSign is measured on a personal laptop, and our source code is made publicly available [10].
1.2. Organization
The rest of this paper is organized as follows. Section 2 presents and compares related works. Section 3 provides important preliminaries. Section 4 describes the system and security model of our PriSign system, while Section 5 describes its construction. Section 6 contains a security analysis and Section 7 a performance analysis, while Section 8 presents our conclusions.
2. Related Work and Comparison
Elmufti et al. [4] proposed an ASSO scheme suitable for the Global System for Mobile communication (GSM) system, in which the GSM network operator provides a single sign-on service for users. They combined the security features of GSM with digital signatures to allow users to access arbitrary third-party services anonymously. In their scheme, a new one-time identity is generated and used to authenticate a trusted third party (TTP) each time a user accesses a service. After authenticating the user, TTP forwards the one-time identity of the user to the service provider; therefore, the service provider cannot infer the user’s real identity from this one-time identity. Although their scheme achieves the unlinkability of user identities, it makes the verification services vulnerable to a single point of failure due to the need for the TTP when verifying user service requests. In our scheme, users can directly access services without TTP involvement.
Han et al. [5] proposed a generic construction of dynamic ASSO schemes with strong security based on CCA-secure broadcast encryption [11,12], strongly existentially unforgeable signature [13,14], and zero-knowledge proof [15,16]. In their construction, registered users can obtain an encrypted credential of their public key from an identity provider (IDP) along with the set of services they want to access. Users can use this credential to access all designated services without requiring different credentials for different services. Furthermore, when the user presents their credentials, a zero-knowledge proof of the user’s private key should be computed to prevent the sharing of credentials. Unfortunately, as all designated verifiers can know users’ public keys, this scheme cannot achieve unlinkability of user identities.
Wang et al. [6] proposed a generic construction of the ASSO scheme that is transformed from dynamic group signatures [17,18]. In their scheme, users register with a central authority and obtain a group signing key. When accessing a service, a user generates a group signature using his group signing key. The service provider checks whether the user is authorized to access the service by verifying the correctness of the group signature. In addition, the central authority can use the tracing algorithm of the group signature scheme to trace users’ identities. However, all service providers can verify users’ access requests; in our scheme, on the other hand, a user can designate the verifier of service requests.
Lee et al. [7] proposed a provably secure ASSO scheme based on extended Chebyshev chaotic maps [19,20]. In their scheme, an issuer generates ephemeral keys to users and service providers. When accessing a service, a user and a service provider need to use their ephemeral keys to exchange a session key to grant the service. Compared to the scheme based on modular exponential computations of the elliptic curve, their scheme is more efficient; however, each service provider knows user identities when generating session keys, which compromises user privacy.
Han et al. [8] utilized Au and colleagues’ BBS+ signature [21] and zero-knowledge proof of knowledge [22] in constructing an ASSO scheme for designated services. The main contribution of their construction is to protect the privacy of both user identities and their service requests. Their scheme allows users to obtain tickets from the ticket issuers in order to access multiple services, while the tickets contain a set of authentication tags that can only be verified by designated verifiers. Designated verifiers can verify that their corresponding tags cannot be linked to the user’s service request. However, unlike our scheme, their scheme does not support fine-grained access control of tickets nor proxy re-verification of access tokens.
Recently, Han et al. [9] proposed a new ASSO scheme with proxy re-verification using BBS+ Signature [21], zero-knowledge proof of knowledge [22], and identity-based encryption [23,24]. Their scheme is an improvement of the scheme in [8] to achieve proxy re-verification of services by introducing a trusted central verifier (CV). In case the designated verifier is unavailable when verifying user access tokens, the CV can authorize a proxy verifier to complete the verification of access tokens on behalf of the original verifier. Unfortunately, the setting of a CV does not improve the stability of verification services; moreover, their scheme does not support token-hiding and fine-grained access control.
The closest parallel to ASSO is the attribute-based electronic ticket (e-ticket) system [25,26,27]. In such systems, users can buy tickets from issuers using the attribute-based credentials requested from the CA, and then use the tickets to access multiple services. Han et al. [25] first proposed a privacy-preserving e-ticket system, using attribute-based credentials derived from Boneh–Boyen Signature (BBS) [28] and efficient set membership proof and range proof [29]. Next, Feng et al. [26] utilized structure-preserving signatures on equivalence class [30] and dynamically malleable signatures [31] to construct efficient and strong privacy protection in a transferable attribute-based ticket scheme. Shi et al. [27] proposed an electronic ticketing system to address the problem of existing electronic ticketing systems being challenging to deploy in resource-constrained devices and unable to prevent ticket sharing among unauthorized devices. Similar schemes [25,26,27] have achieved user anonymity and fine-grained access control; however, unlike our scheme, none of them support token-hiding and designating verifiers.
Table 1 summarizes a detailed comparison between PriSign and related ASSO schemes [4,5,6,7,8,9]. Comparisons are conducted in terms of unlinkability, designated verifiers, proxy re-verification, threshold keys issuance, token-hiding, traceability, and fine-grained access control. Unlinkability means that an ASSO scheme can protect users’ identities from being linked by malicious verifiers, even if they collude. Designated verifiers mean that an ASSO scheme allows users to designate a verifier for access tokens without any non-designated verifiers being able to determine the correctness of tokens. Proxy re-verification means that an ASSO scheme allows a proxy verifier to perform token verification services on behalf of the original verifier. Threshold key issuance means that an ASSO scheme allows multiple CVs (or policymakers) to generate verification keys for designated verifiers or proxy verifiers using a threshold approach. Token-hiding means that an ASSO scheme hides user service requests from all non-designated verifiers. Traceability means that an ASSO scheme can de-anonymize a user’s identity. Fine-grained access control means that an ASSO system supports users’ obtaining different types of tickets according to attribute disclosure policies. Table 1 indicates that among all schemes in our comparison, only PriSign supports all desirable features, making it a preferred solution in practice.

Table 1.
Functional comparison.
3. Preliminaries
In this section, we recall the definitions of complexity assumption and the cryptographic primitives used in the construction scheme. The abbreviations used in this paper are summarized in Table 2.

Table 2.
Nomenclature.
3.1. Bilinear Pairing
Let , , and be cyclic groups of prime order p. Let g and be generators of and , respectively. The mapping is a bilinear map if it has three properties: (1) bilinearity: , and , and we have ; (2) non-degeneracy: ; (3) computability: e can be efficiently computed. We denote a bilinear group . Our scheme is based on the Type-III pairing [32], which means that there is no efficiently computable homomorphism between and .
3.2. Complexity Assumptions
- Symmetric Discrete Logarithm (SDL) Assumption: Let be a bilinear group. Given and , the SDL assumption holds in if no efficient adversary can compute x with non-negligible probability.
- Decisional Diffie–Hellman (DDH) assumption: Let be an cyclic group of prime order and g be a generator of ; given , the DDH assumption holds in the group if no efficient adversary can distinguish from an element z randomly chosen from .
- Bilinear Decisional Diffie–Hellman (BDDH) Assumption: Let be a bilinear group; given , the BDDH assumption holds if no efficient adversary can distinguish from an element z randomly chosen from .
3.3. Structure-Preserving Signatures
Groth’s structure-preserving signatures (SPS) [33] consist of the following probability polynomial-time (PPT) algorithms:
- : On input a security parameter and a positive integer l, this algorithm generates a bilinear group and outputs public parameters .
- : On input public parameters , this algorithm selects and a generator , then computes . It outputs a secret key and a public key .
- : To sign l messages (), the signer selects , computes ; and , then outputs the signature .
- : To verify the signature on messages , this algorithm checks two pairing equations, and . If both equations are satisfied, it outputs 1; otherwise, it outputs 0.
Groth’s SPS scheme [33] is existentially unforgeable under chosen message attacks (EUF-CMA). In this paper, we use this signature scheme to create credentials for the public key of the ticket issuer.
3.4. Pointcheval–Sanders Signatures
The multiple-message Pointcheval–Sanders (PS) signatures [34] consist of the following PPT algorithms:
- : On input of a security parameter and a positive integer q, this algorithm generates a bilinear group and outputs public parameters .
- : On input public parameters , this algorithm selects and computes . It outputs a secret key and a public key .
- : To sign messages (), the signer selects , computes , and outputs the signature .
- : To verify the signature on messages , this algorithm checks two equations, and . If both equations are satisfied, it outputs 1; otherwise, it outputs 0.
PS signature achieves EUF-CMA secure status under the PS assumption [34].
3.5. Inner-Product Functional Encryption
An inner-product functional encryption (IPFE) [35,36] scheme over the set of attributes consists of the following PPT algorithms:
- : On input of a security parameter , this algorithm outputs a master private key and a master public key .
- : On input of a master private key and a characteristic vector , this algorithm outputs a policy key .
- : On input of a master public key , an attribute vector , and a message M, this algorithm outputs a ciphertext C.
- : On input of a policy key and a ciphertext C, this algorithm outputs the message M if ; otherwise, it outputs the failure symbol ⊥.
An IPFE [36] scheme is secure if it is attribute-hiding; we introduce the definition of attribute-hiding in Supplemental Material A.
3.6. Zero-Knowledge Signature of Knowledge
Zero-knowledge signature of knowledge (ZKSoK) [37] for an NP-relation with the language consists of the following algorithms:
- : On input of a security parameter , this algorithm outputs a public parameter .
- : On input of a message m and a relation , this algorithm it outputs a ZKSoK: .
- : On input of a message m, a ZKSoK , and a statement y, this algorithm returns 1 if is valid; otherwise, it returns 0.
A ZKSoK is - [37] if it satisfies correctness, simulatability, and extractability.
4. System and Security Model
In this section, we describe the system and security model of our PriSign system.
4.1. System Model
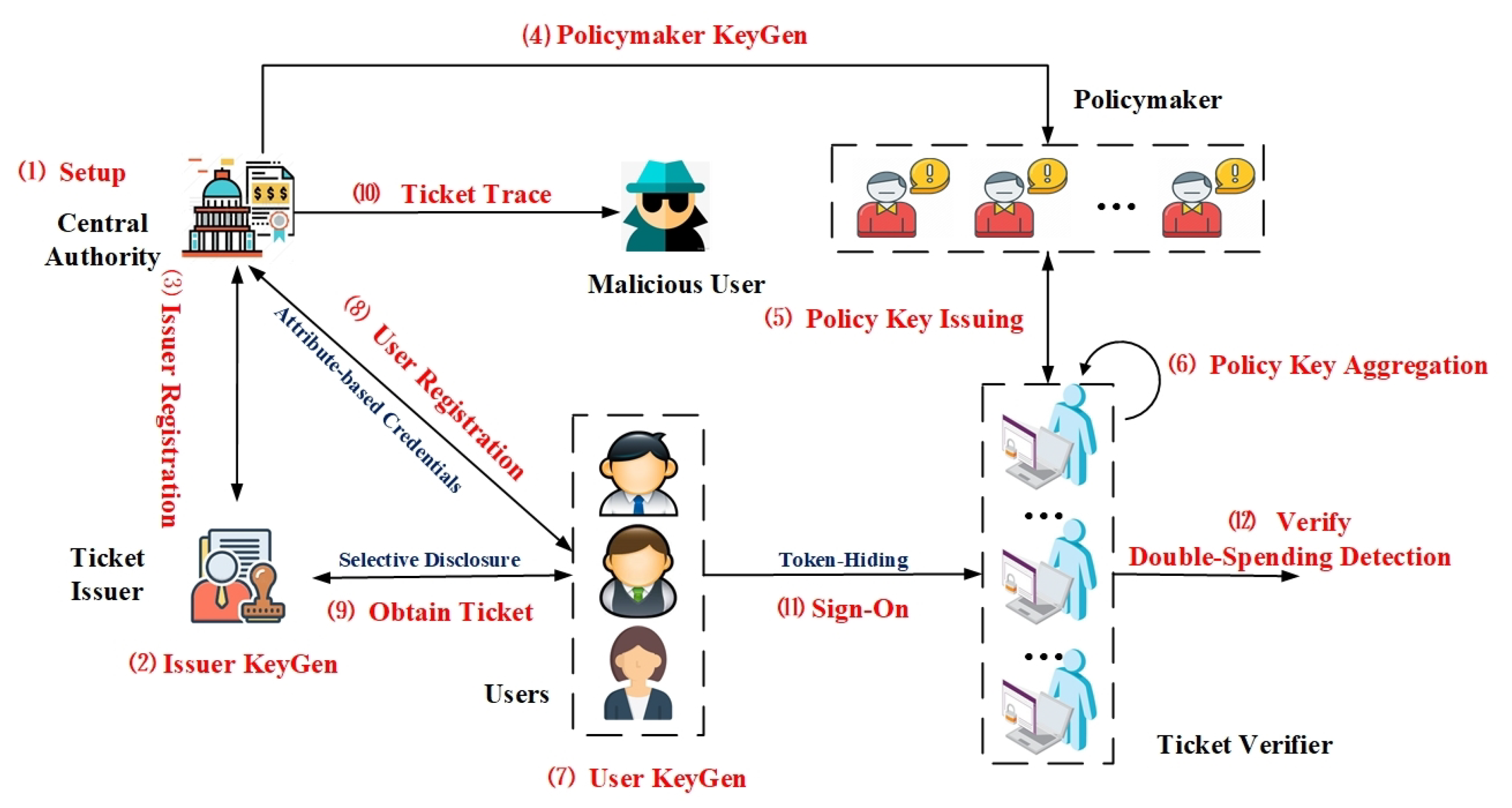
As shown in Figure 1, the architecture of a PriSign scheme consists of five types of parties: a central authority (CA), a ticket issuer (), policymakers (), users (), and ticket verifiers (). The specific role of each party is described below.
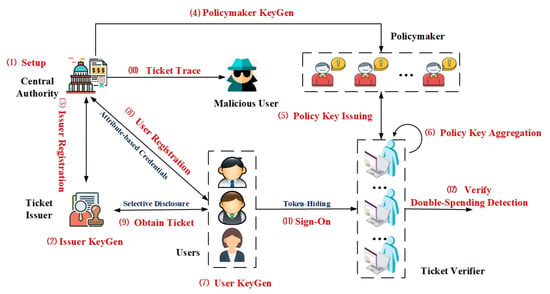
Figure 1.
Architecture of PriSign.
- CA is a trusted global party responsible for setting up the system (step ➀), providing certification service for the ticket issuer (step ➂) and all users (step ➇) as well as issuing keys for a group of policymakers (step ➃). Moreover, CA can trace the identities of malicious users (step ➉).
- I is a ticket issuer and should register with CA (step ➁ and step ➂). I is tasked to verify any user’s credentials according to attribute disclosure policies generated by itself and to issue tickets for users (step ➈).
- P is an independent policymaker which receives keys from CA (step ➃) and is responsible for issuing a share of the policy key for each verifier and binding this share to the verifier’s identity (step ➄). The PriSign scheme is set up with n policymakers, of which t policymakers can cooperate to issue complete policy keys for verifiers. If a verifier is offline, t policymakers can cooperate to issue a new key with the same policy as the offline verifier that is bound to the identity of a new proxy verifier. This proxy-verifier can replace the offline verifier in order to complete the verification of tokens that are designated to be verified by the offline verifier.
- U with with a set of attributes should apply for a credential from CA (steps ➆ and ➇). To obtain a ticket, U needs to present a credential to I anonymously and disclose a subset of attributes to prove that the attribute disclosure policy enforced by I is satisfied (step ➈). To access a designated service with a ticket, U computes an access token of the ticket using an attribute vector that matches the designated verifier’s policy (step ⑪).
- V should request that each of t online policymakers receive a share of the policy key bound to its identity (step ➄) and aggregate them into a complete policy key (step ➅). V with a complete policy key that matches the user’s attribute vector then provides token verification services for those users who designate it as the verifier, and can detect any double-spending tickets (step ⑫).
In practical applications, in order to prevent users from accessing services unrestricted, tickets applied by users from issuers can only be used once, such as movie tickets and traffic tickets. However, electronic tickets are easily copied and shared, meaning that malicious users must be prevented from double-spending. In this paper, we use the pre-generated double-spending identity as the unique identity of the ticket; if the verifier detects that the double-spending identity is repeated, it suspends access.
4.2. Formal Definition
The notation used in the scheme is summarized in Table 3. The PriSign scheme consists of the following PPT algorithms:

Table 3.
Summary of notation.
- : This algorithm is operated by CA, which inputs a security parameter , a number of user attributes q, a number of policymakers n and threshold value t, and a policy length k, then outputs the system parameters , a main key pair , and a user registration list , where contains a matching function over the set of attribute vectors and the set of policies . To simplify the description, the remaining algorithms take as the input by default.
- : This algorithm is operated by the ticket issuer and outputs a secret key and public key .
- : This algorithm operates by interacting between I and CA to issue a public key credential for I. I takes as inputs, while CA takes and as inputs. It returns either a credential for I if the execution of the algorithm succeeds, or ⊥ if the execution fails.
- : This algorithm is operated by CA to issue keys for n policymakers. It inputs , , and outputs a private key and a verification key for each P, where . Note that t policymakers can cooperate to recover the complete key used to generate policy keys for verifiers.
- This algorithm is operated by a policymaker P with index i to generate a share of a policy key for a verifier with identity and policy . It inputs , a verifier’s identity , and a policy , and outputs a share of policy key .
- ; This algorithm is operated by V, which receives t shares of the policy key from t policymakers and aggregates them into a complete policy key. It inputs , , t shares of policy key , and , then outputs a complete policy key .
- : This algorithm is operated by U and outputs a private key , a public key , and a tracing key .
- : This algorithm is operated by interacting between U and CA to issue an attribute-based credential for U. U takes the identity , , , and set of attributes as inputs, while CA takes , , and as inputs. It returns either a credential for U and updated user registration list if the execution of the algorithm succeeds, or ⊥ if the execution fails.
- : This algorithm operates by interacting between U and I to issue a ticket for U. U takes , , , , an attribute disclosure policy (), and a context as inputs, while I takes , , and as inputs. It outputs either a credential presentation , a ticket , the ticket’s double-spending identity , and validity period if the execution of the algorithm succeeds, or if the execution fails, ⊥. Note that should satisfy an attribute disclosure policy generated by I to pass I’s verification, and CTX is a random value to prevent replay attacks.
- : This algorithm is operated by CA, which takes , , and as inputs, and outputs either a user’s identity if the execution of the algorithm succeeds or ⊥ if the execution fails.
- : This algorithm is operated by U to create an access token to a designated verifier with the policy . It takes , , , an attribute vector that matches the policy (i.e., ), and as inputs, then outputs an access token .
- : This algorithm is operated by a designated verifier V that takes , , , and as inputs. It outputs 1 if the token is validated and not double-spending, and 0 otherwise.
Correctness. A PriSign scheme is correct if it satisfies the following conditions: (1) access tokens generated by honest users can be verified by designated verifiers; (2) the identities of users who have successfully obtained tickets can be traced by the CA. The formal correctness definition is shown in Supplemental Material E.1.
4.3. Overflow of PriSign
As shown in Figure 1, the working flow of a PriSign scheme is described as follows. CA initializes the system and outputs public parameter , a main key pair , and a user registration list (PriSign.Setup step ➀). To be a legitimate ticket issuer, I generates a private and public key pair () (PriSign.IssuerKeyGen step ➁) and authenticates to CA to obtain their public key credential (PriSign.IssuerReg step ➂). To achieve stable policy key generation in an unstable cloud environment, CA issues keys to n policymakers such that t of these policymakers cooperate to generate the complete policy keys for verifiers (PriSign.PolMakKeyGen step ➃); t policymakers then generate a share of the policy key for the respective verifier with identity and policy (PriSign.IssPolKey step ➄) and the verifier aggregates the t shares into a complete policy key (PriSign.AggrPolKey step ➅). Suppose a verifier with policy is offline. In this case, t policymakers can cooperate to issue a new key with the policy for a proxy verifier with identity ; this proxy verifier can replace the offline verifier to complete the verification of tokens that are designated to be verified by the offline verifier. When joining the system, each U generates a private and public key pair () and a tracing key (PriSign.UserKeyGen step ➆), then U authenticates to CA to obtain their attribute-based credentials (PriSign.UserReg step ➇). To obtain a ticket, U authenticates to I by computing a credential presentation and disclosing a subset of attributes, then I issues a ticket for U (PriSign.ObtTkt step ➈). At this point, CA can trace the identities of users (PriSign.Trace step ➉). When accessing a designated service, U computes an access token of the ticket using an attribute vector that matches the designated verifier’s policy (PriSign.SignOn step ⑪). The designated verifier with the policy key verifies the validity of the token and detects whether it is double-spending (PriSign.Verify step ⑫).
4.4. Threat Model
We assume that the central authority CA is a globally trusted party in the system. The ticket issuer I is assumed to be honest but curious, in the sense that while it is honest in issuing tickets for users according to the attribute disclosure policies, it is curious about obtaining users’ undisclosed attributes and real identities. Policymakers P are globally trusted parties in the system, assuming that at least t out of n policymakers in a cloud environment simultaneously provide policy key generation services online. Users U are assumed to be malicious; they either forge the credential presentations to illegally obtain tickets, or directly forge tokens to illegally access designated services. Verifiers V are assumed to be honest but curious; V honestly verifies tokens of the users who designated it as a verifier and prevents double-spending of tickets, but is curious about the real identities of the users. In addition, it is curious about knowing the token information of users who did not designate it as the verifier.
4.5. Security Model
In this section, we adopt a game-based model to define the security properties of the PriSign scheme, including its unforgeability, unlinkability, and token-hiding. All security definitions use the following global variables and oracles. There is a challenger and a PPT adversary in the game; is responsible for initializing the system, issuing keys for all policymakers, and controlling all global variables and oracles; and interacts with through the oracles to break the scheme.
Global Variables.
: a set storing each time CA issues a credential for an honest user .
: a set of corrupt user identities ;
: a set storing when CA issues a credential for the ticket issuer.
: a set storing each time t policymakers cooperate to generate a policy key for a verifier with policy .
: a set storing each time I issues a ticket for an honest user .
: a set storing each time U create an access token to a designated verifier with a policy .
Oracles.
−: It is an oracle that can be used to issue a public key credential for the ticket issuer. It generates a key pair by running , and then issues a credential to the ticket issuer by running . Finally, it adds to and returns .
−: an oracle that can be used to corrupt the ticket issuer by returning .
−: an oracle that can be used to generate a policy key for a ticket verifier with a policy . If , then it returns ⊥; otherwise, it runs , then runs , and finally adds to .
−: an oracle that can be used to corrupt a ticket verifier with the policy by returning .
−: an oracle that can be used to issue an attribute-based credential for an honest user with an attribute set . If , then it returns ⊥; otherwise, it generates keys by running , then issues a credential to user by running . Finally, it adds to .
−: an oracle that can be used to corrupt an honest user . If , then it returns ⊥. If , then it removes from and adds to . Finally, it returns .
an oracle that can be used to play the honest ticket issuer issuing a ticket to an honest user . If , it returns ⊥; otherwise, it runs . Finally, it adds to .
an oracle that can be used to play the corrupted ticket issuer issuing a ticket to an honest user . If , it returns ⊥; otherwise, it runs , where the ticket issuer’s side is executed by the adversary. Finally, it adds to .
an oracle that can be used to play the honest ticket issuer issuing a ticket to a corrupt user . If , it returns ⊥; otherwise, it runs , where the user’s side is executed by the adversary. Finally, it adds to , where * is unknown.
an oracle that can be used to play an honest user with an attribute vector creating a token to a designated verifier with the policy . If , it returns ⊥; otherwise, it runs . Finally, it adds to and returns .
−: a challenge oracle in the unlinkability of credentials experiment, where the adversary playing as the ticket issuer is challenged to distinguish credential presentations computed by two different users. It takes two identities of users and an attribute disclosure policy as inputs, then runs , where . Finally, it returns . Note that the attributes disclosed by both users should be the same, i.e., .
−: a challenge oracle in the unlinkability of tokens experiment, where the adversary playing as a designated ticket verifier with the policy is challenged to distinguish access tokens computed by two different users. It takes two identities of users and an attribute vector that matches the policy (i.e., ) as inputs. It first runs , where , then runs . Finally, it returns .
−: a challenge oracle in the token-hiding experiment, where the adversary playing as a non-designated ticket verifier with the policy is challenged to distinguish access tokens derived from two different tickets. It takes two tickets , an attribute vector that does not match the policy ((i.e., )), and as inputs. It runs , where , then returns .
4.5.1. Unforgeability
The unforgeability of credentials protects honest ticket issuers from malicious users. The adversary wins the game by forging a credential presentation of an honest user or an unregistered user in the algorithm.
Definition 1

(Unforgeability of credentials). The unforgeability of credentials is defined by experiment in Figure 2. The users’ credentials are unforgeable if, for any PPT adversary having access to the oracles , there is a negligible function such that

Figure 2.
Unforgeability of credentials.
The unforgeability of tokens protects ticket verifiers from malicious users. If an adversary can forge a token not issued by the ticket issuer, this wins the game.
Definition 2

(Unforgeability of tokens). The unforgeability of tokens is defined by experiment in Figure 3. The users’ tokens are unforgeable if, for any PPT adversary having access to the oracles , there is a negligible function such that

Figure 3.
Unforgeability of tokens.
4.5.2. Unlinkability
The unlinkability of credentials protects honest users from a curious ticket issuer. In the PriSign.ObtTkt algorithm, the curious ticket issuer cannot distinguish between the credential presentations of two honest users with non-negligible probability.
Definition 3

(Unlinkability of credentials). The unlinkability of credentials is defined by experiment in Figure 4. The users’ credentials are unlinkable if, for any PPT adversary having access to the oracles and , there is a negligible function such that

Figure 4.
Unlinkability of credentials.
The unlinkability of tokens protects honest users from curious designated verifiers. In this experiment, the adversary can control all verifiers by querying the oracle , and even the designated verifier cannot distinguish the tokens of two honest users with non-negligible probability.
Definition 4

(Unlinkability of tokens). The unlinkability of tokens is defined by experiment in Figure 5. The users’ tokens are unlinkable if, for any PPT adversary having access to the oracles and , there is a negligible function such that

Figure 5.
Unlinkability of tokens.
4.5.3. Token-Hiding
Token-hiding protects honest users from curious non-designated verifiers. In the PriSign.Sign algorithm, any non-designated verifiers cannot distinguish the tokens of two different tickets with non-negligible probability.
Definition 5

(Token-hiding). Token-hiding is defined by experiment in Figure 6. Users’ tokens are hidden if, for any PPT adversary having access to the oracles and , there is a negligible function such that

Figure 6.
Token-hiding.
5. Construction of PriSign
In this section, we provide a detailed description of the PriSign system’s construction.
5.1. Challenges and Intuitions
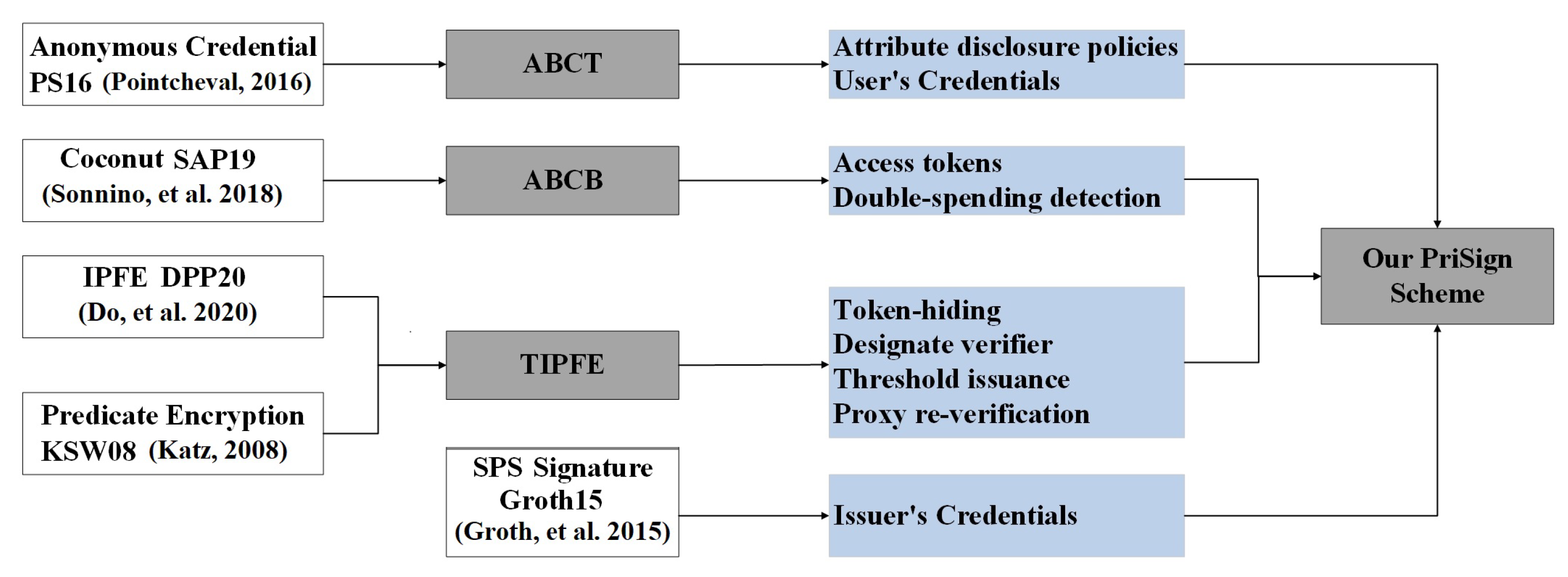
The schemes described in [33,34,35,36,38] form the basis of our construction; the challenge is to combine and adapt them to ensure that the final scheme satisfies the system and security model proposed in Section 4. As shown in Figure 7, we summarize the dependencies between the building blocks used by PriSign along with a roadmap highlighting our contributions in gray boxes.
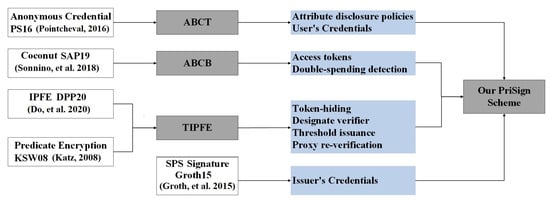
Figure 7.
Building blocks and roadmap [33,34,35,36,38].
First, we construct an attribute-based credential with traceability (ABCT) scheme from the anonymous credential in [34] and utilize it to create users’ credentials. Because our ABCT scheme supports attribute disclosure proofs with unlinkability, the ticket issuer can issue different types of tickets for users according to different selective disclosure policies in the PriSign scheme, thereby realizing fine-grained access control of services. In addition, this enables PriSign to support traceability of users.
Second, we construct an attribute-based credential with blindness (ABCB) scheme from the anonymous credential in [38] and utilize it to issue tokens for users. Our ABCB scheme supports issuing credentials based on both unblinded and blinded attributes simultaneously. Therefore, when issuing a ticket, the double-spending identity of the ticket can be used as the blinded attribute and the ticket’s validity period as the unblinded attribute.
Third, we construct a threshold inner-product functional encryption (TIPFE) scheme from the inner-product functional encryption (IPFE) in [35] and predicate encryption scheme in [36]. We use TIPFE’s encryption algorithm to hide tokens, TIPFE’s inner product predicate as the matching function to designate verifiers, and TIPFE’s threshold key issuance to achieve stable policy key generation for verifiers in cloud environments. Finally, the SPS [33] scheme enables us to implement public key credential issuance of the ticket issuer.
5.2. New Results and Building Blocks
5.2.1. Attribute-Based Credentials with Traceability
We construct an attribute-based credential with traceability (ABCT) scheme from the anonymous credential scheme in [34]. Compared with the original scheme [34], our ABCT scheme is improved in three aspects: (1) we enable users to generate public and private key pairs independently and obtain credentials of attributes set and the public key without disclosing their private keys; (2) we extend the feature to support malicious user identity tracing while protecting user privacy; and (3) we modify the credential presentation algorithm (Show) to support efficient selective disclosure, which is essential to support fine-grained access control.
: On input of a security parameter and a positive integer q, this algorithm generates a bilinear group and sets , where q is the attribute number for user.
: This algorithm is operated by an issuer to generate their public private key pair. The issuer chooses and computes and for . Then, it initializes a user registration list and outputs a private key and public key .
: This algorithm is operated by a user to generate their public private key pair. The user chooses a private key , then computes their public key and tracing key .
: This algorithm operates by interacting between a user and an issuer to create an attribute-based credential for the user.
- : The user computes a ZKSoK , then sends their identity , attribute set , and to the issuer.
- : After is verified, the issuer chooses and computes , . Then, it sets and returns .
- : The user accepts the credential if holds.
: This algorithm is operated by a user to anonymously present a credential while disclosing a subset of attributes , where . The user chooses , computes , , and computes a ZKSoK . Finally, the user outputs a credential presentation . Note that CTX is a random value used to prevent replay attacks.
: This algorithm is operated by a verifier. The verifier outputs 1 if the user’s attributes satisfy an attribute disclosure policy enforced by the verifier, , and is verified, and outputs 0 otherwise.
: This algorithm is operated by the issuer to trace the identity of a user who generates the presentation . The issuer outputs if there exists a tuple in satisfying ; otherwise, it outputs ⊥.
The details of the ZKSoK and the correctness analysis of our ABCT scheme are shown in Supplemental Material B. Naturally, our ABCT scheme satisfies the unlinkability and unforgeability the same as the anonymous credential scheme in [34]. In this paper, we use the ABCT scheme to issue a credential for the public key and attributes set of a user.
5.2.2. Attribute-Based Credentials with Blindness
We construct an attribute-based credential with blindness (ABCB) scheme by making two crucial modifications to the anonymous credential in [38]: (1) we streamline the threshold issuance functionality of the original scheme to ensure that there is only one issuer in the ABCB scheme and (2) we extend it to support both blind issuing of user attributes and adding non-blind attributes to user credentials by the issuer in the issuing credential algorithm. In short, attributes of user credentials can come from both user and issuer, and attributes from the user are hidden from the issuer.
: On input of a security parameter and a positive integer l, this algorithm generates a bilinear group and sets .
: The issuer chooses , then computes and for . Then, it outputs a private key and public key .
: This algorithm is used to issue attribute-based credentials for users, with attributes consisting of two parts: (1) attributes that the user owns are hidden from the issuer and (2) attributes that the issuer adds to the user .
- : The user chooses a secret key , then computes a public key and a group element , chooses a random , and computes the ElGamal encryption for each (): . The user computes a ZKSoK and sets .
- : After is verified, the issuer recomputes and returns , where are computed as follows: .
- .The user computes and sets . The user accepts the credential if holds.
: The user chooses , computes , , and computes a ZKSoK . The user outputs a token .
: The verifier outputs 1 if the user’s attributes satisfy an attribute disclosure policy enforced by the verifier, , and is verified; otherwise, it outputs 0.
The details of the ZKSoK and the correctness analysis of our ABCB scheme are shown in Supplemental Material C. Naturally, our ABCB scheme satisfies the unlinkability, unforgeability, and blindness requirements, the same as the anonymous credential scheme in [38]. In this paper, we use the ABCB scheme to create tickets for users.
5.2.3. Threshold Inner-Product Functional Encryption
Threshold inner-product functional encryption (TIPFE) is inspired by Inner-product functional encryption (IPFE) [35]. First, we realize the threshold key extraction algorithm using the linear feature of IPFE’s key extraction algorithm. Of course, this modification sacrifices its traceability, which is unnecessary in this application. Second, we use the transformation in [36] to convert the predicate-only scheme into a full-fledged predicate encryption scheme.
: This algorithm is operated by a central authority to generate public parameters and a master key pair for the system.
- Set
- Randomly choose
- Compute , and , and set
This algorithm is operated by the central authority to issue shared keys for n policymakers, where t policymakers cooperate to recover the master key.
- Choose polynomials of degree with coefficients in , denoted as , and set
- Compute and where , and set
- Compute where , and set
: This algorithm is operated by a policymaker i to issue a share of a policy key for a receiver with identity and a characteristic vector .
- Set and compute
- Compute
: This algorithm is operated by a receiver to aggregate t received shares of policy keys into a compact policy key.
- For each , check
- For each , compute
- Compute
This algorithm is operated by a sender to encrypt a message M with an attribute vector .
- Randomly choose , then compute
- Compute
- Set
: This algorithm is operated by a receiver to decrypt the ciphertext using a policy key.
- If , compute
Theorem 1.
Our TIPFE scheme satisfies attribute-hiding under the BDDH assumption.
The correctness analysis and formal proof of our TIPFE scheme are provided in Supplemental Material D. In this paper, we use the TIPFE scheme to achieve token-hiding and proxy re-verification.
5.3. Concrete Construction
In this section, we present a concrete instantiation of the PriSign scheme based on the ABCT scheme in Section 5.2.1, the ABCB scheme in Section 5.2.2, the TIPFE scheme in Section 5.2.3, and Groth’s SPS scheme [33].
- : As shown in Figure 8, CA runs to generate public parameters (a Type-III bilinear group) for other algorithms of PriSign scheme, runs to generate keys used to issue public-key credentials for issuers, runs to generate keys used to issue attribute-based credentials for users, and runs to generate the keys used to issue keys for policymakers. Finally, it sets the public parameters , master secret key , master public key , and user registration list .
 Figure 8. Setup algorithm.
Figure 8. Setup algorithm. - : The ticket issuer runs to generate its secret key and public key used to issue tickets for users.
- : As shown in Figure 9, CA computes an SPS signature on the issuer’s public key and treats it as the issuer’s credential. The details of are shown in Supplemental Material E.2.
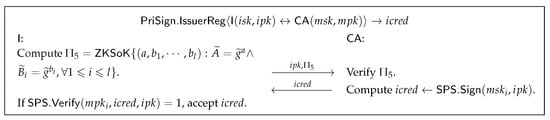 Figure 9. Issuer Registration algorithm.
Figure 9. Issuer Registration algorithm. - : CA runs to generate keys for all policymakers.
- : The policymaker i runs to issue a share of the policy key to a verifier with identity and policy .
- : The verifier runs to obtain a compact policy key.
- : A user runs to create their private key, public key, and tracing key.
- : CA and a user run to create a credential for the user.
- : As shown in Figure 10, I computes a ZKSoK to prove to the user that it has been authenticated by CA. After verifying I’s and credential , U computes a credential presentation by executing , then randomly selects a double-spend identity for the ticket, blinds it by executing , and sends to I. I verifies the correctness of the user credential and chooses a validity period for the ticket, then computes a ticket by executing and returns . Finally, the user restores the ticket by executing .
 Figure 10. Obtain Tickets algorithm.
Figure 10. Obtain Tickets algorithm. - : CA runs to trace the user’s identity.
- : As shown in Figure 11, U computes a ticket presentation by executing , then randomly selects an encryption key K and encrypts the presentation information using the AES-CTR algorithm [39,40] to achieve token-hiding. Finally, U encrypts K using the attribute vector that matches the policy , i.e., , to achieve designated verification, and returns .
 Figure 11. Sign-On algorithm.
Figure 11. Sign-On algorithm. - As shown in Figure 12, the designated verifier with policy key recovers key K by executing and decrypts the ticket presentation information using the AES-CTR algorithm. Then, it checks whether is within the validity period and checks all tickets with the same in the history to detect whether the ticket is double-spending. Finally, V verifies the correctness of the ticket presentation by executing .
 Figure 12. Verify algorithm.
Figure 12. Verify algorithm.
6. Security Analysis
We define the following theorems to formalize that our construction satisfies all the desired security arrangements.
Theorem 2.
Our PriSign scheme is correct.
Proof.
Naturally, if the ABCT scheme, the ABCB scheme, the TIPFE scheme, and Groth’s SPS scheme satisfy correctness, then our PriSign scheme is correct. □
Theorem 3.
Our PriSign scheme satisfies the unforgeability of credentials if the SDL assumption holds and the PS signature is unforgeable.
Proof.
The proof is provided in Supplemental Material E.3.1. □
Theorem 4.
Our PriSign scheme satisfies the unforgeability of tokens if the PS signature is unforgeable.
Proof.
The proof is provided in Supplemental Material E.3.2. □
Theorem 5.
Our PriSign scheme satisfies the unlinkability of credentials if the DDH assumption holds in .
Proof.
The proof is provided in Supplemental Material E.3.3. □
Theorem 6.
Our PriSign scheme satisfies the unlinkability of tokens if the ABCB scheme satisfies the same.
Proof.
The proof is provided in Supplemental Material E.3.4. □
Theorem 7.
Our PriSign scheme satisfies token-hiding if the TIPFE scheme satisfies attribute-hiding and the AES-CTR algorithm is CPA-secure.
Proof.
In the PriSign.SignOn algorithm, we use the AES-CTR algorithm to hide the presentation of tickets and the TIPFE scheme to hide the AES encryption key. According to the definitions of attribute-hiding and CPA-secure, it can be directly concluded that our scheme is token-hiding. □
7. Performance Analysis
In this section, we present a performance analysis of PriSign from both the theoretical and experimental aspects.
7.1. Theoretical Analysis
In Table 4 and Table 5, the proposed PriSign system is compared with state-of-the-art ASSO systems [8,9] in terms of computation and storage overheads. Let , , and be the element sizes in group , , and , respectively; here, , , and represent the time cost for the exponential in group , , and the pairing computations, respectively.

Table 4.
Computation overhead.

Table 5.
Storage overhead.
Table 4 presents the storage cost of the algorithms in our PriSign system, including Setup, IssuerReg.I, IssuerReg.CA, IssPolKey, AggrPolKey, UserReg.U, UserReg.CA, ObtTkt.U, ObtTkt.I, SignOn, and Verify. Because the systems in [8,9] do not support policy issuing with thresholds, the performance comparison does not include IssPolKey and AggrPolKey. As shown in Table 4, even though our scheme supports token-hiding and designating verifiers, it is nonetheless able to achieve constant complexity of service access (SignOn) and verification (Verify) under the selected parameter k. In addition, it takes only a single exponentiation operation in for a policymaker to generate a policy key for a verifier (IssPolKey); while the computational complexity of the aggregate key is linear () to the threshold value (AggrPolKey), t is fortunately small in actual deployments. Because the systems in [8,9] do not support attribute-based fine-grained access control, the computational cost of obtaining tickets and sign-on in their systems is independent of q. Obviously, when , the computational cost of our system is close to that of the systems in [8,9].
Table 5 presents the computation cost of the algorithms in our PriSign system, including , , , , , , , , , , and . As shown in Table 5, the user credential , ticket seller credential , ticket , and access token all have constant size in the PriSign scheme. The storage overhead primarily consists of the mast public key , for which it is only necessary to store one copy for each user. In addition, when the storage cost of our system is close to that of the systems in [8,9], even with our system’s has additional support for token-hiding and policy issuing with thresholds.
7.2. Experimental Analysis
We implemented the PriSign scheme using MIRACL [41], Type-III pairing [32], and the Barreto-Naehrig curve (BN-256) [42], and tested the system’s performance at the AES-100 bit security level. The source code of our implementation is available at [10]. We ran our implementation on a personal laptop (HUAWEI Matebook 14) with an AMD Ryzen-5 4600H with a Radeon Graphics 3.00 GHz CPU, 16GB RAM, and 512GB SSD running the Ubuntu Kylin 16.04 operating system.
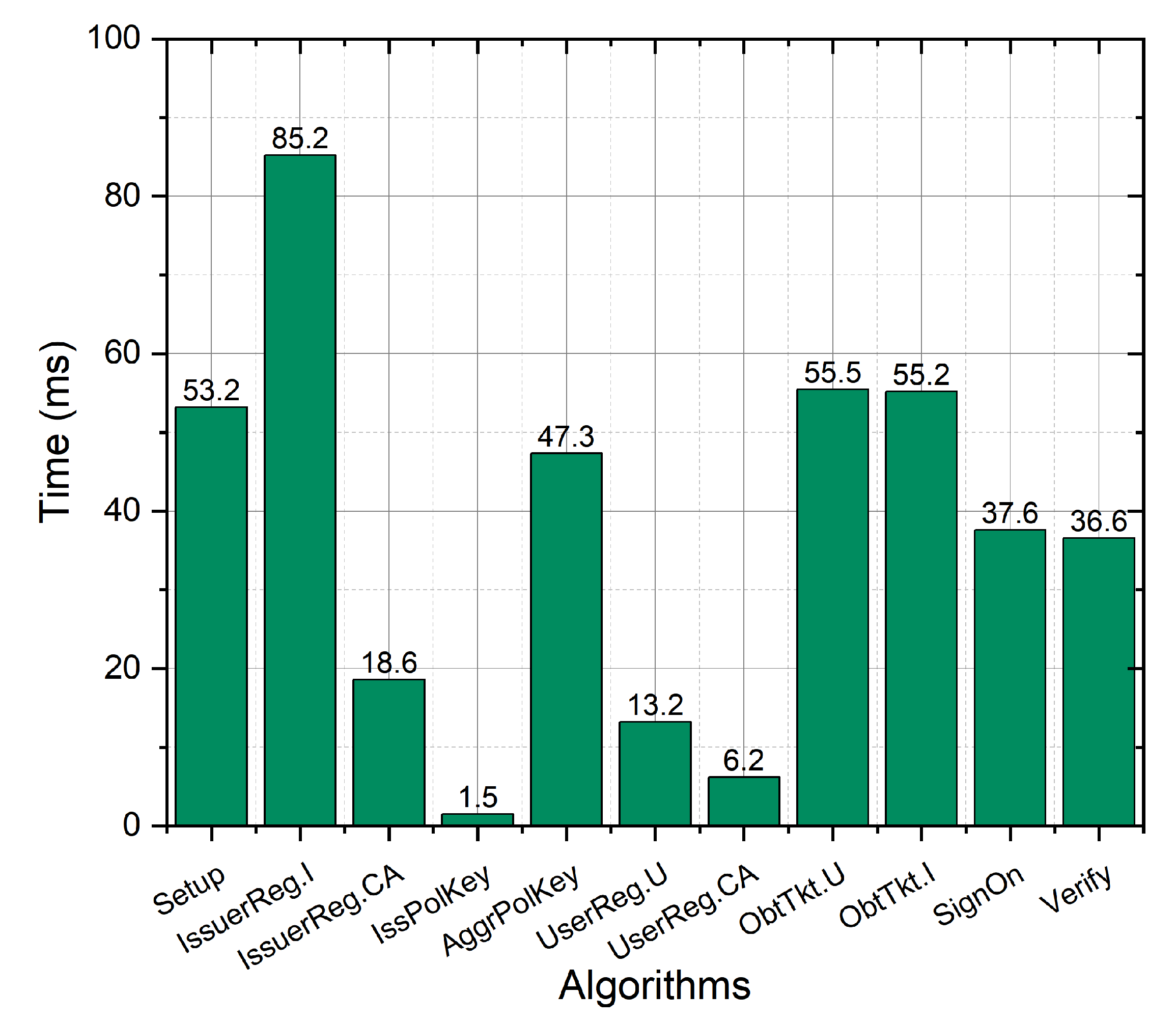
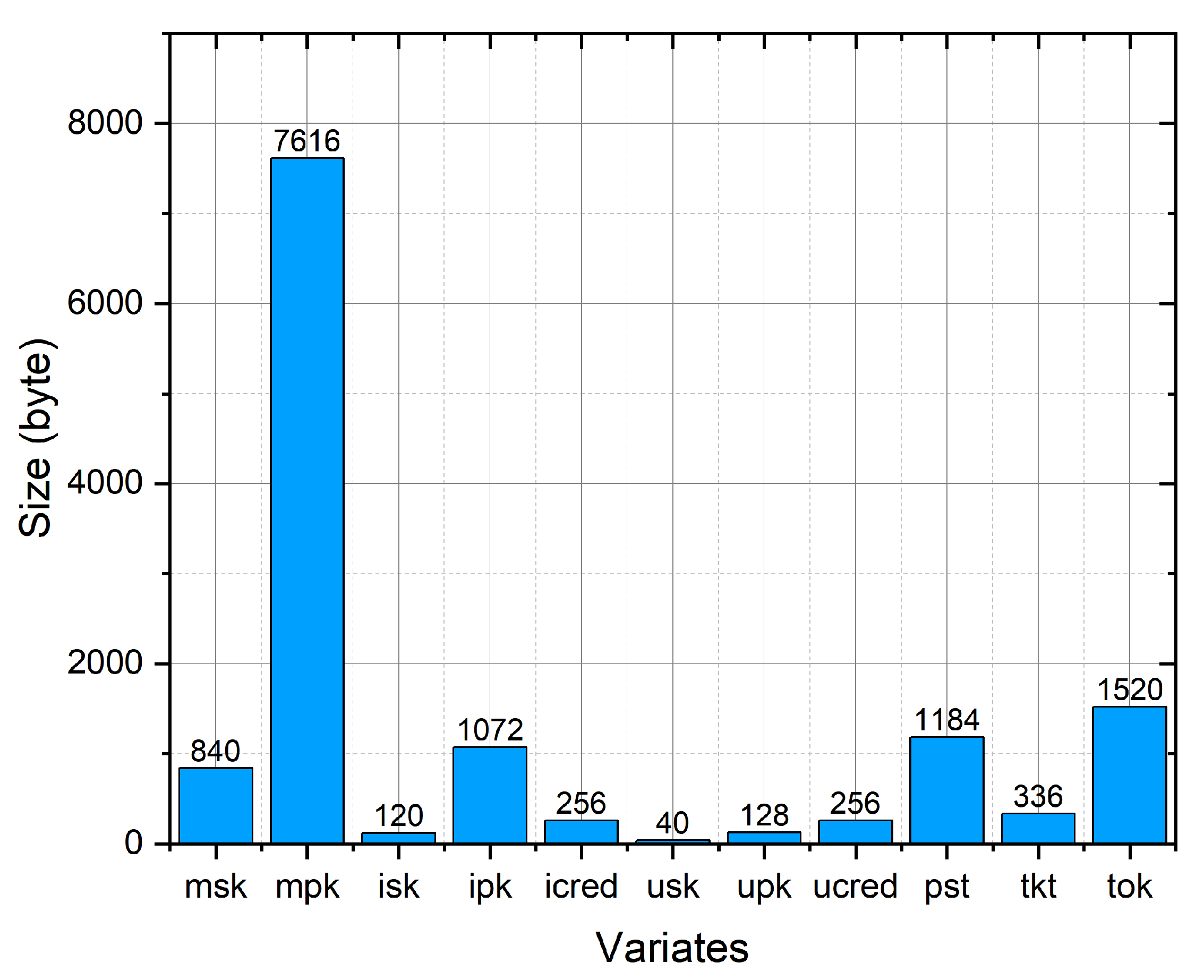
In Figure 13 and Figure 14, we show the computational and storage overheads of all algorithms at , where each timing result is computed as the average over ten iterations.
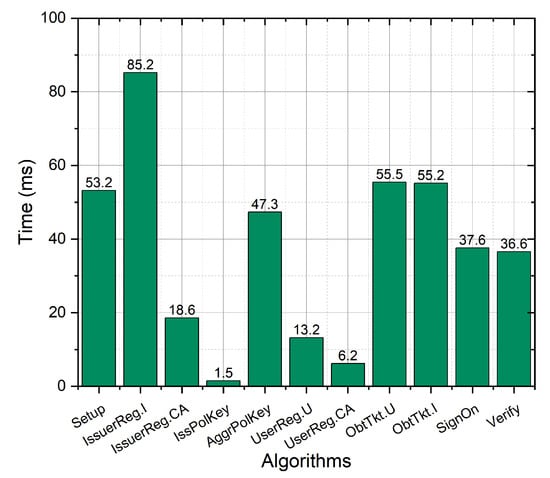
Figure 13.
Execution time of algorithms.
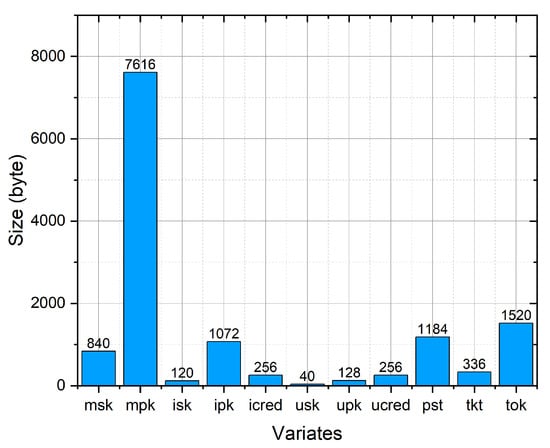
Figure 14.
Storage size of algorithms.
As shown in Figure 13, the Setup algorithm in the PriSign scheme takes 53.2 s. For ticket seller registration, IssuerReg.I and IssuerReg.CA cost 85.2 ms and 18.6 ms, respectively. For policy key generation, IssPolKey and AggrPolKey cost 1.5 ms and 47.3 ms, respectively. For user registration, UserReg.U and UserReg.CA cost 13.2 ms and 6.2 ms, respectively. The most frequently used PriSign algorithms are ObtTkt, SignOn, and Verify. When obtaining a ticket, ObtTkt.U and ObtTkt.I cost 55.5 ms and 55.2 ms, respectively, while when accessing the service, SignOn and Verify cost 37.6 ms and 36.6 ms, respectively. The algorithm that consumes the most time is IssuerReg.I, which takes 85.2 ms; fortunately, it only needs to be executed once for each new issuer. In the algorithm for obtaining tickets, the time required by the user and the issuer is similar, at about 55 ms, while in the sign-on algorithm the time consumed by the user and the verifier is about 37 ms. The above conclusions are consistent with the results in Table 4. In practice, this millisecond time consumption is very friendly to both users and the server.
As shown in Figure 14, for the CA, the storage of private key and public parameters in the PriSign scheme takes 840 bytes and 7616 bytes, respectively. For the issuer, the storage of the private key , public key , and credential takes 120 bytes, 1072 bytes, and 256 bytes, respectively. For the user, the storage of the private key , public key , and credential takes 40 bytes, 128 bytes, and 256 bytes, respectively. For obtaining tickets, the storage of the presentation and ticket takes 1184 bytes and 336 bytes, respectively. For the sign-on protocol, the storage of the token takes 1520 bytes. We note that all storage consumption values are byte scale, which is not a burden on the users or the server.
In order to evaluate the performance in a real test, we compared the execution time with the system in [8,9]. In order to fairly compare performance, we used the following settings during testing: (1) because the systems in [8,9] do not support attribute-based fine-grained access control, we set and in the experiment; (2) because the systems in [8,9] require a fixed number of designated verifiers while ours does not need this to be specified, we set in the experiment; (3) the remaining parameters were set as .
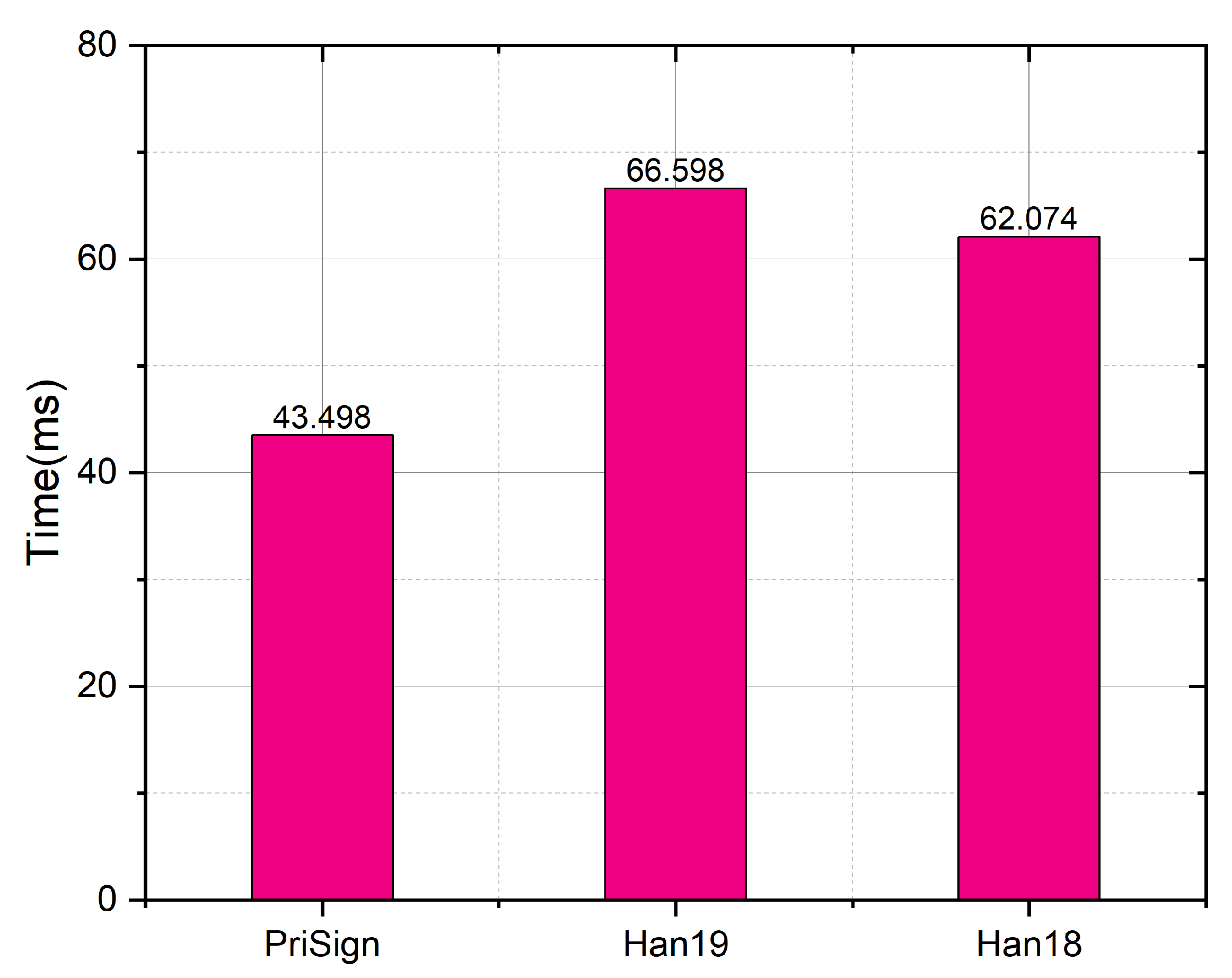
As shown in Figure 15, we compared the ObtTkt.U algorithm in our system to the systems in [8,9]. The computational overheads are 43.4 ms, 62.1 ms, and 65.5 ms, respectively, for our system and the systems in [8,9]. Our system is 30% faster than the system in [8] and 33.8% faster than the system in [9].
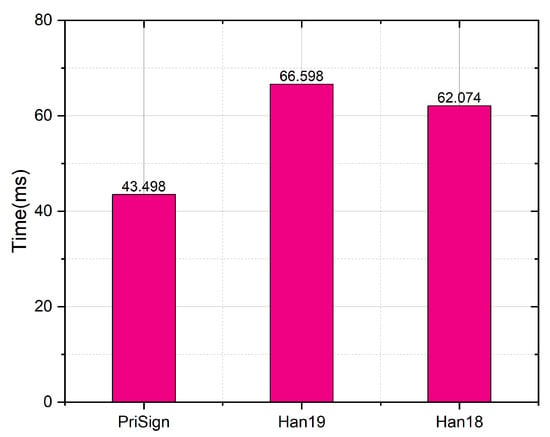
Figure 15.
Time comparison with Han19 [9] and Han18 [8] in ObtTkt.U.
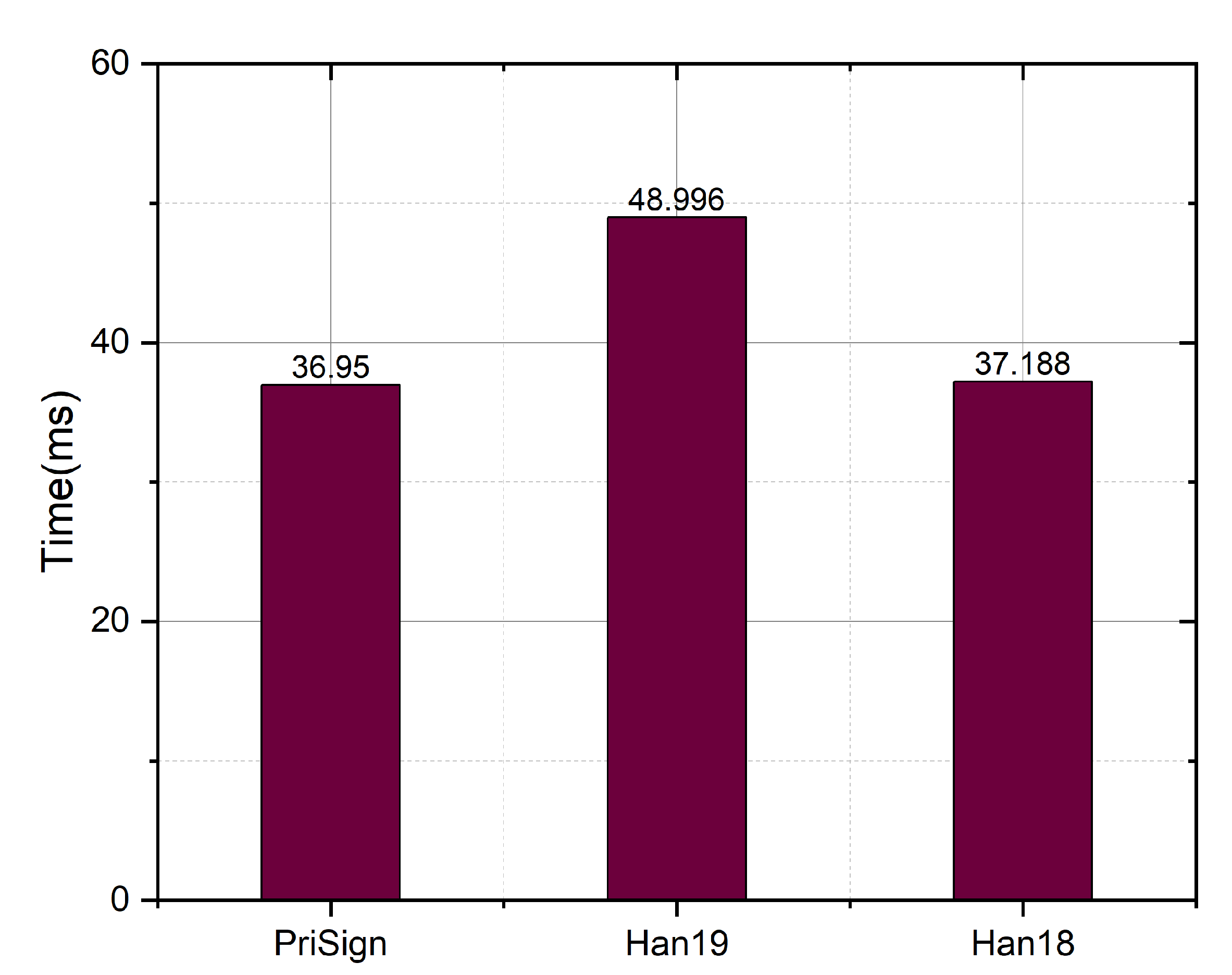
As shown in Figure 16, we compared the ObtTkt.I algorithm in our system with the systems in [8,9]. The computational overheads are 36.9 ms, 37.2 ms, and 48.9 ms, respectively, for our system and the systems in [8,9]. Our system performs as well as the system in [8], and is 24% faster than the system in [9].
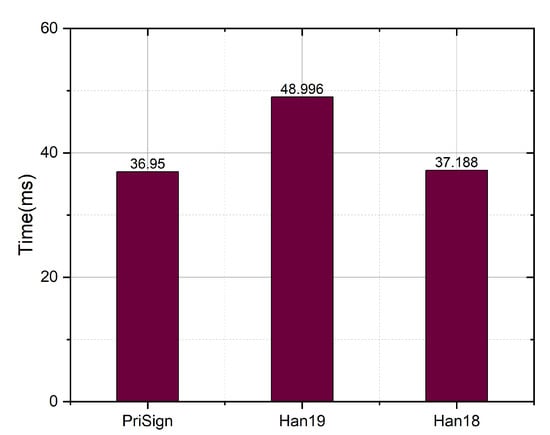
Figure 16.
Time comparison with Han19 [9] and Han18 [8] in ObtTkt.I.
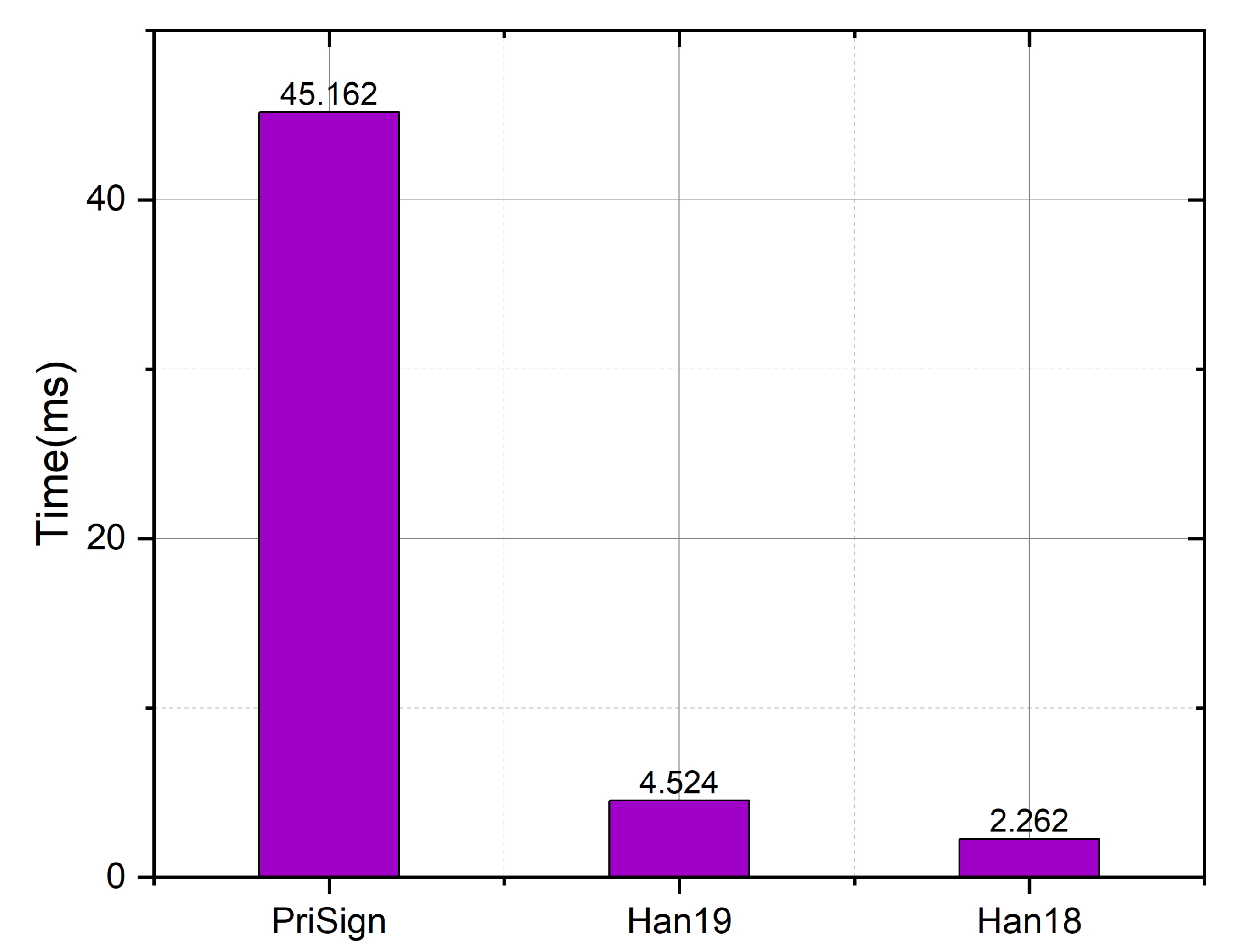
As shown in Figure 17, we compared the SignOn algorithm in our system with the systems in [8,9]. The computational overheads are 45.2 ms, 2.3 ms, and 4.5 ms, respectively, for our system and the systems in [8,9]. Our system is required to perform TIPFE encryption operations due to the need to support token-hiding, resulting in higher computing consumption than the systems in [8,9]. However, our computing costs are nonetheless on the second scale, and as such are suitable for deployment in real-world applications.
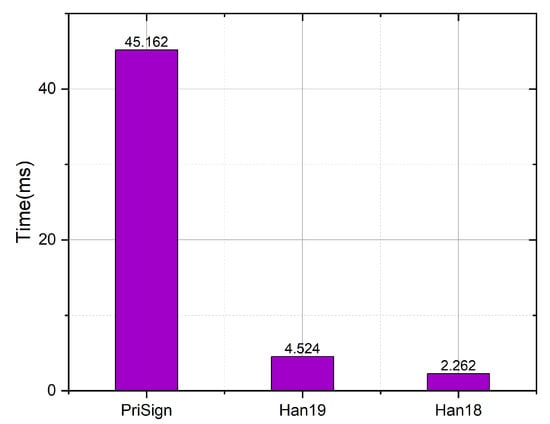
Figure 17.
Time comparison with Han19 [9] and Han18 [8] in SignOn.
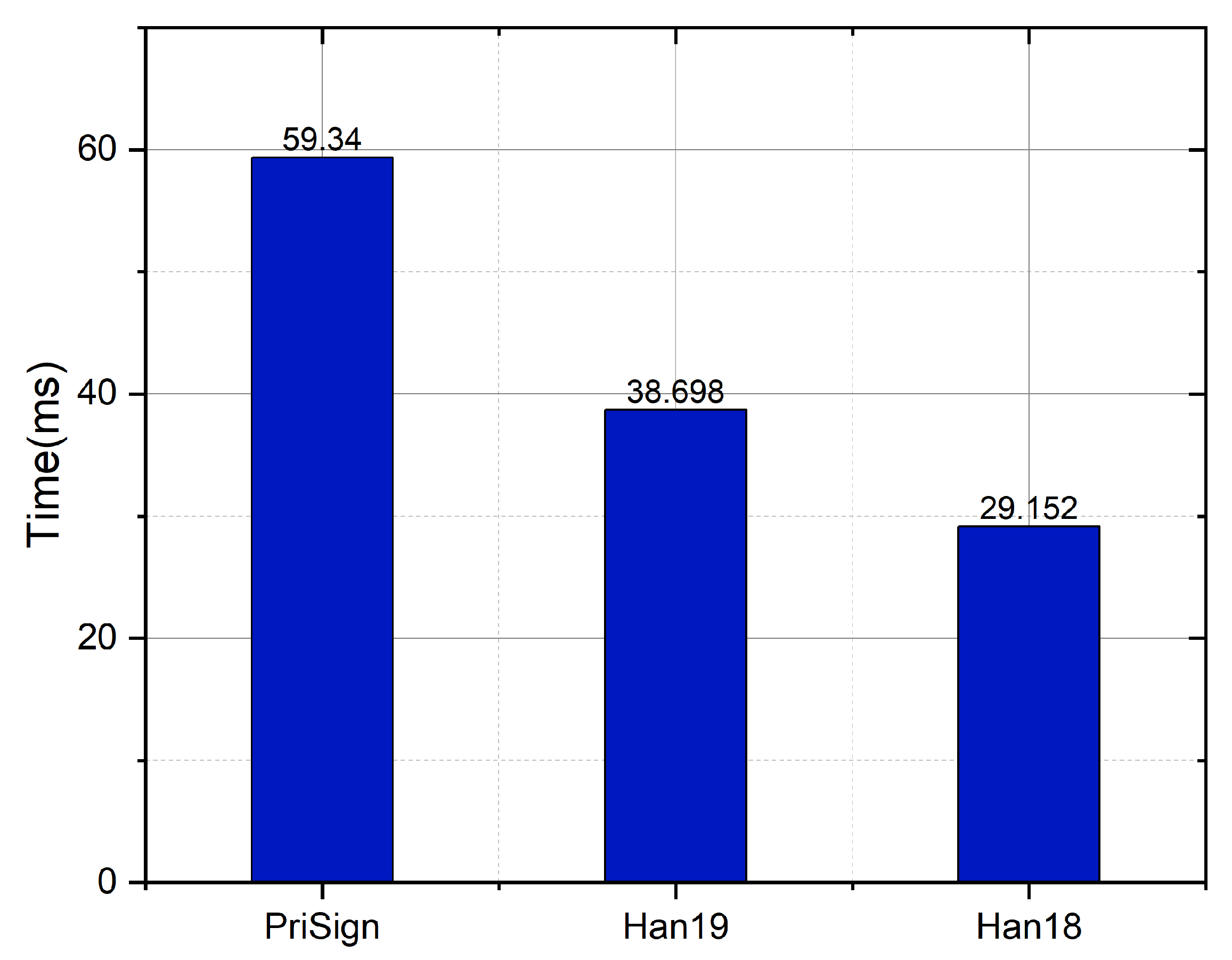
As shown in Figure 18, we compared the Verify algorithm in our system with the systems in [8,9]. The computational overheads are 59.3 ms, 29.1 ms, and 38.7 ms, respectively, for our system and the systems in [8,9]. Although our system has a higher computational cost due to its support for token-hiding, the execution efficiency is nonetheless at the same level as the systems in [8,9], making it suitable for real-world applications.
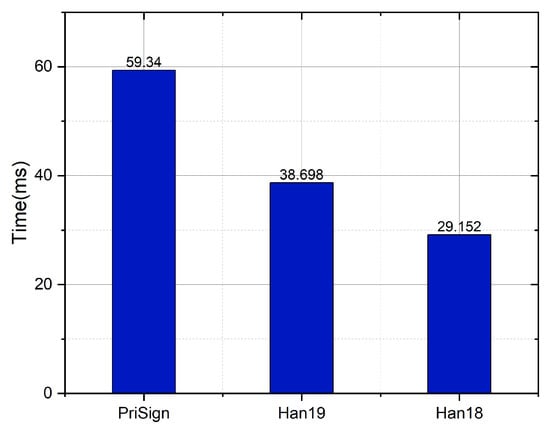
Figure 18.
Time comparison with Han19 [9] and Han18 [8] in Verify.
8. Conclusions
In this paper, we introduce the notion of PriSign to solve the problem of fine-grained access control, token-hiding, and stability of verification services for cloud environments in an ASSO system. First, we redefine the system model of PriSign and provide formal security definitions, including unforgeability, unlinkability, and token-hiding. Second, we provide a concrete construction using the ABCT scheme from Section 5.2.1, the ABCB scheme from Section 5.2.2, the TIPFE scheme from Section 5.2.3, and the SPS signature scheme in [33]. Finally, we provide formal security definitions and proofs and describe our implementation of the algorithms used in the PriSign scheme on a personal laptop to demonstrate its practicability.
Note that there is a relatively higher computing overhead due to our adoption of TIPFE for token-hiding and policy issuing. To further address this problem, we intend to explore new efficient construction schemes for TIPFE in the future along with other approaches for achieving token-hiding.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/app13020727/s1.
Author Contributions
Conceptualization, H.X. and R.S.; methodology, R.S., Y.Y. and H.X.; validation, R.S., Y.Y., H.X. and H.F.; formal analysis, H.F., G.S. and J.Z.; writing—original draft preparation, R.S., Y.Y. and H.X.; writing—review and editing, H.F. and G.S.; visualization, G.S. and J.Z.; project administration, G.S.; funding acquisition, H.F. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Program of China under Grant 2018YFB0803600 and the National Natural Science Foundation of China under Grant No.61872091.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no potential conflict of interest with respect to the research, authorship, or publication of this article.
References
- Recordon, D.; Reed, D. OpenID 2.0: A platform for user-centric identity management. In Proceedings of the Second ACM Workshop on Digital Identity Management, Alexandria, VA, USA, 3 November 2006; pp. 11–16. [Google Scholar]
- MIT Kerberos: Kerberos: The Network Authentication Protocol. 2017. Available online: https://web.mit.edu/kerberos/ (accessed on 20 November 2022).
- European Union. General data protection regulation. Off. J. Eur. Union 2016, 49, L119. Available online: https://gdpr-info.eu (accessed on 20 November 2022).
- Elmufti, K.; Weerasinghe, D.; Rajarajan, M.; Rakocevic, V. Anonymous authentication for mobile single sign-on to protect user privacy. Int. J. Mob. Commun. 2008, 6, 760–769. [Google Scholar] [CrossRef]
- Han, J.; Mu, Y.; Susilo, W.; Yan, J. A generic construction of dynamic single sign-on with strong security. In Proceedings of the International Conference on Security and Privacy in Communication Systems, Singapore, 7–9 September 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 181–198. [Google Scholar]
- Wang, J.; Wang, G.; Susilo, W. Anonymous single sign-on schemes transformed from group signatures. In Proceedings of the 2013 5th International Conference on Intelligent Networking and Collaborative Systems, IEEE, Xi’an, China, 9–11 September 2013; pp. 560–567. [Google Scholar]
- Lee, T.F. Provably secure anonymous single-sign-on authentication mechanisms using extended Chebyshev chaotic maps for distributed computer networks. IEEE Syst. J. 2015, 12, 1499–1505. [Google Scholar] [CrossRef]
- Han, J.; Chen, L.; Schneider, S.; Treharne, H.; Wesemeyer, S. Anonymous single-sign-on for n designated services with traceability. In Proceedings of the European Symposium on Research in Computer Security, Barcelona, Spain, 3–7 September 2018; Springer: Cham, Switzerland, 2018; pp. 470–490. [Google Scholar]
- Han, J.; Chen, L.; Schneider, S.; Treharne, H.; Wesemeyer, S.; Wilson, N. Anonymous single sign-on with proxy re-verification. IEEE Trans. Inf. Forensics Secur. 2019, 15, 223–236. [Google Scholar] [CrossRef]
- PriSign [Online]. Available online: https://github.com/PriSign/PriSign (accessed on 20 November 2022).
- Boneh, D.; Waters, B. A fully collusion resistant broadcast, trace, and revoke system. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 211–220. [Google Scholar]
- Dodis, Y.; Fazio, N. Public key trace and revoke scheme secure against adaptive chosen ciphertext attack. In Proceedings of the International Workshop on Public Key Cryptography, Miami, FL, USA, 6–8 January 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 100–115. [Google Scholar]
- Boneh, D.; Shen, E.; Waters, B. Strongly unforgeable signatures based on computational Diffie-Hellman. In Proceedings of the International Workshop on Public Key Cryptography, New York, NY, USA, 24–26 April 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 229–240. [Google Scholar]
- Goldwasser, S.; Micali, S.; Rivest, R.L. A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 1988, 17, 281–308. [Google Scholar] [CrossRef]
- Feige, U.; Fiat, A.; Shamir, A. Zero-knowledge proofs of identity. J. Cryptol. 1988, 1, 77–94. [Google Scholar] [CrossRef]
- Goldreich, O.; Micali, S.; Wigderson, A. Proofs that yield nothing but their validity or all languages in NP have zero-knowledge proof systems. J. ACM (JACM) 1991, 38, 690–728. [Google Scholar] [CrossRef]
- Bellare, M.; Shi, H.; Zhang, C. Foundations of group signatures: The case of dynamic groups. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 14–18 February 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 136–153. [Google Scholar]
- Nguyen, L.; Safavi-Naini, R. Efficient and provably secure trapdoor-free group signature schemes from bilinear pairings. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Jeju Island, Korea, 5–9 December 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 372–386. [Google Scholar]
- Bergamo, P.; D’Arco, P.; De Santis, A.; Kocarev, L. Security of public-key cryptosystems based on Chebyshev polynomials. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 1382–1393. [Google Scholar] [CrossRef]
- Xiao, D.; Liao, X.; Deng, S. Using time-stamp to improve the security of a chaotic maps-based key agreement protocol. Inf. Sci. 2008, 178, 1598–1602. [Google Scholar] [CrossRef]
- Au, M.H.; Susilo, W.; Mu, Y. Constant-size dynamic k-TAA. In Proceedings of the International Conference on Security and Cryptography for Networks, Maiori, Italy, 6–8 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 111–125. [Google Scholar]
- Camenisch, J.; Kiayias, A.; Yung, M. On the portability of generalized schnorr proofs. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cologne, Germany, 26–30 April 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 425–442. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–229. [Google Scholar]
- Chatterjee, S.; Menezes, A. On cryptographic protocols employing asymmetric pairings—The role of Ψ revisited. Discret. Appl. Math. 2011, 159, 1311–1322. [Google Scholar] [CrossRef]
- Han, J.; Chen, L.; Schneider, S.; Treharne, H.; Wesemeyer, S. Privacy-preserving electronic ticket scheme with attribute-based credentials. IEEE Trans. Dependable Secur. Comput. 2019, 18, 1836–1849. [Google Scholar] [CrossRef]
- Feng, H.; Shi, R.; Yuan, F.; Li, Y.; Yang, Y. Efficient strong privacy protection and transferable attribute-based ticket scheme. J. Commun. 2022, 43, 63–75. [Google Scholar]
- Shi, R.; Feng, H.; Xie, H. Privacy-preserving attribute ticket scheme based on mobile terminal with smart card. J. Commun. 2022, 43, 26–41. [Google Scholar]
- Boneh, D.; Boyen, X. Short signatures without random oracles. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 56–73. [Google Scholar]
- Camenisch, J.; Chaabouni, R.; Shelat, A. Efficient protocols for set membership and range proofs. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security (ASIACRYPT’08), Melbourne, Australia, 7–11 December 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 234–252. [Google Scholar]
- Fuchsbauer, G.; Hanser, C.; Slamanig, D. Structure-preserving signatures on equivalence classes and constant-size anonymous credentials. J. Cryptol. 2019, 32, 498–546. [Google Scholar] [CrossRef]
- Blömer, J.; Bobolz, J. Delegatable attribute-based anonymous credentials from dynamically malleable signatures. In Proceedings of the International Conference on Applied Cryptography and Network Security, Leuven, Belgium, 2–4 July 2018; Springer: Cham, Switzerland, 2018; pp. 221–239. [Google Scholar]
- Galbraith, S.D.; Paterson, K.G.; Smart, N.P. Pairings for cryptographers. Discret. Appl. Math. 2008, 156, 3113–3121. [Google Scholar] [CrossRef]
- Groth, J. Efficient fully structure-preserving signatures for large messages. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Auckland, New Zealand, 29 November–3 December 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 239–259. [Google Scholar]
- Pointcheval, D.; Sanders, O. Short Randomizable Signatures. In Topics in Cryptology—CT-RSA 2016; Sako, K., Ed.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9610. [Google Scholar]
- Do, X.T.; Phan, D.H.; Pointcheval, D. Traceable inner product functional encryption. In Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 24–28 February 2020; Springer: Cham, Switzerland, 2020; pp. 564–585. [Google Scholar]
- Katz, J.; Sahai, A.; Waters, B. Predicate encryption supporting disjunctions, polynomial equations, and inner products. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Istanbul, Turkey, 13–17 April 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 146–162. [Google Scholar]
- Chase, M.; Lysyanskaya, A. On signatures of knowledge. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 78–96. [Google Scholar]
- Sonnino, A.; Al-Bassam, M.; Bano, S.; Meiklejohn, S.; Danezis, G. Coconut: Threshold issuance selective disclosure credentials with applications to distributed ledgers. arXiv 2018, arXiv:1802.07344. [Google Scholar]
- NIST. Advanced Encryption Standard (AES). 2001. Available online: http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf (accessed on 20 November 2022).
- NIST. Recommendation for Block Cipher Modes of Operation (Meth-ods and Techniques). 2001. Available online: http://csrc.nist.gov/publications/nistpubs/800-38a/sp800-38a.pdf (accessed on 20 November 2022).
- MIRACL Ltd. [Online]. Available online: https://github.com/miracl/MIRACL (accessed on 20 November 2022).
- Fan, J.; Vercauteren, F.; Verbauwhede, I. Faster Fp-Arithmetic for Cryptographic Pairings on Barreto-Naehrig Curves. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Lausanne, Switzerland, 6–9 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 240–253. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).