Crystal Plasticity Finite Element Modeling on High Temperature Low Cycle Fatigue of Ti2AlNb Alloy
Abstract
1. Introduction
2. Experiment and Modeling Theory
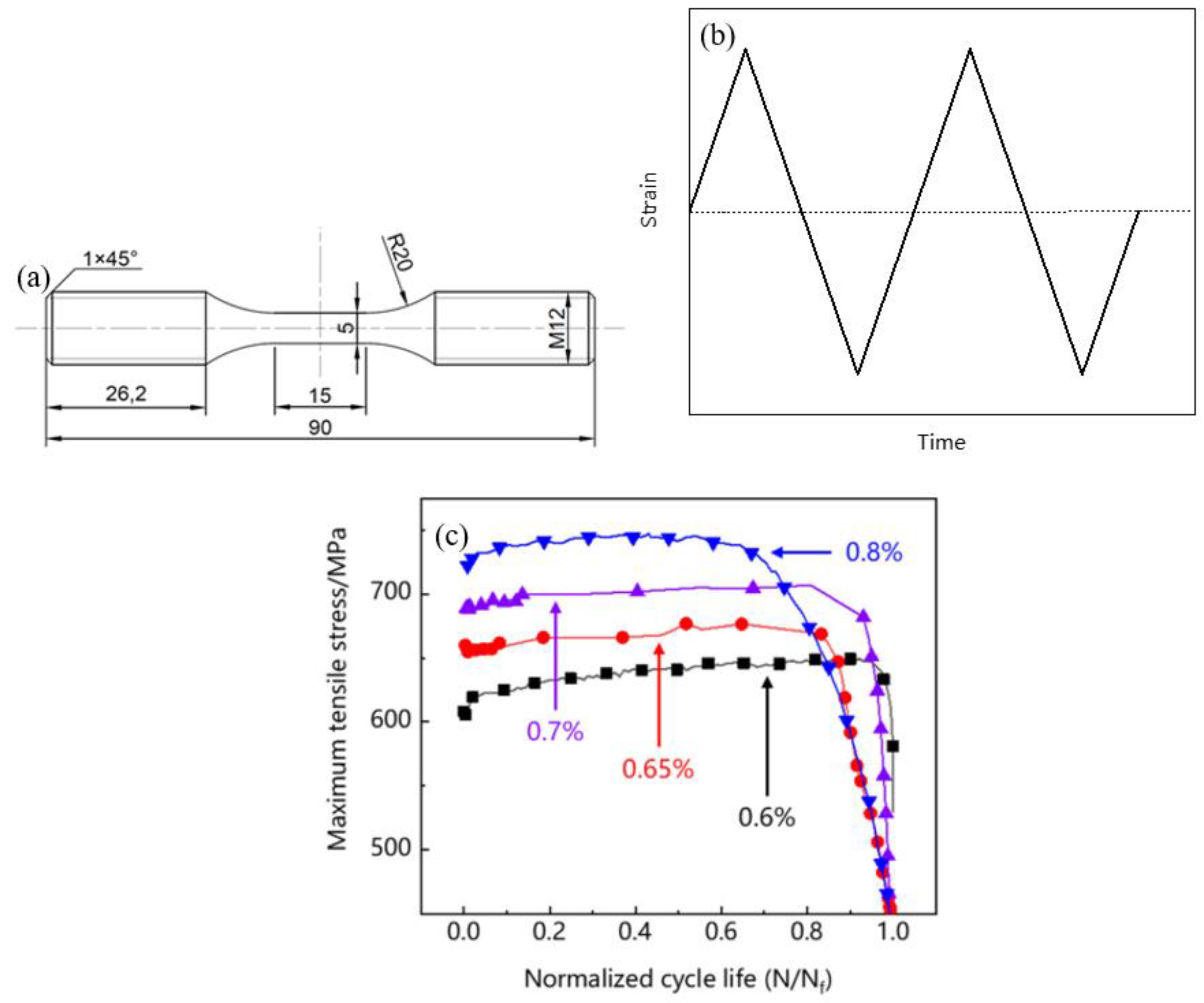
2.1. Experiment Materials and Procedures
2.2. Chaboche Cyclic Deformation Constitutive Model
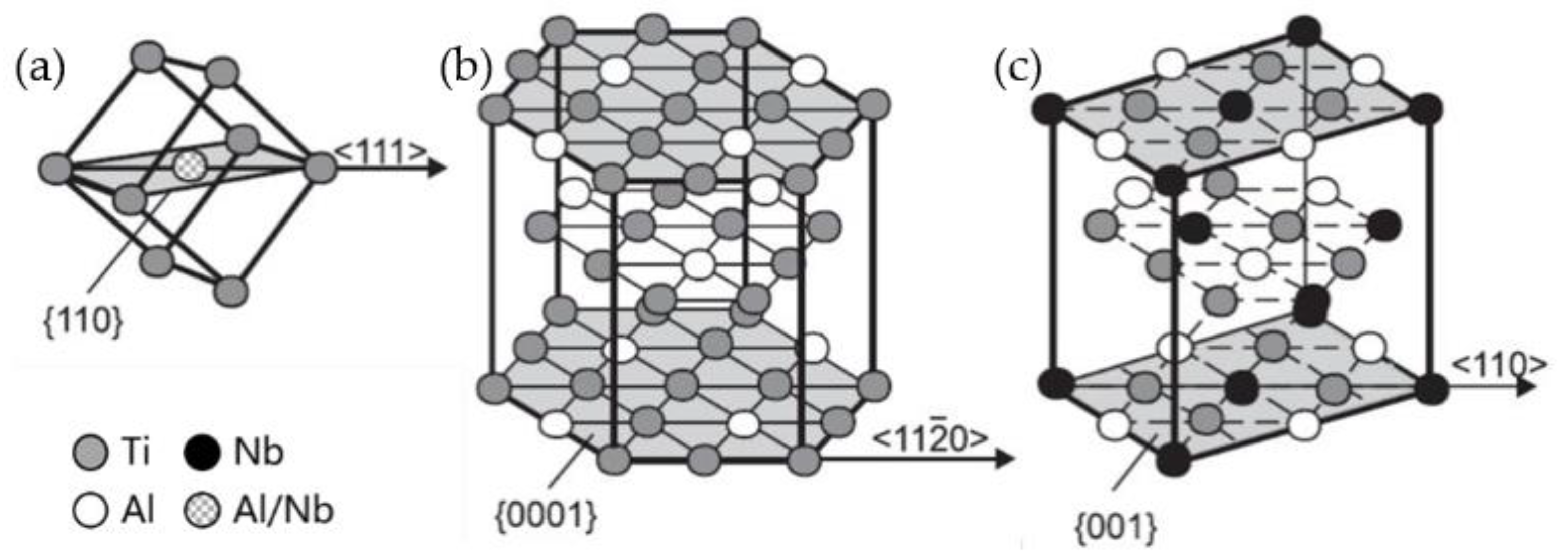
2.3. Crystal Plasticity Finite Element Model
3. Model Parameters Identification and Validation
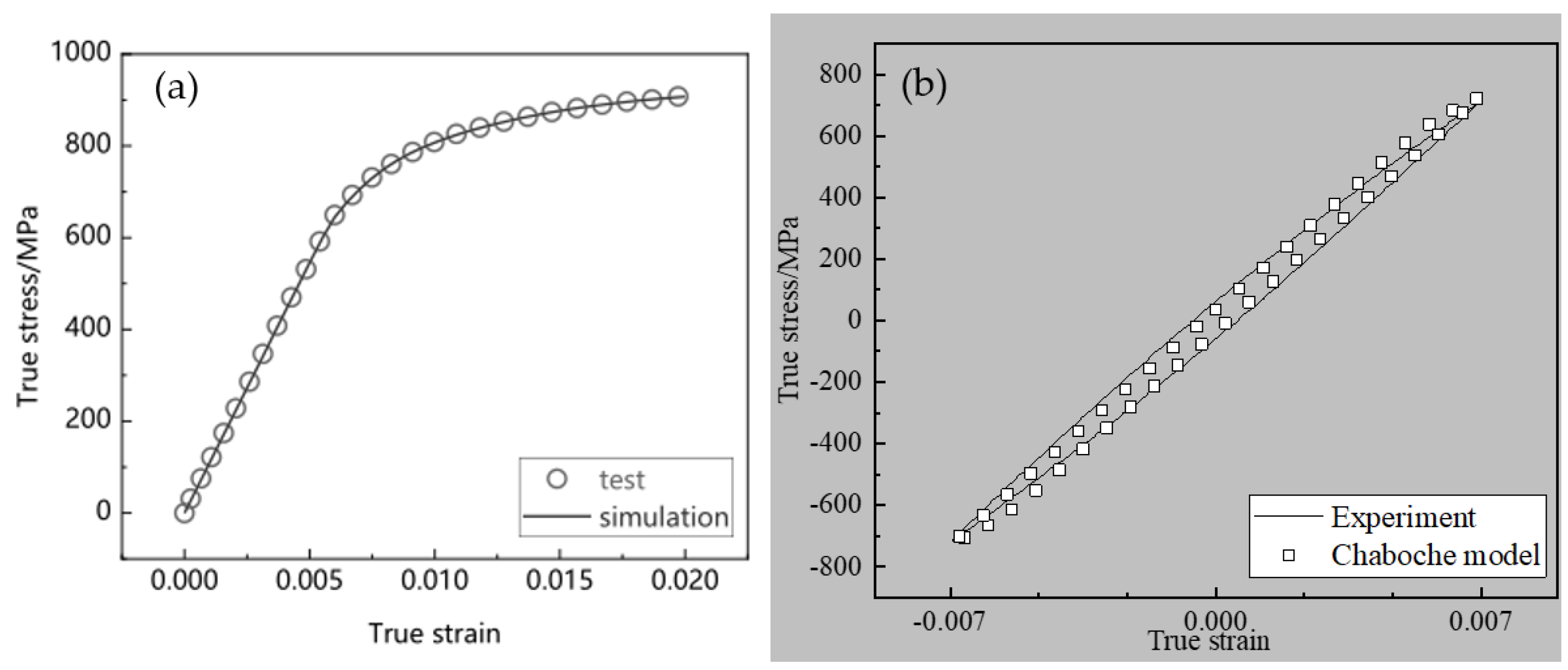
3.1. Chaoboche Cyclic Deformation Constitutive Model
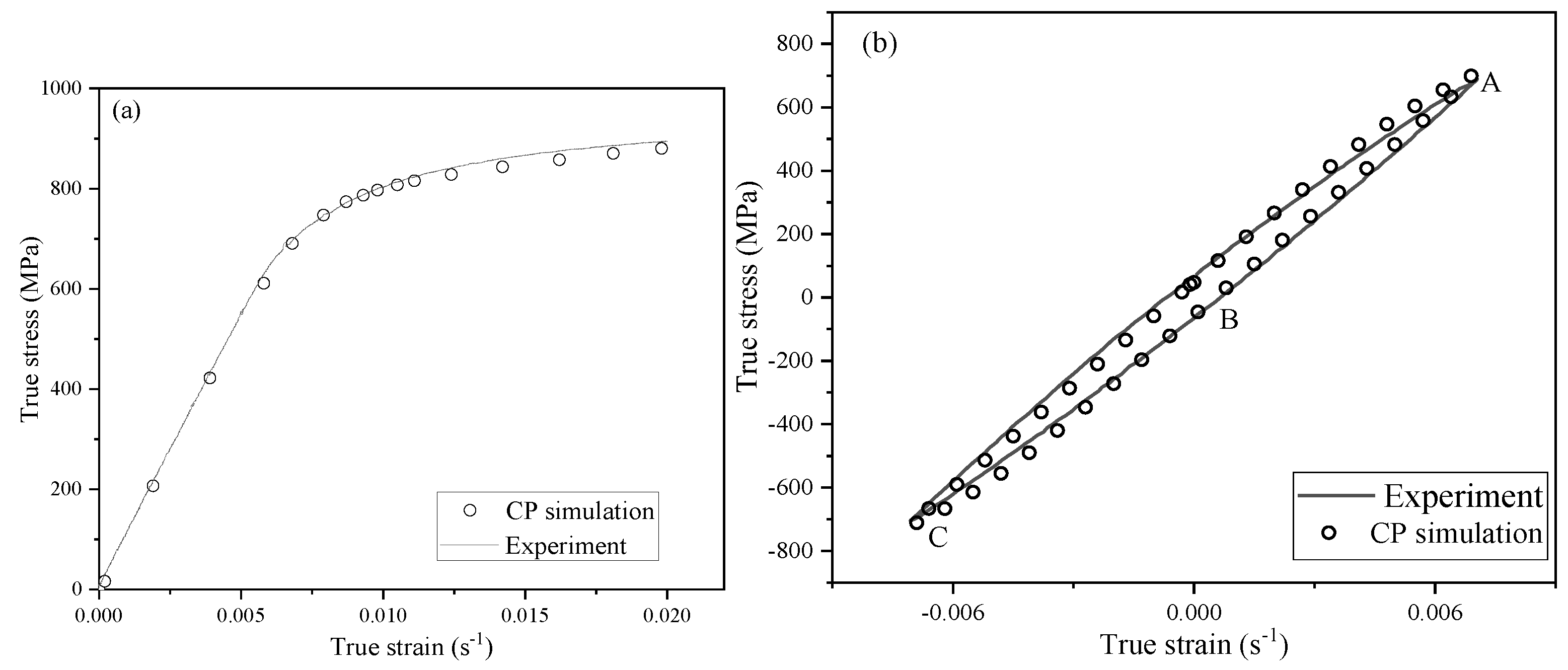
3.2. Crystal Plasticity Finite Element Model
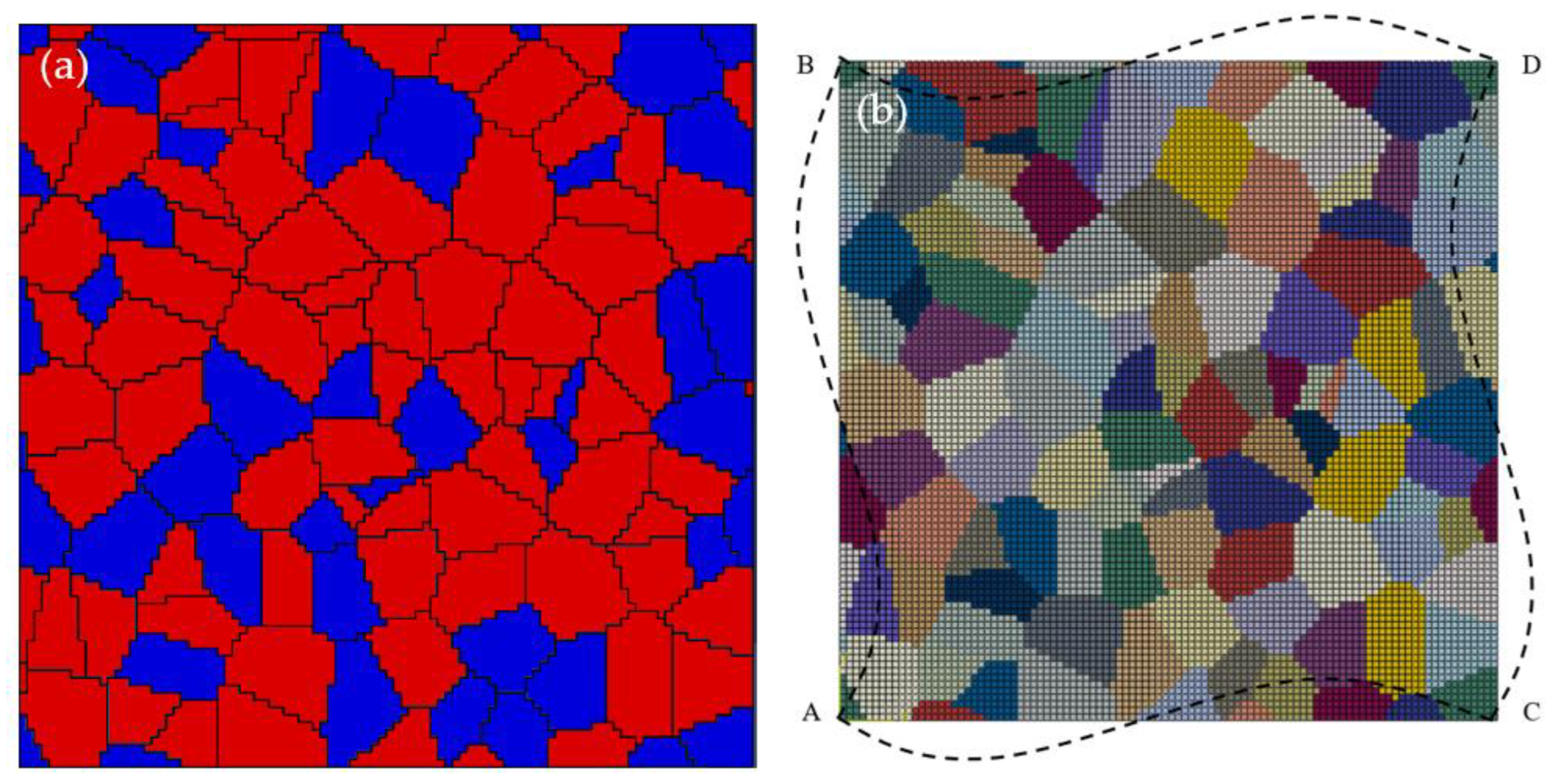
3.2.1. RVEs and Boundary Conditions
3.2.2. Identification of Material Parameters
4. Results and Discussion
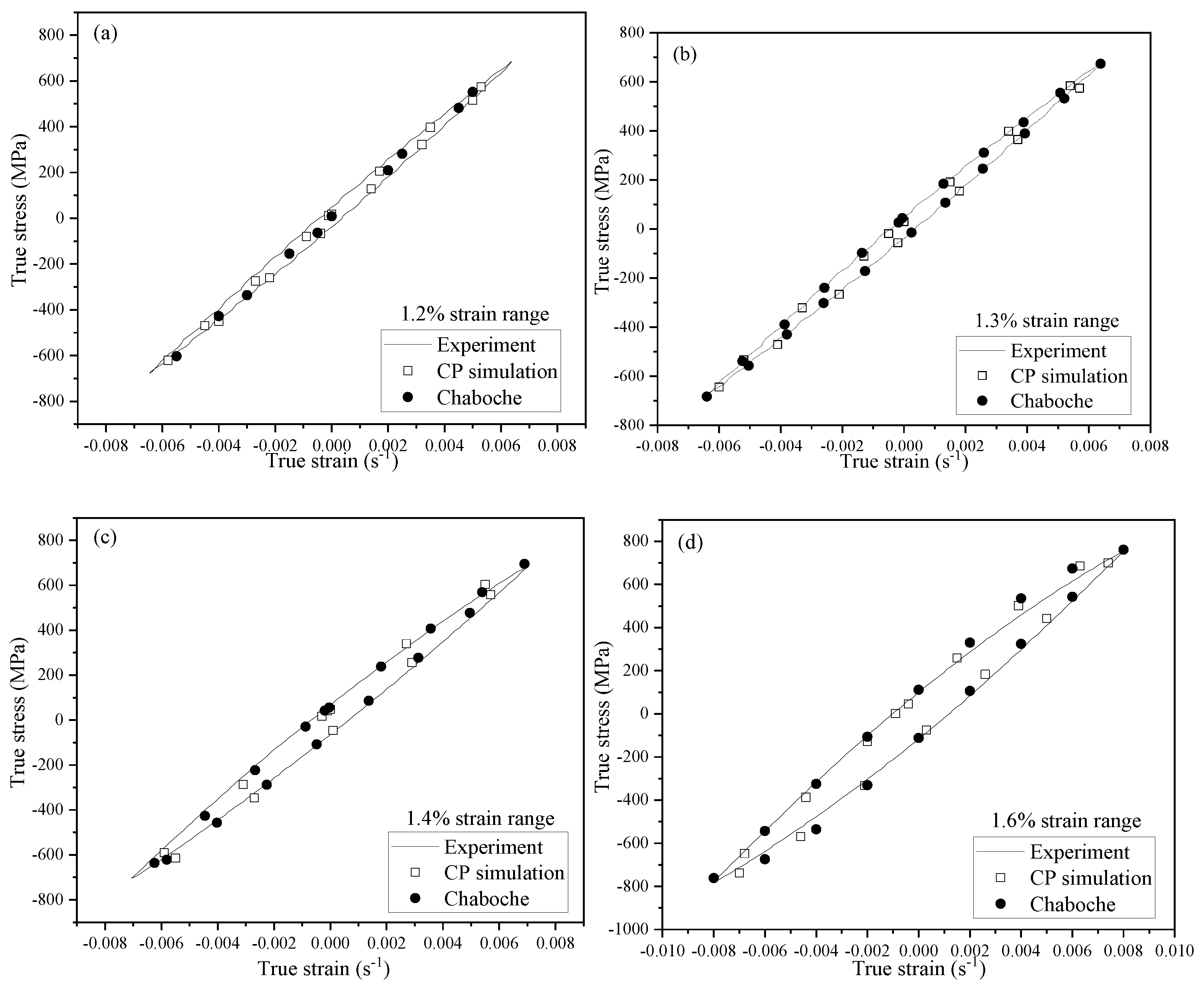
4.1. Comparison of Simulation Ability between Cyclic Deformation Model and CPFEM
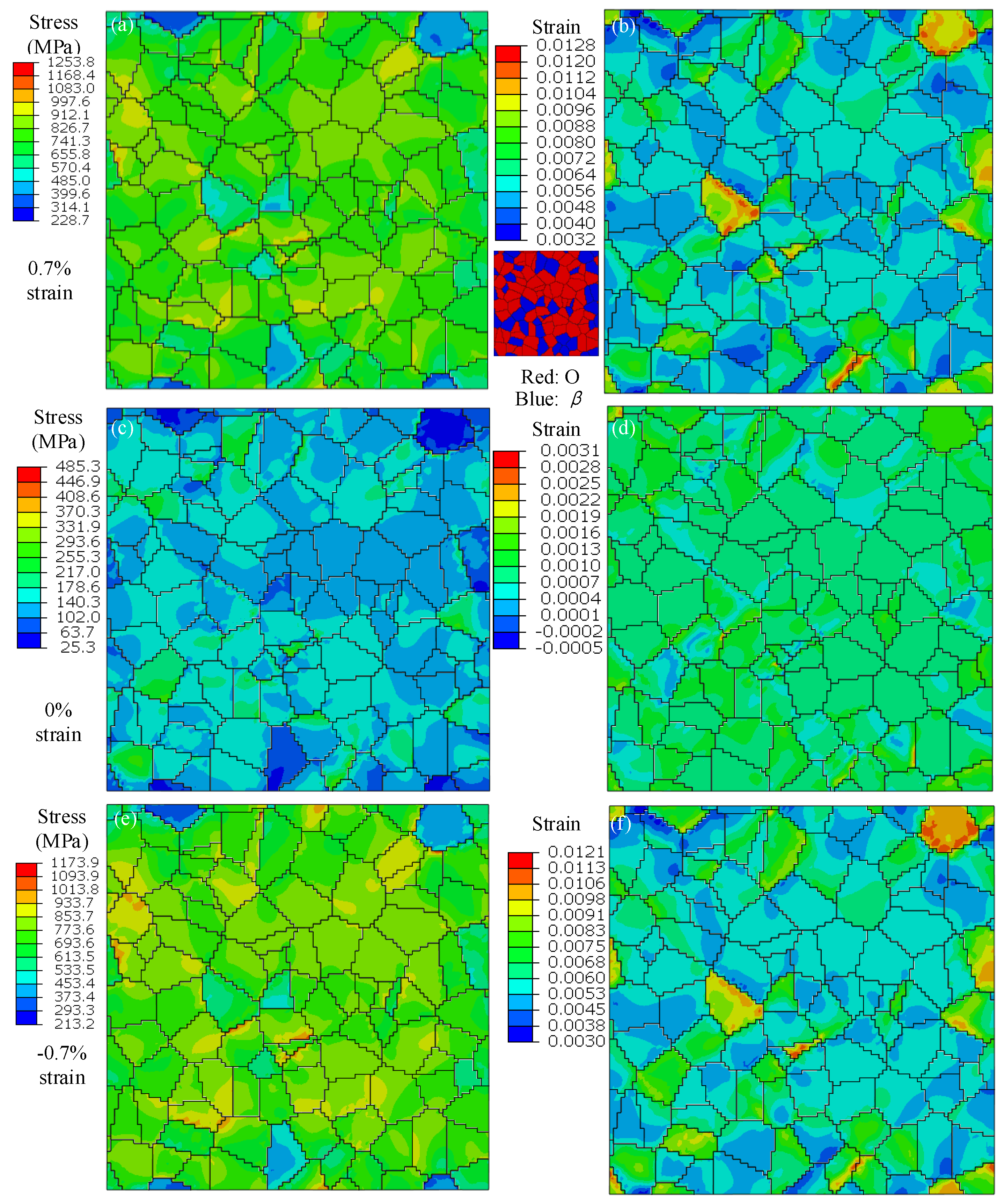
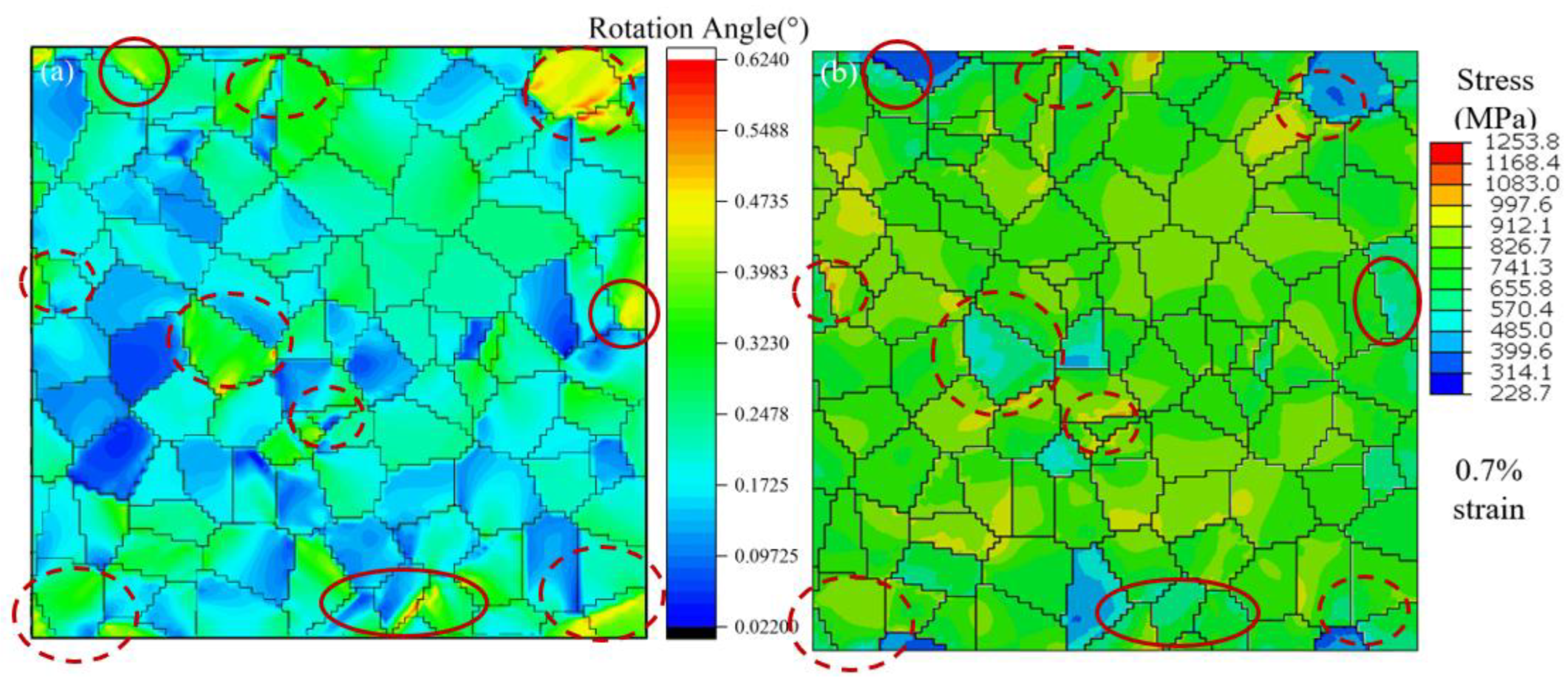
4.2. Strain and Stress Distribution between the O Phase and b Phase
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xue, L. A Unified Expression for Low Cycle Fatigue and Extremely Low Cycle Fatigue and Its Implication for Monotonic Loading. Int. J. Fatigue 2008, 30, 1691–1698. [Google Scholar] [CrossRef]
- Coffin, J. Low Cycle Fatigue—A Review; General Electric Co., Research Lab.: Schenectady, NY, USA, 1962. [Google Scholar]
- Li, P.; Li, Q.Q.; Jin, T.; Zhou, Y.Z.; Li, J.G.; Sun, X.F.; Zhang, Z.F. Comparison of Low-Cycle Fatigue Behaviors between Two Nickel-Based Single-Crystal Superalloys. Int. J. Fatigue 2014, 63, 137–144. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, Y.; Xu, D.K.; Lin, Y.C.; Chen, X. Low Cycle Fatigue and Creep-Fatigue Interaction Behavior of Nickel-Base Superalloy GH4169 at Elevated Temperature of 650 °C. Mater. Sci. Eng. A 2016, 655, 175–182. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Inui, H.; Kishida, K.; Matsumuro, M.; Shirai, Y. Gamma Titanium Aluminide Alloys. MRS Online Proc. Libr. (OPL) 1994, 364. [Google Scholar] [CrossRef]
- Kim, Y.-W. Gamma Titanium Aluminides: Their Status and Future. JOM 1995, 47, 39–42. [Google Scholar] [CrossRef]
- Kumpfert, J. Intermetallic Alloys Based on Orthorhombic Titanium Aluminide. Adv. Eng. Mater. 2001, 3, 851. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, A.; Qu, S.; Shen, J.; Chen, D. Microstructure and Low Cycle Fatigue of a Ti2AlNb-Based Lightweight Alloy. J. Mater. Sci. Technol. 2020, 44, 140–147. [Google Scholar] [CrossRef]
- Fang, B.; Cao, J.; Li, P. Behavior of Alloy Ti—24% Al—15% Nb—1% Mo under Conditions of Low-Cycle Fatigue at High Temperatures. Met. Sci. Heat Treat. 2009, 51, 471–475. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, M.; Ye, T.; Liang, Y.; Ren, Y.; Dong, C.; Lin, J. Microstructure Stability and Micro-Mechanical Behavior of as-Cast Gamma-TiAl Alloy during High-Temperature Low Cycle Fatigue. Acta Materialia 2018, 145, 504–515. [Google Scholar] [CrossRef]
- Ding, J.; Liang, Y.; Xu, X.; Yu, H.; Dong, C.; Lin, J. Cyclic Deformation and Microstructure Evolution of High Nb Containing TiAl Alloy during High Temperature Low Cycle Fatigue. Int. J. Fatigue 2017, 99, 68–77. [Google Scholar] [CrossRef]
- Kruml, T.; Petrenec, M.; Obrtlíka, K.; Polák, J.; Buček, P. Influence of Niobium Alloying on the Low Cycle Fatigue of Cast TiAl Alloys at Room and High Temperatures. Procedia Eng. 2010, 2, 2297–2305. [Google Scholar] [CrossRef]
- Koo, G.-H.; Kwon, J.-H. Identification of Inelastic Material Parameters for Modified 9Cr–1Mo Steel Applicable to the Plastic and Viscoplastic Constitutive Equations. Int. J. Press. Vessel. Pip. 2011, 88, 26–33. [Google Scholar] [CrossRef]
- Dornelas, V.M.; Oliveira, S.A.; Savi, M.A.; Pacheco, P.M.C.L.; de Souza, L.F.G. Fatigue on Shape Memory Alloys: Experimental Observations and Constitutive Modeling. Int. J. Solids Struct. 2021, 213, 1–24. [Google Scholar] [CrossRef]
- Chandran, K.S.R. A Physical Model and Constitutive Equations for Complete Characterization of S-N Fatigue Behavior of Metals. Acta Mater. 2016, 121, 85–103. [Google Scholar] [CrossRef]
- Ma, L.; Luo, Y.; Wang, Y.; Du, W.; Zhang, J. Constitutive and Damage Modelling of H11 Subjected to Low-cycle Fatigue at High Temperature. Fatigue Fract. Eng. Mat. Struct. 2017, 40, 2107–2117. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.; Ma, K.; Shi, T.; Qian, Z.; Liang, K.; Dong, F. A Thermomechanical Constitutive Model for Investigating the Fatigue Behavior of Sn-rich Solder under Thermal Cycle Loading. Fatigue Fract. Eng. Mat. Struct. 2022, 45, 1953–1968. [Google Scholar] [CrossRef]
- Han, Q.; Lei, X.; Rui, S.-S.; Su, Y.; Ma, X.; Cui, H.; Shi, H. Temperature-Dependent Fatigue Response of a Fe44Mn36Co10Cr10 High Entropy Alloy: A Coupled in-Situ Electron Microscopy Study and Crystal Plasticity Simulation. Int. J. Fatigue 2021, 151, 106385. [Google Scholar] [CrossRef]
- Pan, Y.B.; Dunne, F.P.E.; MacLachlan, D.W. A Mechanistic and Stochastic Approach to Fatigue Crack Nucleation in Coarse Grain RR1000 Using Local Stored Energy. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 505–520. [Google Scholar] [CrossRef]
- Ozturk, D.; Shahba, A.; Ghosh, S. Crystal plasticity FE study of the effect of thermo-mechanical loading on fatigue crack nucleation in titanium alloys. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 752–769. [Google Scholar] [CrossRef]
- Ashton, P.J.; Jun, T.-S.; Zhang, Z.; Britton, T.B.; Harte, A.M.; Leen, S.B.; Dunne, F.P. The effect of the beta phase on the micromechanical response of dual-phase titanium alloys. Int. J. Fatigue 2017, 100, 377–387. [Google Scholar] [CrossRef]
- Leyens, C.; Peters, M. (Eds.) Titanium and Titanium Alloys: Fundamentals and Applications; Wiley-vch: Weinheim, Germany, 2006. [Google Scholar]
- Wang, Y.; Wang, X.; Yang, Y.; Lan, X.; Zhang, Z.; Li, H. Study on Creep-Fatigue Mechanical Behavior and Life Prediction of Ti2AlNb-Based Alloy. Materials 2022, 15, 6238. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Van, K.D.; Cordier, G. Modelization of the Strain Memory Effect on the Cyclic Hardening of 316 Stainless Steel. 1979. Available online: https://repository.lib.ncsu.edu/bitstream/handle/1840.20/26854/L11-3.pdf?sequence=1 (accessed on 15 April 2022).
- Hill, R.; Rice, J. Constitutive Analysis of Elastic-Plastic Crystals at Arbitrary Strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J. Strain Localization in Ductile Single Crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. Material Rate Dependence and Localized Deformation in Crystalline Solids. Acta metallurgica 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Busso, E.P. Cyclic Deformation of Monocrystalline Nickel Aluminide and High Temperature Coatings. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1990. [Google Scholar]
- Li, K.-S.; Wang, R.-Z.; Yuan, G.-J.; Zhu, S.-P.; Zhang, X.-C.; Tu, S.-T.; Miura, H. A Crystal Plasticity-Based Approach for Creep-Fatigue Life Prediction and Damage Evaluation in a Nickel-Based Superalloy. Int. J. Fatigue 2021, 143, 106031. [Google Scholar] [CrossRef]
- Fournier, B.; Dalle, F.; Sauzay, M.; Longour, J.; Salvi, M.; Caës, C.; Tournié, I.; Giroux, P.-F.; Kim, S.-H. Comparison of Various 9–12% Cr Steels under Fatigue and Creep-Fatigue Loadings at High Temperature. Mater. Sci. Eng. A 2011, 528, 6934–6945. [Google Scholar] [CrossRef]
- Zhang, K.-S.; Ju, J.W.; Li, Z.; Bai, Y.-L.; Brocks, W. Micromechanics Based Fatigue Life Prediction of a Polycrystalline Metal Applying Crystal Plasticity. Mech. Mater. 2015, 85, 16–37. [Google Scholar] [CrossRef]
- Quey, R.; Dawson, P.R.; Barbe, F. Large-Scale 3D Random Polycrystals for the Finite Element Method: Generation, Meshing and Remeshing. Comput. Methods Appl. Mech. Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef]
- Chu, F.; Mitchell, T.E.; Majumdar, B.; Miracle, D.; Nandy, T.K.; Banerjee, D. Elastic Properties of the O Phase in Ti-Al-Nb Alloys. Intermetallics 1997, 5, 147–156. [Google Scholar] [CrossRef]
- Fan, X.G.; Yang, H. Internal-State-Variable Based Self-Consistent Constitutive Modeling for Hot Working of Two-Phase Titanium Alloys Coupling Microstructure Evolution. Int. J. Plast. 2011, 27, 1833–1852. [Google Scholar] [CrossRef]
- Fu, Y.; Lv, M.; Zhao, Q.; Zhang, H.; Cui, Z. Investigation on the Size and Distribution Effects of O Phase on Fracture Properties of Ti2AlNb Superalloy by Using Image-Based Crystal Plasticity Modeling. Mater. Sci. Eng. A 2021, 805, 140787. [Google Scholar] [CrossRef]
- Nandy, T.K.; Banerjee, D. Deformation Mechanisms in the O Phase. Intermetallics 2000, 8, 1269–1282. [Google Scholar] [CrossRef]
- Wen, D.-X.; Lin, Y.C.; Li, X.-H.; Singh, S.K. Hot Deformation Characteristics and Dislocation Substructure Evolution of a Nickel-Base Alloy Considering Effects of δ Phase. J. Alloy. Compd. 2018, 764, 1008–1020. [Google Scholar] [CrossRef]
- Li, H.; Fu, M. Deformation-Based Processing of Materials, Behavior, Performance, Modeling, and Control; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]


| Ti | Al | Nb | Zr |
|---|---|---|---|
| 55 | 21 | 23 | 1 |
| Test | Strain Range/% | Life |
|---|---|---|
| Fatigue | 1.2 | 9660/cycle |
| 1.3 | 1081/cycle | |
| 1.4 | 742/cycle | |
| 1.6 | 482/cycle |
| E/GPa | Q0/MPa | C1/MPa | γ1 | C2/MPa | γ2 | C3/MPa | γ3 |
|---|---|---|---|---|---|---|---|
| 109.191 | 570 | 1,634,660 | 25,468 | 142,294 | 1405.3 | 36,262 | 187.15 |
| Parameter | Unit | Value(O|β) | ||
|---|---|---|---|---|
| Elastic constants | C11 | GPa | 184 | 135 |
| C12 | GPa | 86.2 | 113 | |
| C44 | GPa | 49 | 55 | |
| Flow parameters | s−1 | 120 | 120 | |
| F0 | kJ/mol | 150 | 250 | |
| τ0 | MPa | 200 | 200 | |
| Hardening parameters | hB | MPa | 1000 | 950 |
| rD | MPa | 8 | 10 | |
| Ssat | MPa | 250 | 160 | |
| S0 | MPa | 300 | 225 | |
| hαβ | MPa | 350 | 350 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, Z.; Wang, X.; Yang, Y.; Lan, X.; Li, H. Crystal Plasticity Finite Element Modeling on High Temperature Low Cycle Fatigue of Ti2AlNb Alloy. Appl. Sci. 2023, 13, 706. https://doi.org/10.3390/app13020706
Wang Y, Zhang Z, Wang X, Yang Y, Lan X, Li H. Crystal Plasticity Finite Element Modeling on High Temperature Low Cycle Fatigue of Ti2AlNb Alloy. Applied Sciences. 2023; 13(2):706. https://doi.org/10.3390/app13020706
Chicago/Turabian StyleWang, Yanju, Zhao Zhang, Xinhao Wang, Yanfeng Yang, Xiang Lan, and Heng Li. 2023. "Crystal Plasticity Finite Element Modeling on High Temperature Low Cycle Fatigue of Ti2AlNb Alloy" Applied Sciences 13, no. 2: 706. https://doi.org/10.3390/app13020706
APA StyleWang, Y., Zhang, Z., Wang, X., Yang, Y., Lan, X., & Li, H. (2023). Crystal Plasticity Finite Element Modeling on High Temperature Low Cycle Fatigue of Ti2AlNb Alloy. Applied Sciences, 13(2), 706. https://doi.org/10.3390/app13020706







