Abstract
A network model of epidemic spread accounting for inhomogeneous population district division is investigated. Motivated by the COVID-19 pandemic, we analyze the effects of infection development in the area, for example, of a city divided into several population districts. The districts are characterized by a certain intensity of contact inside and with inter-district communication that can be generally controlled by the authorities. Specifically, we consider the effect of the central district, which is the hub of infection. We investigate how the interaction strength influences the city’s level of epidemic development. We obtained that the final infected amount in the district rises with an increasing degree of connection with the hub. However, the model situation was not limited by the first outbreak but included the subsequent waves of infection. We obtained that the appearance and disappearance of subsequent waves of infection essentially depended on the intensity of communication with the infected hub. Our results suggest the mechanism where stricter communication policy can negatively affect the subsequent infection waves.
1. Introduction
The COVID-19 pandemic has caused over 500 million confirmed cases and over 6 million deaths globally up to April 2022. At present, different variations of the coronavirus still circulate in many countries, and the global number of COVID-19 cases is still quite high. Obviously, the development of vaccines and special drugs for COVID-19 therapy represents the main instrument in the fight against the pandemic. However, predictions of the infection spread in different conditions also have great significance, specifically for authorities to coordinate the medical care system and economics in epidemic conditions. Countries and cities in the World are quite different in their geographical conditions, technical development, infrastructure, people mobility and services. However, in most of the World’s big cities, there is well-developed infrastructure, transport and territorial division with industrial, market, dormitory and other areas. It makes the conditions of epidemic development strongly inhomogeneous between certain districts. It may not be so critical, for example, for seasonal flu, which is relatively fast and not so deadly. However, the situation is different for COVID-19, which has a much longer infection period and may survive without people carriers for a long time [1,2]. It means that developed city infrastructure and transport communication may play a significant role in infection dynamics. In terms of epidemic prediction, the classical SIR approach [3]. considering homogeneous populations cannot be directly applied to the current pandemic.
During more than two years of the pandemic, many mathematical models describing qualitatively and quantitatively COVID-19 development have been proposed [4,5,6,7,8]. Models demonstrate their satisfactory performance, especially for limited areas [9], although there are other points of view [10]. It should be noted that the modified SIR models require more complex data for development, and due to the presence of little information and lack of reliable data regarding this newly emerged disease, the simple SIR model has been the choice of many investigators [11]. These over-simplified models ignore the factors that have a great effect on the course of the disease and cannot reproduce such effects as secondary and subsequent waves. The other issue affecting the spread of the virus is the behavioral changes considerably related to the social and cultural context of the population [10,12,13]. Rocha et al. [14] simulated disease spread using SI and SIR models on an empirical temporal network of sexual contacts. To simulate models in an empirical network of sexually transmitted infections, the authors mapped the sampled network onto a time-ordered list. Their results indicate that the network was not dense enough to support sexually transmitted infection outbreaks. Another similar approach was used in the work [15]. The authors defined a multitype, stochastic SIR dynamical epidemic model on a strongly connected graph. The stochastic SIR model for the spread of an epidemic within and between nodes showed a standard finite-time convergence result for a branching process. One of the most unique techniques was shown in the work [16]. The model contains a mix of discrete and continuous times with interaction described as a Bernoulli process of a finite number of binary random variables. Lazerbnik et al. [17] presented another type of hybrid model that is based on a SIRD model for two age classes using eight populations and a spatial model where these populations are distributed in space and time between places. Among the most recent research, a spatio-temporal modeling framework was used in the work [18]. In their model for each population class, the authors estimated the intensity of the spatial-temporal point process that originated from each observed point pattern of infected individuals by incorporating the estimates of the total number of infectious derived from the SIR model into the mean component of the point process. The question of quarantine’s influence on the flow of infection still requires further research [19,20,21,22]. One of the possible approaches was described in the work [23]. In that work, an intervention policy that relies on the strategic deployment of inspection units was shown.
In this study, we address the effects of the inhomogeneous structure of a modern city population on epidemic development. We assumed that a given territory is divided into several districts. Inside those districts, the population is homogeneous and described by a SIR-like model. Interaction between the districts is described by a contact matrix that defines the communication level between certain districts. As a result, we proposed a network-based SIR model capable of incorporating such factors as boundaries crossing limitations to assess how communication between the hub and other districts can affect the infection spread. The novelty of the proposed model involves combining a network approach and accounting for infection without a host.
2. Materials and Methods
Schematically, we divide a territory into a set of interacting districts (in Figure 1).
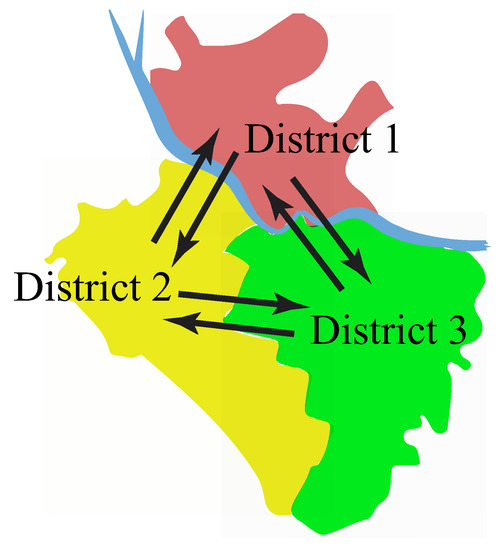
Figure 1.
Schematic representation of a territory with interacting districts.
We consider the following network system describing k interacting districts:
here is the number of susceptible individuals of the i-th region, is the infected, is recovered and is the non-human carriers (viruses). The independent variable is time t, measured in days. The coefficient denotes the number of carriers (viruses) emitted by an infected individual, is the probability of infection in the case of contact between a susceptible and an infected subject, is the probability of recovery (usually, it is interpreted as the rate of recovery, since the average duration of the subject is in the state of infection is days), is the probability of losing immunity and the appearance of the re-infection possibility, is the probability of death, is the immigration of the population for the i-th region and is the interaction coefficient between the j-th and i-th districts given from the communication matrix (P). The relative degree of openness of the borders, which is relevant for modeling quarantine events [24], b denotes the coefficient of natural loss of carriers and d is the degree of contagiousness of the carrier (virulence). It should be noted that in the case of (complete closure of boundaries), the system degenerates in the case of infecting one subject in the absence of the remaining infection [25]. In general, model Equation (1) includes four equations. The first describes the dynamics of the exposed, the second describes the dynamics of the infected, the third describes the dynamics of the recovered and the fourth describes the dynamics of the virus population. Compared to the classical SIR model, the first term of Equations (1)1 and (1)2 includes the dependence on the degree of interaction within the network . The second term of Equation (1)2 describes the transition of the cured to the exposed population. term in Equation (1)2 represents the dynamics of infecting people without contact with another infected person. of Equation (1)3 represents the dynamics of recovery. The term shows the production of viruses by the infected, and the term represents the natural death of the virus.
If we consider the behavior of the model for a separate area ( and ), then the matrices of infection and the transition could be calculated as follows:
The spectral radius of the matrix can be considered as an assessment of the main reproductive number:
Strictly speaking, there will be a separate reproductive number for each district. However, given the specifics of the model and the possibility of dividing a single entity into separate districts, the average number can be represented as follows:
3. Results
To study the basic effects of the spread of infection in the case of various interactions between districts, we used a simplified model with zero levels of immigration and mortality. To check the main effects of the net with several interacting districts, the communication matrix was set to be symmetrical as follows:
where the initial appearance of infected individuals in the first district was implied, the spread of infection in the districts interacting with the first one was identical. This matrix reflects a homogeneous but densely populated area, including three districts. Three closely spaced homogeneous settlements can be considered to be of this type. Since the interaction within a district is conditionally considered active, the values on the main diagonal are set to 1. The interaction between districts is considered equal and given p due to less active interaction between districts, both due to natural causes and possible restrictions.
The dynamics of Equation (1) were identical for districts 2 and 3. The number of infected individuals demonstrated a big first wave in the time period from 20 to 30 days, with a recovery period from 30 to 40 days and a second lower wave from 30 to 50. Initially, infected district 1 demonstrated the maximal value of infected in the first wave, while the second and third districts were only slightly lower due to the high interaction within each district.
We observed significant reductions in both the maximum and the end values in the case of even partial closure of boundaries. At the same time, the apex of the maximum also falls on later values, and at boundaries that are more open, the occurrence of secondary and subsequent infection waves begins. The difference between the infection waves in the first district and bound districts was especially noticeable in the first infection wave when the degree of openness of the boundaries between the districts is lower than 0.4. A lower degree causes a bigger delay between the maximums of the infected reached by the first wave.
To check the effect of the presence of the central district (a hub), as well as the observed difference between the second and third districts, the communication matrix was taken in the following form:
The assumptions underlying the construction of this matrix include the homogeneity of districts, as well as the varying degrees of interaction within districts. The second and third districts were located on the outskirts and had weak interaction between themselves. Most of the population is assumed to be interested in spending time in the hub rather than an outskirt. The first district was treated as a hub, and its level of exposure to other districts can vary. Another reason for the significant difference in the main diagonal numbers of Equation (7) is the desire to demonstrate the difference in dynamics for objects with medium and weak interactions. Typical curves for a strong bond () are shown in Figure 2. The number of infected demonstrated a big first wave in the time period from 30 to 40 days, a recovery period from 40 to 60 days and a second lower wave from 180 to 220. For comparison, the figure also shows a graph for the time series of an unaltered SIR model that does not demonstrate any secondary or consequent waves. The numerical simulation showed that despite the fact that the probability of internal infection in the third area is five times lower than in the second, the final number of infected differs only by 10%. The graphs of the total infected over time for the degree of opening of the borders for the districts were similar to the dynamics with the case of symmetric links, despite the difference in the probability of infection inside the districts and were primarily determined by the degree of relationship with a hub, which can be seen for the first wave, but the flow and final values of the infected dependent from the internal probabilities of infection with small communication values a hub. The final amount of infected in the district increases with a degree of connection with a hub. The peak of the wave (maximal number) of infected individuals for secondary and subsequent waves 3 and 4 are shown in Figure 3. The graphs demonstrate growth for the communication values with the hub within the limits from to . However, for the () maximal value of infected individuals, the second wave even decreases while peaks of subsequent waves barely change. For the relatively big values of , the maximal values converge to a constant.
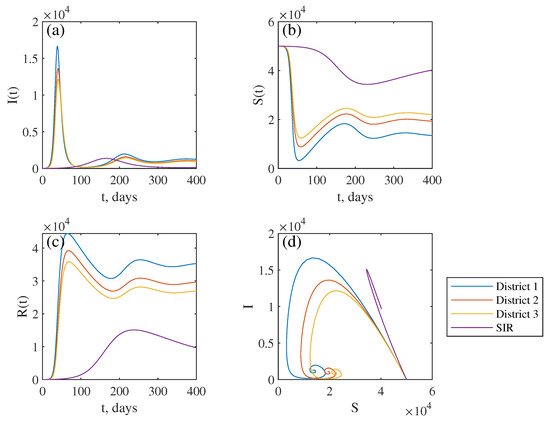
Figure 2.
The time series of infected (a), susceptible (b) and recovered (c). The phase portrait for three districts (d), obtained for the values of the system parameters with the communication matrix (7): , , , , , ; the violet line represents time series unaltered SIR model with the same parameters.
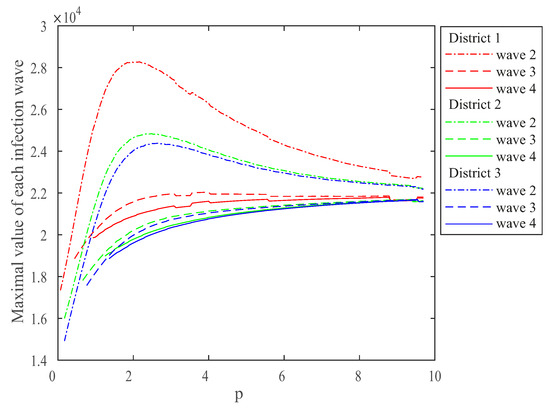
Figure 3.
The dependence of the maximum number of infected in the second and subsequent waves in districts (red—1, green—2, blue—3) on the degree of openness of the boundaries between the hub and other districts (p).
The final number of infected demonstrates a slow upward slope on the dependence of the final number of infected in districts (red—1, green—2, blue—3) on the degree of openness of the boundaries between the hub and other districts, as shown in Figure 4. The numerical simulation showed that despite differences in infection probability, the final number of infected is quite similar. For the very low values of p (), differences between the hub and rural districts are sufficient (more than 10 times) as the graphs demonstrate upward growth. However, for the values , the final number of infected in the hub area is only twice as large for for the and districts and keeps diminishing with the degree of openness of the boundaries between the hub and other districts. With a sufficiently large degree of openness, the whole city could be seen as one homogenous entity.
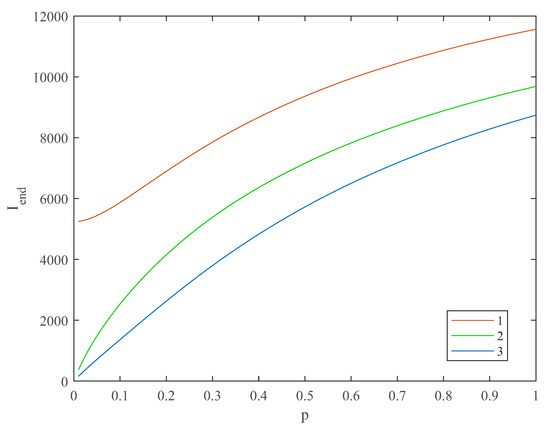
Figure 4.
The dependence of the final number of infected in districts (red—1, green—2, blue—3) on the degree of openness of the boundaries between the hub and other districts (p).
As a demonstration of the practical application of the work, the situation on Shikoku Island was examined. Shikoku is the smallest of the four main islands of Japan and has a population of about 2.8 million people. This territory was chosen to reduce the possible effect of migration, as well as due to its territorial and administrative division into regions. Tokushima, Kagawa, Ehime and Kochi prefectures are located on the island. The infection rates for these regions were taken from public datasets [26,27] for the last three months (22 October–30 December 2022). Through empirical fitting of model parameters, it was possible to qualitatively reproduce the dynamics of the number of infected using the communication matrix in Equation (8).
For comparison by region, the data are shown in Figure 5. Although the applicability of the model for the practical situation is demonstrated in a similar way, the model system, in this case, was applied without taking into account the current information on internal and external migration, as well as specific limiting measures expressed in quantitative terms due to the lack of open information. Obtaining a more accurate real prediction in each specific situation requires a separate study, which is beyond the scope of the current work.
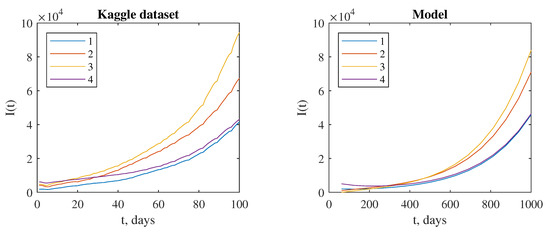
Figure 5.
The dynamics of the infection cases in the prefectures and districts (Tokushima—1, Kagawa—2, Ehime—3, Kochi—4) for the Kaggle dataset and model data with the parameters n = , , , , , .
4. Discussion
The resulting dynamics were primarily determined by the degree of relationship with the hub. It can be explained by the existence of undetected infectious people and the effect of the control measures [28]. This can be seen for the first wave, but the flow and final values of infected depended on the internal probabilities of infection with small communication values with the hub. The final amount of infected in the district rises with an increasing degree of connection with the hub. However, this dependence was close to a logarithmic form [29]. Despite the difference in the likelihood of infection within the districts, infection curves are primarily determined by the degree of relationship with the hub, which can be seen for the first wave, but the flow and final values of infected depended on the internal probabilities of infection with a small interaction level with the hub. The occurrence and disappearance of subsequent waves [30] of infection on the degree of relationship with a hub were non-linear, and with a large extent relationship, the number of waves even decrease, and their amplitude was committed to a constant value, as shown. The main cause of the process of maximal infection wave values can be homogenous infection spread caused by the influence of the central hub. It should be noted that the occurrence of the first infection wave in the time period from 20 to 30 days matches well with the real data [31]. The expectation of the subsequent waves in the half-year period was also reported for some countries [32,33]. From the beginning of the COVID-19 flash, both the proposed capacities and the demand for trips have fallen sharply. The situation worsened along with the spread of the virus. After the announcement of a global pandemic, air travel was reduced against the background of long large-scale lockdowns and restrictions on trips introduced in most countries of the World. Analysis of the economic consequences of the International Civil Aviation Organization shows that in April 2020, when almost all countries introduced a complete or partial Lockdown, air movement dropped sharply to zero with an unprecedented reduction of more than 60% [34]. Some works do not find detectable effects of shelter-in-place orders during the first wave of the COVID-19 pandemic on disease spread or deaths, but only measurable effects on mobility that dissipate over time [35,36].
To date, it seems clear that an important factor influencing the success of the fight against COVID-19 has been the adequate response of people to both government regulations to prevent the spread of the disease and personal attitudes toward the pandemic. Belief in the effectiveness of government measures and a sense of personal risk (including fear of infection and death) contribute to adherence to rules for prevention and the prevention of further spread of infection. Within the framework of the modern understanding of the situation (regional and country aspects of behavior, perception and evaluation of the situation by region, age, professional and ethno-cultural communities), the role of the nation-state and socio-cultural influences impacted society during the pandemic.
In work [37], the authors estimated the extent to which the relaxation of social distancing affected epidemic control and specific effective reproduction number. They found that the relaxation of statewide social distancing measures was associated with a reversal of the downward trend in the transmission of SARS-CoV-2 that had been achieved after these measures were implemented. In all but 9 states, the reversal returned the estimated reproduction number above 1.0 within 8 weeks of the initial relaxation of social distancing measures, leading to increased transmission, an increased number of cases and an increased number of deaths. These patterns were apparent irrespective of the specific kinds of social distancing measures that were rescinded and also irrespective of key indicators of epidemic severity that have been heretofore used by many jurisdictions to guide relaxation decisions. These results can be explained with the help of our model, showing how it can negatively affect the subsequent infection wave values since affected regions include some amount of infection hubs.
Shiva and co-authors [38] used COVID-19 deaths from 169 countries to estimate the effect of the lockdown on the number of deaths 1–8 weeks later. The study finds that stricter lockdowns reduce deaths 4 weeks later but is insignificant 8 weeks later and have the greatest effect in high-income countries. Our results also highlight the importance of using ‘smart’ or ‘targeted’ lockdown policies on the grounds that country-specific conditions call for designing particular policies that work better given underlying circumstances.
5. Conclusions
Thus, we developed a non-linear network-based SIR epidemic model describing the spread of coronavirus in a territory composed of communicating districts. In the example of a hub district that we can describe, for example, a market district with a higher rate of infection spread, we demonstrated that the emergence and subsequent waves of infection disappearance on the degree of relationship with the hub were non-linear. It was also illustrated that for a higher degree of communication with the hub, the number of waves decreased. Finally, our model qualitatively predicts the possibility of control of time dynamics of infected cases by playing with the communication level between interacting districts. In fact, the government should have taken stronger and harsher measures to increase isolation during the first wave. Meanwhile, the quarantine can be lifted after the first two waves, as the values of the maximum number of infected in the second and subsequent waves will decrease; thus, it is limitedly helpful to control the spread of the epidemic disease. Practical application can be convenient for cases when it is possible to draw conditional boundaries between regions and divide the region into smaller areas. By changing the parameters of the connectivity matrices, it is possible to simulate the situation with the level of restrictions both between and within districts. This will allow a more balanced approach to making decisions about restriction measures.
Author Contributions
Conceptualization, V.K. (Viktor Kazantsev) and A.H.; methodology, V.K. (Viktor Kazantsev) and V.K. (Vladimir Khorev); software, V.K. (Vladimir Khorev); validation, V.K. (Viktor Kazantsev); formal analysis, V.K. (Vladimir Khorev); investigation, V.K. (Vladimir Khorev) and V.K. (Viktor Kazantsev); resources, V.K. (Viktor Kazantsev); data curation, V.K. (Viktor Kazantsev) and A.H.; writing—original draft preparation, V.K. (Vladimir Khorev) and A.H.; writing—review and editing, V.K. (Viktor Kazantsev), A.H. and V.K. (Vladimir Khorev); visualization, V.K. (Vladimir Khorev); supervision, A.H.; project administration, A.E and V.K. (Viktor Kazantsev); funding acquisition, V.K. (Viktor Kazantsev). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Foundation for Basic Research (grant 20-04-60078), AEH was also supported by the Programme for Supporting Leading Scientific Schools in the Russian Federation (grant NSh-589.2022.1.2).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pan, Y.; Zhang, D.; Yang, P.; Poon, L.L.M.; Wang, Q. Viral load of SARS-CoV-2 in clinical samples. Lancet Infect. Dis. 2020, 20, 411–412. [Google Scholar] [CrossRef] [PubMed]
- Chin, A.W.H.; Chu, J.T.S.; Perera, M.R.A.; Hui, K.P.Y.; Yen, H.L.; Chan, M.C.W.; Peiris, M.; Poon, L.L.M. Stability of SARS-CoV-2 in different environmental conditions. Lancet Microbe 2020, 1, e10. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics: V. Analysis of experimental epidemics of mouse-typhoid; a bacterial disease conferring incomplete immunity. J. Hyg. 1939, 39, 271–288. [Google Scholar] [CrossRef] [PubMed]
- Gounane, S.; Barkouch, Y.; Atlas, A.; Bendahmane, M.; Karami, F.; Meskine, D. An adaptive social distancing SIR model for COVID-19 disease spreading and forecasting. Epidemiol. Methods 2021, 10, 20200044. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Filippo, A.D.; Matteo, A.D.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Abou-Ismail, A. Compartmental Models of the COVID-19 Pandemic for Physicians and Physician-Scientists. SN Compr. Clin. Med. 2020, 2, 852–858. [Google Scholar] [CrossRef]
- Fokas, A.S.; Dikaios, N.; Kastis, G.A. Mathematical models and deep learning for predicting the number of individuals reported to be infected with SARS-CoV-2. J. R. Soc. Interface 2020, 17, 20200494. [Google Scholar] [CrossRef]
- Deldar, M.; Ghorabi, S.T.; Sayehmiri, K. SIR Model for Estimations of the Coronavirus Epidemic Dynamics in Iran. J. Biostat. Epidemiol. 2020, 6, 101–106. [Google Scholar] [CrossRef]
- Lai, C.C.; Hsu, C.Y.; Jen, H.H.; Yen, A.M.F.; Chan, C.C.; Chen, H.H. The Bayesian Susceptible-Exposed-Infected-Recovered model for the outbreak of COVID-19 on the Diamond Princess Cruise Ship. Stoch. Environ. Res. Risk Assess. 2021, 35, 1319–1333. [Google Scholar] [CrossRef]
- Moein, S.; Nickaeen, N.; Roointan, A.; Borhani, N.; Heidary, Z.; Javanmard, S.H.; Ghaisari, J.; Gheisari, Y. Inefficiency of SIR models in forecasting COVID-19 epidemic: A case study of Isfahan. Sci. Rep. 2021, 11, 4725. [Google Scholar] [CrossRef]
- Liu, Y.; Gayle, A.A.; Wilder-Smith, A.; Rocklöv, J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Travel Med. 2020, 27. [Google Scholar] [CrossRef]
- Bavel, J.J.V.; Baicker, K.; Boggio, P.S.; Capraro, V.; Cichocka, A.; Cikara, M.; Crockett, M.J.; Crum, A.J.; Douglas, K.M.; Druckman, J.N.; et al. Using social and behavioural science to support COVID-19 pandemic response. Nat. Hum. Behav. 2020, 4, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Kastalskiy, I.A.; Pankratova, E.V.; Mirkes, E.M.; Kazantsev, V.B.; Gorban, A.N. Social stress drives the multi-wave dynamics of COVID-19 outbreaks. Sci. Rep. 2021, 11, 22497. [Google Scholar] [CrossRef] [PubMed]
- Rocha, L.E.C.; Liljeros, F.; Holme, P. Simulated Epidemics in an Empirical Spatiotemporal Network of 50, 185 Sexual Contacts. PLoS Comput. Biol. 2011, 7, e1001109. [Google Scholar] [CrossRef] [PubMed]
- Montagnon, P. A stochastic SIR model on a graph with epidemiological and population dynamics occurring over the same time scale. J. Math. Biol. 2019, 79, 31–62. [Google Scholar] [CrossRef]
- Holme, P. Fast and principled simulations of the SIR model on temporal networks. PLoS ONE 2021, 16, e0246961. [Google Scholar] [CrossRef]
- Lazebnik, T.; Bunimovich-Mendrazitsky, S. The Signature Features of COVID-19 Pandemic in a Hybrid Mathematical Model—Implications for Optimal Work–School Lockdown Policy. Adv. Theory Simul. 2021, 4, 2000298. [Google Scholar] [CrossRef]
- Amaral, A.V.R.; González, J.A.; Moraga, P. Spatio-temporal modeling of infectious diseases by integrating compartment and point process models. Stoch. Environ. Res. Risk Assess. 2022. [Google Scholar] [CrossRef]
- Estrada, E. COVID-19 and SARS-CoV-2. Modeling the present, looking at the future. Phys. Rep. 2020, 869, 1–51. [Google Scholar] [CrossRef]
- Boccaletti, S.; Mindlin, G.; Ditto, W.; Atangana, A. Closing editorial: Forecasting of epidemic spreading: Lessons learned from the current covid-19 pandemic. Chaos Solitons Fractals 2020, 139, 110278. [Google Scholar] [CrossRef]
- Boccaletti, S.; Ditto, W.; Mindlin, G.; Atangana, A. Modeling and forecasting of epidemic spreading: The case of COVID-19 and beyond. Chaos Solitons Fractals 2020, 135, 109794. [Google Scholar] [CrossRef] [PubMed]
- Prasse, B.; Achterberg, M.A.; Ma, L.; Mieghem, P.V. Network-inference-based prediction of the COVID-19 epidemic outbreak in the Chinese province Hubei. Appl. Netw. Sci. 2020, 5, 35. [Google Scholar] [CrossRef] [PubMed]
- Alexi, A.; Rosenfeld, A.; Lazebnik, T. A Security Games Inspired Approach for Distributed Control of Pandemic Spread. Adv. Theory Simul. 2022, 5, 2200631. [Google Scholar] [CrossRef]
- Wood, J.; McCaw, J.; Becker, N.; Nolan, T.; MacIntyre, C.R. Optimal Dosing and Dynamic Distribution of Vaccines in an Influenza Pandemic. Am. J. Epidemiol. 2009, 169, 1517–1524. [Google Scholar] [CrossRef]
- Tien, J.H.; Earn, D.J.D. Multiple Transmission Pathways and Disease Dynamics in a Waterborne Pathogen Model. Bull. Math. Biol. 2010, 72, 1506–1533. [Google Scholar] [CrossRef]
- Lisphilar. Number of Novel Corona Virus 2019 Cases in Japan. 2022. Available online: https://www.kaggle.com/datasets/lisphilar/covid19-dataset-in-japan (accessed on 12 January 2023).
- Science Council of Japan. Area-Specific Data for COVID-19 Statistics in Japan. 2022. Available online: https://www.scj.go.jp/ja/member/iinkai/2bu/linklist.html (accessed on 12 January 2023).
- Ivorra, B.; Ferrández, M.; Vela-Pérez, M.; Ramos, A. Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China. Commun. Nonlinear Sci. Numer. Simul. 2020, 88, 105303. [Google Scholar] [CrossRef]
- Singh, B.C.; Alom, Z.; Hu, H.; Rahman, M.M.; Baowaly, M.K.; Aung, Z.; Azim, M.A.; Moni, M.A. COVID-19 Pandemic Outbreak in the Subcontinent: A Data Driven Analysis. J. Pers. Med. 2021, 11, 889. [Google Scholar] [CrossRef]
- Cacciapaglia, G.; Cot, C.; Sannino, F. Multiwave pandemic dynamics explained: How to tame the next wave of infectious diseases. Sci. Rep. 2021, 11, 6638. [Google Scholar] [CrossRef]
- Saikia, D.; Bora, K.; Bora, M.P. COVID-19 outbreak in India: An SEIR model-based analysis. Nonlinear Dyn. 2021, 104, 4727–4751. [Google Scholar] [CrossRef]
- Durán-Olivencia, M.A.; Kalliadasis, S. Understanding Soaring Coronavirus Cases and the Effect of Contagion Policies in the UK. Vaccines 2021, 9, 735. [Google Scholar] [CrossRef]
- Ranjan, R.; Sharma, A.; Verma, M.K. Characterization of the Second Wave of COVID-19 in India. medRxiv 2021, 121, 85–93. [Google Scholar] [CrossRef]
- Dray, L.; Schäfer, A.W. Initial Long-Term Scenarios for COVID-19’s Impact on Aviation and Implications for Climate Policy. Transp. Res. Rec. J. Transp. Res. Board 2021, 036119812110450. [Google Scholar] [CrossRef]
- Dave, D.; Friedson, A.I.; Matsuzawa, K.; Sabia, J.J. When do shelter-in-place orders fight covid-19 best? policy heterogeneity across states and adoption time. Econ. Inq. 2020, 59, 29–52. [Google Scholar] [CrossRef] [PubMed]
- Berry, C.R.; Fowler, A.; Glazer, T.; Handel-Meyer, S.; MacMillen, A. Evaluating the effects of shelter-in-place policies during the COVID-19 pandemic. Proc. Natl. Acad. Sci. USA 2021, 118, e2019706118. [Google Scholar] [CrossRef] [PubMed]
- Tsai, A.C.; Harling, G.; Reynolds, Z.; Gilbert, R.F.; Siedner, M.J. Coronavirus Disease 2019 (COVID-19) Transmission in the United States Before Versus After Relaxation of Statewide Social Distancing Measures. Clin. Infect. Dis. 2020, 73, S120–S126. [Google Scholar] [CrossRef]
- Shiva, M.; Molana, H. The Luxury of Lockdown. Eur. J. Dev. Res. 2021, 34, 503–523. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).