Construction of an Accurate Wheat-Grain Model Based on X-ray Tomography and Bonding Parameters by Discrete Element
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials
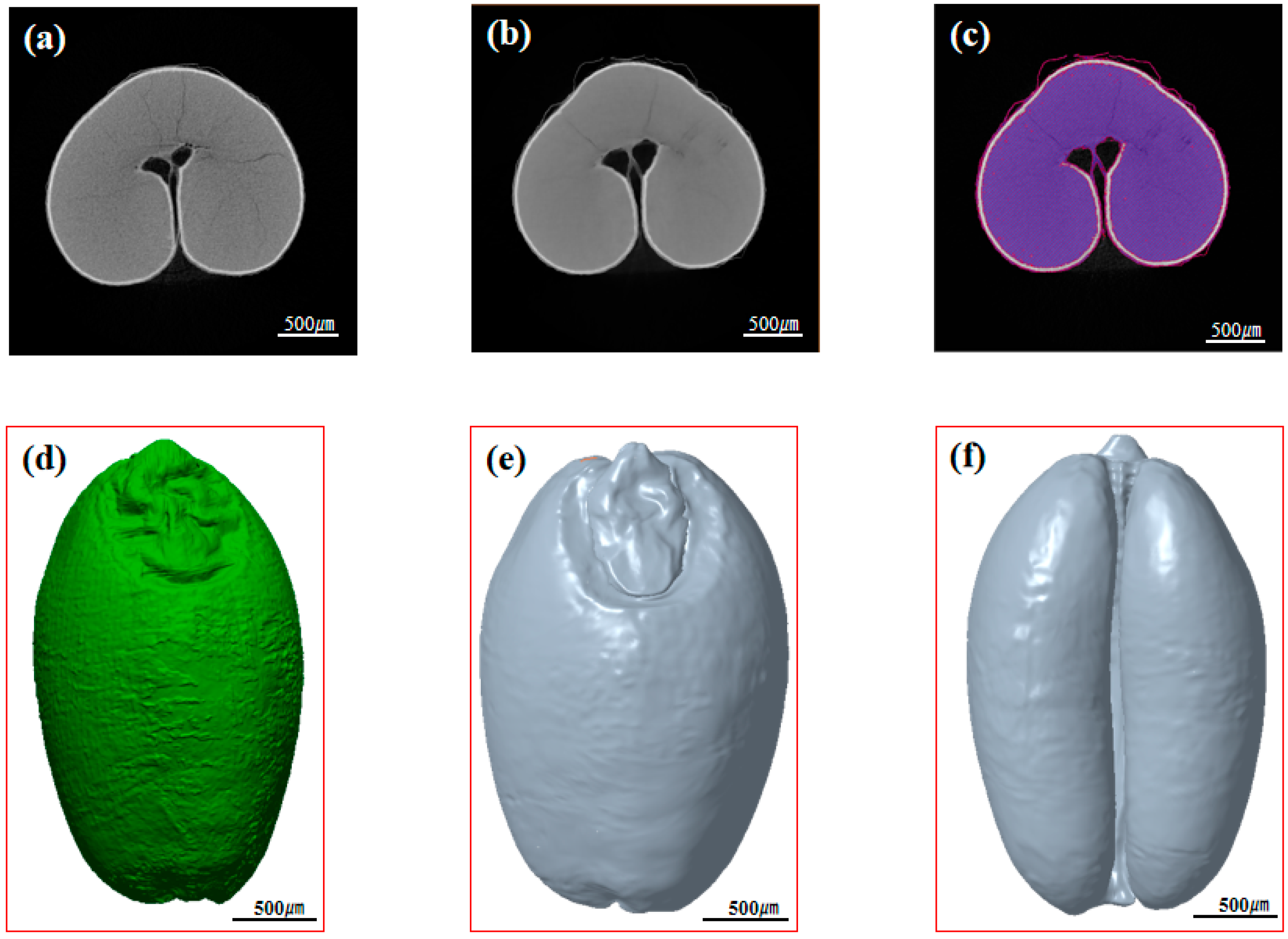
2.2. Reconstruction of Three-Dimensional Model of Wheat Grain
2.2.1. Image Acquisition
2.2.2. Image Processing
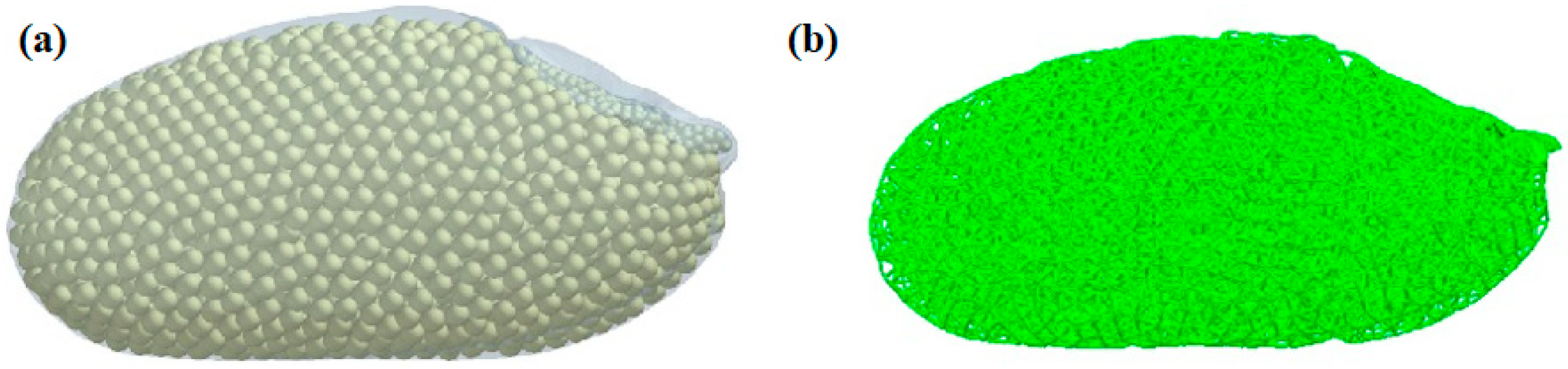
2.3. Construction of Discrete-Element Simulation Model of Wheat Grain
2.3.1. Discrete-Element Contact Model
2.3.2. Discrete-Element Simulation Model of Wheat Grain
2.4. Uniaxial Compression Experiment
2.5. Test Factors
2.6. Experimental Design
2.6.1. Single-Factor Test Design
2.6.2. Plackett–Burman Test Design
2.6.3. Steepest-Ascent Experiment Design
2.6.4. Box–Behnken Test Design
3. Results
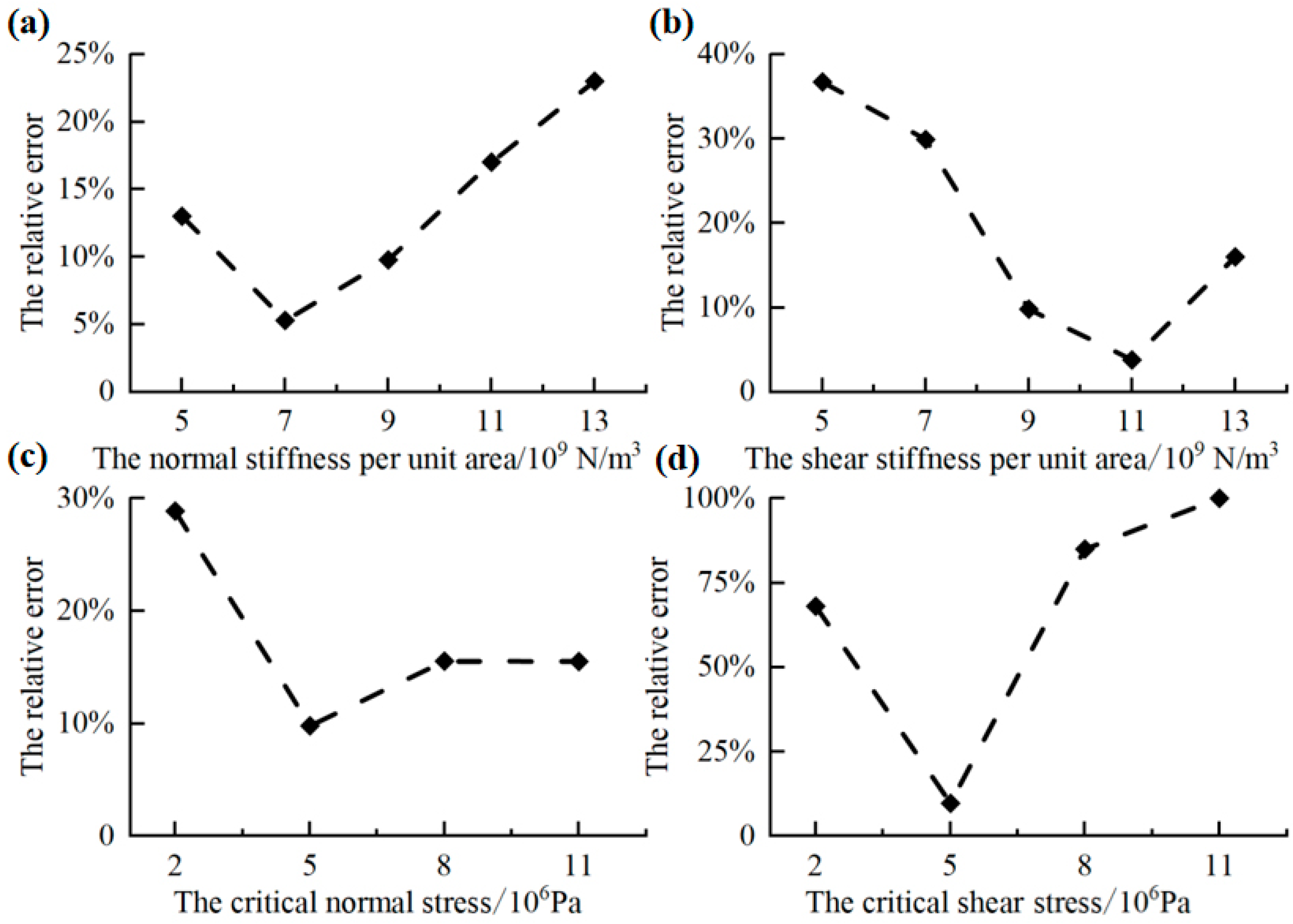
3.1. Single-Factor Test
3.2. Plackett–Burman Test
3.3. Steepest-Ascent Experiment
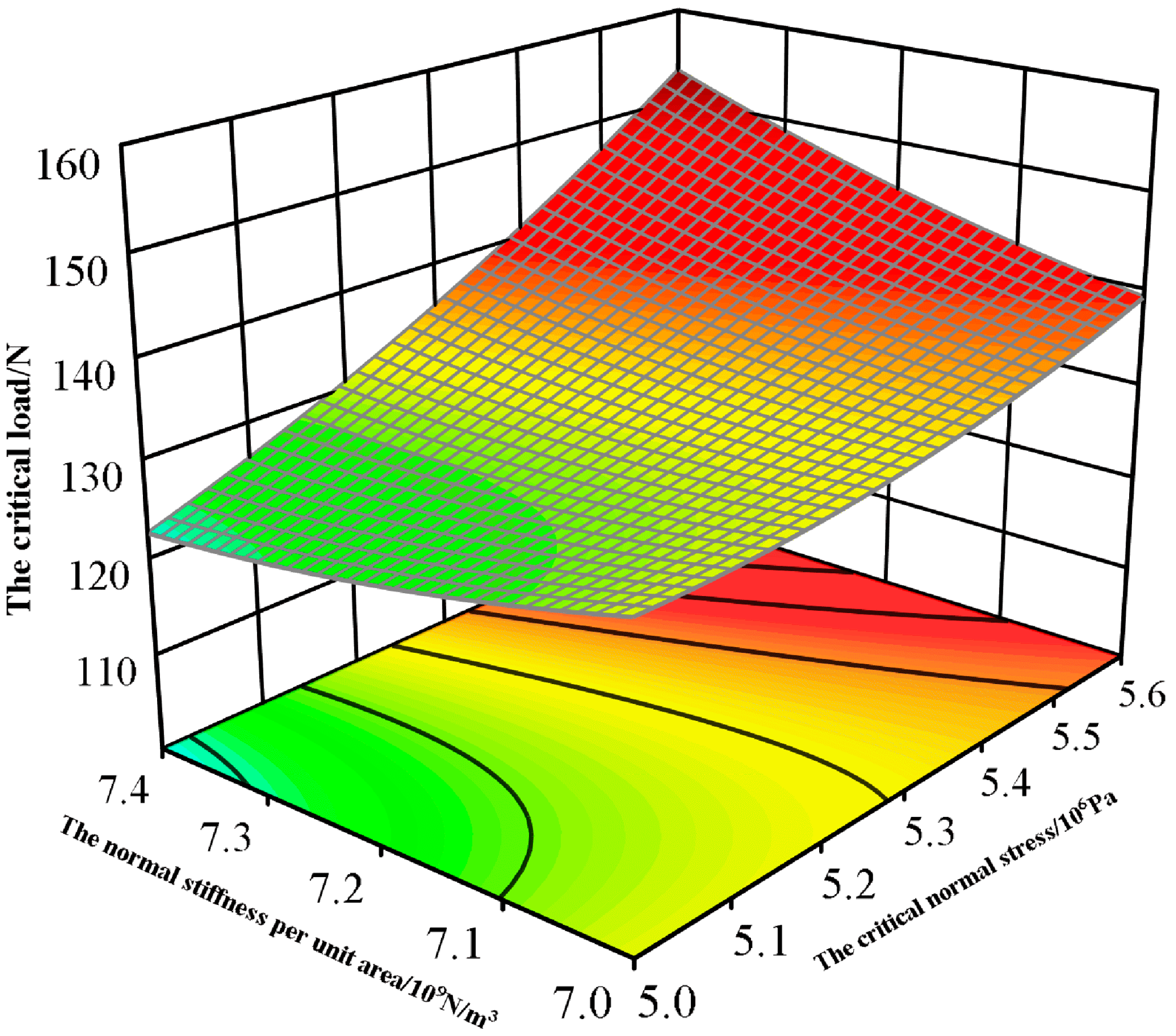
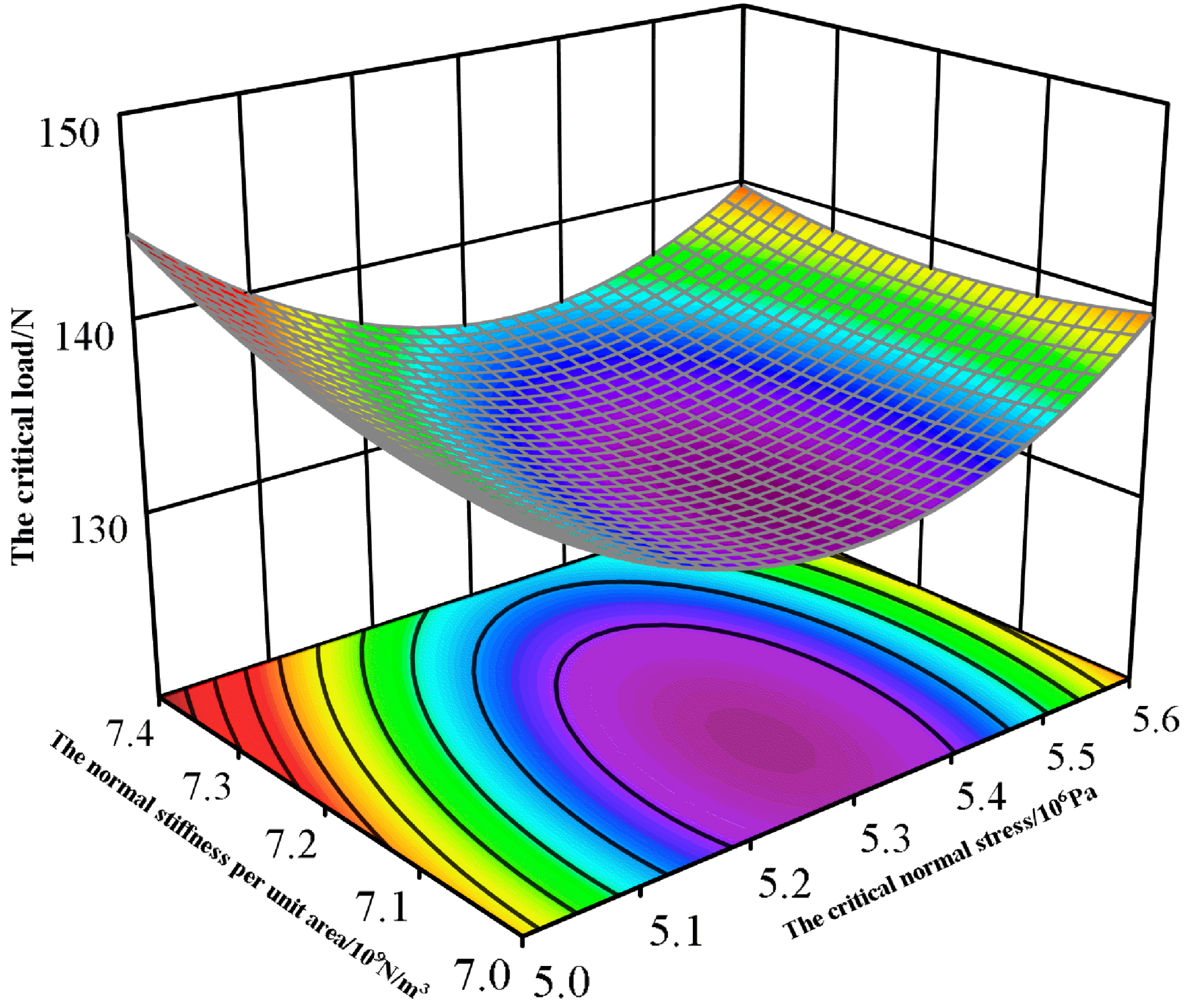
3.4. Box–Behnken Test
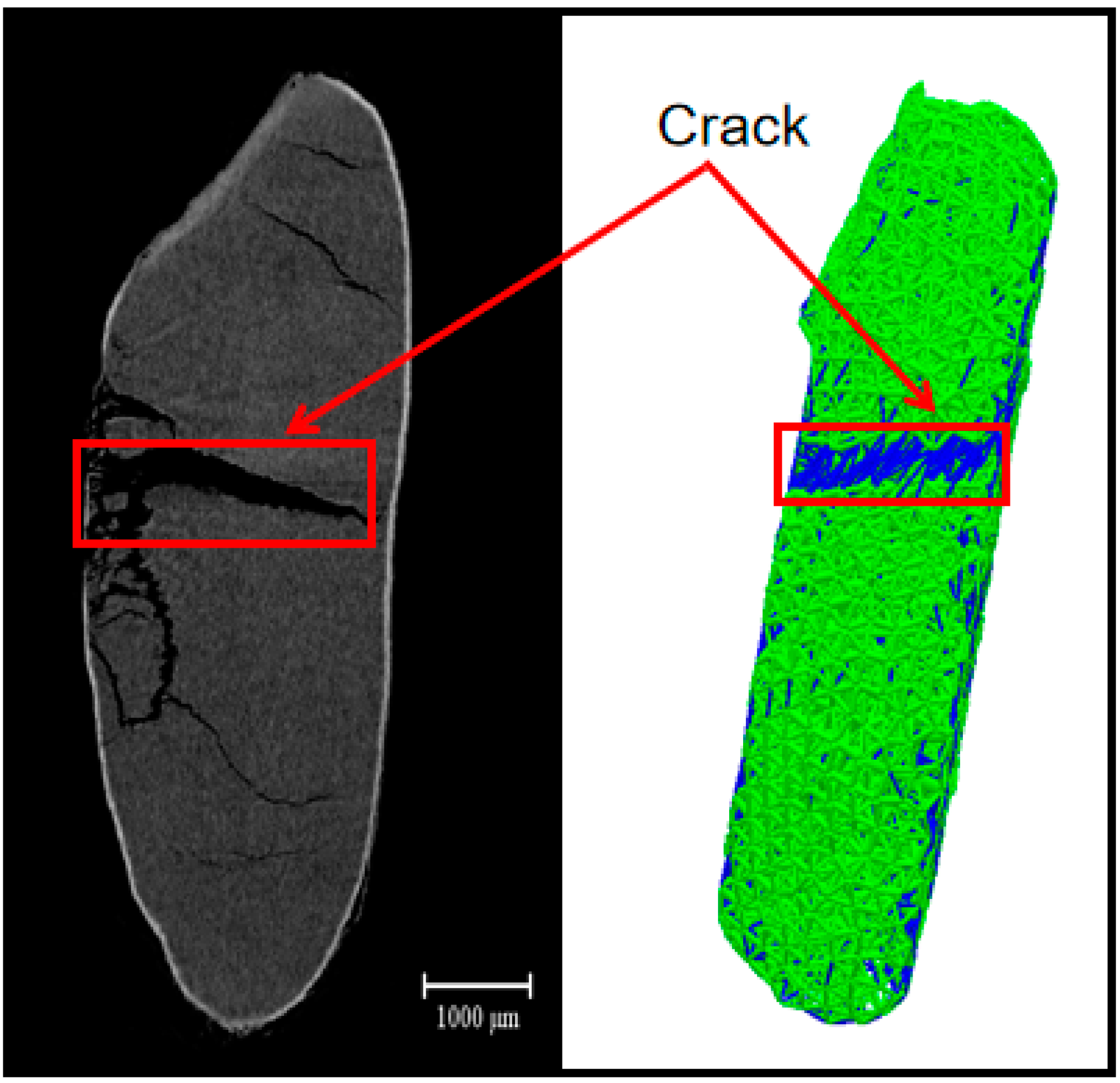
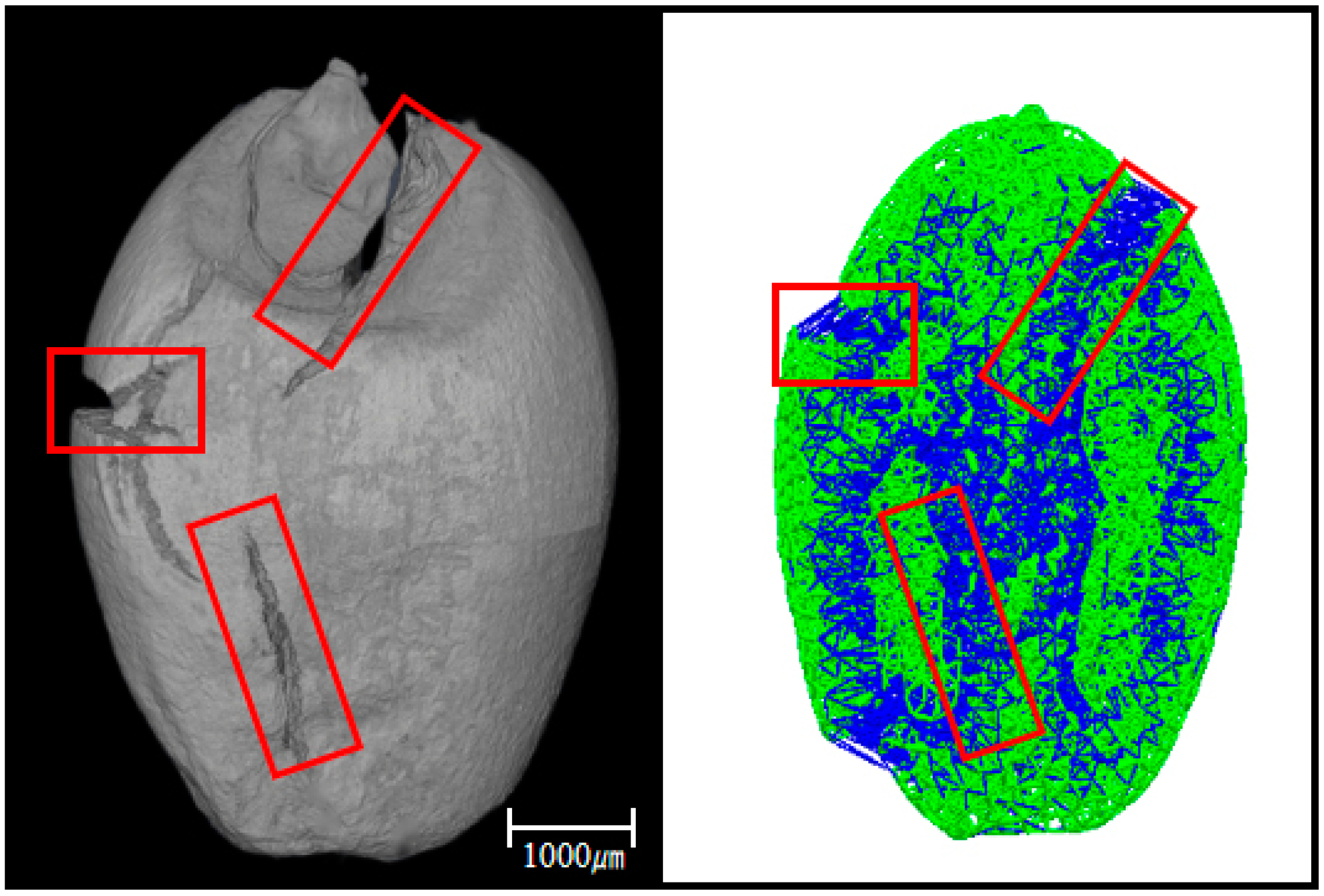
3.5. Optimal Parameters and Model Validation
4. Conclusions
- (1)
- An accurate outer contour model of wheat grain was established, and the various tissue models could be obtained by separating the embryo, endosperm, and other tissues in the model.
- (2)
- A discrete-element simulation model of wheat grains was constructed by filling the tissue models of various parts of wheat grains with particles of different radii.
- (3)
- In the uniaxial compression test, the critical load of wheat crushing was 118.821 N. Through the single-factor test and the Plackett–Burman test, the significant factors affecting the relative error between the critical load test value and the simulation value was identified: critical tangential stress. The influence of critical normal stress and unit area normal stiffness on both was relatively small.
- (4)
- The steepest-climbing test was used to reduce the horizontal range of significant factors, followed by the Box–Behnken response surface test. Through the analysis of the test results, a quadratic polynomial regression equation was obtained. An ANOVA showed that the regression equations have a highly significant and a high fit. The regression equation was optimized and solved to obtain the optimal parameters as follows: the normal stiffness per unit area was 7.392 × 1010 N/m3, the critical normal stress was 5.293 × 106 Pa, and the critical tangential stress was 5.001 × 106 Pa. The critical load of 122.392 N in the verification test and the physical error of 118.821 N was 3%, which verified the reliability of the simulation parameters of the wheat-grain crushing model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, W.; Peng, S. Research on the construction of safety management and operation mechanism of grain storage and transportation in China. Soc. Sci. Shandong Prov. 2014, 6, 179–183. [Google Scholar]
- Voicu, G.; Tudosie, E.-M.; Ungureanu, N. Some mechanical characteristics of wheat seeds Obtained by Uniaxial Compression Tests. UPB Sci. Bull. Ser. D Mech. Eng. 2013, 75, 265–278. [Google Scholar]
- Barrer, G.N.; Mendez-Mendez, J.; Arzate-Vazquez, I.; Calderón-Domínguez, G.; Ribotta, P.D. Nano- and micromechanical properties of wheat grain by atomic force microscopy (AFM) and nano-indentation (IIT) and their relationship with the mechanical properties evaluated by uniaxial compression test. J. Cereal Sci. 2019, 90, 102830. [Google Scholar] [CrossRef]
- Jia, F.; Zhou, X.; Chen, F. The Calculations and Simulation Testing on the Elastic Modulus of Wheat. Interdiscip. Sci. Comput. Life Sci. 2015, 7, 200–204. [Google Scholar] [CrossRef]
- Cheng, Y.; Sun, X. The relationship between the crushing resistance of wheat grain and its quality traits. Grain Oil Process. 2008, 12, 84–86. [Google Scholar]
- Li, D.; Mao, Z. Analysis of the microstructure of rice after natural air drying. J. Agric. Eng. 2003, 19, 156–159. [Google Scholar]
- Zhang, K.; Huang, J.; Yang, M.; Zhang, F.; Huang, X.; Zhao, C. Finite element analysis and experimental verification of winter wheat grain extrusion characteristics. J. Agric. Eng. 2010, 26, 352—356+391. [Google Scholar]
- Peng, F.; Fang, F.; Wang, H. Modeling and testing of barley kernels based on 3D laser scanning. J. Agric. Mach. 2018, 49, 342–348. [Google Scholar]
- Zhu, K.; Hui, Y.; Zhou, Y.; Wang, H.; Zhang, Y.; Li, H.; Chen, Y.; Zheng, J.; Bai, L. Construction of wheat grain model and discrete element parameter calibration based on X-ray tomography. Chin. J. Grain Oil 2022, 37, 218–223. [Google Scholar]
- He, Y.; Wu, M.; Xiang, W. Progress in the application of the discrete element method in agricultural engineering. China Agric. Bull. 2017, 33, 133–137. [Google Scholar]
- Zhao, H.; Huang, Y.; Liu, Z. Applications of Discrete Element Method in the Research of Agricultural Machinery: A Review. Agriculture 2021, 11, 425. [Google Scholar] [CrossRef]
- Chen, Y.; Zeng, X.; Wang, J. Harvest machine virtual environment model and simulation platform construction. J. Agric. Mach. 2019, 50, 159–166. [Google Scholar]
- Zeng, Z.; Ma, X.; Cao, X. Application status and prospect of discrete element method in agricultural engineering research. J. Agric. Mach. 2021, 52, 1–20. [Google Scholar]
- Zhang, N.; Cao, X.; Wang, X.; Sun, Y. Determination of simulation parameters of rice mill. Food Mach. 2023, 39, 95–100. [Google Scholar]
- Don, G.; Yang, Y.; Guo, Y.; Liu, X.; Yu, C.; Du, J.; Zhang, J. EDEM simulation analysis of seed filling characteristics of different soybean varieties. J. Henan Agric. Univ. 2019, 53, 93–98. [Google Scholar]
- Zhang, R.; Jiao, W.; Zhou, J.; Qi, B.; Liu, H.; Xia, Q. Calibration of discrete element model parameters for rice seeds with different filling particle radii. J. Agric. Mach. 2020, 51, 227–235. [Google Scholar]
- Wang, M.; Wang, W.; Yang, L.; Hou, M. The corn seed particle modeling method based on EDEM. J. Henan Agric. Univ. 2018, 52, 80—84, 103. [Google Scholar]
- Li, J.; Liu, X.; Zou, L.; Yin, R.; Yang, K.; Yuan, J. Discrete element modeling method and experimental verification of spinach main–root. Agric. Mech. Res. 2021, 43, 181–185. [Google Scholar]
- Shu, C.; Yang, J.; Wan, X.; Yuan, J.; Liao, Y.; Liao, Q. Simulation calibration and experiment of simulation parameters of discrete rapeseed seed extract. J. Agric. Eng. 2022, 38, 34–43. [Google Scholar]
- Zhu, H.; Qian, C.; Bai, L.; Li, H.; Mou, D.; Li, J. Optimizing the corn straw discrete element model based on Plackett-Burman test design and response surface method. J. China Agric. Univ. 2021, 26, 221–231. [Google Scholar]
- Liu, W.; Su, Q.; Fang, M.; Zhang, J.; Zhang, W.; Yu, Z. Parameters Calibration of Discrete Element Model for Corn Straw Cutting Based on Hertz-Mindlin with Bonding. Appl. Sci. 2023, 13, 1156. [Google Scholar] [CrossRef]
- Chen, L.; Xue, J.; Mou, X.; Ma, X.; Liu, W.; Liu, Y.; Xiang, J. Study on the parameter calibration method of cassava seed stem simulation based on discrete element. Jiangsu Agric. Sci. 2023, 51, 198–205. [Google Scholar]
- Zhou, Y.; Hui, Y.; Feng, L. Construction of a three-dimensional precision model based on X-ray. Chin. J. Grain Oil 2018, 33, 7–11. [Google Scholar]
- Fang, R. Numerical Analysis of Discrete Elements for Stress and Wear of Shield Disc Hob. Master’s thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Rackl, M.; Hanley, K.L. A methodical calibration procedure for discrete element models. Powder Technol. 2017, 307, 73–83. [Google Scholar] [CrossRef]
- Zhu, K. Study on the Construction and Crushing Characteristics of Wheat Grain Morphology and Structure. Master’s Thesis, Henan University of Technology, Zhengzhou, China, 2021. [Google Scholar]
- Liu, F. Discrete Element Modeling of Wheat Particles and Short Stalks in the Cleaning Device. Ph.D. Thesis, Northwest A & F University, Xianyang, China, 2018. [Google Scholar]
- Yu, Y.; Ren, S.; Li, J.; Chang, J.; Yu, S.; Sun, C.; Chen, T. Calibration and Testing of Discrete Element Modeling Parameters for Fresh Goji Berries. Appl. Sci. 2022, 12, 11629. [Google Scholar] [CrossRef]



| Project | Parameter | Number |
|---|---|---|
| Material parameter | Wheat Poisson ratio | 0.4 |
| Steel plate Poisson ratio | 0.3 | |
| Wheat Young’s modulus/Mpa | 244.24 | |
| Steel plate Young’s modulus/Mpa | 206,000 | |
| Wheat density/(kg/m3) | 1350 | |
| Steel plate density/(kg/m3) | 7500 | |
| Contact parameter | Wheat-wheat recovery coefficient | 0.46 |
| Wheat-wheat static friction coefficient | 0.185 | |
| Wheat-wheat rolling coefficient of friction | 0.046 | |
| Wheat-steel plate recovery coefficient | 0.48 | |
| Wheat-static friction coefficient of steel plate | 0.23 | |
| Wheat-steel plate rolling friction coefficient | 0.05 |
| Wheat Tissue | Fill the Radius | Contact Radius |
|---|---|---|
| Embryo | 0.05/mm | 0.1/mm |
| Epidermal and endosperm | 0.1/mm | 0.12/mm |
| Test | X1 | X2 | X3 | X4 | Test Relative Error/% |
|---|---|---|---|---|---|
| 1 | 1 | 1 | −1 | 1 | 70.53% |
| 2 | −1 | 1 | 1 | −1 | 19.24% |
| 3 | 1 | −1 | 1 | 1 | 107.16% |
| 4 | −1 | 1 | −1 | 1 | 68.13% |
| 5 | −1 | −1 | 1 | −1 | 5.11% |
| 6 | −1 | −1 | −1 | 1 | 7.09% |
| 7 | 1 | −1 | −1 | −1 | 5.48% |
| 8 | 1 | 1 | −1 | −1 | 16.14% |
| 9 | 1 | 1 | 1 | −1 | 19.04% |
| 10 | −1 | 1 | 1 | 1 | 75.70% |
| 11 | 1 | −1 | 1 | 1 | 102.96% |
| 12 | −1 | −1 | −1 | −1 | 4.65% |
| Factor | Sum of Squares | df | Mean Square | F Value | p Value |
|---|---|---|---|---|---|
| model | 1.47 | 4 | 0.37 | 9.00 | 0.0068 |
| X1 | 0.17 | 1 | 0.17 | 4.07 | 0.0835 |
| X2 | 0.011 | 1 | 0.011 | 0.27 | 0.6203 |
| X3 | 0.21 | 1 | 0.21 | 5.03 | 0.0599 |
| X4 | 1.09 | 1 | 1.09 | 26.66 | 0.0013 |
| Test | X1 | X3 | X4 | Critical Load/N | Relative Error/% |
|---|---|---|---|---|---|
| 1 | 7 | 5 | 5 | 110.44 | 7.05% |
| 2 | 7.4 | 5.6 | 5.6 | 158.428 | 33.33% |
| 3 | 7.8 | 6.2 | 6.2 | 167.921 | 41.32% |
| 4 | 8.2 | 6.8 | 6.8 | 205.096 | 72.61% |
| 5 | 8.6 | 7.4 | 7.4 | 216.869 | 82.52% |
| 6 | 9 | 8 | 8 | 246.144 | 107.16% |
| Test | X1 | X3 | X4 | Critical Load/N |
|---|---|---|---|---|
| 1 | −1 | −1 | 0 | 139.446 |
| 2 | 1 | −1 | 0 | 144.169 |
| 3 | −1 | 1 | 0 | 139.635 |
| 4 | 1 | 1 | 0 | 139.244 |
| 5 | −1 | 0 | −1 | 130.844 |
| 6 | 1 | 0 | −1 | 122.793 |
| 7 | −1 | 0 | 1 | 138.881 |
| 8 | 1 | 0 | 1 | 153.638 |
| 9 | 0 | −1 | −1 | 131.19 |
| 10 | 0 | 1 | −1 | 133.078 |
| 11 | 0 | −1 | 1 | 153.902 |
| 12 | 0 | 1 | 1 | 148.864 |
| 13 | 0 | 0 | 0 | 127.358 |
| 14 | 0 | 0 | 0 | 135.727 |
| 15 | 0 | 0 | 0 | 135.272 |
| 16 | 0 | 0 | 0 | 134.104 |
| 17 | 0 | 0 | 0 | 131.865 |
| Source | Sum of Squares | df | Mean Square | F Value | p Value |
|---|---|---|---|---|---|
| model | 1142.34 | 9.00 | 126.93 | 18.55 | 0.0004 |
| X1 | 15.23 | 1.00 | 15.23 | 2.23 | 0.1793 |
| X3 | 7.77 | 1.00 | 7.77 | 1.14 | 0.3218 |
| X4 | 748.46 | 1.00 | 748.46 | 109.41 | <0.0001 |
| X1X3 | 6.54 | 1.00 | 6.54 | 0.96 | 0.3608 |
| X1X4 | 130.05 | 1.00 | 130.05 | 19.01 | 0.0033 |
| X3X4 | 11.99 | 1.00 | 11.99 | 1.75 | 0.2271 |
| X12 | 6.78 | 1.00 | 6.78 | 0.99 | 0.3525 |
| X32 | 177.29 | 1.00 | 177.29 | 25.92 | 0.0014 |
| X42 | 24.34 | 1.00 | 24.34 | 3.56 | 0.1012 |
| Residual | 47.88 | 7.00 | 6.84 | ---- | 0.9921 |
| Lack of Fit | 1.04 | 3.00 | 0.35 | 0.03 | 0.0004 |
| Pure Error | 46.85 | 4.00 | 11.71 | ---- | 0.1793 |
| Cor Total | 1190.22 | 16.00 | ---- | ---- | 0.3218 |
| CV = 1.9%, R2 = 0.9598, AdjR2 = 0.9098, PredR2 = 0.9246, Adep Precision = 15.755 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Shang, W.; Hui, Y.; Shi, C.; Gao, J.; Zhang, Y.; Liu, J.; Cheng, D.; Zhu, K. Construction of an Accurate Wheat-Grain Model Based on X-ray Tomography and Bonding Parameters by Discrete Element. Appl. Sci. 2023, 13, 9265. https://doi.org/10.3390/app13169265
Zhou Y, Shang W, Hui Y, Shi C, Gao J, Zhang Y, Liu J, Cheng D, Zhu K. Construction of an Accurate Wheat-Grain Model Based on X-ray Tomography and Bonding Parameters by Discrete Element. Applied Sciences. 2023; 13(16):9265. https://doi.org/10.3390/app13169265
Chicago/Turabian StyleZhou, Ying, Wenyu Shang, Yanbo Hui, Chuang Shi, Ju Gao, Yongzhen Zhang, Juanjuan Liu, Dongdong Cheng, and Kang Zhu. 2023. "Construction of an Accurate Wheat-Grain Model Based on X-ray Tomography and Bonding Parameters by Discrete Element" Applied Sciences 13, no. 16: 9265. https://doi.org/10.3390/app13169265
APA StyleZhou, Y., Shang, W., Hui, Y., Shi, C., Gao, J., Zhang, Y., Liu, J., Cheng, D., & Zhu, K. (2023). Construction of an Accurate Wheat-Grain Model Based on X-ray Tomography and Bonding Parameters by Discrete Element. Applied Sciences, 13(16), 9265. https://doi.org/10.3390/app13169265





