1. Introduction
Federated learning is a decentralized machine learning paradigm that enables collaborative model training without the need for centralized data aggregation. Multiple parties, such as devices or organizations, participate by computing model updates or gradients locally and exchanging them with a central server [
1]. Due to its characteristics, federated learning has gained increasing attention, particularly in the fields of healthcare, finance, and the Internet of Things (IoT) [
2,
3,
4]. However, in federated learning, the importance of protecting the privacy of participants cannot be overlooked [
2]. Therefore, protecting sensitive information becomes a challenging task in the ever-evolving landscape of federated learning. Based on this premise, group signatures have emerged as an effective tool for protecting user privacy due to their anonymity and traceability properties.
Group signature, as a special type of digital signature [
5], is a research hotspot in public key cryptography. In the group signature scheme, each member of the group is issued with a signing key, allowing them to generate signatures anonymously by using the signing key (anonymity); if there is an abuse of signature power by malicious group members, the group signature scheme has an entity called the group manager, which can break anonymity by deriving specific signatories from the signature. Due to the characteristics of group signature, it can be applied in federated learning to achieve anonymity preservation and parameter integrity, as well as to prevent dishonest participants from transmitting malicious data, etc.
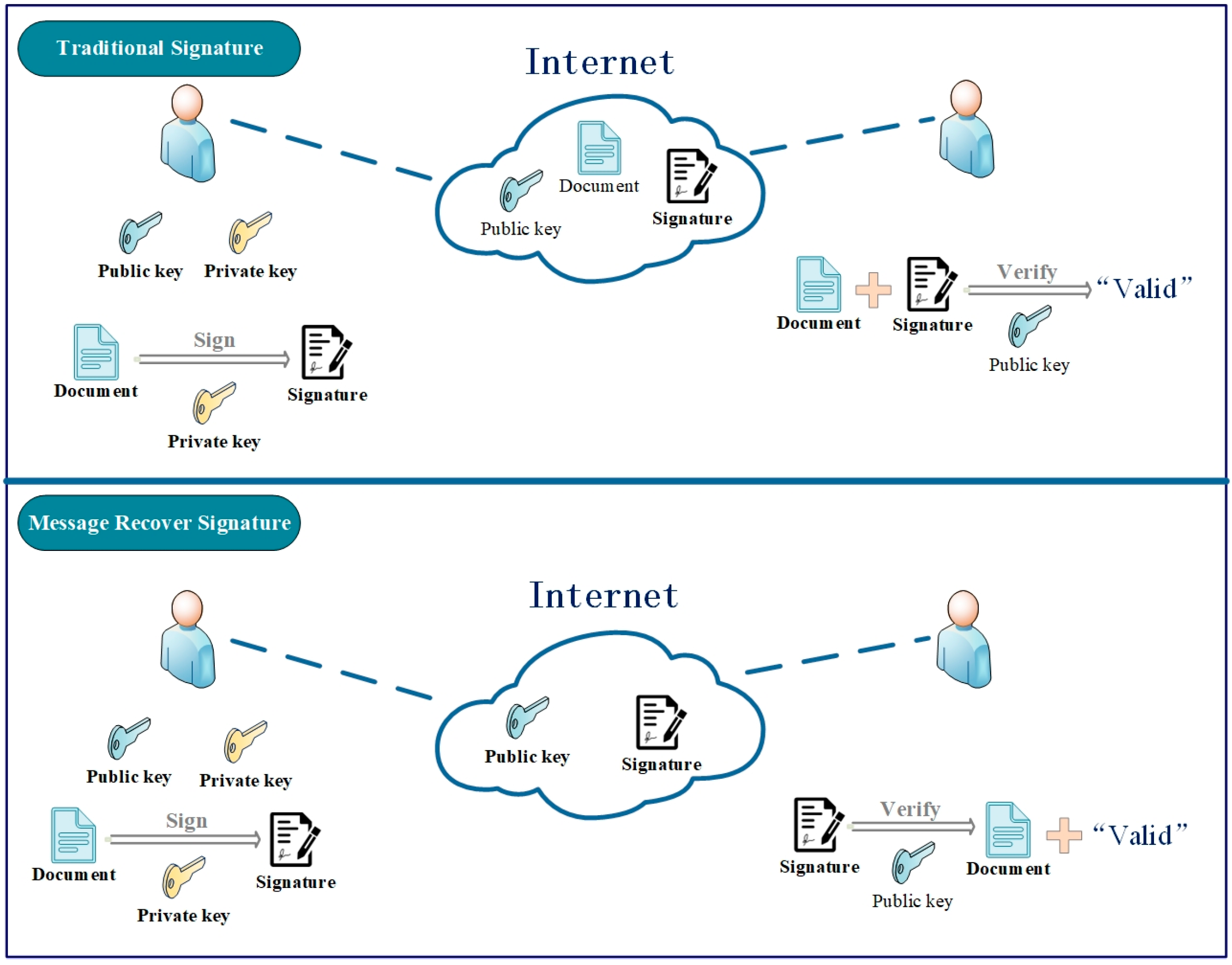
However, in conventional group signatures, to ensure message integrity, signers must send the message along with the signature to the verifier. This poses a significant problem: during the process of verifying the correctness of the signature, the verifier needs to receive all the parameters of the message–signature pairs, with the message often taking up a significant portion. To address the above problem, Nyberg et al. [
6] introduced the concept of message recovery: It enables the sender to avoid sending the signed message and to send only the signature, and it can recover the message while confirming the validity of the signature. This obviously decreases the quantity of information that needs to be transferred, which saves transmission bandwidth. Moreover, it is more convenient for both the sender and the receiver. The implementation of message recovery is considered as an encoding method [
7,
8], as it involves adding additional information to the signature to achieve message recoverability. Since then, Islam et al. [
9] have proposed a signature scheme for message recovery with specified verifiers based on elliptic curves and bilinear pairs, and the scheme was proven to be secure under the stochastic prediction model. In 2020, Kazmirchuk et al. [
10] proposed a provably secure elliptic curve-based digital signature authentication scheme with message recovery. Their scheme uses a hash token function instead of a hash function, allowing for reversed signature and verification procedures and message recovery from the signature r-component. In 2013, Tian et al. [
11] first introduced the concept of message recovery to lattice-based cryptography. In 2023, Wu et al. [
12] proposed an identity-based proxy signature scheme on the lattice, and it also worked with message recovery. The difference between traditional digital signatures and message recovery signatures is shown in
Figure 1.
Nevertheless, to the best of our knowledge, the group signature schemes currently proposed do not possess the functionality of message recovery. This will directly result in group members having to send additional messages to the verifier. Therefore, constructing a group signature scheme with message recovery (GS-MR) will reduce the amount of data received by the verifier and provide greater transparency and application scalability to group privacy scenarios. Furthermore, in domains such as federated learning, the GS-MR scheme has significant advantages over traditional group signature schemes. For example, in federated learning, participants train the model locally and send the model parameter updates to a central server, which aggregates these parameter updates and distributes the aggregated model parameters to the participants. The GS-MR scheme can be used to verify the integrity of the model parameters transmitted by the central server and to recover the original model update information. This ensures that the model parameters are not tampered with during the transmission process and provides verifiability of the results to the participants. In addition, in certain scenarios, such as model analysis or debugging of model updates, federated learning may require the recovery of the original participant data without centralizing the raw data on the central server. The GS-MR scheme can facilitate the recovery of participants’ original data from the group signatures, eliminating the need for centralized data collection. This helps protect the privacy of subscriber data and reduces the need for data transmission.
With the continuous breakthroughs in the field of quantum computing, group signature schemes based on traditional number theory constructions are becoming insecure. In 1996, Ajtai [
13] introduced the lattice as a cryptographic system with a special algebraic structure. In the post-quantum era, lattice-based cryptography has become a hot research topic in cryptography because of its high asymptotic efficiency, parallelizability, and simplicity of operation. In addition, probabilistic polynomial-time efficient methods for solving difficult problems on lattice do not yet exist under quantum computers [
14]. Thanks to the multiple advantages of lattices, Gordon et al. [
15] pioneered the construction of the first lattice-based group signature scheme. Gordon’s scheme has high theoretical value, but its signature length is too long to be of practical consequence. Ling et al. [
16] proposed the first lattice-based constant-size group signature scheme at PKC 2018. They used the “restricted guessing” technique of Ducas and Micciancio’s signature scheme [
17] and solved the problem of linear growth of the signature size, but the parameters of their scheme were set too large and there were soundness errors in NIZK proof in their scheme. In the subsequent research on lattice-based group signature constructions, numerous improved schemes have been proposed [
18,
19,
20,
21,
22,
23]. Furthermore, many lattice-based group signature schemes have been proven to be secure in the standard model, such as [
24]. However, to the best of our knowledge, a lattice-based GS-MR scheme has not been proposed thus far. Therefore, we aim to construct a lattice-based GS-MR scheme to provide potential security assurance for federated learning scenarios in the quantum era.
Our Contribution
We constructed the first lattice-based GS-MR scheme from lattice assumption. In the GS-MR scheme, the message will be recovered in full while the signature is verified as being correct. Therefore, in the rest of this paper, we will use the verification parameter to represent the total size of the message–signature required for the verification phase. The specific contributions are as follows:
- (1)
We construct a GS-MR based on the Abe-Okamoto signature scheme [
25] (ASS) combined with the sign-hybrid-encrypt framework. In the key generation phase, we combine a ring version of Boyen’s signature scheme (BSS) with an algorithm for generating ring trapdoors to distribute private signing keys to the group members. In the signature generation phase, the member’s identity ID is first encrypted into cipher text using a double encryption algorithm with CCA-security [
26] (LPR encryption scheme) to ensure the anonymity and traceability of the group member’s identity; The encrypted result is then used as part of the input to the LSS combined with the ASS to generate the final signature.
- (2)
We prove that the GS-MR scheme satisfies correctness (with message recoverability), full anonymity, and traceability under the random oracle model (ROM). In addition, the anonymity of GS-MR relies on ring learning with errors assumption (RLWE), and the traceability of GS-MR relies on the short integer solution assumption (RSIS).
- (3)
We have experimentally performed some simple evaluations of the proposed GS-MR scheme, which include a comparison of the key and verification parameters, respectively. Then, we compare three existing lattice-based group signature schemes [
19,
24,
27] with the proposed GS-MR scheme and perform an exhaustive verification parameter size analysis. According to the results of the analysis, the proposed GS-MR scheme reduces the verification parameter size by an average of 39.17%.
The structure of this paper is as follows. In
Section 2, we introduce the symbols, lattice, the RSIS and RLWE problems, and some algorithms. In
Section 3, we introduce the definition and security model of the GS-MR scheme. Then, we introduce the proposed scheme in
Section 4. The security analysis is shown in
Section 5.
Section 6 presents the efficiency analysis. The last section is a summary of the paper.
4. Scheme Construction
In the proposed GS-MR scheme, each group member has a fixed length of identity information . The parameters of GS-MR are as follows: Let be the security parameter, and be the maximum group members. Specifically, let Gaussian parameters and and modulus be prime, where and . The noise boundary of is set to an integer and satisfies and . Choose four hash functions: ,, and to be modeled as random oracles.
The GS-MR scheme we proposed is as follows:
given
and
, the group manager performs Algorithm 1.
| Algorithm 1: |
| 1: |
| 2: |
| 3: do |
| 4: |
| 5: |
| 6: , such that |
| 7: |
| 8: |
| 9: , , , |
| 10: |
| 11: , , |
given
, message
, signing key
and a group member’s identity set
, the signer runs Algorithm 2.
| Algorithm 2: |
| 1: do |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: to |
| 9: |
| 10: |
| 11: |
| 12: |
| 13: do |
| 14: if , then |
| 15: else calculate , and outputs with probability . |
| 16: |
| 17: |
| 18: Output: |
given
, signature
and identity set
, the verifier performs Algorithm 3.
| Algorithm 3: |
| 1: |
| 2: do |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: |
| 10: |
| 11: |
| 12: |
given
, signature
, and tracking key
, the group manager performs Algorithm 4.
| Algorithm 4: |
| 1: |
| 2: do |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: |
| 10: |
| 11: |
| 12: |
| 13: |
5. Security Analysis
We prove that the proposed GS-MR scheme satisfies correctness (validation correctness, message recoverability, and open correctness), full anonymity, and traceability.
Theorem 1 (correctness). The GS-MR scheme is correct.
Proof of Theorem 1. - (1)
Verification correctness and message recoverability.
Given a legal and valid signature, the following equation holds:
Then, we have
and since
we can recover the message
From it, and the message must satisfy . On the other hand, when and , where , according to Lemma 1, satisfies with overwhelming probability; when , we have , and where , according to Lemma 2, is statistically indistinguishable from Gaussian distribution . Therefore, for all , is established with overwhelming probability.
The correctness of opening depends on the accuracy of the underlying LPR encryption, and the parameter settings described in
Section 4. of this paper meet the correctness requirements of the encryption scheme, assuming that
is a signature generated by an honest member
through the algorithm
Regarding the validity of the open algorithm, we show that
where
. Note that
and
, it can therefore be concluded that
. Next, we determine the value of the
based on the value of each component of
. The algorithm
then recovereds the
with a probability of 1. □
Theorem 2 (full anonymity). The GS-MR scheme meets full anonymity under ROM if the problem is hard.
Proof of Theorem 2. Let be any PPT adversary in Definition 1; the following proves that the GS-MR scheme satisfies the anonymity requirement by showing that the four games are indistinguishable.
is denoted as the experiment with in GAME I. First, the system is set up, and the challenger calls the algorithm to generate , , and . Then, sends and to . is permitted to make the following adaptive queries:
- (a)
Signing query: makes a signing query on an index and a message , and then returns the signature to .
- (b)
Opening query: makes an opening query on a signature , calls the algorithm to output a member identity , and returns the member’s identity to ; otherwise, it returns to .
selects two indexes with and a message , and sends them to . Then, calls the signature algorithm and sends the signature to .
was modified from When calling the algorithm to generate a signature, calculate and in addition to the remaining steps in the signature generation process (calculate the values of and according to the scheme described above).
is identical to with the exception that chooses rather than .
is identical to . □
Lemma 6. and are computationally indistinguishable.
Proof of Lemma 6. In the and games, the difference in signatures lies in the calculation of . According to Lemma 2, the value produced via rejection sampling in is statistically equivalent to the value produced by the Gaussian distribution (statistical distance less than ). In , the value of is taken from the Gaussian distribution and so the games and are computationally indistinguishable. □
Lemma 7. and are computationally indistinguishable.
Proof of Lemma 7. The indistinguishability of computation between and (where in the context of the GAME I model) is proved in the same way as described above. □
Lemma 8. If the problem is hard, and are computationally indistinguishable.
Proof of Lemma 8. Games and are similar, except for the computation of the part containing member information in the signature (which includes the identity of the member ). Therefore, it is only necessary to prove that the signature generated in and the signature in are indistinguishable in computation.
The
and
can be seen as the LPR encryption of different member identities (
and
) according to the LPR encryption scheme [
26], which is indistinguishable (satisfies IND-CCA security) under the
assumption. Therefore, for an adversary
,
and
are indistinguishable in computation. Combined with the above proof,
and
are statistically indistinguishable. Therefore,
and
are indistinguishable in computation. □
In conclusion, are statistically indistinguishable. Therefore, for any adversary , when facing GAME I defined at the beginning of this paper, the advantage of winning the game is , indicating that has no advantage in winning the anonymity game. It can be inferred that the GS-MR scheme satisfies the anonymity requirement.
Theorem 3 (full traceability). The GS-MR scheme meets full traceability under ROM if the problem is hard.
Proof of Theorem 3. When proving the traceability of the GS-MR scheme, there are two key components: (1) The algorithm generates legal signatures that can be traced back to the identities of their signers. (2) No adversary can forge a legal and untraceable group signature. First, as shown in Theorem 1, the GS-MR scheme is proven to correctly open any valid signature and query the identity details of the signer. Therefore, the following proof focuses on the second point, namely, that it is impossible for any PPT adversary to successfully construct a legally and untraceable signature. □
Let be any PPT algorithm defined in Definition 6 that can forge a signature with a non-negligible advantage after numerous inquiries. Then, a challenger can be built to solve the problem with a non-negligible advantage.
Let the challenger maintain three lists , and initialize them as empty. Then, honestly runs the algorithm of the scheme, with input security parameter and maximum member group , randomly selects , generates , and then sends and to . In response to ’s inquiry, replied as follows ( had conducted relevant queries and queries prior to performing signing and corrupt queries):
- (a)
query. selects N polynomial vectors to . first checks list . If has previously submitted the same query, directly returns the same query result. Otherwise, selects a random vector and returns it to . For this query, records in the list .
- (b)
query. selects a message , and , and submits them to . first checks list . If has previously submitted the same query, directly returns the same query result. Otherwise, selects a random vector and returns it to . For this query, records in the list .
- (c)
Corrupt query. inputs , if , terminates the game; if , sends the signing key to . For this query, records in the list .
- (d)
Signing query. inputs and message , if , will modify in the algorithm to , and return the signature to ; if , honestly runs the algorithm and returns the signature to . For this query, records in the list .
After a series of queries, outputs a forged group signature . If the signature satisfies Definition 6, it implies that wins GAME II. We analyzed the following two aspects:
- (1)
Assuming that
is a valid signature and satisfies
. Since the signature is valid, it follows that
; Furthermore, since the signature
forged by
can satisfy the verification correctness, we have
. As the collision probability of the hash-oracle is negligible, we can see that
and
, and therefore we can conclude that
since
, it follows that
is a solution to the
problem.
- (2)
Assuming
, the forged signature
produced by the adversary
satisfies the following condition
Since the above condition can be verified by the algorithm
, we have
From Equations (11) and (12), we can obtain
Since is a solution to the problem.
Based on the proof of the two above cases, if the adversary wins GAME II, then the challenger will obtain a solution to the problem. However, the problem is to solvedifficult under the parameters provided in this paper, and so cannot satisfy the two conditions mentioned above. Therefore, the GS-MR scheme has full traceability.
6. Implementation and Efficiency Analysis
As proof of concept, in order to understand the practicality of group signatures with recoverable messages, we simply performed some implementations of the GS-MR scheme. We have shown implementations of the GS-MR, which were experimented with using an AMD Ryzen 5 5600G @ 3.90GHz CPU with 16GB of RAM. The programs were compiled using SageMath and Python 3.8. A selection of some program parameters were first shown. Then, based on these parameters, some corresponding outputs in the GS-MR scheme were experimentally derived. In
Table 1, we summarize the theoretical estimates of the key size and signature size of GS-MR, where “
denotes
elements in a set
”.
We followed the parameter settings of Luo et al. [
37] and also considered the security of the parameter settings in this paper.
To keep working safely, set , , and .
For the Gaussian parameter in
, we chose
and according to Pino [
38], let
.
For Gaussian parameters in rejection sampling, we chose .
For the choice of in rejection sampling, according to Definition 4, if then the probability of and is greater than . Then, we can fix .
Specifically, we will use the following specific parameters for our experiments:
,.
,.
,.
In
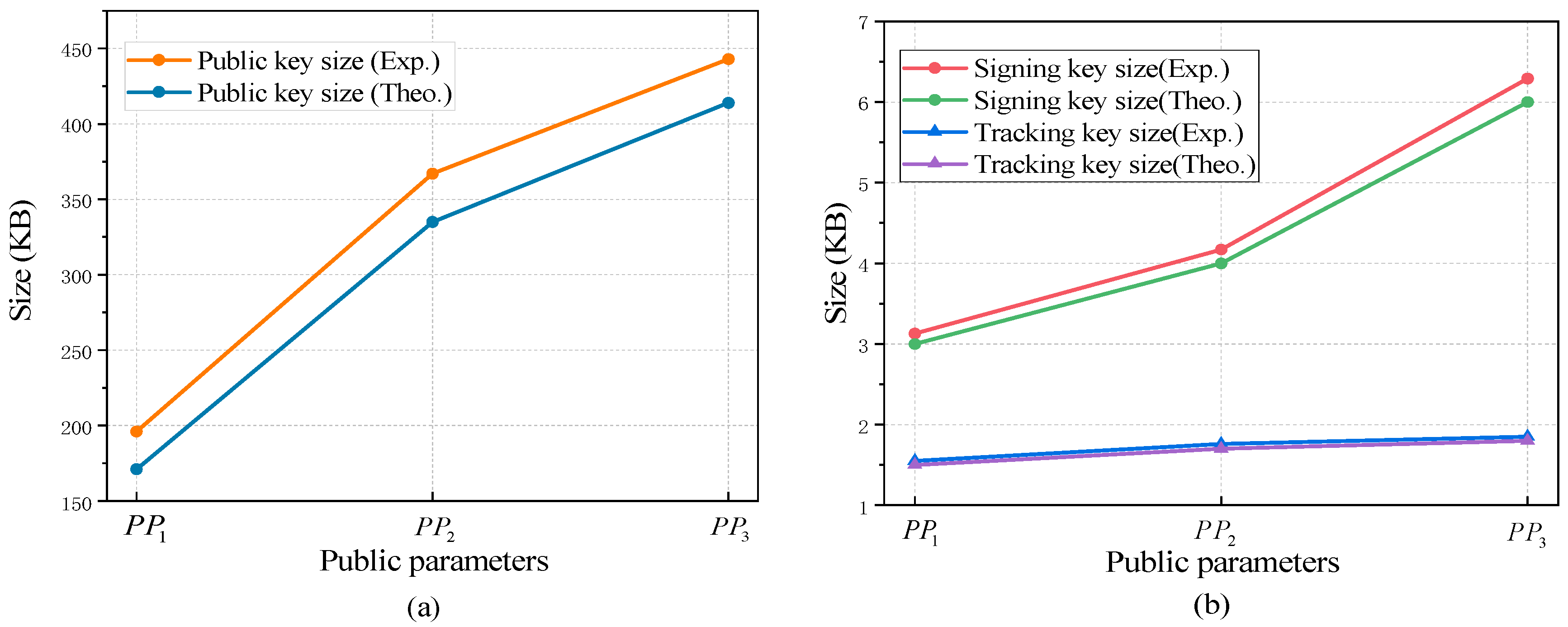
Table 2, we summarize the real output key values of the GS-MR scheme (i.e., public key, signing key, and tracking key) for three specific parameters compared to their theoretical estimates. For a more intuitive display, we plotted
Figure 3 to visualize the variations in key sizes under different parameter settings. Based on
Table 2 and
Figure 3a, it can be observed that the storage cost of our GS-MR scheme mainly lies in the group public key. In
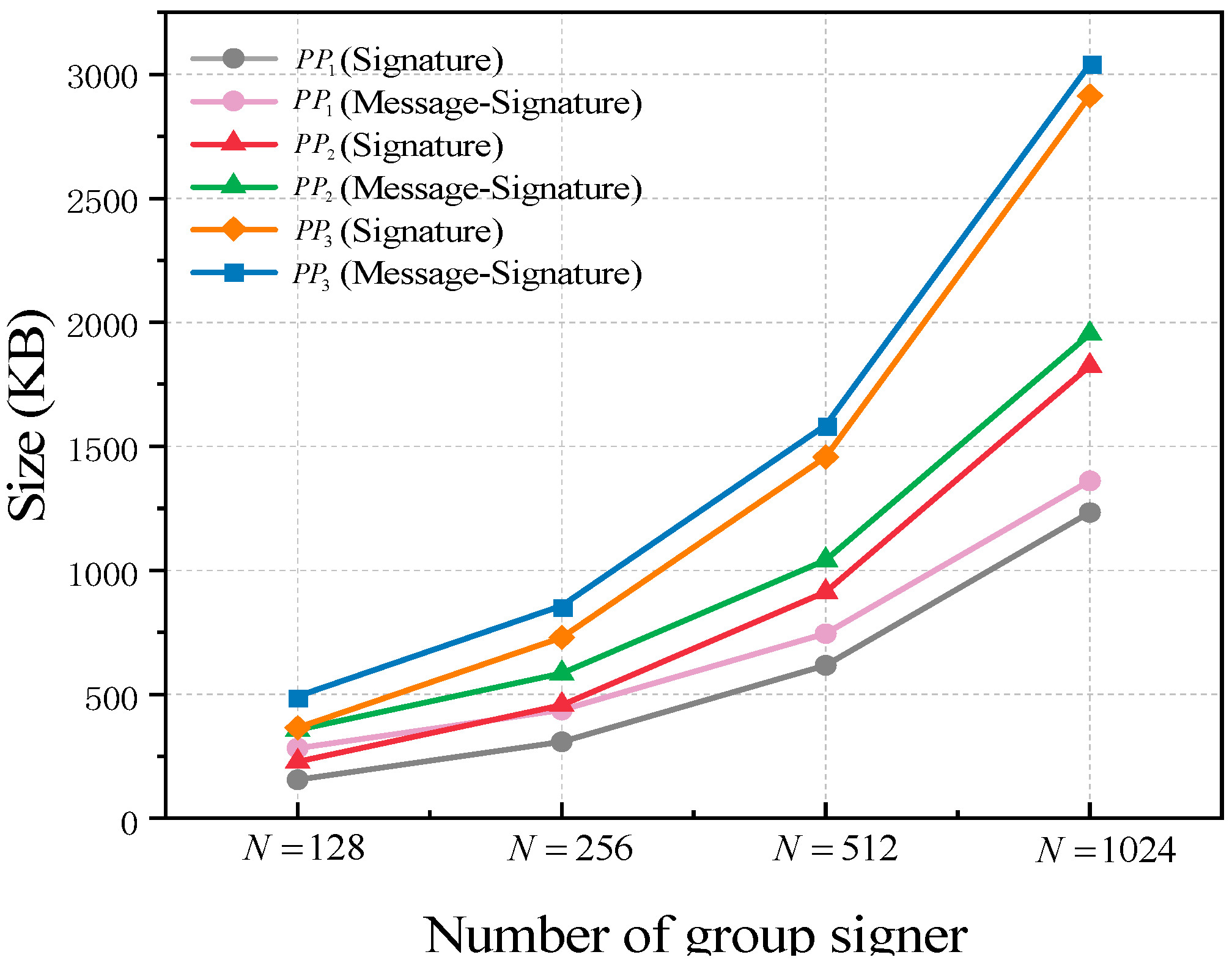
Figure 3b, it can be seen that the signing key and tracking key of the GS-MR scheme are only the size of single-digit KB under the three sets of parameters. Although the signed message is not to be used as an input parameter in the verification phase, we also performed a comparative experiment with the signature and message–signature pairs. Subsequently, we conducted 10 experiments for each of the specific group orders 128, 256, 512, and 1024 to compare the signature size and the total length of message-signature under different scenarios (for
Section 4, we fixed the value of
). Based on the experimental results, we evaluated the average signature size, as shown in
Table 3 and
Figure 4, which indicates that the signature size of GS-MR increases linearly with the number of group members. With a fixed message, the proportion of the message size decreases as the group size increases. However, we believe that our GS-MR scheme is still feasible. Particularly in small group environments with a low channel bandwidth and poor communication quality, the proposed GS-MR scheme can ensure a smaller total parameter transmission and alleviate concerns regarding the impact of channel noise on message transmission.
To further demonstrate the advantages of the GS-MR scheme, we performed a progressive efficiency analysis and verification parameter size comparison between three lattice-based group signature schemes and the GS-MR scheme. They were, respectively, the group signature scheme with indexed attribute-based signature (ABS) proposed by Katsumata et al. [
24], the group signature scheme with forward security and constant size proposed by Canard et al. [
27], and the lattice-based dynamic group signature scheme proposed by Huang et al. [
19]. In
Table 4, we compare these three group signature schemes [
19,
24,
27] with the GS-MR scheme, where
is the security parameter and
is the number of group members. From
Table 4, it can be seen that the group public keys in [
19,
24,
27] are all related to the maximum number of group members
, whereas the public and private keys in our scheme and [
19] are fixed values. However, in this paper, we needed to use the lattice-based delegation algorithm to generate member signing keys, causing the signature length to be linearly related to
. However, none of the above compared schemes have message recovery in the verification phase.
For a more intuitive comparison, we chose fixed values for these schemes to compare the size of the verification parameter for different schemes under the same number of group members. We selected some fixed parameters while ensuring the security of the above comparison schemes. Let
, and
. Finally, all schemes select a fixed message
in the signature generation stage, where
. The comparison of the size of the verification parameters is shown in
Table 5 and
Figure 5.
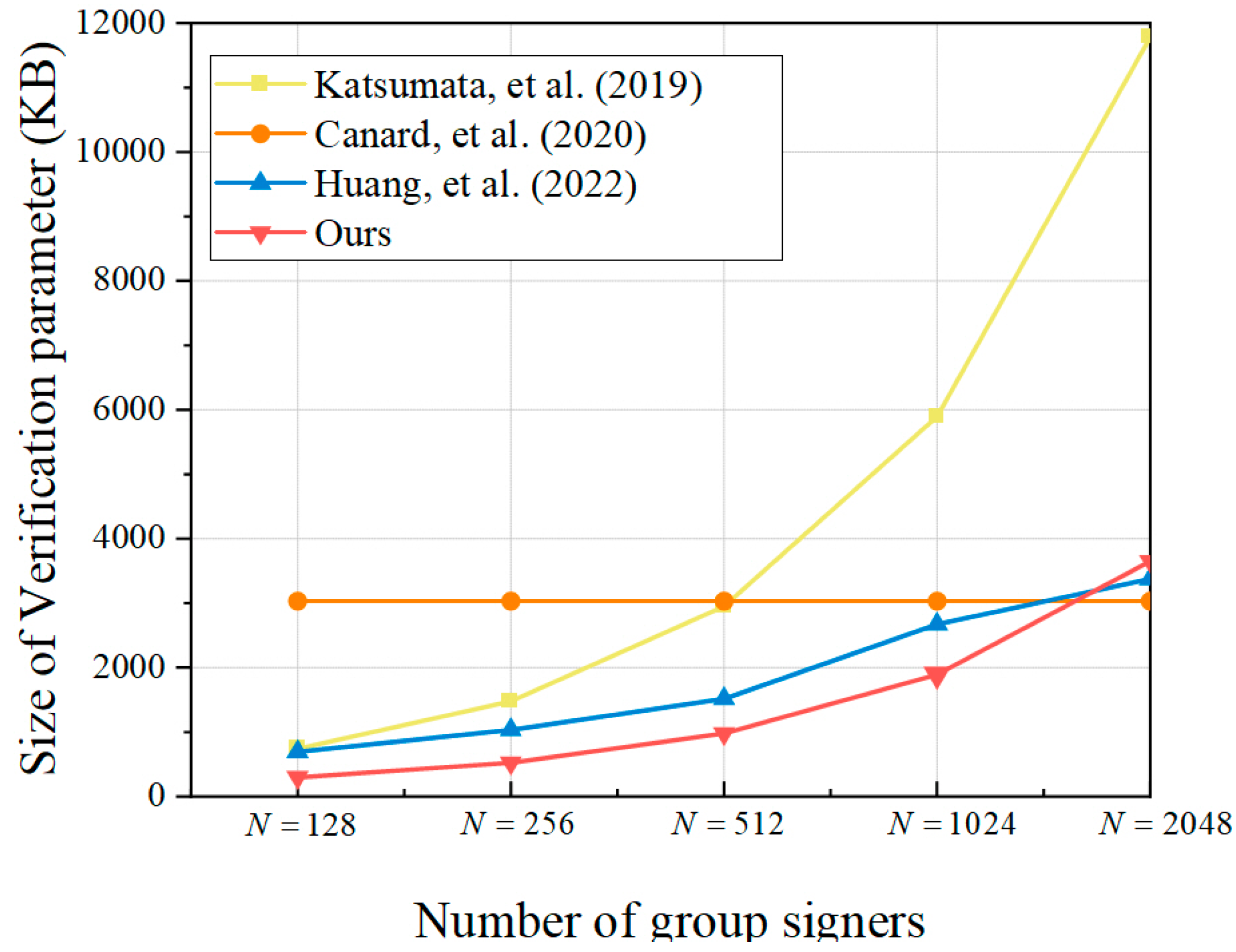
From
Figure 5, it can be seen that compared to the other three schemes, the size of the verification parameters in the GS-MR scheme is the shortest when the number of group members
is considered, with an average reduction of 53.02%. However, the signature size of GS-MR increases linearly with
, and at
, the verification parameter size is no longer advantageous compared to the Canard scheme [
27] and the Huang scheme [
27]. Overall, the proposed GS-MR scheme reduces the verification parameter size by an average of 39.17% compared to the schemes of [
19,
24,
27].