Two-Dimensional Mesoscale Finite Element Modeling of Concrete Damage and Failure
Abstract
1. Introduction
2. Two-Dimensional Heterogeneous Mesostructures of Concrete
2.1. Aggregate Size Distribution
2.1.1. Random Circular and Ellipsoidal Aggregates
2.1.2. Random Polygon Aggregates
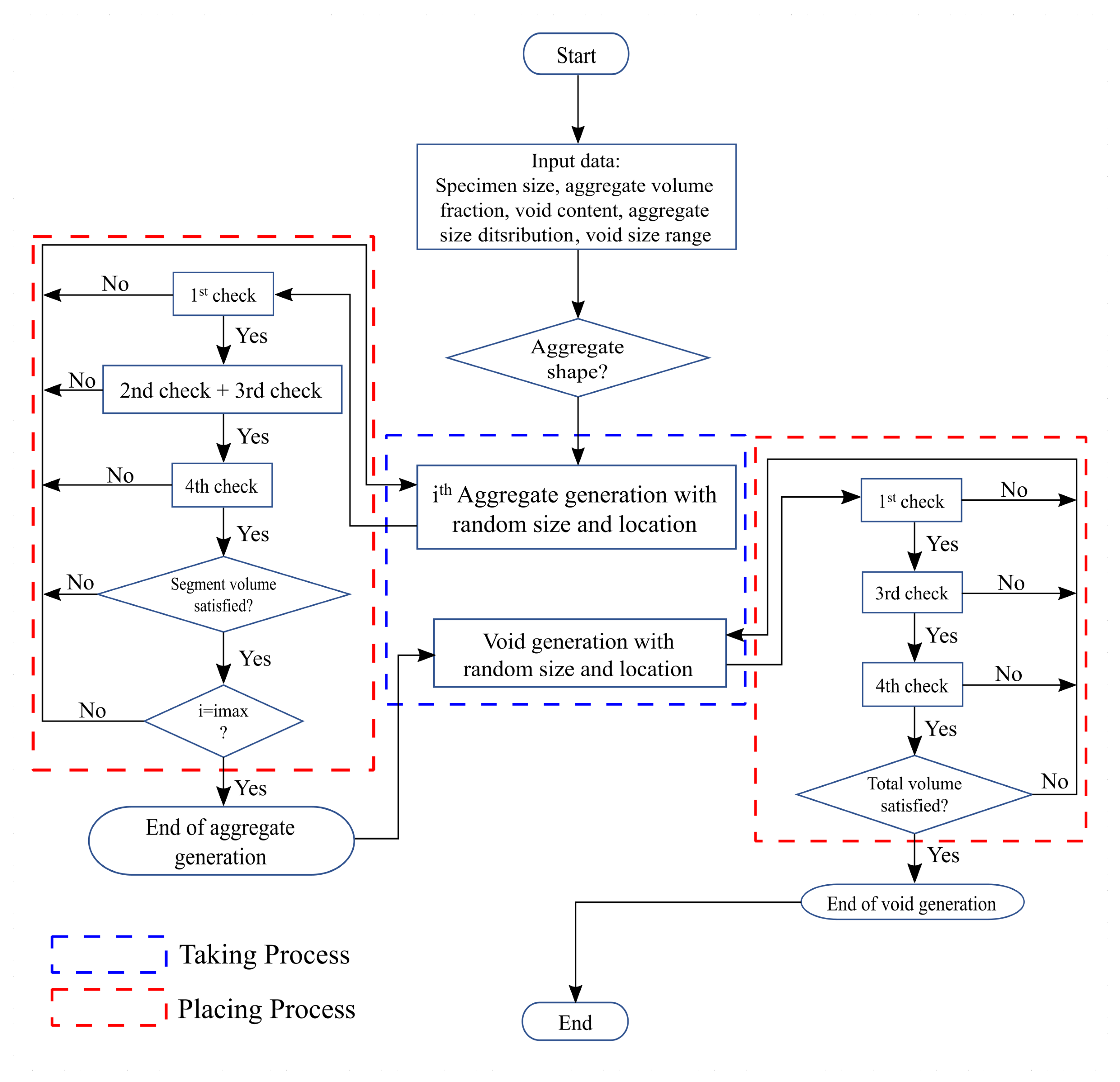
2.2. Aggregate Packing
- The aggregate must be placed completely within the boundaries of the concrete specimen without crossing them.
- The newly placed aggregate must not overlap with already placed aggregates.
- A small gap should be left between each two positioned aggregates to create a mortar layer thickness between the aggregates.
- Check 1The first condition is satisfied if all vertices of the generated aggregate lie within the boundary of the mesoscale concrete specimen. For the transfer of the generated aggregate within the boundaries of the concrete specimen, a translation vector is generated by extracting a random coordinate whose origin is at the center of the coordinate system. The chosen random value must be within the main frame of the mesoscale specimen. After the translation process, the coordinates of all vertices are compared with the main frame coordinates of the concrete, and if an overlap is detected, a new translation vector is built until the first condition is satisfied.
- Check 2 and Check 3Intersection check 2 and check 3 are carried out simultaneously. Assume that the constructive Equation of the newly placed aggregate particle is denoted by . To perform intersection check 2, the value of is calculated using the constructive vertices of each already placed aggregate. If the value of is equal to or smaller than one, this indicates that at least one already placed aggregate has an intersection with the new aggregate and the newly placed aggregate must be removed from the main frame. In addition, intersection check 3 is performed automatically by setting the minimum value of in intersection check 2 to 1.2. In this way, a small gap between the aggregate particles is realized. Therefore, the small gap condition is simultaneously fulfilled in this step.
- Check 4The fulfillment of intersection check 2 and check 3 is a necessary condition. However, it is not sufficient, because in the developed Python code, the placement process always starts with the aggregates with larger sizes and it may happen that the newly placed aggregate is exactly inside the already placed aggregate without intersecting its boundaries. This condition cannot be detected by intersection check 2. To solve this problem, the constructive Equation of the already placed aggregate is established and its value is checked with the vertices of the newly placed aggregate. In this condition, if the result of the constructive equation becomes less than one, it shows that the smaller newly placed aggregate is exactly inside a larger aggregate and this aggregate must be removed from the main frame.
3. Automatic Generation of Cohesive Elements
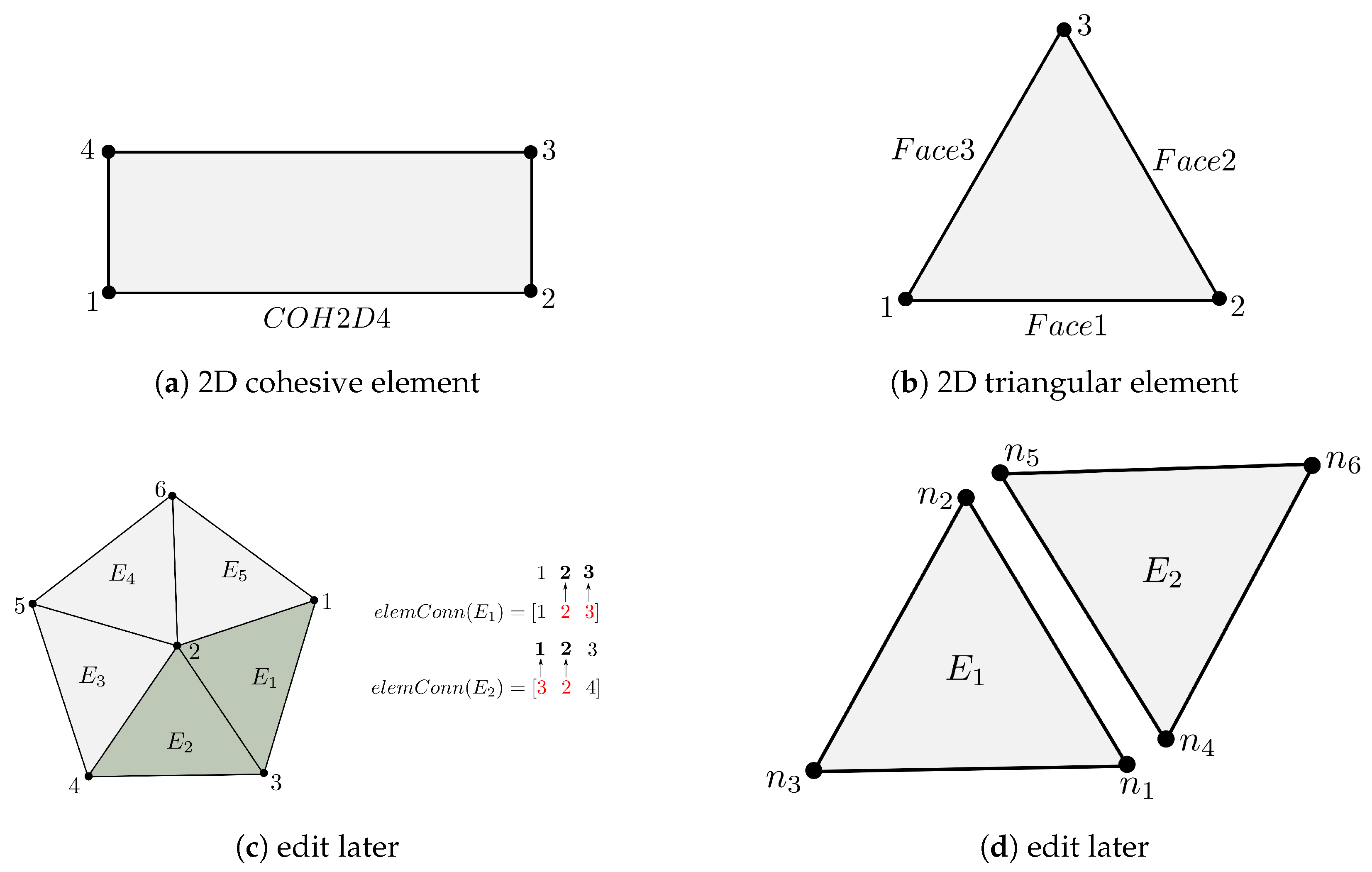
- Step 1: InitializationThe initial FE mesh file generated by Abaqus/CAE is imported into the Python code, and by processing the node and element data, three main data structures are generated. A unique specific ID number is assigned to each node and element in the first and second data structures, and the corresponding coordinates and element connectivity list are stored, respectively. It is worth mentioning that the assigned ID numbers are positive integers. The element connectivity list represents all nodes that constitute an element. As illustrated in Figure 3b, the element connectivity list of a triangular element is [1-2-3]. Element sets are stored in the third data structure, and the elements in each set are assigned a specific material ID. In this context, element sets, which are automatically written to the original FE mesh file, represent a specific region of discretized geometry. The elements forming the mortar matrix are labeled with the material ID equal to zero, whereas the elements constituting the aggregates would have different material ID numbers. The material ID numbers for aggregates are positive integers, and the corresponding value for each aggregate depends on the name of the aggregate’s element set in the original FE mesh file. For instance, if the name of the element set of a particular aggregate in the initial FE mesh file is one, the elements that constitute that aggregate will be labeled with a material ID of one. Material IDs enable the generation of cohesive interface elements at different phases of the concrete mesostructure.
- Step 2: Construction of node connectivity listA data structure called the node connectivity list (ndConnL) is created that stores the element IDs of all elements that contain a particular node. The node connectivity list of each node is determined by traversing the element connectivity list of all elements so that all possible elements containing a given node in their element connectivity list are identified.
- Step 3: Identification of ITZ nodesThe nodes located at the interface of the aggregates and mortar matrix are identified. For this purpose, the node connectivity list of each node is called from the corresponding data structure in Python, and in the second step, the corresponding material ID of each element in the node connectivity list is determined. Then, the extracted material IDs are compared with each other. If the material IDs are not unique, then the corresponding node is in the ITZ zone.
- Step 4: Identification of adjacent elementsIn this step, every two neighboring elements that share a common face will be identified. To this end, the node connectivity list of each node is called. Then, an extraction of the element connectivity lists of all elements contained in the node connectivity list is performed. A comparison is made between all element connectivity vectors, and when the number of common nodes between two elements reaches two, it means that these two elements are adjacent. This process is performed for all elements, and the element IDs of the adjacent elements are stored in a separate data structure.
- Step 5: Assigning face typeFace type is assigned to each of the two adjacent elements identified in the previous step, and the corresponding face type of each element is stored in a separate data structure. Figure 3b illustrates a two-dimensional triangular element with its corresponding node numbering. As can be seen, a 2D triangular element has three faces consisting of the segments defined by the nodes [1–2] for face 1, nodes [2–3] for face 2, and nodes [3–1] for face 3. To assign the face type to each element, first, the element connectivity list of each two adjacent elements is extracted. Then, new numeric labels are assigned to the components of the element connectivity list. These new numerical labels are integer positive numbers ranging between 1 and 3. As mentioned earlier, adjacent elements have two common nodes; in this state, the corresponding new numerical labels of the common nodes are extracted for each adjacent element. Based on the new numerical labels of the common nodes, the face type is identified and assigned to each element. As Figure 3c illustrates, nodes [2–3] represent the common interface between elements and . With respect to the corresponding new numerical labels of the common nodes, Face 2 is assigned to element and face 1 is assigned to element .
- Step 6: Multiplication of cohesive nodesThose nodes that are located at the interface of two adjacent elements are multiplied, and in this way cohesive nodes are generated. It is worth mentioning that if the node connectivity list has n members, n − 1 new nodes are generated and the original node is always assigned to an element with the smallest element ID in the node connectivity list. After this operation, interface nodes do not exist anymore and each created node is allocated to a different element. Therefore, it is crucial to update the element connectivity list of each element after the generation of cohesive nodes.
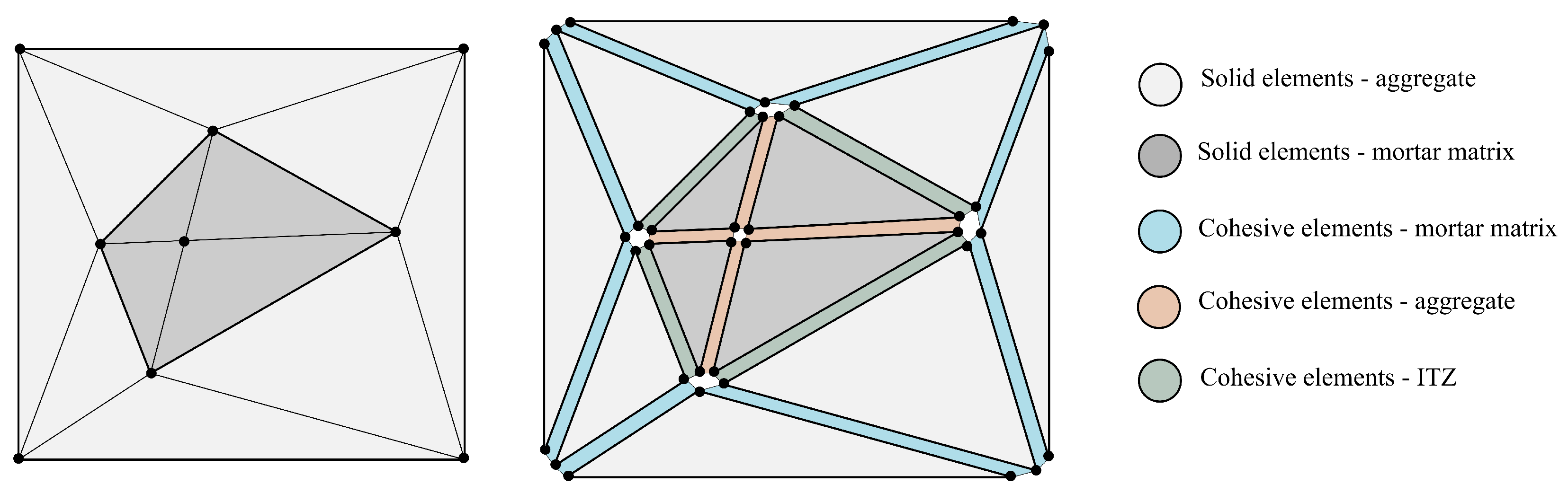
- Step 7: Generation of cohesive elementsFor this purpose, the updated element connectivity list and face type of each two adjacent elements are retrieved, and with these data at hand, the element connectivity list of a four-node cohesive element (COH2D4) is written. The traction–separation law (TSL) is implemented as the material property of cohesive elements which is based on the deformation vector of the nodes. As shown in Figure 3d, the first two nodes (, ) belong to the bulk element and the other two nodes (, ) belong to the to the bulk element . When there is no deformation, node coincides with , and node coincides with node . The distance between these nodes determines the interface separation. Since the finite element solver can distinguish between the opening and closing of the cohesive element with respect to its element connectivity list, its node arrangement must be written correctly in a counterclockwise manner. The triangular elements can have any orientation in space, but the node numbering is always as illustrated in Figure 3b. It is worth mentioning that the face type of the adjacent elements helps to write the element connectivity list of the cohesive elements in a counterclockwise fashion, which leads to a correct distinction between the opening and closing of cohesive elements. Figure 4 represents the generated cohesive element in three different regions of the concrete mesostructure.
| Algorithm 1: Algorithm to generate cohesive elements. |
| Input: FE mesh file of Abaqus |
| Output: Generated cohesive elements |
Initialization;
Construct Node Connectivity list (ndConntL);
Identification of ITZ nodes;
Identification of adjacent elements;
Assign FaceType object to adjacent elements;
Duplicating nodes;
Generation of Cohesive Elements;
|
4. Finite Element Modeling
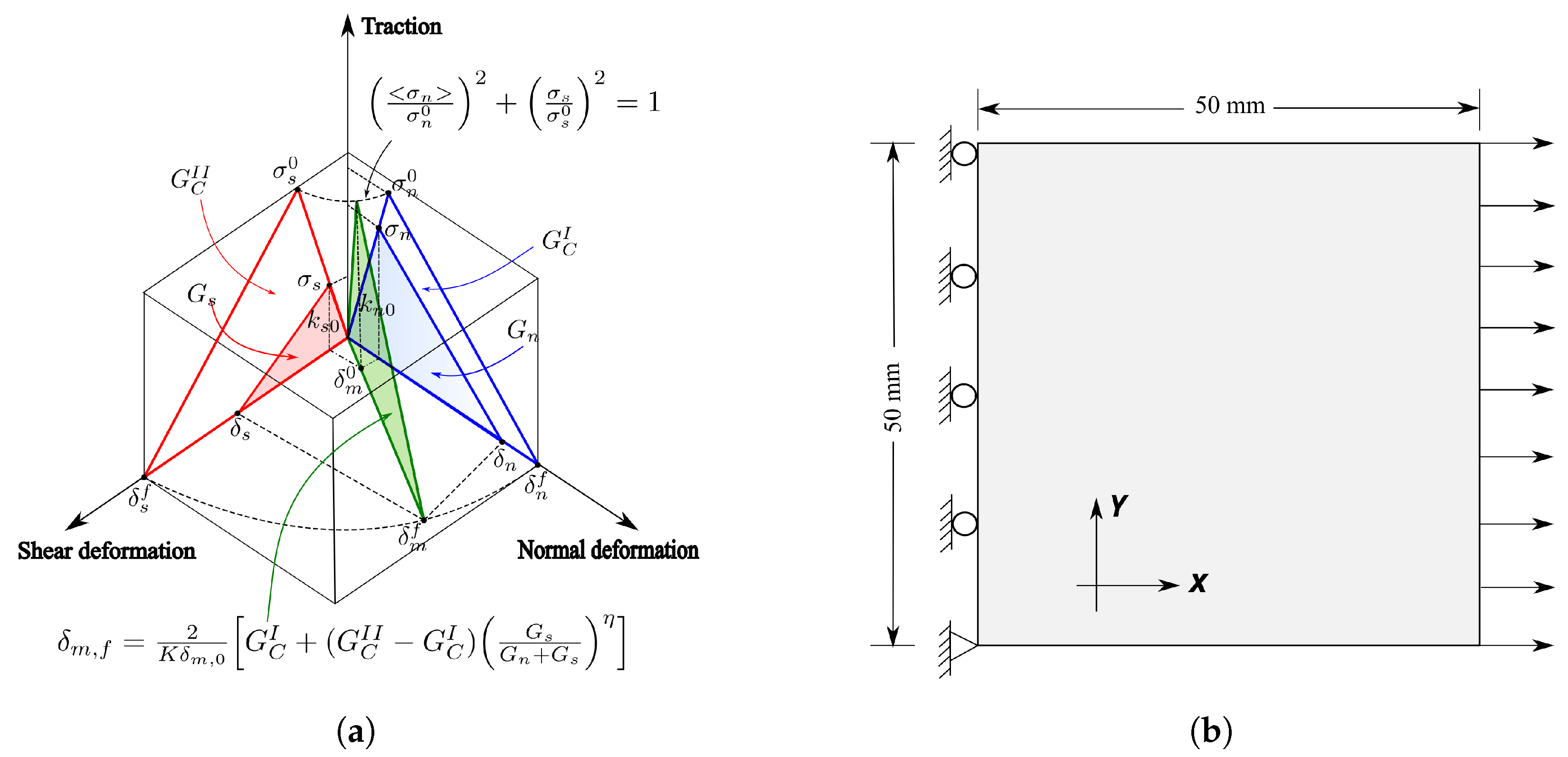
4.1. Model Description
4.2. Constitutive Behavior of CIEs
5. Results
5.1. Model Parameters
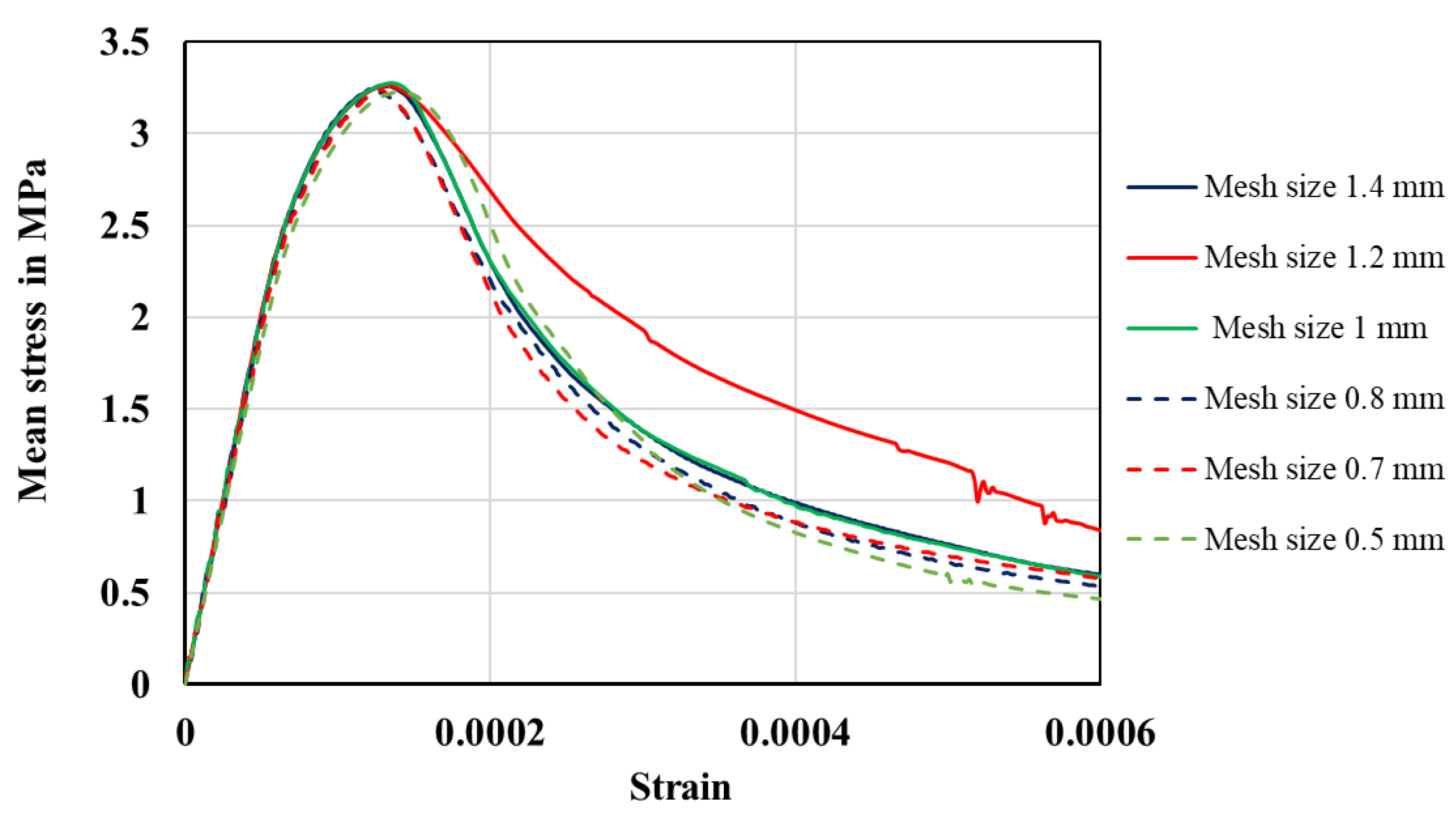
5.2. Mesh Convergence Study
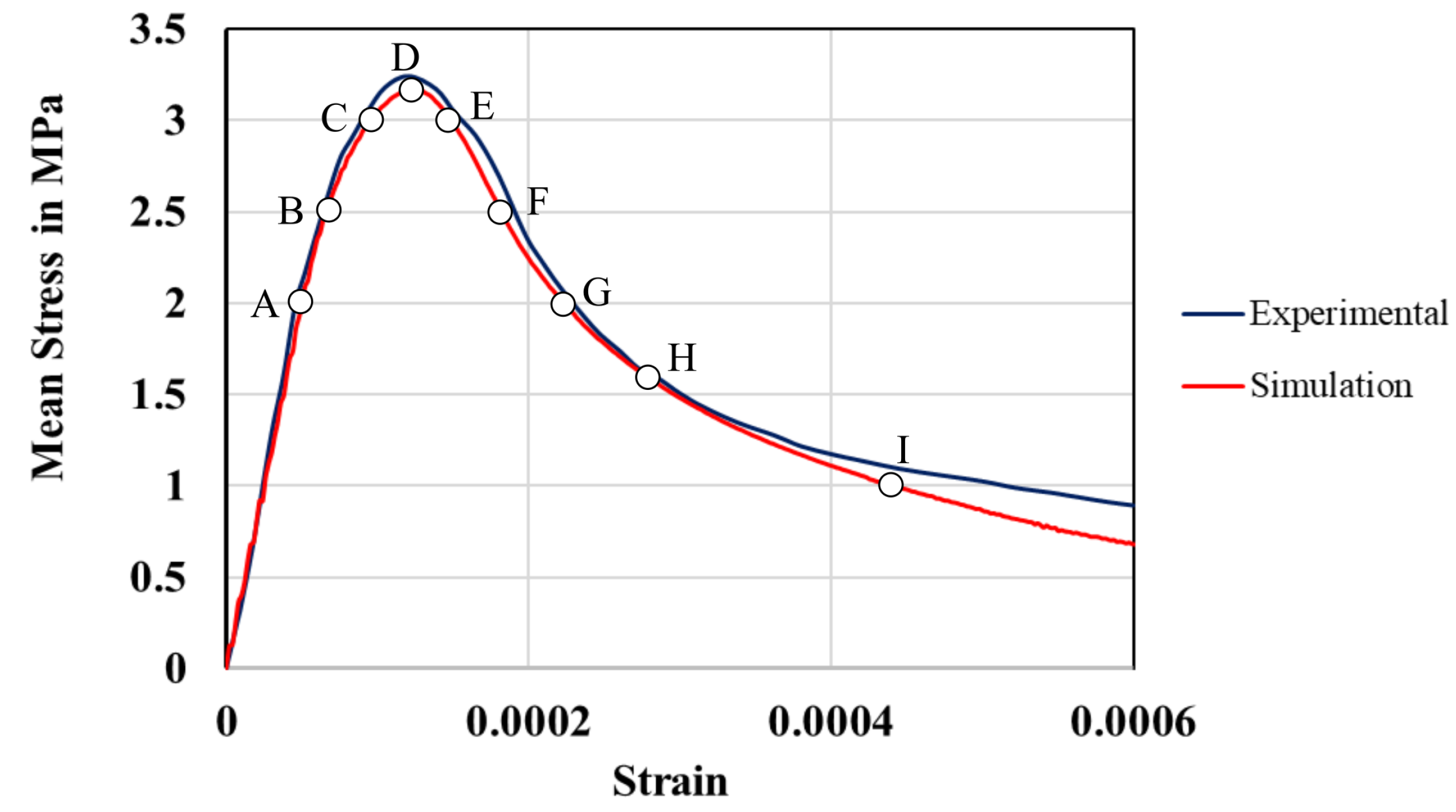
5.3. Uniaxial Tension Simulation
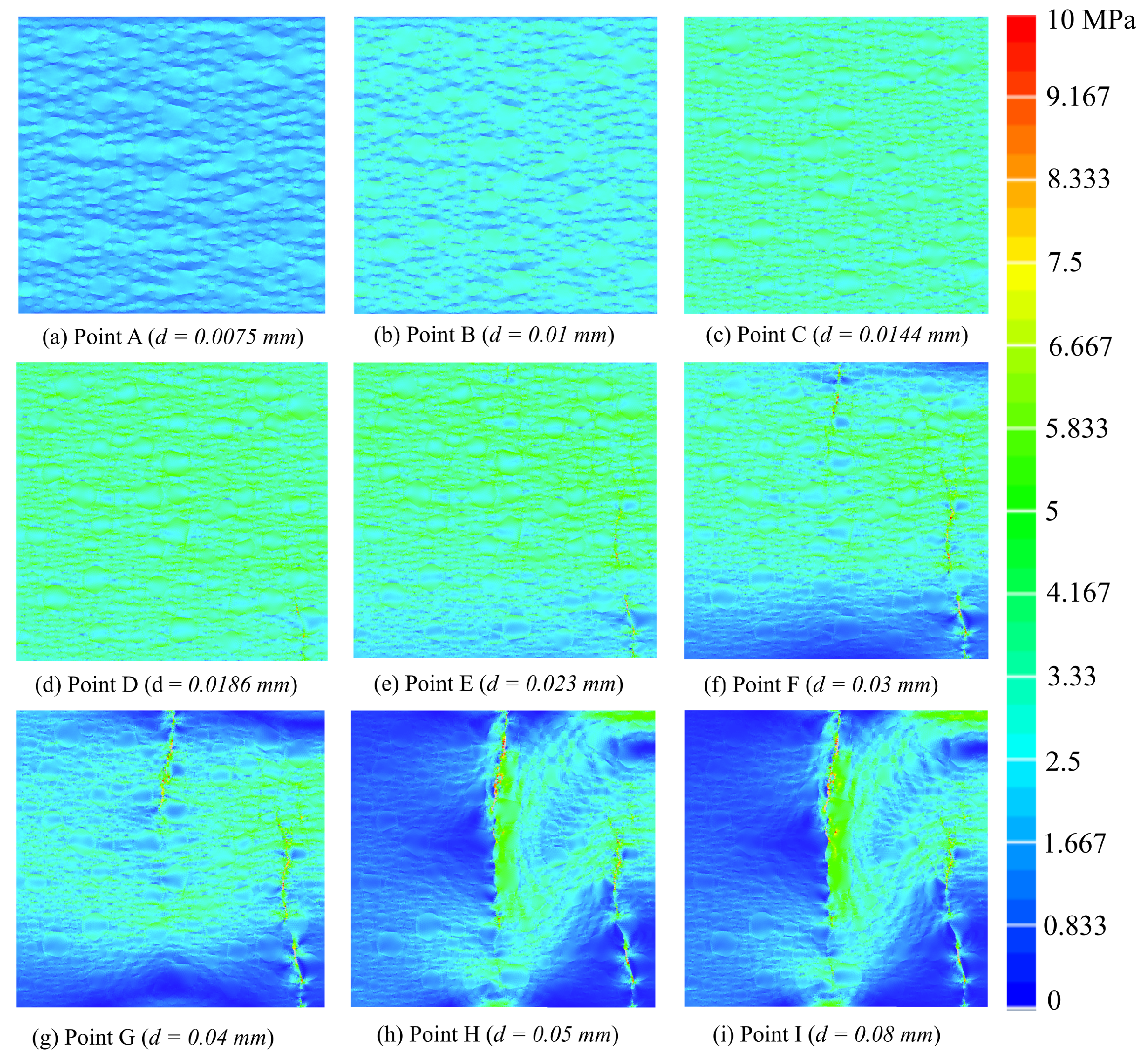
5.4. Propagation of Microcracks and Formation of Macrocracks
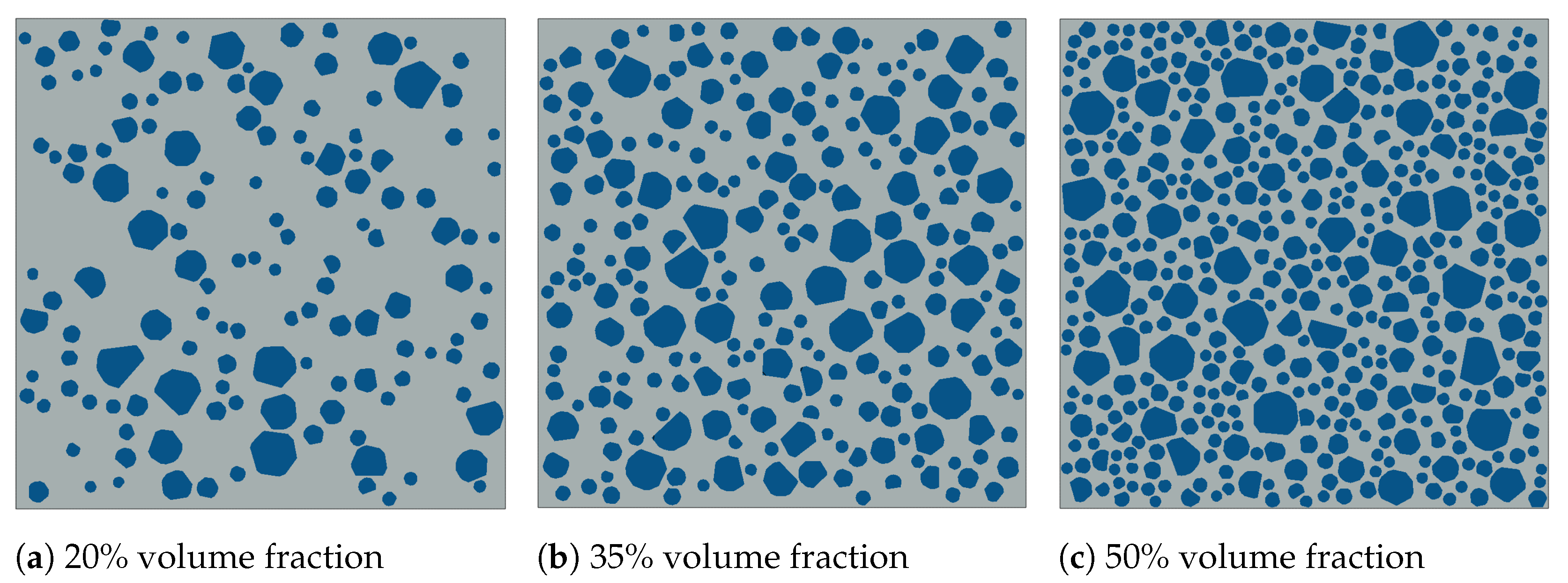
5.5. Effect of Aggregate Content
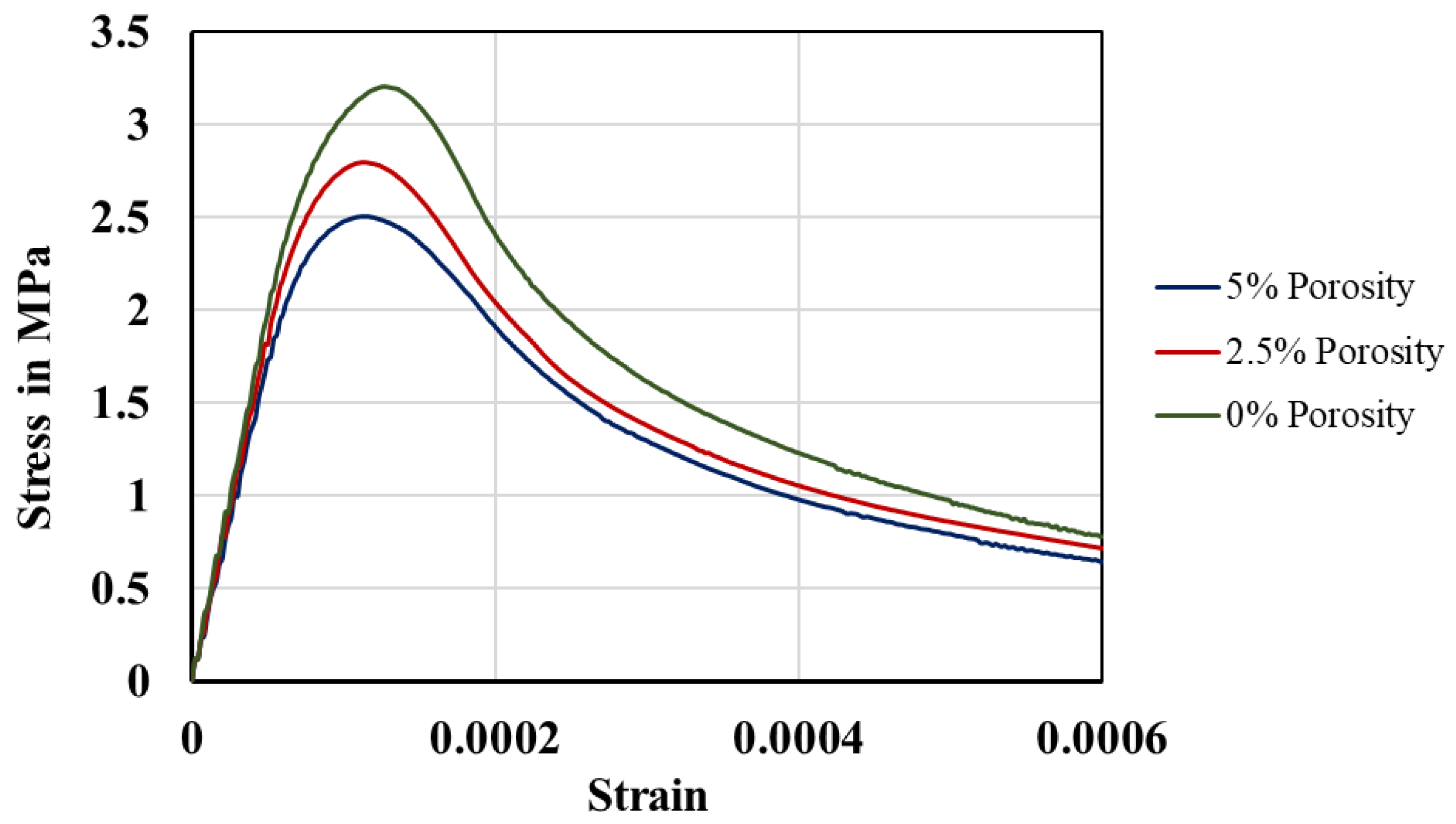
5.6. Effect of Volume Porosity
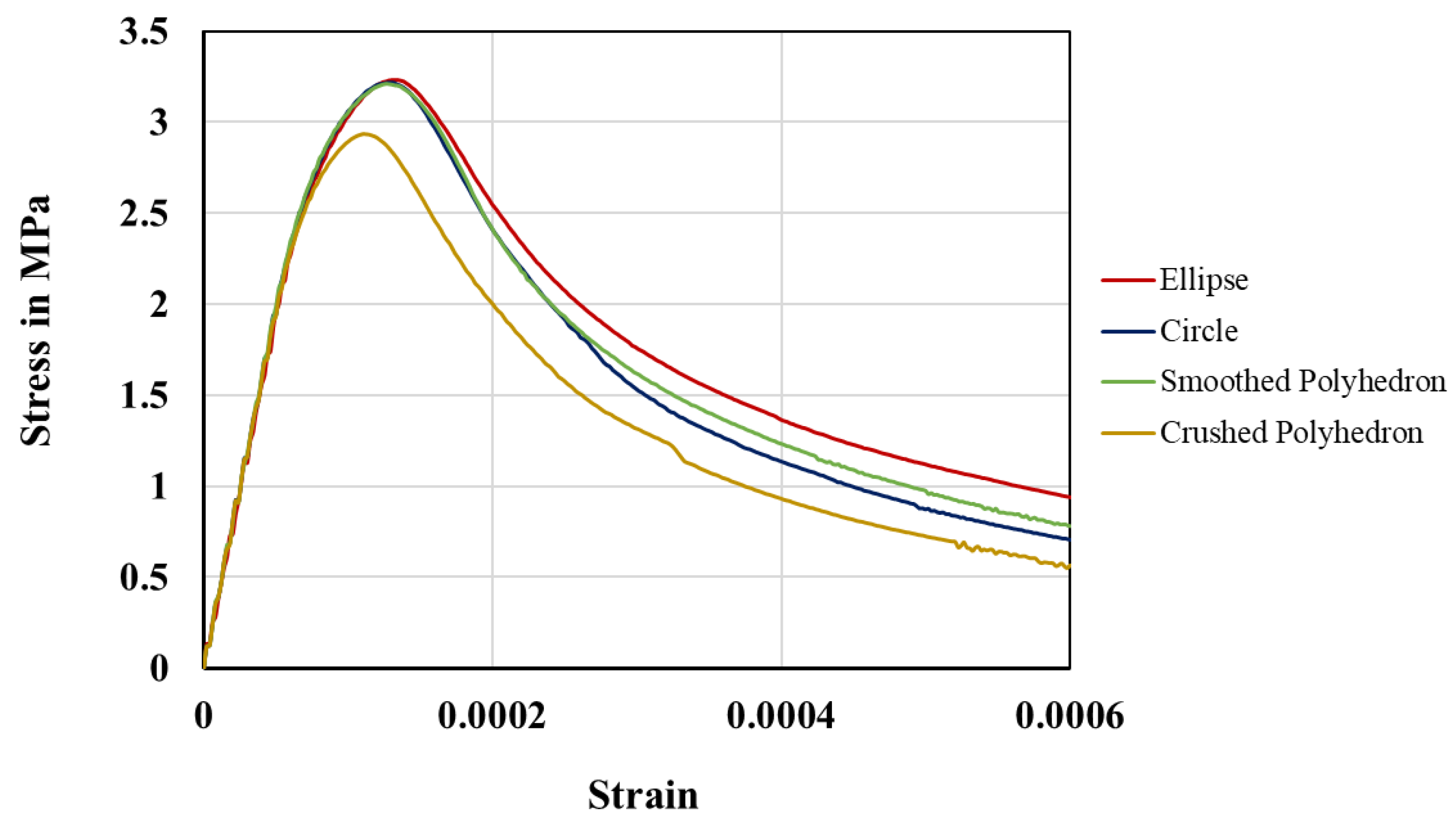
5.7. Effect of Aggregate Shape
6. Conclusions
- Two different macrocrack patterns are observed in the mesoscale simulation of concrete specimens under the uniaxial tension loading condition. In the first type, the microcracks merge to form a failure macrocrack. This type of macrocrack leads to a sharp decrease in the load-carrying capacity of the concrete specimen immediately after the onset of the softening zone. Thus, less energy is dissipated until complete failure. In the second type, the coalescence of microcracks leads to the formation of two or more failure macrocracks. In this condition, a more gradual softening response is observed, and, therefore, more energy is dissipated until complete failure.
- Under tensile loading of concrete specimens, the damage starts to initiate first in the ITZ zone, which is known to be the weakest phase, and as the specimen is further loaded, the microcracks propagate through the mortar matrix, resulting in a decrease in the stiffness of the concrete.
- The tensile strength and strain at which the softening zone begins are lower for the crushed aggregates than for the circular and elliptical aggregates. This can be explained by the local stress concentration at the sharp edges of the crushed aggregates. Therefore, the strength of the concrete may be overestimated in the mesoscale simulation with circular and elliptical aggregates.
- It is found that the modulus of elasticity of concrete is linearly proportional to the total volume fraction of aggregate particles, whereas the ductility of concrete is inversely proportional to the volume fraction of aggregates.
- An increase in the volume fraction of coarse aggregate leads to a reduction in the maximum tensile strength and the load-carrying capacity of the concrete specimens. This can be explained, on the one hand, by the increase in the weak aggregate–mortar interface and, on the other hand, by enhanced crack bridging mechanisms, especially in zones where a higher concentration of aggregates is observed.
- An increase in the total volume fraction of porosity leads to a reduction in the maximum tensile strength and load-bearing capacity. This is attributed to the fact that a higher content of voids facilitates the initiation and propagation of cracks. This case shows the importance of considering voids in the mechanical and fracture modeling of concretes with high void content.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yılmaz, O.; Molinari, J.F. A mesoscale fracture model for concrete. Cem. Concr. Res. 2017, 97, 84–94. [Google Scholar] [CrossRef]
- Unger, J.F.; Eckardt, S. Multiscale modeling of concrete. Arch. Comput. Methods Eng. 2011, 18, 341–393. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.J.; Yates, J.; Jivkov, A.; Zhang, C. Monte Carlo simulations of mesoscale fracture modelling of concrete with random aggregates and pores. Constr. Build. Mater. 2015, 75, 35–45. [Google Scholar] [CrossRef]
- Yang, Z.J.; Li, B.B.; Wu, J.Y. X-ray computed tomography images based phase-field modeling of mesoscopic failure in concrete. Eng. Fract. Mech. 2019, 208, 151–170. [Google Scholar] [CrossRef]
- Li, S.; Li, Q. Method of meshing ITZ structure in 3D meso-level finite element analysis for concrete. Finite Elem. Anal. Des. 2015, 93, 96–106. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, X.; Liu, Y.; Wu, D.; Song, C. Three-dimensional mesoscale modelling of concrete composites by using random walking algorithm. Compos. Sci. Technol. 2017, 149, 235–245. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, X.; Zhang, D.; Xue, L.; Sun, S.; Stránskỳ, J.; Wang, Y. Morphological reconstruction method of irregular shaped ballast particles and application in numerical simulation of ballasted track. Transp. Geotech. 2020, 24, 100374. [Google Scholar] [CrossRef]
- Naderi, S.; Zhang, M. An integrated framework for modelling virtual 3D irregulate particulate mesostructure. Powder Technol. 2019, 355, 808–819. [Google Scholar] [CrossRef]
- Van Mier, J.; Van Vliet, M. Influence of microstructure of concrete on size/scale effects in tensile fracture. Eng. Fract. Mech. 2003, 70, 2281–2306. [Google Scholar] [CrossRef]
- Leite, J.; Slowik, V.; Mihashi, H. Computer simulation of fracture processes of concrete using mesolevel models of lattice structures. Cem. Concr. Res. 2004, 34, 1025–1033. [Google Scholar] [CrossRef]
- Eliáš, J.; Stang, H. Lattice modeling of aggregate interlocking in concrete. Int. J. Fract. 2012, 175, 1–11. [Google Scholar] [CrossRef]
- Grassl, P.; Grégoire, D.; Solano, L.R.; Pijaudier-Cabot, G. Meso-scale modelling of the size effect on the fracture process zone of concrete. Int. J. Solids Struct. 2012, 49, 1818–1827. [Google Scholar] [CrossRef]
- López, C.M.; Carol, I.; Aguado, A. Meso-structural study of concrete fracture using interface elements. I: Numerical model and tensile behavior. Mater. Struct. 2008, 41, 583–599. [Google Scholar] [CrossRef]
- Wang, Z.; Kwan, A.; Chan, H. Mesoscopic study of concrete I: Generation of random aggregate structure and finite element mesh. Comput. Struct. 1999, 70, 533–544. [Google Scholar] [CrossRef]
- Schlangen, E.; Van Mier, J. Simple lattice model for numerical simulation of fracture of concrete materials and structures. Mater. Struct. 1992, 25, 534–542. [Google Scholar] [CrossRef]
- Schlangen, E.; Garboczi, E.J. Fracture simulations of concrete using lattice models: Computational aspects. Eng. Fract. Mech. 1997, 57, 319–332. [Google Scholar] [CrossRef]
- Bolander, J., Jr.; Saito, S. Fracture analyses using spring networks with random geometry. Eng. Fract. Mech. 1998, 61, 569–591. [Google Scholar] [CrossRef]
- Cusatis, G.; Bažant, Z.P.; Cedolin, L. Confinement-shear lattice CSL model for fracture propagation in concrete. Comput. Methods Appl. Mech. Eng. 2006, 195, 7154–7171. [Google Scholar] [CrossRef]
- D’Addetta, G.A.; Ramm, E. A microstructure-based simulation environment on the basis of an interface enhanced particle model. Granul. Matter 2006, 8, 159–174. [Google Scholar] [CrossRef]
- Zubelewlcz, A.; Bažant, Z.P. Interface element modeling of fracture in aggregate composites. J. Eng. Mech. 1987, 113, 1619–1630. [Google Scholar] [CrossRef]
- Ma, G.; Xie, Y.; Long, G.; Tang, Z.; Zhou, X.; Zeng, X.; Li, J. Mesoscale investigation on concrete creep behaviors based on discrete element method. Constr. Build. Mater. 2022, 342, 127957. [Google Scholar] [CrossRef]
- Yu, Y.; Zheng, Y.; Zhao, X.Y. Mesoscale modeling of recycled aggregate concrete under uniaxial compression and tension using discrete element method. Constr. Build. Mater. 2021, 268, 121116. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, J.; Zhang, Z.; Song, X. Mesoscale damage modelling of concrete by using image-based scaled boundary finite element method. Int. J. Damage Mech. 2021, 30, 1281–1311. [Google Scholar] [CrossRef]
- Yu, J.C.; Wang, J.T.; Pan, J.W.; Guo, N.; Zhang, C.H. A dynamic FEM-DEM multiscale modeling approach for concrete structures. Eng. Fract. Mech. 2023, 278, 109031. [Google Scholar] [CrossRef]
- Sherzer, G.L.; Alghalandis, Y.F.; Peterson, K.; Shah, S. Comparative study of scale effect in concrete fracturing via Lattice Discrete Particle and Finite Discrete Element Models. Eng. Fail. Anal. 2022, 135, 106062. [Google Scholar] [CrossRef]
- Caballero, A.; López, C.; Carol, I. 3D meso-structural analysis of concrete specimens under uniaxial tension. Comput. Methods Appl. Mech. Eng. 2006, 195, 7182–7195. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Haefner, S.; Eckardt, S.; Koenke, C. A geometrical inclusion-matrix model for the finite element analysis of concrete at multiple scales. In Proceedings of the 16th IKM 2003, Weimar, Germany, 10–12 June 2003. [Google Scholar]
- Barenblatt, G.I. The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-symmetric cracks. J. Appl. Math. Mech. 1959, 23, 622–636. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, M.; Jivkov, A.P. Computational technology for analysis of 3D meso-structure effects on damage and failure of concrete. Int. J. Solids Struct. 2016, 80, 310–333. [Google Scholar] [CrossRef]
- Rezaei, S.; Mianroodi, J.R.; Khaledi, K.; Reese, S. A nonlocal method for modeling interfaces: Numerical simulation of decohesion and sliding at grain boundaries. Comput. Methods Appl. Mech. Eng. 2020, 362, 112836. [Google Scholar] [CrossRef]
- Ying, J.; Guo, J. Fracture Behaviour of Real Coarse Aggregate Distributed Concrete under Uniaxial Compressive Load Based on Cohesive Zone Model. Materials 2021, 14, 4314. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Ouyang, X.; Sun, X. Numerical Investigation of Asphalt Concrete Fracture Based on Heterogeneous Structure and Cohesive Zone Model. Appl. Sci. 2022, 12, 11150. [Google Scholar] [CrossRef]
- Zhang, B.; Nadimi, S.; Eissa, A.; Rouainia, M. Modelling fracturing process using cohesive interface elements: Theoretical verification and experimental validation. Constr. Build. Mater. 2023, 365, 130132. [Google Scholar] [CrossRef]
- Luo, Q.; Wang, W.; Sun, Z.; Wang, B.; Xu, S. Statistical analysis of mesoscopic concrete with random elastic modulus. J. Build. Eng. 2021, 33, 101850. [Google Scholar] [CrossRef]
- Naderi, S.; Zhang, M. Meso-scale modelling of static and dynamic tensile fracture of concrete accounting for real-shape aggregates. Cem. Concr. Compos. 2021, 116, 103889. [Google Scholar] [CrossRef]
- Naderi, S.; Zhang, M. 3D meso-scale modelling of tensile and compressive fracture behaviour of steel fibre reinforced concrete. Compos. Struct. 2022, 291, 115690. [Google Scholar] [CrossRef]
- Guinea, G.; El-Sayed, K.; Rocco, C.; Elices, M.; Planas, J. The effect of the bond between the matrix and the aggregates on the cracking mechanism and fracture parameters of concrete. Cem. Concr. Res. 2002, 32, 1961–1970. [Google Scholar] [CrossRef]
- Wittmann, F.; Roelfstra, P.; Sadouki, H. Simulation and analysis of composite structures. Mater. Sci. Eng. 1985, 68, 239–248. [Google Scholar] [CrossRef]
- Roelfstra, P. A Numerical Approach to Investigate the Properties of Numerical Concrete. Ph.D. Thesis, EPFL-Lausanne, Lausanne, Switzerland, 1989. [Google Scholar]
- Zohdi, T. Computational optimization of the vortex manufacturing of advanced materials. Comput. Methods Appl. Mech. Eng. 2001, 190, 6231–6256. [Google Scholar] [CrossRef]
- Zhou, R.; Song, Z.; Lu, Y. 3D mesoscale finite element modelling of concrete. Comput. Struct. 2017, 192, 96–113. [Google Scholar] [CrossRef]
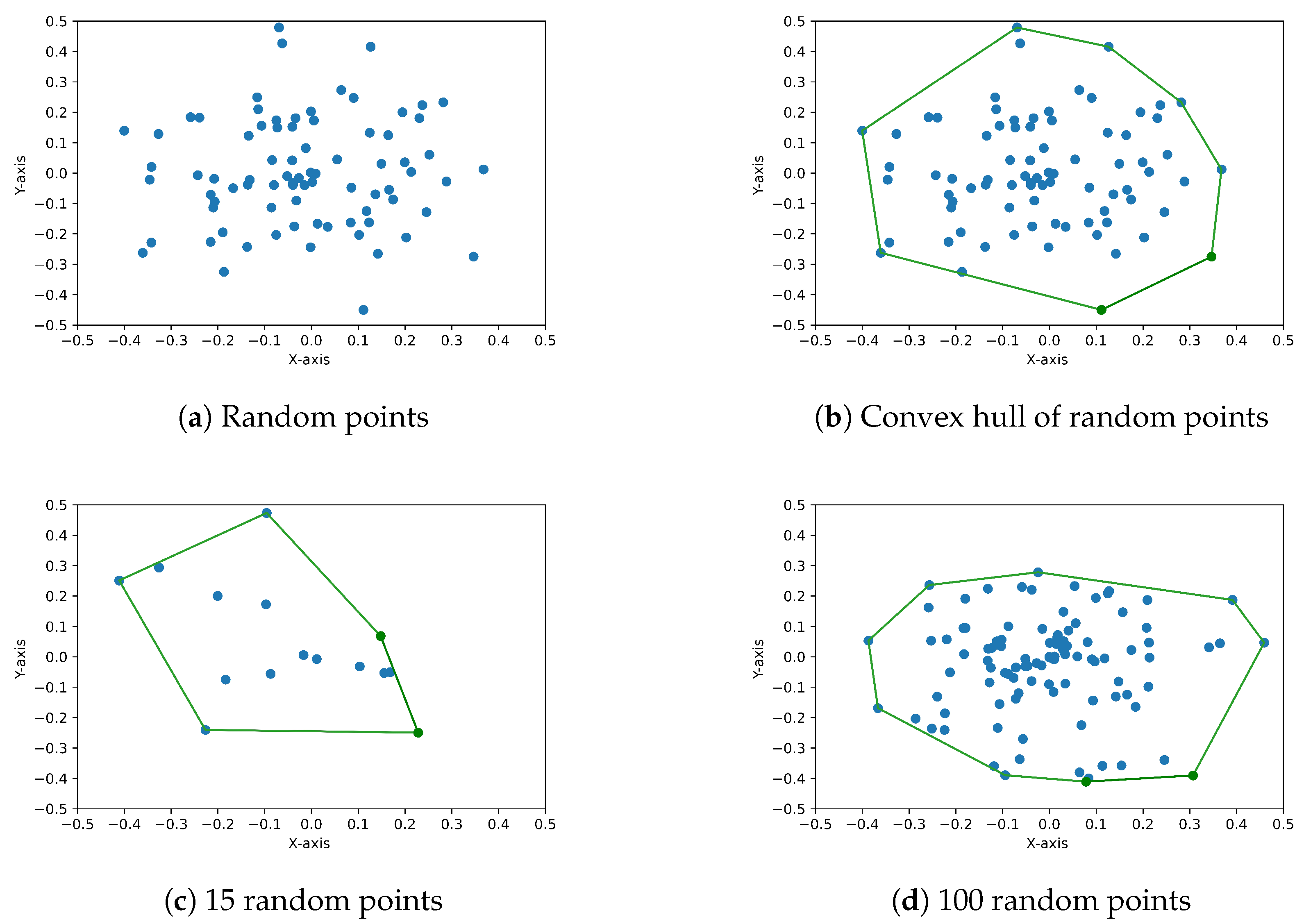
- Jarvis, R.A. On the identification of the convex hull of a finite set of points in the plane. Inf. Process. Lett. 1973, 2, 18–21. [Google Scholar] [CrossRef]
- Xiong, X.; Xiao, Q. Meso-scale simulation of concrete based on fracture and interaction behavior. Appl. Sci. 2019, 9, 2986. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Xi, X.; Yang, S.; Li, C.Q.; Cai, M.; Hu, X.; Shipton, Z.K. Meso-scale mixed-mode fracture modelling of reinforced concrete structures subjected to non-uniform corrosion. Eng. Fract. Mech. 2018, 199, 114–130. [Google Scholar] [CrossRef]
- Schwalbe, K.; Scheider, I.; Cornec, A. Guidelines for Applying Cohesive Models to the Damage Behaviour of Engineering Materials and Structures; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Camanho, P.P.; Dávila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials; No. NAS 1.15: 211737; Technical Report; NASA: Washington, DC, USA, 2002. [Google Scholar]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Ren, X.; Yang, W.; Zhou, Y.; Li, J. Behavior of high-performance concrete under uniaxial and biaxial loading. ACI Mater. J. 2008, 105, 548. [Google Scholar]
- Kim, S.M.; Al-Rub, R.K.A. Meso-scale computational modeling of the plastic-damage response of cementitious composites. Cem. Concr. Res. 2011, 41, 339–358. [Google Scholar] [CrossRef]
- Hordijk, D.A. Tensile and tensile fatigue behaviour of concrete; experiments, modelling and analyses. Heron 1992, 37, 79. [Google Scholar]
- Rodrigues, E.A.; Manzoli, O.L.; Bitencourt, L.A., Jr.; Bittencourt, T.N. 2D mesoscale model for concrete based on the use of interface element with a high aspect ratio. Int. J. Solids Struct. 2016, 94, 112–124. [Google Scholar] [CrossRef]
- Du, X.; Jin, L.; Ma, G. Numerical modeling tensile failure behavior of concrete at mesoscale using extended finite element method. Int. J. Damage Mech. 2014, 23, 872–898. [Google Scholar] [CrossRef]
- Guo, H.; Ooi, E.; Saputra, A.; Yang, Z.; Natarajan, S.; Ooi, E.; Song, C. A quadtree-polygon-based scaled boundary finite element method for image-based mesoscale fracture modelling in concrete. Eng. Fract. Mech. 2019, 211, 420–441. [Google Scholar] [CrossRef]
- Yu, J.; Li, G.; Ren, Z.; Wei, Z.; Tang, J.; Li, Z.; Si, X.; Zhao, Z. Mixed-mode I-II mesoscale fracture behavior of concrete determined by the realistic aggregate numerical model. Constr. Build. Mater. 2019, 226, 802–817. [Google Scholar] [CrossRef]






| (mm) | (mm) | ||
|---|---|---|---|
| 15 | 100 | 6.7 | |
| 13 | 93.09 | 7.2 | |
| 11 | 85.63 | 8 | |
| 9 | 77.45 | 13.7 | |
| 6 | 63.24 | 14.45 | |
| 3.5 | 48.30 |
| Parameter | Aggregate | Mortar | TSL-ITZ | TSL-Mortar | TSL-Aggregate |
|---|---|---|---|---|---|
| Elastic modulus, E (GPa) | 72 | 28 | - | - | - |
| Poission’s ratio, | 0.16 | 0.2 | - | - | - |
| Elastic stiffness, (MPa/mm) | - | - | |||
| Maximum normal stress, (MPa) | - | - | 2.4 | 4 | - |
| Maximum shear stress, (MPa) | - | - | 10 | 30 | - |
| Normal mode fracture energy, (N/mm) | - | - | 0.02 | 0.06 | - |
| Shear mode fracture energy, (N/mm) | - | - | 0.4 | 1.2 | - |
| B-K criterion material parameter, | - | - | 1.2 | 1.2 | - |
| Aggregate Diameter (mm) | Volume Fraction 50% | Volume Fraction 35% | Volume Fraction 20% |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najafi Koopas, R.; Rauter, N.; Lammering, R. Two-Dimensional Mesoscale Finite Element Modeling of Concrete Damage and Failure. Appl. Sci. 2023, 13, 8971. https://doi.org/10.3390/app13158971
Najafi Koopas R, Rauter N, Lammering R. Two-Dimensional Mesoscale Finite Element Modeling of Concrete Damage and Failure. Applied Sciences. 2023; 13(15):8971. https://doi.org/10.3390/app13158971
Chicago/Turabian StyleNajafi Koopas, Rasoul, Natalie Rauter, and Rolf Lammering. 2023. "Two-Dimensional Mesoscale Finite Element Modeling of Concrete Damage and Failure" Applied Sciences 13, no. 15: 8971. https://doi.org/10.3390/app13158971
APA StyleNajafi Koopas, R., Rauter, N., & Lammering, R. (2023). Two-Dimensional Mesoscale Finite Element Modeling of Concrete Damage and Failure. Applied Sciences, 13(15), 8971. https://doi.org/10.3390/app13158971






