Abstract
The performance optimization and reliability of electromagnetic orbital launchers need to take into account the uncertainties that exist in the manufacturing and service processes. Considering that it is difficult to identify the problem of the parameter probability distribution in advance for electromagnetic orbital launchers, this paper uses the interval number to describe the uncertain variables and realizes the conversion of uncertainty optimization into deterministic optimization problems based on interval sequential relations; moreover, it establishes interval uncertainty optimization methods. The converted deterministic optimization problem is solved by combining a high-precision proxy model with an optimization algorithm to search for the optimal solution set. Finally, reliability estimation is achieved by taking the armature of the electromagnetic orbital launcher as the optimization object. The computational example proves that the method is able to deal with the optimization problem of the parameter interval of an electromagnetic orbital launcher containing uncertain parameters and has good engineering applicability.
1. Introduction
The armature plays a crucial role as one of the key components in the electromagnetic orbital launcher, and the design parameters of the armature directly affect the launcher’s performance [1,2]. However, in the armature design process, challenges arise in acquiring the design parameters, modeling the armature appropriately, and dealing with uncertainties associated with these design parameters. As a result, there has been limited research investigating the impact of the design parameters on the armature’s performance and developing optimization methods for armature design.
Nowadays, the most commonly used electrical equipment performance optimization scheme is a combination of a proxy model and algorithm to find the best solution, first based on existing data to establish a proxy model between the design parameters and performance data, and then using genetic algorithm [3], particle swarm optimization (PSO) [4], and the differential evolution algorithm [5] based on the proxy model.
In the field of the deterministic optimization of electrical equipment, Yun Wen et al. [6] selected the efficiency and power density of an axial motor as the optimization objective and obtained the optimal Pareto solution set for the motor optimization variables by multi-objective genetic algorithm search, which improved the motor power density by 20.82%. Xu et al. [7] used the response surface methodology combined with genetic algorithm to optimize the cogging torque of an axial flux permanent magnet motor. The results showed that the cogging torque could be reduced from 2.14 to 0.18 N·m, and the peak-to-peak value of the torque ripple was only 3.5% of the rated output torque. Moreover, the values of the no-load back EMF and the rated output torque were almost invariable before and after optimization. Byungkwan et al. [8] proposed an adaptive particle swarm optimization algorithm for reluctance motor optimization, which converged faster than the standard particle swarm optimization algorithm and had an improved ability to search for a better solution set. Li et al. [9] used a multiple swarm genetic algorithm with a strong search capability for the multi-objective optimization of the thrust density, thrust fluctuation, and loss using the dimensions of the permanent magnets and toroidal windings of a coreless permanent magnet linear synchronous motor as variables. It was verified that the optimal design results obtained by MPGA were in good agreement with the design objectives under different weight coefficients. Tamas et al. [10] optimized transformer winding shapes based on a fast non-dominated ranking genetic algorithm NSGA-II with an elite strategy, and the example validation results showed a 10% improvement in efficiency. Daneshmand et al. [11] used the simulated annealing algorithm as well as genetic algorithm to achieve the multi-objective optimal design of a high-temperature superconducting transformer’s volume and loss. Here, three simple scenarios were considered for optimization: Scenario 1: one-variable and one-constraint two-objective functions; Scenario 2: two-variable and one-constraint three-objective functions; and Scenario 3: two-variable and one-constraint four-objective functions. Li et al. [12] analyzed the track geometry size characteristics based on a simulation model of an electromagnetic rail gun system and optimized the design of the track size using genetic algorithm, with the optimization objective of increasing the kinetic energy of the armature exit.
The optimization of the design parameters of the electromagnetic orbital launcher can be achieved to a certain extent using these deterministic optimization methods, but the extensive uncertainties that exist in its design and service process are not considered, making it difficult to achieve a reliable design.
In the optimization processes of electrical equipment, there are always uncertainties, such as loads, material properties, geometric characteristics, and boundary conditions [13,14]. The uncertainties can be classified as random, fuzzy, and unsure. According to the mechanism and physical meaning of the uncertainty factors, there are three uncertainty optimization theories, namely stochastic planning, fuzzy planning, and non-probabilistic, corresponding to three uncertainty models, namely the probabilistic model, fuzzy model, and convex model [15,16].
In the field of the uncertainty optimization of electrical equipment, Li et al. [17] established an uncertainty optimization model using the interval order and interval probability density method for the processing of composite materials under strong impact loads with high difficulty and error, and they solved the model via the interval nested optimization method based on a radial basis function neural network. Ramin et al. [18] proposed a structural damage identification algorithm under an interval number optimization algorithm for the uncertainty damage identification problem, which considered the uncertainty in variables and provided support for structural health diagnosis under uncertainty. Cai et al. [19] proposed an effective interval uncertainty powertrain suspension system analysis and design optimization method. The method takes the uncertainty parameters of the powertrain suspension system as interval variables and proposes an effective method to quickly calculate the inherent frequency of the system and decouple the lower and upper bounds, which improves the computational efficiency. Tang et al. [20] proposed a method to solve nonlinear problems using an interval linear programming approach, which is based on the idea of transforming an uncertainty optimization problem into several sensitivity analysis and deterministic linear optimization problems to be solved sequentially. Wang et al. [21] proposed an interval uncertainty optimization method for the dynamic responses of artillery structures considering robustness and economy, based on nonlinear interval programming and nested optimization solution strategies. Yang Fan et al. [22] established a wind-storage-vehicle capacity stochastic planning method for wind power output uncertainty with multi-scenario operation simulation, which can efficiently participate in source–load interactions and obtain a capacity configuration with better robustness. Sanad et al. [23] proposed a reliability design optimization method for wind turbine towers that can accurately take into account the uncertainty of wind loads and material properties, and the results showed that the optimal design of the tower can be accurately achieved to meet the target reliability. Zhang Yongbin et al. [24] considered the uncertainty of the output power of distributed power sources, established a distribution network grid planning model based on fuzzy theory, and solved the model by combining it with genetic algorithm.
Probabilistic and fuzzy models require sufficient uncertainty information to establish probability distribution functions and fuzzy affiliation functions, which is often difficult for practical engineering problems and the applications are more limited. From the perspective of uncertainty modeling, interval number optimization is a special case of convex model optimization. It uses the upper and lower bounds of uncertainty parameters, i.e., intervals, to describe the volatility of the values. Interval design optimization does not need to calculate the probability distribution functions of uncertain design variables, and it characterizes the uncertainty ranges of variables by interval ranges, which requires relatively low quantities and accuracy in data and is relatively easy to calculate. Thus, it has obvious advantages in practical engineering applications [25,26]. Currently, the interval uncertainty optimization method has achieved more and better results in problems where explicit expressions can be established. However, the mapping relationship between the design parameters and performance data of electromagnetic orbital launchers is complex, and it is not possible to establish accurate computational equations, so a proxy model based on machine learning is needed. Therefore, this paper carries out the interval uncertainty optimization method based on a proxy model to realize the reliability design of an electromagnetic orbital launcher considering uncertainty factors.
In Section 2 of this thesis, the information of the electromagnetic track emitter is provided. Section 3 introduces the theory of uncertainty optimization based on intervals, which transforms the existing uncertainty problem into a deterministic problem. In Section 4, the process of optimization based on interval uncertainty is presented. Section 5 uses the optimization method to optimize the design parameters of an electromagnetic orbit emitter and analyzes the optimization results.
2. Description of the Optimization Object
An electromagnetic orbital launcher is a new type of kinetic energy weapon produced based on electromagnetic launch technology. It has the advantages of high firing efficiency, a fast response, and good controllability, which have resulted in its large application prospects in military and civilian fields. The setting of the model size, parameters, and structures is a key step in the study of electromagnetic orbital launchers. Different shapes of the armature structures have different pivot rail contact states, firing efficiency, and performance, but the objective laws of their responses are consistent. In this paper, a U-shaped electromagnetic orbital launcher is used as the research object, and the established electromagnetic orbital launcher model is shown in Figure 1.
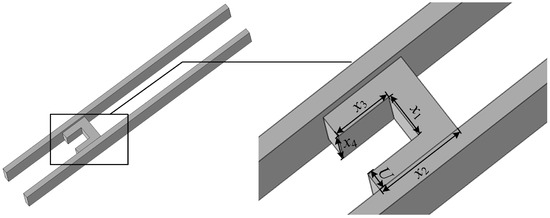
Figure 1.
Finite element model of electromagnetic orbital launcher.
The trapezoidal excitation current is a widely used model loading technique in engineering practice. Figure 2 illustrates the parameters of the excitation current. The excitation process can be divided into three phases [27]:
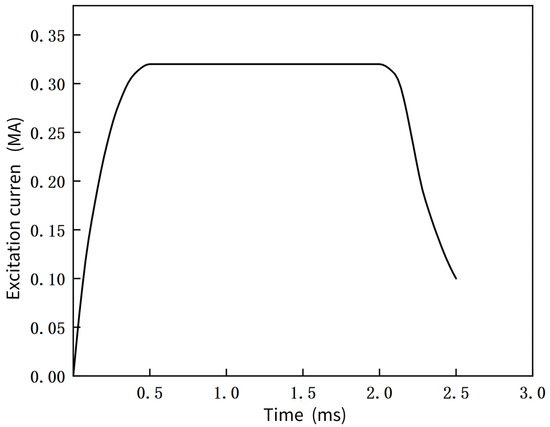
Figure 2.
Schematic diagram of excitation current.
- The increasing phase lasts from 0 to 0.5 ms, during which the current rises from 0 to 0.32 MA;
- The constant phase extends from 0.5 ms to 2.0 ms, with the current maintaining a steady value of 0.32 MA;
- The decreasing phase occurs from 2.0 ms to 2.5 ms, where the current gradually decays from 0.32 MA to 0.1 MA.
In the finite element model, the excitation current enters through the lower face of the upper track, passes through the armature, and then exits from the lower face of the lower track.
Based on the finite element simulation results of the armature electromagnetic thrust and the maximum current density at the contact surface of the armature rail at the moment of 1.0 ms during the current constant phase, an interval multi-objective optimal design of the armature with uncertain parameter variables is obtained for the electromagnetic orbital launcher. The armature tail width , armature length , armature tail length , and armature tail height are selected as design variables X, and the armature electromagnetic thrust and the maximum current density at the pivot rail contact surface are selected as optimization objectives. The data before the optimization of the electromagnetic orbital launcher are shown in Table 1, and the ranges of its design parameters are taken as shown in Table 2.

Table 1.
Data before optimization of electromagnetic orbital launcher.

Table 2.
Value ranges of design parameters.
3. Uncertainty Analysis Based on Interval Theory
3.1. Description of the Interval Optimization Model
According to interval mathematics, the interval number is defined as
where and denote the lower and upper bounds of the interval, respectively. can also be defined as
where and denote the midpoint and radius of the interval , respectively:
The geometric description of the interval is shown in Figure 3.
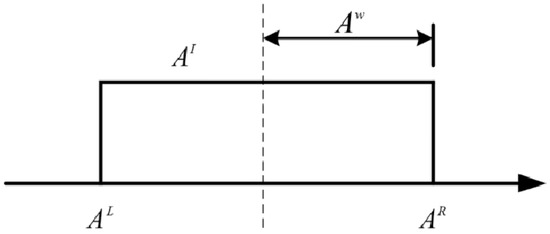
Figure 3.
Geometric description of interval.
Using the interval number to describe the uncertainty of the parameters, the nonlinear interval number optimization problem of the general form (formulated and transformed below using the single-objective problem as an example, and similarly for the multi-objective problem) can be formulated as
where X is the n-dimensional design vector with values ranging from . U is the q-dimensional interval uncertainty vector, whose values are in the range of . is the i-th uncertainty vector. f is the nonlinear objective function on X and U.
In the optimization process, due to the existence of U, the possible values of under any determined X will be an interval, so the traditional deterministic optimization methods cannot solve the problem directly. Therefore, it is necessary to transform the uncertainty optimization problem to solve the nonlinear interval number optimization problem.
3.2. Interval Order Relationship Conversion Model
The interval order relationship can be used to qualitatively determine the advantages and disadvantages of two intervals. By comparing the merits of different objective function intervals, the merits of the corresponding design vectors can be evaluated, and then the optimal design vector can be found. For optimization problems, the following are the five interval order relations that are commonly used.
- (1)
- Interval order relationship :expresses a preference for the upper and lower boundaries of the interval.
- (2)
- Interval order relationship :expresses a preference for the midpoint and radius of the interval.
- (3)
- Interval order relationship :expresses a preference for the lower bound and midpoint of the interval.
- (4)
- Interval order relationship :expresses a preference for the lower bound of the interval.
- (5)
- Interval order relationship :expresses a preference for the upper bound of the interval.
3.3. Transformation of Uncertainty Optimization Problems
The interval sequence relation has a more intuitive engineering meaning and good engineering practicality, so this paper chooses the interval sequence relation [28,29]. For any design vector X, the possible range of values of the objective function is
where
Based on the interval order relation , a judgment can be made: if the objective function has a midpoint and a radius , then the design vector is superior to . Then, the objective function in Equation (5) can be converted into
where, for any X, the midpoint and radius of the uncertain objective function can be calculated based on Equations (12) and (13). The objective function boundaries and can be obtained by
Optimizing is equivalent to improving the “average design performance” of the objective function under uncertainty, while optimizing is equivalent to reducing the “sensitivity” of the objective function under uncertainty, thus ensuring design reliability.
For subsequent optimization solutions, the linear weighting method is used to further transform
where is the multi-objective evaluation function, is the multi-objective weight factor, is the parameter that ensures that and are non-negative, and and are the regularization factors of the multi-objective function.
4. Process of Interval Uncertainty Optimization Method
4.1. Interval Uncertainty Optimization System
A two-layer optimization structure system is employed to address the transformed problem, with the outer layer focusing on the optimization of the design variables and the inner layer focusing on the optimization of the uncertainty variables. The flowchart of this two-layer optimization system is depicted in Figure 4. This paper specifically applies the two-layer optimization approach to the structural optimization of modern electrical equipment.
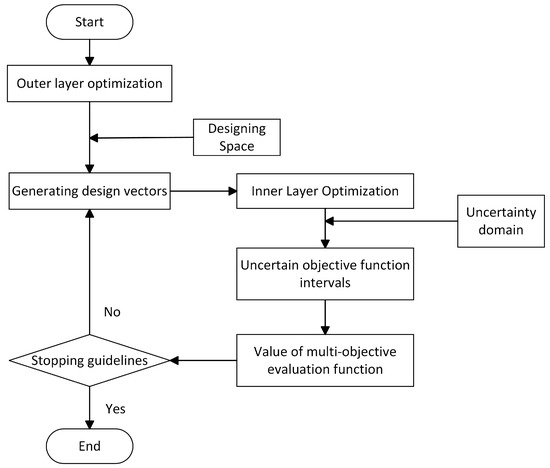
Figure 4.
Flowchart of two-layer optimization system.
In the outer layer optimization, multiple design vector individuals are generated using an optimization algorithm. Each individual then undergoes the inner layer optimization process. The inner layer utilizes an optimization algorithm and a high-precision proxy model to maximize and minimize the responses within the uncertainty domain. This process determines the midpoint and radius values of the objective function and subsequently calculates the evaluation function value for the objective.
Finally, the algorithm evaluates the stopping criterion. If the criterion is satisfied, the optimization process concludes, and the values of the design variables corresponding to this point represent the optimized results. If the criterion is not satisfied, the optimization search continues.
4.2. Algorithm Implementation Process
When using the interval-based uncertainty optimization method, the specific implementation process is as follows.
- (1)
- Sampling in the mixed space (design space and uncertainty domain) to obtain multiple sets of samples consisting of design variables X and uncertainty variables U.
- (2)
- For any sample , the uncertain objective function value is calculated by the finite element simulation model, which constitutes the sample set of the inner layer proxy model.
- (3)
- The design variables and uncertainty variables are used as inputs, and the uncertain objective function values are used as outputs to build an inner layer high-precision proxy model.
- (4)
- For each sample X, two inner-level optimizations of andare performed to find the lower bound and upper bound of the objective function, respectively. The optimization solution process is shown in Figure 5.
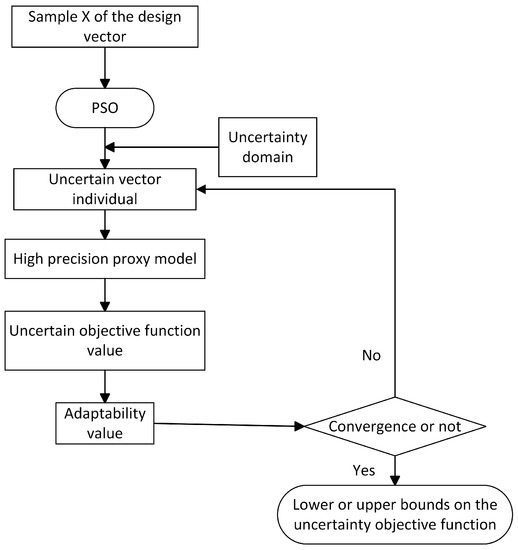 Figure 5. The boundary of the objective function.
Figure 5. The boundary of the objective function. - (5)
- An outer proxy model is established, with the design vector X as input and the lower bound and the upper bound of the uncertain objective function at X as output, to realize the nonlinear mapping between the input and output.
- (6)
- The trained outer proxy model is combined with the optimization algorithm to solve the transformed Equation (18) problem, as shown in Figure 6. For the design vector individuals generated by the PSO optimization algorithm, the interval of the objective function is obtained directly by the outer proxy model, and then the optimal solution or optimal solution set is selected by calculating the fitness value based on the multi-objective evaluation function.
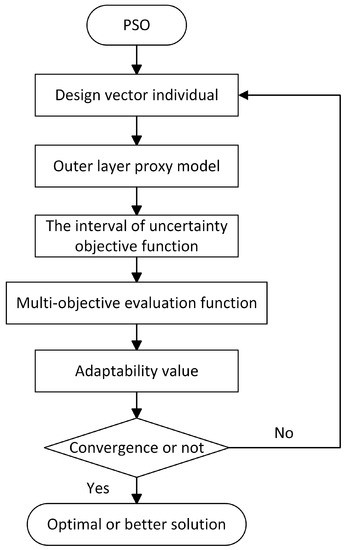 Figure 6. Flowchart of optimization solution process.
Figure 6. Flowchart of optimization solution process.
5. Multi-Objective Optimization Algorithm Example
The armature electromagnetic thrust of the electromagnetic orbital launcher is directly related to the exit velocity of the projectile; the higher the , the higher the exit velocity. The maximum current density at the contact surface of the armature track reflects the armature ablation; the smaller the , the less likely it is that the armature will ablate [30]. Therefore, and are used as the optimization objective functions. One of the main problems encountered in the design of electromagnetic railguns is transition, which refers to the transition from solid–solid contact to solid–arc solid contact on the contact surface of the pivot rail. When transition occurs, there must be an intermediate gap filled by plasma at the contact surface of the pivot rail, and this intermediate gap is caused by friction and wear, resulting in material loss on the contact surface of the pivot rail, and thus in transition. The armature has to bear not only high stress but also high temperatures caused by Joule heat and friction heat in the process of dynamic emission with a large current load and ultra-high speed. The contact surface of the armature rail will wear and corrode, and then the thickness of the armature tail will change [31]. Therefore, the armature tail thickness is treated as an uncertainty variable at U to better match the actual operating conditions of the electromagnetic orbital launcher. Thus, the uncertainty optimization problem can be established as follows:
To facilitate the creation of multi-objective optimization problems, this paper optimizes the opposite of , i.e., finds the minimum value of . The optimization problem can be converted as follows:
This paper seeks to find reasonable design parameter variables that make the electromagnetic thrust value as large as possible and the maximum current density at the contact surface as small as possible (considering the average design performance, i.e., the midpoint value of the objective function) and cause the electromagnetic thrust and the maximum current density at the contact surface to have the smallest radius values (i.e., with the smallest performance fluctuation interval). Thus, the optimization model can be described as follows:
A multi-objective evaluation function is applied to the above equation with the following parameters: is 0.5, is 0, and and are 1.0. Then, this optimization problem can be transformed into
In this complex multi-objective optimization scenario, a dual-layer model, featuring a deep belief networks (DBN) and deep neural network (DNN), known as DBN-DNN, is deployed. The architecture comprises an inner layer and an outer layer, both utilizing the DBN-DNN model, with the strategic selection of three hidden layers. Each layer is equipped with a distinct number of neurons: 30, 24, and 18, respectively.
We use PyTorch, a Python-based machine learning library, to build the DBN-DNN model, and we verify the reliability of the model with the PyCharm software. Firstly, the greedy unsupervised learning algorithm is used to initialize the DBN. The input vector, as the input of the first restricted Boltzmann machine (RBM) visual layer in the DBN network, is trained by the contrastive divergence (CD) algorithm to obtain the connection weight and node bias vector of RBM1. After the training of RBM1, the output of its hidden layer is used as the input of the visible layer of RBM2 for training. It is carried out in sequence, i.e., starting from the input layer, each two layers is trained as an RBM, layer by layer. After all RBM training is complete, the entire DBN initialization is complete. Compared with the traditional method of the random initialization of artificial neural network weight parameters, this training method can effectively solve the problems of low training efficiency and falling into local optimal. After layer by layer training, the DBN output feature vector is used as the input of the deep neural network, so that the deep neural network can be trained quickly, effectively, stably, and reliably. Finally, the BP algorithm is used to train the DNN supervised to fit labeled data, and a DBN-DNN model is obtained.
The Adam optimizer combines the advantages of Adagrad in dealing with sparse gradients and RMSprop in dealing with non-stationary targets, and it can calculate different adaptive learning rates for different parameters. In this article, the Adam optimizer is selected in the PyTorch library and the learning rate is set to 0.0001. The activation function employed here is the Rectified Linear Unit (ReLU). The prediction error for the outer layer proxy model can be found in Table 3.

Table 3.
Outer proxy model prediction error.
Upon testing, 100 data groups are randomly selected for a comparative analysis. The predicted outcomes of the outer proxy model are juxtaposed with the results derived from the optimization method. The comparison reveals a high degree of consistency between the predicted and actual values, with negligible instances of marked deviation. This robust correlation indicates the efficacy and predictive accuracy of the established outer proxy model. The prediction effect of the outer proxy model is shown in Figure 7 and Figure 8.
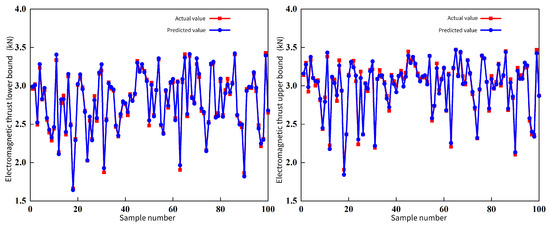
Figure 7.
lower bound and upper bound.
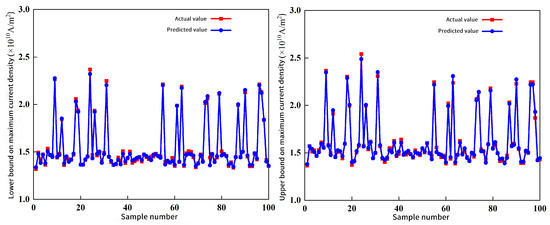
Figure 8.
lower bound and upper bound.
The single-objective PSO algorithm is deployed for internal optimization, while the multi-objective particle swarm optimization (MOPSO) algorithm is employed for external optimization. Here, the number of iterations is fixed at 200.
Due to the nature of multi-objective optimization, it is difficult to find a single global optimal solution. More commonly, the process culminates in the acquisition of a series of Pareto optimal solution sets. The computational results corresponding to 50, 100, 150, and 200 iterations are visually represented in Figure 9. Notably, the disparity between the optimization values at 150 and 200 iterations and those at 100 iterations is minuscule. Additionally, the optimization values at 150 and 200 iterations are practically identical. This consistency suggests that the optimization results reach a state of convergence, indicative of the algorithm’s effective convergence performance.
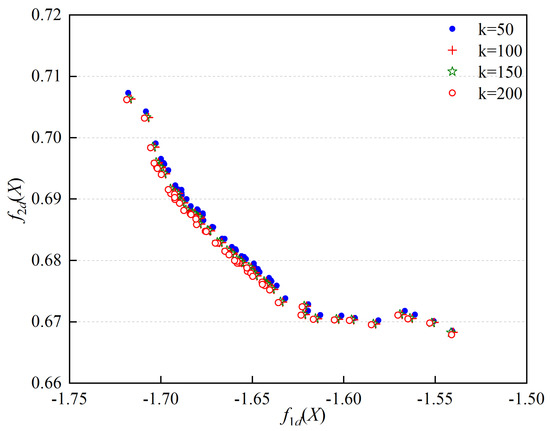
Figure 9.
Pareto solution sets with different iterations.
Upon inspecting the distribution of points within the solution set, it appears to be quite uniform. The multi-objective evaluation function reaches a minimum value of −1.71869, concurrently with the multi-objective evaluation function achieving a maximum value of 0.70619. At the same time, hits a maximum value of −1.54101, which corresponds with the reaching its minimum value of 0.66790. These observations offer important insights into the dynamics and efficiency of the optimization process.
For the analysis of the problem as stated in Equation (20), the set of interval Pareto optimal solutions obtained post-transformation is represented in Figure 10. Moreover, the analysis of the original problem, i.e., Equation (19), reveals that the maximum value of the midpoint of electromagnetic thrust is 3.46843 kN, and, concurrently, the midpoint of the maximum current density at the contact surface peaks at 1.40412 × A/m.
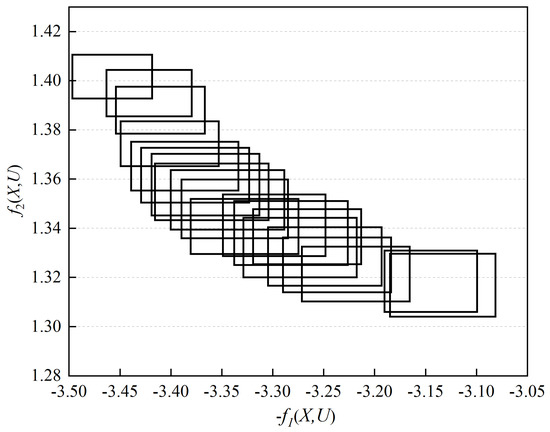
Figure 10.
Interval non-inferior solution set distribution.
Under the influence of uncertain parameters, the fluctuation range of electromagnetic thrust is [3.43738, 3.49947] kN, and for the maximum current density at the contact surface, it is [1.39587, 1.41237] × A/m. The minimum value of the electromagnetic thrust midpoint is 3.13619 kN, during which the contact surface maximum current density midpoint is at its lowest, 1.31852 × A/m. The fluctuation range of the electromagnetic thrust, influenced by uncertain parameters, is [3.08201, 3.19037] kN, and for the maximum current density at the contact surface, it is [1.30423, 1.33281] × A/m.
Five solutions are uniformly chosen from the Pareto solution set, as outlined in Table 4. By comparing the data in Table 1 and Table 4, it is apparent that the optimized values in the interval range of the armature electromagnetic thrust, after considering interval uncertainty, see an improvement of approximately 7.5∼17.4%. Simultaneously, the values in the interval range of the pivot rail contact surface current density decrease by approximately 9.5∼4.1% compared to the initial values, without significant alteration of the transmitter design parameters.

Table 4.
Data before optimization of electromagnetic orbital launcher.
Interval multi-objective optimization proves effective in enhancing both the electromagnetic thrust and the maximum current density of the contact surface of the electromagnetic orbital launcher. Moreover, it enables the efficient selection of the armature structure size to meet varying performance control requirements. For instance, if a designer prioritizes electromagnetic thrust, they can opt for the data set of group 5; if the maximum current density value of the contact surface is of more concern, they should choose the data from group 1; if the designer wishes to consider both the electromagnetic thrust and the maximum current density of the contact surface, the data sets from groups 2, 3, and 4 would be most suitable.
Table 5 presents the comparative results regarding the objective evaluation function values derived from the optimization of the fifth Pareto solution and the actual evaluation function values computed using the finite element method. According to the data in the table, the discrepancies between the objective evaluation function values calculated by the surrogate model and the actual objective evaluation function values are 1.44% and 1.57%, respectively. This outcome serves to further confirm the practicality and validity of the surrogate model.

Table 5.
Armature optimization results of electromagnetic orbital launcher.
For this optimization problem, the traditional optimization method is used to optimize it deterministically, without considering the influence of uncertain parameters, and then the method established in this paper is used to optimize its design by considering the uncertainty of the parameters; the non-inferiority solution sets obtained by the two methods are shown in Figure 11.
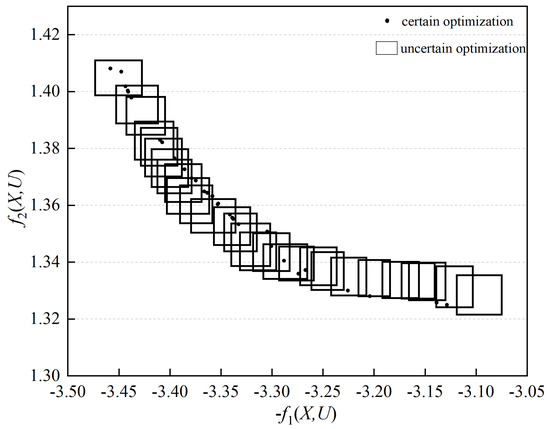
Figure 11.
Interval non-inferior solution set distribution.
As is visible from the figure, the deterministic optimization method, due to its disregard for the uncertainty factors of the electromagnetic orbital launcher in real-world conditions, bases its decision making on specific values of the objective function at each design vector. Consequently, the Pareto optimal solution set achieved is a series of Pareto points.
Conversely, the methodology proposed in this paper acknowledges that the armature tail thickness is not constant owing to frictional wear. It employs interval numbers to denote the uncertainty of the armature tail thickness and integrates this into the optimization design process. As a result, the value of the objective function is also an interval. The upper and lower limits of this interval are the critical values ascertained when taking into account parameter uncertainty. The Pareto optimal solution set, in this case, is a series of interval solutions.
Considering that the current paper addresses a minimization problem and that the Pareto front is concave, the optimization result is satisfactory. Our method offers a more fitting depiction of the performance variations of the electromagnetic orbital launcher due to uncertainty. Furthermore, it ensures the reliability of the optimization results, an attribute of paramount importance for the reliability estimation of the electromagnetic orbital launcher. The approach also provides a valuable reference point for designers when addressing real-world engineering problems.
6. Conclusions
In this paper, an interval-based uncertainty optimization method for electromagnetic orbital launchers is established to realize the reliability estimation of electromagnetic orbital launcher armatures.
- 1.
- The uncertainty of variables is described using interval numbers, and the conversion of uncertainty optimization problems into deterministic optimization problems is achieved based on interval order relations.
- 2.
- The DBN-DNN algorithm is used to build a high-precision proxy model to predict the performance of electromagnetic orbital launchers. It is also combined with the particle swarm optimization algorithm to solve the transformed deterministic optimization problem.
- 3.
- The results of the multi-objective optimization algorithm for the electromagnetic orbital launcher show that the optimized solution set obtained by the method contains interval rather than deterministic values, it is able to handle interval optimization problems with uncertain parameters, and the performance is improved compared with that before optimization.
The series of interval non-inferiority solution sets obtained in the optimization examples can appropriately describe the performance fluctuations caused by uncertainty in the electromagnetic orbital launcher and can consider the uncertainty in the manufacturing and service processes to improve the performance stability of the product in operation.
Author Contributions
Conceptualization, L.J.; methodology, L.L. and J.S.; software, J.S.; validation, L.L. and Y.Y.; formal analysis, L.L. and J.S.; investigation, Y.Y.; resources, L.L.; data curation, L.L., Y.Y. and X.Z.; writing—original draft preparation, Y.Y.; writing—review and editing, Y.Y. and X.Z.; visualization, J.S. and X.Z.; supervision, L.J.; project administration, L.J.; funding acquisition, L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Major Research Program of the National Natural Science Foundation of China, grant number 92066206; the Project of the National Natural Science Foundation of China, grant number 51977148; and the Local Science and Technology Development Projects Guided by the Central Government, grant number 226Z4503G.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data, models generated or used during the study appearance in the submitted article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dang, S.G. Research on Shape Design and Contact Characteristics of Several Typical Solid Armatures. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2016. [Google Scholar]
- Gao, B.; Qiu, Q.X.; Xi, W.J.; Ma, X.K. Analysis and Experimental Research on Multi field Coupling of Electromagnetic Railgun Armature. J. Electr. Eng. 2020, 35, 341–345. [Google Scholar]
- Xu, B.; Yao, Y.Y. Adaptive Dual Population Genetic Algorithm and Its Application in Electromagnetic Field Optimization Design. J. Electr. Eng. 2013, 28, 183–187. [Google Scholar]
- Cheng, Z.; Dong, M.N.; Yang, T.K.; Han, L.J. Parameter Identification of Photovoltaic Cell Model Based on Adaptive Chaos Particle Swarm Optimization Algorithm. J. Electr. Eng. 2014, 29, 245–252. [Google Scholar]
- Wu, G.F.; Cui, Y.; Liu, H.; Zhang, L. Decoupling calibration method for three-dimensional electric field sensors based on differential evolution algorithm. J. Electr. Eng. 2021, 36, 3993–4001. [Google Scholar]
- Wen, Y. Application of Multi-Objective Hybrid Genetic Algorithm in the Optimization Design of Permanent Magnet Motors. Master’s Thesis, North China Electric Power University, Beijing, China, 2017. [Google Scholar]
- Xu, L.J.; Xu, Y.L.; Gong, J.L. Analysis and Optimization of Cogging Torque in Yokeless and Segmented Armature Axial-Flux Permanent-Magnet Machine with Soft Magnetic Composite Core. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar]
- Son, B.; Kim, J.S.; Kim, J.W.; Kim, Y.J.; Jung, S.Y. Adaptive Particle Swarm Optimization Based on Kernel Support Vector Machine for Optimal Design of Synchronous Reluctance Motor. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Li, L.Y.; Tang, Y.B.; Liu, J.X.; Pan, D.H. Application of Multiple Population Genetic Algorithms in the Optimization Design of Coreless Permanent Magnet Linear Synchronous Motors. Proc. Chin. Soc. Electr. Eng. 2013, 33, 69–77+14. [Google Scholar]
- Tamás, O.; Pavel, K.; David, P.; Ivo, D. FEM-based transformer design optimization technique with evolutionary algorithms and geometric programming. Int. J. Appl. Electromagn. Mech. 2021, 64, S41–S49. [Google Scholar]
- Vahdati Daneshmand, S.; Heydari, H. A Diversified Multiobjective Simulated Annealing and Genetic Algorithm for Optimizing a Three-Phase HTS Transformer. IEEE Trans. Appl. Supercond. 2016, 26, 1–10. [Google Scholar] [CrossRef]
- Li, X.J.; Wang, Z.H.; Wu, H.R. Analysis and Optimization Design of Geometric Dimensional Characteristics of Electromagnetic Cannon Track. J. Ballist. 2015, 36, 54–58. [Google Scholar]
- Tao, Y.R. Multi Disciplinary Uncertainty Optimization Design Method Based on Convex Models. Ph.D. Thesis, Hunan University, Changsha, China, 2010. [Google Scholar]
- Wang, X.D. Research on Uncertainty Optimization Theory and Solution Methods Based on Interval Numbers. Master’s Thesis, Chang’an University, Xi’an, China, 2012. [Google Scholar]
- Meng, X.J. Research on Multidisciplinary Reliability Design Optimization Methods Considering Mixed Uncertainty. Ph.D. Thesis, Beijing University of Technology, Beijing, China, 2016. [Google Scholar]
- Hu, J.M. Research on a Robust Optimization Design Method for Random and Cognitive Uncertainty. Master’s Thesis, China Academy of Engineering Physics, Chengdu, China, 2012. [Google Scholar]
- Li, Z.X.; Yang, G.L.; Xu, F.J.; Wang, L.Q. Interval uncertain optimization for damping fluctuation of a segmented electromagnetic buffer under intensive impact load. Def. Technol. 2021, 17, 884–897. [Google Scholar] [CrossRef]
- Cai, B.H.; Shangguan, W.B.; Lü, H. An efficient analysis and optimization method for powertrain mounting systems involving interval uncertainty. Appl. Sci. 2022, 12, 1–21. [Google Scholar] [CrossRef]
- Ghiasi, R.; Noori, M.; Kuok, S.; Silik, A.; Wang, T.; Pozo, F.; Altabey, W. Structural Assessment under Uncertain Parameters via the Interval Optimization Method Using the Slime Mold Algorithm. Appl. Sci. 2022, 12, 1876. [Google Scholar] [CrossRef]
- Tang, J.C.; Fu, C.M.; Mi, C.J.; Liu, H.B. An interval sequential linear programming for nonlinear robust optimization problems. Appl. Math. Model 2022, 107, 256–274. [Google Scholar] [CrossRef]
- Wang, L.Q.; Yang, G.L.; Xiao, H.; Sun, Q.Q.; Ge, J.L. Interval optimization for structural dynamic responses of an artillery system under uncertainty. Eng. Optim. 2020, 52, 343–366. [Google Scholar] [CrossRef]
- Yang, F.; Wang, W.Q.; He, S.; Zhan, H.L.; Cheng, J. Stochastic planning of wind storage vehicle capacity based on multi scenario operation simulation. HV Tech. 2023, 49, 1161–1171. [Google Scholar]
- Al-Sanad, S.; Wang, L.; Parol, J.; Kolios, A. Reliability-based design optimisation framework for wind turbine towers. Renew. Energy 2021, 49, 942–953. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Nie, M.L.; Zhang, J.P.; Song, H.; Chi, M.W.; Yi, Q.Y. Fuzzy Programming of Distribution Network Framework Considering the Uncertainty of Distributed Power Sources. J. Electr. Eng. 2019, 34, 258–263. [Google Scholar]
- Li, D.; Zhang, S.J.; Xiao, Y.H. Interval Optimization-Based Optimal Design of Distributed Energy Resource Systems under Uncertainties. Energies 2020, 13, 3465. [Google Scholar] [CrossRef]
- Liu, Y.; Jeong, H.K.; Collette, M. Efficient optimization of reliability-constrained structural design problems including interval uncertainty. Comput. Struct. 2016, 177, 1–11. [Google Scholar] [CrossRef]
- Yang, K.S.; Kim, S.H.; Lee, B.; An, S.; Lee, Y.H.; Yoon, S.H.; Koo, I.S.; Jin, Y.S.; Kim, Y.B.; Kim, J.S. Electromagnetic Launch Experiments Using a 4.8-MJ Pulsed Power Supply. IEEE Trans. Plasma Sci. 2015, 43, 1358–1361. [Google Scholar] [CrossRef]
- Jin, X. Research on Interval Value Function Optimization Problems Based on Interval Number Order Relations. Master’s Thesis, Chongqing University of Posts and Telecommunications, Chongqing, China, 2022. [Google Scholar]
- Pang, X.Q. Research on the Ranking Relationship of Interval Numbers and Its Application in Multi Attribute Decision Making of Interval Fuzzy Preference Relationships. Master’s Thesis, Guangxi University, Nanning, China, 2022. [Google Scholar]
- Liu, Y.; Guo, W.; Zhang, T.; Fan, W. Double layer armature structure design and its electromagnetic force and current density distribution. J. Proj. Rocket. Missil. Guid. 2020, 40, 160–164. [Google Scholar]
- Gao, X. Ansys of the Wear Characteristics of the Rail-Armature of Electromagnetic Railgun. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).